Логические основы ЭВМ

 Логические основы ЭВМ

Данные в компьютере запоминаются в двоичной системе, и ре- зультаты проверки логических выражений тоже можно представлять в двоичной системе. Из этого следует, что одни и те же устройства компьютера могут применяться для обработки и хранения как число- вой информации, так и логических переменных. Элементарные схе- мы компьютера реализуют обработку сигнала по функциям И, ИЛИ, НЕ.

С помощью этого набора можно реализовать любую логиче- скую функцию, описывающую работу устройств компьютера. Рас- смотрим, к примеру, схему сложения одноразрядных двоичных чисел с учетом возможности переноса в старший разряд:

0 + 0 = 0; 0 + 1 = 1; 1 + 0 = 1; 1 + 1 = 10₂

Если оба слагаемых равны единице, то сумма становится дву- значной. В том разряде, в котором находились слагаемые, получается 0, а единица переходит в старший разряд. Введем обозначения: сла- гаемые – А и В, значение суммы в разряде слагаемых – S, перенос в старший разряд – Р, перенос из младшего разряда – Р₀,. Таблица ис- тинности для значения, этого примера выглядит так:

Из этой таблицы видно, что значение переноса можно полу- чить по операции конъюнкции: P = А B. Значение суммы в трех пер- вых строках получается по операции дизъюнкции, а последнее значе- ние – это инверсия Р, и всю таблицу можно описать функцией S = (A v B) (A B). Эта функция описывает работу одноразрядного полу- сумматора процессора.

В полном одноразрядном сумматоре учитывается третье сла- гаемое: величина, переносимая в этот разряд из младшего разряда. Обозначим ее Р₀. Таблица истинности с учетом этой величины вы- глядит следующим образом:

Из таблицы видно, что перенос в старший разряд надо делать тогда, когда значение 1 принимают хотя бы два слагаемых. Этому соответствует формула Р = (A B) v (B P₀) v (A P₀). Для значения суммы во всех строках, за исключением последней, подходит форму-

ла S₁ = (A v B v P₀)   P. Для последней строки годится выражение S₂

= (A   B   P₀). Окончательная формула, которая описывает результа- ты суммирования в одноразрядном сумматоре при всех возможных вариантах, выглядит так:

S = (A v B v P₀)    P v (A    B    P₀)

Так же как и в электрических схемах, для базовых типов логи- ческих преобразований установлены условные обозначения, которые облегчают понимание сложных логических схем. Они отражают тип преобразования информации, отвлекаясь от структуры электронной схемы, которая реализует это преобразование. На рис. 2.1 приведены условные обозначения этих преобразований.

Схема «И»

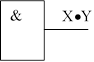X Y

Схема «ИЛИ»

X                          XvY

Y

Схема «И-НЕ»

Схема «ИЛИ-НЕ»

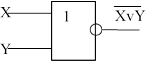
Схема «НЕ»

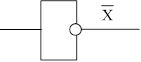Х

Рис. 2.1. Условные обозначения базовых логических элементов

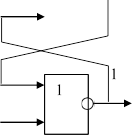
На рис. 2.2 Приведена логическая схема триггера. Это устрой- ство может хранить 1 бит информа-

ции. Триггеры используются как разряды оперативной памяти и памя- ти процессора. В обычном состоянии триггер хранит сигнал 0. Для записи 1 на вход S подается сигнал 1. Прой- дя по схеме он формирует на выходе Q сигнал 1 и устойчиво хранит его после того, как сигнал S исчезнет. Для того, чтобы сбросить этот сигнал

S(1)

1

0

Q

R

Рис. 2.2. Логическая схема триггера

и подготовиться к приему нового на вход R подается сигнал 1, кото- рый приводит триггер к «нулевому» состоянию.