Мастер-класс "Анализ математической информации через применение активных приёмов технологии критического мышления"

Тема семинара: Формирование учебных компетенций учащихся через инновационные подходы в организации работы с текстом.

Тема мастер-класса: Анализ математической информации через применение активных приёмов технологии критического мышления

Проблема осмысления математического текста прослеживается в следующих процессах: отделение математического содержания от нематематического;  определение отношений, логико-математических связей внутри текстового содержания; различение существенной информации и второстепенной, выделение лишней, недостаточной информации для решения поставленной учебной задачи.

К сожалению, эти проблемы приводят  к непониманию математики, как учебного предмета в целом.

Математическая информация, содержание которой в виду её универсальности, краткости, лаконичности, имеет свои трудности. Важно сформировать представление о математическом тексте, как о тексте.

Большую роль в этом направлении я отвожу активным приёмам технологии критического мышления.

Думать критически означает проявлять и использовать исследовательские методы, ставить перед собой вопросы и осуществлять планомерный поиск ответов через вдумчивую работу с информацией.

В основе технологии РКМЧП лежит базовая модель урока, состоящая из трех фаз: стадия вызова, стадия осмысления, рефлексия.

В идеале  желательно проводить урок полностью в данной технологии. У меня это получается редко, но я приспособилась вводить фрагментарно в структуру урока трёхфазность при работе с отдельными заданиями. А самое главное поняла, что в ТКМ работа с информацией имеет пятиступенчатую конструкцию.

.

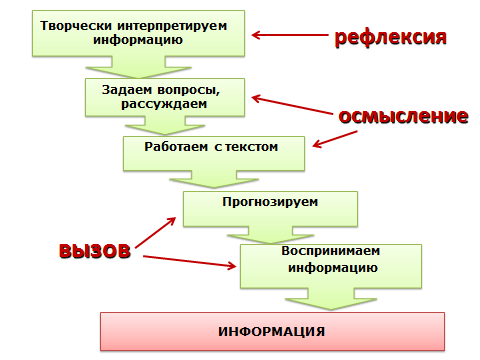
Далее  эти пять ступенек я провела через трёхфазность.

 В стадию вызова у меня вошли два этапа работы с информацией – принятие информации и прогноз. В стадию осмысления вошла конкретная работа по анализу текста. И в стадию рефлексии – обличение понятой информации в творческую форму.  

Целью стадии вызова является актуализация имеющихся у ученика знаний, вызов устойчивого интереса к изучаемой теме; мотивация к учебной деятельности.

Через перечисленные  приёмы … организуем работу с математической информацией на стадии вызова.

1. Рассказ-предположение по “ключевым” словам.

2. Верные – неверные утверждения (Верите ли вы, что…)

3. Перепутанные логические цепочки.

Возьмите листы голубого цвета и выполните задания в группах.

1 группа

Прием “ Рассказ-предположение по “ключевым” словам (фразам)”

         По ключевым словам нужно составить рассказ или расставить их в определенной последовательности, а затем, на стадии осмысления искать подтверждение своим предположениям, расширяя материал.

         По выражениям-описаниям догадайтесь, о каком математическом понятии  идёт речь. Докажите: величина непостоянная, можно измерять сравнивать, находить, занимаемое пространство плоской фигуры, измеряется в квадратных единицах.

2 группа

Прием – Игра “ Верите ли вы?” или “Данетка”

Учитель задает вопросы, на которые учащиеся должны ответить “да” или “нет”. У каждого на парте таблица, как на доске. Учитель читает вопросы, а ученики ставят в первой строке плюс (да), если согласны с утверждением, и минус (нет), если не согласны. Вторая строка у вас пока останется пустой. В течение урока ученики обращаются к таблице и видят, насколько были правы.

Определите истинность ли ложность математических  высказываний.

3 группа

Перепутанные логические цепочки

Модификация приема «Ключевые термины». Дополнительным моментом является расположение на доске ключевых слов (фраз)  в специально «перепутанной» логической последовательности. После знакомства с текстом учащимся предлагается восстановить нарушенную последовательность.

1. Восстановите нарушенную последовательность на уровне фразы.

2. Из полученных фраз составьте логическую цепочку действий  по нахождению площади.

Чтобы найти площадь прямоугольной фигуры, нужно…

Знать (измерить)  / длину и ширину этой фигуры.

Если значения длины и ширины известны, /  умножаем их.

Если неизвестна длина или ширина,  / выполняем арифметические действия с целью / её нахождения.

Ответ записываем  / в квадратных единицах.

Защита применяемых приёмов стадии вызова.

- Сформулируйте математическое понятие, с которым нам предстоит работать на мастер классе… ПЛОЩАДЬ

Целью стадии  осмысление является получение и первичное осмысление новой информации, включение  её в систему имеющихся знаний.

Возьмём листы жёлтого цвета и проанализируем ситуацию через приёмы: «Толстые и   тонкие вопросы», «Ромашка Блума», «Кластер». На работу в группах 5 минут.

У Лизиной бабушки Веры Петровны в деревне дом с участком земли. Участок прямоугольной формы, 30 метров в ширину и 43 метра в длину. Дом занимает 90 м², огород занимает половину участка, ещё 85 м² разные хозяйственные постройки, сад – 300 м², цветник вдвое меньше, чем сад. Оставшаяся часть участка отведена Лизе для игр. На какой площади можно играть Лизе, если четвёртую  часть отведенного ей пространства занимает вольер Мухтара? Как вы думаете, хватит ли ей этого пространства для игр?

1 группа

Прием "Толстые и   тонкие вопросы"

         Для более успешной адаптации во взрослой жизни детей необходимо учить различать те вопросы, на которые можно дать однозначный ответ (тонкие вопросы), и те, на которые ответить столь определенно не возможно (Толстые вопросы). Толстые вопросы - это проблемные вопросы, предполагающие неоднозначные ответы.

         Продолжите формулирование вопросов с целью более точного представления ситуации.

2 группа

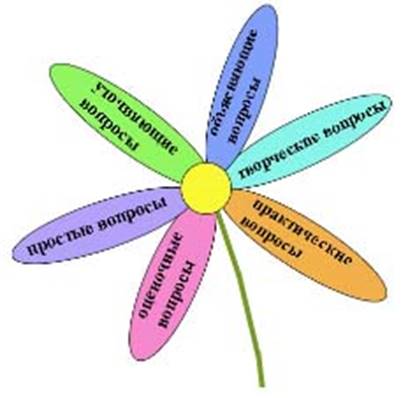
Ромашка Блума

" Ромашка Блума." состоит из шести лепестков, каждый из которых содержит определенный тип вопроса. Таким образом, шесть лепестков – шесть вопросов:

1. Простые вопросы — вопросы, отвечая на которые, нужно назвать какие-то факты. вспомнить и воспроизвести определенную информацию: "Что?", "Когда?", "Где?", "Как?".

2. Уточняющие вопросы. Такие вопросы обычно начинаются со слов: "То есть ты говоришь, что…?", "Если я правильно понял, то …?", "Я могу ошибаться, но, по-моему, вы сказали о …?". Целью этих вопросов является предоставление учащемуся возможностей для обратной связи относительно того, что он только что сказал. Иногда их задают с целью получения информации, отсутствующей в сообщении, но подразумевающейся.

3. Интерпретационные (объясняющие) вопросы. Обычно начинаются со слова "Почему?" и направлены на установление причинно-следственных связей. "Почему листья на деревьях осенью желтеют?". Если ответ на этот вопрос известен, он из интерпретационного "превращается" в простой. Следовательно, данный тип вопроса "срабатывает" тогда, когда в ответе присутствует элемент самостоятельности.

4. Творческие вопросы. Данный тип вопроса чаще всего содержит частицу "бы", элементы условности, предположения, прогноза: "Что изменилось бы ...", "Что будет, если ...?", "Как вы думаете, как будет развиваться сюжет в рассказе после...?".

5. Оценочные вопросы. Эти вопросы направлены на выяснение критериев оценки тех или иных событий, явлений, фактов. "Почему что-то хорошо, а что-то плохо?", "Чем один урок отличается от другого?", "Как вы относитесь к поступку главного героя?" и т.д.

6. Практические вопросы. Данный тип вопроса направлен на установление взаимосвязи между теорией и практикой: "Как можно применить ...?", Что можно сделать из ...?", "Где вы в обычной жизни можете наблюдать ...?", "Как бы вы поступили на месте героя рассказа?".

         Сформулируйте 6 групп вопросов, позволяющих представить предлагаемую ситуацию с разных позиций.

3 группа

         Прием «Кластер»

         Выделение смысловых единиц текста и графическое оформление в определенном порядке в виде грозди. Ведущим приемом могут стать гроздья (кластеры). Делая какие-то записи, зарисовки для памяти, мы, часто интуитивно, распределяем их особым образом, компонуем по категориям. Грозди - графический прием в систематизации материала. Наши мысли уже не громоздятся, а "гроздятся", то есть, располагаются в определенном порядке. Правила очень простые. Рисуем модель солнечной системы: звезду, планеты и их спутники. В центре звезда - это наша тема, вокруг нее планеты - крупные смысловые единицы, соединяем их прямой линией со звездой, у каждой планеты свои спутники, у спутников свои.

         Представьте предлагаемую ситуацию в форме кластера. Как видите «Грозди» разного размера. Догадайтесь, почему, и внесите в них информацию.

Прием “Корзина идей”

         Все требуемые сведения кратко записываются и помещаются в “корзину” идей (без комментариев), даже если они ошибочны. В корзину идей можно “сбрасывать” факты,  мнения,  имена, проблемы, понятия, имеющие отношение к теме урока. Далее в ходе урока эти разрозненные в сознании ребенка факты или мнения, проблемы или понятия могут быть связаны в логические цепи.

          Все ошибки исправляются далее, по мере освоения новой информации.

         - Какой проблемный  вопрос озвучивался в ситуации? Ответьте…

- Я держу в руках «корзину»,  которую мы наполним идеями для решения проблемы.

1).   43*30 = 1290 (м²) –S усадьбы.

2). 1290 : 2 = 645 (м²) – S огорода.

3). 300 : 2 = 150(м²) – S цветника.

4). 645 + 300 + 150 + 90  +  85= 1270 (м²) – S без Лизиного участка.

5). 1290 – 1270 = 20 (м²) – S Лизиного участка.

6). 20 : 4 = 5 (м²) – S площадь вольера.

7). 20 – 5 = 15 (м²) – S места для игр.

Третья стадия – рефлексия. Цель -  целостное осмысление, обобщение полученной информации; анализ  собственного отношения и уровня понимания полученной  информации.

15 м² для игр… Это много или мало? Посмотрим на это с позиции ребёнка. Ему будет мало. Давайте методом мозгового штурма сформулируем предложения по поводу расширения участка. Я Вера Петровна. Вы – Лиза. Убеждайте!