Мастер класс «Комбинаторные задачи»

Мастер класс «Комбинаторные задачи»

учителя начальных классов МБОУ Кыштовская СОШ №

 Кузменковой Надежды Васильевны

Многие  жизненные проблемы требуют для своего решения комбинаторного подхода, умения просчитать все возможные варианты и с учетом дополнительных условий выбрать наилучший. Поэтому весьма актуальным является формирование и развитие таких качеств мышления учащихся, как системность, гибкость, многовариантность, избирательность. Все эти качества характеризуют комбинаторный стиль мышления.

Имея огромное развивающее значение, комбинаторика является базой для изучения теории вероятностей и основ математической статистики, постепенно занимающих прочные позиции в школьном образовании.

В рамках традиционного подхода к преподаванию математики введение элементов теории вероятностей предполагает предварительное знакомство с комбинаторикой. Этот раздел математики очень важен в обучении школьников, т.к. он в большей степени, чем другие разделы способствует развитию мышления учащихся. Благодаря решению комбинаторных задач, развитие мышления младших школьников (переход от практического вида к теоретическому) становится более осуществимым.

Комбинаторные задачи – это задачи, требующие осуществления перебора всех возможных вариантов или подсчета их числа.

В действующих учебниках математики число комбинаторных задач очень мало и используются задачи только некоторых видов. Поэтому возникает необходимость в отборе комбинаторных задач, которые можно и нужно включать в начальный курс математики.

Обучение решению комбинаторных задач проводится в три этапа:

1)    подготовительный этап, цель которого формирование мыслительных операций в процессе решения комбинаторных задач с помощью хаотического перебора;

2)    основной этап, цель – ознакомление учащихся с методом организованного перебора;

3)    этап отработки умений выполнять организованный перебор, цель – отработать у учащихся умения решать комбинаторные задачи.

Рассмотрим подробно методику решения комбинаторных задач на каждом этапе.

На подготовительном этапе предлагаются задачи на развитие познавательных способностей, на активизацию таких мыслительных процессов как анализ, синтез, обобщение и классификация.

На данном этапе решаются задачи двух видов:

v задачи-игры;

v «жизненные» задачи (задачи, решаемые в повседневной деятельности человека).

Для обеспечения мотивации решения таких задач можно предложить детям задачи в виде игр.

1.Правила игры «Башенки». (шкатулка чудес, кубики трёх цветов)

Ведущий кладет в коробку три кубика разного цвета, например, зеленого, синего и желтого цветов и говорит, что будет брать, не глядя, по одному кубику и составлять башенку следующим образом: первый кубик – нижний этаж, второй – средний, третий – верхний. Игрокам предлагается нарисовать башенку, изображая кубики квадратами соответствующего цвета. Затем кубики вынимаются из коробки. Тот, кто угадал, становится победителем. Вопрос: сколько различных башенок надо нарисовать, чтобы быть уверенным, что, сколько бы башенок мы не составляли, среди рисунков всегда окажется нужный, и ты всегда будешь выигрывать?

Решение:

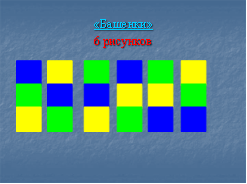
Методические указания: в процессе игры учащиеся могут придти к выводу, что если рисуешь одну башенку, то можешь получить как задуманный, так и другой порядок цветов. Именно тогда целесообразно задать вопрос задачи (сколько различных башенок надо нарисовать, чтобы быть уверенным, что, сколько бы башенок мы не составляли, среди рисунков всегда окажется нужный, и ты всегда будешь выигрывать?).

Используя электронный вариант сборника, важно предусмотреть это условие, т.е. открыть вопрос не вместе с задачей, а позже, когда учащиеся сделают вывод. После того, как ученики нарисуют все башенки, ответ можно проверить с помощью электронного варианта.

Игру можно предложить в конце урока математики в качестве дополнительного материала. Далее мы  предлагаем задачи, показывающие возможность применения комбинаторики в повседневной деятельности человека («жизненные» задачи). Данные задачи можно предлагать учащимся в конце уроков математики.

Задача 2.  (раздать модели купюр)

У кассы кинотеатра стоят четверо ребят. У двух из них сторублевые купюры, у других двух – пятидесятирублевые. (Учитель вызывает 4 учеников к доске и дает им модели купюр). Билет в кино стоит 50 рублей. В начале продажи касса пуста. (Учитель вызывает «кассира» и дает ему «билеты»). Как должны расположиться ребята, чтобы никому не пришлось ждать сдачи?

Методические указания: для решения задачи целесообразно разыграть сценку, с помощью которой можно найти два возможных варианта решения:

1)    50 рублей, 100 рублей, 50 рублей, 100 рублей;

2)    50 рублей, 50 рублей, 100 рублей, 100 рублей.

Задача 3.  (раздать рисунки,  треугольники – парусы, клей)

4 парусника готовились к соревнованиям. У каждого был свой корабль. Судьи решили, что надо раскрасить паруса, чтобы парусники были видны издалека, и было ясно, кто из спортсменов идет впереди, кто запаздывает. Покажите, как по-разному раскрасили паруса, если было всего две краски?

Методические указания: после прочтения задачи учитель может повесить заготовленные заранее модели парусников на доску, чтобы учащимся было легче сориентироваться в ситуации.

Решение:

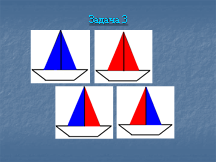
 Далее учитель обсуждает с учениками возможные варианты, после чего ответы проверяются с помощью электронного варианта «Сборника…».

Таким образом, на подготовительном этапе создается положительная мотивация и эмоциональная подготовка учащихся к дальнейшему решению комбинаторных задач.

На основном этапе учащиеся знакомятся с разными способами решения комбинаторных задач.

На данном этапе решаются задачи четырех видов:

v задачи, решаемые методом организованного перебора;

v задачи, решаемые с помощью таблиц;

v задачи, решаемые с помощью графов;

v задачи, решаемые с помощью дерева возможных вариантов.

Для начала мы предлагаем ознакомить учащихся с методом организованного перебора. При решении данных задач важно обучить детей выполнять перебор не хаотически, а соблюдая определенную последовательность перебора всех вариантов решений.

Задача 4.(раздать изображение воздушных шаров)

 В магазине продают воздушные шары: красные, желтые, зеленые, синие. Какие наборы можно составить из двух разных шаров? Сколько наборов у тебя получилось?

Решение:

            Методические указания: следует обратить внимание учащихся на то, что при выборе двух шаров не имеет значения, какой из них находится справа, а какой слева. Но при расположении шаров необходимо пользоваться организованным перебором.

Далее мы предлагаем ознакомить учащихся с другим способом решения комбинаторных задач – с помощью таблиц.

Перед тем, как знакомить учащихся с новым способом решения комбинаторных задач, необходимо актуализировать знания детей о таблицах, выделить существенные признаки таблиц и сформулировать определение понятия «таблица», например такое: таблица – это перечень сведений, числовых данных, приведенных в определенную систему и разнесенных по графам (строкам и столбцам).

            Задача 5. Запиши в нужные клетки таблицы следующие числа: 23, 32, 11, 31, 22, 33, 13. Какие числа нужно записать в оставшиеся клетки?

         Методические указания: перед решением данной задачи необходимо вспомнить с учащимися разрядный состав чисел, используемых в решении задачи.  Проверку решения можно осуществить при помощи электронного варианта «Сборника…», открывая постепенно числа в таблице.

5.1 Проверь, правильно ли заполнена таблица?

         Методические указания: как и перед решением предыдущей задачи необходимо вспомнить с учащимися разрядный состав чисел, используемых в решении задачи.  Проверку решения можно осуществить при помощи электронного варианта «Сборника…», открывая числа в таблице по столбикам.

Далее знакомим учащихся с новым способом решения комбинаторных задач – с помощью графов.

Задача 6.

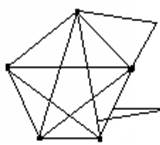
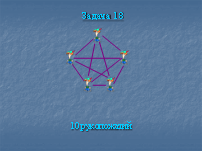
 Пятеро друзей встретились после каникул и обменялись рукопожатиями. Каждый, здороваясь, пожал руку. Сколько всего было сделано рукопожатий?

         Методические указания: для начала необходимо выяснить с учащимися, как можно обозначить каждого человека (быстрее и удобнее изображать людей точками, которые располагаются примерно по кругу, чтобы записи были понятными и наглядными). Рукопожатия удобно обозначить черточками. Сначала составить рукопожатия одного человека (точку соединить со всеми остальными), потом перейти к другому человеку. Проведенные линии помогут увидеть, с кем он уже поздоровался, а с кем нет. Составить недостающие рукопожатия. Так действовали до тех пор, пока все не поздоровались друг с другом.

Проверять решение можно как постепенно, открывая поэтапно стрелки, так и целиком открыв весь граф на слайде электронного варианта «Сборника…».

Далее знакомим учащихся с применением одной из разновидностей графа – деревом возможных вариантов при решении комбинаторных задач.

            Задача 7. Какое число зашифровано в выделенном пути?
Покажи путь, в котором зашифровано число 5571.

                                                                                                   единицы тысяч

                                                                                                         сотни

                                                                                                        десятки

                                                                                                        единицы

          С детьми выясняется, что данный вид графа, если его перевернуть будет похож на дерево, на котором растут ветки с листьями. Наше дерево  отличается тем, что растет сверху вниз, потому что так удобнее располагать объекты в нужной последовательности. Такой вид графа называется деревом возможных вариантов.

Далее с детьми следует проанализировать структуру дерева возможных вариантов: дерево возможных вариантов начинается строго с определенного объекта (цифра 5 обозначает первый разряд при чтении показанных на дереве чисел), такой объект в структуре дерева называется корнем дерева; дерево возможных вариантов показывает последовательности вариантов выбора объектов (определенный порядок расположения кубиков в башенках и цифр, из которых состоят четырехзначные числа), они называются ветвями дерева.

На этапе отработки умений выполнять организованный перебор предлагается решать комбинаторные задачи разными способами (методом организованного перебора, с помощью таблиц, с помощью графов), тем самым, с одной стороны, закрепляя умение решать такие задачи с помощью различных приемов перебора, с другой – осуществляя действие самоконтроля, являющееся необходимым компонентом учебной деятельности.