Мастер класс "Красота првлекает, а математические фокусы увлекают"

Муниципальное бюджетное образовательное учреждение дополнительного образования «Кош-Агачский Центр дополнительного образования детей»

Мастер - класс

"Красота привлекает, а математические фокусы увлекают"

                Составитель:

Аспенбетова Роза Антаевна  

педагог дополнительного образования

     МБОУ ДО «Кош-Агачский ЦДОД»

Кош-Агач

2024

Форма проведения: мастер -класс

Эпиграф: В математике есть своя красота, как в живописи и поэзии. (Н.Е. Жуковский)

Лучший способ изучить что-либо - это открыть самому. (Д. Пойа)

Математика заключает в себе не только истину, но и высочайшую красоту – красоту холодную и строгую, подобную красоте скульптуры. Бертран Рассел

.

План проведения

 I.Вступительная часть (пояснительная записка, цели, задачи, актуальность, практическая значимость темы, оборудование, ознакомление с содержанием мастер класса)

 II. Демонстрационная часть (сообщение обучающегося, знакомство с математическими фокусами)

 III.Практическая часть (отгадывание математических фокусов)

 IV. Заключение (обсуждение результатов мастер класса, рефлексия)

Организационный момент.

Мастер-класс будет проводиться одновременно для  обучающихся  8-9-х классов. Педагоги выполняют роль наблюдателей и консультантов.

I.Вступительная часть

Пояснительная записка

Интеллектуальное развитие человека предполагает интерес, любознательность и стремление к развитию – это заложено природой, поэтому важно поддерживать это и находится в состоянии постоянного интереса к миру и тому, что происходит вокруг. Я стараюсь делать это в рамках своего направления. Создание нестандартных ситуаций на занятий творческого объединения мне часто в этом помогает.

Главное не забывать, что математические «способности» связаны с любознательностью и активностью ребенка! Существует такая статистика: любопытные и активные дети, которые многим интересуются и не боятся пробовать новое, успевают по математике  гораздо лучше, чем дети, которые боятся проявлять свою природную любознательность. Родители и, конечно же мы, в этом смысле имеем на руках все козыри. Нужно всего лишь поддерживать интерес ребенка к окружающему миру, учить его задавать вопросы, искать решения, не бояться ошибок и понимать, что незнание – это первый шаг к постижению тайны.

Математические фокусы – это эксперименты, основанные на математических знаниях, на свойствах фигур и чисел, обличенные в экстравагантную форму. Понять суть того или иного эксперимента – это значит понять пусть небольшую, но очень важную математическую закономерность.

Способность человека отгадывать задуманные другими числа кажется удивительной для непосвященных. Поэтому для детей – это что-то магическое и не постижимое изначально. Но когда мы помогаем им узнать секреты фокусов, то тем самым мотивируем их не только на угадывание принципа работы (что невозможно без математической модели), но и на придумывание своих.

Так же и мы- педагоги  учимся всю жизнь, находимся в постоянном развитии и всю трудовую жизнь являемся исследователями. Поэтому я, например, очень люблю различные мастер-классы. Даже если я уже бываю знакома с той или иной методикой или идеей то всё равно наблюдать и участвовать очень интересно, потому что каждый педагог-мастер излагает по-своему, привносит своё оформление.

 На мастер классе  хочу доказать, что математические фокусы помогают развивать память, сообразительность, способность мыслить логически, совершенствовать навыки устного счета и, наконец, просто повышают заинтересованность учеников в математике, что должно улучшить качество их знаний.

Цель:

·         познакомить  обучающихся с историей  возникновения математических фокусов;

·         научить обучающихся разгадывать фокусы;

·         способствовать развитию умений анализировать, сравнивать, обобщать, выделять главное; развивать осознанную математическую речь; развитие познавательного интереса обучающихся;

·         содействовать воспитанию таких качеств как: самостоятельность, целеустремленность, настойчивость, целенаправленность, трудолюбие, аккуратность, ответственность

Задачи:

- Продолжить формирование навыков контроля результатов деятельности.

- Способствовать развитию коммуникативных навыков. Развивать умение анализировать, обобщать материал, выступать перед аудиторией, развивать интеллектуальные, творческие и исследовательские способности, активизировать интерес к учебным предметам.

- Формирование логического, абстрактного, эвристического, системного мышления.

Актуальность данной темы довольно велика, так как математика представлена в более игровой форме, но с развивающей целью. Данные в фокусах действия могут производить все дети. Когда выполняются вычисления,  ребенок считает,  думает и размышляет. Также математические фокусы производят впечатление и привлекают, создавая у детей интерес узнавать больше.

Практическая значимость математических фокусов.

Многие утверждают, что математические фокусы не только  влияют на мышление человека, но и развивают вычислительные навыки, быстроту реакции. Навыки, которые отвечают за этот раздел мозга, задействуются как в стереометрии и механике, так и в физике и инженерии. Ребенок, играясь, сам того не замечая, приучается к дисциплине логического мышления и последовательности, когда понимает алгоритм решения.

А после показа не самого сложного математического фокуса главное - не торопиться с разгадкой. Можно рассмотреть несколько подобных примеров, убедиться, что снова у всех получилось одно и то же число и посоветовать разобраться с этим дома, используя любые источники. И, как показывает практика, свои домашние задания в школе они начинают выполнять именно с этого задания. Что мы этим параллельно достигаем? А не что иное, как формирование метапредмтных результатов обучения. 

Необходимое оборудование и наглядные материалы.

- оборудование для демонстрации презентации,

- раздаточный материал на столы для групповой работы,

- коробки продуктов со штрих кодом.

- календари

Фото и рисунки с заданиями и решениями.

Вступительное слово педагога

Добрый день дорогие дети, уважаемые коллеги!                                          Человек по-разному открывает красоту. Один из этих путей – путь логического мышления. Сегодня мы совершим путешествие в красоту с помощью математической логики. На мастер - классе постараемся развить математические способности, одним словом развивать хоть чуточку математической одаренности. Сегодня наш мастер- класс  точно никому не покажется скучным, ведь оно будет посвящено фокусам. Причём это будут не фокусы с бумагой, монетами или лентами, это будут фокусы с числами и действиями над ними. Фокусов много, но точнее – это эксперименты, основанные на математике, на свойствах фигур и чисел. Чтобы их понять, нужно использовать элементы школьной алгебры и геометрии.

А теперь скажите,  как вы понимаете смысл слов, которые вы видите на слайде: 1) В математике есть своя красота, как в живописи и поэзии.

 (Н.Е. Жуковский).  Он был заслуженным профессором Московского университета, почётным членом Московского университета, а также членом-корреспондентом Императорской Академии наук по разряду математических наук.

2) Математика заключает в себе не только истину, но и высочайшую красоту – красоту холодную и строгую, подобную красоте скульптуры. Бертран Рассел

Британский философ, специалист по математической логике)

II. Демонстрационная часть

История возникновения математических фокусов. (Сообщение ученика)

Математические фокусы возникли несколько тысяч лет до нашей эры. Родиной фокусов гипотетически является Древний Египет. С античных веков знакомы головоломки Пифагора и Архимеда.

Леонтий Филиппович Магницкий в своей книге «Арифметика, сиречь наука числительная, с разных диалектов на славянский язык переведенная и воедино собрана и на две книги разделена…» первый упоминает о математических фокусах. Магницкий изучал математические фокусы для «утехи и, особенно для изощрения ума учащихся»

Михаил Юрьевич Лермонтов интересовался математикой, он увлекался математическими фокусами, некоторые фокусы придуманы им. Фокус, придуманный великим русским поэтом: «Задумать любое число, прибавить к нему 25, прибавить еще 125, отнять 36, вычесть задуманное число, остаток умножить на 5, полученное число разделить на 2. Результат: 285»

В основе всех математических фокусов лежат законы математики. Каждый фокусник должен знать свойства чисел, в чём и состоит секрет фокуса. Математические фокусы развивают мыслительные операции, полезны для людей любых возрастных групп.

В мастер классе я рассмотрела фокусы, которые на мой взгляд являются наиболее интересными и полезными для обучающихся. (Презентация)

Знакомство с  фокусами и их секретами

III.Практическая часть (отгадывание математических фокусов)

1.Математический фокус.  Попросить учеников задумать число. После это число он должен умножить на 2, прибавить к результату 8, разделить результат на 2 и от полученного результата отнять задуманное число. Фокус выполнять очень быстро. После того, как они закончили вычислять, я раздаю им листочки с их ответами, делая вид, что у каждого он разный. Потом я предлагаю им показать свои ответы. В результате у всех написано число 4.

Пример 1. Ученик задумал число 7. Имеем: 7•2=14; 14+8=22; 22:2=11; 11-7=4.

Пример 2. Ученик задумал число 23. Имеем: 23•2=46; 46+8=54; 54:2=27; 27-23=4.

А в 8 классе, когда уже пройдена тема «Преобразование рациональных выражений», они уже понимают и могут доказывать независимость результата преобразования от переменной. И у доски можно это без труда доказать: пусть загаданное число – это Х, тогда:

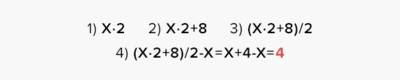
Мы получили 4 независимо от изначально загаданного числа. Используя подобную смену деятельности на уроке, мотивация просто зашкаливает.

3. Математический фокус -Угаданный день рождения

Содержание этого математического фокуса. Объявите зрителям, что вы сможете угадать день рождения любого незнакомого человека.

• Вызовите любого желающего и предложите ему умножить на 2 число дня своего рождения
• Затем пусть зритель сложит получившееся произведение и число 5,
• теперь пусть умножит на 50 полученную сумму.
• К этому результату необходимо прибавить номер месяца рождения (июль — 7, январь — 1)
• вслух назвать полученное число.

Через секунду вы называете день и месяц рождения зрителя. Секрет этого математического фокуса. Все очень просто. В уме от того числа, которое назвал зритель, отнимите 250. У вас должно выйти трехзначное или четырехзначное число. Первая и вторая цифры — день рождения, две последние — месяц.

4. Математический фокус - Отгадывание числа

• Для этого математического фокуса Вам понадобятся:
• заранее приготовленные листы бумаги (по числу детей),
• карандаши или ручки (по числу детей).

Представиться детям как великий математик, дрессировщик цифр, читающий чужие мысли. Попросите зрителей задумать какое-нибудь число. Вопрос вы можете задать абсолютно любой, например: сколько дней в неделю вы хотели бы кататься на велосипеде, есть манную кашу, не ходить в школу, бегать по лужам. Весь смысл не в вопросе, а в задуманном зрителями числе.

Раздайте зрителям бумажки и ручки и дайте задание письменно ответить на ваш вопрос. Пусть каждый напишет, сколько дней в неделю он хотел бы есть морковку(мороженое).

Теперь пусть каждый умножит это число на 2, затем к полученному числу морковок прибавит 5, после чего умножит эту сумму на 50. Теперь пусть каждый сделает следующее: если в этом году уже был день рождения, прибавить 1 750, если нет — 1 749. Теперь из этого числа каждый должен вычесть свой год рождения и к этому числу прибавить 7.

Содержание фокуса.

Предлагаю  задумать трехзначное число и записать его на бумаге. При загадывании числа должно быть выполнено одно условие: цифра сотен не должна быть равна цифре единиц и не должна быть на единицу меньше или больше ее. Если вы еще путаетесь в сотнях и единицах, то на первом месте в трехзначных числах стоят сотни, на втором десятки, на третьем единицы (например, подойдет число 531).

• Теперь  должны перевернуть задуманное число, т.е. написать цифры в обратном порядке (135).
• Затем  должны взять эти два числа и из большего вычесть меньшее (531 - 135).
• Получившуюся разницу снова нужно перевернуть (396; 693) и сложить эти два числа (396 + 693).
• Потом один из обучающихся должен прибавить к полученной сумме 100, второй — 200, третий — 300 и т. д.
• Теперь  можно отгадать, что получилось у каждого, но при том условии, что они к своему последнему числу прибавят цифру 1 089. У первого ученика, прибавлявшего 100, получится 1 189, у второго — 1 289, у третьего — 1 389.

Теперь попросите любого из зрителей назвать получившуюся цифру.

Должно получиться двухзначное или трехзначное число. Первая цифра — количество морковок, остальные — возраст человека. Секрет фокуса. Сколько бы ни прибавляли и ни отнимали, это все хитрости алгебры. Только ваши зрители не догадываются об этом, весь секрет фокуса в тех числах, которые вы заставляете их прибавлять, отнимать, делить.

Вот как это выглядит. Например, вы загадали 2 дня в неделю для поедания морковки.

• Теперь умножьте 2 на 2, получится 4.
• Потом к 4 прибавьте 5, получится 9, затем 9 умножьте на 50, получится 450.
• Допустим, ваш день рождения 18 июля 1997 г. Например, сейчас сентябрь-месяц и ваш день рождения уже прошел.
• Значит, прибавьте к 450 число 1 750, получится 2 200.
• Теперь из числа 2 200 вычтите год рождения 1997, получится 203, к этому числу прибавьте 7.
• Результат — 210 (2 дня и 10 лет).

Во втором случае из числа 2 199 вычтите 1 997, получится число 202, прибавьте 7, получится 209. Значит, загадано 2 дня морковки и 9 лет загадавшему.

Совет: Перед выполнением этого математического фокуса раздайте зрителям калькуляторы, чтобы они не ошиблись в вычислениях, а для себя на первое время запишите на карточке порядок действий с цифрами: на что умножить, что прибавить, из чего вычесть.

Секрет фокуса.

Для того чтобы узнать, что получилось, вам не нужно знать задуманное число. Главное — прибавлять к числу 1 089 то число (100, 200, 300, 400...), которое они прибавляли в самом конце. Для того чтобы не перепутать, у кого что получилось, в самом конце фокуса можно раздать карточки с цифрами 100, 200, 300 и попросить держать их при отгадывании конечного результата.

5. Фокус на определение настоящего товара от подделки

Например, покупая газировку, конфеты, или кофе, вы, разумеется, видели на упаковке штрих-код. Что бы это значило? С помощью него зашифрована информация о некоторых наиболее существенных параметрах продукции. Согласно этой системе, каждому виду изделия присваивается свой номер состоящий чаще всего из 13 цифр:

·         Первые две – код страны

·         Последующие 5 – код изготовителя

·         Еще 5 наименование товара

·         И последняя – знак товара или контрольная цифра

В последнее время очень много нелегальных производств подпольной продукции, но как же простому покупателю отличить где подделка, а где настоящий товар?? Именно в этом нам и поможет МАТЕМАТИКА. Каждый кто хорошо умеет считать может без особых усилий раскрыть тайну магических цифр.

Вот эта формула: Сложите цифры, стоящие на четных местах. Полученную сумму умножьте на три. Сложите цифры, стоящие на нечетных местах, кроме последней. Сложите два предыдущих результата. А теперь от этой суммы отбросьте первую цифру. Из десяти вычтите последний получившийся результат. И радуйтесь - вычисления можно закончить. Если у вас получилась цифра, равная последней, контрольной, значит перед вами оригинальный продукт. Если цифры не совпадают, перед вами, скорее всего, подделка.

Можно ли проверить подлинность купюры евро по серийному номеру?
Подлинность единой европейской валюты можно проверить по ее серийному номеру. Букву нужно заменить на ее порядковый номер в английском алфавите и сложить с остальными цифрами, затем у получившегося числа сложить все цифры и т.д. до тех пор пока не останется одна цифра. Если эта цифра не равна 8, то купюра фальшивая.

Стремительно изменяется мир и сама жизнь. В неё входят новые технологии. Только математика и решение задач в традиционном понимании не изменяют себе. Математические законы проверены и систематизированы, поэтому человек в важные моменты может положиться на неё, решить любую задачу. Математика не подведёт.

Свой мастер – класс мне хотелось бы закончить, перефразируя высказывание Гете: «Часто говорят, что цифры управляют миром; по крайней мере, надеюсь, что мой мастер – класс вас убедил в том, что цифры показывают, как он управляется»

Рефлексия

Составить синквейн к слову ФОКУС

Интересный, познавательный

Вычисляет, обучает, развивает

Математические Фокусы связаны с числами

Логика

Закончить наше занятие хочется словами:

Открытый мир - всегда задача,
Смекай, отгадывай, твори                                                                                                        

Решай - и ждет тебя удача!                                                                                                                                                                                                                                                                                               

И будешь ты- на высоте!

Список использованной литературы и источников

1. Я.И.Перельман «Арифметические фокусы»

2. Я.И.Перельман «Фокусы и развлечения»

3. Я. И Перельман «Занимательная алгебра» Москва «Наука» 1970

4. 365 веселых игр и фокусов. Москва АСТ - пресс 2005

5. moikompas.ru/compas/focus_pocus  

6. deltadim.narod.ru/matfocus.htm  

7. nauka.relis.ru/52/0002/52002048.htm

8. http://www.youtube.com/watch?v=gZdmFmjOTPI

Скачано с www.znanio.ru