Мастер класс "Создать проблему? Без проблем!"

Белоусова А.И. учитель математики ГБОУ Херсонской области «Приморская школа Скадовского муниципального округа

Мастер класс

Создать Проблему? Без проблем!

Добрый день уважаемые коллеги!

Я думаю, что с ситуацией «зрелищности вам не хватает» мы все часто сталкиваемся и на своих уроках. Учитель рассказывает, показывает иллюстрации, но некоторые ученики его не слышат, поскольку голова занята совсем другим. Как до таких «достучаться», и «вернуть» их на урок?

Каждый преподаватель стремится найти наиболее эффективные методы обучения, которые способствуют развитию учащихся. Я считаю, что я для себя нашла такие методы и хочу этим поделиться с вами.

Великий Сократ сказал: «Человек глубоко постигает лишь то, до чего додумывается сам»

Действительно, открывать самому интересно, следовательно, меняется отношение обучающихся к учебе. Предложите ребенку поучаствовать в составлении определения, доказательстве фактов, иногда даже при планировании урока, т. е. «заразите» его поиском пути решения заданной проблемы, и вы увидите горящие глаза своего ученика

Коллеги, хору выслушать ваши версии о теме моего мастер класса? (выслушиваю)

Свой мастер класс я назвала «Создать проблему? Нет проблем!»  Предлагаю вам ознакомиться с  приемами и методами создания проблемных ситуаций на уроках математики, которые использую я.

Что значит создать проблемную ситуацию?  Ввести противоречие, столкновение, которое вызывает реакцию удивления и затруднения.

·        Вы можете выполнить это задание?

·        В чем затруднение?

·        Почему не получается выполнить?

·        Что вас удивляет?

·        Какова же будет тема урока?  И т.д.

 Существует масса приемов создания проблемных ситуаций

1.Предварительные домашние задания или задания, на материале учебника, в которых нет готового ответа.

2. Задания с элементами исследования.  

3. Использование экспериментов и жизненных наблюдений (осознание неточности своих представлений вызывает потребность в новых знаниях)

4. Постановка проблемных вопросов и организация дискуссий. Вопрос является проблемным, если он для школьников новый, интересный, содержащий противоречия. Различные мнения учащихся усиливают ситуацию проблемности и активизируют поиск.

5.Предложение выполнить практическое действие, на первый взгляд, не вызывающее затруднений.

6. Создание ситуации выбора (столкновение различных точек зрения) или сообщение противоположных мнений.

7.Учитель сам ставит проблему.

8.Ученикам дается задание, в процессе выполнения которого рождается проблемная ситуации.

9.Перед учащимися ставится вопрос, ответить на который они должны, прослушав объяснение учителя и сделав соответствующие выводы.

Итак предлагаю ознакомиться с некоторыми примерами создания проблемы на уроке

Примеры:

1. Создание проблемных ситуаций через решение задач, связанных с жизнью (практико-ориентированные задачи)

Пример 1. 5 кл. Тема «Проценты»

«За участие в конкурсе эрудитов наш класс получил премию 2000р. 75% мы с вами решили отдать на благотворительность в реабилитационный центр г. Скадовск и 25%в приют для животных. Сколько денег мы отдали в приют?»

Сначала у детей радость и ликование. Но я возвращаю их к реальному вопросу. Сможем ли мы ответить на этот вопрос? Вот тут затруднение (побуждение к осознанию противоречия). Ученики отвечают: «А как же мы вам поможем, если мы не знаем, что такое процент?» (побуждение к формулировке проблемы). Проблемная ситуация создана. Ребята сами формулируют проблему «Что же такое процент?» Высказываются  различные предположения (какое-то число, дробь, деньги и т.д). С помощью учителя ученики формулируют гипотезу: «Процент- это сотая часть». В конце урока доводят решение данной задачи до конца и делают вывод о важности и нужности темы «Проценты» в нашей жизни. Затем участвуют вместе со мной в возможном распределении денег. Я вижу их радостные лица.

Пример. 8 класс. Тема «Теорема Пифагора»

« На охоте с двух отвесных скал два первобытных охотника заметили козла и разом в него выстрелили, причем стрелы достигли цели одновременно. Охотники одновременно начали спуск к добыче с одинаковой скоростью. Кому достанется козел?

Проблемная ситуация очевидна при построении математической модели практической задачи. Её можно сопровождать вопросами:

- Как на чертеже изобразить скалы?

- Как изобразить путь каждой стрелы?

- Как изобразить путь каждого охотника?

- Что означает тот факт, что стрелы достигли цели одновременно? (CD=CE)

Использование только того факта, что отрезки равны не  приведет к решению данной задачи. Возникает проблема: Существует ли зависимость между катетами и гипотенузой? И как она формулируется?

Для решения этой проблемы организую поиск формулировки, предложив задание по рядам: Построить прямоугольные треугольники с катетами 3 и 4, 12 и 5, 6 и 8 см, измерить гипотенузу, результаты занести в таблицу. Далее обсуждаем разные гипотезы и приходим к выводу: квадрат гипотенузы равен сумме квадратов катетов.

2. Создание проблемных ситуаций через использование занимательных заданий.

Пример 1.    7 кл. Тема: «Линейная функция»

Обычная форма задания.  Функция задана формулой  У = Х + 6. Найдите значение функции при Х = 0, 4, -6, 1.

Занимательная форма задания.  Приглашаю к доске ученика, даю ему карточку, на которой  написано  У = Х + 6. На доске заготовлена таблица:

Один ученик из класса называет какое-нибудь значение Х. Ученик у доски вписывает это число в таблицу и, поставив его в формулу, находит и вписывает в таблицу соответствующее ему значение У. Затем другой ученик из класса называет другое значение Х и ученик у доски проделывает те же операции. Возникает проблема: “Угадать” формулу, записанную на карточке. Проблемная ситуация создана. Гипотеза: для того чтобы угадать формулу, надо найти какую-то закономерность. Продолжаем подставлять значения х и находим закономерность, и делаем вывод: зная закономерность, легко угадать формулу. В итоге выигрывает тот ученик, который первый назовет формулу.

Пример№2 9 кл. «Сумма первых n членов геометрической прогрессии»

Однажды незнакомец постучал в окно к богатому купцу и предложил такую сделку: « Я буду ежедневно в течение 30 дней приносить тебе по 100 000 руб. А ты мне в первый день за 100 000 руб. дашь 1коп., во второй день за 100 000 руб. – 2 коп.и так каждый день будешь увеличивать предыдущее число денег в 2 раза. Если тебе выгодна сделка, то с завтрашнего дня начнем».

Купец обрадовался такой удаче. Он подсчитал, что за 30 дней получит от незнакомца 3 000 000 руб. На следующий день пошли к нотариусу и узаконили сделку.

Создается проблемная ситуация. Кто в этой сделке проиграл: купец или незнакомец?

Учащиеся предлагают записать геометрическую прогрессию и найти сумму 30-ти ее членов: 1,2,4,8,16,32,128,…, но понимают, что это трудоемко. Вопрос: А можно ли решить эту задачу более рациональным способом?

Ученики говорят да, если будем знать формулу суммы членов конечной геометрической прогрессии. Формулируем тему урока и выводим формулу.

, q или

S₃₀ = 2³⁰ – 1 = 1073741823 (коп.) = 10 737 418,23 (руб). Ответ очевиден!

3. Создание  проблемных ситуаций через решение задач на внимание и сравнение.

Пример 2. Третьекласснице Даше учительница дала задание сосчитать, сколько треугольников изображено на рисунке. Она нашла 5 треугольников. Подошла  Лена и нашла 7 треугольников. Кто из них прав? Попробуем посчитать вместе.

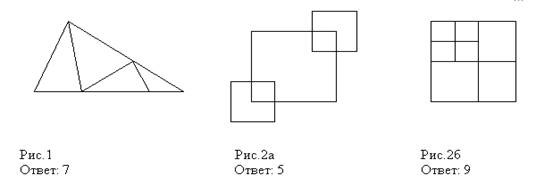
Сможете ли вы сосчитать все треугольники? Затруднение для учащихся. Проблема: как же их сосчитать? Предлагают гипотезы (считаем все подряд, которые найдём, считаем сначала все маленькие, затем побольше, считаем все слева направо и т.д.). Проверяем предположения на практике. Выбираем лучший вариант.  Делаем вывод, что Лена посчитала лучше (наверное, она старше и умнее или просто внимательнее!).

Определите, сколько треугольников вы видите на рис.1 и квадратов на рис.2а, 2б?

4.Одним из самых интересных методов, по мнению учеников,  являются исследовательские и лабораторные работы. Да, да уважаемые биологи и в математике есть такое…

Приглашаю 6 человек (фокус-группа)

1.          Создание проблемной ситуации.

Всем очевидно ясно, что это  старое колесо от самопрялки какую математическую модель оно напоминает?

 – окружность.

(Слайд 4) Ось колеса – центр окружности, спица – радиус, две спицы, лежащие на одной прямой – диаметр.  Их  легко измерить с помощью линейки.  Для прочности деревянные колеса в старину обивали металлическим ободом. Как узнать, сколько метров металлической пластины потребуется, для того чтобы обить данное колесо снаружи?

Давайте измерим длину окружности. В чем трудность? Да, к сожалению, специального прибора для измерения длины окружности нет. Но и это не останавливало человека. Предложите свой способ измерения длины окружности (обсуждение в группах).

-- верёвкой

Ниткой, веревкой удобно пользоваться для измерения длины окружности малого радиуса. А как быть, если требуется измерить длину окружности предмета круглой формы большого размера, например, трубы завода? С помощью нитки и веревки это сделать можно, но весьма трудоемко и результат таких измерений может быть неточным.

Ещё древние находили длину окружности по формуле С=Пхд  Д это диаметр окружности.

Вопрос: а что же такое п? пока для нас это тайна

Приглашаю вас в лабораторию раскрытия тайн.

^ Работа в группах по 2 человека.

У вас на столах лежат 3 круга с отмеченным центром, а также ниточка. Как можно измерить длину окружности, которая является границей круга? (С помощью ниточки). Измерьте, пожалуйста, и запишите результат измерения в таблицу. С помощью линейки измерьте диаметр круга и результат измерения занесите в таблицу.

Тема: «Нахождение значения числа П».

Цель: с помощью эксперимента найти значение числа П

Оборудование: предмет, имеющий форму цилиндра, рулетка, линейка, микрокалькулятор.

Ход работы

Делайте так:

1.          С помощью рулетки измерьте длину окружности предмета.

2.          Сделайте запись С = …

3.          Линейкой измерьте диаметр окружности.

4.          Сделайте запись D =…

5.          Найдите отношение длины окружности к её диаметру (разделите с помощью калькулятора длину окружности на диаметр).

6.          Сделайте запись. Ответ округлите до десятых.

7.          Занесите полученные результаты в таблицу на доске.

Вывод: закончите предложение «Число П равно от …до…»

Лист МЕБИУСА

Пока фокус группа работает мы с вами немного поэкспериментируем. Посмотрите на эту полоску бумаги. Что я получу если склею ее концы? (Цилиндр, Кольцо…) Сколько сторон у него? Сколько поверхностей? (две)

Однажды служанка немецкого геометра Августа Фердинанда Мёбиуса сшила неправильно концы ленты, чем сподвигла математика к великому открытию. А именно, удивительной фигуры, названной лентой Мебиуса.

Как вы думаете сколько сторон у данной ленты? Поверхностей? (одна)

Проведем эксперимент

Возьмем нами приготовленный лист Мёбиуса и разрежем склеенную ленту посередине, вдоль пунктирной линии. Как вы думаете, что получится? Конечно, если бы мы не перекрутили ленту перед склейкой, все было бы просто: из одного широкого кольца получилось бы два узких (это тоже лучше продемонстрировать). А что сейчас?

Получилось не два кольца, а одно, вдвое уже, но зато вдвое длиннее. К тому же перекручено оно не один раз, а два.

Что же из этого свойства следует? А следуют удивительные превращения ленты, если разрезать ее вдоль. Точно посередине - вы уже пробовали. А вот если разрезать ленту на расстоянии 1/3 ее ширины от края, то получаются два кольца - но! - одно большое и сцепленное с ним маленькое. Если же разрезать еще и маленькое кольцо вдоль посередине, то у вас окажется весьма "затейливое" переплетение двух колец - одинаковых по размеру, но разных по ширине. Чудеса?.. Попробуйте сами!

Итак, наши исследователи готовы? Какие значения вы получили? Найдём среднее арифметическое ваших результатов                                            

Первым ввел обозначение отношения длины окружности к диаметру современным символом π английский математик Джонсон в 1706 г. В качестве символа он взял первую букву греческого слова «периферия», что в переводе означает «окружность».

П это бесконечная дробь, Точное значение π  неизвестно и сейчас.

 Но современные машины могут определить до миллиона знаков после запятой.

П=3,1415926…

В дальнейшей работе мы будем использовать значение П =3,14

И так, теперь мы можем узнать, сколько сантиметров металлической пластины потребуется, для того чтобы обить данное колесо.

Дано: R = 27 см,  3,14.

Найти: С.

Решение. С = 2R;   С = 2 · 3,14 · 27 = 169,56(см).

Ответ: 169,56см.

ИТОГ. Исследование проведено. На уроке кроме исследовательской работы удачно использовалась работа в парах. Сотрудничество и взаимопомощь  принесли  желаемый  результат. Проблема решена.

Имея успех в небольших исследованиях на уроках, некоторые ребята вовлекаются в более серьёзные исследования, требующие много времени.

Вывод:

Сегодня я попыталась показать вам, что создание проблемных ситуаций на уроках  самым естественным образом развивает у школьников творческую активность. Нельзя заставлять ребёнка слепо штудировать предмет в погоне за общей успеваемостью. Необходимо давать ему  возможность экспериментировать и не бояться ошибок, воспитывать у учащихся смелость быть не согласным с учителем. Всякий раз при разрешении проблемной ситуации я с удовольствием наблюдаю, как ребята не только усваивают новое для себя, но и переживают этот процесс как «открытие» ещё чего-то неизвестного: кто сдержанно, а кто с нетерпением и  восторгом. А мне на каждом уроке приходится думать о том, как ободрить их, заставить поверить в свои силы, снова увидеть горящие глаза. Именно это заставляет меня искать что-то новое, всегда быть в поиске.