
Урок по теме: Коррекция знаний по теме «Повторение». Ряд натуральных чисел.
Цели:
· образовательные: сформировать у учащихся понятие натуральных чисел, научиться распознавать натуральные числа и приводить примеры, рассмотреть свойства натурального ряда чисел;
· развивающие: развивать мыслительную деятельность, интуицию, мотивацию практической значимости данной темы, культуру математической речи;
· воспитательные: продолжить формирование навыков контроля и самоконтроля учащихся, коммуникативных навыков, культуры умственного труда, эстетических навыков оформления записи на доске и в тетради, усидчивость.
Ход урока:
1. Организационный момент. Приветствие учеников.
2. Мотивация урока.
Кто сказал, что математика скучна,
Что она сложна, суха, тосклива?
В этом вы не правы, господа,
Знайте: математика – красива!
Вам приятно жить в опрятном доме,
Где у каждой вещи место есть?
Математика создать порядок может,
И за это ей хвала и честь!
Сколько в ней самой изящных линий,
Мощных формул, строгих теорем,
Тот не назовет её красивой,
кто с наукой не знаком совсем!
Математика – самая древняя из наук, она была и остается необходимой людям. Слово «математика» греческого происхождения. Оно обозначает «наука», «размышление». Математику уже затем учить надо, что она ум в порядок приводит. М.В. Ломоносов.
Число- одно из самых основных понятий математики. Оно разрешает выражать результаты счета или измерений. Сколько карандашей в пенале? Сколько листов в тетради? Чтобы ответить на эти вопросы необходимо уметь считать, а сделать это можно только при помощи чисел. Сегодня мы и поговорим о натуральных числах, которые используются при счете.
3. Актуализация опорных знаний.
Работа над типичными ошибками, допущенными в к/р.
Устный счет(задания в презентации).
4. Изучение нового материала
- Сколько тебе лет?
- Сколько цветов в радуги?
- Сколько предметов ты будешь изучать в этом учебном году?
После получения ответов учитель напоминает ученикам, что названные числа имеют нечто общее - используются для счета.
Страна Натуральных Чисел – это необыкновенная, замечательная страна, в которой живут, трудятся и властвуют натуральные числа. Интерес к изучению чисел возник у людей в глубокой древности, и вызван он был не только практической необходимостью. Привлекала необычайная магическая сила Числа, которым можно выразить количество любых предметов. Натуральными числами обозначались и боги, и космос, и люди, и их взаимоотношения. Поэтому изучению натуральных чисел уделялось особое почтительное внимание. «Фундаментом математических знаний, от которого зависит прочность дальнейшего математического образования, является знание принципа образования натурального ряда чисел», – говорил выдающийся педагог В.А.Сухомлинский.
1. Наименьшим натуральным числом является 1.
2. Наибольшего натурального числа не существует.
3. Все натуральные числа, записанные в порядке роста, образуют ряд натуральных чисел.
Например: 1, 2, 3, 4, 5, ... - ряд натуральных чисел; 1, 2, 4, 5 - не является рядом натуральных чисел.
Просмотр презентации. Работа с учебником.
5. Закрепление нового материала.
Устно:
· Приведите примеры использования натуральных чисел для счета:
а) одушевленных предметов;
б) неодушевленных предметов.
· Приведите примеры использования натуральных чисел для измерения:
а) массы; б) расстояния; в) времени.
· С помощью учебного пособия назовите пропущенные в тексте натуральные числа:
а) «В учебнике по математике для 5 класса __ страниц, __ глав, __ пунктов»;
· Назовите числа, которые не являются натуральными.
· Продолжите счет до пятого числа: 815, 816, …
· Продолжите счет до пятого числа: сто первый, сто второй, …
· Назовите порядковый номер:
а) буквы «Е» в русском алфавите,
б) буквы «Е» в записи слова «МАТЕМАТИКА»,
в) месяца «СЕНТЯБРЬ» в последовательности месяцев календарного года,
г) своей фамилии в списке учащихся в классном журнале.
· Какое число в натуральном ряду идет за числом 78?
· Какое число в натуральном ряду предшествует числу 45?
· Сколько чисел стоит в натуральном ряду между числами 5 и 54?
Решить №________________(у доски и в тетрадях)
6. Физкультминутка.
Рисуй глазами треугольник.
Теперь его переверни.
И вновь глазами по периметру веди.
Рисуй восьмерку вертикально.
Ты головою не крути,
А лишь глазами осторожно
Ты вдоль по линиям води.
И на бочок ее клади.
Теперь веди горизонтально,
И в центре ты остановись.
Глазки крепко закрываем,
Дружно до пяти считаем.
Глаза открываем мы, наконец.
Зарядка окончилась. Ты молодец!
7. Самостоятельная работа.
Решить №____
8. Итоги урока. Д/з. Рефлексия.
Ответьте на вопросы:
· Какие знания понадобились тебе на уроке?
· Что называется рядом натуральных чисел
· Является ли нуль числом натуральным?
· Ряд натуральных чисел имеет конечное число?
· Какое вы знаете наименьшее двухзначное число?
· Какое вы знаете наибольшее трехзначное число?
· Что понравилось на уроке больше всего?
· Какими словами можешь выразить свое настроение как результат работы на уроке?
· Д/з: выучить____, вопросы с.___, решить №___________
Составить синквейн к слову «Математика». Работа в группах.
Математика
Интересная, великая
Думать, спорить, доказывать
В порядок ум приводит
Гениально!
Урок по теме: Цифры. Десятичная запись числа
Цели:
· образовательные: формировать представление о роли разрядов и классов в записи натурального числа и навык представления натурального числа в виде суммы разрядных слагаемых, познакомить с нумерацией разрядов и их названиями, а также с названиями классов в записи натурального числа, создать условия для совершенствования навыка чтения и записи натуральных чисел.
· развивающие: развивать мыслительную деятельность, интуицию, мотивацию практической значимости данной темы, культуру математической речи;
· воспитательные: продолжить формирование навыков контроля и самоконтроля учащихся, коммуникативных навыков, культуры умственного труда, эстетических навыков оформления записи на доске и в тетради, усидчивость.
Ход урока:
1. Организационный момент. Приветствие учеников.
2. Мотивация урока.
Математику уже затем учить надо, что она ум в порядок приводит. М.В. Ломоносов.
Число - одно из самых основных понятий математики. Оно разрешает выражать результаты счета или измерений. Сколько карандашей в пенале? Сколько листов в тетради? Чтобы ответить на эти вопросы необходимо уметь считать, а сделать это можно только при помощи чисел. Сегодня мы и поговорим о натуральных числах, которые используются при счете.
3. Актуализация опорных знаний. Проверка Д\з.
Беседа с классом.
1. Как называются числа, которые мы использовали повторяя таблицу умножения?
2. Для чего используются натуральные числа?
3. Назовите самое маленькое натуральное число?
4. Что мы используем в записи натуральных чисел?
5. Сколько цифр мы используем, чтобы записать любое натуральное число?
6. Зависит ли значение цифры от ее места в записи числа?
7. Какой цифрой обозначают отсутствие разряда?
8. Относят ли нуль к натуральным числам?
4. Изучение нового материала. Просмотр презентации
Мы уже знаем, что натуральные числа – это числа, которые используют при счёте. Любое натуральное число можно записать с помощью десяти цифр.
Практическая деятельность потребовала ни только умение считать, но и умение записывать числа. В старину для записи натуральных чисел использовались и особые рисунки, и черточки, и буквы.
В настоящее время принята десятичная система счисления, в которой числа записывают при помощи десяти знаков: 0,1,2,3,4,5,6,7,8,9. Эти знаки называют цифрами.
При этом одна и та же цифра имеет различное значение в зависимости от места, где она расположена в записи числа.
Пример: в записи числа 777 первая справа цифра 7-семь единиц, вторая- семь десятков, третья-7 сотен.
Поэтому десятичную систему счисления называют позиционной.
Важную роль в десятичной системе счисления играет число 10.
Десять единиц называют десятком, десять десятков-сотней,10 сотен тысячей.
Натуральные числа, записанные одной цифрой, называют однозначными, а записанные несколькими цифрами-многозначными.
Примеры.
Первая цифра справа в десятичной записи числа называется цифрой первого разряда, вторая цифрой второго разряда и т.д.
Первая цифра слева в записи натурального числа называют цифрой высшего разряда. она всегда отлична от нуля.
Чтобы прочитать многозначное число цифры в его записи разбивают справа на лево на группы по три цифры в каждой. Эти группы называются классами.
Первый класс справа называют классом единиц, второй класс тысяч, третий миллионов и т.д.
Пример:
148 951 784 296
148 миллиардов 951 миллион 784 тысячи 298
!Каждое натуральное число можно записать в виде суммы разрядных слагаемых.
Пример: 99 состоит из 9 десятков и 9 единиц 99=9*10+9*1
3278 состоит 3 тысяч 2 сотен 7 десятков и 8 единиц 3278=3*1000+2*100+7*10+8*1
Способ записи чисел, которым мы пользуемся, называется десятичной позиционной системой счисления. Значение цифры зависит от ее места (позиции) в записи числа.
Кроме натуральных чисел мы знаем еще число 0 (нуль). При счёте число 0 (нуль) не используется, а означает оно «ни одного». Поэтому число 0 не является натуральным!
Занимательная пауза
А может, вы знаете, как появились натуральные числа?
Эти числа появились в глубокой древности, когда людям понадобилось вести счет окружающих предметов, плодов, животных.
Само слово «натуральный» означает в русском языке то же самое что «естественный».
А слово natura – по латински – есть природа.
Арабы принесли к нам способ записи чисел, которыми мы пользуемся из Индии. Однако в самой Индии до последнего времени цифры выглядели совсем не так, как в Европе.
В Древней Греции поступали очень просто: греки не стали выдумывать специальные знаки для цифр, а использовали буквы.
1-обозначалиА,2-Б,3-Г.
Греческий алфавит похож на русский в этом нет ничего удивительного, так как славянский алфавит создан на основе греческого монахами Кириллом и Мефодием.
Сегодня мы познакомимся с римскими цифрами.
I, II, III, V, VI, C, D , M (работа с учебником с.______)
С помощью этих цифр с применением сложения и вычитания в римской нумерации записывают и другие числа.
В справочный материал: если меньшая цифра стоит после большей, то она прибавляется к большей, если меньшая цифра стоит перед большей, то она вычитается из большей.
Великим достижением математиков было изобретение десятичной системы записи чисел, хорошо нам известной в ней используют только 10 цифр их называют арабскими.
5. Закрепление нового материала.
Ответить на
вопросы с._____
Решить №________________(у доски и в тетрадях)
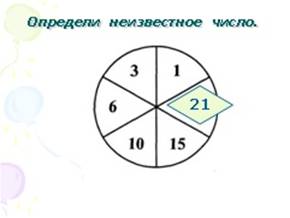
Логическое задание:
6. Физкультминутка.
Игра «Цифра – число». Правила игры: учитель называет числа и цифры. Дети встают, если называется число, садятся - при названии цифры.
Все поднялись.
Встали в ряд.
Изучали мы разряд.
А сейчас мы отдохнем,
Руки, ноги разомнём.
Потянулись, улыбнулись.
Все нагнулись, разогнулись.
Подтянули плечики.
Прыгаем, кузнечики.
И в ладоши три хлопка.
Головою три кивка.
Мы глазами поморгаем.
Физкультуру уважаем.
Это бодрости заряд!
Шшш…(успокаиваем детей, показываем, что можно
сесть)
Изучаем мы разряд…
7. Самостоятельная работа.
Математический диктант:
1. Запишите наименьшее двузначное число(10)
2. Запишите наименьшее трехзначное число, в котором все цифры различны. (102)
3. Запишите наибольшее трехзначное число (999)
4. Запишите двузначное число, в котором число десятков в семь раз больше цифры его единиц (включаем логику: чтобы выполнялось условие подходит только 71).
5. Запишите двузначное число, в котором число единиц равно наибольшему из однозначных чисел, а число десятков на три меньше числа единиц. (69)
6. Сумма цифр двузначного числа равна наибольшему из однозначных чисел, а число десятков на два меньше этой суммы. Запишите это число. (72)
7. Число, предшествующее 76(75)
8. Число, следующее за 99(100)
9. Число, расположенное между 18 и 20(19)
10. В одних сутках… часов(24)
11. В 1 км…дм(100)
Затем – самопроверка.
8. Итоги урока. Д/з. Рефлексия «Лестница успеха».
Д/з: выучить п.___, решить №___________/
Дополнительное задание: сочинить сказку о цифрах и числах (можно с
иллюстрациями)
Завершим урок на лирической нотке. Ведь
как сказал А.С. Пушкин: «Вдохновение нужно в математики, как и в поэзии».
Наука математики прекрасна,
С ней небоскребы строить не опасно!
С ней можно строить мачты и мосты,
И создавать огромные ракеты,
С ней мы осуществим свои мечты:
Одни займут в механике посты,
Другие полетят к иным планетам.
Одни проникнут в недра тайн земных,
Возьмут другие руль комбайна в руки.
У нас путей не может быть других,
Как лишь к труду, к передовой науке!
Всем, кто в учебе видит свет,
От математики - привет!
Урок: «Отрезок. Длина отрезка»
Цель урока:
· Образовательные задачи: содействовать развитию у учащихся навыков построения отрезков, находить их длину, умения их обозначать и читать.
· Развивающие задачи: развивать творческую сторону мыслительной деятельности; создавать условия для проявления познавательной деятельности учащихся; содействовать развитию математического кругозора, мышления, речи, памяти, внимания.
· Воспитательные: способствовать выявлению и раскрытию способностей учащихся; воспитывать познавательную активность учащихся; прививать самостоятельность и любознательность.
Ход урока
1.Организационный момент.
2. Мотивация урока.
Ребята. Сегодня у нас необычный урок. Мы начнём знакомство с одним из разделов математики, который изучает фигуры и их свойства. Это – геометрия – одна из наиболее древних наук. Появление и развитие геометрических знаний связано с практической деятельностью людей: земледелие, строительство, желание украсить свой быт и одежду....Первые геометрические факты найдены в вавилонских клинописных таблицах и египетских папируса. Неоценимый вклад в развитие геометрии был внесен древнегреческими математиками. “Не обучавшийся геометрии пусть не входит в эту дверь”. Такая надпись была сделана над дверью дома, в котором Платон занимался со своими учениками. Первым, кто начал получать новые геометрические факты при помощи рассуждений, был древнегреческий математик Фалес (VI век до н.э.). Наибольшее влияние на все последующее развитие геометрии оказали труды греческого ученого Евклида, жившего в Александрии в III веке до н.э. Сочинение Евклида "Начала" почти 2 тысячи лет служило основной книгой, по которой изучали геометрию. В настоящее время геометрия – это целая наука, занимающаяся изучением геометрических фигур. В ней изучаются формы, размеры, взаимное расположение предметов независимо от их других свойств: массы, цвета, плотности, вкуса и т. п.
3. Актуализация опорных знаний. Проверка д/з.
Устный счет
«Математическая разминка»(светофор)
1. Если математическое утверждение верно, то показывается карточка зеленого цвета. Если нет – то красного.
а) В одном сантиметре 10 дециметров.
б) Прямая не имеет концов.
в) В записи числа «Одна тысяча» три нуля.
г) Для записи натуральных чисел употребляются одиннадцать цифр.
д) Последующее натуральное число отличается от предыдущего на единицу.
е) Цифра «нуль» означает отсутствие разряда?
ж) Две точки можно соединить двумя отрезками? (Если у вас нет ответа на этот вопрос, то наберитесь терпения и подождите некоторое время. Ответ на него мы узнаем сегодня).
4. Изучение нового материала. Просмотр презентации.
Откройте тетради, запишите число, классная работа и тему сегодняшнего урока “Отрезок. Длина отрезка”
Точка – основное геометрическое понятие. В переводе с латинского языка слово точка – результат мгновенного касания, укол.
Задание 1.
Отметить в тетради точку. Обозначить её. Обозначить – значит дать имя. Имя точки – большая буква латинского алфавита
Задание 2.
С помощью линейки провести в тетради линию. В переводе с латинского языка слово линия – льняная нить. На линии отметьте точки A, B
Часть линии, заключённая между двумя точками, называется отрезком. Обозначается отрезок двумя точками, которые являются его концами.
Задание 3.
Начертить в тетради отрезки AB, CD, NM, KL.
Каждый из этих отрезков имеет длину. Как сравнить длины отрезков? Нужно их измерить. Для этого можно воспользоваться измерителем
Задание 4.
С помощью какого инструмента можно построить и измерить длину отрезка?
С помощью линейки. Выполнить №58.
Геометрическая пауза.
Сравнить:

Можно измерять шагами.
Можно измерять локтями.
И линейкою, и веткой,
Сантиметром и рулеткой.
Папа говорил мне так:
- Пусть нашей мерой будет шаг.
Шаг муравьишки - миллиметр.
Шаг у людей - примерно метр...
-А километр? - воскликнул я.
Отец сказал: - Ну, что ж,
Стань великаном и, шутя,
На километр шагнёшь.
Об измерительных приборах и единицах измерения длин
Задание 5.
Измерьте длины отрезков №52. Назови больший.
Длину отрезка АВ называют также расстоянием между точками А и В.
Для измерения длин применяют различные единицы длины (демонстрация слайда № 11).
Миллиметр, сантиметр, дециметр, метр, километр.
1 см = 10 мм, 1 дм =10 см, 1 м = 10 дм = 100 см, 1 км = 1000 м.
Задание 6.
Выразите в сантиметрах: 8 дм 6 см; 40 мм; 3 м 5 см.
Выразите в метрах: 3 км 300м; 7 км 90 м.
Меры длины, которые мы используем сейчас, были не всегда. На Руси, в старину, длину измеряли с помощью частей тела.
5. Физкультминутка.
Вы на славу потрудились,
И немного утомились,
Дружно скажем нам пора,
Сделать важные дела.
1. Нарисуйте правой рукой четыре квадрата.
2. Нарисуйте левой рукой три треугольника.
3. Нарисуйте кончиком носа букву В два раза.
6. Закрепление нового материала.
Ответить на
вопросы с._____
Выполнить № 58
7. Самостоятельная работа.
Постарайтесь выполнить следующие задания
Запишите в тетрадь ответы на вопросы:
· Какие точки лежат на отрезке AB?
· Какие точки не лежат на отрезке AB?
· Какие точки лежат между точками А и О?
· Какие точки лежат между точками В и M?
· Сколько отрезков на рисунке?
Проверьте правильность выполнения задания
8. Итоги урока.
Наше занятие подходит концу. Пожалуйста, поделитесь с нами своими мыслями о сегодняшнем занятии (хотите одним предложением).
Вам для этого помогут слова:
Сегодня вы познакомились с понятием точка, отрезок –…(отвечают ученики),
Узнали, как и с помощью чего можно измерить длину отрезка – …(отвечают ученики),
Применили полученные знания на практике.
Д/З: выучить п.2, решить №53,60.
В качестве домашнего задания предлагаю вам творческую работу. Сделайте сообщение или презентацию на одну из тем: “Старинные русские меры длины”, “Мера длины в различных странах”
Тема урока: « Ломаная».
Цели:
1.Образовательная: обучение учащихся понятию ломаной, как фигуры соединенных под углом отрезков; понятием звено; замкнутая, незамкнутая ломаная, нахождение ее длины; формирование умения строить ломаные линии.
2.Развивающая: развивать логическое мышление, пространственное воображение, внимание, память, фантазию.
3.Воспитательная: воспитывать чувство взаимовыручки, товарищества, внимательного отношения друг друга при работе на уроке, умение слушать ответы учащихся и объяснение учителя.
ХОД УРОКА.
I. Орг. момент. Эмоциональный настрой на урок.
Проверь дружок
Ты готов начать урок?
Все ль на месте,
Все ль в порядке-
Ручка, книжка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
Оформление в тетради: число, тема
Мотивация урока. Слово учителя: Сегодня на уроке вас ожидает много интересных заданий, новых открытий; а помощниками будут вам: внимание, находчивость, смекалка.
II. Актуализация знаний учащихся
Викторина, работа в командах.
Математический диктант.
1) 4 миллиона 23 тысячи 150;
2) 2 тысячи 35;
3) сколько чисел между 15 и 27;
4) в сантиметрах: 3 м 9 см;
5) в сантиметрах: 4 дм 7 см;
6) в метрах и километрах: 1350 м;
7) наибольшее двузначное число;
8) число, следующее за 998;
9) число цифр;
10) длина отрезка в 2 раза большая 13 см;
11) длина отрезка на 6дм меньшая 15 дм;
12) что больше 1км или 100 дм?
III. Изучение нового материала.
1) Работа с магнитными палочками: - Посмотрите что у меня в руках?
-Что оно вам напоминает? (ломаная)
-Посмотрите и определите, какая у меня ломаная? (не замкнутая)
-А теперь? (замкнутая)
-Теперь самостоятельно постройте ломаную.
-Из скольких частей она состоит?
-Как называется каждая часть ломаной?
-Найдите и покажите вершины ломаной?
-Сколько их?
Ломаная - геометрическая фигура состоящая из точек, соединенных отрезками.
Точки называются вершинами ломаной а отрезки - звеньями ломаной.
Длиной ломаной называется сумма длин ее звеньев.
Виды ломаной:
ü замкнутая ломаная - такая ломаная, если
конец ее последнего звена совпадает с началом первого звена.
ü Незамкнутая (простая), если ее звенья не пересекаются.
IV. Закрепление материала
А теперь давайте закрепим наши знания, умения и навыки практически, при этом мы будем использовать опорный конспект.
1) Задание по опорным конспектам;
Делаем рисунок ломаной, обозначаем прописными латинскими буквами вершины, показываем звенья
2) Работа с учебником;
-Что вы видите на рисунках?(ломаные)
-Какая из ломаных имеет больше звеньев? Меньше звеньев?
-Какая из ломаных самая длинная?
-Как доказать? (нужно измерить длину)
-А как измерить длину ломаной? (измерить длину каждого звена и результаты сложить)
-Делаем запись в тетрадь:
АВСD=АВ+ВС+СD
-Какие виды ломаной вы видите? (замкнутые и незамкнутые)
3) Физ.минутка ;
Из-за парт мы выйдем дружно,
Но шуметь совсем не нужно,
Встали прямо, ноги вместе
Поворот кругом, на месте.
Хлопнем пару раз в ладошки
И потопаем немножко.
4) Решение задач;
1. Постройте ломаную в виде буквы русского алфавита, состоящую из двух, трех и более звеньев.
2.Найдите
длину ломанной. Е
А C
 |
В D
3.Построить ломаную АВСDЕК, длина которой равна 36 см и найти ее звено, если соответствующие ее звенья равны: АВ=5см, СD=6 см, DЕ=8 см, ЕК=10 см.
5) Физ.минутка для глаз
6) Самостоятельная работа: решить №_______
V. Обобщение и вывод по работе на уроке
-С чем мы сегодня познакомились? (с ломаными)
-Какие они бывают? (замкнутые и незамкнутые)
-Как найти длину ломаной? (измерить длину каждого звена и результаты сложить)
VI. Подведение итогов
1. выставление оценок;
2. рефлексия
-Сегодня на уроке я узнал…
-Сегодня на уроке я научился…
-Сегодня на уроке мне понравилось…
-Новые знания мне пригодятся…
VII. Домашнее задание
Выучить п._____, решить №______
Окончен урок и выполнен план
Спасибо огромное вам
За то, что упорно и дружно трудились,
И знания точно уж вам пригодились.
Дата_____ Класс________Тема: Прямая. Луч. Отрезок.
Цель:
Образовательные: научить обучающихся различать прямую, луч, отрезок. Познакомить с общепринятыми обозначениями фигур.
Развивающие: развивать мыслительные операции, математические способности, логическое мышление.
Воспитательные: воспитывать ответственность, дружелюбие, умение работать в группе.
Ход урока.
1. Организация начала урока.
Ну-ка, проверь, дружок!
Готов ли ты начать урок?
Всё ль на месте? Всё ль в порядке?
Книжка, ручка и тетрадка…
Проверили? Вот здорово!
К уроку всё готово!
2. Активизация знаний обучающихся. Проверка д/з.
Верным помощником на уроке у нас будет самая маленькая геометрическая фигура Весёлая точка.
Прочитайте числа: 180000509, 300001700, 608600005003
Какое число нужно вписать в последнюю клетку?
+23
|
 |
 |
|
||||||||||
 |
 |
 |
|||||||||||
![]()
![]()
![]()
![]()
![]()
 |
Выразите в дециметрах: 50 см, 230 см, 67 м, 800 м.
Выразите в метрах : 600 см, 30 дм, 2 км, 12000 мм.
3. Мотивация урока. Анаграммы. Просмотр презентации.
Расшифруйте слова: МАЯПРЯ, РЕЗООТК, КАТОЧ, ЧУЛ
-Это слова «прямая», «отрезок», «луч», «нитки», «точка».
-Все ли расшифрованные слова вам знакомы?
-А где вы с ними встречались?
(На уроке математики, а нитки на уроке труда).
-Какое слово лишнее?
(Нитки. Они не относятся к уроку математики).
-Но все эти слова сегодня помогут нам сделать открытие.
Сообщение темы и цели урока.
-Рассмотрите фигуры на доске.
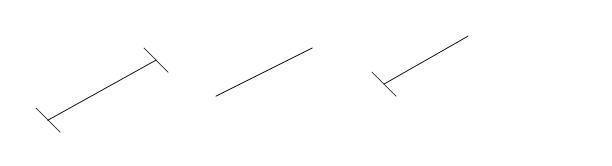
- На какие группу их можно разбить?
(В ходе рассуждения можно разбить на 2 группы- «отрезки» и «прямые»)
-Но возникает проблема: куда можно отнести фигуру
4. Изучение нового материала.
-Сравните фигуру с уже известными нам.
-Что можно сказать?
-Можно ли эту фигуру назвать отрезком? Почему?
-Может её включим в группу прямых? Почему?
-Тогда давайте выполним одну операцию.
-В руках у меня 2 катушки тесьмы. Мы раздвигаем их в разные стороны.
-Что заметили?
(Это прямая линия, только в воздухе)
-Можно ли её продолжить в обоих направлениях?
-А эту прямую можно изобразить на доске?
(Чертим на доске, а дети в тетради).
 А
А
а
В
Без начала и без края линия прямая,
Хоть 100 лет по ней идти,
Не найдёшь конца пути.
- У людей есть имена, у животных клички.
-А прямую линию можно обозначить одной или двумя буквами.
- Предложите имя прямой линии.
Вывод: У прямой линии нет ни начала, ни конца.
Мы можем изобразить только маленькую часть прямой линии. Её можно продолжить.
-Наша Весёлая Точка поможет нам ещё поработать с прямой линией.
-Поставьте точку, проведите через неё прямую линию.
-Можно ещё провести линию через эту точку?
-Сколько прямых линий можно провести через одну точку?
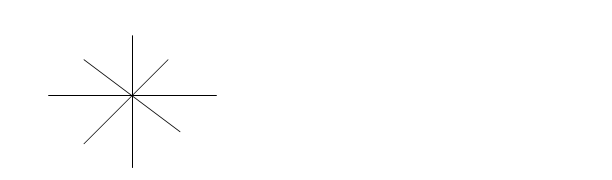
-Поставьте 2 точки. Через эти точки проведите прямую линию. Можно ли ещё провести?
А К
![]()
Вывод: Через одну точку можно провести сколько угодно линий, а через 2 точки – только одну.
-Теперь нашу прямую линию я разрежу.
(К месту разреза прикреплю Солнышко).
-Что получилось?
-На что похоже?
(Луч солнца)
О новой фигуре разносится весть
Конца пусть в ней нет,
Начало-то есть!
И солнце, тихонько взойдя из-за туч,
Сказало: «Друзья, назовём его луч!»
-Можно ли продолжить луч со стороны разреза?
(Нет, мешает круг и нечего продолжать)
-А с другой стороны?
(Можно продолжить до бесконечности)
СРАВНИТЕ: Луч и прямую линию.
(Прямую линию можно продолжить в обе стороны, а луч только в одну. Луч имеет начало)
-Начертите луч на доске и в тетради
-Луч обозначается двумя прописными буквами.
На первом месте всегда указывается начало луча.
-Поставьте точку, проведите луч, а ещё можно провести из этой точки, ещё…
-Какие лучи бывают?
(Солнечные лучи, лампа, фонарик и т.д.)
Вывод: Луч – это прямая линия, ограниченная с одной стороны. Из одной точки можно провести бесконечное множество лучей.
-У луча я отрезаю ту часть, которую можно продолжить…и прикреплю ещё одну точку.
-Что получилось?
(Отрезок)
-Линия, ограниченная с двух сторон.
СРАВНИТЕ: Луч и отрезок.
-У луча есть только начало, а отрезок имеет и начало и конец.
-Можно отрезок изобразить на доске и в тетради?
Точки две поставь в тетради,
Чтоб потом нарисовать между ними
Под линеечку – прямую,
И окажется, мой друг,
Что отрезок вышел вдруг,
Только точкам имена дать ты
Не забудь!
-Отрезок обозначается двумя буквами, но порядок при чтении и записи не имеет значения.
Вывод: Отрезок – это прямая, ограниченная с двух сторон.
-Что нового узнали об этих фигурах?
Вывод: Луч, прямая и отрезок – это геометрические фигуры.
Работа с учебником с.18-20.
5. Физкультминутка.
Раз, два, три, четыре, пять,-
Все умеем мы считать,
Отдыхать умеем тоже,
Руки за спину заложим,
Голову поднимем выше
И легко – легко подышим,
Раз – подняться, потянуться,
Два – согнуться, разогнуться,
Три – в ладоши три хлопка,
На четыре – руки шире,
Пять – руками помахать,
Шесть – за парту тихо сесть.
6. Закрепление изученного материала.
(На доске изображены геометрические фигуры)
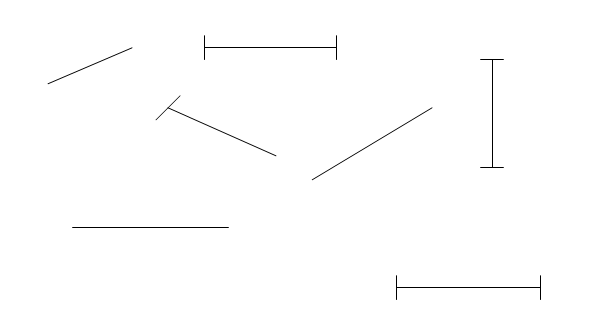
-Найдите отрезок, луч, прямую.
-Обоснуйте свой ответ.
-Можно ли сказать, что они пересекающиеся?
-А могут ли они пересечься?
7. Обучающая самостоятельная работа.
№54 (рис.35), 77(1)
8. Домашнее задание.
На дом вам будет дано следующее задание: п. 2, решить № 74, 42.
В тетради начертить прямую, отрезок, луч.
9. Подведение итогов урока. Рефлексия.
-Соедините названия фигуры с фигурой.
Подберите правильное название.
ОТРЕЗОК ЛУЧ ПРЯМАЯ линия![]()
![]()
![]()
![]()
![]()
ПРЯМАЯ линия – не имеет начала и конца; можно обозначать одной или двумя буквами; через одну точку можно провести сколько угодно линий, через две – только одну.
ЛУЧ- прямая, ограниченная с одной стороны; продолжать можно только в одну сторону; из одной точки можно провести сколько угодно лучей; лучи бывают разные.
ОТРЕЗОК – прямая линия, ограниченная с двух сторон; на одной прямой может быть несколько отрезков; любую прямую можно превратить в отрезок.
Нарисовать свое настроение в виде солнышка в конце урока. «Лестница успеха».
-Вы сегодня дружно и творчески работали (Оценивается работа обучающихся).
-Спасибо всем! Урок окончен.
Тема урока: «Шкала. Координатный луч»
Цели урока:
1. Познакомить с понятиями: единичный отрезок, координата, координатный луч; научить записывать координаты точек, по заданным координатам находить положение точки на координатном луче.
2.Развивать умения анализировать, сравнивать, обобщать; внимание, память, воображение и мышление; математическую культуру речи и письма
3. Воспитывать доброжелательные отношения среди обучающихся в работе парами, чувство уверенности в себе, умение работать в коллективе.
Ход урока.
1. Орг. момент. Настрой на урок.
2. Мотивация урока.
Я рада вас видеть на уроке математики и начать мне его хочется со слов французского философа Ж.Ж. Руссо (1712-1778гг.): "Вы - талантливые дети! Когда-нибудь вы сами приятно поразитесь, какие вы умные, как много и хорошо умеете, если будете постоянно работать над собой, ставить новые цели и стремиться к их достижению…” Я желаю вам уже сегодня на уроке убедиться в этих словах, ведь вас ждёт открытие новых знаний при изучении нового материала.
3. Актуализация опорных знаний. Проверка д/з.
Устный счет: повторяем таблицу умножения в парах.
Решить пример № 435(1), задачу на построение № 63.
Математический диктант на знание теоретического материала по теме «Отрезок, прямая, луч»
4. Изучение нового материала.
Открыли тетради, построили луч, расположенный горизонтально, отметили начало луча точкой О, внизу подписали число 0, – эту точку О назовём точкой отсчёта, отсюда мы начнём движение …(вправо), пройдя какое – то расстояние мы попали в точку А , внизу видим подписанное число 1. Какое же расстояние мы можем пройти до данного числа?
Отрезок ОА называется единичным отрезком,
Подумайте и попробуйте теперь сами поставить числа 2, 3, 4, а над ними подпишите точки В, С, …Числа – 0, 1, 2, 3,… называют координатами точек О, А, В, С, …. Это число, показывающее местоположение точки на числовом луче, т. е. “адрес” точки.
Как мы назовём луч, о котором идёт речь? Координатный луч.
Найдите в учебнике п.3 определение координатного луча. Работа в парах с учебником: с.25. История слова «шкала». Шкалы вокруг нас: с.26, 27
5. Физминутка. Зарядка «Геометрическая»
6. Закрепление нового материала. Решить устно №80, 81, 83, у доски № 84
7. Самостоятельная работа. Выполнить тестовые задания.
8.
|
Вариант 1 |
Вариант 2 |
|
№1. На каком рисунке правильно изображены точки С(7) и В(3)?
№2. Укажите координаты точек А, В и С.
1) А(3),В(6),С(9) 2) А(2),В(6),С(8) 3) А(9),В(7),С(3) 4) А(3),В(7),С(9) №3.Решите уравнение: х+223 = 1308 1) 1805; 2) 1085; 3) 1531; 4) 3056. № 4. Число: тридцать миллиардов двести тысяч восемь - это: 1) 300 200 008; 2) 30 000 200 080; 3) 30 000 200 008; 4) 30 000 020 008. №5. Выразите в сантиметрах 2км 5м 4см.
№6. В школе 542 учащихся. Среди них - 269 мальчиков. Кого в школе больше мальчиков или девочек? На сколько?
№7.Сколько и каких различных трехзначных чисел можно составить с помощью цифр 7 и 3?
|
№1. На каком рисунке правильно изображены точки С(8) и В(4)?
№2. Укажите координаты точек А, В и С.
1) А(3),В(6),С(9) 2) А(2),В(7),С(9) 3) А(9),В(7),С(3) 4) А(3),В(7),С(9) №3.Решите уравнение: с-127=353 1) 480; 2) 226; 3) 408; 4) 155. №4. Число: триста семьдесят миллиардов шестьдесят миллионов восемьсот тысяч четыре - это: 1) 307 060 080 004; 2) 370 600 080 004; 3) 370 060 800 040; 4) 370 060 800 004. №5. Выразите в граммах Зт 2кг 72г. №6. В саду 142 дерева, из которых 61 - яблони, а остальные - груши. Каких деревьев в саду больше и на сколько? №7. Сколько и каких различных трехзначных чисел можно составить с помощью цифр 5 и 1?
|
9. Итоги урока. Оценивание. Рефлексия «Шкала самооценки».
Что понравилось на уроке?
- Что запомнилось?
- Что получилось?
- В чем затруднился?
Выучить п.3, решить №85, 89, 99*.
Тема: Сравнение натуральных чисел.
Цели:
- учить сравнивать натуральные числа; многозначные натуральные числа; сравнивать величины;
- развивать аналитические способности, логическое мышление, развивать умение анализировать и оценивать свою работу и ответы одноклассников;
- воспитывать доброжелательное отношение к окружающим людям, взаимопонимание, взаимную ответственность, умение осуществлять взаимопомощь.
Ход урока.
1. Организационный этап
Учитель приветствует учащихся, проверяет их готовность к уроку; Добрый день, дорогие ребята! Улыбнитесь друг другу, пожелай те хорошего настроения! С каким настроением вы пришли на урок математики?
Математику, друзья,
Не любить никак нельзя.
Очень строгая наука,
Очень точная наука,
Интересная наука –
Это математика!
2 . Актуализация знаний. Проверка д/з.
1. Новые знания нам будет очень трудно осваивать без умения быстро и верно считать, поэтому, как всегда, начнем урок с устного счета (работа в парах).
Возьмитесь за руки, покажите, что вы пара. Проверка таблицы умножения.
С каким понятием мы познакомились на прошлом уроке? Что называется координатным лучом? Задание на построение точек с заданными координатами на координатном луче: № 92, 93.
Как найти расстояние между точками на координатном луче? №94, 95-с/р.
Работа в парах с учебником: История слова «шкала». Шкалы вокруг нас: с.26, 27
Устно выполнить задания №80, 81, 86.
3. Постановка целей, задач урока, мотивационная деятельность учащихся.
1) Какие числа применяются для счета предметов?
2) Сколько цифр и какие используют для записи натуральных чисел? Назовите первые десять натуральных чисел.
3) Назовите по порядку первые четыре класса в записи натуральных чисел.
4) Как читают многозначные числа?
5) Сколькими отрезками можно соединить точки М и Р? Как называются точки М и Р?
6) Как сравнивают два отрезка?
7) Назвать единицы измерения длины.
8) Есть ли края у плоскости? Имеет ли прямая концы? Сколько прямых можно провести через две точки?
9) На сколько лучей разбивает прямую АВ точка К? Назвать эти лучи. Какие лучи называются дополнительными?
10) Чем отличается координатный луч от луча?
- Для чего нужно уметь сравнивать числа? (ответы учащихся) Какие величины мы умеем сравнивать?
- Цель нашего урока: Вывести правило сравнения чисел и научиться его применять.
4. Первичное усвоение новых знаний.
Из двух однозначных натуральных чисел, записанных в строку по указанному образцу, меньше то, которое находится левее, и больше то, которое находится правее.
Например, число 1 меньше числа 2, число 1 меньше, чем число 7, число 6 меньше любого из чисел 7, 8 и 9. А 2 больше 1; 7 больше, чем 4; 6 больше любого из чисел 1, 2, 3, 4 и 5.
Для краткой записи используют знак меньше «<» и знак больше «>», которые располагают между сравниваемыми числами. Например, запись 3<7 означает, что 3 меньше, чем 7, а запись 8>5 означает, что 8 больше, чем 5.
Запись, в которой присутствуют два натуральных числа и один из знаков «<» или «>» между этими числами, называют неравенством. Неравенства, как и равенства, бывают верными и неверными.
Пример верного неравенства 2<9, а неравенство 5>8 - неверное.
- Сравнение однозначного и многозначного натуральных чисел.
Примем за правило, что любое однозначное натуральное число меньше любого многозначного натурального числа.
В качестве примера запишем несколько верных неравенств:
9<10, 4<42, 300>3, 3043>7. А вот неравенства 6>11, 543<5 и 9>1000 - неверные.
- Осталось разобраться со сравнением многозначных чисел.
Для начала разберемся со сравнением двух неравных многозначных натуральных чисел, записи которых состоят из равного количества знаков. Прежде чем продолжить чтение, рекомендуем освежить в памяти информацию из раздела разряды натурального числа, значение разряда.
Сравнение таких чисел проводится поразрядно слева направо до нахождения неравных значений разрядов. Меньшим (большим) будем считать то число, у которого значение соответствующего разряда меньше (больше).
Для применения озвученного правила нам понадобиться принять еще одну условность: будем считать, что число 0 меньше любого натурального числа, и что нуль равен нулю (напомним, что число 0 не относится к натуральным числам).
Пример: Сравните два двузначных числа: 35 и 65
Очевидно, данные натуральные числа не равны и их записи состоят из двух знаков. Сравниваем значения разряда десятков, в результате имеем неравенство 3<6, следовательно, 35<65.
Пример: Сравните натуральные числа 302 и 307.
Очевидно, данные натуральные числа не равны и они оба трехзначные. Сначала сравниваем значения разряда сотен. Имеем равенство 3=3, поэтому переходим к сравнению значений разряда десятков. Опять имеем равенство 0=0, поэтому переходим к сравнению значений разряда единиц. Теперь имеем неравенство 2<7, из которого делаем вывод, что 302<307.
Осталось разобраться со сравнением двух многозначных натуральных чисел, записи которых состоят из неравного количества знаков.
В этих случаях, меньшим (большим) будем считать то число, запись которого состоит из меньшего (большего) количества знаков.
Пример: Сравните многозначные натуральные числа 40392 и 92248812.
Запись числа 40392 состоит из 5 знаков, а запись числа 92248812 – из 8 знаков. Так как 5<8, то число 40392 меньше, чем число 92248812.
4. Первичное усвоение новых знаний.
Учимся читать числовое неравенство: 108, 109, 110 устно
Учимся писать числовое неравенство: №116, 117 письменно, 122.
Сравнение чисел на координатном луче: №118, 124 у доски.
5. Физминутка для рук.
6. Самостоятельная работа:
Разгадав анаграмму, вы узнаете следующее задание: ШЕРИ ЧАДУЗА
Решить № 125.
7. Подведение итогов урока. Д/з. итоги урока.
Д/з: выучить п.4, решить № 119, 123, 130.
-Какую задачу мы ставили на уроке?
-Удалось решить нам поставленную задачу?
-Что еще нужно сделать?
-Где можно применить новое знание?
-Что на уроке у вас хорошо получалось?
-Над чем еще нужно поработать?
Тема: «Округление натуральных чисел»
Цели:
1. Орг. Момент. Эмоциональный настрой на урок. Мотивация урока.
– Здравствуйте, ребята! Я рада вас видеть, готовыми к новым открытиям.
– Чему мы научились на прошлом уроке?
2. Актуализация знаний и фиксация затруднения в деятельности. Проверка д/з.
Устно решить № 1, 4, 8, письменно №5(1) с.326.
–Давайте вспомним таблицу разрядов.

Я подготовила вам предложения, из данных предложений найдите числа и постараемся заполнить таблицу:
Задание классу. Выбрать предложения, в
которых речь идет о приближенных значениях.
1. В корзине 15 яблок.
2. Расстояние между Мариуполем и Мангушем равно
25 км.
3. На полке 40 книг.
4. Население города 42000 человек
5. В алфавите 33 буквы.
6. Ближайшее расстояние от Земли до Венеры составляет тридцать восемь миллионов километров
7. Вес индийского слона составляет две тысячи семьсот кг.
Запишем эти числа. Назовите разряды чисел.
Какие из этих чисел характеризуют точную, а какие приближенную величину?
3. Изучение нового материала.
В жизни мы часто имеем дело с приближенными значениями. Иногда просто невозможно точно сосчитать, а иногда не нужно точно знать, сколько чего либо. Например: всего на планете живет около 350 тысяч видов растений; в словаре русского языка Ожегова на титульном листе указано, что в нем около 57000 слов (хотя можно было бы подсчитать их точное количество).
1) Отметьте число 2583 на шкале и округлите его с точностью:
К каким числам ближе лежит 2583?
2580
2590 2583 ![]()
2500
2600 2583 ![]()
2000
3000 2583 ![]()
![]()
![]()
![]()
2) Сформулируйте и обоснуйте свой вариант алгоритма округления чисел.
На доске фиксируются разные варианты ответов и выслушиваются обоснования выполнения задания.
– Какое задание вы должны были выполнить?
– Как вы думаете, почему мы видим с вами разные ответы и услышали разные обоснования выполнения заданий? (У нас нет единого правила округления натуральных чисел.)
– Какую цель мы оставим перед собой? (Вывести правило округления натуральных чисел.)
– Сформулируйте тему урока. (Округление натуральных чисел.)
– Обратимся к первому рисунку, что вы наблюдаете? (Число 2583 стоит на отрезке ближе к числу 2580.)
– Какое число будет приближённым значением числа 2583, если мы будем округлять до десятков? (Число 2580.)
– Проанализируем
получившееся приближённое равенство 2583 ![]() 2580,
что произошло? (Цифра, стоящая в разряде десятков не изменилась, а цифру,
стоящую в разряде единиц заменили 0.)
2580,
что произошло? (Цифра, стоящая в разряде десятков не изменилась, а цифру,
стоящую в разряде единиц заменили 0.)
– Рассмотрим
второй рисунок, какой вывод вы можете сделать? (Так как число расположено на
отрезке ближе к числу 2600, значит, получим равенство: 2583 ![]() 2600.)
2600.)
– Проанализируем
получившееся приближённое равенство 2583 ![]() 2600,
что произошло? (Цифра, стоящая в разряде сотен увеличилась на 1, а цифры,
стоящие в разрядах десятков и единиц заменили 0.)
2600,
что произошло? (Цифра, стоящая в разряде сотен увеличилась на 1, а цифры,
стоящие в разрядах десятков и единиц заменили 0.)
– Почему в первом случае округляемая цифра не изменилась, а во втором случае увеличилась на 1? (Если учащиеся не смогут ответить на вопрос, обратить их внимание на цифру, следующую за округляемой цифрой.)
Вывод: в первом примере следующая цифра 3, меньше 5 (середина отрезка), а во втором случае цифра 8, больше 5.
– Какой вывод можно сделать? (Если следующая цифра, стоящая за округляемой меньше 5, то округляемая цифра не меняется, если следующая цифра, стоящая за округляемой больше 5, то округляемая цифра увеличивается на 1.)
– Что вы можете сказать о
третьем примере? (Число стоит по середине отрезка, значит можно брать при
округлении и число 2000 и 3000, но число 2583 ближе расположено ближе к 2600, а
2600 ближе к 3000, значит 2583 ![]() 3000.)
3000.)
– Если следующая цифра, стоящая за округляемой равна 5, что будем делать с округляемой цифрой? (Увеличивать на 1.)
– Сформулируйте полностью правило округления натуральных чисел. (Учащиеся предлагают свои варианты формулировок, учитель корректирует и правило фиксируется на доске.)
Затем работа с учебником с. 298.
Зарядка для глаз.
5. Первичное закрепление во внешней речи
Задание а) округлить до сотен: 372, 2428, 691, 5971, 93, 42 .
б) округлить до тысяч: 14572, 23854, 2473, 9857,99999,637,421.
Работа за закрытой доской проверяется всем классом.
Работа в парах. Задача.
Маша задумала число и, округлив его до десятков, получила 470.Какое число могла задумать Маша? Назовите самое большое из возможных вариантов . Назовите самое маленькое .(465,466, 467, 468,469,470,471,472,473,474),(474),(465)
Ответы проверяются коллективно.
6. Самостоятельная работа с самопроверкой по эталону
1.Округлите до десятков 237 856
а) 237 800; б)237 860; в)240 000; г)237 850.
2.Округлите до сотен 541 823
а)541 820; б) 500 000; в)541 800; г)541 900.
3.Округлите до тысяч 481 536
а)480 000; б)500 000; в)482 000; г)481 000.
4.Округлите до сотен тысяч 532 451
а)500 000; б)600 000; в) 530 000; г)532 500.
После выполнения задания учащиеся проверяют по эталону, фиксируют результаты знаком «+» при совпадении ответов, знаком «?» при не совпадении ответов, проводится анализ и исправления ошибок.
7. Рефлексия деятельности на уроке
– Что нового вы узнали?
– Где может использоваться округление чисел?
– Какие знания нам помогли вывести правило округления?
– Какие затруднения у вас были при выполнении самостоятельной работы?
– Проанализируйте свою работу на уроке.
8. Итоги урока. Домашнее задание
Знать правило округления, № 5(4), 7, 9 с.326.
Урок обобщения и систематизации знаний по теме «Натуральные числа»
Цели урока:
· Образовательные - обеспечить повторение, обобщение и систематизацию материала по теме "Натуральные числа". Создать условия контроля (самоконтроля) усвоения знаний и умений.
· Развивающие - способствовать формированию умений применять приемы: сравнения, выделения главного, переноса знаний в новую ситуацию, развития математического кругозора, мышления и речи, внимания и памяти.
· Воспитательные - воспитывать интерес к математике, активность, мобильность, умение общаться, общую культуру.
Ход урока
I. Организационный момент.
Проверка готовности к уроку. Учитель настраивает детей на урок, желает победы и высоких результатов.
2. Мотивация.
Чтобы спорилось нужное дело,
Чтобы в жизни не знать неудач,
Мы в поход отправляемся смело,
В мир загадок и сложных задач.
Не беда, что идти далеко,
Не боимся, что путь будет труден,
Достижения людям
Никогда не давались легко.
Сегодняшний урок мы проведем не как обычно, сегодня мы будем играть.
Я предлагаю вам отправиться в морское путешествие по бескрайнему океану "Натуральных чисел". Предупреждаю: мы отправляемся в интересное путешествие, оно таит в себе множество опасностей, которые потребуют от вас мужества, хладнокровия, сообразительности и конечно знаний математики.
Цель нашего урока - обобщить и систематизировать знания по теме "Натуральные числа", выяснить насколько хорошо вы усвоили эту тему.
3. Актуализация опорных знаний. Проверка д/з.
Прежде чем отправляться в плавание соберем наш багаж:
А) сверка решения д/з с записью на доске;
Б) игра «Верю - не верю» с использованием светофоров..
1. Число 0 - натуральное.
2. Площадь измеряется в квадратных единицах.
3. Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
4. Произведение трех одинаковых множителей можно записать в виде куба числа.
5. Грань прямоугольного параллелепипеда - отрезок.
6. Куб - один из видов прямоугольного параллелепипеда.
7. В одном дециметре 10 мм.
В добрый путь!
4. Обобщение и систематизация знаний по теме "Натуральные числа".
Отправляемся в путешествие. В добрый путь!
1 этап путешествия. Натуральный залив. Просмотр презентации.
Предлагается ответить на вопросы.
- Где применяются натуральные числа?
- Какие цифры используются для записи натуральных чисел?
- Нуль относится к натуральным числам?
Как читают многозначные числа?
Какие классы вы знаете?
«Все прекрасно благодаря числу» ( Пифагор)
«Красота спасет мир»
Пифагор много путешествовал по странам Востока, Египетские жрецы и вавилонские халдеи привили Пифагору пристрастие к восточным таинствам и числовой мистике. Возвратившись на родину, Пифагор создал школу. Пифагор проповедовал, что всю природу, всю вселенную, все на свете можно свести к натуральным числам и их отношениям. «Все есть число», «числа правят миром» - искренне верил Пифагор. Учение о числах было одной из составных частей его религии. Он считал, что через числа можно выразить все закономерности в мире. Пифагорейцы обожествляли числа.
Число 1 означало огонь, 2 – землю, 3 – воду, 4 – воздух, 5 – символизирует любовь, 6 – холод, 7 – разум, свет.
Пифагор впервые разделил числа на четные и нечетные, простые и составные. Четные числа считались несчастливыми, а нечетные – счастливыми. Эта традиция сохранилась и поныне: дарить на праздник нечетное, на похороны – четное число цветков.
Но большие числа они не называли.
Ц. М. Архимед научился называть громадные числа. Просто единица – единица чисел первых, миранду миранд, то есть 100 000 000 – единица вторых чисел. Но хотя названия громадных чисел у Архимеда уже были – обозначать он их не умел: не хватало самой малости…нуля.
2 этап путешествия. Вычислительная лагуна.
Устный счет
|
17 ·5 ·2 |
33 ·4 · 25 |
15+7+13 |
85+17+15 |
Работа у доски.
Длина хвоста Васьки: (599+289):24-23+11, а Мурки: (512+256):32+16-15. Чей же хвост длиннее?
3 этап путешествия. Остров Логики
Проверим, как вы сообразительны и сможем ли мы преодолеть этот остров.
1) В корзине лежат 5 яблок. Разделите их между пятью лицами так, чтобы каждый получил по яблоку, и одно яблоко осталось в корзине.
2) У родителей 5 сыновей. У каждого есть сестра. Сколько всего детей у родителей.
3) Сколько граней у неочищенного шестигранного карандаша?
4) Если дождь идет в 12 часов ночи, то может ли быть через 72 часа солнечная погода?
Тренировка внимания.
 Учитель
показывает ребятам плакат и обращается к ним: «Внимательно посмотрите на
плакат. Вам дается 1 секунда, после чего плакат будет убран, а вы должны
сложить три числа, которые были на нем, и назвать сумму этих чисел».
Учитель
показывает ребятам плакат и обращается к ним: «Внимательно посмотрите на
плакат. Вам дается 1 секунда, после чего плакат будет убран, а вы должны
сложить три числа, которые были на нем, и назвать сумму этих чисел».


Вы просто суперсообразительны и поэтому сможете попасть в Геометрическую бухту. Там нас ждет в гости замечательный абориген. Он не верит, что на корабле собрались умнейшие пятиклассники, и решил устроить нам проверку с помощью волшебного кроссворда.
4 этап путешествия. Геометрическая бухта.
5. Самостоятельная работа «Бермудский треугольник».
Вы, наверное, слышали, что это очень опасное место, в котором пропадают корабли.
Сейчас каждому из вас придется приложить немало усилий для того, чтобы благополучно вернуться домой. Решить №_____
6. Подведение итогов. Рефлексия «Микрофон»
Подведем итог нашего путешествия.
Учитель благодарит детей за продуктивную и интересную работу.
7. Домашнее задание.
· Повторить п.1-4. Решить №__________
· Нарисовать страну "Натуральных чисел".
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.