Математика в истории

Нальгиева З., студентка II курса

кафедра педагогики и методики начального обучения

                                              Аушева М. Б., научный руководитель, ст. преподаватель

ФГБОУ ВО «Ингушский государственный университет»

г. Магас, Республика Ингушетия

Математика в истории

        В истории математики выделяются несколько этапов развития математических знаний. Рассмотрим некоторые из них:

1.  Формирование понятия геометрические фигуры и числа как идеализация реальных объектов и множество  однородных  объектов.

       Появление счёта и измерения, которые позволили сравнивать различные числа, длины, площади и объёмы.

Самой древней математической деятельностью был счет. Счет был необходим, чтобы следить за поголовьем скота и вести торговлю. Древние люди добывали себе пищу охотой. На крупного зверя – бизона или лося – приходилось охотиться всем племенем: в одиночку ведь с ним и не справишься. Чтобы добыча не ушла, ее надо было окружить, ну вот хотя бы так: пять человек справа, семь сзади, четыре слева. Даже в те времена, когда человек не знал таких слов, как «пять» или «семь», он мог показать числа на пальцах рук. Таким образом, первобытные племена с помощью соотношения чисел с частями тела, главным образом с пальцами рук и ног, занимались счетом.

       В современное время такое соотношение используют родители и учителя, дабы облегчить детям  изучение счета.

       Для первобытных людей важную роль играла форма окружавших их предметов. По форме и цвету, они отличали съедобные грибы от несъедобных, пригодные для построек породы деревьев от тех, которые годятся лишь на дрова, вкусные орехи от горьких и т.д. Особенно вкусными казались им орехи кокосовой пальмы, которые имеют форму шара. А добывая каменную соль, люди наталкивались на кристаллы, имевшие форму куба. Так, овладевая окружающим их миром, люди знакомились с простейшими геометрическими формами.

    Уже 200 тысяч лет тому назад были изготовлены орудия сравнительно правильной геометрической формы, а потом люди научились шлифовать их. Специальных названий для геометрических фигур, конечно, не было. Говорили: «такой же, как кокосовый орех» или «такой же, как соль» и т.д. 

       А когда люди стали строить дома из дерева, пришлось глубже разобраться в том, какую форму следует придавать стенам и крыше, какой формы должны быть бревна. Сами того не зная, люди все время занимались геометрией: женщины, изготавливая одежду, охотники, изготавливая наконечники для копий или бумеранги сложной формы, рыболовы, делая такие крючки из кости, чтобы рыба с них не срывалась.

       Изготавливая наконечники для копий или бумеранги сложной формы, рыболовы, делая такие крючки из кости, чтобы рыба с них не срывалась.

      Когда стали строить здания из камня, пришлось перетаскивать тяжелые каменные глыбы. Для этого применялись катки. И заметили, что перекатка проще, если взять кусок дерева с почти одинаковой толщиной в начале и в конце. Так люди познакомились с одним из важнейших тел – цилиндром. Скалками цилиндрической формы пользовались и женщины, раскатывая белье после стирки.

     Перевозить грузы на катках было довольно тяжело, потому, что сами древесные стволы весили много. Чтобы облегчить работу, стали вырезать из стволов тонкие круглые пластинки и с их помощью перетаскивать грузы. Так появилось первое колесо.

      Но не только в процессе работы знакомились люди с геометрическим фигурами.

         Издавна они любили украшать себя, свою одежду, свое жилище (бусинки, браслеты, кольца, украшения из драгоценных камней и металлов, роспись дворцов).

    2. Изобретение арифметических операций. Накопление эмпирическим путем (методом проб и ошибок) знаний о свойствах  арифметических действий, о способах измерения площадей и объемов простых фигур и тел.

       Понятие о натуральных числах формировалось постепенно и осложнялось неумением первобытного человека отделять числовую абстракцию от её конкретного представления. Вследствие этого счёт долгое время оставался только вещественным — использовались пальцы, камешки, пометки.

С распространением счёта на большее количества появилась идея считать не только единицами, но и, так сказать, пакетами единиц, содержащими, например, 10 объектов. Эта идея немедленно отразилась в языке, а затем и в письменности. Принцип именования или изображения числа (нумерация) может быть^:

• аддитивным (один+на+дцать, XXX = 30)
• субтрактивным (IX, девя-но-сто)
• мультипликативным (пять*десят, три*ста)

Для запоминания результатов счёта использовали зарубки, узелки и т. п. 

Первым  способом «записи» чисел были зарубки на палке. Хорошо, если число небольшое – десятки или, в крайнем случае, сотни. А если тысячи? Пока сосчитаешь зарубки, чтобы «прочитать» число, пройдет больше часа. Очень неудобная «запись»! И вот примерно пять тысяч лет назад почти одновременно в разных странах – Вавилонии, Египте, Китае – родился новый способ записи чисел.

   Только, прежде чем говорить об этом, давайте разберемся, как мы записываем числа сейчас.

   Мы пользуемся всего десятью цифрами, но с помощью этих десяти значков – цифр – можем записать любое число. Как это получается? Возьмем какое – нибудь число, например 189. Чтобы получить это число, надо сложить: 1 сотню + 8 десятков + 9 единиц = 189.

Оказывается, каждое число состоит из ступенек: единиц, десятков, сотен, тысяч – и так далее. Математики называют такие ступеньки разрядами. В начальной школе многозначное число делят на разряды для проведения различных операций над ними (сложение, вычитание,  умножение, деление).

     В Древнем Вавилоне считали не десятками, а шестидесятками. Математик сказал бы, что система счета была там не десятичная, как у нас, а шестидесятеричная. Число шестьдесят играло у них такую же роль, как у нас десять.

Интересно, что до сих пор мы иногда пользуемся вавилонской системой счета. Как вы думаете, почему в нашем часе 60 минут, а в минуте 60 секунд? Наверное, это осталось в наследство от вавилонян!

     Очень интересная система счета была у народа майя, который жил в Средней Америке. Они считали двадцатками, - у них была двадцатеричная система счета. Числа от 1 до 20 обозначались точками и черточками. Если под числом был нарисован особый значок в виде глаза, это значило, что число надо увеличить в двадцать раз. Выходит, что изображение глаза играло у майя ту же роль, что у нас цифра нуль. Только они рисовали глаз не рядом с числом, а под ним.

Главной мерой длины у египтян служил локоть. Локоть делился на семь «ладоней», «ладонь» – на четыре «пальца». Как и многие другие народы, в качестве мерок длины египтяне использовали части человеческого тела. Но люди бывают разного роста, и локти у них не одинаковые. Египтяне это, конечно, понимали. Для того чтобы измерения получались точными и не происходило никакой путаницы, они придумали образцовые меры: локоть, ладонь и палец, общие для всего Египта. Теперь было уже не важно, какой длины руки у человека, который хотел, что-либо измерить. Он мерил не своим, а «общим» локтем.

Древнеегипетская письменность основывалась на иероглифах. Система счисления того периода также уступала вавилонской. Египтяне пользовались непозиционной десятичной системой, в которой числа от 1 до 9 обозначались соответствующим числом вертикальных черточек, а для последовательных степеней числа 10 вводились индивидуальные символы. Последовательно комбинируя эти символы, можно было записать любое число. С появлением папируса возникло так называемое иератическое письмо-скоропись, способствовавшее, в свою очередь, появлению новой числовой системы. Для каждого из чисел от 1 до 9 и для каждого из первых девяти кратных чисел 10, 100 и т.д. использовался специальный опознавательный символ. Дроби записывались в виде суммы дробей с числителем, равным единице. С такими дробями египтяне производили все четыре арифметические операции, но процедура таких вычислений оставалась очень громоздкой.

 .

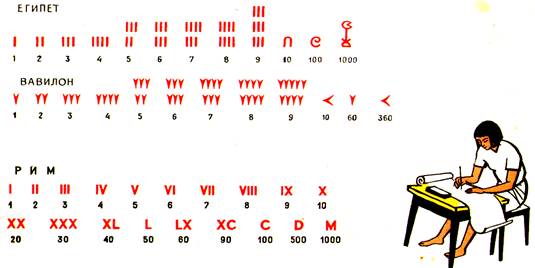    В Китае существовала система счета  Сучжо́у. Цифры Сучжоу или хуама 花碼 — десятичная позиционная система записи чисел.

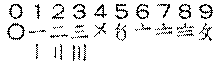
Цифры Сучжоу (蘇州碼子 или 苏州码子: sūzhōu mǎzi)

Древнекитайские цифры для счётной доски.

          Цифры Сучжоу — единственная отчасти сохранившаяся система, основанная на счете. Эта система сформировалась на базе более древней системы цифр, которые выкладывались палочками для вычислений на счётной доске, использовавшейся в Южной Сун. Долгое время расчёты велись почти только на счётной доске. На бумаге записывался результат.

       Вместе с арифметическими действиями развивалось  и геометрия. А именно способы измерения площадей и объёмов различных фигур. В основном эти знания использовались в архитектуре.  

Само слово «геометрия» по–гречески означает « землемерие». Ученые считают, что эта наука зародилась еще у самых древних египетских земледельцев. После каждого разлива Нила им приходилось заново разбивать поля на участки, находить их границы. А для этого надо было уметь измерять площади различных фигур : ведь поле может иметь какую угодно форму. Особенно тщательно поля измеряли чиновники фараонов , которые собирали с земли налоги.

       Древние египтяне были замечательными математиками и инженерами. Известные  многим пирамиды созданы егептянами. Самая большая пирамида – пирамида Хеопса – выше сорокаэтажного дома. Даже сейчас поднять на такую высоту и расставить вплотную друг к другу тысячи многотонных каменных «кубиков» было бы не простым делом. А ведь у египтян не было ни подъёмных кранов, ни мощных домкратов.

    Все пирамиды имеют совершенно одинаковую правильную форму. И стоят они не как попало: одна сторона пирамиды смотрит всегда точно на восток, другие – на север, юг и запад. Но ведь построить (хотя бы на бумаге) правильную пирамиду совсем не просто. Даже сейчас люди учатся этому только в средней школе. А египтяне умели строить пирамиды уже пять тысяч лет назад!

Список литературы

1. Бурбаки Н. Очерки по истории математике / Пер. И. Г. Башмаковой под ред. К. А. Рыбникова.   2007. 

2. Глейзер Г. И. История математики в школе— М.: Просвещение, 1981.

3. Башэ, К.Г. Игры и задачи, основанные на математике / К.Г. Башэ. 2012г.

Скачано с www.znanio.ru