Материал для учителя

Беседа

Если внимательно присмотреться к большинству механических движений, которые происходят в природе, то можно заметить, что многие из них осуществляются по криволинейным траекториям. И одним из самых грандиозных примеров такого движения является бесспорно движение планет! (Учитель рассказывает о движении Луны — естественного спутника Земли.)

Вопрос классу: Приведите примеры криволинейного движения, которые встречается в природе и в технике.

Любую криволинейную траекторию можно «упростить», то есть свести к более простой форме  дуге окружности (рис. 3)

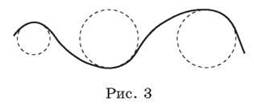
Вопрос классу: как будет направлена скорость движения тела в этом случае?

Можно выбрать настолько малую участок дуги AB (рис. 4), что она почти не будет отличаться от прямолинейного отрезка. Тогда скорость движения довольно легко изобразить. Мы видим, что направление скорости от точки к точке меняется.

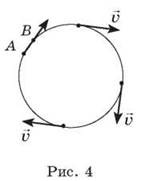
Вопрос классу: Как в математике называются линии, вдоль которых в нашем случае направленные скорости движения? (Касательные.)

Вывод. Во время движения по кругу скорости направлены по касательным.

Рассмотрим частный случай криволинейного движения — равномерное вращение тела по окружности.

Запись в тетрадь: Движение по окружности называется равномерным, если числовое значение скорости не изменяется.

Вопрос классу: Почему в определении равномерного движения речь идет именно о числовом значении скорости? (Потому что мы видели на рисунке, что направление скорости в каждой точке меняется.)

Для описания равномерного вращения тела по окружности используют характеристику — период вращения.

Запись в тетрадь: Период вращения T — это время одного полного оборота.

Вопрос классу:

• В каких единицах СИ должна измеряться период вращения исходя из определения? (В секундах.)

• Чему равен период вращения секундной стрелки часов? минутной? часовой?

• Чему равен период вращения Земли вокруг своей оси? вокруг Солнца?

С периодом вращения связана еще одна важная характеристика вращательного движения — частота вращения.

Запись в тетрадь: Частота вращения (ν) – число оборотов, которое тело совершает в единицу времени. Измеряется в системе СИ в обратных секундах.

Формула для нахождения частоты:

где  – полное время вращения;  – число оборотов

Частота и период – обратно пропорциональные величины:

 Вопрос классу: Период вращения Земли вокруг собственной оси равен 24 час. Сколько оборотов делает Земля за 1 час? (Ответ: 1/24 часть оборота.)

Вопрос классу: Тело делает 2 оборота за секунду. За какое время тело совершит один оборот, то есть чему равен период вращения? (Ответ: T = 1/2 с.)

В случае равномерного движения:  = S/t.

В случае движения по окружности: S = 2πR, а время, за которое преодолевается это расстояние, соответствует периоду вращения, то есть t = T.

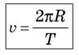
Помимо линейной скорости, криволинейное движение характеризуется угловой скоростью (ω)

Угловой скоростью (ω) называют отношение изменения угла, на который повернулось тело, ко времени, за которое этот поворот произошел. Измеряется в системе СИ в радианах, деленных на секунды.

Формула для нахождения угловой скорости:

где  – изменение угла;  – время, за которое произошел поворот на угол .

Для того чтобы связать угловую и линейную скорость, рассмотрим один полный оборот тела по окружности:

-путь тела будет равен длине окружности:

- угловое перемещение будет равно :

- время полного оборота равно периоду:

Подставим эти данные в формулы для скоростей:

 – угловая скорость

– линейная скорость

 – связь между линейной и угловой скоростью

Центростремительное ускорение связано с линейной скоростью формулой:

Зная, что , получаем формулу, которая связывает центростремительное ускорение с угловой скоростью:

Скачано с www.znanio.ru