
Лекция 4.
Сети Петри
Основные соотношения. Для формального описания структуры и взаимодействия параллельных систем и процессов, а также анализа причинно-следственных связей в сложных системах используются сети Петри (англ. Petri Nets), называемые N-схемами.
Графы специального вида, получившие в дальнейшем название “Сети Петри” были впервые введены Карлом Петри в 60-х годах. В следующем десятилетии начался “бум” разработок в этом направлении. Популярность сетей Петри вызвана удачным представлением различных типов объектов, присутствующих во многих моделируемых системах и “событийным” подходом к моделированию.
Формально N-схема задается четверкой вида
N = <B, D, I, O>,
где В – конечное множество символов, называемых позициями, B
¹ O;
D – конечное множество символов, называемых переходами D ¹ O,
B Ç D = O; I
– входная функция (прямая функция инцидентности)
I: B ´ D ® {0,
1}; О – выходная функция
(обратная функция инцидентности),
О: B ´ D ® {0, 1}.
Таким образом входная функция I отображает переход dj
в множество входных позиций bj Î
I(dj), а выходная функция O отображает переход dj
в множество выходных позиций bj Î О(dj). Для каждого перехода
dj Î D
можно определить множество входных позиций перехода I(dj)
и выходных позиций перехода O(dj) как
I(dj) = { bi Î B | I(bi, dj) = 1 },
O(dj) = { bi Î B | O(dj, bi) = 1 },
i = ![]()
![]() ; j =
; j = ![]() ; n = | B |, m =
| D |.
; n = | B |, m =
| D |.
Аналогично для каждой позиции bi Î B вводятся определения множеств
входных переходов позиции I(bi) и выходных переходов
позиции O(bi):
I(bi) = { dj Î D | I(dj, bi,) = 1 },
O(bi) = { dj Î D | O(bi, dj) = 1 }.
Графически N-схема изображается в виде двудольного ориентированного мультиграфа, представляющего собой совокупность позиций и переходов (рис. 1). Граф N-схемы имеет два типа узлов: позиции и переходы, изображаемые O и | соответственно. Ориентировочные дуги соединяют позиции и переходы, причем каждая дуга направлена от элемента одного множества (позиции или перехода) к элементу другого множества (переходу или позиции). Граф N-схемы является мультиграфом, так как он допускает существование кратных дуг от одной вершины к другой.
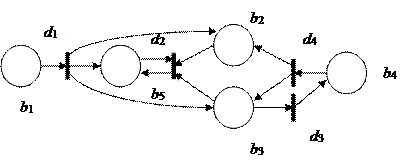 |
Рис. 1. Графическое изображение N-схемы
Пример. Представим формально N-схему, показанную в виде графа на рис. 1:
N = <B, D, I, O>,
B = <b1, b2, b3, b4, b5>,
D = <d1, d2, d3, d4>.
Входные позиции перехода Выходные позиции перехода
I(d1)={b1}, O(d1)={b2, b3, b5},
I(d2)={b2, b3, b5}, O(d2)={b5},
I(d3)={b3}, O(d3)={b4},
I(d4)={b4}. O(d4)={b2, b3}.
Возможные приложения N-схем. Приведенное
представление
N-схемы может использоваться только как отражение статики моделируемой
системы (взаимосвязи событий и условий), но не позволяет отразить в модели
динамику функционирования моделируемой системы. Для представления динамических
свойств объекта вводится функция маркировки (разметки) позиций М: В
® {0, 1, 2, …}. Маркировка М
есть присвоение неких абстрактных объектов, называемых метками (фишками),
позициям N-схемы, причем количество меток, соответствующее каждой
позиции, может меняться. При графическом задании N-схемы разметка
отображается помещением внутри вершин позиций соответствующего числа точек
(когда количество точек велико, ставят цифры).
Маркированная (размеченная) N-схема может быть описана в виде NМ = <B, D, I, O, M>.
Функционирование N-схемы отражается путем перехода от разметки к
разметке. Начальная разметка обозначается как М0: В ® {0, 1, 2, …}.
Смена разметок происходит в результате срабатывания одного из переходов dj
Î D сети.
Правило срабатывания перехода
Функционирование многих систем можно описать в терминах состояний системы и изменения ее состояний. При моделировании динамики системы состояние, или маркировка сети Петри, сменяется согласно правилу запуска перехода:
1) переход разрешен, если все входные значения b помечены не менее чем w(b, d) фишками, где w(b, d) - вес дуги от b к d;
2) запуск разрешенного перехода носит случайный характер (в зависимости от наступления или ненаступления соответствующего события.
3) запущенный переход d изымает w(b, d) фишек из каждой своей входной позиции и добавляет w(d, b) фишек в каждую свою выходную позицию. Здесь w(d, b) - вес дуги, ведущей из d в b.
Наиболее интересны сети Петри тем, что они позволяют представлять и изучать в динамике поведение системы параллельных процессов в программе или в любом другом дискретном устройстве.
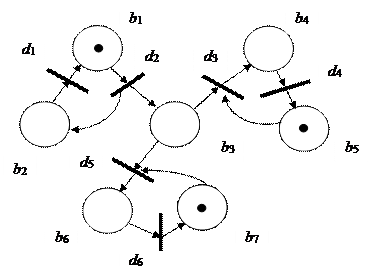
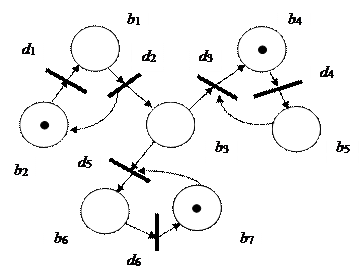
Пример. Рассмотрим размеченную N-схему с
начальной разметкой M0 = {1, 0, 0, 0, 1, 0, 1}, которая
приведена на рис. 2.8, а. При такой начальной разметке N-схемы
единственным готовым к срабатыванию является
переход d2, срабатывание которого ведет к смене разметки на M1,
где
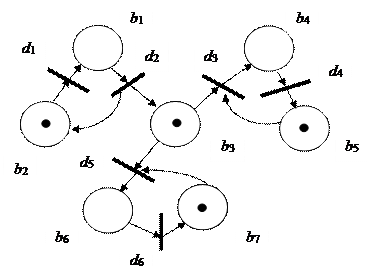
M1 = {0, 1, 1, 0, 1, 0, 1} (рис. 2).
Рис.2. Пример функционирования размеченной N-схемы:
 а
а
б
 |
 в
в
г
 |
д
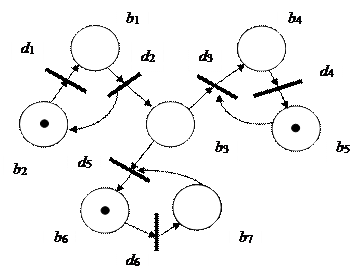 |
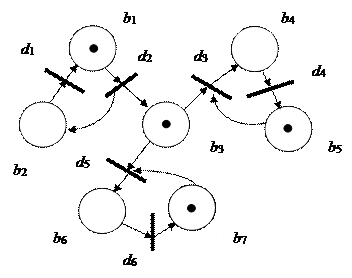
Рис. 2. (Окончание)
При разметке M1 возможно срабатывание переходов d1 d3 и d5. В зависимости от того, какой переход сработал первым, получается одна из трех возможных новых маркировок (рис. 2., в, г, д). Функционирование N-схемы продолжается до тех пор, пока существует хотя бы один возможный переход.
Таким образом, N-схема выполняется путем запусков переходов под управлением количества меток и их распределения в сети. Переход запускается удалением меток из его входных позиций и образованием новых меток, помещаемых в выходные позиции. Переход может запускаться только тогда, когда он разрешен. Переход называется разрешенным, если каждая из его входных позиций имеет число меток, по крайне мере равное числу дуг из позиции в переход.
Важной особенностью моделей процесса функционирования систем с использованием типовых N-схем является простота построения иерархических конструкций при моделировании параллельных и конкурирующих процессов в системах.
В применении к программированию можно представлять себе переходы как процедуры, а позиции - как переменные или буфер. Фишка свидетельствует о том, что переменная/буфер имеет значение, а если позиция имеет, к примеру, 3 фишки, то это может интерпретироваться как наличие трех разных значений в буфере.
Пример. Требуется описать с помощью сети Петри функционирование системы из предприятий A, В и С. Предприятия А и В поставляют узлы Х1 и X2 соответственно, а на предприятии С происходит сборка, в каждый сборочный узел входит один узел X1 и два узла X2. На рис. 2.10 предприятиям А, В и С соответствуют переходы t1, t2 и t3.
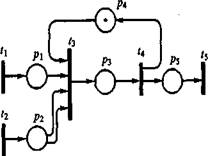
Рис. 3. Сеть Петри для примера
Срабатывание перехода t3 происходит только в том случае, если, во-первых, в позиции pl имеется метка, а в позиции р2 - не менее двух меток, что означает поступление от предприятии А и В соответствующих комплектующих, и, во-вторых, имеется метка в позиции p4, что означает, что предприятие С закончило сборку предыдущего изделия и готово приступить к сборке следующего. Пока очередное изделие не будет собрано, метки в p4 не будет, следовательно, запросы, пришедшие во входные позиции р1 и р2, вынуждены ожидать срабатывания перехода t4. Переходам t1, t2 и t3 поставлены в соответствие процедуры вычисления задержек срабатывания. Задержки в первых двух переходах равны интервалам времени между появлениями готовых узлов, задержка в t3 равна времени сборки изделия.
Сеть Петри - инструмент для моделирования динамических систем. Теория сетей Петри делает возможным моделирование системы математическим представлением ее в виде сети Петри, анализ которой помогает получить важную информацию о структуре и динамическом поведении моделируемой системы.
Возможно несколько путей практического применения сетей Петри при проектировании и анализе систем. В одном из подходов сети Петри рассматриваются как вспомогательный инструмент анализа. Здесь для построения системы используются общепринятые методы проектирования, затем построенная система моделируется сетью Петри, и построенная модель анализируется. Анализ результатов выполнения может сказать о том, в каких состояниях пребывала или не пребывала система, какие состояния в принципе не достижимы. Однако, такой анализ не дает числовых характеристик, определяющих состояние системы.
В другом подходе весь процесс проектирования и определения характеристик проводится в терминах сетей Петри. В этом случае задача заключается в преобразовании представления сети Петри в реальную информационную систему.
Несомненным достоинством сетей Петри является математически строгое описание модели. Это позволяет проводить их анализ с помощью современной вычислительной техники.
Поведенческие свойства сетей Петри
1. Достижимость.
Достижимость является фундаментальным понятием, необходимым для изучения динамических свойств любой системы. Запуск разрешенного перехода приводит к перераспределению фишек в сети (смене маркировки) по правилу перехода. Последовательности запусков соответствует последовательность маркировок. Маркировка Мn достижима из маркировки М0, если существует последовательность запусков, приводящих от М0 к Мn.
Множество всех маркировок, достижимых в сети (N, M0) от М0, обозначается как R(N, M0), или просто R(M0).
Таким образом, проблема достижимости в сетях Петри заключается в том, чтобы при заданной маркировке Мn в сети (N, M0) установить принадлежность Mn к множеству R(M0).
Граф достижимости
Множество разметок, достижимых в порядке срабатывания сети, представляется разверткой сети.
Множество достижимых разметок удобно представлять графом достижимости, который показывает все достижимые разметки и последовательности срабатываний переходов, приводящих к ним.
Пример. Следующая сеть (рис. 4а.) определяет управление двумя параллельно протекающими процессами с синхронизацией. Граф достижимости показан на рис. 4в. Граф развертки сети бесконечен (рис 4б), однако после состояния М3 в каждой ветви повторяется один и тот же фрагмент и потому возможно конечное представление графа достижимости (рис. 4в).
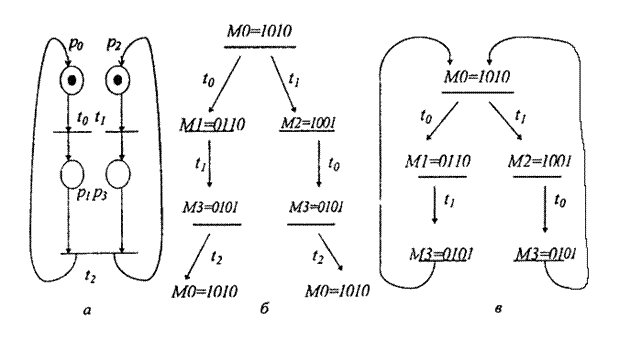
Рис. 4. Пример сети Петри (а) с ее графом развертки (б) и графом достижимости (в).
2. Ограниченность.
Другое направление исследования функционирования сети Петри связано с изменением количества фишек в конкретной или произвольной позиции в процессе функционирования сети.
Сеть Петри называется К-ограниченной, или просто ограниченной, если для любой маркировки, достижимой от маркировки М0, количество фишек в любой позиции не превышает некоторого числа К, т .е. М(р) <= К для любого р и любой маркировки М, принадлежащей R(M0). Сеть Петри (N, M0) называется безопасной, если она 1-ограниченна.
Позиции сети Петри часто моделируют буферы или регистры, служащие для хранения промежуточных результатов. Проверка ограниченности или безопасности сети гарантирует отсутствие переполнения буферов или регистров при любой фактической последовательности запусков переходов.
Безопасная сеть никогда, не допустит, чтобы в переменную было положено новое значение, если старое еще не было использовано по назначению. Нарушения этого правила часто являются причиной ошибок в параллельных программах.
В другой интерпретации переход может представлять некоторое устройство. Устройство может (но не должно) сработать, если выполнились все входные условия. Если несколько переходов готовы сработать, то срабатывает один из них (любой), или некоторые из них, или все.
Рассмотрим пример конвейера. Пусть есть три обрабатывающих устройства t0, t1, t2 организованные в виде конвейера. Это могут быть, например, станки на заводе или функциональные устройства конвейерного процессора и вообще любой конвейер, в котором каждое обрабатывающее устройство выполняет лишь часть общей работы, а результат будет выработан лишь последним из них.
Особенностью нашего конвейера является ограниченность емкости мест p1 и р2; место p1 может вместить лишь два результата (место p1 сети является 2-ограниченым) предшествующего этапа работы конвейера (вырабатывается переходом t0 ), а место p2 - 3-ограниченным. Символ n в месте р0 означает наличие n фишек в нем, n - целое положительной число.
Сеть Петри, обеспечивающая необходимое прямое управление, приведена на рис. Понятно, что в месте p1 не может накопиться более 2 фишек при любых порядках срабатывания переходов сети.
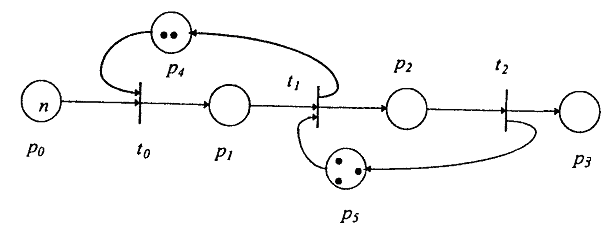
Рис. 5. Пример сети Петри, моделирующей работу конвейера.
3. Активность.
Понятие активности тесно связано с отсутствием возможности взаимной блокировки (тупиковых ситуаций) в операционной системе. Сеть Петри активна (или, что эквивалентно, маркировка М0 сети Петри активна), если независимо от достигнутой от М0 маркировки, для любого перехода существует последовательность дальнейших запусков, приводящая к его запуску. Это означает, что для активной сети Петри при любой последовательности запусков полностью исключена возможность взаимной блокировки.
4. Обратимость и базовое состояние.
Сети Петри обратима, если для любой маркировки М из R(M0) маркировка М0 достижима от М. Иными словами, в обратимой сети всегда можно вернуться к начальной маркировке (состоянию). Во многих задачах необязательно возвращаться в начальное состояние, но достаточно иметь возможность вернуться в базовое состояние. Поэтому условие обратимости можно ослабить и определить понятие базового состояния. Маркировка М' называется базовым состоянием, если она достижима от любой маркировки М из R(M0).
Задача о конечности функционирования сети Петри
Одна из основных проблем в теории сетей Петри - задача о конечности функционирования сети (о достижении тупиковой разметки).
Суть проблемы состоит в ответе на вопрос для данной конкретной сети - существует ли такая последовательность срабатывания переходов, которая приводит сеть к тупиковой разметке (т.е. разметке, при которой ни один переход не может сработать)?
Более того, анализ сетей позволяет утверждать, что ненкоторые сети всегда приходят к тупиковой разметке. Это математическое утверждение (теорема!) может быть строго доказано.
Заметим, что хотя некоторые сети обязательно останавливается, т.е. достигают тупиковой разметки, но сами эти тупиковые разметки могут быть различны.
Свойство достижения конечной разметки присуще далеко не всем сетям. Существуют сети, всегда приходящие к тупиковой разметке, сети, никогда не попадающие в тупик, сети, которые могут остановиться, а могут и нет.
Инструментальные средства моделирования с помощью сетей Петри позволяют запустить сеть Петри в работу (провести имитационное моделирование) и посмотреть, достигнет лисеть тупиковой разметки или нет.
Пример использования сети Петри при анализе состояний дедлока.
Сети Петри оказались удобным средством для анализа такого свойства параллельной системы, как наличие или отсутствие дедлоков. Состояние дедлока возникает, когда запрос ресурсов в системе не может быть удовлетворен и система останавливается (ни один переход не может сработать).
Рассмотрим пример на рис. 6. Сеть А определяет циклическое неограниченное срабатывание переходов t1, t2, t3. При срабатывании переходы t2 и t3 потребляют единицу ресурса из места р3 каждый. Можно представить себе для определенности, что место р3 содержит два участка памяти (буферы), которые операционная система может динамически выделять программе по ее запросу. Пока процесс, управляемый сетью А, выполняется один, ситуации дедлока не возникает. Но если появляется идентичный процесс, выполняющийся параллельно А и управляемый сетью В (рис. 6), тогда возникает конкуренция за ресурс в месте р3.
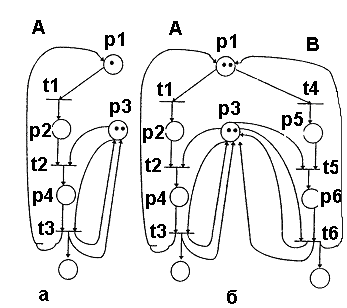
Рис 6. Пример сети Петри, моделирующей состояние системы без дедлока (а) и с дедлоком (б).
Ситуация дедлока возникает при такой последовательности срабатываний переходов сети: t1, t4, t2, t5. И в этом состоянии имеем дедлок: ни один переход не может сработать. Однако сеть будет нормально функционировать, если в позиции p1 оставить одну фишку, т.е. разрешить выполняться либо процессу А, либо процессу В, но не обоим одновременно.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.