4.8. Механізм масообмінних процесів.

      4.8.1. Основні моделі процесу масопереносу.

      Як указувалося вище, точний математичний опис процесів масопередачі зустрічає дотепер нездоланні труднощі, тому для їхнього опису запропонований ряд наближених гіпотетичних моделей.

      При розробці моделей масопереносу звичайно приймають допущення про те, що на поверхні розділу фази знаходяться в стані рівноваги, а загальний опір процесу переносу складається із суми опорів двох фаз, тобто процес масопереносу підкоряється правилу адитивності фазових опорів. Із цих допущень випливає, що на границі розділу фаз відсутній опір процесу (це означає, що рівновага на границі встановлюється дуже швидко – у всякому разі, швидше зміни середньої концентрації в ядрі фази, що для цілого ряду процесів масопереносу доведено експериментально).

      Плівкова (двоплівкова) модель Льюіса й Уітмена. Відповідно до цієї моделі по обидва боки поверхні контакту фаз утворюються нерухомі або ламінарні плівки (рис.4.5), у яких перенос речовини здійснюється тільки молекулярною дифузією. Ці плівки відокремлюють поверхню контакту фаз від ядра потоку, у якому концентрація практично постійна, усі зміни концентрації речовини відбуваються у плівці.

      Відповідно до плівкової моделі інтегрування рівняння (4.21а) приводить до виразу ,               (4.29)

де δ_пл – товщина пограничної плівки,

Відповідно, з рис.4.5.:

      Порівнюючи останні рівняння з рівнянням (4.27), одержимо

                                             (4.30)

      З рівнянь (4.30) випливає, що коефіцієнт масовіддачі β обернено пропорційний товщині плівки, яка визначається гідродинамічними умовами: чим більше турбулентність фаз, тим менше δ_пл  і, отже, тим вище коефіцієнт β. Рівняння (4.30) також показують, що за плівковою моделлю коефіцієнт масовіддачі повинен лінійно залежати від коефіцієнта молекулярної дифузії, що в більшості випадків не підтверджується експериментально. Крім того, ця теорія не враховує деформації поверхні контакту фаз і переносу речовини турбулентними пульсаціями.

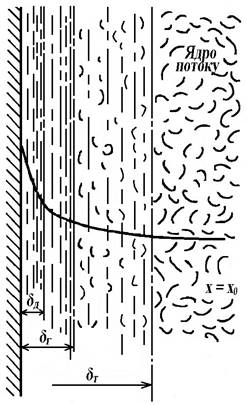
      Модель дифузійного пограничного шару є подальшим розвитком плівкової моделі, у ній відображений вплив гідродинамічних умов на процес масопереносу. За цією моделлю пограничний шар складається з трьох  (буферному) підшарі товщиною   концентрація речовини, яка є постійною в ядрі потоку, поступово знижується при наближенні до границі. У цьому шарі молекулярні і турбулентні сили в'язкості порівнянні між собою . Зі зменшенням масштабу пульсацій у другому (в’язкому) підшарі товщиною  концентрація знижується істотно швидше. І, нарешті, усередині тонкого дифузійного підшару товщиною  молекулярний перенос стає основним, при цьому _,. Товщина дифузійного пограничного шару визначається при цьому з залежності:

                       ,               (4.31)

де m – показник ступеня, що відображує закон загасання турбулентного переносу поблизу границі розділу фаз; для систем «рідина-тверде тіло»  m=3, а для систем «газ (пара)-рідина» і «рідина-рідина»  m=2.

       Розрахунок по рівняннях (4.29) і (4.31) приводить для систем «тверде тіло-рідина» до співвідношення М~D^0,66, а для систем «газ (пара)-рідина» і «рідина-рідина» - до М~D^0,5, що в значно більшому ступені відповідає експериментальним даним.

      Модель відновлення поверхні фазового контакту (модель проникнення або пенетраційна модель) припускає нестаціонарність процесу масопереносу, при цьому передбачається, що турбулентні пульсації постійно підводять до поверхні розділу фаз свіжу рідину і змивають порції рідини, що вже прореагувала з газом (парою), тобто кожен елемент поверхні рідини взаємодіє з газом (парою) протягом деякого часу τ (час контакту або відновлення), після чого даний елемент обновлюється. На основі цієї моделі, приймаючи час контакту τ постійним для всіх елементів поверхні, Хігбі одержав рівняння для визначення коефіцієнта масовіддачі:

                                                                                              (4.32)

      Як випливає з рівняння (4.32), швидкість переносу за пенетраційною моделлю, як і за моделлю дифузійного пограничного шару, М~D^0,5, що підтверджується експериментом.

      Кишинівський, приймаючи час контакту також постійним, замінює в рівнянні (4.32) коефіцієнт молекулярної дифузії D коефіцієнтом ефективної дифузії D_еф, який дорівнює сумі коефіцієнтів молекулярної D_м і турбулентної D_т дифузії.

      Запропоновано й інші моделі механізму масопереносу. Слід зазначити, що приведені вище моделі можна використовувати для розрахунку процесів тільки в окремих випадках, тому що внаслідок надзвичайної складності турбулентних двофазних потоків практично неможливе визначення в них поверхні контакту фаз, розподілу концентрацій у фазах і інших параметрів, необхідних для розрахунку.

     

      4.8.2. Зв'язок між коефіцієнтами масовіддачі і масопередачі.

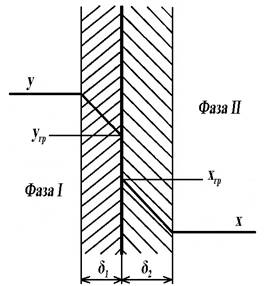
      Розглянемо процес масопередачі з фази Ф_у у фазу Ф_х приймаючи, що для нескінченно малого інтервалу лінія рівноваги є прямою, тобто у_р=mx, а робоча лінія також описується рівнянням прямої у = Ах + В. Допустимо, що на границі розділу фаз установлюється рівновага, тобто опір масопереносу практично відсутній. У такий спосіб передбачається адитивність фазових опорів.

      При сталому процесі рівняння масовіддачі для фази Ф_у має вигляд:

                                                  dМ = β_у·(y – у_гр) dF,                                        (4.33)

а для фази Ф_х  -

                                                  dM = β_х·(х_гр – х) dF,                                        (4.34)

      У рівнянні (4.34) х_гр=у_гр/m і х=у_р/m, звідки одержимо

                 .   (4.34а)

      Перетворимо рівняння (4.33) і (4.34а) щодо опору в кожній з фаз:

1/β_у = (у-у_гр) dF/dM,          m/β_x  = (у_гр-y_р) dF/dM.

     Склавши ці вираження, одержимо в лівій частині загальний опір R_y процесу масопереносу:

R_y = (1/β_у)+(m/β_x)= (у-у_р) dF/dM.

     Запишемо останнє рівняння щодо величини dM:

   ,      (4.35)

але   або .     (4.36)

     Рівняння (4.36) виражає адитивність фазових опорів. Із його врахуванням рівняння (4.35) прийме вид

                                                                                        (4.37)

або для всієї поверхні масопередачі F

                                                    .                                              (4.38)

      Аналогічно, якщо рушійна сила процесу виражається по фазі Ф_х, одержимо

                                               ,                                        (4.39)

                                                    ,                                              (4.40)

де .                                                                  (4.41)

      Таким чином, К_у і К_х, які називають поверхневими коефіцієнтами масопередачі, залежать від величин коефіцієнтів масовіддачі β_у і β_х. Якщо коефіцієнт β_х великий, то 1/β_у>>m/β_х і К_у≈β_у, тобто стадією, яка лімітує процес, у даному випадку буде дифузійний опір у фазі Ф_у. Якщо великі значення β_у і m, то 1/β_х>>1/(mβ_y) і К_x≈β_x і відповідно стадією, яка лімітує процес у цьому випадку, буде дифузійний опір у фазі Ф_х.

      У промислових апаратах при реалізації масообмінних процесів між газами (парами) і рідинами, а також між двома рідинами, що не змішуються, особливо в тих випадках, коли одна з контактуючих фаз знаходиться в дисперсному стані (барботажні, розпорошувальні апарати і т.п.), міжфазна поверхня F не завжди піддається безпосередньому вимірові. У таких випадках часто користуються не поверхневими, а об'ємними коефіцієнтами масовідддачі і масопередачі, які виражають кількість речовини, що переходить за одиницю часу в 1 м³ робочого об’єму апарата при рушійній силі процесу, рівній одиниці:

                                 K_vy= aK_y;  K_vx = aK_x; β_vy = aβ_y; β_vx = aβ_x,

де a = F/V  - питома поверхня контакту фаз (тобто поверхня фазового контакту F, утворена в 1 м³ робочого об’єму апарата V), м²/м³.

      Тоді рівняння масопередачі (4.38, 4.40) можуть бути записані у виді:

                                                                          (4.42)

      Рівняння масовіддачі  в цьому випадку приймають вид, аналогічний рівнянням (4.27):

                                                             (4.43)

      Значення K_vy і K_vx визначають за рівняннями адитивності фазових опорів аналогічно (4.36, 4.41).