Методическая разработка "Изложение основных теорем и формул вероятностей"

 

 

 

 

 

 

 

 

 

 

МЕТОДИЧЕСКАЯ РАЗРАБОТКА

ЛЕКЦИОННОГО ЗАНЯТИЯ № 11

по теме:

«Изложение основных теорем и формул вероятностей»

 

Дисциплина: Математика

 

Специальность 31.02.01. Лечебное дело

 

Курс 1               

 

 

 

 

 

 

 

 

Балашов 2022

СОДЕРЖАНИЕ

 

1.	Пояснительная записка……………………………………….	4
2.	Технологическая карта……………………………………….	5
3.	План изложения теоретического материала……………..….	6
4.	Содержание теоретического материала…….……………….	6
5.	Контрольно-оценочный материал……………………………	14
6.	Список рекомендуемой литературы…………………………	15

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Пояснительная записка

Данная методическая разработка предназначена для реализации требований Федерального государственного образовательного стандарта среднего профессионального образования по специальности 31.02.01 – «Лечебное дело» к минимуму содержания и уровню подготовки выпускников по учебной дисциплине «Математика».

Тема «Изложение основных теорем и формул вероятностей» входит в программу по дисциплине «Математика» и занимает в ней значительное место, т.к. навыки, полученные при изучении данной темы необходимы для изучения других смежных тем и для профессиональной деятельности среднего медицинского работника.

Основная цель данного занятия состоит в том, чтобы дать студентам набор математических знаний и навыков, необходимых для изучения других программных дисциплин, использующих в той или иной мере математику, для умения выполнять практические расчеты, для формирования и развития логического мышления.

В данной работе последовательно формулируются основные теоремы, рассматриваются  основные задачи и методы их решения, технологии применения этих методов к решению практических задач. Изложение сопровождается подробными комментариями и многочисленными примерами.

На данное занятие отводится 2 учебных часа. Изучение нового материала проходит в виде лекции с последующим закреплением через решение задач. Контроль уровня усвоения нового материала проводится в форме беседы со студентами. Методами обучения служат устный опрос, метод упражнений. Формы обучения имеют фронтальный, индивидуальный и групповой характер. Самостоятельная работа предполагает выполнение типовых расчетов и решение задач.

 

Технологическая карта лекционного занятия

 

Учебные цели занятия: изучение основных теорем и формул вероятностей.

знать:

1. Теорему сложения вероятностей несовместных событий.

2. Формулу условной вероятности.

3. Теорему умножения вероятностей независимых событий.

 

ОК 1–5, 12

Тип занятия: информационная, проблемная, эвристическая, бинарная

                                                 (нужное подчеркнуть)

Уровень освоения: 2

Материальное обеспечение учебного занятия:

1. Ноутбук, проектор.

2. Мультимедийная презентация

 

Распределение рабочего времени на учебном занятии:

 

Содержание занятия	Время	Методические указания
1. Организационный момент	2 мин	Взаимное приветствие. Проверка состава студентов и их готовности к занятию.
2. Формулировка темы, ее мотивация	3 мин	Сообщение темы занятия, раскрытие её теоретической и практической значимости.
3. Определение целей занятия	2 мин	Сообщение целей занятия. План занятия.
4. Работа над изучаемым материалом	60 мин	Изложение нового материала, конспектирование студентами основных понятий и теорем.
5. Закрепление нового материала	20 мин	С целью закрепления изученного материала идёт повторение основных понятий и определений, решение примеров
6. Подведение итогов занятия. Задание на дом	3 мин	Подведение итогов занятия, работа группы в целом и отдельных студентов. Выдача домашнего задания.

 

 

 

План изложения теоретического материала

 

1. Теорема сложения вероятностей несовместных событий.

2. Формула условной вероятности.

3. Теорема умножения вероятностей независимых событий.

 

Содержание теоретического материала

1. Теорема сложения вероятностей несовместных событий

Суммой конечного числа событий называется событие, состоящее в наступлении хотя бы одного из них.

Сумму двух событий обозначают символом А+В, а сумму n событий символом А₁+А₂+ … +А_n.

Теорема сложения вероятностей: вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

 или

Следствие 1. Если событие А₁, А₂, … ,А_n образуют полную систему, то сумма вероятностей этих событий равна единице.

.

Следствие 2. Сумма вероятностей противоположных событий  и  равна единице.

.

Задача №1. Имеется 100 лотерейных билетов. Известно, что на 5 билетов попадает выигрыш по 20000 руб., на 10 - по 15000 руб, на 15 - по 10000 руб., на 25 - по 2000 руб. и на остальные ничего. Найти вероятность того, что на купленный билет будет получен выигрыш не менее 10000 руб.

Решение:

Пусть А, В, и С- события, состоящие в том, что на купленный билет падает выигрыш, равный соответственно 20000, 15000 и 10000 руб. так как события А, В и С несовместны, то

.

Ответ: 0,3.

Задача №2. На заочное отделение техникума поступают контрольные работы по математике из городов А, В и С. Вероятность поступления контрольной работы из города А равна 0,6, из города В - 0,1. Найти вероятность того, что очередная контрольная работа поступит из города С.

Решение:

События «контрольная работа поступила из города А», «контрольная работа поступила из города В» и «контрольная работа поступила из города С» образуют полную систему, поэтому сумма их вероятностей равна единице:

, т.е. .

Ответ: 0,3.

Задача №3. Вероятность того, что день будет ясным, . Найти вероятность  того, что день будет облачным.

Решение:

События «день ясный» и «день облачный» противоположные, поэтому

, т.е .

Ответ: 0,15.

 

2. Формула условной вероятности

При совместном рассмотрении двух случайных событий А и В возникает вопрос:

Как связаны события А и В друг с другом, как наступление одного из них влияет на возможность наступления другого?

Простейшим примером связи между двумя событиями служит причинная связь, когда наступление одного из событий обязательно приводит к наступлению другого, или наоборот, когда наступление одного исключает возможность наступления другого.

Для характеристики зависимости одних событий от других вводится понятие условной вероятности.

Определение. Пусть А и В - два случайных события одного и того же испытания. Тогда условной вероятностью события А или вероятностью события А при условии, что наступило событие В, называется число .

Обозначив условную вероятность , получим формулу

, .

Задача №1. Вычислить вероятность того, что в семье, где есть один ребенок- мальчик, родится второй мальчик.

Решение:

Пусть событие А состоит в том, что в семье два мальчика, а событие В - что один мальчик.

Рассмотрим все возможные исходы: мальчик и мальчик; мальчик и девочка; девочка и мальчик; девочка и девочка.

Тогда ,  и по формуле находим

.

Ответ: 0,3.

 

3. Теорема умножения вероятностей независимых событий

Событие А называется независимым от события В, если наступление события В не оказывает никакого влияния на вероятность наступления события А.

Теорема умножения вероятностей: вероятность одновременного появления двух независимых событий равна произведению вероятностей этих событий:

.

Вероятность появления нескольких событий, независимых в совокупности, вычисляется по формуле

.

Задача №1. В первой урне находится 6 черных и 4 белых шара, во второй- 5 черных и 7 белых шаров. Из каждой урны извлекают по одному шару. Какова вероятность того, что оба шара окажутся белыми.

Решение:

Пусть  - из первой урны извлечен белый шар; - из второй урны извлечен белый шар. Очевидно, что события   и  независимы.

Так как , , то по формуле  находим

.

Ответ: .

Задача №2. Прибор состоит из двух элементов, работающих независимо. Вероятность выхода из строя первого элемента равна 0,2; вероятность выхода из строя второго элемента равна 0,3. Найти вероятность того, что: а) оба элемента выйдут из строя; б) оба элемента будут работать.

Решение. Пусть событие А- выход из строя первого элемента, событие В- выход их строя второго элемента. Эти события независимы (по условию).

а) Одновременное появление А и В есть событие АВ. Следовательно,

.

б) Если работает первый элемент, то имеет место событие  (противоположное событию А- выходу этого элемента из строя); если работает второй элемент- событие В. Найдем вероятности событий  и :

;

.

Тогда событие, состоящее в том, что будут работать оба элемента, есть  и, значит,

.

Ответ: 0,56.

Рассмотрим задачи с применением формул комбинаторики.

Задача №3. В ящике находится 15 качественных и 5 бракованных деталей. Наудачу извлекаются 2 детали. Найти вероятность того, что:

а) обе детали будут качественными;

б) одна деталь будет качественной, а одна – бракованной; 

в) обе детали бракованны.

Решение:

1) Всего: 15 + 5 = 20 деталей в ящике. Вычислим общее число исходов: 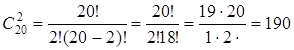способами можно извлечь 2 детали из 20 из ящика.

2) Рассмотрим событие А – обе извлечённые детали будут качественными: 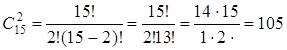 способами можно извлечь 2 качественные детали.

По классическому определению вероятности:  .

3) Рассмотрим событие В – одна деталь будет качественной, а одна – бракованной. Одна извлечённая деталь будет качественной: 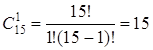, а другая бракованной 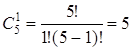, тогда по теореме умножения  способами можно извлечь 1 качественную деталь и 1 бракованную детали.

По классическому определению: .

4) Рассмотрим событие С – обе извлечённые детали бракованными: 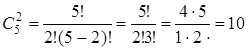 способами можно извлечь 2 бракованные детали.

По классическому определению: .

Проверка: вычислим сумму вероятностей событий, образующих полную группу: , что и требовалось проверить.

Ответ: а) ; б) ; в).

Задача №4. Найти вероятность того, что при бросании двух игральных костей в сумме выпадет:

а) пять очков;

б) не более четырёх очков;

в) от 3-х до 9 очков включительно.

Решение:

1) Найдём общее количество исходов: 6 способами может выпасть грань 1-го кубика и 6 способами может выпасть грань 2-го кубика; по правилу умножения комбинаций, всего: 6*6=36 возможных комбинаций. Иными словами, каждая грань 1-го кубика может составить упорядоченную пару с каждой гранью 2-го кубика. Условимся записывать такую пару в виде , где  – цифра, выпавшая на 1-м кубике,  – цифра, выпавшая на 2-м кубике. Например:

 – на первом кубике выпало 3 очка, на втором – 5 очков, сумма очков: 3 + 5 = 8;

  – на первом кубике выпало 6 очков, на втором – 1 очко, сумма очков: 6 + 1 = 7;  – на обеих костях выпало 2 очка, сумма: 2 + 2 = 4.

Очевидно, что наименьшую сумму даёт пара , а наибольшую – две «шестёрки».

а) Рассмотрим событие:  – при бросании двух игральных костей выпадет 5 очков.

Запишем и подсчитаем количество исходов, которые благоприятствуют данному событию:

Итого: 4 благоприятствующих исхода. По классическому определению:
 – искомая вероятность.

б) Рассмотрим событие:  – выпадет не более 4-х очков. То есть, либо 2, либо 3, либо 4 очка. Снова перечисляем и подсчитываем благоприятствующие комбинации, слева я буду записывать суммарное количество очков, а после двоеточия – подходящие пары:

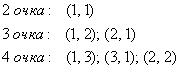
Итого: 6 благоприятствующих комбинаций. Таким образом:
 – вероятность того, что выпадет не более 4-х очков.

в) Рассмотрим событие:  – выпадет от 3-х до 9 очков включительно. Здесь можно пойти прямой дорогой, но… что-то не хочется. Да, некоторые пары уже перечислены в предыдущих пунктах, но работы все равно предстоит многовато.

Как лучше поступить? В подобных случаях рациональным оказывается окольный путь. Рассмотрим   – выпадет 2 или 10 или 11 или 12 очков. противоположное событие: противоположному событию благоприятствует значительно меньшее количество пар:

Итого: 7 благоприятствующих исходов.

По классическому определению:  – вероятность того, что выпадет меньше трёх или больше 9-ти очков.

Далее пользуемся тем, что сумма вероятностей противоположных событий равна единице:

 – вероятность того, что выпадет от 3-х до 9 очков включительно.

Ответ: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Контрольно-оценочный материал

(фронтальный опрос по пройденной теме)

1. Какие события называют несовместными? Приведите примеры.

2. Сформулируйте теорему сложения вероятностей несовместных событий.

3. Что называют условной вероятностью?

4. По какой формуле вычисляется условная вероятность?

5. Какое событие называется независимым? Приведите примеры.

6. Сформулируйте теорему умножения вероятностей независимых событий.

 

Задание на дом

Выучить основные теоремы и формулы теории вероятности, решить задачу.

Задача 1. Имеется 1000 лотерейных билетов. Известно, что на 10 билетов попадает выигрыш по 10000 руб., на 10 - по 5000 руб, на 20 - по 1000 руб., на 25 - по 2000 руб. и на остальные ничего. Найти вероятность того, что на купленный билет будет получен выигрыш не менее 10000 руб.

 

 

 

 

 

 

 

 

 

 

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

 

Основная литература:

1.   Балдин К. В. Математика и информатика: учебное пособие / К.В. Балдин, В. Н. Башлыков, А. В. Рукосуев., В. Б. Уткин под рук. Балдина К. В.- М.: КНОРУС, 2020.

2.   Гилярова М. Г. Математика для медицинских колледжей /М. Г. Гилярова. - Р.н/Д.: Феникс, 2018

Дополнительная литература:

1.   Колесов В. В., Романов М. Н. Математика для медицинских колледжей / В. В. Колесов, М. Н. Романов. - Р.н/Д.: Феникс, 2018

Интернет – ресурсы:

1.       Математика для всех. Доступ: http://konkurs-kenguru.ru

2.       Материалы по математике в Единой коллекции цифровых образовательных ресурсов Доступ: http://www.math.ru

3.       Математические олимпиады для школьников. Доступ: http://www.math-on-line.com

4.       Математические олимпиады и олимпиадные задачи. Доступ: http://www.olimpiada.ru

 

 

 

 

 

 

 

 

 

 

Скачано с www.znanio.ru