Методическая разработка «Методика проведения устной контрольной работы»

Муниципальное бюджетное учреждение

«Школа № 82»

г.о. Тольятти Самарской области

Методическая разработка

«Методика проведения устной контрольной работы»

Автор: Родионова Галина Михайловна,

учитель математики МБУ «Школа № 82"

г.о. Тольятти

Самарской области

2021

 О методике проведения устной контрольной работы

На доске написан пример, ученики решают его устно. Через некоторое время учитель просит поднять руку тех, кто решил. Если с примером справилась большая часть класса, то ученики в тетрадях ставят номер примера и пишут ответ. В противном случае добавляется время для поиска ответа. Ответ записывают только по команде учителя.

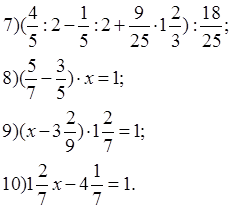Если цель этой работы не только проверить знания, но и ещё раз отработать какие-то вопросы теории, то разбор решения происходит сразу после того, как записан ответ. Тогда следующий пример составляется так, чтобы при его решении можно было использовать те приемы, с которым они встретились при разборе. Поясню сказанное:

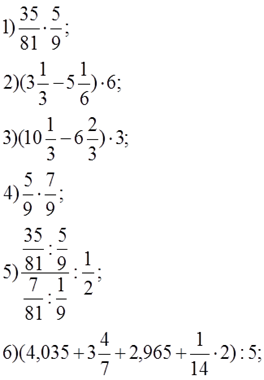
Первый пример контрольной работы по теме «Действия с дробями»             (VI класс) подобран так, чтобы его могли быстро решить все ученики. Второй пример дан на применение распределительного закона. Для     решения третьего примера требовалось заметить, что

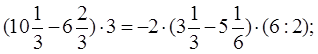а значит, в ответе получается число, противоположное результату второго примера. Ответ четвертого примера следует из первого. В пятом примере необходимо заметить, что в знаменателе делимое и делитель каждый в 5 раз меньше, чем соответственно делимое и делитель числителя. Отсюда вывод: дробь равна единице. Шестой и седьмой примеры на применение законов сложения. В восьмом примере сначала следует найти разность    -          и заметить, что х – число, обратное этой разности. Девятый пример  – аналогичен восьмому, только, может быть, несколько труднее, а десятый – это то же уравнение, что и девятое, только в левой части его раскрыты скобки.

Таким образом, ученики вынуждены неоднократно возвращаться к ранее решенным примерам. Это полезный прием. Ведь часто ученики решают задачи по принципу узнавания ситуации: «А я знаю!» И тогда, выполняя действия по тому же алгоритму,  что и в ранее решенной задаче, не видя в условии задачи нового элемента, который отличает ее от предыдущей , они не в состоянии увидеть более простого решения.

Устная контрольная работа несколько отличается от  традиционной контрольной. Здесь ученик как бы сам себя контролирует при помощи заданий учителя. Сам он делает выводы об уровне усвоения, учитель не видит его неудач. Поэтому устная контрольная работа чаще имеет обучающий характер.

Если контрольная  проводится с целью проверки знаний, то разбор ее делается после выполнения всей работы. Затем ученикам сообщается, за сколько примеров ставится «5», за сколько «4» (других отметок не ставится). Ученики говорят свою отметку учителю, которая и выставляется в журнал.

Итак, ученик поставлен в ситуацию, когда он вынужден работать в темпе, заданном учителем, контролировать свои действия и использовать весь материал темы. Очевидно что, хотя этот урок и называется устной контрольной работой, не всегда контроль является главной его целью. Сверхзадача урока – обучение рациональным приемам работы, без которых невозможно творчество. Работа может занимать как часть урока, так и весь урок (в старших классах).

Приведу примеры нескольких   таких  контрольных по  некоторым темам математики и алгебры.

Тема . Формулы сокращенного умножения

Упростить:

1)    (a –b)(a + b) ;    2) (a + b)(a - b) ;   3) ( b –a)(a + b) ;    4) (- a –b)(a + b) ;   

5) (- a –b)(a - b) ;    6) (2a –2b)(a + b) ;   7)  ( b – x)( a + b) ;   

Разложите на множители:

8)  a² – b² = (  – )(  +  );   9) 4a² – b² = (  –  )(  +  );  10)  a⁸ – b⁸ =       (  – )(  +  );

10)  a¹⁰ – b¹⁰ = (  – )(  +  );    11)   a²ⁿ – b²ⁿ = (  – )(  +  );

 12)  a³² – b³² = (  – )(  +  );

Примеры контрольных работ:

Тема. Решение уравнений  (6 класс)

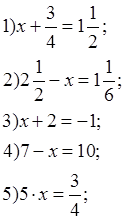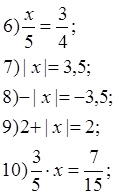Нетрудно увидеть , что работа это проверочная - уравнения составлены так, что среди них нет даже двух аналогичных. За 10 решенных примеров ставятся  две пятерки, за 8-9 –пять, за 6-7 –четыре.

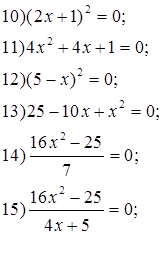
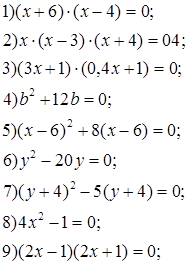Тема. Решение уравнений  (8  класс)

Тема. Теорема Виета   (8 класс)

1)    Не решая уравнения, найти сумму  и произведение их корней:

а) х² -  11х +20 = 0;    б)  2х² -  25х +18 = 0;      в) 2 х² -  5х + 18 = 0;

2)  Найти корни уравнения, применяя теорему Виета:

 а) х² -  16х +5 = 0;    б)  х² -  7х +12 = 0;      в)  х² -  8х + 15 = 0;

3)  Составьте приведенное квадратное уравнение, если его корни:

а) х₁ = - 3, х₂ = 1;    б) х₁ = - 3, х₂ = - 4;         в)  х₁ = 5, х₂ = 6; 

      4)  Не решая уравнение    х² +5х - 1 = 0, найти:

а) сумму корней;   б) произведение  корней ;   в) квадрат  суммы  корней ;

в) суммы квадратов  корней ;  д)   +    ;

     5)  Один из корней  уравнения  х² + рх – 18 =0 равен 2.  Найти  р и другой корень .

     6)  Один из корней  уравнения  х² + 6х – q = 0 равен 1.  Найти  q и другой корень.

     7)  Один из корней  уравнения  х² + 2pх – 6 = 0 равен  -3.  Найти  p  и другой корень.

    8)  Один из корней  уравнения  х² - 7х – 3p = 0 равен  7.  Найти  p  и другой корень.

    9) Дано   уравнение   2х² - 5х – 6 = 0. 

а)  Можно ли утверждать, что оба его корня положительные?

б)  Можно ли утверждать, что   модуль отрицательного корня больше?

в)  Внесите изменение в данное уравнение, чтобы модуль отрицательного корня был больше.

Контрольная составлена из примеров, аналогичных тем,  которые решались  на предыдущих уроках в классе и дома. Поэтому она носит, с одной стороны, проверочный характер, с другой стороны, так как содержит ряд примеров, решаемых одним способом, дает возможность ученикам ликвидировать пробелы в знаниях, если они имеются.

Список использованной литературы:

Алгебра 8 кл..учебник для общеобразоват. учреждений: Мордкович А.Г.– М.: Мнемозина, 2010 ;

Математика 6: учеб.для общеобразоват. учреждений :  Н.Я.Виленкин,  В.И. Жохов и др.– М.: Мнемозина, 2007;

А.А.Окунев Спасибо за урок, дети!:Кн. для учителя:- М.:Просвещение , 1988.