Методическая разработка открытого урока на тему: "Линейная функция"

Методическая разработка открытого урока на тему: "Линейная функция"

Цели урока:

• повторить материал по данной теме;
• расширить знания учащихся по применению линейной функции в различных областях естествознания;
• оценить знания учащихся;
• прививать умение самостоятельно работать и оценивать свои знания.

Универсальные учебные действия

Личностные Умение самостоятельно делать свой выбор в мире мыслей, личностная саморефлексия, мотивация к познанию, учебе.

Регулятивные Умения организовывать свою деятельность, увидеть проблему, соотносить результат своей деятельности с целью и оценивать его.

Познавательные  умения результативно мыслить, извлекать информацию, добывать новые знания, анализировать, обобщать, сравнивать для получения необходимого результата.

Коммуникативные Умения общаться с людьми, доносить свою позицию до других.

Задачи:

1.      Образовательные: способствовать понимаю учащимися практической значимости изучаемого материала;

2.      Развивающие: совершенствовать навыки построения графиков линейных функций; способствовать развитию информационной, учебно- познавательной и коммуникативной компетенций учащихся.

3.      Воспитывающие: воспитывать культуру речи, аккуратность, внимательность при построении графиков линейных функций

Основной дидактический метод: продуктивный.

Частные методы и приемы:

1.      Метод проблемной ситуации.

2.      Метод поводящего диалога.

3.      Поисковый.

4.      Наглядный.

5.      Дифференцированный подход

Основной дидактический метод: продуктивный.

Частные методы и приемы:

1.      Метод проблемной ситуации.

2.      Метод поводящего диалога.

3.      Поисковый.

4.      Наглядный.

5.      5.Дифференцированный подход

Дидактические и технические средства: Презентация; доска; учебники.

 Планируемые результаты

Личностные: умение самостоятельно делать свой выбор в мире мыслей

Предметные: проведенный урок будет способствовать формированию стремления применять полученные знания на практике и положительного отношения и интереса к изучению математики.

Метапредметные: находить нужную информацию; формирование компетентности в предметной области.

Ход урока

1. Организованный момент: учитель сообщает тему и план урока.

2. Устная работа.

Фронтальный опрос. 1.

• Сформулируйте определение линейной функции.
• Что является графиком линейной функции?
• Как построить график линейной функции?
• Какую функцию называют прямой пропорциональностью?
• Как построить график функции y = kx?
• Как расположен в координатной плоскости график функции y = k x при k>0 и при k<0?  слайды

2.Линейная функция вокруг нас.

Домашнее задание учащихся к уроку было творческое: подобрать материал, и, если возможно, наглядно оформить материал по теме: “Где пользуется и применяется линейная функция”.

Ученики подобрали материал из различных областей естествознания и нашли линейную зависимость между:

- массой тела и силой тяжести: Fтяж = mg;

- массой тела и плотностью вещества

- калорийность и жирностью молока.

. №3 Задана функция: y = 0,2x – 3 . Индивидуальная работа у доски.

Найдите: 1) y(-2)  2) x , если y = 5;

4 Тест

Дана функция y = 2x – 3. Вычислите значения функции при x = -3 и x = 1. Запишите сумму получившихся значений:

а) -9; б) -1; в) -10; г) 2.

2. Для функции y = -1,5x – 5. Найдите значение x, при котором y = 1.

а) -1,5; б) -4; в) -2; г) 2,5.

3. Укажите координаты точки пересечения графиков функций y = 1,5x – 2 и y = 4 – 0,5x.

а) (3; 2,5); б) (-3; -6,5); в) (; -1,.5); г) (-; -2,5).

График функции y = k x+5 проходит через точку М(-7;12). Найдите k.

а) 1; б) -1; в) -6; г) .

Ответ: (через 8 минут откидная доска открывается, на котором находятся ответы к тесту). Учащиеся сами оценивают свою работу.

5. Построить график линейной функции.

I вар.: y = -1/2*x + 2

II вар.: y = 2 – 0,5x

Один ученик производит выполнение построения графика на доске.

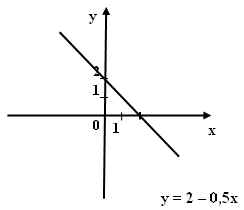
6. Работа с построенным графиком.

Определить

- значение аргумента, если y = - 3;

- значение функции, если x = - 2;

- какое-нибудь значение аргумента, при котором y > 0;

- какое-нибудь значение аргумента, при котором y < 0;

- координаты точек пересечения с осями координат.

7. Определение другим способом (аналитическим) координат точек пересечения с осями координат графика функции.

Аналитический способ. Функция задана формулой: y = -0,6х + 3

Определить координаты точки пересечения графика функции с осью абсцисс с осью ординат. У доски определяют координаты графика два ученика:  ответ

8. Построить графики функций и исследовать свойства этих функций.

• 1 вариант у = 3х – 1, у = 3х + 5, у = 3х.
• 2 вариант у = -5х + 2, у = -5х – 3, у = -5х.
• 3 вариант у = 4х – 1, у = -3х + 2, у =

Представители от каждого варианта рассказывают о результатах своих исследований, отвечая на вопросы.

• Графики, каких функций вы строили? Ответ. Графики линейных функций и прямой пропорциональности.
• Что является графиком каждой функции? Ответ. Графиками являются прямые.
• Как ведут себя прямые, являющиеся графиками линейных функций с одинаковыми коэффициентами при х Ответ. Графиками являются параллельные прямые.
• Как ведут себя прямые, являющиеся графиками линейных функций с разными коэффициентами при х? Ответ. Графики этих функций пересекаются.

Обсудив вместе с остальными учащимися полученные результаты, сравнив их и выявив закономерности взаимного расположения графиков линейных функций, переходим к выводу. слайд

Вывод: При одинаковых значениях k, графиками линейных функций являются параллельные прямые, а при различных значениях – графики пересекаются.

9. Работа по готовому чертежу.

Определить какому из графиков соответствует каждая функция:

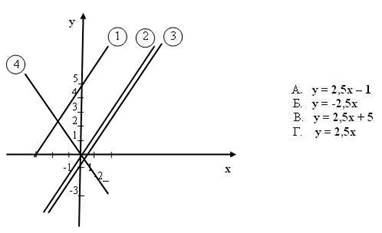
Устно с учащимися разбирается выбор соответствующих функций и определяется (обобщается) геометрический смысл коэффициентов “k” и “b” в уравнении прямой: y = kx + b.

10. По этому же чертежу определяется взаимное расположение графиков линейных функций.

Учащиеся формулируют признак, по которому можно определить, не выполняя построения прямых: каково взаимное расположение прямых на координатной плоскости. 11 Определение координат точки пересечения графиков функций. Работа с учебником

У доски ученик выполняет № 383 (а).

12.Домашнее задание №327.328.

13.С учетом работы в течение всего урока комментируются и оцениваются ответы учащихся

Рефлексия. Скажите, ребята, а что нового вы узнали сегодня на уроке?