Методическая разработка открытого урока по алгебре в 10 классе на тему: «Показательная функция, уравнения, неравенства»

Цели:  

—  Обобщить и закрепить теоретические знания методов,      умения и навыки решения показательных уравнений и неравенств на основе свойств показательной функции.

—  Развивать монологическую речь, правильное оформление решений КИМов ЕГЭ, вычислительные навыки.

—  Воспитывать трудолюбие, терпение, усидчивость, умение слушать товарищей, работать в группе.

План урока:

1.Организационный момент. Через 1,5 года вы подойдете к важной черте вашей жизни к итоговой аттестации. С какими заданиями вы уже можете справиться. Что вы изучали на последних уроках. Сегодняшний урок –урок обобщения .

Слайд (4-9): тема “Показательная функция , при ,   при ее графики и свойства”
Слайд (4) Актуализация опорных знаний.  Блиц – опрос.

1. Какая функция называется показательной?

2.Свойства показательной функции?

3.График  показательной функции?

4.Свойства степени?

5. Какое уравнение называют показательным?

6.Способы решения показательных уравнений?

7.Показательные неравенства?

8.Как решать показательные неравенства?

9.Какова область определения  функции у=0,3х?

10.Каково множество значений функции у=3х?

11.Возрастает или убывает  показательная функция

12.Определить при каком значении а, функция

 проходит через точку А(1;2)

13

Слайд(10-15): анализ методов решения показательных уравнений. Диагностика уровня формирования  практических навыков. Выбор  уравнений указанным методом.

Слайд (17) Указать способы решения показательных уравнений.

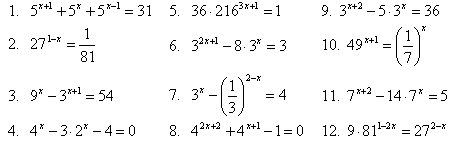
Слайд (18) Диагностика уровня формирования  практических навыков

Сейчас мы работаем по теме показательные неравенства

Слайд(16)

Слайд(19): Решение показательных неравенств.

Слайд(20).

 Слайд(21) Математический диктант. Если ответ правильный то «+»; если неверный то «-» 

Слайд (22) Ответ.

- + - - -

Слайд(23) Работа учащихся группами.                                                                   

       Разгадай ребус.

В данном задании зашифровано имя математика, которых впервые ввёл понятие показательной функции ( Лейбниц)

Слайд(24)

Для внеаудиторной работы предлагается учащимся подготовить небольшие сообщения по теме : «Готфрид Лейбниц»

Пауза «И в шутку и всерьез»                           

После напряжённой работы предлагаю вам слегка отдохнуть и ответить на несколько шуточных вопросов, где нужны не только знания , но и чувство юмора.

- Самая нелюбимая оценка ученика?

- Утверждение, принимаемое без доказательств.

- Проверка учеников на выживание?

- Независимая переменная в функ

Слайд(25). Найдите корень уравнения или сумму корней

1.2

2.3

3.1

4.0

Слайд (26). Ответ

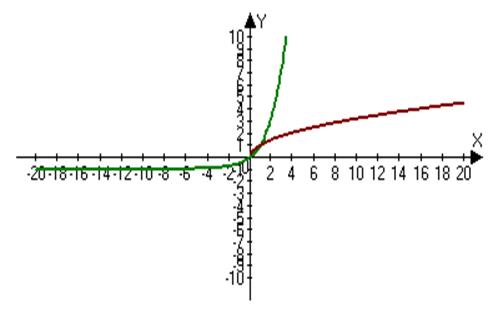
1. 2

2. 3

3. 1

4. 0

Слайд (27). Решить неравенство

Слайд (28). Ответ

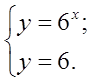 Слайд (29). Решить неравенство

Слайд (30). Ответ

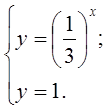
 Самостоятельная работа.

Раздаются карточки с заданиями ЕГЭ. Учащиеся решают в тетради, а выбранный ответ записывают в ранее заготовленную таблицу и сдают учителю.

1 вариант

1.Укажите промежуток, которому принадлежит корень уравнения

1)  ;        2) ;       3)   ;       4)  .

2.Найдите произведение корней уравнения

1) -6;             2) -4;            3) 4;              4) 6

3. Найдите промежуток, которому принадлежит корень уравнения

1) ;        2) ;        3) ;           4) .

4.Решите неравенство

1) ;         2) ;              3) ;           4) .

5.Найдите число целых отрицательных решений неравенства

1) 6;            2)  2;          3) 5;           4) 4

           2 вариант

1.Укажите промежуток, которому принадлежит корень уравнения

1)  ;        2) ;       3)   ;       4)  .

2.Найдите сумму корней уравнения

1) -2;             2) 0;            3) 1;              4) 2

3. Найдите промежуток, которому принадлежит корень уравнения

1) ;        2) ;        3) ;           4) .

4.Решите неравенство

1) ;         2) ;              3) ;           4) .

5.Найдите число целых отрицательных решений неравенства

>1

1) 6;            2)  12;          3) 10;           4) 11

Слайд(31). Ответ

1 вариант

2 вариант

Поведение итогов, выставление оценок по всем видам работ , проведённых в течение урока.

Домашнее задание. Задание на карточках.