Методическая разработка по теме "Математика в профессиях"

Кировское областное государственное профессиональное образовательное бюджетное учреждение «Кировский сельскохозяйственный техникум имени дважды Героя Социалистического Труда А. Д. Червякова»

Методическая разработка по теме

«Математика в профессиях»

 

Преподаватель:

Князева С. В.

 

 

 

 

 

 

 

 

 

г. Котельнич

 2022 г.

 

Содержание

1.                 Введение........................................................................................2

2.                 Математика – часть нашей жизни...............................................3

3.                 Математика в профессиях:

3.1.    Бухгалтер........................................................................................4

3.2.    Газовик............................................................................................7

3.3.    Механик..........................................................................................9

3.4.    Автомеханик..................................................................................10

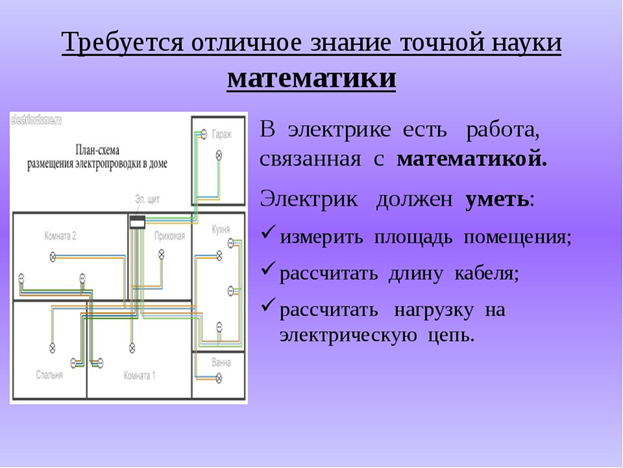
3.5.    Электрик.........................................................................................14

3.6.    Технолог общественного питания...............................................17

4.                 Заключение.....................................................................................29

5.                 Приложения

5.1.    Приложение 1…………………………………………………….31

5.2.    Приложение 2…………………………………………………….40

5.3.    Приложение 3…………………………………………………….42

6.                 Информационные источники........................................................43

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1.Введение.

Наука под названием математика в мире профессий необходима буквально повсюду, более того, она необходима на каждом шагу в повседневной жизни человека. Без нее невозможно не только построить дом, но и соорудить даже собачью будку, посчитать мелочь в кармане и купюры в бумажнике, измерить расстояние до соседского забора.

Из истории известно, что древние греки рекомендовали изучать математику для познания окружающего мира, а римляне для того, чтобы строить города, дорожную и мостовую инфраструктуру, отмерять земельные участки легионерам. Если бы наши предки не знали математики, разве изобрели бы они самолет или ракету, холодильник или телевизор, автомобиль или велосипед?

Трудно перечислить все профессии в которых нужна математика, однако это не станет препятствием, для того чтобы рассказать о важной роли, которую имеет математика в профессиях людей.

Приходя в наш техникум учиться, многие студенты на уроках математики часто задают один и тот же вопрос:  а зачем нам это нужно, где в жизни пригодится нам эта математика, для чего её вообще нужно изучать, если мы пришли конкретно получить специальность. Поэтому цель данной методической разработки – показать, как и где применяется математика в тех специальностях, по которым  получают образование в нашем техникуме, какие конкретные математические задачи приходится решать специалистам этих  профессий.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2. Математика – часть нашей жизни

«Нет ни одной области математики, как бы абстрактна она не была, которая когда-нибудь не окажется применимой к явлениям действительного мира».

Н. И. Лобачевский

Математика (греч. mathematike, от mathema - знание, наука) - наука, в которой изучаются пространственные формы и количественные отношения. Математика дает людям методы изучения и познания окружающего мира, методы исследования как теоретических, так и практических проблем.

Не раз приходилось слышать фразу о том, что математика - страна без границ. Несмотря на свою банальность, фраза о математике имеет под собой очень веские основания. Математика в жизни человека занимает особое место. Мы настолько срослись с ней, что попросту не замечаем её.

А ведь с математики начинается всё. Ребёнок только родился, а первые цифры в его жизни уже звучат: рост, вес.Малыш растет, не может выговорить слова "математика", а уже занимается ею, решает небольшие задачи по подсчету игрушек, кубиков. Да и родители о математике и задачах не забывают. Готовя ребёнку пищу, взвешивая его, им приходится использовать математику. Ведь нужно решить элементарные задачи: сколько еды нужно приготовить для малыша, учитывая его вес.

В школе математических задач приходится решать очень много и сложность их с каждым годом растет. Они не просто учат ребенка математике и определённым действиям. Математические задачи развивают мышление, логику, комплекс умений: умение группировать предметы, раскрывать закономерности, определять связи между явлениями, принимать решения.

Очень часто решения таких задач являются просто математическим расчётом. Занятия математикой, решение математических задач развивает личность, делает её целеустремленнее, активнее, самостоятельнее.

Те, кто хорошо разбираются в математике, успешно могут решать задачи, аргументировать свой выбор, могут  критически оценить себя и своих одноклассников. Да и успеваемость по остальным предметам, кроме математики, оказывается у них, как правило,  на порядок выше. Именно математическое мышление помогает им в этом.

Математика встречается и используется в повседневной жизни, следо-вательно определенные математические навыки нужны каждому человеку. Не правда ли, нам приходится в жизни считать (например, деньги), мы по-стоянно используем (часто не замечая этого) знания о величинах, характеризующих протяжённости, площади, объёмы, промежутки времени, скорости и многое другое. Всё это пришло к нам на уроках арифметики и геометрии и сгодилось для ориентации в окружающем мире.

Во время учёбы в вузе, на работе и дома нужно постоянно решать задачи, и не только математические. Какова вероятность успешной сдачи экзамена по математике? Сколько денег нужно заработать, чтобы купить квартиру? Каким должен быть объём вашего дома и сколько для этого нужно приобрести кирпича. Как правильно рассчитать, чтобы родилась девочка или мальчик? И тут на помощь придёт математика. Она следует за человеком везде, помогает ему решать задачи, делает его жизнь намного удобнее.

Математические знания и навыки необходимы практически во всех профессиях, прежде всего, конечно, в тех, что связаны с естественными науками, техникой и экономикой.

Также в наше время существует  необходимость применения матема-тических знаний и математического мышления врачу, лингвисту, историку, и трудно оборвать этот список, настолько важно математическое образование для профессиональной деятельности в наше время. Следовательно, математика и математическое образование нужны для подготовки к будущей профессии.

Философское постижение Мира, его общих закономерностей и основ-ных научных концепций также не возможно без математики. И потому математика необходима для формирования мировоззрения.

3.     Математика в профессиях

3.1.Математика в профессии бухгалтера.

Когда неожиданно задают вопрос, в каких профессиях нужна математика, то первое, что приходит на память это, конечно же, профессия бухгалтера. Тут, как говорится, сам Всевышний велел бухгалтерам быть хорошими математиками. От их математических способностей в некоторых случаях зависят судьбы даже компаний и фирм. Чего стоит ошибиться бухгалтеру в расчетах налоговых отчислений или начисления зарплаты сотрудникам? В первом случае – это штрафные санкции со стороны налоговиков, а то и уголовное дело от прокуратуры, а во втором - скандал и потеря репутации организации.

На знаниях математики основываются такие прикладные профессии, как бухгалтер или экономист, весьма востребованные в наше время. Чтобы уметь высчитывать НДС, или делать любые другие бухгалтерские расчеты, по сути, нужно уметь быстро получать решение математических задач. Бухгалтерия невозможна и нереализуема без применения математики.

В России профессия бухгалтера стала особенно востребованной в начале 90-х годов, когда на рынок вышли тысячи предприятий малого и среднего бизнеса. Бухгалтерия необходима на любом предприятии, любой фирме, абсолютно неважно, какого рода деятельности. Основные бухгалтерские понятия всегда имеют под собой математическую основу, и любой бухгалтерский расчет – это математический расчет, основанный на тех же математических правилах, терминах, законах и понятиях.

 История развития бухгалтерии начинается в глубокой древности. Еще первобытные хозяйственники вели бухгалтерию. Учет тех лет начинался и заканчивался в головах людей, его ведущих, а единственным учетным регистром для бухгалтера тех лет служил он сам. Реализация этой потребности запоминать была бы невозможна без развития алфавита и цифр. Неслучайно и язык, и математика получили толчок к развитию именно благодаря хозяйственной деятельности, торговле и бухгалтерии. Многие математики рассматривали бухгалтерский учет как частный случай прикладной математики.

Бухгалтерский учет в его современном понимании - это продолжение вне человека его способности запоминать то, что происходит в хозяйстве. В этой профессии как в никакой другой профессии нужна математика. Именно в математике бухгалтерский учет позаимствовал одну из главных своих качеств - точность. Она необходима для выполнения расчетов, неслучайно бухгалтеров еще называют счетными работниками.

На гербе бухгалтеров, признанном интернациональной эмблемой счетных работников, изображены солнце, весы, кривая Бернулли и начертан девиз: "Наука, доверие, независимость". Солнце символизирует освещение бухгалтерским учетом финансовой деятельности, весы - баланс, а кривая Бернулли - символ того, что учет, возникший однажды, будет существовать вечно.

Бухгалтер - лицо, ответственное за финансовый учет и отчетность организации. Его задачи: вовремя и правильно заплатить налоги, отчитаться перед государственными органами и собственниками компании, организовать работу с клиентами и партнёрами организации, следить за финансовым состоянием предприятия и так далее. Основными качествами, которые следует иметь бухгалтеру, являются: математические способности, аналитический склад ума, усидчивость и скрупулезность. Кроме того, необходим высокий уровень внимания, счетно- аналитические способности, хорошая оперативная память, склонность к работе с числами, эмоциональная устойчивость, склонность к систематической работе с литературой; аккуратность, сосредоточенность, терпение, а также ответственность и организованность. В практической работе бухгалтер постоянно встречается со всеми арифметическими действиями, с начислением простых и сложных процентов, широко использует матричную модель взаимосвязи счетов, теорию множеств, математическую логику.

Наконец, математика нужна для алгоритмизации учетных процессов. Это предусматривает составление математического  описания учетной задачи (составление алгоритма и программы ее реализации на ЭВМ).  Математическая модель бухгалтерского учета имеет перспективу быть понятой и принятой специалистами в любой стране мира, т.к. язык математики обладает необходимым единообразием в понимании. Глобальная математическая модель бухгалтерского учета и формирования финансовой отчетности - это ключ к взаимопониманию между бухгалтерами и финансовыми аналитиками всех стран мира. В основу ее построения положены понятия как корреспонденция счетов и бухгалтерская проводка в терминах и элементарных операциях матричной алгебры. Производство, торговля, сфера обслуживания, финансовые и государственные учреждения – всюду нужны бухгалтера, человеку с такой профессией всегда найдется рабочее место. И для того чтобы быть хорошим бухгалтером, настоящим специалистом, нужно всегда, в любых случаях, уметь решать математические задачи.

 Рассмотрим некоторые задачи, решаемые каждым бухгалтером:

Сколько за месяц получит работник больницы, если норма его работы

160 ч., оклад 5550 руб., а отработано 170 ч.? Ответ: 9750 руб.

 2. Нужно составить расчёт о расходе лекарств за месяц. Условие такое: на складе имеются лекарства на сумму 35000р., поступило на склад с аптеки лекарств на сумму 12000р. Осталось после раздачи лекарств на сумму 29000р. Ответ: 18000 руб - расход . Бухгалтеру приходится  решать множество специфических задач, где без  математических расчётов просто не обойтись. (Приложение 1).

Ещё математика является не только мощным средством решения прикладных задач и универсальным языком науки, но также и элементом общей культуры. Поэтому математическое образование следует рассматривать как важнейшую составляющую в системе фундаментальной подготовки современного бухгалтера. В бухгалтерии важно не знание математики, а умение применять её на практике.

         Таким образом, бухгалтерия и математика, по сути, неразделимы, не может быть никакой бухгалтерии без знания математики.

 

3.2. Математика в профессии газовика

Газовик – это профессия, которая приносит неоценимую тепло и уют всему человечеству. Это газ в наших домах, благодаря которому работают электростанции и горит свет в наших домах. С чем же в первую очередь у людей ассоциируется профессия "газовик"? Правильно, газ - значит деньги, а газовик - значит большая зарплата. А ведь многие совершенно не знают иной стороны медали. Газовик - это профессия, которая дает возможность познать все краски недр нашей земли: местами золотой, серебряной, а местами угольно черной.

В любую погоду, днем и ночью, во всех местах требуется своевременно, ответственно, при строгом соблюдении технических норм, грамотно и безопасно выполнять свои профессиональные обязанности.

Газовик – это профессия, окутанная в романтический ореол судьбы. Газовик, ровно, как и нефтяник, постоянно покидает обжитые места в поисках новых месторождений, он работает в условиях суровой тайги и тундры, безводных пустынь и бескрайних степей. Кроме того, профессии «газовик» - это еще и постоянные физические нагрузки, бытовая неустроенность, значительные нервные перегрузки, высокая заболеваемость и производственный травматизм.  Газовик – это человек, который самоотверженно добывает для своей страны столь ценное «голубое золото». Ведь газ – это, прежде всего -тепло ,а также, химия, удобрения, различные красители, синтетические материалы и взрывчатое вещество.

Газ – это полезное ископаемое, которое концентрируется в подземном хранилище, образовавшееся в результате постепенного формирования земной коры. Сегодня по длинным газопроводам газ переносится под давлением на расстояния в тысячи километров, обеспечивая дома, металлургические заводы и электростанции горючим.  Добыча природных ископаемых, таких как газ, влечет за собой значительный выброс различного рода вредных и взрывоопасных веществ, несомненно, присутствующих в газе. Вот почему газовик – это риск и опасность. Но есть и положительная сторона, от которой не скрыться, газовики – творцы современной экономики страны. Ведь именно развитие экономики является вечным прогрессом всего народа и всей эволюции в целом.  Газовик – профессия неотъемлемого звена, которое так яро служит всем людям во благо. 

И, конечно, газовикам, как и представителям других профессий, тоже приходится решать задачи, связанные с математическими расчётами: определять давление, массу, объём газа в баллонах, длину и массу труб для проложения газопроводов и многое другое.

Рассмотрим например такую задачу:

Найти массу десятиметровой трубы, диаметром 1420мм, сделанной из стального листа толщиной 22 мм. Плотность стали 7600кг\м³. Сколько тонн таких стальных труб потребуется, чтобы уложить газопровод Уренгой- Ужгород, длина которого 4451км?

Эта и многие другие задачи показывают необходимость знания математики и применения её в профессии газовиков.

 

3.3. Математика в профессии механика

Будущий специалист «Техник – механик» будет  выполнять операции по техническому обслуживанию и ремонту автотранспортных средств, контролировать техническое состояние автомобилей с помощью диагностического оборудования и приборов, управлять автотранспортными средствами. Следовательно, математика в этой профессии просто необходима.

Эта профессия позволяет увеличивать сроки эксплуатации автомобиля, осуществлять своевременную профилактику его функционального состояния, что обеспечивает безопасность дорожного движения.

При ремонте автомобилей и тракторов все детали и механизмы подбираются по номерам, размерам с использованием инструментов, которые без знаний математики -  просто металлолом (микрометр, штангенциркуль …).

Область машины,  где пригодятся знания по математике:

1. Для подбора поршней к цилиндрам вычисляют зазор между ними.

2. Регулировка люфта рулевого управления.

3.Регулировка автомобильных фар.

Описание этих видов деятельности подробно рассмотрено в профессии автомеханика.

Как и всякая наука, математика имеет свою историю, подчас не менее интересную, чем история войн, государств, великих личностей. На протяжении тысячелетий – от зари человечества, когда первые математические символы – числа только появлялись и имели причудливую, непонятную для нынешнего человека форму до современности, эпохи компьютеров, работающих на основе математических законов – формировалась математическая наука.

С помощью решения производственных задач с применением математического аппарата можно определить тормозной путь, при экспертном доказательстве вины водителя, определить безопасную дистанцию.[2]

Задача 1.

  Индикаторная мощность двигателя внутреннего сгорания (ДВС) на маховике равна 150 л.с.. Чему равна эффективная мощность этого ДВС?

Эффективная мощность всегда меньше индикаторной на 10%-15%, так как часть индикаторной мощности расходуется на преодоление сил трения.     150-10% = 150-15= 135 л.с.[1]

Задача 2.

Определить тормозной путь легкового автомобиля с ϑ=80км/ч на сухом асфальта-бетоне, если при ϑ=40км/ч он составляет — 14,5 метров.

Тормозной путь примерно равен квадрату скорости –S=ϑ². Если при 40 км/ч, S_торм. = 14,5м, то при 80 км/ч: 14,5*4~58 метров.[1]

 

Задача 3.

Определить безопасную дистанцию при ϑ=90км/ч.

Безопасной считается дистанция, которую автомобиль проходит за 2 секунды.

Чтобы узнать безопасную дистанцию, мы должны узнать расстояние, пройденное автомобилем за секунду, и умножить её на 2.(90:10*3)*2=27*2~54 метра.

Не будем забывать, что специальность, которую получают в нашем техникуме,  называется «Механизация сельского хозяйства», поэтому кроме всех рассмотренных выше задач, специалистам этого профиля приходится также решать и множество задач, связанных с сельским хозяйством. (Приложение 2).

Таким образом,  для профессии механика всегда необходимо уметь решать задачи на движение, проценты, площади и объемы, составление уравнений и систем уравнений.

 

3.4. Математика в профессии автомеханика

Математика в профессии автомеханика тоже играет не последнюю роль. Выставить параметры необходимого развала – схождения колес автомобиля, отрегулировать свет фар и зазоры клапанов в двигателе, рассчитать остаточный ресурс мотора и всего автомобиля, даже зазор в свечах зажигания невозможно выставить без математических знаний. Между прочим, от всего перечисленного зависит безопасность, как самого автомобиля, так и водителя, а также его пассажиров и других людей, которые находятся на дороге.

Ответственность автомеханика, можно сравнить с ответственностью врача, потому что его ошибка в математических расчетах может привести к дорожной аварии с последствиями для жизни и здоровья людей.

Автомеханик – это рабочий широкого профиля, который выполняет операции по техническому обслуживанию и ремонту автотранспортных средств, контролирует техническое состояние автомобилей с помощью диагностического оборудования и приборов, управляет автотранспортными средствами. Немного из  истории профессии «автомеханик»...

Первые самоходные коляски появились в XVIII веке в разных странах мира. В течение длительного времени они видоизменялись и совершенствовались. Но, как всякий механизм, они требовали ухода и ремонта в случае поломки. Этим могли заниматься только люди, хорошо разбирающиеся во внутреннем устройстве автомобиля. Так появилась новая профессия – автомеханик или автослесарь. Эта профессия позволяет увеличивать сроки эксплуатации автомобиля, осуществлять своевременную профилактику его функционального состояния, что обеспечивает безопасность дорожного движения.

 

Виды деятельности профессии автомеханика:
1..Установление технического диагноза путем внешнего осмотра и инструментального контроля;

2.. Своевременное и качественное проведение технического обслуживания автомобиля;

 3. Осуществление ремонта автомобиля и его деталей.

 

Где именно при ремонте автомобиля пригодятся знания по математике?

Рассмотрим,  какие именно математические знания, умения и навыки необходимы автомеханику на определенных этапах работы.

1. Автомобильные фары. Для того, чтобы зеркало фар отражало лучи параллельным пучком, зеркалу нужно придать форму параболоида вращения, внутри которого в отдельной точке находится лампочка. Параболоид вращения – это поверхность, которая образуется при вращении параболы вокруг её оси. В курсе алгебры  изучается  тема «Квадратичная функция и её свойства».

2. Изготовление шестерёнок. Чтобы изготовить шестеренку надо окружность разделить на n-равных частей. С этой задачей мы встречались на уроках геометрии: научились при помощи циркуля , линейки и транспортира делить окружность на любое количество равных частей. Здесь используется формула для вычисления угла правильного n-угольника.

3. Подбор поршней к цилиндрам. Для подбора поршней к цилиндрам вычисляют зазор между ними. Зазор определяется как разность между замеренными диаметрами поршня и цилиндра. Номинальный зазор равен 0,025-0,045 мм, предельно допустимый – 0,15 мм.

Диаметр поршня измеряют микрометром в плоскости, перпендикулярной оси поршневого пальца, на расстоянии 51,5 мм днища поршня.

4.Установка катафотов. Отражающая поверхность световозвращателей сделана из множества прямоугольных пирамидок, попавший на них свет от внешнего источника отражается точно в обратном направлении, то есть в сторону того же источника. Благодаря этому в свете фар своего автомобиля можно заметить на дороге или обочине машину с выключенными габаритными огнями.

5.Проверка рулевого управления.

Пустить двигатель и установить колеса прямо.Слегка повернуть рулевое колесо в одну и другую сторону.

В случае, если люфт  составляет более 30 мм, необходимо проверить рулевое управление и все детали рулевого механизма на чрезмерный люфт.

На легковом автомобиле люфт не должен превышать 10 градусов, на грузовом — 25 градусов, на автобусе — 20 градусов.

Ещё можно предложить разобрать решения следующих нескольких производственных задач с применением математического аппарата:

Задача 1. Индикаторная мощность ДВС на маховике 150 л. с. Чему равна эффективная мощность этого ДВС ?

Задача 2. Определить максимальный крутящий момент на вторичном валу КПП, если этот момент на маховике равен 45 ? а передаточное число первой передачи – 7?

Задача 3. Плотность электролита полностью заряженной АКБ – 1.27 г/см³. При очередном ТО-2 показания амперметра – 1,22 г/см³. На сколько % разрядилась батарея и допускается ли ее эксплуатация в зимнее время?

Задача 4. реакция водителя не должна превышать – 1 сек. Какое расстояние пройдет автомобиль за 1 секунду при V = 80 км/ч.

Задача 5. Определить безопасную дистанцию при V = 90 км/ч.

Задача 6. Определить тормозной путь легкового автомобиля при  V = 40 км/ч на сухом асфальтобетонном покрытии, если при  он составляет 14.5 м.

Задача 7. Выдержит ли ледовая переправа грузовой автомобиль КАМАЗ-4310 массой 16000 кг, если толщина льда – 45 см?

Убедились, знание математики не только нужны, но и необходимы каждому автомеханику, чтобы он был грамотным, любящим свою работу специалистом. В конце урока можно с детьми провести интеллект- шоу, предложив следующие интересные вопросы:

1.С чей легкой руки безбрежное пространство, которое бороздят космические корабли и спутники получило название «Космос». (Пифагора).

2.Кто ввел в химическую практику весы? (Ломоносов).

3.В каком году и кто начал проводить эксперименты с двигателем внутреннего сгорания?(1884г.Евгений Александрович Яковлев).

4.Назовите фамилию немецкого инженера, который является изобретателем автомобиля. В 1885 году он построил первый в мире автомобиль. Патент на изобретение этого автомобиля был получен им в 1886 году. (Бенц)

5.Назовите марку автомобиля, которую выпускал в Советском Союзе завод «Коммунар». Мощность двигателя – 30,1 кВт, (40 лошадиных сил), скорость – 118 км/ч. (Запорожец)

6.Известно, что первый светофор представлял из себя вращающийся газовый фонарь, который излучал сигналы красного и зеленого цветов. Этот светофор был установлен в Лондоне в декабре 1868 года и предназначался для транспортных средств, что облегчало переход пешеходов через улицу. В январе 1869 года устройство взорвалось, ранив полицейского, и эта идея регулирования движения была реализована впоследствии только через 40 лет. Назовите фамилию человека, который изобрел светофор. (Найт)

Естественно, на этом обязанности автомеханика, связанные с математикой, не заканчиваются. Тема столь глубока, что ей можно посвятить отдельную статью, рассматривая каждый индивидуальный случай по отдельности.

3.5.          Математика в профессии электрика.

Электрик - специалист, занимающийся техническим обслуживанием, эксплуатацией и ремонтом электромеханического и технического оборудования на производстве и в быту.

 Данная профессия возникла в 19 веке вместе с появлением первых электростанций, и в первую очередь была вызвана необходимостью прокладывать провода и кабеля. Совершенствование электротехники привело к разветвлению профессии на более узкие специальности и в настоящее время их насчитывается несколько десятков: электрик-электромонтажник, электрик – электрослесарь, техник  электрик, электрик – электромеханик и проч. Огромная сфера обслуживания  данных специалистов начинается с автоматических выключателей, розеток и бытовой электропроводки, а заканчивается ремонтом линий электропередач, монтажом и наладкой электрооборудования, проектированием систем электроснабжения, измерением сопротивления изоляции кабеля.

В своей работе электрик  должен иметь базовые знания по физике, математике, черчению, прикладной механике. Знать устройство, технические характеристики и принципы действия обслуживаемых приборов, датчиков. Понимать виды и причины их повреждений, правила ремонта оборудования.

В строительных, монтажных и ремонтно-строительных организациях  электрик выполняет слесарные работы при монтаже электроконструкций. Делает разметку электроконструкций с помощью геометрии и черчения по образцам и чертежам, устанавливает электрооборудование.                                                                                                                                                                                                                                                                                                                                                                                    

Электрик должен обладать высоким чувством ответственности, быть осторожным, предусмотрительным и наблюдательным. Ему необходимы хорошая зрительная память, хорошее зрение, слух и обоняние, хладнокровие, ясность мысли, способность к логическому мышлению (а ведь именно изучение математики прекрасно развивает логическое мышление!), настойчивость и твердость характера, хорошая координация движений и ловкость рук, дисциплинированность и организованность.

Выпускник техникума, освоивший специальность «Электрификация сельского хозяйства» должен знать: основы электро и радиотехники, высшую математику, электрические схемы монтируемого оборудования, правила эксплуатации, ремонта и наладки обслуживаемого оборудования, правила техники безопасности; должен уметь: читать и составлять схемы, выполнять слесарные и сварочные работы, определять неисправности эксплуатируемого оборудования и устранять ихВсе открытия в области электричества, опирались на знания, в первую очередь математики, а так же физики и химии…

Какой же электрик без математики? Проверка наличия цепи и замеры переходных сопротивлений между заземлителями и заземляющими проводниками, заземляемым оборудованием (элементами) и заземляющими

 

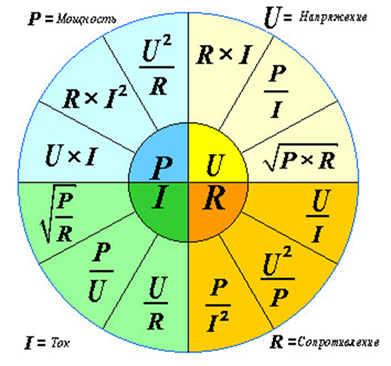проводниками. Измерение сопротивления изоляций кабелей, обмоток электродвигателей, аппаратов, вторичных цепей и электропроводок, и электрооборудования напряжением до 1000В.– Чтобы справиться с этими задачами, электрику кроме специальных знаний: технические характеристики оборудования, виды повреждений, правила ремонта и проч., пригодятся базовые знания по математике, физике, черчению и механике.

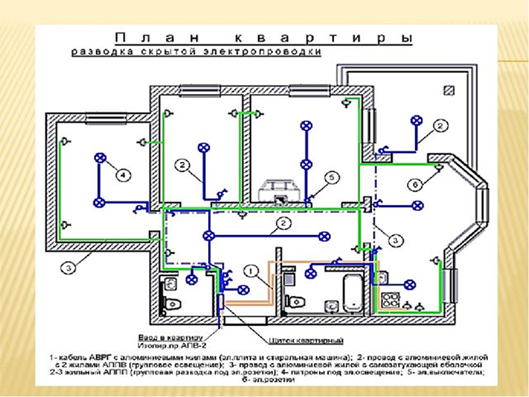
Схема электроснабжения коттеджа с системой TN-C-S.  Разобраться в этой схеме, не зная математики, – невозможно!

 

Можно сказать с уверенностью, что профессия электрика не утратила своей популярности за прошедшее столетие.

Недаром в обществе сегодня бытует поговорка: «Если электрик спит, значит, все хорошо».

От мастеров своего дела зависит безопасность, эффективность работы всех производств, частных компаний, офисов, жилых объектов.

Тем не менее, некоторые изменения все же произошли. В первую очередь, они коснулись качественной составляющей работы электрика. Если раньше знания примитивных схем и устройств было вполне достаточно, то сегодня передовые технологии требуют постоянного совершенствования и «обновления» технической информации.

В руках электриков находятся тысячи жизней, и груз ответственности не может не оказывать на них давления. А возникновение какой-либо аварийной ситуации на производстве — это «страшный сон» для любого специалиста. Тем не менее, обслуживание электрооборудования стало призванием для многих сотен молодых квалифицированных сотрудников.

         Таким образом, выбирая для себя профессию электрика, +следует помнить, что в ВУЗе или техникуме, колледже или специализированном образовательном центре от вас потребуется отличное знание сложных наук, и в первую очередь – математики!

 

3.6.          Математика в профессии технолога общественного питания.

Одной из главных специальностей в сфере производства продуктов общественного питания является технолог.

Первыми технологами по контролю  за качеством приготовленной пищи можно считать людей, которые дегустировали королевскую еду. Им короли доверяли безоговорочно. В настоящее время профессия технолога общественного питания востребована как никогда ранее в связи с развитием и расширением сети  предприятий общественного питания. 

В России так называемые предприятия общественного питания в виде трактиров, корчм возникли в конце XVIII века наряду с возникновением кулинарии как науки.  Контролировать качество пищи, приготовленной нанятыми людьми, приходилось хозяевам заведений. Таким образом  и возникла профессия технолога общественного питания.

В настоящее время технолог общественного питания – это специалист, занимающийся разработкой, производством и контролем качества кулинарной и кондитерской продукции, обслуживанием потребителей и оказанием услуг в качестве технолога на предприятиях общественного питания различных организационно-правовых форм.

Технолог общественного питания должен обладать такими личностными качествами, как ответственность, честность, аккуратность, терпеливость, выдержанность, выносливость, развитое воображение, оригинальность, изобретательность.

Работа технолога общественного питания связана с работой с таблицами, результатами анализов, что позволяет отнести ее по предмету труда к типу «Человек – Знаковая система».

Математика используется не только в науке, но и в кулинарии при приготовлении пищи.  Немного из истории кулинарии.
«CULINARIUS» – в Древнем Риме «искусство приготовления пищи».
КУЛИНАРИЯ  высоко ценилась во все времена, но при этом она всегда подчинялась законам капризной моды точно так же, как искусство изготовления одежды, украшений и предметов интерьера.
         Существует множество рецептов блюд, которые названы по имени знаменитых людей, а также в честь поваров, создавших их. К таким блюдам относятся например, бешамель, сэндвич и другие.
На самом деле, все этапы приготовления пищи, в том числе покупка продуктов питания, расходы бюджета требуют некоторые математические знания.

Математика в кулинарии имеет большое значение, так как для приготовления любого блюда должен соблюдаться рецепт. В рецепте указывается точное соотношение продуктов, которое необходимо соблюдать в процессе приготовления.

При взвешивании продуктов в кулинарии используются математические величины - масса и объём. Ими тоже необходимо уметь пользоваться. Единицы времени играют далеко не последнюю роль в приготовлении блюд.                Приготовленные блюда нужно умело делить на порции, в чём нам опять же поможет математика.
        Например, для того, чтобы приготовить японский омлет с рисом ( омурайсу ), нам необходимо уметь читать список ингредиентов и уметь их применять. На 1 порцию нам потребуются: 

Яйцо — 1 штука
Молоко — 2 ст. ложки
Рис отварной — 3 ст. ложки
Колбаса — 2 ломтика (можно использовать отварную курицу )
Кетчуп — 2 ст. ложки
Зелень свежая — 20 грамм
Перец черный молотый — по вкусу
Соль — по вкусу.
        Если мы хотим приготовить больше одной порции, то уже придётся с помощью математики рассчитывать количество каждого ингредиента по отдельности.
         В кулинарии мы используем преобразования. Многие рецепты написаны в имперских единицах. Некоторые новые рецепты и измерительные приборы обозначены в метрических единицах (например, миллилитры).

По характеру труда профессия технолога общественного питания предполагает проектирование, разработку новых образцов, принятие нестандартных решений, требует независимого оригинального мышления.

         Технолог должен уметь хорошо работать со сборником рецептур : составлять технологические карты,  калькуляционные карты,  акты проработки,  работать с таблицами; рассчитывать сырьё на полуфабрикаты и готовые блюда; потери при тепловой обработке, минимизацию расходов.

Каждое блюдо должно весить определенное количество граммов и продукты имеют свойство терять вес при готовке. Технологу надо уметь рассчитывать количество продуктов для получения готовых блюд так,  чтобы не было недостачи и излишков.

В профессии «Технолог общественного питания» знания математики необходимы и широко применяются в его профессиональной деятельности.

 

Технолог должен знать алгоритм приготовления блюд.

Например, рассмотрим технологическую схему приготовления котлетной массы из мяса:

 

 

 

1. Нарезают мясо.    

 

2. Мясо пропускают.

 

3. Подготавливают хлеб для котлетной массы.

 

4. Добавляют соль, перец.                   

 

5.Массу перемешивают и выбивают.

 

6. Просеивают размолотые сухари, муку.  

 

7.  Готовят полуфабрикаты.  

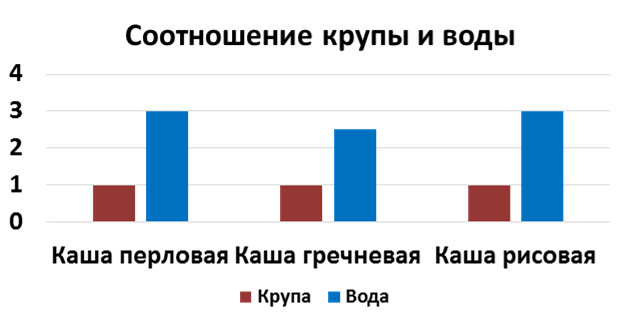
Технолог должен знать,  в каких пропорциях подбирать компоненты для приготовления блюд. Например, рассмотрим пропорции воды и крупы для приготовления каши:

Технолог общественного питания должен обязательно уметь определять влажность продуктов, рассчитывать дневную норму питания в процентах, производить калькуляцию и учёт продуктов питания. Поэтому, конечно, важны для этой профессии математические задачи на проценты.

Задача 1. Повару необходимо приготовить 15 порций бифштекса по 200 г в каждой. Сколько необходимо взять мяса, если известно, что мясо при варке теряет 35% своей массы.

Решение:

1)Найдем сначала сколько всего должно получится готовой продукции:

15х0,2=3кг

2)Обозначим за Х кг количество мяса, которое требуется для приготовления бифштекса. Тогда Х кг – это 100%, а 3кг – это 65%. Отсюда находим Х:

Х=3х100/65

Х≈4,6 кг

Ответ: ≈4,6 кг мяса требуется для приготовления 15 порций бифштекса

Задача 2. Врачи рекомендуют дневную норму твоего зимнего питания распределить на 4 приема: утренний завтрак –  0,2; второй завтрак – 0,1;

обед – 0,5; ужин – 0,2. Запиши предлагаемую норму в процентах.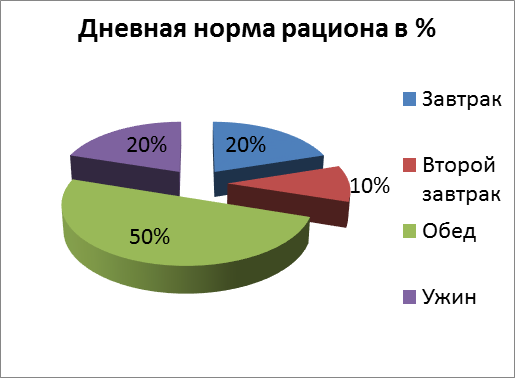

Технолог рассчитывает объём посуды, количество жидкости для точного расчёта количества порций. Поэтому важны задачи нахождения площадей и объёмов.

Задача 3. Кастрюля имеет форму цилиндра, образующая которого 45 см, а диаметр основания 50 см. Можно ли приготовить в этой кастрюле 350 порций кипячёного молока, если при нагревании объём молока увеличивается в 1,1 раз.

Решение:

1) Найдём сначала объём молока, который необходимо вскипятить: 350* 0,2=70л.

2) Найдём объём молока при нагревании:   7* 1,1=77л.

3) Найдём объём кастрюли: V=πr²h

V=3,14*625*45=88300мл=88,3л.

4) 88,3>77, следовательно в данной кастрюле можно приготовить требуемое по условию задачи количество молока.

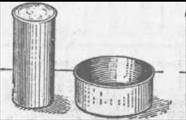Задача 4. Имеется две кастрюли. Которая из них вместительнее - правая, широкая или левая,втрое более высокая, но вдвое более узкая?

Решение:

1) Найдём объём правой кастрюли: V₁=r²h

2) Найдём объём левой кастрюли:

V₂ =π*)²*3h =πr²h

Следовательно, V₁>V₂

Ответ: Объём правой кастрюли больше, чем объём левой.

Геометрические фигуры в оформлении блюд.

 В оформлении блюда применяются различные геометрические фигуры, например, шар, тор, усеченный конус, параллелепипед.

А на самом деле их намного больше – параллелепипед,  шар, усечённый конус, тор. Например, торты – это крупные кондитерские изделия в форме низкого цилиндра, эллипса, прямоугольника, треугольника, квадрата и т. д.

Стейк или бифштекс – это толстый кусок обжаренного мяса, как правило,  в форме шайбы, т. е. цилиндра.

Желе – это студень,  полученный из соков плодов и ягод, чаще всего в форме усеченной пирамиды.

 И таких примеров может быть множество!

Например, пончик с дыркой посередине имеет форму тороида (геометрической фигуры). Дырка предназначается для того, чтобы извлечённый из горячего масла пончик был нанизан на стержень, с которого потом продукт кладётся в кулёк или на тарелку покупателю.

 

 

 Или, например, какой-нибудь пудинг имеет форму усеченного конуса из-за того, что его охлаждение производится в специальной форме или посуде, имеющую углубленность.

 

 

 

Как видите,  разные формы у блюд не случайны.

 

Интересный факт:

 если положить продукт под крышку в форме пирамиды, то он не испортится. Находясь под пирамидой, долго не закисает молоко, сырое мясо, расположенное на высоте 1/3 от основания не гниет, а мумифицируется, табак и кофе улучшают свой вкус, при длительном хранении крупа, мука, овощи, фрукты надолго остаются свежими.

Формы нарезки

 Форма нарезки тоже относится по большей части к геометрии. Ведь все продукты при нарезке приобретают определенную форму, например в виде кубика, соломки, кружочков и т. д.

 От формы и размера нарезки многое зависит:

 1) вкус блюда 2) время приготовления 3) внешний вид.

Почему от формы нарезки овощей меняется вкус блюда?

 Потому что если нарезать тонко овощи, их вкусы перемешаются между собой. А если порезать покрупней, то каждый овощ даст  свой вкус и вы почувствуете его аромат, а перемешиваясь во рту, ароматы овощей создадут целую гамму вкусов.  Так что если хочется что-то единообразное, то надо резать мелко, а если хочется сначала отведать каждый вкус, а уж потом, (пережевав),  соединить, то резать покрупней. И это касается не только салатов, но и горячих блюд.

Если порезать продукт, в данном случае мясо, крупным куском, то оно будет готовиться долго, хотя в этом тоже есть свои плюсы. Во-первых, так готовят многие блюда, чтобы сохранить нужные нашему организму белки (при тепловой обработке они разрушаются). Во-вторых, некоторые сорта мяса, например, говядина, готовясь большим куском и «не прожариваясь» до конца, имеют более нежный и сочный вкус.  Маленькие кусочки быстрее готовятся, и имеют большее преимущество в приготовлении других блюд с самыми разными продуктами. Такими примерами могут служить плов, каурма-шурпа, борщ, паэлья и др.

И без внешнего вида не обойтись. Форма нарезки придает более красивый вид блюду.

В нашем техникуме есть курс «Введение в кулинарное искусство», где на первом занятии  объясняют  формы нарезки в теории и на практике.

 

 

Карвинг – это художественная резьба (в данном случае по овощам). Здесь применяются самые необыкновенные и самые разные геометрические фигуры: цилиндры, кубы, конусы и многое другое.

 

        

Математика в цвете.

 В блюде основными частями являются:         объём, форма и цвет. В данном случае мы рассмотрим кондитерскую часть. Кондитер – это в первую очередь художник, а художнику важен цвет. Именно для этого возьмем за пример ок-рашивание белкового крема различными видами красителя.

 

Пищевые красители– пищевые добавки, придающие, усиливающие или восстанавливающие окраску пищевого продукта. Они подразделяются на натуральные и синтетические; на водорастворимые (т. е. которые растворяются водой) и жирорастворимые (растворяемые в жире); на жидкие, гелевые и порошкообразные (употребляются в сухом виде или разводятся сначала водой).

Существует множество задач, которые нужно решить технологу, чтобы правильно применить  красители при приготовлении различных блюд.

 Задачи  заключаются в том, чтобы рассчитать количество красителя на количество крема. Или количество сухого красителя на количество воды (ко-торой его разводят). (Приложение 3).

Подобные задачи можно решать и не только с различными видами крема, но и с айсингом. Айсинг (от англ. Icing) – это сахарно-белковая рисовальная масса для изготовления объемных кондитерских украшений.

Интересные факты:  оказывается, цвет влияет на аппетит. Исследования показали, что аппетит зависит даже от цвета посуды.

Если блюда находятся на посуде желтого цвета, человек, съев меньше чем обычно, быстрее чувствует себя сытым.  Посуда красного цвета тревожит и беспокоит, блюда на такой посуде выглядят неаппетитно. Голубая посуда прекрасно подходит для салатов, но не для кофе или чая. За столом с голубым сервизом часто возникают споры.  Тарелки чёрного цвета вызывают чувство брезгливости и ухудшают вкусовые качества еды.  Белая посуда подчёркивает достоинства пищи; особенно аппетитны в белых тарелках супы. Точно так же и с цветами самого блюда – главной его чертой должен быть не только вкус, но и внешний вид.

Свойство оранжевого и жёлтого цвета возбуждать аппетит и стимулировать работу органов пищеварения незаменимо на кухне. Жёлтый и красный его    улучшают, чёрный, зелёный, серый, синий — снижают. Кстати, синий и все его оттенки — самые «несъедобные» цвета, лучшее средство для снижения аппетита.

Форма и цвет – это две неразделимые части в любом блюде и являются основной составляющей всего изделия. Главное при оформлении блюда – это правильно все рассчитать, т. е. найти подходящий цвет и сделать правильную форму своего изделия.

В профессии «Технолог общественного питания» знания математики необходимы и широко применяются в его профессиональной деятельности:

Мы убедились, что людям этой профессии постоянно приходится в своей работе решать множество задач, напрямую связанных с математикой и математическими расчётами.

Таким образом, при подготовке к профессии технолога общественного питания следует уделить большое внимание приобретению математических знаний и навыков.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4. Заключение.

«Никакой достоверности нет в науках там,

 

где нельзя приложить ни одной

 

из математических наук, и в том,

 

что не имеет связи с математикой»

 

Леонардо да Винчи.

 

«Зачем нам Математика?»

Если бы не было Математики, не было бы многих профессий. Математика нужна в любомделе, в любой профессии. Каждому нужна математика.

Лётчику — чтобы набрать нужную высоту, дворнику — чтобы посчитать сколькопесканужно насыпать на тот или иной участок, ну а учёным она нужна больше всех. Кто-то скажет: «Да математика нужна только математикам и физикам». Но не всё так просто. Археологу нужно произвести расчёты на какой глубине копать, а это тоже математика. Ихтиологу — сколько рыб в этом году вывелось.

Математика нужна каждому и везде. Без математики ничего не обходится. Без математики не движется прогресс, без неё мы не смогли бы сделать даже маленькое дело. Математика — наука, как прошлого, так и будущего.

Не каждый человек с начала своего образовательного пути знает, какую профессию он приобретет в будущем, но благодаря ответственному отношению к изучению математики, каждый обеспечивает себя необходимыми знаниями, качествами, которые необходимы в

его дальнейшей профессиональной деятельности.

Каждому из людей как дома, так и на работе приходиться делать те или иные расчеты, иногда простые, а иногда и сложные расчеты. В одном случае для вычислений достаточно калькулятора, в другом – нужна специальная вычислительная техника. Иногда эти расчеты требуют использования лишь простых математических операций, а иногда нужны сложные формулы алгоритмических и тригонометрических вычислений.

Помимо этого, некоторые расчеты требуют владения приемами геометрических измерений, разбираться в информации, которая представлена в виде таблиц, диаграмм и графиков, схем алгоритмов выполнения различных заданий. Еще древние заметили, что математика заставляет человека постоянно думать. И в подтверждение этого первый «российский университет» М.В. Ломоносов говорил, что математику нужно учить потому, что она приводит в порядок мысли человека. Математику называют «царицей всех наук», потому что математический стиль мышления и методы мышления применяются не только лишь в физике, технических и астрономических науках, она применяется и, казалось бы в таких далеких от нее науках, как биология, химия, в экономических науках, а также в метеорологии и археологии.

Таким образом, все профессии, которые получают наши студенты по окончанию техникума, не являются исключением и также неразрывно связаны с математическими вычислениями, и в той или иной мере используют  математические знания.

Поэтому трудно переоценить применение математики в профессиях, которые связаны с вышеперечисленными и многими другими науками, так или иначе, использующих «царицу всех наук».

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Приложение 1.

Задача 1. Заработная плата Иванова Михаила Евгеньевича по основному месту работы 25 000 рублей. Он подрабатывает и получает дополнительно ещё 9000 рублей. Его расходы за коммунальные платежи составляют 4000 ежемесячно. Михаил хочет взять кредит с 1.02.2017 на 1 год (12 месяцев) под  19%. Найти:  платежеспособность (P), максимальный размер кредита (Sp),составить график примерного расчета платежей по кредиту.

Решение

Дч- среднемесячный доход;

Чистый доход (Дч) =25000+9000-4000=30000

k- коэффициент в зависимости от величины Дч;

k платежеспособности=0.7(до 45 тыс.руб.)

k=0.7 при Дч в сумме до 45000 руб. (или эквивалента этой суммы в иностранной валюте) включительно;

k=0.8 при Дч в сумме свыше 45000 руб. (или эквивалента этой суммы в иностранной валюте);

k(ипотека)=0.8 при Дч в сумме свыше 21000 руб. и 0,9 при Дч в сумме от 21000 руб. и выше;

t-срок кредитования, мес.

t=12 месяцев

P=Дч*k*t=30000*0.7*12=252000

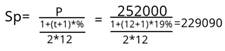
Ежемесячная сумма основного долга =

Ежемесячные проценты(1) =

Ежемесячный платеж по кредиту (1) = Ежемесячная сумма основного долга + +Ежемесячные проценты=19090,83+3339,06=22429,89

Сумма основного долга (2) = Сумма основного долга (1)- Ежемесячная сумма =

=229090-19090,83=209999,17

Ежемесячные проценты(2) =

Ежемесячный платеж по кредиту (2) = 19090,83+3388,75=22479,58

Сумма основного долга (3) = Сумма основного долга (2)- Ежемесячная сумма основного долга =209999,17-19090,83=190908,34

Ежемесячные проценты(3) =

Ежемесячный платеж по кредиту (3)= 19090,83+2981,31=22072,14

 

График примерного расчета платежей по кредиту:

 

№ месяца	Сумма основного долга	Ежемесячная сумма основного долга	Ежемесячные проценты	Ежемесячный платеж по кредиту
1	229090	19090,83	3339,06	22429,89
2	209999,17		3388,75	22479,58
3	190908,34		2981,31	22072,14
4	171817,51		2772,62	21863,45
5	152726,68		2385,05	21475,88
6	133635,85		2156,48	21247,31
7	114545,02		1848,41	20939,24
8	95454,19		1490,65	20581,48
9	76363,36		1232,27	20323,10
10	57272,52		894,39	19985,22
11	38181,70		616,14	19706,97
12	19090,87		308,07	19398,90

 

Задача 2. Петров Алексей Юрьевич 10.01.2016 оформил вклад на 1 год (12 месяцев) на сумму 10000 рублей под 8%.В течение года он 5.02.2016 внес 5000, 15.03.2016 снял 1500, 6.06.2016 внес 30000, 10.10.2016 снял 6000, 11.12.2016 внес 9000.Найти процент на конец закрытия вклада, рассчитать капитализацию.

Решение

Дч=10000+5000-1500+30000-6000+9000=46500

 46500*8%=3720- проценты на конец закрытия вклада.

Расчет капитализации:

Январь (с 10 по 31): 

Февраль(с 1 по 5):

Февраль (с 6 по 29):

Март (с 1 по 15): 

Март (с 16 по 31): 

Апрель (с 1 по 30): 

Май (с 1 по 31):

Июнь (с 1 по 6):

Июнь (с 7 по 30):

Июль (1 по 31):

Август (с 1 по 31):

Сентябрь (с 1 по 30):

Октябрь (с 1 по 10):

Октябрь (с 11 по 31):

Ноябрь (с 1 по 30):

Декабрь (с 1 по 11):

Декабрь (с 12 по 31):

Январь (с 1 по 9):

Задача 3.Начислить зарплату работникам одного из техникумов Кировской области.

 

	ФИО			Оклад			Премия
	Петров П.А.			37000=00			15 %
	Сидоров С.И.			35000=00			11%
	Иванова И.Б.			30000=00			10%
	Швецов В.П.			29000=00			10%
	Козлов К.Д.			20000=00			-
	Вещев В.Г.			21000=00			5%
	Дерябин Д.Е.			14000=00			-
	Мухина М.К.			18000=00			-
	Нестеров Н.М.			14000=00			2%
	Мешков О.Г.			10000=00			-
	Копейкин Н.Ю.			13000=00			3%
	Пименов Г.С.			17000=00			5%
	Хлебникова Т.А.			15000=00			4%
ФИО	Должность	Дни	Оклад	Премия	Всего начислено	Аванс		Дети	Под. налог	Всего удержано	Сумма выдачи
Петров П.А.	Директор	22	37000=00	5550=00	42550=00	5000=00		2	5167=50	10167=50	32382=50
Сидоров С.И.	Зам. директора	21	33409=09	3674=99	37084=08	6000=00		1	4638=93	10638=93	26445=15
Иванова И.Б.	Главный бухгалтер	20	27272=73	2727=27	29999=99	-		-	3900=00	3900=00	26100=00
Швецов В.П.	Бухгалтер	22	29000=00	2900=00	31900=00	-		1	3965=00	3965=00	27935=00
Козлов К.Д.	Завуч	19	17217=72	-	17272=72	-		2	1881=45	1881=45	15391=26
Вещев В.Г.	Завхоз	22	21000=00	1050=00	22050=00	5000=00		-	2866=50	7866=50	14183=50
Дерябин Д.Е.	Охранник	15	9545=45	-	9545=45	6000=00		1	1058=90	7058=90	2486=54
Мухина М.К.	Педагог	21	17181=81	-	17181=81	-		2	1869=63	1869=63	15312=17
Нестеров Н.М.	Электрик	18	11454=54	229=09	11863=63	4000=00		-	1518=87	5518=87	6164=75
Мешков О.Г.	Водитель	10	4545=45	-	4545=45	-		1	408=90	408=90	4136=55
Копейкин Н.Ю.	Педагог	14	8272=72	248=18	8520=90	-		1	925=71	925=71	7595=18
Пименов Г.С.	Мастер	21	16227=27	811=36	17038=63	2000=00		2	1851=02	3851=02	13187=60
Хлебникова Т.А.	Воспитатель	22	15000=00	600=00	15600=00	-		2	1664=00	1664=00	13936=00

 

 

Решение

Петров П.А.

Оклад - 37000=00 (т.к. 22 раб. дня)

Премия = 37000 * 15% =5550

Всего начислено=Оклад+Премия=37000+5550=42550

Под. налог = Всего начислено – Налоговый вычет¹ *13%=42550-2800*13%=5167

Всего удержано = Аванс + Подоходный налог =5000+5167,50=10167,50

Сумма выдачи = Всего начислено – Всего удержано = 42550– 5167,50 =32382,50

Сидоров С.И.

Оклад- (

Премия = 33409=09*11%= 3674=99

Всего начислено=Оклад+Премия=33409,09+3674,99=37084,08

Под. налог = Всего начислено – Налоговый вычет*13%=37084=08-1400*13%=4638=93

Всего удержано = Аванс + Подоходный налог =6000+4638,93=10638,93

Сумма выдачи = Всего начислено – Всего удержано =37084,08-10638,93=26445,15

Налоговый вычет на детей- это один из видов государственных льгот родителям, на содержании которых находятся несовершеннолетние дети или учащиеся до 24 лет.

Сумма за 1 ребенка-1400=00

Сумма за 2-х детей-2800=00

Сумма за 3-х и более детей-3000=00

 

Задача 4.Заполнить кассовую книгу на 9 ноября 2017 года.

№ документа	Документ и содержание операции		Сумма Руб.
	Остаток на 09.10.2017		123000=00
002	Из кассы выдано ГСМ		1300=00
003	От Иванова возврат подотчетных сумм в кассу		4589=00
004	В банк на расчетный счет депонированная з/п		3000=00
005	В кассу за аренду		11570=00
006	Оганову расходы по командировке		1400=00
007	В кассу за платные услуги		5460=00
008	Под отчет Петровой на хоз. расходы	564=00
009	Получены деньги за обучение от Петрова	5400=00
010	Получены деньги за обучение от Иванова	6400=00
011	Получены деньги за обучение от Макарова	3400=00
012	Выплата отпускных	70000=00

 

№ доку- мента

От кого получено или кому выдано

№ корреспон- дирующего счета, субсчета

Приход, руб.коп

Расход, руб.коп.

Л И Н И Я О Т Р Е З А

№ доку- мента

От кого получено или кому выдано

№ корреспон- дирующего счета, субсчета

Приход, руб.коп

Расход, руб.коп.

1

2

3

4

5

1

2

3

4

5

Остаток на начало дня

123000=00

Х

002

Из кассы выдано ГСМ

1300=00

003

От Иванова возврат подотчетных сумм в кассу

4589=00

004

В банк на расчетный счет депонированная зарплата

3000=00

005

В кассу за аренду

11570=00

006

Оганову расходы по командировке

1400=00

007

В кассу за платные услуги

5460=00

008

Под отчет Петровой на хоз. расходы

564=00

009

Получены деньги за обучение от Петрова

5400=00

Итого за день

36819=00

76264=00

010

Получены деньги за обучение от Иванова

6400=00

Остаток на конец дня

83555=00

Х

011

Получены деньги за обучение от Макарова

3400=00

В т.ч. на зарплату, выплаты соц.характера и стипендии

-

Х

012

Выплата отпускных

70000=0

Кассир

Сидорова

Сидорова Ю.А.

подпись

расшифровка подписи

Перенос

Записи в кассовой книге проверил и документы в кол-ве

шести

приходных и   расходных

прописью

пяти

прописью

получил Бухгалтер

Михайлова

Михайлова К.Н.

подпись

расшифровка подписи

 

Задача 5.Расчитать лимит остатка кассы:

1)    за апрель 2017 года;

2)    за февраль-апрель 2017 года.

Формула расчета лимита наличных денежных средств по кассе:

L = V / P * N,

где  L — это лимит кассы,

V — объем всех поступлений за расчетный период,

P — расчетный период, который должен составлять не более 92-х дней,

N — количество дней, от одной сдачи наличных в банк до другой сдачи (не должен превышать 7 рабочих дней).

1) Расчетный период за апрель 2017 года. Его продолжительность 22 дня. Допустим, наличные сдаются в банк один раз в 4 дня. Поступление наличных денежных средств в кассу за этот период составило 560 000 рублей.

Решение

2) Расчетный период за февраль-апрель 2017 года. Его продолжительность 62 дня. Наличные сдаются 1 раз в 10 дней. Поступление наличных денежных средств в кассу за этот период составило 750 000 рублей.

Решение

 

 

 

 

 

 

 

 

 

 

Приложение 2.

Задача 1. За один рабочий день в уборочную комбайнёр должен убрать озимой пшеницы с 15 га. С 1 га набирается примерно 1,5 тонны пшеницы, так как год 2017 трудный был, то  1 тонна стоит в среднем 10000 руб. Сколько может заработать денег фермерское хозяйство благодаря работе одного комбайнера в течение месяца?

Задачи с использованием формул вызывают наибольшую трудность в решении. В практической жизни очень часто приходится использовать ту или иную формулу.

Как известно, роль грубых кормов в питании жвачных животных чрезвычайно велика, так как они способствуют нормальной работе желудка и кишечника, а от этого зависит не только продуктивность, но и здоровье наших питомцев. Приходится перевозить тонны сена. Нужно знать, сколько сена за одну перевозку можно перевезти, сколько раз нужно съездить, сколько нужно транспорта, бензина, и др….

Количество заготовленного сена определяют по объему стога (скирды) и массы в кубических метрах. Для этого измеряют длину (Д), ширину (Ш) и перекидку (П) скирды или стога. Длину определяют с двух сторон на высоте одного метра от земли. Ширину измеряют с обеих сторон на высоте 0,5 м и высчитывают среднюю величину. Перекидку измеряют поперек скирды от земли с одной стороны через вершину скирды, с другой − в 2-3-х местах для определения средней длины.

Объем скирды определяется по формуле О=Д (П+Ш):4• (П+Ш):4.

Задача 2. Определить объём стога, если перекидка равна 15 м, ширина 5 м, а длина 10 м.

Решение: объем скирды в кубических метрах составит: О=10(5+15):4• (5+15):4. Таким образом, объем стога или скирды будет равен 250 м³.

Для приближённого подсчёта объёма сена в скирде пользуются следующей формулой: V = (0,52l — 0,45а) ab, где V - объём сена в м³, l - длина «перекидки», т. е. длина линии BCD в метрах, а - ширина скирды (ВD) в метрах, b —длина скирды (АВ) в метрах.

Пользуясь этой формулой, подсчитать вес сена в скирде, если а = 4 м; b = 8 м;  l =10 м; вес 1 м3 равен 70 кг. Ответ: 7616 кг

Задача 3. Для перевозки убранного урожая хозяйству нужны автомобили. Нужно транспортировать 45 тонн на 1300 км. Услуги перевозчиков приведены в таблице. Какой перевозчик выберет хозяйство и какова будет стоимость перевозки?[3]

Перевозчик	Стоимость перевозки одним автомобилем (на 100 км)	Грузоподъёмность автомобилей (тонн)
А	3700 руб	3,5
Б	4300 руб	5
В	9800 руб	12

Задача 4. Проверка сеялки в поле.

Саженью надо отмерить длину 278 м и ширину 3,6 м. Отмеренная площадь равна 278 *3,6 = 1000,8 м²  или 0,1 га. Если норма высева 250 кг/га, то на эту площадь надо засыпать 25 кг, чтобы всё высеялось.

Все эти практические примеры доказывают непосредственную связь математики с сельскохозяйственной практикой.

Приложение 3.

Задачи  на  расчёт количества красителя на количество крема. Или количество сухого красителя на количество воды (которой его разводят).

Задача № 1.  1 капля красителя окрашивает полностью 100 г белкового крема. Сколько нужно капель красителя для полного окраса 600 г  крема? Задача элементарная.

 Делаем пропорцию:

1 капля – 100 г

Х капель – 600 г

1) 600 г*1 к/100 г = 6 (капель)

 Ответ: 6 капель красителя нужно, чтобы полностью окрасить 600 граммов белкового крема.

Задача № 2.  Как мы решили в задаче № 1: 600 г белкового крема полностью окрашивается 6 каплями пищевого красителя и это 100%-ный цвет. Нам нужен цвет немножко светлее, т. е. пищевого красителя нужно добавить меньше. Например, нам нужно не 100%-ный цвет, а 80%. И дальше все также составляем пропорцию:

 6 капель – (600 г) – 100%

Х капель – (600 г) – 80%

1) 80%*6 к/100% = 4,8.   Это примерно 5 капель.

Ответ: 5 капель нужно, чтобы окрасить в более светлый цвет 600 грамм белкового крема.

Задача № 3. Сухой краситель(100% концентрация) 1 г нужно разбавить водой. Сколько нужно воды, чтобы получить 70% жидкий краситель.

1 г красителя – 100%

Х воды — х%

100% — х = 70%

 Находим х: 100% — 70% = 30%

 А дальше составляем пропорцию:

 1 г – 100%

Х воды – 30%

30%*1 г/100% = 0, 3 мл воды

Ответ: 30% (0, 3 мл) воды потребуется, чтобы развести 1 г сухого пищевого красителя 100%-ного.

 

 

 

 

Информационные источники.

1.   Васильева, Г.Н. Технологии и методики обучения математике / Г.Н. Васильева, И.В. Косолапова. – Пермь: Изд-во пермского педагогического университета, 2002. – 340 с.

2.   Депман И.Я.,  Виленкин Н.Я. За страницами учебника математики. – М.: Просвещение, 2009.

3.   Кларин М.В. Инновации в обучении. Метафоры и модели – Москва, Наука, 1997.

4.   poznajvse.com›auto/70-za-pjat-sek-do-avarii/

5.   yandex.ru/images› рисунок безопасная дистанция.

6.   http://www.moeobrazovanie.ru/

7.   http://hijos.ru/2012/08/08/matematika-v-zhizni-lyudej/

8.   http://ext.spb.ru/

9. http://www.scienceforum.ru/

10. М. И. Башмаков, Математика. Сборник задач профильной направленности – М. : Издательский центр «Академия», 2013

 

 

Скачано с www.znanio.ru