Методическая разработка по теме "Подготовка к ЕГЭ. Решение задач с экономическим содержанием"

МБОУ «Шлиссельбургская средняя общеобразовательная школа №1 с углубленным изучением отдельных предметов»

Методическая разработка по теме

«Подготовка к ЕГЭ.

Решение задач с «экономическим содержанием»

                                                                                             Ламанцева Нина Михайловна,

                                                                                             учитель математики  высшей

                                                                                            квалификационной категории   

Г. Шлиссельбург

Ленинградская область

2024 год

Подготовка к ЕГЭ

Решение задач с «экономическим содержанием»

I Задача: Взят кредит (К), через определенный промежуток времени на него начисляется процент (П), после чего клиент производит  платеж (Х). Выплаты производятся равными платежами несколько раз (n). Каков этот платеж?

Решение:

1)Через первый промежуток времени:

К+0,01П*К=(1+0,01П)*К-новый долг

(1+0,01П)*К-Х=-оставшийся долг после первой выплаты.

2)Через второй промежуток времени:

+0,01П*=(1+0,01П)*-новый долг

(1+0,01П)*-Х=-оставшийся долг после второй выплаты.

3)Аналогично через третий промежуток:

(1+0,01П)*-Х=-оставшийся долг

Пусть долг был выплачен тремя равными платежами, тогда

 =0

Обозначим для удобства: 1+0,01П=р

р(р-Х)-Х=0

-рХ-Х=0

(рК-Х)-рХ-Х=0

К-Х-рХ-Х=0

Х(+р+1)=

Х=

Аналогично, если произведено  n равных платежей, то

Х=

№1. 31 декабря Иван Иванович взял в банке 4290000 рублей в кредит под 14,5% годовых. Схема выплаты кредита следующая-31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т.е. увеличивает долг на 14,5%), затем Иван Иванович переводит в банк Х рублей. Какой должна быть сумма Х, чтобы долг был выплачен двумя равными платежами (т.е. за два года)?

Решение:

К=4290000; П=14,5; n=2

Х=;           р=1+0,01*14,5=1,145

Х=

Ответ: платеж составляет 2622050 рублей.

№2. 31 декабря Иван Иванович взял в банке 6944000 рублей в кредит под 12,5% годовых. Схема выплаты кредита следующая-31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т.е. увеличивает долг на 12,5%), затем Иван Иванович переводит в банк Х рублей. Какой должна быть сумма Х, чтобы долг был выплачен тремя  равными платежами (т.е. за три  года)?

Решение:

К=6944000; П=12,5; n=3

Х=; р=1+0,01*12,5=1,125

Х=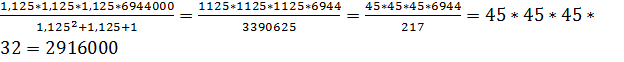

Ответ: платеж составляет  рублей.

№3. 31 декабря Владимир взял в банке некоторую сумму в кредит под 14% годовых. Схема выплаты кредита следующая-31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т.е. увеличивает долг на 14%), затем Владимир переводит в банк 4548600 рублей. Какую сумму взял Владимир в банке, если он выплатил долг двумя равными платежами?

Решение:

К=?; П=14; n=2; Х=4548600

Х=;           р=1+0,01*14=1,14

К=

К=

Ответ: сумма, взятая в банке,  составляет 7490000 рублей.

II Задача: Взят кредит (К), через определенный промежуток времени на него начисляется процент (П), после чего клиент производит  платеж . Выплаты производятся не обязательно равными платежами несколько раз (n), но известно, что каждый платеж не более, чем Х. Каково минимальное количество таких платежей?

Решение:

1)Если бы на кредит не начислялись проценты, то количество платежей, каждый из которых равен максимально возможному числу(Х), равно , следовательно искомое количество платежей n>.

2)После каждой очередной выплаты долг уменьшается (<К, < и т.д.), следовательно каждое очередное увеличение долга за счет процентов не более, чем 0,01П*К, а значит за n платежей выплаченная сумма не более, чем 0,01П*К*n.

№4. 1 января 2015 года Александр взял в банке 1,1 млн рублей в кредит. Схема выплаты кредита следующая-1 числа каждого следующего месяца банк начисляет 1% на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Александр переводит в банк платеж. На какое минимальное количество месяцев Александр может взять кредит, чтобы ежемесячные выплаты были не более 275 тыс. рублей?

Решение:

1) Если бы на кредит не начислялись проценты, то

1100000:275000=4 (мес.)

Значит количество платежей n>4.

2)ежемесячное начисление процентов составляет не более, чем

0,01*1100000=11000 (руб.)

3) Пусть n=5

1100000+11000*5=1100000+55000=1155000(руб.) всего выплачено за 5 месяцев.

275000*5=1375000 (руб.)

1155000<1375000, значит Александр сможет выплатить кредит за 5 месяцев.

Ответ: минимальное количество месяцев-5.

№5.Степан хочет взять в кредит 1,2 млн рублей. Погашение кредита происходит раз в год равными суммами (кроме , может быть, последней) после начисления процентов. Ставка процента 10% годовых. На какое минимальное количество лет может Степан взять кредит, чтобы ежегодные выплаты были не более 290 тысяч рублей?

Решение:

1) Если бы на кредит не начислялись проценты, то

1200000:290000=4 (ост.40000)

Значит количество платежей n>4.

2)ежемесячное начисление процентов составляет не более, чем

0,1*1200000=120000 (руб.)

3) Пусть n=5

1200000+120000*5=1800000 (руб.) Значит должно быть выплачено не более 1800000 руб.

290000*5=1450000 (руб.)

1450000 не больше 1800000, следовательно нет уверенности в том, что за 5 лет кредит будет выплачен.

Можно сосчитать, сколько рублей будет выплачено за 5 лет и сделать вывод, сколько лет еще необходимо:

1)1,1*1,2-0,29=1,03 (руб.) оставшийся долг после 1-го года

2)1,1*1,03-0,29=0,843 (руб.) оставшийся долг после 2-го года

3)1,1*0,843-0,29=0,6373 (руб.) оставшийся долг после 3-го года

4)1,1*0,6373-0,29=0,41103 (руб.) оставшийся долг после 4-го года

5)1,1*0,41103-0,29=0,162133 (руб.) оставшийся долг после 5-го года

0,162133<0,29, значит необходимо 6 лет для выплаты кредита.

Ответ: 6 лет.

№6. 1 января 2015 года Алексей взял в банке 1,1 млн рублей в кредит. Схема выплаты кредита следующая-1 числа каждого следующего месяца банк начисляет 2% на оставшуюся сумму долга (то есть увеличивает долг на 2%), затем Алексей  переводит в банк платеж. На какое минимальное количество месяцев Алексей  может взять кредит, чтобы ежемесячные выплаты были не более 220 тыс. рублей?

Решение:

1) Если бы на кредит не начислялись проценты, то

1100000:220000=5 (мес.)

Значит количество платежей n>5.

2)ежемесячное начисление процентов составляет не более, чем

0,02*1100000=22000 (руб.)

3) Пусть n=6

1100000+22000*6=1100000+132000=1232000(руб.) всего выплатить  за 6 месяцев.

220000*6=1320000 (руб.)

1232000<1320000, значит Алексей сможет выплатить кредит за 6 месяцев.

Ответ: минимальное количество месяцев-6.

№7. 1 января 2015 года Василий Михайлович  взял в банке 1,1 млн рублей в кредит. Схема выплаты кредита следующая-1 числа каждого следующего месяца банк начисляет 1% на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем  Василий Михайлович  переводит в банк платеж. На какое минимальное количество месяцев  Василий Михайлович  может взять кредит, чтобы ежемесячные выплаты были не более 137, 5 тыс. рублей?

Решение:

1) Если бы на кредит не начислялись проценты, то

1100000:137500=8 (мес.)

Значит количество платежей n>8.

2)ежемесячное начисление процентов составляет не более, чем

0,01*1100000=11000 (руб.)

3) Пусть n=9

1100000+11000*9=1100000+99000=1199000(руб.) всего выплатить  за 9 месяцев.

137500*9=1237500 (руб.)

1199000<1237500, значит Василий Михайлович  сможет выплатить кредит за 9 месяцев.

Ответ: минимальное количество месяцев-9.