Методическая разработка «Удивительная математика»

Мастер-класс на тему «Удивительная математика»

учителя математики

Бадирхановой Рукият Салиховны

Добрый день уважаемые коллеги! Очень рада видеть всех Вас!  Хочу пожелать хорошего настроения, творчества и позитива!

Я Бадирханова Рукият Салиховна,  работаю учителем математики в МБОУ «Нововикринская средняя школа». Сегодня я хотела бы провести для Вас небольшой мастер-класс.

И начать со слов французского математика Блеза Паскаля: «Предмет математики настолько серьезен, что полезно не упускать случая делать его немного занимательным».

Принято считать, что математика точная наука, которая состоит из «сухих» чисел и не прощает каких-либо неточностей. Да это так… И очень часто у ребят возникает предвзятое отношение к математике, они приходят в школу, заранее зная, что математика — это сложно. Но в то же время без нее никуда. Поэтому у каждого человека должны быть сформированы основные вычислительные навыки.

Именно поэтому я сегодня хочу продемонстрировать Вам, как я стараюсь переубедить ребят, как я показываю им, что математика – это интересная и удивительная наука.

И одним из приемов, который позволяет заинтересовать учащихся в теме урока - это начать урок с удивления - с какого-то события, вопроса, необычного факта, поразительного сравнения, необычной связью между, казалось бы, совершенно не связанными вещами.

Например, урок на тему «Площадь» можно начать с новости о том, что где-то построили самый большой в мире стадион или телескоп. Дети начнут интересоваться: «Где он находится? А каких он размеров?» И тут учитель может предложить им, самим попробовать определить его площадь,  зная его размеры.

 Удивлять детей нужно не только в начале. Интересные и занимательные моменты должны быть включены на протяжении всего урока.

Например:  

1.      Сумма углов треугольника и четырехугольника

2.1. В курсе геометрии 7 класса мы изучали теорему о сумме углов треугольника.  Узнали, что эта теорема одна из важнейших теорем в геометрии.

 Существует несколько геометрий, и в каждой из них, сумма углов треугольника трактуется по-разному.

В геометрии Лобачевского сумма углов треугольника всегда меньше 180.

В геометрии Евклида сумма углов всегда равна 180.

В геометрии Римана – сумма углов больше 180.

Доказательство этой теоремы можно показать на практике, используя перпендикулярность прямых и бумажного треугольника.

1. Берём обычный лист бумаги.

2. Вырезаем из него произвольный треугольник.

3. Проводим в нём высоту к большей стороне.

4. Сгибаем правый угол к проведённой высоте

5. Повторяем это же действие с левым углом.

Дальше  сгибаем верхний угол к основанию перпендикуляра, получается что, сумма углов равен 180.

А теперь чему равна сумма углов четырехугольника?

2.      «Волшебные кружочки»

Сейчас я раздам каждому из Вас 10 кружочков, и попрошу построить из них вот такой треугольник (на экране). Теперь Вам необходимо переставить 3 кружочка так, чтобы картинка перевернулась.

Это задание позволило нам раскрыть Вашу логику, пространственное восприятие и скорость мышления

3.На столе разноцветные геометрические фигуры и составить из них пчелу, домик, цветок или что-то другое.  Какой вид будет у финального изображения, не показывайте.  А теперь можно показать исходное изображение к удивлению всех.

После показываем свои изображения и повторяем:

1.Геометрические фигуры на плоскости.

2.Свойства геометрических фигур.

3.      Применение теоремы «Пика»

Сегодня я покажу вам замечательную, универсальную, на мой взгляд, очень полезную, формулу нахождения площадей геометрических фигур. Эта тема довольно актуальна для нас тем, что задания на нахождение площадей фигур являются обязательными как на ОГЭ, так и на ЕГЭ, да и просто знать её, уметь ею пользоваться будет для каждого из нас совсем не лишним.

Итак, создатель формулы Георг Александр Пик. Родился Георг Пик в еврейской семье. До одиннадцати лет Георг получал образование дома (с ним занимался отец), затем он пошел в четвертый класс гимназии. В 1875 г. он сдал выпускные экзамены и поступил университет. Пик поступил в университет в Вене в 1875 году. И уже в следующем году он опубликовал свою первую работу по математике, ему было всего лишь семнадцать лет. Он изучал математику и физику.

Больше всего Пик известен, своей теоремой, которую так и называют теорема Пика, которая появилась в его восьмистраничной работе 1899 года. Эта теорема привлекла довольно большое внимание и начала вызывать восхищение своей простотой и элегантностью.

В чем же красота и элегантность этой теоремы? Во-первых, в том, что она проста. Давайте вместе для себя откроем новую информацию из мира математики.

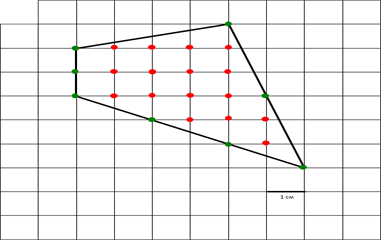
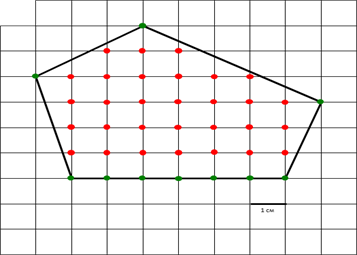
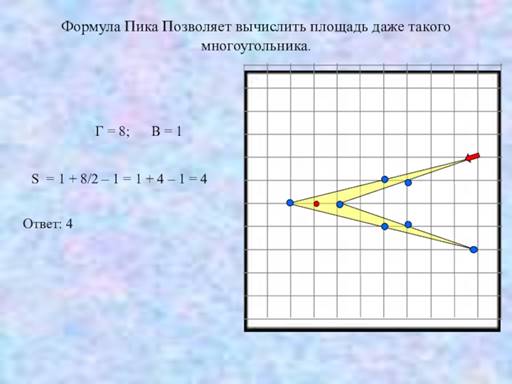
Формула: S=Г/2+В-1

Г – количество узлов на границе многоугольника (на сторонах и вершинах)

В – количество узлов внутри многоугольника

Формула выполняется, если вершины многоугольника находятся в точках целочисленной решётки. Рассмотрим основные понятия: «решетка» и «узел». Что такое решётка? Решёткой в этой теореме является клеточная поверхность бумаги, где располагается фигура . Именно на ней производятся действия связанные с этой формулой.

Что такое узел? Узел – это пересечение горизонтальной и вертикальной линии.

Привести примеры подобных интересных и занимательных заданий можно очень много. Это могут быть и различные логические задачи, и ребусы, и кроссворды, математические цепочки, различные диктанты (математические и графические), задания на готовых чертежах и т.д.

Выполнение всех этих задания способствует развитию пространственного мышления, логики, математической грамотности и самое главное ИНТЕРЕСА к математике.

Я могу сказать, что чем чаще я применяю такие приемы и методы обучения на своих уроках, тем выше их активность на уроке, и тем выше их уровень вычислительных навыков.

В течение жизни мы решаем множество задач. И если каждую отдельно решенную задачу рассматривать как распустившийся цветок, то в результате мы получим огромный, красивый букет.

Пусть все задачи,  которые встают перед вами, будут решены, а букет только из распустившихся цветов.

Спасибо за внимание.