Методическая разработка урока математики в 6 классе "Окружность и круг"

Урок математики в 6 классе.

 

Тема: «Окружность и круг».

 

Цели урока:

-            познакомить с  понятием окружности, круга и их элементов,  

-            изучить формулу длины окружности,  

-            формирование умения применять ее при решении задач, получать значение числа

_ в ходе выполнения практической работы;

-            развивать познавательный интерес учащихся, познакомить их с историческим материалом;

-            прививать учащимся навык самостоятельности в работе, 

-            воспитывать трудолюбие, аккуратность.

 

 

Ход урока.

1.Организационный момент.

 

Ребята, послушайте, какая тишина!

Это в школе начались уроки. Мы не будем тратить время зря,  И приступим все к работе.

 

2. Мотивация урока.

 

Ребята, какие геометрические фигуры мы изучили? (Прямоугольник, треугольник, квадрат...)

В канун нового года принято украшать елку и мы с вами будем этим сегодня заниматься. Но елка наша будет непростая, а математическая.

 

 

Какие фигуры мы с вами не изучали еще? Попробуйте отгадать загадку.

 

Нет углов у меня,

И похож на блюдце я,

На тарелку и на крышку, На кольцо, на колесо.

Кто же я такой, друзья? (Круг)

 

У круга есть одна подруга, Знакома всем ее наружность!

Она идет по краю круга

И называется -…(окружность)

 

Да, именно эти фигуры нам понадобятся сегодня для нашей математической елки.  Итак, тема нашего урока: «Окружность и круг».

 

3. Изучение нового материала.   

 

Выходит девочка с моделью окружности (с ней в паре работает мальчик, который с места задает вопросы):

-   А я – окружность. Внутри меня есть точка непростая.

 Зовется центром, от точек всех моих он равноудален.

-   В каких же отношеньях ты с прямой? - Смотря с какой.

  Внутри меня, ее отрезок  хордою зовут.

  Чем ближе к центру, тем она длинней.

-   Что будет, если хорда через центр пройдет?

-   О!!! Ее диаметром геометр назовет. - А сколько у тебя диаметров? - Ох, много…   Их бесконечность, выражаясь строго.   При том, заметьте, что из них любой   Всегда есть радиус двойной. - А радиус?

-   То всякая прямая, что к центру тянется, его соединяя

  С любой из точек, мне принадлежащих, Точнее, на окружности лежащих.

 

 Из истории.

Недаром древние греки считали окружность совершеннейшей и  «самой круглой» фигурой. И в наши дни в некоторых ситуациях, когда хотят дать особую оценку, используют слово «круглый», которое считается синонимом слова «полнейший»:

круглый отличник, круглый сирота и т.п.

Также считают и колесо – одно из самых замечательных изобретений человека.

Наверное, весь секрет кроется в свойствах удивительной линии – окружности.

Давайте сделаем вывод и «соберем» разбежавшиеся правила.

 

Начало:

Окружность – замкнутая линия без самопересечений…

Круг – это часть плоскости,…

Радиус – это отрезок, соединяющий… Диаметр – это отрезок, соединяющий…

Хорда - это отрезок, соединяющий…

Диаметр – это хорда,…

 

Конец:

…все точки которой находятся на одинаковом расстоянии от центра.

…ограниченная окружностью.

…две точки окружности.

…проходящая через центр.

…соединяющий центр окружности с любой точкой на окружности.

…две точки окружности и проходящий через центр.

 

Назвать радиус, центр, диаметр, хорду окружности, изображенные на рисунке.

 

  

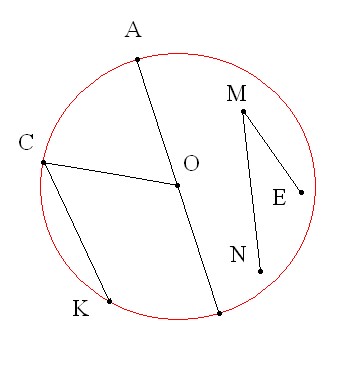
-   Что изображено красным цветом? (Окружность) - Что можно вырезать из бумаги? (Круг)

-   А какая связь между ними?

 

 

Историческая справка.

Окружность – самая простая кривая линия. Радиус – происходит от латинского слова «радиус» - «спица колеса». Хорда – греческое слово и переводится – «струна». Диаметр – «диаметрос» - тоже греческое слово, переводится – «поперечник».

 

Скажите, а с помощью какого инструмента мы можем построить окружность?

 

Загадка 

 

Танцевальное движенье

Совершеннейшей ноги

И круги, круги, круги Вызывают восхищенье.

Балерина создавала

Точный круг в один момент, Подивился ей немало  Достославный геометр.

О прекрасной балерине

Вспоминал частенько он Не по этой ли причине

... был изобретён.

 

(Циркуль)

 

Из истории возникновения циркуля.

 

Циркуль от латинского слова “circulus” - круг, окружность (“circa” - вокруг, кругом, то есть цирк – это круг)

Сейчас уже нельзя сказать, кто именно изобрел этот инструмент - история не сохранила для нас его имя, но легенды Древней Греции приписывают авторство Талосу, племяннику знаменитого Дедала, первого «воздухоплавателя» древности.  История циркуля насчитывает уже несколько тысяч лет - судя по сохранившимся начерченным кругам, инструмент был знаком еще вавилонянам и ассирийцам (II - I века до нашей эры). На территории Франции, в галльском кургане был найден железный циркуль (I век нашей эры), во время раскопок в Помпеях было найдено много древнеримских бронзовых циркулей.

 

Давайте вместе построим несколько шариков для нашей математической елочки, радиусы которых равны 2см, 4см и 5см 5мм. Разукрасьте их.

 

 

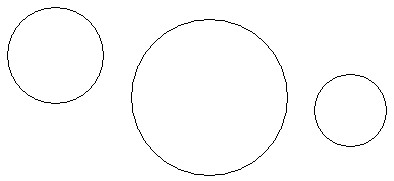
Постройте на каждом из них радиус и диаметр. Измерьте, чему равен диаметр каждого шарика. Какой можно сделать вывод? правильно, длина диаметра в 2 раза больше радиуса. Если обозначить r – радиус, а d – диаметр, тогда: d=2 r.

 

Я тоже для вас приготовила елочные шарики (картонные кружочки разных радиусов разных цветов, по 3 на одну парту).

Давайте измерим длину каждой окружности. В чем трудность? Да, к сожалению, специального прибора для измерения длины окружности нет. Но и это не останавливало человека. Предложите свой способ измерения длины окружности (обсуждение в группах).

Еще древние греки умели находить длину окружности по формуле  С = π d  или С = 2πr  , где d - диаметр окружности, а  - радиус окружности. А что это за число π?

 

4. Первичное закрепление нового материала.

Рассмотрим на практической работе один из способов нахождения числа .

Если «опоясать» окружность ниткой, а затем ее «распрямить», то длина нитки будет приблизительно равна длине окружности. У вас имеются 3 круга различных диаметров. Измерьте длину окружности  и диаметр каждого и найдите отношение длины  к  диаметру окружности. Результаты измерений заносятся в таблицу:

 

№ опыта	Длина окружности (С)	Диаметр (d)	Значение π =С: d
1
2
3

 

Если измерения выполнены достаточно точно, то у всех должно получиться значение π  приблизительно равное 3,1-3,2.

Из истории.

Еще в древности людям были известны многие геометрические фигуры, в том числе окружность и круг. Об этом свидетельствуют археологические раскопки. Еще тогда приходилось решать задачи на вычисление длины окружности. Сейчас известно, что значением числа  π в разные времена считали различные числа. Так, в Древнем Египте (ок. 3500 лет назад) считали π = 3,16; древние римляне полагали, что π= 3,12. Все эти значения были определены опытным путем. Великий ученый Древней Греции

Архимед определил, что значение π находится в следующих пределах   3 <π<3 .

Легенда гласит, что когда древнегреческий город Сиракузы, где жил в своё время Архимед, захватили римляне, учёный, занимаясь научными исследованиями, чертил окружности на песке. Солдату, который пришёл убить его, он воскликнул: “Убей меня, но не тронь моих кругов”.

С помощью современных электронно – вычислительных машин число «пи» было вычислено точностью до миллиона знаков после запятой. Для обозначения частного от деления длины окружности на диаметр впервые букву π использовал английский математик Джонс в 1706 г., но общепринятым это обозначение стало благодаря работам великого математика Эйлера. Он вычислил для числа я 153 десятичных знака.

 

Для закрепления в памяти рационального выражения π – числа Архимеда (π =22/7) - может оказаться полезной шутка из учебника Магницкого: Двадцать две совы скучали  На больших сухих суках. 

Двадцать две совы мечтали

 О семи больших мышах,  О мышах довольно юрких  В аккуратных серых шкурках.  Слюнки капали с усов  У огромных серых сов.

 

Его значение 3, 14159265358…

 

Желающим запомнить поможет мнемоника - придумывание стихотворных, легко запоминающихся фраз, число букв, в каждом слове которых указывает соответствующую цифру.

 

Мнемонические правила

 

Чтобы нам не ошибаться, Надо правильно прочесть: Три, четырнадцать, пятнадцать, Девяносто два и шесть.

 

Надо только постараться

И запомнить всё как есть:

Три, четырнадцать, пятнадцать, Девяносто два и шесть.

 

Три, четырнадцать, пятнадцать, Девять, два, шесть, пять, три, пять. Чтоб наукой заниматься,

Это каждый должен знать.

 

Можно просто постараться И почаще повторять:

«Три, четырнадцать, пятнадцать, Девять, двадцать шесть и пять».

 

5.Самостоятельная работа.

К нам на нашу математическую елочку пришли Колобок, Снеговик. Давайте их нарисуем и вычислим с помощью формулы С = 2πr  длину окружности.

 

1) Рисуем колобка, окружность радиусом 4 см и разукрашиваем цветными карандашами.

 

 

 

2)Рисуем снеговика, радиусы окружностей которого 3 см, 4,5 см и 6 см. Затем разукрашиваем.

 

 

 

 

Из истории.

Неофициальный праздник «День числа Пи» отмечается 14 марта, которое в американском формате дат (месяц/день) записывается как 3.14, что соответствует приближённому значению числа π.

Ещё одной датой, связанной с числом π, является 22 июля, которое называется «Днём приближённого числа Пи» (англ. Pi Approximation Day), так как в европейском формате дат этот день записывается как 22/7, а значение этой дроби является приближённым значением числа π.

 

 

 

Памятник числу «пи» на ступенях перед зданием Музея искусств в Сиэтле.

 

 

6. Итоги урока.  Д/з.

1.         Вычислите длину окружности, если r =5см.

2.         Вычислите длину окружности, если d = 100 м.

3.         Ученики организовали соревнования по фигурному катанию на велосипедах. В этих соревнованиях нужно было проехать четыре круга по окружности радиусом 3 м. Какое расстояние проехали велосипедисты в этом виде фигурного катания?  Творческое задание: по возможности придумать стихотворную фразу для запоминания числа π.

 

 

Рефлексия.

1.     С какой геометрической фигурой мы познакомились?

2.     Что надо знать, чтобы построить окружность?

3.     С помощью какого инструмента мы ее строим?

4.     Чему равно число π?

5.     Что нового, интересного узнали? 6. Что понравилось?

 

Наша математическая елка украшена, гости в сборе. Осталось только поздравить вас с наступающим Новым Годом.

 

Пусть Новый год вам принесет

Со снегом - смех,

С морозом - бодрость, В делах успех,

А в духе - твердость.

Пусть все заветное свершится

И, пересилив даль дорог,

Надежда в дверь к вам постучится И тихо ступит на порог.

 

Удачи вам!

Спасибо за урок!