
Методическая разработка
внеклассного мероприятия для учащихся
6 класса
" Математическая викторина".
Разработчик: учитель математики МБОУ "Школа №125" , г. Нижний Новгород Алекаева Валентина Алексеевна.
№1 В шесть рядов.
Расставить 24человека в шесть рядов так, чтобы каждый ряд состоял из пяти человек.
№2 Девять нулей.
Девять нулей расставлены так, как здесь показано:
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
Задача состоит в том, чтобы перечеркнуть все нули, проведя только четыре прямые линии. Чтобы облегчить отыскание решения, прибавлю еще, что все девять нулей перечеркиваются, не отрывая карандаша от бумаги.
№3 Две шашки.
На пустую шашечную доску надо поместить две различные шашки. Сколько различных положений могут они занимать на доске?
 №4
Лунный серп.
№4
Лунный серп.
Эту фигуру лунного серпа требуется разделить на шесть частей, проведя всего только две прямые линии. Как это сделать?
№5 Землекопы.
Пять землекопов в пять часов выкапывают 5м канавы. Сколько землекопов в 100 часов выкопают 100 м канавы?
№6 Сколько машин?
В мастерской отремонтировано в течение месяца 40 машин – автомобилей и мотоциклов. Всех колес выпущено было из ремонта ровно 100. Спрашивается, сколько было в ремонте автомобилей и мотоциклов.
№7 Почем лимоны?
Три дюжины лимонов стоят столько рублей, сколько дают лимонов на 16 рублей. Сколько стоит дюжина лимонов?
№8 Вздорожание и подешевление.
Товар на 10% вздорожал, потом на 10% подешевел. Когда цена его была ниже: до вздорожания или после подешевления?
№9 Кошки и котята.
Из прилагаемого рисунка вы видите, что четыре кошки и три котенка весят 15 кг, а три кошки и четыре котёнка весят 13 кг. Сколько же весит каждая кошка и каждый котенок в отдельности? Предполагается, что все взрослые кошки весят одинаково; котята также весят поровну

№10 Три и семь.
Часы бьют три. И пока они бьют, проходит 3 секунды. Сколько же времени должны употребить часы, чтобы пробить семь?
 №11
Который час?
№11
Который час?
- Куда спешите?
- К шести часовому поезду. Сколько минут осталось до отхода?
- 50 минут назад было вчетверо больше минут после трех. Что означает этот странный ответ? Который был час?
№12 Стадо коров.
Некто раздал своим
сыновья стадо коров. Старшему он дал одну корову и ![]() всех остальных; второму
– две коровы и
всех остальных; второму
– две коровы и ![]() всех остальных; третьему
– три коровы и
всех остальных; третьему
– три коровы и ![]() всех остальных;
четвертому четыре коровы и
всех остальных;
четвертому четыре коровы и ![]() всех остальных и т.д
Так разделено было все стадо между сыновьями без остатка. Сколько было сыновей,
и какова была численность стада?
всех остальных и т.д
Так разделено было все стадо между сыновьями без остатка. Сколько было сыновей,
и какова была численность стада?
№13 В ожидании трамвая.
Три брата, возвращаясь из театра домой, подошли к трамвайной остановке, чтобы вскочить в первый же вагон, который подойдет. Вагон не показывался, и старший брат предложил подождать.
- Чем стоять здесь и ждать, - ответил средний брат, - лучше пойдем вперед. Когда вагон догонит нас, тогда и вскочим, а тем временем часть пути будет уже за нами – скорее домой приедем.
- Если уж идти, - возразил младший брат, - то не вперед, по движению, а в обратную сторону: тогда нам, конечно, скорее попадется встречный вагон; мы раньше и домой прибудем.
Так как братья не могли убедить друг друга, то каждый поступил по-своему: старший остался ожидать на месте, средний пошел вперед, младший – назад. Кто из трех братьев приехал домой раньше? Кто из них поступил благоразумнее?
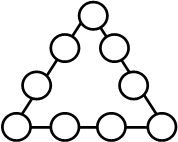 №14 Числовой треугольник.
№14 Числовой треугольник.
Все значащие цифры разместить в кружках треугольника так, чтобы сумма их на каждой стороне равнялась 17.
№15 Три четверти человека.
Одного бригадира полеводческой бригады спросили, сколько у него в бригаде человек. Он ответил довольно замысловато:
- Людей немного: три четверти нас да еще три четверти человека – вот и всего у нас людей.
Можете ли вы разгадать, сколько человек было в этой бригаде?
№16 Почтовые марки.
Гражданин купил на 5 рублей марок трех родов: в 50 копеек, в 10 копеек и в 1 копейку – всего 100 штук. Можете ли вы сказать, сколько штук марок разного рода он купил?

 №17
Две кружки.
№17
Две кружки.
Одна кружка вдвое выше
другой, зато другая в ![]() раза шире. Которая
кружка вместительнее?
раза шире. Которая
кружка вместительнее?
№18 Что тяжелее.
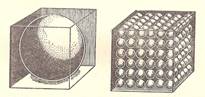
Имеются два одинаковых кубических ящика. В левый положен большой железный шар диаметром во всю высоту ящика. Правый наполнен маленькими железными шариками, уложенными так, как показано на рисунке. Который ящик тяжелее?
Ответы для математической
викторины 6 класса.
№1 В шесть рядов.
 Расставить
24человека в шесть рядов так, чтобы каждый ряд состоял из пяти человек.
Расставить
24человека в шесть рядов так, чтобы каждый ряд состоял из пяти человек.
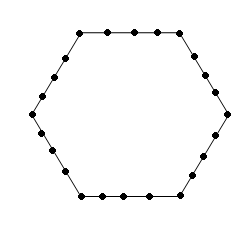
Решение. Требованию задачи легко удовлетворить,
если расставить людей в форме шестиугольника,
как показано на рис.
∙№2 Девять нулей.
Девять нулей расставлены так, как здесь показано:
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
 Задача
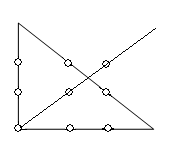
состоит в том, чтобы перечеркнуть все нули, проведя только четыре прямые
линии. Чтобы облегчить отыскание решения, прибавлю еще, что все девять нулей
перечеркиваются, не отрывая карандаша от бумаги.
Задача
состоит в том, чтобы перечеркнуть все нули, проведя только четыре прямые
линии. Чтобы облегчить отыскание решения, прибавлю еще, что все девять нулей
перечеркиваются, не отрывая карандаша от бумаги.
Решение. Задача решается так, как показано на рис.
№3 Две шашки.
На пустую шашечную доску надо поместить две различные шашки. Сколько различных положений могут они занимать на доске?
Решение. Первую шашку можно поместить на любое из 64 полей доски, то есть 64 способами. После того как первая поставлена, вторую шашку можно поместить на какое либо из прочих 63 полей. Значит, к каждому из 64 положений первой шашки можно присоединить 63 положения второй шашки. Отсюда общее число различных положений двух шашек на доске:
64![]()
 №4
Лунный серп.
№4
Лунный серп.
![]()

![]()
![]() Эту
фигуру лунного серпа требуется разделить на шесть частей, проведя всего только
две прямые линии. Как это сделать?
Эту
фигуру лунного серпа требуется разделить на шесть частей, проведя всего только
две прямые линии. Как это сделать?
Решение.
![]()
№5 Землекопы.
Пять землекопов в пять часов выкапывают 5м канавы. Сколько землекопов в 100 часов выкопают 100 м канавы?
Решение. На удочку этой задачи легко попасться: можно думать, что если 5 землекопов в 5 часов вырыли 5 м канавы, то для выкопки в 100 часов 100м понадобиться 100 человек. Однако это совершенно неправильное рассуждение: понадобиться те же 5 землекопов, не больше.
В самом деле,5 землекопов в 5 часов выкапывают 5м; значит, 5 землекопов в 1 час вырыли бы 1 м, а в100 часов – 100 м.
№6 Сколько машин?
В мастерской отремонтировано в течение месяца 40 машин – автомобилей и мотоциклов. Всех колес выпущено было из ремонта ровно 100. Спрашивается, сколько было в ремонте автомобилей и мотоциклов.
Решение. Если бы все 40 машин были мотоциклы, то общее число колёс равнялось бы 80, т.е. на 20 меньше, чем в действительности. Замена одного мотоцикла автомобилем влечет за собой увеличение общего числа колес на два: разница уменьшается на два. Очевидно, надо сделать 10 таких замен, чтобы свести разницу к нулю. Итак, автомобилей было10, а мотоциклов – 30.
Действительно: 10![]() .
.
№7 Почем лимоны?
Три дюжины лимонов стоят столько рублей, сколько дают лимонов на 16 рублей. Сколько стоит дюжина лимонов?
Решение.
Мы знаем, что 36 лимонов стоят столько рублей, сколько на 16 рублей дают
лимонов. Но 36 штук стоят: 36 ![]()
А на 16 рублей дают штук:
![]()
Значит, 36 ![]()
Если бы первую часть не делили на цену штуки, то в левой части получили бы больше в ( цену штуки) раз, т.е. 16 :
36 ![]() ) =16
) =16
Если бы левую часть не
множили на 36, то в правой части получили бы меньше в 36 раз : ![]() ) =
) =![]()
Ясно что цена штуки равна
![]() =
=![]() рубля, а стоимость
дюжины лимонов равна
рубля, а стоимость
дюжины лимонов равна
![]()
![]()
№8 Вздорожание и подешевление.
Товар на 10% вздорожал, потом на 10% подешевел. Когда цена его была ниже: до вздорожания или после подешевления?
Решение. Ошибочно
считать, что цена в обоих случаях одинакова. Сделаем соответствующие выкладки.
После вздорожания товар стоил 110%, или 1,1 первоначальной цены. После же
подешевления цена его составляла 1,1 ![]() первоначальной. Значит,
после подешевления товар стал на 1
первоначальной. Значит,
после подешевления товар стал на 1![]() дешевле, чем
вздорожания.
дешевле, чем
вздорожания.
№9 Кошки и котята.
Из прилагаемого рисунка вы видите, что четыре кошки и три котенка весят 15 кг, а три кошки и четыре котёнка весят 13 кг. Сколько же весит каждая кошка и каждый котенок в отдельности? Предполагается, что все взрослые кошки весят одинаково; котята также весят поровну.

Решение. Сравнивая оба взвешивания, легко видеть, что от замены одной кошки одним котенком вес груза уменьшился на 2 кг. Отсюда следует, что кошка тяжелее котенка на 2 кг. Зная это ,заменим при первом взвешивании всех 4 кошек котятами: у нас будет тогда всех 4 + 3 = 7 котят, весить они будут вместе не 15 кг, а на 2∙4,т. Е. на 8 кг. меньше. Значит,7 котят весят 15 – 8 = 7 кг. Отсюда ясно, что котенок весит 1 кг, взрослая кошка 1+ 2 =3 кг.
№10 Три и семь.
Часы бьют три. И пока они бьют, проходит 3 секунды. Сколько же времени должны употребить часы, чтобы пробить семь?
Решение. Обычно отвечают: «7 секунд». Но такой , ответ, как сейчас увидим, неверен. Когда часы бьют 3, мы наблюдаем 2 промежутка:
1) между первым и вторым ударом;
2) между вторым и третьим ударом.
Оба
промежутка длятся 3 секунды; значит, каждый продолжается вдвое меньше – именно
1![]() секунды. Когда же часы
бьют 7, то таких же промежутков бывает 6. Шесть раз по 1
секунды. Когда же часы
бьют 7, то таких же промежутков бывает 6. Шесть раз по 1![]() секунды составляет 9
секунд. Следовательно часы «бьют 7» ( т. е. делают 7 ударов) в 9 секунд.
секунды составляет 9
секунд. Следовательно часы «бьют 7» ( т. е. делают 7 ударов) в 9 секунд.
 №11
Который час?
№11
Который час?
- Куда спешите?
- К шести часовому поезду. Сколько минут осталось до отхода?
- 50 минут назад было вчетверо больше минут после трех. Что означает этот странный ответ? Который был час?
Решение. Между 3 и 6 часами 180 минут. Число минут , остающихся до 6 часов, найдется, если 180 – 50,т.е. 130, разделим на такие 2 части, из которых одна в 4 раза больше другой. Значит, надо найти пятую часть от 130. Итак, было без 26 минут шесть.
№12 Стадо коров.
Некто раздал своим
сыновья стадо коров. Старшему он дал одну корову и ![]() всех остальных; второму
– две коровы и
всех остальных; второму
– две коровы и ![]() всех остальных; третьему
– три коровы и
всех остальных; третьему
– три коровы и ![]() всех остальных;
четвертому четыре коровы и
всех остальных;
четвертому четыре коровы и ![]() всех остальных и т.д.
Так разделено было все стадо между сыновьями без остатка. Сколько было сыновей,
и какова была численность стада?
всех остальных и т.д.
Так разделено было все стадо между сыновьями без остатка. Сколько было сыновей,
и какова была численность стада?
Решение. Решать задачу арифметически ( т.е. не прибегая к уравнениям) надо с конца.
Самый младший сын получил
столько коров, сколько было всех сыновей; ![]() остального
стада он получить с
остального
стада он получить с
верх того не мог, т.к. остатка после него никакого не было.
Далее: предыдущий сын
получил коров одной меньше, чем было всех сыновей, и![]() остального
стада. Значит, то, что досталось самому младшему сыну, составляет
остального
стада. Значит, то, что досталось самому младшему сыну, составляет ![]() доли этого остального.
доли этого остального.
Отсюда вытекает, что число коров, полученное самым младшим сыном, должно делиться на 6 без остатка.
Попробуем допустить, что
этот младший сын получил 6 коров, и посмотрим, годится ли это предположение.
Если самый младший получил 6 коров, то, значит, он был шестой сын, и всех
сыновей было 6. Пятый сын получил 5 коров, да еще![]() от 7, т.е. всего 6
коров. Соображаем, что оба последних сына получили 6 + 6 = 12 коров, которые
составляют
от 7, т.е. всего 6
коров. Соображаем, что оба последних сына получили 6 + 6 = 12 коров, которые
составляют ![]() оставшегося после
наделения 4 сына. Полный остаток равен 12 :
оставшегося после
наделения 4 сына. Полный остаток равен 12 : ![]() = 14 коровам;
следовательно, 4 сын получил 4 +
= 14 коровам;
следовательно, 4 сын получил 4 + ![]() = 6.
= 6.
Вычислим остаток стада
после наделения третьего сына: 6 + 6 + 6, т.е. 18, есть ![]() этого остатка; поэтому полный
остаток 18 :
этого остатка; поэтому полный
остаток 18 : ![]() = 21. Третьему сыну
досталось 3 +
= 21. Третьему сыну
досталось 3 + ![]() = 6.
= 6.
Точно таким же образом узнаем, что второй и первый сыновья получили тоже по 6 коров.
Допущение наше оказалось правдоподобным: всех сыновей было 6, а коров в стаде 36.
Нет ли еще других решений? Допустим, что сыновей было не 6, а 12; окажется, что такое допущение не годится. Непригодно и число 18. Дальше не для чего и испытывать: 24 и больше сыновей быть не могло.
№13 В ожидании трамвая.
Три брата, возвращаясь из театра домой, подошли к трамвайной остановке, чтобы вскочить в первый же вагон, который подойдет. Вагон не показывался, и старший брат предложил подождать.
- Чем стоять здесь и ждать, - ответил средний брат, - лучше пойдем вперед. Когда вагон догонит нас, тогда и вскочим, а тем временем часть пути будет уже за нами – скорее домой приедем.
- Если уж идти, - возразил младший брат, - то не вперед, по движению, а в обратную сторону: тогда нам, конечно, скорее попадется встречный вагон; мы раньше и домой прибудем.
Так как братья не могли убедить друг друга, то каждый поступил по-своему: старший остался ожидать на месте, средний пошел вперед, младший – назад. Кто из трех братьев приехал домой раньше? Кто из них поступил благоразумнее?
Решение. Младший брат, пойдя назад по движению, увидел идущий навстречу вагон и вскочил в него. Когда этот вагон дошел до места, где ожидал старший брат, последний вскочил в него. Когда этот вагон дошел до места, где ожидал старший брат, последний вскочил в него. Немного спустя тот же вагон догнал шедшего впереди среднего брата и принял его. Все 3 брата очутились в одном и том же вагоне и, конечно, приехали домой одновременно. Однако благоразумнее всего поступил старший брат: спокойно ожидал на одном месте, он устал меньше других.
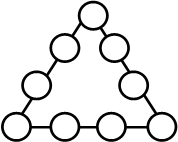 №14 Числовой треугольник.
№14 Числовой треугольник.
Все значащие цифры разместить в кружках треугольника так, чтобы сумма их на каждой стороне равнялась 17.
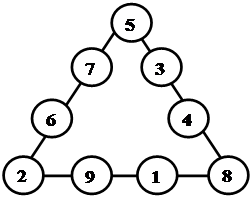
Решение. Средние цифры каждого ряда можно переставить и получить, т.о., еще ряд решений.
№15 Три четверти человека.
Одного бригадира полеводческой бригады спросили, сколько у него в бригаде человек. Он ответил довольно замысловато:
- Людей немного: три четверти нас да еще три четверти человека – вот и всего у нас людей.
Можете ли вы разгадать, сколько человек было в этой бригаде?
Решение.![]() бригады да еще
бригады да еще ![]() человека составляют всю
бригаду. Значит, эти
человека составляют всю
бригаду. Значит, эти![]() человека есть
недостающая четверть бригады. Полная бригада в 4 раза больше, чем
человека есть
недостающая четверть бригады. Полная бригада в 4 раза больше, чем ![]() человека. Но
человека. Но ![]() человека, взятые 4 раза,
составляют 3. Итак, в бригаде было 3 человека.
человека, взятые 4 раза,
составляют 3. Итак, в бригаде было 3 человека.
№16 Почтовые марки.
Гражданин купил на 5 рублей марок трех родов: в 50 копеек, в 10 копеек и в 1 копейку – всего 100 штук. Можете ли вы сказать, сколько штук марок разного рода он купил?
Решение. Гражданин купил:
50- копеечных марок 1 штуку
10- копеечных марок 39 штук
1- копеечных марок 60 штук
Всех марок 1 + 39 + 60 = 100 штук. А стоят они 50 + 390 + 60 = 500 копеек.

 №17
Две кружки.
№17
Две кружки.
Одна кружка вдвое выше
другой, зато другая в ![]() раза шире. Которая
кружка вместительнее?
раза шире. Которая
кружка вместительнее?
Решение. Та
кружка, которая в 1![]() раза шире, при равной
высоте была бы вместительнее в
раза шире, при равной
высоте была бы вместительнее в ![]() , т. е. в 2
, т. е. в 2![]() раза. Т.к. она ниже
только в 2 раза, то в конечном итоге она все же вместительнее, чем высокая
кружка.
раза. Т.к. она ниже
только в 2 раза, то в конечном итоге она все же вместительнее, чем высокая
кружка.
№18 Что тяжелее.
Имеются два одинаковых кубических ящика. В левый положен большой железный шар диаметром во всю высоту ящика. Правый наполнен маленькими железными шариками, уложенными так, как показано на рисунке. Который ящик тяжелее?
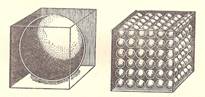
Решение. Правый куб представим себе состоящим из маленьких кубиков, в каждом из которых помещается шарик. Легко видеть, что большой шар занимает такую же долю целого куба, какую составляет каждый малый шарик от малого кубика. Число всех малых шариков и кубиков не трудно определить: 6∙6∙6=216. 216 шариков составляет по объему такую же долю от216 кубиков, как и один шарик от одного кубика, т.е. такую же, как и большой шар от большего куба. Отсюда ясно, что в обоих ящиках содержится одинаковое количество металла и, следовательно, вес их должен быть один и тот же.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.