МЕТОДИЧЕСКАЯ РАЗРАБОТКА ЗАНЯТИЯ «Классическая постановка транспортной задачи. Метод потенциалов» ПО ДИСЦИПЛИНЕ ЕН.01 МАТЕМАТИКА для студентов IІ курса специальности 23.02.01 Организация перевозок и управление на транспорте (по видам)

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

ДОНЕЦКОЙ НАРОДНОЙ РЕСПУБЛИКИ

ГОСУДАРСТВЕННОЕ ПРОФЕССИОНАЛЬНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«ДОНЕЦКИЙ ТРАНСПОРТНО-ЭКОНОМИЧЕСКИЙ КОЛЛЕДЖ»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

МЕТОДИЧЕСКАЯ РАЗРАБОТКА ЗАНЯТИЯ

 

 «Классическая постановка транспортной задачи. Метод потенциалов»

 

ПО ДИСЦИПЛИНЕ ЕН.01 МАТЕМАТИКА

 

для студентов IІ курса

специальности     23.02.01 Организация перевозок

 и управление на транспорте (по видам)

 

 

                                                             

 

 

 

 

 

2020 год

 

 

Методическая разработка занятия по дисциплине ЕН.01 Математика

 

 

 

Подготовила Воловик О.В. – преподаватель математики Государственного профессионального образовательного учреждения «Донецкий транспортно-экономический колледж», специалист высшей категории – 2020.

 

 

В разработке представлена методика проведения занятия по дисциплине ЕН.01 Математика для студентов IІ курса специальности     23.02.01 Организация перевозок  и управление на транспорте (по видам)  по теме «Классическая постановка транспортной задачи. Метод потенциалов»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рассмотрено и одобрено на заседании цикловой комиссии естественно- математических дисциплин ГПОУ «Донецкий транспортно-экономический колледж»

Протокол № 5  от 2 декабря 2020г.

Председатель цикловой комиссии    ____________ Н.А. Дулина

ВВЕДЕНИЕ

 

         Данная методическая разработка составлена в соответствии с рабочей программой учебной дисциплины ЕН.01 Математика. Рабочая программа учебной дисциплины ЕН.01 Математика является частью основной профессиональной образовательной программы в соответствии с ГОС по специальности СПО 23.02.01 Организация перевозок и управление                                                  на транспорте (по видам) и соответствующих общих и профессиональных компетенций.

В основе программы дисциплины лежат следующие нормативные документы:

-          Закон Донецкой Народной Республики  «Об образовании» от 25.06.2015 года;

-          Государственный образовательный стандарт среднего профессионального образования по специальности 23.02.01 Организация перевозок и управление                                                  на транспорте (по видам);

-          Приказ МОН ДНР № 328 от 20.07.2015 г  «О  порядке организации и осуществления образовательной деятельности по образовательным программам среднего профессионального образования»;

-          Учебный план УЗ СПО ДонТЭК по специальности 23.02.01 Организация перевозок и управление на транспорте (по видам).

Математика является фундаментальной дисциплиной. На ней базируется преподавание, как дисциплин естественнонаучного цикла, так и специальных дисциплин.

Математика является не только мощным средством решения прикладных задач и универсальным языком науки, но также и элементом общей культуры

 

 

 

 

 

Учебная дисциплина: ЕН.01 Математика

         Тема занятия: «Классическая постановка транспортной задачи. Метод потенциалов»

Вид занятия: лекция

         Тип занятия: изучения новых знаний

         Цель занятия:

методическая:

-    совершенствование навыков применения активных и интерактивных методов обучения с целью создания условий для активной творческой самостоятельной работы студентов и формирования их познавательных способностей.

дидактическая:

-   обобщение и систематизация знаний о задачах линейного программирования;

-   формирование  навыков  построения математической модели транспортной задачи;

-   отработка алгоритма решения транспортной задачи методом потенциалов.

воспитательная:

-    воспитание и развитие разносторонних интересов личности;

-    воспитание ответственного отношения к учебному труду, воли и настойчивости для достижения конечных результатов при расчетах транспортной задачи;

-    воспитание умения работать в команде, чувства коллективизма, ответственности за результат совместной деятельности.

развивающая:

-    развитие познавательных интересов и творческих способностей студентов, психологических способностей студента, обеспечивающих его адаптацию в дальнейшей жизни, научить студентов учиться посредством личностно-ориентированного подхода;

-    способствовать совершенствованию операций умственной деятельности: анализ, синтез, классификация, способность наблюдать и делать выводы, выделять существенные признаки.

        

 

 

 

 

 

Литература:

основная:

1. Математическое программирование. Учебное пособие студентов специальностей " учет и аудит», «банковское дело», «Финансы»/ составитель Г. Г. Пенина.- Донецк, ДонДУЕТ, 2004.

дополнительная:                                           

1. Высшая математика для экономистов: Учебник для вузов/ Под ред. проф. Н.Ш. Кремера. – 2-е изд., перераб. и доп. – М..ЮНИТИ, 2012.

Интернет-ресурсы:

1. https://open-lesson.net/(Методические разработки занятий)

2. https://www.metod-kopilka.ru/ (Методические разработки занятий)                                                   

 

 

 

 

 

 

 

 

 

 

 

СТРУКТУРА ЗАНЯТИЯ

I    Организационный момент

      –  дата – перекличка студентов – дежурство –  проверка готовности студентов к занятию

 

II  Сообщение темы,  целей  и основных задач занятия, место темы в общей структуре дисциплины

 

III  Мотивация учебной и познавательной деятельности

Термин ТРАНСПОРТНАЯ ЗАДАЧА ассоциируется с перемещением груза от поставщиков к потребителям. Решение данной задачи позволяет разработать наиболее рациональные пути и способы транспортирования товаров, устранить чрезмерно дальние, встречные, повторные перевозки. Всё это сокращает время продвижения товаров, уменьшает затраты предприятий и фирм, связанные с осуществлением процессов снабжения сырьём, материалами, топливом, оборудованием и т. д. Вместе с тем алгоритм и методы решения транспортной задачи могут быть использованы при решении некоторых задач, не имеющих ничего общего с транспортировкой груза. Всё зависит от того, как интерпретируются так называемые тарифы. Так, например, при решении задачи обеспечения материальными ресурсами при производстве продукции товары, находящиеся на складе, физически не перемещаются, но при этом увеличивается их стоимость в результате расходов на хранение. Таким образом, товар как бы перемещается во времени, а значит, задачу по минимизации расходов на осуществление процесса обеспечения ресурсами можно решить с помощью транспортной задачи.

Впервые высказывание о важности решения задач линейного программирования и, в частности, транспортной задачи было сделано в прошлом веке. Тогда же были предложены методы решения этих задач. У истоков создания теории линейного программирования стоял русский учёный – Л. В. Канторович. Широкое практическое использование этой теории началось после появления вычислительных машин. Это связано с тем, что при реализации методов линейного программирования требуется выполнять многочисленные последовательные арифметические операции. Ошибка в одном действии приводила к неверному результату и поиску верного решения путём повторного утомительного расчёта.

 

 

IV  Усвоение новых знаний и закрепление изученного материала

 

Мы рассмотрим классическую транспортную задачу – это задача об оптимальном плане перевозок грузов из пунктов отправления в пункты потребления, встречается чаще всего в практических приложениях линейного программирования.

На каждом предприятии есть отдел логистики. Его работа заключается в организации рационального процесса продвижения товаров от производителей к потребителям, создания инфраструктуры товародвижения. Логисты обязательно должны уметь работать в Word, Excel, Access. По окончании колледжа вы можете работать логистами. Логистов иначе называют «транспортными богами».

Сегодня на занятии нам необходимо разобрать транспортную задачу,  научиться строить математическую модель этой задачи и решать ее.

Как всегда изучение теоретического материала будем сопровождать примерами.

Проблема транспортной задачи была впервые формализована французским математиком Гаспаром Монжем в 1781 году, который выполнил работу о наиболее экономном способе перемещения масс для строительства военных укреплений.

А основное продвижение было сделано советским математиком и экономистом Леонидом Канторовичем.

В 1939 году к 26-летнему профессору-математику, обратились за консультацией сотрудники лаборатории планерного треста, которым нужно было решить задачу о наиболее выгодном распределении материала между станками. Эта задача сводилась к нахождению максимума линейной функции, заданной на многограннике. Максимум такой функции достигался в вершине, однако число вершин в этой задаче достигало миллиарда. Поэтому простой перебор вершин не годился. Леонид Витальевич писал: “оказалось, что эта задача не является случайной. Я обнаружил большое число разнообразных по содержанию задач, имеющих аналогичный математический характер: наилучшее использование посевных площадей, выбор загрузки оборудования, рациональный раскрой материала, распределение транспортных грузопотоков…  Это настойчиво побудило меня к поиску эффективного метода их решения”. И уже летом 1939 года была сдана в набор книга Л.В.Канторовича “Математические методы организации и планирования производства”.

Поэтому иногда эта проблема называется транспортной задачей Монжа — Канторовича.

В 1975 году академик Л.В.Канторович и американец профессор Т.Купманс получили Нобелевскую премию по экономическим наукам за “вклад в разработку теории и оптимального использования ресурсов в экономике”.

 

1. Постановка транспортной задачи

 

Предположим, что в m пунктах отправления (производства)  хранится однородный груз, имеющийся соответственно в количествах  единиц, который требуется доставить в каждый из n пунктов назначения (потребления)  соответственно в количествах единиц. Стоимость перевозки (тариф) единицы продукции из в  известна для всех маршрутов  и  равна   (i = 1,…, m; j = 1…, n).

Требуется составить такой план перевозок, при котором весь груз из пунктов отправления вывозится, и запросы всех пунктов потребления удовлетворяются, а суммарные транспортные расходы минимальны.

Чтобы мы могли решать данную задачу нам необходимо записать ее математическую модель.

Наша задача найти значения х, которые удовлетворяют системе ограничений и целевой функции.

При этом нам понадобятся несколько определений:

Определение:   Построенный план называется опорным, если в нем отличны от нуля m+n-1 базисных перевозок, а остальные перевозки равны 0.

Определение:   Опорный план называется оптимальным, если он приводит к минимальной суммарной стоимости перевозок.

Перейдем  к решению задачи.

Так как транспортная задача является задачей линейного программирования, то её можно решать симплекс-методом.

 

Условия задачи удобно располагать в таблице,  вписывая в ячейки количество перевозимого груза ≥ 0  из в , а в маленькие клетки – соответствующие тарифы  .
 

 

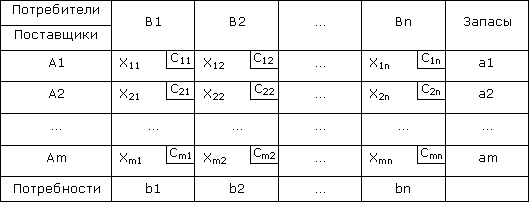
Итак, наша задача заключается в нахождении таких неотрицательных величин  , которые удовлетворяли бы системам

 

,

 

а целевая функция     была бы минимальной.

 

 

2. Метод потенциалов

 

Этот метод используется для решения многих распределительных задач, содержащих большое число переменных и отвечающих требованию целочисленности решения. Таким, в частности, являются транспортные задачи, на них и будет проиллюстрирован алгоритм метода. Теоретические основы метода таковы:

·        необходимым и достаточным условием существования решения является баланс между спросом и предложением;

·        по загруженным ячейкам определяют систему потенциалов: 

,

      где  - потенциал строки;

             - потенциал столбца;

             - тариф соответствующей ячейки.

·        В оптимальном распределении сумма строки и столбца не должна превосходить тариф соответствующей не загруженной ячейки;

·        Количество поставок должно равняться величине , где m-число поставщиков, n-число потребителей.

Метод потенциалов осуществляется в три этапа:

1. Построение первоначального опорного плана (начальное распределение грузов).

2. Оценка оптимальности распределения грузов с помощью системы потенциалов.

3. Улучшение плана перевозок, если оно возможно.

Второй и третий этапы повторяются до тех пор, пока решение не станет оптимальным.

I этап.  Построение первоначального опорного плана

Начальное распределение можно выполнять разными способами: способом северо-западного угла, способом наименьших тарифов, двойного преимущества, способом Фогеля, способу Лебедева-Тихомирова и др. Наиболее простым и легко реализуемым на ЭВМ является способ северо-западного угла. Он заключается в том, что от каждого поставщика, начиная с первого, вывозят весь груз с учетом потребностей потребителей. Распределение завершено, если весь груз от поставщиков вывезен, а каждый потребитель получил необходимый объем.

Рассмотрим пример: есть три поставщика () и три потребителя

 (), известны мощности поставщиков, спрос потребителей и     тарифы на перевоз груза (табл.1). 

Таблица 1

Потребители	Мощность	В1	В2	В3	Ui
Поставщики		200	250	200
A1	250	5   200	4   50 -	1   + (4)	0
A2	150	1   (3)	3   150	3   (1)	-1
A3	250	1   (2)	2   50 +	3   - 200	-2
	Vk	5	4	5	-

 

Установим, прежде всего, наличие баланса между спросом и предложением:   250+150=250=650,  200+250+200=650. Баланс есть.

Теперь распределим груз, начиная с первой верхней ячейки, отсюда и название способа - северо-западный угол. Распределение завершено, необходимо определить затраты (величину Z) и оценить оптимальность решения:  .

 

II этап.  Оценка оптимальности решения

По загруженным ячейкам составим систему уравнений для потенциалов, предварительно проверив количество заполненных клеток. Их должно бать . Именно столько и есть. Сумма потенциалов строки и столбца должна равняться транспортным тарифам загруженных ячеек; на основе чего получаем систему для потенциалов:

 .

Имеем систему из 5 уравнений с 6 неизвестными, поэтому один из потенциалов примем равным 0. Чаще всего берут  и находят все остальные потенциалы:

 .

Теперь необходимо проверить выполнение второго условия оптимальности решения: сумма потенциалов для незаполненной ячейки не должна превышать величину тарифа в ней.

 

Условие оптимальности ни для одной из пустых ячеек не выполняется. Стоит улучшить решение.

 

III этап.  Построение нового распределения

Из всех ячеек, для которых условие оптимальности не выполняется, выбирают ту, у которой расхождение наибольшее. Если таких ячеек несколько, то выбирают клетку с меньшим тарифом. Ее обозначают знаком “+”. Начиная от выбранной ячейки, строят прямоугольную фигуру, все остальные вершины которой находятся в заполненных ячейках. Знаки вершин чередуют.

Вид фигуры предопределяется распределением поставок.

Из всех клеточек, отмеченных знаком минус, выбирают самый маленький груз. Его перемещают вдоль прямоугольной фигуры, прибавляя, если стоит знак"+", и, вычитая, если стоит знак “-“. Все изменения отображаются в новой таблице. Величины, не участвующие в перераспределении, в новую таблицу переносят без изменения. Обратимся к примеру: в таблице 1 знаком “-“ отмечены две ячейки, выбираем наименьший груз 50 и перемещаем его вдоль прямоугольной фигуры. Все изменения показаны в табл.2. получено новое распределение: необходимо оценить его, поэтому возвращаемся ко II этапу алгоритма.

 

Таблица 2

Потребители	Мощность	В1	В2	В3	Ui
Поставщики		200	250	200
A1	250	5   200  -	4	1   +  50	0
A2	150	1   (7) +	3   - 150	3   (1)	3
A3	250	1   (6)	2   + 100	3   - 150	2
	Vk	5	0	1	-

 

.

Проверим число заполненных ячеек. Их по-прежнему 5. Снова находим потенциал. Причем можно не составлять систему, а использовать правила:

1. В 1 строке берем 0.

2. Неизвестный потенциал столбца равна разности между тарифом заполненной ячейки и известным потенциалом строки.

3. Неизвестный потенциал столбца равна разности между тарифом заполненной ячейки и известным потенциалом столбца.

Чередуя и правила, найдем потенциалы.

Проверку оптимальности также можно проводить непосредственно в таблице, ставя «точку», если условие выполняется, и, указывая в круглых скобках величину расхождения в случае невыполнения условия.

В нашем примере наибольшее расхождение между суммой потенциалов и тарифами – в ячейке (2;1). Строим прямоугольную фигуру и заметим, что две клеточки., отмечены знаком « - », имеют одинаковую наименьшую величину 150, - этот факт ведет к вырожденного распределения. И действительно, после перемещения получим таблицу 3, в которой число загруженных ячеек равно 4.

 

 

 

 

 

 

Таблица 3

Потребители	Мощность	В1	В2	В3	Ui
Поставщики		200	250	200
A1	250	5   50  -	4   + (2)	1   200	0
A2	150	1   150	3	3	-4
A3	250	1   0 +	2   - 250	3	-4
	Vk	5	6	1	-

 

 

Вырожденности может появляться и исчезать при переходе от таблицы к таблице. Чтобы продолжить решение такой задачи, вводят нулевые поставки, соответствующие ячейки считают условно заполненными. Нулей будет столько, сколько не хватает поставок. Их вписывают в ячейки, имеющие малые затраты, и при этом следят, чтобы не получался замкнутый цикл (прямоугольная фигура, во всех вершинах которого – заполненные ячейки). В данном примере стоит вписать один ноль и лучше всего в ячейку (3;1). Дальнейшее решение обычное: находят потенциалы, проверяют условие оптимальности. После очередного перераспределения получим таблицу 4.

Таблица 4

Потребители	Мощность	В1	В2	В3	Ui
Поставщики		200	250	200
A1	250	5	4   50	1   200	0
A2	150	1   150	3	3	-2
A3	250	1   50	2   200	3	-2
	Vk	3	4	1	-

 

Задача опять стала не вырожденною – число загруженных ячеек равна 5. Условие оптимальности выполняется. Размещение грузов видно из таблицы. Найденные суммы расходов на каждом этапе решения: . На каждом этапе получали решение лучше предыдущего.

 

Замечание 1. Если мы имеем дело с открытой транспортной задачей, то для ее решения необходимо сначала обеспечить баланс между спросом и предложением. Для этого вводят дополнительного поставщика, если спрос превышает предложение, в противном случае вводят дополнительного потребителя. Если добавляют поставщика, то его “мощностью” будет величина, которую не хватает до баланса, транспортные тарифы принимают равными нулю. Аналогично действуют, если добавляют потребителя. В дальнейшем решение проводят по изложенному выше алгоритму. Введение дополнительного поставщика или потребителя имеет вполне определенное экономическое объяснение. В первом случае мы определяем, какому потребителю выгоднее недопоставить груз, исходя из интересов всех участников, во втором случае – у какого поставщика целесообразнее всего оставить часть груза.

 

Замечание 2. Ранее был подробно рассмотрен способ северо-западного угла для начального распределения грузов. Число итераций (таблиц)можно уменьшить, если воспользоваться способом наименьших тарифов. Он заключается в анализе всей матрицы тарифов, выборе наименьших значений и максимальном заполнении соответствующих ячеек таблицы. Эти действия выполняются до тех пор, пока не будет распределен весь груз и удовлетворен спрос всех потребителей в результате заполнения одной из ячеек исключается из рассмотрения некий поставщик или потребитель. При этом дополнительные участники транспортной задачи принимаются во внимание в последнюю очередь.

 

V  Домашнее задание

Выполнить: ИНДИВИДУАЛЬНАЯ РАБОТА по теме «Линейное программирование»  ЗАДАНИЕ 3 (номер варианта соответствует нумерации в журнале учебной группы).

 

VI Подведение итогов занятия

– достижение цели занятия – рекомендации – рефлексия

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Скачано с www.znanio.ru