
Методическая система учителя математики
Тарасовой Татьяны Ивановны
Повышение уровня учебной мотивации школьников при изучении математики
Учение, лишенное всякого интереса и взятое только силой принуждения, убивает в ученике охоту к овладению знаниями. Приохотить ребенка к учению гораздо более достойная задача, чем приневолить.
К.Д. Ушинский
Математика является одной из важнейших наук, ведь именно с ней человек встречается каждый день в своей жизни. Поэтому учителю необходимо развивать у детей интерес к этому предмету.
Главной задачей при обучении математике своих учеников считаю научить их
видеть красоту науки и необходимость изучения математики и, как следствие:
- научиться ставить цели;
- организовывать свою работу, планируя деятельность на шаг вперёд;
- оценивать результаты своего труда,
- быть способными осваивать и применять знания в незнакомых ситуациях,
Педагог должен стремиться к тому, чтобы обучение приносило радость каждому обучающемуся. Между педагогом и ребенком должен возникать интеллектуальный контакт, позволяющий избежать насильственного процесса передачи знаний, когда учащийся сопротивляется, а учитель пытается заставить его получить очередную порцию новых сведений. Во время работы приходилось наблюдать на уроках математики отсутствие интереса у ряда учеников к предмету. Учитель, особенно в начале обучения, должен так излагать предмет, чтобы заинтересовать учащихся, сделать предмет доступным для понимания. Вместе с тем, нельзя всё учение свести к интересу. Учение требует и черновой работы и волевого усилия.
Как правило, с детьми я работаю, начиная с 5-го класса и до 11-го. В работе можно выделить следующие ступени:
I Работа с обучающимися 5-7 классов: основное направление - комплексное формирование мотивации к изучению предмета.
II Работа с обучающимися 8-9 классов: основное направление – осуществление педагогической поддержки ребят с выраженным интересом к изучению предметов математики + развитие мотивационной сферы обучающихся с частично сформированным стимулом к учению (внешними мотивами).
III Работа с обучающимися 10-11 классов: основное направление – целенаправленное развитие мотивированных учащихся, обладающих способностями к точным наукам + педагогическое сопровождение старшеклассников с чётко сформированным внешним мотивом к учению (подготовка к ЕГЭ).
На I ступени: содержание образования предлагается на творческом уровне (уровне максимума), а административный контроль его усвоения – на уровне стандарта. Поэтому все дети, в том числе и более подготовленные, имеют возможность получить образование на максимально возможном для себя уровне. В 5-6 классе очень важно научить понимать, учить и применять правила – первые математические алгоритмы.
Мы обязательно решаем в 5-6 классах задания из учебника повышенной сложности, решаем дополнительные задания на контрольных работах, решаем задачи на факультативных занятиях. Все дети разные: кто-то из них выполнит все задания и пойдет дальше, а другие сделают часть, но после участия в обсуждении заданий более высокого уровня трудности, воспримут обязательный уровень как легкий для себя. Такой подход дает возможность многим ученикам быть нацеленными на успех, работать с увлечением.
Уже в это время, в 5-6 классах, выделяются ребята, которые изучают математику более успешно. Именно сейчас в полной мере можно наблюдать проявление двух основных составляющих успешного ученика – природных способностей к математике и трудолюбивой усидчивости. Ну и, по моему мнению, главная отличительная черта будущего успешного ученика - получать удовольствие от процесса решения задач.
В 7 классе мы начинаем изучать геометрию. Это уникальный предмет, в котором наиболее тесно переплетаются логический и интуитивный аспекты. Анри Пуанкаре писал: «Доказывают при помощи логики, изобретают при помощи интуиции». Геометрия, как никакой другой предмет способствует развитию обоих качеств. Я вообще считаю, что геометрия и есть единственная настоящая математика, а все остальные разделы – своего рода прикладные инструменты. Умение воспроизвести доказательство теоремы, знать все формулировки – это «обязательный минимум» для хорошиста. Вот тут количество «четвёрок» в классе может уменьшиться вдвое. Именно на этом этапе семиклассники встречаются с трудностями, преодоление которых для определенной части обучающихся является непосильным. Для кого-то в силу природных возможностей, а для кого - из-за недостаточной усидчивости. Воистину, «Нет царского пути в геометрию!» Все факультативные занятия в 7 классе я посвящаю именно геометрии. В 7 классе окончательно становится понятно, кто из ребят готов изучать математику на повышенном уровне.
На II ступени в 8 классе дети, с выраженными способностями к математике решаю более сложные задания. Нужно ориентировать ученика на работу на высоком уровне трудности. Обучающиеся со слабой подготовкой вынуждены больше заниматься, но если не достаточно усидчивости, то успеваемость у них падает. Важная роль на этом этапе отводится факультативным занятиям, именно там мы решаем задачи повышенной и высокой сложности, готовимся к олимпиадам, а с более «слабыми» подтягиваем пройденный материал. Для того, чтобы быть успешным на этом этапе, нужно иметь хорошую подготовку и трудолюбие.
Серьёзная ступень в это время – государственная итоговая аттестация в 9 классе. Всё больше времени уделяется самостоятельной работе обучающихся.
Конечно, не все ученики успешно решат вторую часть экзамена. Но в процессе решения сложных задач и более слабые ребята отрабатывают свои вычислительные навыки, логические умения. Поэтому сложные задачи решать необходимо.
На III ступени работы – в 10-11 классах - основное направление нашей деятельности – целенаправленное развитие мотивированных учащихся, обладающих способностями к точным наукам + педагогическое сопровождение старшеклассников с чётко сформированным внешним мотивом к учению (подготовка к ЕГЭ).
Все учащиеся различаются по своим способностям и интересам, следовательно, для успешности обучения необходимо обеспечить каждому ученику нагрузку, соответствующую его индивидуальным возможностям. Это достигается различными способами: дифференцированными домашними заданиями, необязательными заданиями, дополнительными индивидуальными заданиями. Этой же цели служит индивидуализированный контроль. В 10-11 классах я позволяю себе работать, ориентируясь однозначно на более способных обучающихся. Часто в ущерб менее подготовленным. Я считаю, что обязана дать возможность идти вперёд тем, кто это может и в этом заинтересован и осознанно изучает математику на углублённом уровне. И такие ученики всегда есть. Жаль, что часто не в большинстве.
К изучению математики в математическом классе привлекается разнообразная учебная литература. Помимо специальных учебных пособий используются учебники для массовой школы, экспериментальные учебные пособия, различные сборники задач, книги, освещающие опыт работы в математических классах и содержащие материал обучения.
В связи с модернизацией образования перед собой я ставлю серьёзные задачи. Современный выпускник должен уметь ясно выражать свою мысль, действовать с умом, стремиться к знаниям и совершенству. Стараюсь воспитывать для общества трудолюбивых, предприимчивых, стремящихся к новизне молодых людей. К своим ученикам я отношусь с уважением, считаюсь с их мнением, учу личным примером, черпаю в них силы, вдохновение, веру в себя и в то, что смогу подарить им сегодня что-то хорошее, ну, хотя бы интересный урок. На мой взгляд, каждый день дети должны выходить с урока, проведя время с пользой, но при этом проведя его еще и с удовольствием!
Я очень люблю математику и прекрасно понимаю, что умение решать квадратные уравнения, неравенства или строить графики – это совсем не цель. Поэтому свой предмет я воспринимаю как:
ü гимнастику для ума;
ü отработку практических навыков, которыми они смогут воспользоваться;
ü окно в другой мир, пока не известный детям – мир идеальных абстракций, гармонии, строгой логики и красоты доказательств;
ü «мостик», благодаря которому я имею возможность общаться со своими учениками, делиться с ними опытом, выходящим за рамки предмета.
Моя мечта - научить детей учиться. А для этого, на мой взгляд, нужно изменить роль ученика: из пассивного слушателя превратить его в активного участника образовательного процесса. Это трудно, потому что многие дети просто не хотят учиться, в частности, математике. Нет желания, терпения, усидчивости. Одна из главных проблем нежелания учиться – отсутствие мотивации. Поэтому основополагающей своей целью я поставила создание системы, которая позволит эту самую мотивацию повысить. Необходимо сделать образовательный процесс творческим, а урок превратить в мир интересных открытий. И если ребенок ощутит это, он будет учиться с удовольствием, постепенно открывая новое вокруг себя и в себе. Убеждена, что творческий характер образовательного процесса – необходимое условие здоровьесбережения.
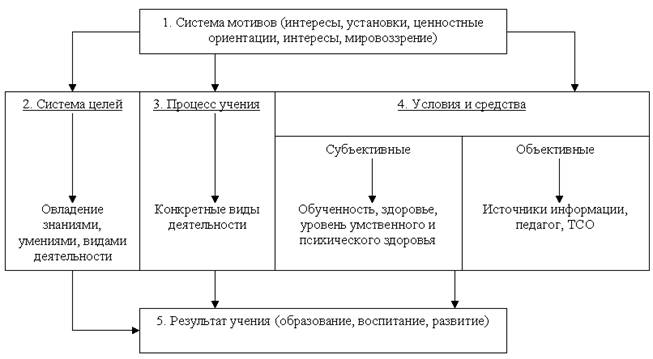
В настоящее время существует множество форм привития познавательного интереса к математике, который может достигаться следующим образом:
1) обогащение содержания математики историческим материалом;
2) решение задач различной степени трудности и нестандартных задач;
3)подчеркивание силы и изящества методов вычислений, доказательств, преобразований и исследований;
4)разнообразием уроков, нешаблонным их построением, включением в уроки элементов придающих каждому уроку своеобразный характер, использование современных технических средств, наглядных пособий, разнообразием устного счета, включением в уроки игровых моментов;
5)активизация познавательной деятельности учащихся на уроке с использованием форм самостоятельной и творческой работы;
6)использование различных форм обратной связи: систематическим проведением опроса, кратковременных устных и письменных контрольных работ, различных тестов, математических диктантов наряду с контрольными работами, предусмотренными планом;
7) разнообразие домашнего задания;
8)установление внутренних и межпредметных связей, показом и разъяснением применения математики в жизни.
В своей работе я использую следующие приемы для мотивации:
ü связь изучаемого материала с жизнью, с достижениями науки и техники;
ü показ недостаточности имеющихся знаний;
ü создание проблемной ситуации;
ü использование художественной и научно-популярной литературы, произведений искусства;
ü использование сравнений;
ü привлечение занимательных приемов, опытов, парадоксов;
ü использование игровых ситуаций и др.
Для повышения мотивации учеников я стремлюсь:
В основу системы мною положены следующие основные принципы:
Отдельно хочется остановиться на некоторых методах обучения, способствующих мотивации. Это, конечно же, метод сравнения - эффективный инструмент не только познания, но и мотивации. Ученики на деле убеждаются, как один материал увязывается с другим. Ребята понимают, как важно учиться не от случая к случаю, а систематически.
За годы работы в школе я обратила внимание на то, что есть такие понятия в математике, при изучении которых дети очень часто путаются или просто забывают их. Если понятие “противоположных чисел” усваивается легко, то понятие “обратное число” забывается очень быстро. И вот тогда на помощь приходит метод сравнения.
|
Число |
Противоположное |
Обратное |
|
3 |
-3 |
1/3 |
|
2/5 |
-2/5 |
5/2=2 1/2 |
|
-7/10 |
7/10 |
-10/7=-1 3/7 |
|
1 3/7 |
-1 3/7 |
7/10 |
|
-1,5 |
1,5 |
10/15=2/3 |
|
1/8 |
-1/8 |
8 |
|
0 |
0 |
Нет |
|
а |
-а |
1/а, при а ≠0 |
Подобная тренировка и сопутствующая беседа при составлении такой таблицы помогает ребятам прочно усвоить тему “Обратные числа” (6 класс) и повторить понятие “противоположное число”, учит сравнивать.
При изучении темы “Десятичные дроби” (5 класс) на первый урок изучения действий с десятичными дробями я приглашаю старшеклассников, и, после того, как будет рассказано о десятичных дробях и истории их возникновения, слово предоставляется гостям: я их прошу показать, как выполняются действия с десятичными дробями.
|
Действия |
Десятичные дроби |
Натуральные числа |
|
Сложение |
72,13+5,16 |
|
|
Вычитание |
102,34-71,56 |
|
|
Умножение |
5,16*2,7 |
|
|
Деление |
25,5 : 15 |
|
Примеры задаются несложные.
Параллельно изучаются следующие темы: “Признаки подобия и равенства треугольников”, “Арифметическая и геометрическая прогрессии”, “Равные фигуры”, “Равновеликие фигуры”.
Например, темы “Равные и равновеликие фигуры” изучаются в виде практической работы. С помощью ножниц конструируем трапеции и параллелограммы из треугольника, из четырехугольника строим треугольники различных видов, и каждый раз проговариваем равновеликие фигуры. Данный прием позволяет надолго запомнить, что мы понимаем под сочетанием слов “равновеликие фигуры”.
При подготовке к выпускным экзаменам параллельно повторяются решение линейных неравенств и квадратичных неравенств x - 18 > 7 и x2 - 18 > 7. Также параллельно изучаются следующие темы: отрезок, луч, прямая; координатная прямая и координатная плоскость; прямые и обратные задачи на части; квадрат разности и разность квадратов; прямые и обратные теоремы; признаки и свойства параллельных прямых и параллелограмма. При изучении темы “Свойства квадратичной функции” закрепление происходит с помощью серии заданий на сходства и различия в графиках.
Аналогично сравниваются графики функций: y=2x; y= 1/2x; y=2/x.
Неоднократные повторения подобных упражнений всегда дают положительный результат.
Достоинство данного метода не только в возможности исключения наиболее характерных ошибок, но и возможности неоднократного повторения многих тем. Это не только метод мотивации через значимость всего, что изучается в математике. Этот метод помогает развить умение анализировать ситуацию, мыслить логически, способствует интеллектуальному развитию личности. Ученик понимает, как важно знать одно, чтобы понимать другое. Развивая из урока в урок умение сравнивать, учитель создает предпосылки для успешного решения следующих заданий:
· Какие числа делятся на 6 и на 15?
· При каких значениях а верно равенство а + | а | = 0 и при каких неверно?
· Найти наибольшее значение выражений - | x | ; 2 - | x | ; -| x - 1 | ; - (x - 1)2 .
Отдельно хочется остановиться на использовании исторического материала в целях мотивации учебного процесса. Ведь, прежде всего, целью математического образования является культурное развитие учащихся. Надо научить детей ценить духовное и материальное богатство, накопленное человечеством, ну а с точки зрения мотивации вопрос можно поставить иначе «человек, не получивший достойного математического образования, не может считаться культурным». В первую очередь, сам учитель должен верить в то, какие потенциальные возможности содержит в себе математика. Это духовное, эстетическое, творческое и интеллектуальное развитие. Факт то, что математика не только развивает, но и служит инструментом для определения уровня развития ребенка, это единственный измерительный инструмент в психологии.
Математика не только развивает интуицию, воображение, логику, но и служит способом определения их развития.
Величайшая личность истории Петр I считал математику одной из важнейших дисциплин. 14 января 1701 года Петр I издал Указ об учреждении первого русского государственного светского учебного заведения, которым стала знаменитая Московская математико - навигацкая школа.
С помощью исторического материала ребятам можно показать, какую уникальную роль сыграла математика в жизни Петра I. И образование М.В.Ломоносова началось с “Арифметики” Магницкого, он назвал ее “вратами своей учености”. И сколько еще таких примеров можно привести и рассказать ученикам на уроке!
Кроме различных форм и методов работы, создающих положительную мотивацию, важным является благоприятный психологический климат. Это обращение к учащимся по имени, опора на похвалу, на одобрение, на добрый, ласковый тон, на ободряющее прикосновения.
При планировании учебного процесса, я ориентируюсь не на какого–то абстрактного среднего ученика, а опираюсь на знания особенностей мотивационной сферы каждого ученика, и класса в целом. Для меня это постоянный поиск оптимального сочетания методов и приемов работы, которые дали бы возможность одним ученикам двигаться дальше, самосовершенствоваться и выходить на более высокий творческий уровень, а другим бы помогли в стабилизации учебного процесса.
Традиционный подход к организации учебного процесса может обеспечить достаточно высокий уровень усвоения знаний, умений и навыков, но он не способствует развитию личности, раскрытию ее потенциала. Поэтому один из перспективных путей развития и повышения мотивации учения я вижу в применении нетрадиционных методов и форм организации урока.
В своей практике использую групповую работу и работу в паре. В условиях групповой работы осуществляется позитивная зависимость группы учащихся друг от друга, так как члены группы рассматривают успех (неуспех) как результат их коллективной деятельности. При этом снижается уровень тревожности, усредняется положительное (отрицательное) влияние индивидуальных способностей и возможностей на результат деятельности. Таким образом, происходит сдвиг в оценке своей деятельности со способностей на усилия, формируется чувство самоуважения. Групповая форма работы позволяет активизировать познавательную деятельность учащихся, продуктивное, творческое усвоение знаний и умений, создавая положительный эмоциональный фон через активный диалог, анализ проблемных ситуаций, деловые игры, мозговой штурм. При такой форме работы ученик учится сопоставлять, сравнивать, оспаривать другие точки зрения, доказывать свою правоту. Умение сопоставлять различные способы позволит ученику не только анализировать, но и прогнозировать свою деятельность, что в свою очередь влияет на формирование самостоятельности, овладения способами самообразования. Развитие умений планировать, ставить задачи находится в прямой зависимости от мотивации.
Работа в паре особенно важна в сфере самоконтроля и самооценки.
Планируя способ включения всех учащихся в деятельность на уроке, думаю о создании мотивационной основы их работы.
Хорошо известно, что ничто так не привлекает внимания и не стимулирует работу ума, как удивительное. Поэтому мною используются такие приемы, которые стимулируют внутренние ресурсы – процессы, лежащие в основе интереса.
Например, 6 класс, тема “Координатная плоскость”. Начинаю с построения всевозможных фигур: самолет, заяц, петух. Учителями годами накапливаются подобные рисунки для уроков. Часть материала я нахожу на страницах интернета, а часть придумываю или ребята придумывают сами. И только после этого мы с ребятами переходим к учебнику: строим точки, отрезки, треугольники, но делается это уже легко и со знанием дела.
В 6 классе при изучении темы “Диаграммы” получается удивительный эффект от принесенных мною рабочих диаграмм. Рассматривая их в виде раздаточного материала, мы с учениками почерпнули настолько богатейшую информацию, что ребята сами захотели отразить работу нашей школы в виде диаграмм. Ученики предлагали отобразить процесс питания в школе, количество учеников, посещающих начальную школу, среднее звено, старшее звено, успеваемость, кто какие секции посещает, сколько девочек, сколько мальчиков и много других предложений.
Интересно учиться, если учитель использует не только материал учебника, по которому занимаются дети, но и занимательный материал, значимый для ученика.
При изучении темы “Последовательности” я использую материал о завещании Франклина потомкам, о легенде о шахматах, о глупом купце, о пирамидах, которые рано или поздно рушатся.
Ребятам интересно на уроках лабораторных работ: мы рассчитываем площади сложных фигур, измеряем расстояния между недоступными точками, с помощью зеркала определяем высоту школ, дерева при изучении темы “Пропорция” или темы “Подобие треугольников”.
Очень важно, чтобы учитель имел установку: любой изучаемый материал увязать с жизнью, показать его значимость. Подбирая материал к уроку, я всегда продумываю моменты, показывающие, почему это очень важно знать. При изучении темы “Масштаб” объявляется конкурс на лучшую планировку посадок на клумбе. Задумки ребят просто поражают. Аналогично рассматриваются и другие темы. Вектора – это метод познания физических процессов; пропорции и отношения необходимо знать, так как это широко применяемый метод познания химических процессов; при изучении окружности материал увязывается с космонавтикой и астрономией.
Большое значение при решении ряда вопросов, относящихся к проблеме математического образования в школе, имеют интегрированные уроки, внеклассная работа, исследовательская и проектная деятельность. Они пробуждают у детей интерес и любовь к предмету, учат их оригинально мыслить, принимать нестандартные решения в сложных жизненных ситуациях. Особое внимание учителю следует уделять внеурочной деятельности по математике. Внеурочная деятельность поддерживает у учеников интерес к предмету. Математические конкурсы, олимпиады школьников являются одной из важных форм внеклассной работы. Они не только помогают выявить одаренных учащихся, но и служат развитию интереса к математической науке. Участие в олимпиаде, конкурсе - первый шаг к научной деятельности. Это особенно важно для школьников, обучающихся в коррекционной школе. Олимпиады дают шанс таким детям добиться признания, как в семье, так и у одноклассников. Необходимо предоставлять учащимся возможность участвовать в исследовательской и проектной деятельности на уроках. Исследовательская деятельность позволяет не только одаренным детям продемонстрировать свои способности, здесь может проявить себя каждый. Успех проекта во многом зависит от правильно выбранной темы, она должна быть интересна ребенку. Во время работы над проектом, учащиеся учатся самостоятельно принимать решения и несут ответственность за свой выбор. Следует развивать творческие возможности у слабых учеников, не давая остановиться в своем развитии более способным детям.
Интегрированный урок – это находка для учителя осуществить межпредметную связь: “гомотетия и обслуживающий труд” (как построить выкройку), “математика и космонавтика”. Математику соединить с биологией можно при изучении темы “Симметрия”. Математика и иностранный язык нашли точки соприкосновения вкладом английских и немецких ученых в математику.
Интегрированный урок – это не только один из впечатляющих мотивационных приемов, у этих уроков есть возможность помочь уйти от перегрузок. Если продумать систему уроков всей школы, с помощью этих уроков можно учебное пространство сделать более однородным, взаимосвязанным.
Важно, чтобы все, что учитель делает на уроке, было значимо ребенку, а потребности учеников 5-го класса отличаются от потребностей старшеклассников. Пятиклассникам очень важно занять достойное положение в коллективе – это ведущий мотив поведения младшего подростка, и поэтому с ним надо организовывать как можно больше коллективных дел, игровых моментов, причем для них важны даже не сами игровые действия, более значим результат игры. У старших подростков появляются другие потребности – быть популярным, им важно утвердиться в собственном мнении, принять самих себя как значимых.
Эффективность созданной мною методической системы подтверждают следующие показатели:
· повышается качество знаний обучающихся;
· сохраняется положительная динамика участия в проектной деятельности;
· повышается способность обучающихся самостоятельно добывать знания, эффективно заниматься самообразованием; увеличивается количество обучающихся, занимающихся проектной деятельностью, показывающих своё умение взаимодействовать, аргументировать свою точку зрения, учитывать точку зрения других, умение работать в команде.
Математика - предмет настолько серьезный, что педагогу чрезвычайно важно использовать любую возможность оживить урок. Учитель должен помочь ученику увидеть в серьезном – курьезное, в скучном - занимательное, в обычном – необычное. Ведь интерес служит стимулом к дальнейшей работе ученика. Роль учителя в этом деле огромная. В первую очередь мы обязаны создать благоприятные условия для того, чтобы ученики смогли постигать новое в науке.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.