Методическая разработка раздела учебной программы по математике( 6 класс)

РАЗДЕЛА УЧЕБНОЙ  ПРОГРАММЫ МЕТОДИЧЕСКАЯ РАЗРАБОТКА  «СЛОЖЕНИЕ И ВЫЧИТАНИЕ  ОБЫКНОВЕННЫХ ДРОБЕЙ С  РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ» Выполнила учитель математики МБОУ Ивановской СОШ  Крохина Александра Михайловна 2013

1. АКТУАЛЬНОСТЬ.  Методическая разработка раздела «Сложение и  вычитание обыкновенных  дробей с разными  знаменателями» является актуальной и имеет  большую теоретическую и практическую  значимость.  Понятие дроби и действия с дробями не  являются элементарными как представляется  математикам и учителям математики.  Нередко действия с дробями вызывают  серьезные затруднения даже у старшеклассников  и студентов. Проблема надежного и четкого  усвоения понятия дроби и свойств дробей  является актуальной.

ДАННЫЙ РАЗДЕЛ ЯВЛЯЕТСЯ  АКТУАЛЬНЫМ ПО РЯДУ ПРИЧИН  Трудности у обучащиюхся в освоении  данного раздела;  Частые ошибки в письменной и устной  речи  Наличие заданий по данной теме в ГИА и  ЕГЭ

ПОЯСНИТЕЛЬНАЯ  ЗАПИСКА Одно из первых математических понятий, с которым ребенок  встречается в школе, ­ понятие о числе. Это понятие является одним из  базовых понятий математики, и его усвоение имеет для учащихся  большое значение.           В школу обычно ребенок приходит, имея представление о натуральных  числах. В процессе изучения математики понятие о числе постепенно  расширяется. Это связано с практическим применением  чисел –  измерением величин. Для этих целей натуральных чисел оказывается  недостаточно: не всегда единица величины укладывается  целое число раз в  измеряемой величине. Для того чтобы выразить результат любого  измерения, необходимо расширить запас чисел, введя новые числа,  отличные от натуральных. Именно так появляются рациональные числа  (т.е. дробные) числа, а затем и иррациональные, которые вместе образуют  множество действительных чисел. На этом расширение понятия о числе  не останавливается, а продолжается, поскольку это необходимо для  других наук и самой математике.

2. ЦЕЛИ И ЗАДАЧИ  РАЗДЕЛА         Цель:  вырабатывать прочные навыки  преобразования дробей, сложения и  вычитания  дробей.        Задачи: Познавательные : ­ формировать навыки работы с дробями;    ­ формировать знание и правильное  употребление  терминов;    ­ развивать логическую культуру, связанную с  процессом выполнения действий с дробями.

РАЗВИВАЮЩИЕ : ­ развивать внимание, интерес к предмету ;    ­  развивать логическое мышление, умение  сравнивать, анализировать;     ­ развивать мыслительные способности,  слуховую и зрительную память,          совершенствовать навыки самостоятельной  работы;     ­ развивать познавательную активность.

ВОСПИТАТЕЛЬНЫЕ:     ­воспитывать любовь и интерес  к предмету;      ­ развивать чувства ответственности как за  личную деятельность, так и за действия в паре  или в группе;       ­воспитывать чувство уверенности в себе

3. ПСИХОЛОГО­ПЕДАГОГИЧЕСКОЕ ОБЪЯСНЕНИЕ  СПЕЦИФИКИ ВОСПРИЯТИЯ И ОСВОЕНИЯ УЧЕБНОГО  МАТЕРИАЛА УЧАЩИМИСЯ В СООТВЕТСТВИИ С  ВОЗРАСТНЫМИ ОСОБЕННОСТЯМИ. Данный раздел разработан с учетом возрастных и психологических особенностей  детей от 10 до 12 лет. Чаще всего этот период относят к подростковому возрасту.  Этот возраст связан с перестройкой всего организма ребенка. Переходный возраст  пронизывает все стороны развития подростка: и анатомо­физиологическое, и  интеллектуальное, и нравственное развитие – и все виды его деятельности.  Подростков очень привлекает  возможность расширить, обогатить свои знания,  проникнуть в сущность изучаемых явлений, установить причинно – следственные  связи. Они испытывают большое эмоциональное удовлетворение от  исследовательской деятельности. Им нравится мыслить, делать  самостоятельные открытия. Большое значение в этом возрасте имеет признание  их умений и достижений, способствование формированию уверенности в  результативности своей деятельности

4. ОЖИДАЕМЫЕ РЕЗУЛЬТАТЫ ОСВОЕНИЯ  РАЗДЕЛА ПРОГРАММЫ Предметные:      ­ усвоение основного свойства дроби, применяемого для преобразования дробей;     ­ обучающиеся должны уметь сокращать дроби;     ­ приводить дроби к новому (общему ) знаменателю;      ­ уметь сравнивать дроби.      Личностные :     ­ уметь излагать свои мысли, аргументировать свою точку зрения;     ­ уметь организовывать свою деятельность;     ­ уметь учитывать позицию собеседника, организовывать и осуществлять  сотрудничество, адекватно передавать информацию.   Метапредметные:      ­ уметь решать учебные задачи;      ­ работать с различными источниками информации;      ­ использовать компьютерные технологии.

ОБОСНОВАНИЕ ИСПОЛЬЗУЕМЫХ В  ОБРАЗОВАТЕЛЬНОМ ПРОЦЕССЕ ПО РАЗДЕЛУ  ПРОГРАММЫ ОБРАЗОВАТЕЛЬНЫХ  ТЕХНОЛОГИЙ, МЕТОДОВ.   При изучении раздела программы используются следующие технологии, методы  и  формы организации  деятельности учащихся: 1. Информационно – коммуникативные: словесные, наглядные, практические.                 Они позволяют активизировать процесс обучения, повысить темп урока, увеличивают объем  самостоятельной  работы  учащихся.  Методы  направлены  на  создание  точных  представлений  об  окружающем  мире  и  могут  быть  представлены  моделями  (наглядные).  Применение  группы  практических  методов  и  приемов  обеспечивают  мыслительную  активность  учащихся  путем  реализации деятельного подхода, повышает эффективность образовательного процесса. 2.Игровые.    Характерной  чертой  данной  технологии  является  моделирование  жизненно  важных  ситуаций, поиск пути их решения

Ведущий метод – игра. Организационными формами могут быть деловые игры,  ролевые и сюжетные – путешествия, дидактическая игра. 3. Коммуникативные      Особенность данной технологии – построение обучения на основе активного  взаимодействия всех участников учебного процесса. Ведущий метод – общение.  Работа в парах, группах, учебный диалог, дискуссия.      4. Исследовательские(проблемно – поисковые)      Он требует реализации педагогической модели – «обучение через открытие».  Организационная форма – совместный поиск решения проблемных ситуаций. Модель  урока: « знаю, но не все; хотел бы узнать – узнал». Обязательное наличие проблемы.  Обучающие приемы: экспериментирование или моделирование. Данный метод  стимулирует самодеятельность учащихся, их стремление к самовыражению,  формирует активное отношение к окружающему миру.             Научить ребенка различным приемам и методам сохранения и укрепления своего  здоровья. Для этого используются различные физкультминутки, гимнастика для  глаз, задачи со здоровьесберегающим содержанием. 5. Здоровьесберегающие

Система знаний  основное свойство  дроби алгоритм сложения  и вычитания  смешанных чисел правило сложения и  вычитания с разными  знаменателями  понятие  несократимой  дроби Система знаний  правило  сравнения способы  сокращения дробей  алгоритм  приведения дроби  НОЗ

СИСТЕМА ДЕЯТЕЛЬНОСТИ Система взаимодействия учителя и учащихся при изучении  раздела  представляет собой совокупность различных видов  деятельности. Познавательная – учащиеся воспринимают и перерабатывают   информацию, воспроизводят знания, тренируются в их применении, умеют  творчески мыслить  и решать практические задачи. Общеучебная  ­ учащиеся самостоятельно добывают знания, работая с  учебной и справочной литературой, раздаточным материалом. Преобразующая  ­ учащиеся в условиях меняющейся ситуации действуют ,  находят причину затруднений, строят новый проект своих действий. Находят  пути решения проблем.  Самоорганизующая – учащиеся самостоятельно ставят учебные цели,  планируют учебную деятельность, овладевают навыками самоконтроля, а  также учатся анализировать и  оценивать себя  с учетом своих возможностей

КАЛЕНДАРНО – ТЕМАТИЧЕСКОЕ  ПЛАНИРОВАНИЕ РАЗДЕЛА № п/п Тема урока Тип урока 1 2 3 Основ­ное свойство дроби Изучение нового  мате­риала Основ­ное свойство дроби Закрепление знаний  и .умений Сокра­щение  дробей Изучение нового  мате­риала Вид контроля Беседа,  индивидуальный и  фронтальный  опрос Практическая работа Матема­тический  диктант Беседа, работа с  учебником Фрон­тальный опрос,  индиви­дуальный  контроль Требован ия к уровню подготов ки Знать основное  свойство дроби и  применять его при  замене дан­ной  дроби равной ей  дробью Знать определение  сокращения дроби. Уметь сокращать  дробь, исполь­зуя  различные приемы  сокраще­ния,  распознавать  несократимые  дроби

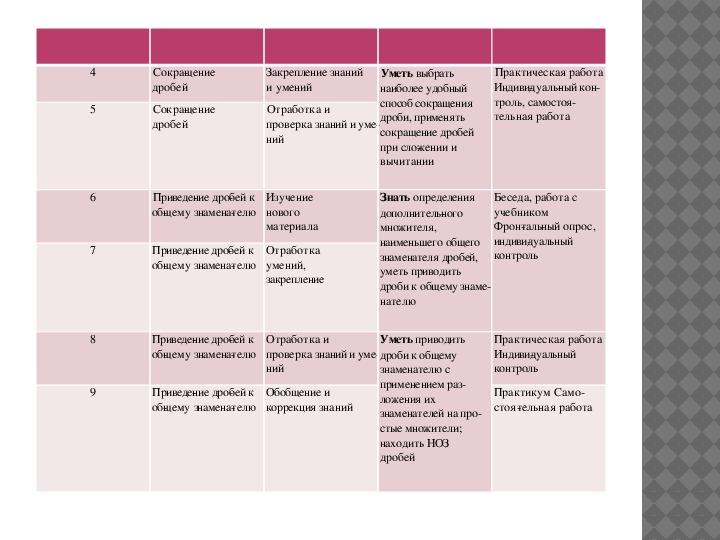
4 5 6 7 8 9 Сокра­щение  дробей Сокра­щение  дробей Закрепление знаний  и умений Отработка и  проверка знаний и уме­ ний Уметь выбрать  наиболее удобный  способ сокращения  дроби, приме­нять  сокращение дробей  при сло­жении и  вычитании Практическая работа  Индиви­дуаль­ный кон­ троль, самостоя­ тельная работа Приведе­ние дро­бей к  об­щему знамена­телю Приведе­ние дро­бей к  об­щему знамена­телю Изучение нового материала Отработка умений, закрепление Приведе­ние дро­бей к  об­щему знамена­телю Отработка и  проверка знаний и уме­ ний Приведе­ние дро­бей к  об­щему знамена­телю Обобщение и  коррекция знаний Беседа, работа с  учебником Фрон­тальный опрос,  индиви­дуальный  контроль Практическая работа  Индиви­дуальный  контроль Практикум Само­ стоя­тельная работа Знать определения  дополнитель­ного  множителя,  наименьшего общего  знаменателя дробей,  уметь приводить  дроби к общему знаме­ нателю Уметь приводить  дроби к общему  знаменателю с  применением раз­ ложения их  знаменателей на про­ стые множители;  находить НОЗ  дробей

10 11 12 Сравне­ние дро­бей с  раз­ными знамена­ телями Изучение нового  мате­риала Сложение и вычита­ние  дро­бей с раз­ными  знамена­телями Изучение нового  мате­риала Сложение и вычита­ние  дро­бей с раз­ными  знамена­телями Закрепление и  обобщение знаний и  умений Знать правило  сравнения дробей с  разными  знаменателями, уметь  применять его при  сравнении дро­бей Беседа, работа с  учебником Фрон­тальный опрос,  индиви­дуальный  контроль Уметь складывать и  вычитать дро­би с  разными  знаменателями, ис­ пользуя  соответствующее  правило Беседа, работа с  учебником Фрон­тальный опрос,  индиви­дуальный  контроль Урок­соревнование (Брейн­ринг) 13­14 Сложение и вычита­ние  дро­бей с раз­ными  знамена­телями Закрепление знаний  и умений Практическая работа  Прове­ рочная­ работа

15 16 17 18 19 Кон­трольная работа № 2 «Сложение и  вычита­ние дро­бей с раз­ными  знамена­телями» Проверка знаний и умении Сложение и вычитание смешанных чисел Изучение нового мате­ риала Сложение и вычитание смешанных чисел Изучение нового мате­ риала Сложение и вычитание смешанных чисел Сложение и вычитание смешанных чисел Закрепление знаний и умений Закрепление знаний и умений Пись­менная работа Беседа, работа с  учебником Фронтальный опрос, индивидуальный  контроль Беседа, работа с  учебником Фронтальный опрос Практикум Математическая эстафета Практическая работа Фронтальный опрос, Уметь сокращать  дроби; сравни­вать,  складывать и вычитать  дроби с разными  знаменателями; приме­ нять изученные  правила для реше­ния  текстовых задач Уметь складывать  смешанные числа Уметь вычитать  смешанные числа Уметь складывать и  вычитать смешанные числа,  применяя из­ вестные свойства  сложения и вы­ читания; решать  уравнения, со­ держащие смешанные  числа; решать  текстовые задачи

20 21 22 Сложение и вычита­ние  сме­шанных чисел Закрепление знаний и  умений Сложение и вычита­ние  сме­шанных чисел Обобщение и  коррекция знаний Кон­трольная работа №3  «Сложение и вычита­ние  сме­шанных чисел» Проверка знаний и  умений Практикум Само­стоя­тельная  работа Практикум Фрон­тальный опрос,  индиви­дуальный  контроль Пись­менная работа Уметь складывать и  вычитать смешанные  числа; решать тексто­ вые задачи и  уравнения с исполь­ зованием изученных  правил

ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА    1.  Н.Я.Виленкин, В.И.Жохов, А.С.Чесноков, С.И.Шварцбурд. Математика, 6.  М.,2009 2.    А.С.Чесноков, К.И.Нешков. Дидактические материалы по математике, 6.  М.,1999. 3.  В.В. Выгорская «Поурочные разработки по математике»,     издательство    «  ВАКО»,2008 г.  Дидактические материалы по математике для 6 класса под редакцией Чеснокова    4. Я. Перельман «Занимательная арифметика» ,Москва 1994г 5. Л.Ф.Фридман «Изучаем математику»,книга для учащихся 5­6 классов 6. Я.И.Груденев «Совершенствование методики работы учителя математики»  издательство «Просвещение», Москва 1990 г

Благодарю за внимание!