ПЕНЗЕНСКАЯ ГОСУДАРСТВЕННАЯ ТЕХНОЛОГИЧЕСКАЯ АКАДЕМИЯ

 

СИСТЕМА

ОТКРЫТОГО

ОБРАЗОВАНИЯ              

 

 

 

 

 

Селезнева С.В.

 

 

 

ТЕХНИЧЕСКИЕ ИЗМЕРЕНИЯ И ПРИБОРЫ

 

Методические рекомендации к выполнению

практических и лабораторных работ

для  специальности 2102 – Автоматизация

технологических процессов и производств

 

 

 

 

 

 

 

 

 

 

Пенза 2010

 

 

УДК 621.317.3

        Ш17

 

 

Селезнева С.В.

Ш17  Технические измерения и приборы. Метод. рекомендации. - 3-е изд, дополненное. Пенза: Издательство Пен. гос. технол. акад, 2010. -54с. 22 ил., 18 табл., 4 библ. назв.

Излагается методика выполнения практических и лабораторных работ с вариантами заданий и контрольными вопросами.

Методические рекомендации подготовлены на кафедре «Автоматизация и управление» Пензенской государственной технологической академии и предназначен для студентов специальности 2102.

Методические рекомендации одобрены и рекомендована Методическим советом Пензенской государственной  технологической академии для использования в учебном процессе.

УДК 621.317.3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Пензенская государственная  технологическая академия, 2010

Селезнева С.В., 2010

 

Работа № 1

Виды измерений

Цель работы – изучение видов измерений, исследование их характеристик.

Краткие пояснения.  Прямые измерения - это измерения, при которых измеряемую величину получают непосредственно по отчетному устройству средства измерений (CИ), например, измерение тока амперметром (рисунок 1.1). Суммарная систематическая погрешность прямых измерений включает погрешности метода, СИ и оператора. При условии статистической независимости этих составляющих  относительная погрешность прямых измерений 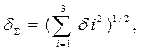    где δ_i - соответствующие составляющие погрешности.

Рисунок 1.1 – Измерение тока амперметром

 

Например, при измерении тока амперметром возникает т.н. погрешность взаимодействия  (погрешность метода), вызванная отличным от нуля внутренним сопротивлением амперметра  R_A ¹0 . При этом подключение амперметра  в измеряемую цепь изменяет сам измеряемый ток. До подключения амперметра ток в цепи равен его действительному значению:  С подключенным амперметром: . Отсюда методическая погрешность измерения тока    Относительная методическая погрешность измерения тока  .

Кроме погрешности взаимодействия в результат измерения вносит вклад погрешность амперметра. Обычно известны классы точности амперметра , выраженные в приведенных или относительных погрешностях (например, 1,0 и означают соответственно g_А=1% приведенной и d_А=1% относительной погрешности амперметра). Если задана приведенная погрешность, то относительная погрешность находится как

где I_max - предел шкалы амперметра.

Относительная  погрешность прямых измерений при этом: .

Экспериментальная погрешность прямых измерений находится как

,

где I^/// - показания амперметра.

Косвенные измерения - это измерения,  при которых измеряемую величину находят из известного соотношения этой величины и других величин, подвергаемых прямым измерениям, например, измерение мощности в нагрузке электрической цепи методом вольтметра-амперметра (рисунок 2.2).Если уравнение измерений имеет вид  ,

где y - измеряемая величина

  - величины, подвергаемые прямым измерениям,

a_i - постоянные коэффициенты,

то суммарная систематическая погрешность косвенных измерений равна:

,

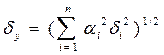где  - относительные погрешности прямых измерений х_i.

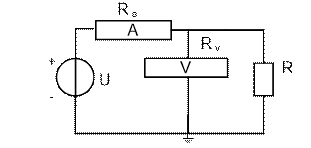
Рис.1.2 Измерение мощности методом  вольтметра-амперметра.

 

Например, для метода вольтметра-амперметра , следовательно погрешность измерения мощности d_р:

 ,

где     d_v, d_I  - погрешности измерений напряжения и тока.

Абсолютные погрешности взаимодействия амперметра  и вольтметра при этом:

;;

где  - сопротивление вольтметра.

Относительные погрешности находятся как

;      .

Как и в рассмотренном выше примере прямых измерений, кроме погрешности взаимодействия в результаты измерений вносят вклад погрешности самих приборов: вольтметра и амперметра. Если известны классы точности амперметра и вольтметра - их приведенные погрешности γ_А и γ_V и пределы шкал  и , то относительные погрешности амперметра  и вольтметра  находятся из формул:

;

 

.

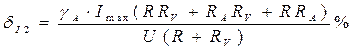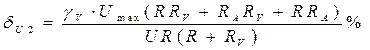Относительная погрешность косвенных измерений мощности δ_ТР складывается геометрически из составляющих погрешностей.

 .

Экспериментальные относительные погрешности измерения мощности:

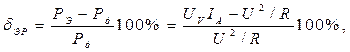
где: Р_Э,  - экспериментальное и действительное значения мощности;

        U_V, I_A – показания вольтметра и амперметра.

Совокупные и совместные измерения - это измерения, при которых значения измеряемых величин получают из системы уравнений, связывающие эти величины и величины, подвергаемые прямым измерениям.

При совокупных измерениях меняются сочетания измеряемых величин, например, измерение сопротивлений R₁  и R₂  путем измерения их параллельного R_пар и последовательного R_посл соединений. Система уравнений при этом:

Решая ее, получим значение R₁ и R₂ .

В совместных измерениях меняются условия измерений. Например, для получения зависимости сопротивления медного терморезистора от температуры  требуется измерить R для 2-х различных температур Т и решить систему уравнений относительно  R₀ и R₁ . При этом, в отличии от совокупных измерений, измеряются неоднородные величины.

      Суммарные систематические погрешности совокупных и совместных измерений определяются также, как погрешности косвенных измерений. При этом применяется уравнение измерений, полученное из системы уравнений относительно измеряемой величины.

 

Практическая работа №1

1. Определить погрешность измерений тока амперметром (рисунок 1.1), для двух значений сопротивлений цепи R=R₁ =№Ом и R=R₂ =10№Ом, где № - номер варианта, если R_A =1Ом; U= 1 B; класс точности амперметра 1,0; I_max =1А. Замечание: учитывается погрешность взаимодействия и погрешности СИ, предельные значения которых определяются классом точности. Провести эти измерения и определить погрешности измерений тока с помощью программной среды “Electronics workbench” на ЭВМ при R_A =1Ом (измеряем I^//) и R_A ®0Ом (измеряем I^/). Исходные, рассчитанные и смоделированные данные занести в таблицу 1.1. Сравнить результаты.

Таблица 1.1

U=1B, RA=1Ом, Imax=1A, γА=1%
	I/, А	I//, А	I///, А	δI1,%	δI2,%	δТI,%	δЭI,%
R=R1=…
R=R2=…

 

2. Определить погрешность измерения мощности методом вольтметра-амперметра (рисунок 1.2) для двух сопротивлений R =R₁=10№Ом и R=R₂=№кОм, если R_A =1Ом, Rv=20кОм, классы точности приборов 1,0. I_max =500 мА, U_max= 1 В, питание U=1 В. Провести эти измерения на ЭВМ и рассчитать погрешности измерений. Сравнить рассчитанные погрешности и погрешности измерений. Исходные, рассчитанные и смоделированные данные занести в таблицу 1.2. Сравнить результаты.

 

 

Таблица 1.2

U=1B, RA=1Ом, RV=20кОм, Imax=500мA, Umax=1B,  γV= γА=1%
	UV, B	IA, А	δI1,%	δI2,%	δU1,%	δU2,%	δТP,%	δЭP,%
R=R1=…..
R=R2=…..

 

 

Лабораторная работа №1

1. Ознакомиться с лабораторными приборами: образцовым вольтметром В7-16 А; стрелочными вольтметром и амперметром на стенде УС-1 (записать их классы точности), макетом работы в виде платы № 3, вставляемой в УС-1, соединительными проводами со штекерами, которые при сборке схемы эксперимента вставляются в гнезда на верхней панели УС-1. Нумерация гнезд для элементов схем показана на откидной крышке УС-1 и в лабораторном журнале.

2. Вставить плату № 3 в разъем УС-1. Измерить действительные значения R_1д , R_2д сопротивлений R₁ , R₂по варианту задания (таблица 1.3) с помощью  В7-16А в режиме омметра. Результату занести в таблицу 1.4.

Таблица 1.3

№	1	2	3	4	5	6	7	8
R1, Ом	200	200	200	10	10	10	2×104	2×104
R2, Ом	104	103	5×103		103	5×103	103	5×103

 

Таблица 1.4

Rд, Ом	Uд, В	U, В	I, мA	R’д, Ом	Iд, мA	DIт, мA	DIэ, мA	R, Ом	, Вт	Вт

 

3. С помощью соединительных проводов собрать схему вольтметра-амперметра (рисунок 1.2). Для этого со встроенного источника УС-1 (2 левых крайних гнезда ) подать напряжение на амперметр и сопротивления R₁ , R₂, таким образом, чтобы токи не превышали предел амперметра. Измерить действительные значения U_1д , U_2д этого напряжения вольтметром В7-16А  и рабочие значения U₁ , U₂ стрелочным вольтметром УС-1,  который непосредственно подключен к источнику напряжения внутри стенда. Измерить протекающие через сопротивления R₁ , R₂ токи I₁ , I₂ прямым способом с помощью амперметра.

4. Измерить действительные значения сопротивлений ,  цепей, состоящих из последовательно соединенных амперметра и сопротивлений R₁ , R₂ прибором В7-16А.  При этом измеряемые цепи отсоединяются от источника напряжения и непосредственно присоединяются  к В7-16А. Определить действительные значения токов I_1д , I_2д ,исходя из действительных значений напряжения U_1д , U_2д и сопротивлений ,.

 

Обработка результатов

1. Рассчитать теоретическую суммарную погрешность  DI_т прямых измерений токов аналогично заданию 1 практической работы. Определить экспериментальные погрешности . Сравнить результаты.

2. Определить мощности в цепи сопротивлений R₁ , R₂ методом вольтметра-амперметра , исходя из показаний вольтметра U₁ , U₂  и амперметра I₁ , I₂. Определить действительные значения мощности , исходя из действительных значений  и . Рассчитать суммарные погрешности: теоретическую  аналогично заданию 2 практической работы и экспериментальную.

3. Сравнить результаты.

 

 

Контрольные вопросы

1. Что такое прямое измерение?

2. Составляющие погрешностей прямых измерений

3. Погрешность взаимодействия

4.Что такое косвенные измерения?

5. Составляющие погрешностей косвенных измерений?

6. Совокупные (совместные) измерения?

7. Какие величины измеряются при совокупных (совместных) измерениях?

8. Что изменяется при совокупных (совместных) измерениях?

9. Составляющие погрешностей совокупных (совместных) измерений?

10. Что такое действительное значение измеряемой величины?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Работа № 2

Виды измерительных сигналов

Цель работы – изучение параметров синусоидальных и импульсных сигналов, измерение их характеристик осциллографом и вольтметрами действительного  и среднего значений.

Краткие пояснения. При описании измерительных сигналов  широко используются элементарные сигналы: постоянный сигнал, синусоидальный и импульсный сигналы (переменное напряжение на рисунке 2.1):

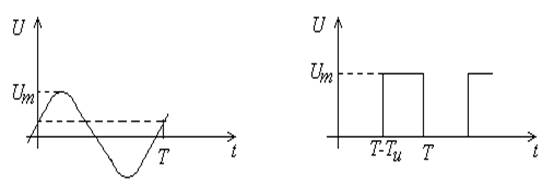
                     а)                                                                   б)

 

Рисунок 2.1 – Напряжение синусоидальной (а) и импульсной (б) форм

 

Синусоидальной сигнал описывается амплитудой U_m, частотой  ω =2π/T ( Т - период сигнала), начальной фазой j:

Импульсный сигнал описывается амплитудой U_m, периодом Т и длительностью импульса Т_u. Аналитически период сигнала выражается с помощью единичных функций:

  где 

Важной характеристикой импульсного сигнала является скважность q - отношение периода Т к длительности импульса Т_u:

  

При анализе переменных сигналов широко используются характеристики среднего значения за период U_ср (постоянная составляющая сигналов), средневыпрямленного значения U_ср.в., действующего, или среднеквадратического значения U_д . Эти характеристики определяются  формулами:

,  ,  

 

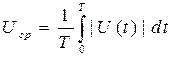Характеристики сигналов связаны между собой коэффициентами формы К_ф и амплитуды К_а :

;      .

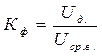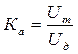Для синусоидальных сигналов  К_ф=1,11, К_а=1,41. Так, если вольтметром действующего значения (например, В7-16) измерено напряжение ,  то амплитуда сигнала

Для импульсных сигналов эти характеристики зависят от значения скважности:

Если вольтметр измеряет действующее значение напряжение V_д или среднее значение  V_ср ,то амплитуда  импульса определяется по формулам:

, .

 

Практическая работа №2

1.     На цепь диод-резистор (рисунок 2.2) подано напряжение sinωt с параметрами U_m и w из таблицы 3.1, где № - номер варианта.

Рисунок 2.2

 

Таблица 2.1

№	Um,B	w,Гц	Uср.вх , В		Uд.вх, В		Uср.R, В		Uд.R, В
			теор.	экспер.	теор.	экспер.	теор.	экспер.	теор.	экспер.
1 2	№ №	50 104

 

Рассчитать для двух значений частоты ω  средние значения сигналов U_ср.вх., и действующие значения сигналов U_д.вх на входе цепи и на сопротивлении R: U_ср._R, U_д.R. При расчете характеристик сигналов на выходе цепи следует учесть однополупериодное выпрямление сигнала, поэтому верхний предел интегрирования в  формулах для среднего и действующего значений при этом равен Т/2. Результаты занести в таблицу 2.1.

Собрать схему 2.2 в среде “Electronics workbench.”на ЭВМ. Измерить напряжение на входе и выходе схемы вольтметрами среднего и действующего значений, в качестве которых используются вольтметр постоянного и переменного токов. Результаты занести в таблицу 2.1. Сравнить расчетные и экспериментальные данные.

2. Определить  средние и действующие значения импульсного сигнала по заданной амплитуде для скважности сигнала по варианту таблицы 2.2. Рассчитать значения в диапазоне q= 1,5¸6 через интервал изменения скважности Dq=0,5 Результаты занести в таблицу 2.2.

 

 

 

Таблица 2.2

№	Um, В	q	Uд, B	Uд.э., В	Uср, В	Uср.э., В
1	№	1,5¸6

 

Измерить  на ЭВМ средние U_ср.э. и действующие U_д.э значения импульсного сигнала для значений U_m и q таблицы 2.2. Для этого напряжение с источника импульсного напряжения подать на вольтметры среднего (вольтметр постоянного тока) и действующего значений (вольтметр переменного тока). Результаты занести в таблицу 2.2. Построить зависимости:  - на одном графике и   -  на другом графике.

Параметры сигналов контролировать осциллографом.

 

Лабораторная работа №2

1. Ознакомиться с приборами, необходимыми для выполнения работы: генератором синусоидального напряжения; генератором импульсных сигналов; универсальным вольтметром;  осциллографом.

2. Подать на вход осциллографа сигнал с генератора синусоидального напряжения с параметрами по варианту из таблицы 2.1. Зарисовать осциллограмму. Определить параметры сигнала U_m, T, f=1/T.

3. Измерить это напряжение вольтметром в режимах измерения постоянного напряжения (среднее значение U_ср) и переменного напряжения (действующее значение U_д). Определить амплитуду U_m из значения действующего напряжения U_д . Сравнить U_m, определенные в п.п. 2 и 3.

4. Подать на вход осциллографа импульсный сигнал с генератора импульсного напряжения с параметрами по варианту таблицы 2.2. Для получения стабильного изображения на экране осциллографа, осуществить его внешнюю синхронизацию от генератора. Определить характеристики U_m, T, T_u, q.

5. Изменяя скважность регулировкой длительности импульса T_u  в диапазоне q=1,5¸6, контролировать значение скважности осциллографом. Параметры U_m,T остаются постоянными. Через интервал изменения скважность Dq=0,5 измерить средние U_ср и действующие U_д значения  импульсного сигнала  вольтметром в режимах измерения соответственно постоянного и переменного напряжения. Результаты занести в таблицу 2.3.

Таблица 2.3

Um=........, B; T=……..., c
Tu, c	q	Uср, В	Uд, В	Um.э.1, В	U m.э.г, В	g1, %	g2,%

 

Обработка результатов

1. Рассчитать из экспериментальных данных амплитуду U_m.э1 и U_m.э.2 импульсного сигнала из значений U_ср. и U_д для каждого значения q.

Сравнить результаты.

2. Рассчитать приведенные погрешности для всех q:

   

где U_m - значение амплитуды, полученное осциллографом. Построить графики , 

3. Сделать вывод о возможности применения универсального вольтметра для измерения характеристик импульсных сигналов.

 

Контрольные вопросы

1. Элементарные сигналы.

2. Какими параметрами оцениваются синусоидальные и импульсные сигналы?

3. Характеристики сигналов.

4. Коэффициенты формы и амплитуды.

5.Что покажет вольтметр среднего значения в цепях синусоидальных сигналов?

6. Как зависит среднее значение импульсных сигналов от скважности импульсов?

7. Можно ли из показаний вольтметра действующего значения определить амплитуду сигналов?

 

Работа № 3

Измерение токов и напряжений

в цепях постоянного тока

Цель работы - изучение способов измерения токов и напряжений в цепях постоянного тока, исследование влияния согласования цепей на точность измерения.

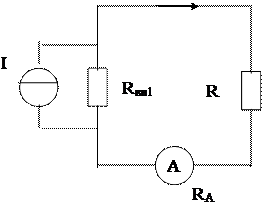
Краткие пояснения. В методе непосредственной оценки амперметр подключается последовательно, а вольтметр - параллельно участку цепи, на котором требуется измерить ток I или напряжение V (рисунок 3.1).

 

 

 

 

 

 

 

 

 

 

 

I

а)                                                                 б)

 

Рисунок 3.1 – Схемы измерения тока (а) и напряжения (б) методом

                                             непосредственной оценки

 

Подключение амперметра и вольтметра меняет режим цепи из-за влияния сопротивлений R_A и R_V самих приборов. Токи (рисунок 3.1-а) и напряжения (рисунок 3.1-б) в цепях до и после подключения амперметра и вольтметра соответственно равны:

;                      ;         

; 

Из-за конечности сопротивлений R_A  и R_V возникает так называемая погрешность согласования, относительные значения которой равны:

;

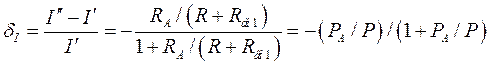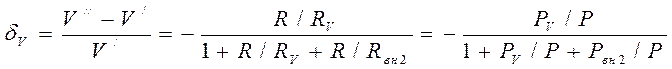где Р_А, Р_V, - мощности, потребляемые соответственно амперметром и вольтметром; P - мощность, потребляемая измерительной цепью.

Для уменьшения погрешности требуется уменьшить мощности, потребляемые амперметром и вольтметром. Это достигается при уменьшении R_A  (при R_A ®0, d_I ®0) и увеличении R_V (при R_V®¥, d_V ®0).

Кроме этого, погрешность может быть уменьшена использованием источников тока и напряжения с оптимальными характеристиками. Погрешности измерений стремятся к нулю, если у источника тока  внутреннее сопротивление стремится к бесконечности (d_I ®0 при R_вн1 ®µ), а у источника напряжения – к нулю (d_V ®0 при R_вн2®0).

На практике для уменьшения погрешностей используют приборы с внутренними сопротивлениями много меньшими (для  амперметра) и много большими  (для    вольтметра) сопротивлений измеряемых цепей.

Чувствительность метода непосредственной оценки определяется отношением приращений показаний приборов к приращениям измеряемых величин

   ;         

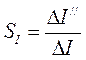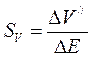
Высокую точность измерения обеспечивают методы сравнения, например, компенсационный метод, который реализуется устройствами, называемыми компенсаторами, или потенциометрами. Наиболее распространена схема компенсации напряжения (рис.3.2). В ней измеряемая ЭДС Е компенсируется равным, но противоположным по знаку известным напряжением  U₀ . Момент компенсации определяется по отсутствию тока в гальванометре Г. При этом E=U₀ , а мощность от объекта измерения не потребляется, т.к.    при I_Г ®0.

Поэтому компенсатор можно считать вольтметром с бесконечным внутренним сопротивлением, а, значит, искажения в измерительную цепь не вносятся.

 

 

 

 

 

 

 

Рисунок 3.2 – Схема измерения E методом сравнения

 

Чувствительность компенсатора определяется отношением приращения показания гальванометра  DI к приращению измеряемой ЭДС  DЕ:

Чувствительность определяется вблизи положения равновесия, т.е. когда показания гальванометра близки к нулю.

 

Практическая работа № 3

1. Определить токи  и относительную погрешность измерения тока δ_Iт методом непосредственной оценки (рисунок 3.1-а) для значения источника тока I=1A и  значений R_вн1=90№ Ом, R=10№ Ом и R_A=1,2,3…10 Ом (взять 10 точек), где № - номер варианта .

2. Собрать схему 3.1-а в программной среде “Electronicsworkbench” на ЭВМ. Ток I^/ _э измеряется «идеальным» амперметром при R_A®0.  Задавая значения параметров из п.1, снять показания амперметра I^//_э1 для всех значений R_А. Рассчитать относительную погрешность измерений. δ_Iэ сравнить ее с погрешностью п.1. Определить чувствительность метода, задавая приращения тока DI=0,1I и снимая изменение показаний амперметра DI^//. Полученные результаты п.1 и п.2 занести в таблицу  3.1.

                                                                                          Таблица 3.1

I=1А	I/т=	I/э=	R=       Rвн1=		DI=0,1А
RА, Ом	I//т, А	I//э, А	Iт, о.е.	Iэ, о.е.	DI//, А	SI, А/А

 

3. Определить напряжения  и относительную погрешность измерения напряжения δ_VТ (для схемы  3.1-б) для ЭДС Е=10В и  значений Rвн₂=1*№, Ом и R=10*№ Ом и диапазона значений R_V=100, 200,....1000 Ом (взять 10 точек).

4. Собрать схему 3.1-б на ЭВМ в программной среде “Electronicsworkbench”. Напряжение U^/э измеряется «идеальным» вольтметром при R_V ® µ .Задавая значения элементов схемы из п.3, снять показания вольтметра U^//_э для всех значений R_V. Рассчитать относительную погрешность δ_Vэ, сравнить ее с погрешностью п.3. Определить чувствительность метода, задавая приращение DЕ=0,1Е и снимая изменение показаний вольтметра DU^//, полученные результаты занести в таблицу 3.2.

 

                                                                                          Таблица 3.2

Е=10В	U/т=	U/э=	R=       Rвн2=		DE=1B
RV, Ом	U//т, В	U//э, B	Vт, о.е.	Vэ, о.е.	DU//, B	SV, B/B

5. Построить графики ,  и  ,   для различных значений R_А и R_V.

6. Собрать схему 2 на ЭВМ. В качестве источника U₀ использовать источник постоянного напряжения с нулевым внутренним сопротивлением (источник образцового напряжения). В качестве гальванометра использовать амперметр с минимально возможным  внутренним сопротивлением. Задавая значения элементов схемы из п.3, измерить ЭДС Е, путем изменения U₀ до тех пор, пока ток через гальванометр не станет равным нулю I=0. В этом случае  Е=U₀ . Рассчитать погрешности измерения δ_Vэ2, сравнить их с погрешностями п.п. 3 и 4. Построить графики погрешностей  для различных значений R_V на том же листе, что и графики п.5. для d_v .

7. Сделать выводы.

 

Лабораторная работа №3

1. Ознакомиться с  лабораторным макетом и оборудованием, необходимым для выполнения работы: учебным стендом УС-1 с встроенным вольтметром и источником ЭДС, образцовым вольтметром В7-16, блоком питания Б5-8. Записать значения сопротивлений вольтметров (по справочным данным).

2. Собрать схему для измерения напряжения (рисунок 3.1-б). Для этого источник ЭДС со стенда УС-1 соединяется с вольтметром на этом же стенде или  с В7-16 через Rвн и R, которые находятся на макете. Задать различные варианты значений элементов схем. Переменным резистором на УС-1 задается значение ЭДС Е.

3. Провести измерения для следующих вариантов значений элементов схем:

I)                                          Rвн»0, R®¥, R_V=20 кОм (1 МОм);

II)                                       Rвн»0, R=20 кОм, R_V=20 кОм (1 МОм);

III)                                    Rвн=20 кОм, R=20 кОм, R_V=20 кОм (1 МОм).

Провести измерения при различных значениях ЭДС от 0 до Vmax (взять 10¸12 значений).

В начале, середине и конце шкалы вольтметра на УС-1 провести измерения чувствительности метода. для этого требуется изменить измеряемую ЭДС на минимальное значение, которое “чувствует” вольтметр, например, так, чтобы показания вольтметра изменились на одно деление шкалы. Приращение ЭДС DV измеряется вольтметром В7-16. показания вольтметра на УС-1 снимается в градусах угла поворота стрелки Da. Чувствительность измерить для всех вариантов значений элементов схем пункта 3.

4. Собрать схему компенсатора (рисунок 3.2). В качестве источника U₀ используется источник ЭДС УС-1, а ЭДС Е - блок питания Б5-8. В качестве гальванометра  Г    используется Rш=10 Ом на макете, ток через который контролируется косвенным путем - измерением на Rш падения, напряжения вольтметром В7-16. Измерение напряжения провести при тех же значениях элементов схем, и значениях  ЭДС , что и  в пункте 3.

Измерить чувствительность компенсационной схемы вблизи положений равновесия. Для этого измеряются приращения тока DI, вызванные приращением DU₀ .Чувствительность измеряется в начале, середине и конце диапазона измерений.

 

Обработка результатов

1. Рассчитать абсолютную, относительную и приведенную погрешности исследованных методов для различных вариантов значений элементов соответствующих схем.

;        ;       ,

где  V- показания вольтметров;

       V_¶ - показания вольтметров при Rвн»0, R®¥, Rv®¥;

     V_max -максимальное значение измеряемого напряжения.

2. Построить графики погрешностей как функции от измеряемого напряжения для различных значений элементов схем на одном листе для каждого из 2-х методов .

3. Рассчитать чувствительность методов. Для метода непосредственной оценки  , для компенсатора .

4. Сравнить методы.

 

Контрольные вопросы

1. Что такое метод непосредственной оценки?

2. Причина возникновения погрешности согласования?

3. Какие входные сопротивления д.б. у идеальных вольтметров и амперметров?

4. Какие внутренние сопротивления д.б. у идеальных источников напряжения и токов?

5. Что компенсируется в одноименном методе?

6. Чем определяется погрешность метода сравнения ?

7.Почему в компенсационном методе не потребляется мощность от источника измеряемого напряжения?

8. Влияют ли сопротивления измерительных приборов и источников измеряемого напряжения на точность измерения в компенсационном методе?

 

Работа № 4

Расширение пределов измерения электроизмерительных приборов постоянного тока

Цель работы – исследование преобразователей тока в напряжение (шунт постоянного тока) и напряжения в ток (добавочный резистор), их использование для измерения токов и напряжений в различных диапазонах.

Краткие пояснения. Для расширения предела измерения амперметра применяется делитель тока: параллельно прибору (ИМ - измерительный механизм) включается шунт - резистор , по которому протекает часть измеряемого тока  (рисунок 4.1). Если  и  - соответственно сопротивления прибора и шунта, то ток через прибор равен:

.

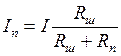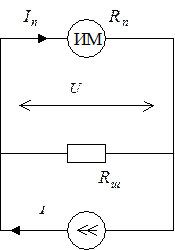
      Рисунок 4.1 – Шунт постоянного тока

 

Сопротивление шунта определяется из этого выражения подстановкой максимального измеряемого тока  и тока полного отклонения прибора  (справочные данные):

,

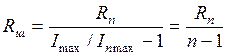где  - число, показывающее во сколько раз увеличивается предел измерения прибора.

Например, если требуется измерить больший в 2 раза ток предела прибора, (), то сопротивление шунта будет равно сопротивлению прибора ().

Зажимы шунта, к которым подводится ток , называются токовыми, а с которых снимается напряжение  - потенциальными. Шунт является преобразователем тока в напряжение. Его функция преобразования (ФП): , т.е. ФП является линейной. Под действием влияющих факторов эта ФП может отличаться от номинальной ФП, которая определяется номинальным значением сопротивления шунта: . Отклонение  от этого значения вызывает погрешность:

,

где  - реальное сопротивление используемого в эксперименте шунта.

Для расширения пределов измерения по напряжению последовательно с прибором (ИМ) включается добавочное сопротивление , на котором падает часть измеряемого напряжения (рисунок 4.2). При этом напряжение на приборе равно 

 

 

Рисунок 4.2 – Добавочное сопротивление

 

Сопротивление  находится, исходя из максимального значения измеряемого напряжения  и максимально возможные падения напряжения на приборе

Например, если требуется измерить напряжение в 2 раза больше предела измерения прибора, то последовательно с ним включается сопротивление, равное сопротивлению прибора.

Добавочное сопротивление  является преобразователем напряжения - ток. Его ФП - ток в цепи ИМ:

,

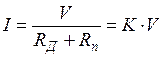где 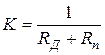   - коэффициент преобразования.

Погрешность этого преобразования вызывается отклонения значения реального добавочного сопротивления  от его номинального значения :

.

 

Практическая работа № 4

1. Определить сопротивления шунта (рисунок 4.1) для расширения пределов измерения амперметра с током полного отклонения и внутренним сопротивлением =1Ом до значения =№A, где № - номер варианта. Какие максимальные токи будут при этом протекать через амперметр и  шунт?

2. Определить сопротивления двухпредельного шунта (рисунок 4.3)  и  для расширения пределов измерения амперметра пункта 1 до значений =№A; =10№A. Рассчитать токи через амперметр и сопротивления шунтов.

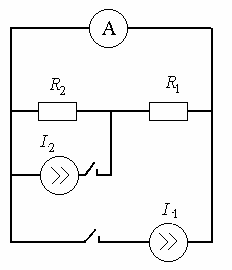
Рисунок 4.3 – Двухпредельный амперметр

 

Замечание: На пределе I₁ используется формула для  с учетом того, что  n=n₁ , а на пределе I₂  используется формула для  с учетом того, что  соединен последовательно с амперметром, т.е.  и того, что n=n₂. Получаем систему уравнений

,

 решая которую находим значения  и .

3. Собрать схемы 4.1 и 4.3 в программной среде “Electronics workbench” на ЭВМ. Задавая значения элементов схем согласно пунктам 1 и 2, измерить токи через амперметр и через сопротивления шунтов путем подключения параллельно сопротивлениям шунтов вольтметров с внутренними сопротивлениями много больше сопротивлений шунтов. Сравнить полученные токи с токами, рассчитанными в пунктах 1 и 2.

4. Изменяя токи от нуля до максимума, снять зависимости , где - падение напряжения на амперметре,  - измеряемый ток (в схеме 4.3 это и ток , и ток ). Построить графики этих зависимостей.

5. Определить значение добавочного сопротивления  (рисунок 4.2) для расширения пределов измерения вольтметра с током полного отклонения =100мА и внутренним сопротивлением =10kOм до значения =10№B. Какие максимальные напряжения будут при этом падать на исходном вольтметре и добавочном сопротивлении?

6. Дана схема двухпредельного вольтметра (рисунок 4.4).

 

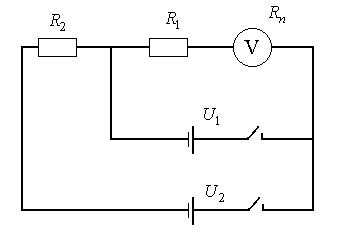
Рисунок 4.4 – Двухпредельный вольтметр.

 

Используя данные значений элементов схемы из предыдущей задачи, определить значения добавочных сопротивлений  и , необходимых для расширения предела измерения вольтметра с =1B до =10№B, =100№B. Какие при этом будут падения напряжений на ,  и ?

7. Собрать схемы  4.2 и 4.4 на ЭВМ. Задавая значения элементов согласно пунктам 5 и 6, определить падение напряжений на всех элементах схем путем измерения соответствующих текущих через них токов, с помощью амперметров с внутренним сопротивлением много меньшим сопротивлений элементов схем. Сравнить п.7 с п.5 и п.6.

8. Изменяя напряжения от максимального значения до нуля, снять зависимости , где  - ток через вольтметр,  - измеряемое напряжение (в схеме 4.4 это и напряжение , и напряжение ). Построить графики этих зависимостей.

9. Сделать выводы.

 

Лабораторная работа № 4

1. Ознакомиться с макетом и приборами, необходимыми для выполнения работы: учебным стендом УС-1 с встроенным вольтметром и ИП милливольтметром и миллиамперметром для расширения пределов измерения.

2. Собрать схему для расширения предела измерения вольтметра (рисунок 4.5), где V - контрольный вольтметр, - милливольтметр, у которого расширяется предел измерения, Кл - ключ.

 

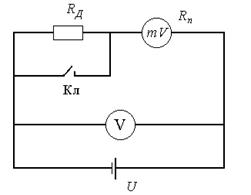
Рисунок 4.5 – Расширение пределов измерения милливольтметра.

3. Замкнуть ключ Кл. Установить стрелку  на максимум .Снять показания вольтметра . Построить градуировочную характеристику для : , где  и  - показания соответственно вольтметров  и . Снять 10 - 15 точек, данные занести в таблицу.

4. Рассчитать , которое требуется для расширения предела измерения  до предела измерения . С помощью омметра установить рассчитанное значение  на переменном резисторе.

5. Подключить резистор с рассчитанным значением  для расширения пределов измерения  до предела измерения . Изменяя напряжение, снять градуировочную характеристику  для  с . Снять 10 - 15 точек от нуля до . Данные занести в таблицу.

 

Обработка результатов

1. Построить графики  пунктов 3 и 5 на одном листе.

2. Рассчитать абсолютную D и приведенную  погрешности преобразования  с  и без него, считая показания вольтметра  действительным значением измеряемого напряжения.

3. Построить графики погрешностей в функции от приложенного напряжения  и .

4. Сравнить характеристики без  и с ним.

 

Контрольные вопросы

1. Почему  включается последовательно с вольтметром?

2. Почему  включается параллельно амперметру?

3. Какая ФП у ?

4. Какая ФП у ?

5. Влияет ли внутреннее сопротивление приборов на значение  и ?

6. Каким должно быть внутреннее сопротивление источников напряжения и тока, чтобы не оказывать заметного влияния на результаты измерения?

 

Работа № 5

Измерение сопротивлений постоянному току

Цель работы – Изучение метода вольтметра-амперметра и мостового метода, сравнение их характеристик.

Краткие пояснения. Метод вольтметра-амперметра. Для измерений малых  применяется схема рисунка 5.1-а. Так как  (), то

  и относительная погрешность при этом   невелика.

 

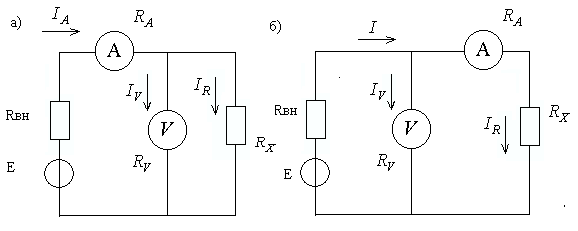
Рисунок 5.1 – Метод вольтметра-амперметра

 

Для измерения больших R применяется схема 5.1-б. Так как .

Относительная погрешность при этом   также невелика. Чувствительность метода равна произведению чувствительности по току и напряжению, т.е.

,

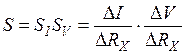 где , ,  - соответственно приращения показаний приборов и измеряемого R.

Мостовой метод (рисунок 5.2) позволяет получить высокую точность. При равновесии моста () верно соотношение:

  или  .

Рисунок 5.2 – Мостовой метод

 

Равновесие достигается изменением  или . Погрешность измерения определяется погрешностями образцовых сопротивлений:

Кроме этого, погрешность вызывается ограниченностью чувствительности гальванометра (Г). Эта погрешность равна

,

где D - порог чувствительности гальванометра;

       - чувствительность гальванометра ,

где   - изменение показаний гальванометра,

      - относительное изменение сопротивления  одного из плеч моста.

В общем случае относительная погрешность измерений определяется по формуле:

,

где  - действительное значение,  - результат измерения.

 

Практическая работа № 5

1. Определить относительную погрешность δ_1Т и δ_2Т двух схем метода вольтметра-амперметра (рисунок 5.1-а,б), для значений R_A=№ Ом, R_V=№ кОм, где № - номер варианта, R_х=1, 10, 10², ……10⁶ Ом (рассчитать для 7 значений). Данные занести в таблицу 5.1.

Таблица 5.1

RA=…..                      RV=…..                  Е=….                      Rвн=…..
Rx, Oм	δ1Т, %	δ2Т, %	Rx1, Oм	Rx2, Oм	δ1э, %	δ2э, %	S1,	S2,	Rx3, Ом	δ3э, %	S3,

 

                                                                                                   Таблица 5.2

 

2. Собрать схемы рисунка 5.1-а,б в среде “Electronics workbench” на ЭВМ. Задавая значения элементов схем по вариантам пункта 1, снять показания вольтметра и амперметра U₁,I₁ и U₂,I₂. Данные занести в таблицу 5.2. Значения Е=10В, R_вн=10№ Ом. Рассчитать по этим показаниям значения сопротивлений R_x1 и R_x2 и относительные погрешности измерений δ_1э  и δ2э, занести их в таблицу 5.1 и сравнить их с погрешностями, полученными в пункте 1.

3. Определить чувствительность методов S₁ и S₂ для данных выше значений элементов схем, задавая приращения  и измеряя приращения показаний приборов ∆I₁, ∆U₁ и ∆I₂, ∆U₂. Данные занести в таблицу 5.2. и таблицу 5.1.

4. Собрать на ЭВМ схему моста (рисунок 5.2). В качестве гальванометра используется амперметр с параметрами п.1. Источник напряжения аналогичен источнику пункта 2. Задаются следующие значения элементов моста: R₂=R₄=R_xmax/2, где R_xmax- максимальное значение R_x из п.1. Для значений R_x из пункта 1 изменением  добиться равновесия моста (I_г=0). Рассчитать значения измеряемых сопротивлений R_x3 и относительных погрешностей измерения δ₃, данные занести в таблицу 5.1. Сравнить погрешности с погрешностями пунктов 1 и 2.

5. Определить чувствительность мостовой схемы S₃, изменяя в положении равновесия значение измеряемого сопротивления DR_x = 0,1R_x и измеряя соответствующее приращений показаний амперметра ∆I₃. Данные занести в таблицы. Сравнить чувствительность мостового метода с чувствительностью метода вольтметра-амперметра.

6. Построить графики погрешностей методов на одном листе и чувствительностей методов на одном листе в функции  . Сделать выводы о характеристиках методов.

 

Лабораторная работа № 5

1. Ознакомиться с лабораторным макетом и приборами, необходимыми для выполнения лабораторной работы: стендом УС-1, с встроенным вольтметром, миллиамперметром и источником постоянного напряжения (ИПН), вольтметром В7-16. Записать их паспортные данные (для вольтметра и миллиамперметра).

2. Измерить действительные значения сопротивлений заданных резисторов с помощью образцового прибора В7-16 в режиме омметра. Данные занести в таблицы 5.3 и 5.4.

                                                                                                         Таблица 5.3

 

 

                                                                                                         Таблица 5.4

Метод непосредствен- ной оценки		Метод вольтметра-амперметра				Мостовой метод
Действительное значение , Ом		, В	, А	, Ом	,	, Ом	, Ом	,

 

3. Собрать поочередно 2 схемы вольтметра-амперметра (рисунок 5.1-а,б) с помощью ИПН, вольтметра и миллиамперметра стенда УС-1 для измерения сопротивлений  на макете. Для каждого   задать такие напряжения , чтобы показания миллиамперметра находились вблизи предела шкалы прибора. Снять показания вольтметра и миллиамперметра. Затем, не изменяя значений , измерить  по схеме 1-б. Полученные результаты занести в таблицу 5.4.

4. Определить чувствительность метода вольтметра-амперметра. Для этого изменить  из пункта 2 на небольшую величину подключением последовательно  известного сопротивления  и измерить приращения показаний вольтметра и миллиамперметра. Полученные результаты занести в табл.5.3.

5. Собрать мостовую схему (рисунок 5.2) для резисторов  из пункта 2. Мост уравновешивается переменным резистором . Разобрать схему. Измерить значение  с помощью прибора В7-16 в режиме омметра. Резистор  подбирается для соответствующих  таким образом, чтобы равновесие моста () достигалось при возможно больших значениях . Добиваясь минимального значения падения напряжения на  изменением , устанавливаем мост в равновесие и определяем .

6. Определить чувствительность мостовой схемы. Для этого вблизи положения равновесия задается небольшое (известное) изменение значения резистора  и снимается соответствующее ему приращение показаний вольтметра В7-16. Полученные результаты занести в таблицу 5.4.

 

Обработка результатов

1. Рассчитать относительные погрешности метода вольтметра-амперметра, используя справочные данные о внутренних сопротивлениях вольтметра и миллиамперметра и о действительных значениях . Определить экспериментальную относительную погрешность измерений по отклонению измеренного и действительного значений .

2. Рассчитать чувствительность метода вольтметра-амперметра.

3. Рассчитать относительные погрешности мостового метода, если погрешность резистора  принять равной половине деления его шкалы. Определить экспериментальную относительную погрешность измерения по мостовой схеме.

4. Рассчитать чувствительность мостового метода.

5. Построить графики погрешностей методов на одном листе и чувствительностей методов на одном листе в функции  . Сделать выводы о характеристиках методов.

 

Контрольные вопросы

1. Какие Вам известны методы измерения сопротивлений?

2. Какой закон лежит в основе метода вольтметра-амперметра?

3. Влияют ли внутренние сопротивления вольтметра и амперметра на результаты измерений?

4. Чем определяется погрешность мостового метода?

5. Каким образом определяется положение равновесия моста?

6. При каких значениях  больше влияние характеристик вольтметра, а при каких - амперметра?

7. Чем определяется чувствительность методов?

Работа № 6

Измерение сопротивлений переменному току

Цель работы – изучение методов измерения емкости , тангенса угла диэлектрических потерь , индуктивности  и добротности  электрических цепей.

Краткие пояснения. В методе одного вольтметра (рисунок 6.1.) напряжение на известной емкости  и индуктивности :

;

,

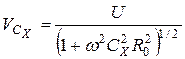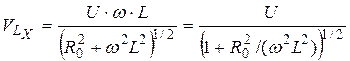где ,  - частота переменного напряжения .

 

 

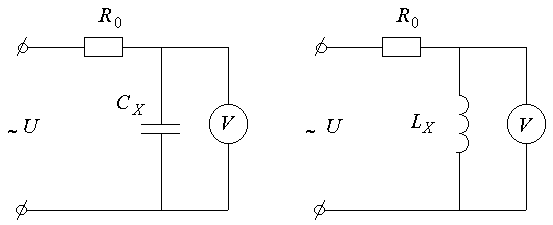
Рисунок 6.1 – Метод одного вольтметра

 

Относительная погрешность метода:

,

где - измеряемое реактивное сопротивление,

      -сопротивление вольтметра переменному току.

Чувствительность метода определяется чувствительностью по напряжению:

,

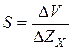где  - приращение показаний вольтметра, соответствующее изменению сопротивления .

Вместо известных сопротивлений могут быть использованы однотипные с измеряемыми реактивные сопротивления:

при измерении  - ,  -  (рисунок 6.2.).

 

 

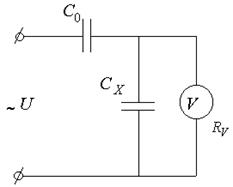
Рисунок 5.2 – Метод одного вольтметра с С₀

 

,

 

где- сопротивление вольтметра.

Откуда

.

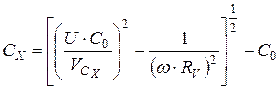Если , то    .

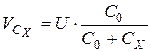Относительная погрешность и чувствительность находятся как в предыдущем примере.

Метод вольтметра-амперметра (рисунок 6.3) использует закон Ома для соответствующих цепей:

   ;      ;

 

 

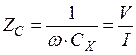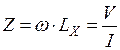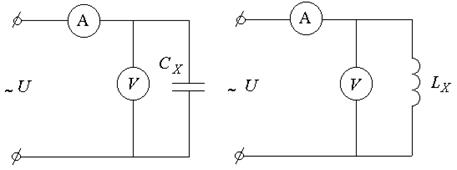
Рисунок 6.3  Метод вольтметра-амперметра

 

Чувствительность метода равна произведению чувствительностей по току и напряжению:

,

где  - приращение показаний приборов, соответствующих изменению измеряемого сопротивления .

Более высокую точность измерения имеют мостовые методы (рисунок 6.4). При равновесии моста (I=0):  , где - полные комплексные сопротивления плеч моста.

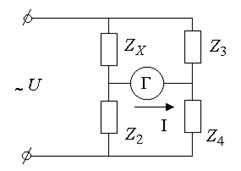
Рисунок 6.4 Мостовой метод

В показательной форме:

 ;                        ;

;             ,

где  - модули полных сопротивлений;

         - фазовые углы (углы между током и напряжением) полных сопротивлений.

Условие равновесия в показательной форме:

,

отсюда получаем:

;    

т.е. при равновесии моста должны быть равны  произведения модулей и суммы и углов. Следовательно, для уравновешивания моста требуется регулировать не менее 2-х параметров моста (так называемые два условия равновесия).

Чтобы мост был частотно-независимым, нужно выбрать одни смежные плечи моста, например,  и  активными, а другие два плеча должны содержать реактивные сопротивления одного типа (емкостные или индуктивные). При этом условие равновесия упрощается, т.к. частоты в равенстве для модулей сокращаются, а

 и .

Погрешность моста определяется погрешностью мер:

,

где  - относительная погрешность соответствующих сопротивлений.

Большое значение для мостов переменного тока имеет возможность так называемого раздельного отсчета, т.е. независимого отсчета активной и реактивной составляющих. Такой отсчет достигается при раздельном влиянии параметров моста на каждое из 2-х условий равновесия (т.е. значения параметров не входят одновременно в оба уравнения). Поэтому требуется чтобы 2 плеча были комплексными (образцовое и измеряемое), а отношения 2-х других плеч было или вещественным или мнимым. При этом если комплексные сопротивления включены в смежные плечи моста, то они должны быть одного характера (или оба последовательно или оба параллельно соединенные), а если в противоположные плечи - то разного.

Чувствительность мостовой схемы определяется вблизи положения равновесия по формулам:

  и  ,

где  - изменение сопротивлений;  - изменение показаний гальванометра.

Если сопротивление комплексное, то общая чувствительность равна сумме чувствительностей по активной и реактивной составляющим:

,

где ,  - изменение активного и реактивного сопротивлений.

Мост Соти (рисунок 6.5) служит для измерения емкостей конденсаторов высокого качества (воздушных и слюдяных). При равновесии

Равновесие достигается или изменением  при , или изменением  при .

 

Рисунок 6.5 – Мост Соти

Практическая работа № 6

1. Определить емкость  и относительную погрешность измерения в методе одного вольтметра (рисунок 6.2) на частотах f=10⁴ Гц, где № - номер варианта, если внутреннее сопротивление вольтметра =10⁶ Ом, входное напряжение =12B, емкость =10^-9 Ф и показание вольтметра  =6 B.

2. Какой ток покажет амперметр в методе вольтметра-амперметра (рисунок 6.3), если параметры входного напряжения , вольтметра , и емкости  взяты из условий и решений задания 1, а сопротивление амперметра Ом?

3. Собрать в среде “Electronics Workbench” на ЭВМ поочередно схемы для измерения емкости  методами одного вольтметра (рисунок 6.2) и вольтметра-амперметра (рисунок 6.3). Задать значение параметров схем и характеристик элементов такие же , что и в пунктах 1 и 2. Снять показания приборов. Рассчитать значения емкостей  и относительных погрешностей методов измерений. Сравнить результаты с результатами пунктов 1 и 2.

4. Определить чувствительность методов в пунктах 1 и 2, задавая относительно небольшие изменения  и измеряя приращения показаний приборов.

5. Собрать на ЭВМ схему моста Соти (рисунок 6.5), в качестве гальванометра используя амперметр с внутренним сопротивлением Ом. Параметры элементов схемы: =12 B; =Ф; =50 кОм ; =100 кОм. Определить чувствительность схемы вблизи положения равновесия моста на частотах, заданных в пункте 1. Результаты работы занести в таблицу 6.1, в которой параметры с индексами  «Т» - рассчитанные, «Э» -  смоделированные на ЭВМ, а S₁,  S ₂,  S ₃,  S ^/₃ – чувствительности методов (в мостовом методе чувствительность рассчитывается по двум формулам).

Таблица 6.1

f, Гц	CxT, Ф	Cxэ, Ф	δТ, о.е	δЭ, о.е	IT, A	IЭ, A	S1, В/Ом	S2,	S3, А/Ом	S3,

 

Лабораторная работа № 6

1. Ознакомиться с  лабораторным макетом и приборами, необходимыми  для выполнения работы: генератором Г3-34, вольтметрами  В7-16 и В7-26, конденсатором переменной емкости (КПЕ). Записать их паспортные данные (внутренние сопротивления вольтметров).

2. Собрать схему метода одного вольтметра (рисунок 6.2) для В7-26 и В7-16. Частоты переменного напряжения с генератора берутся из пункта 1 практической работы. Измерить ёмкости  и  при двух значениях угла поворота КПЕ , взятых из таблицы 6.2 по номеру варианта. Определить чувствительность метода, используя в качестве  разницу в результатах измерений  и .

3. Измерить ёмкости  и  из п.2 методом вольтметра-амперметра (рисунок 6.3). В качестве вольтметра использовать В7-26, а в качестве амперметра - В7-16, которым измеряется падение напряжения на . Параметры переменного напряжения те же, что и в п.2. Определить чувствительность метода.

4. Собрать схему моста Соти (рисунок 6.5). Равновесие моста достигается регулировкой значения емкости  и контролируется вольтметром В7-16 по разнице потенциалов между средними точками моста. Определить чувствительность мостового метода вблизи положения равновесия, изменяя на относительно небольшую величину значение  и снимая соответствующее изменение напряжения на В7-16.

 

                                                                                               Таблица 6.2.

№ вар.	Гц	гц	, град	, град
1	1	1	100	110
2	1,2	1,2	120	130
3	0,8	1,4	140	150
4	0,9	1,3	160	170

 

Обработка результатов

1. Рассчитать относительные погрешности исследованных методов, используя результаты измерений.

2.Рассчитать чувствительность методов.

3. Сравнить результаты практической и лабораторной работ.

 

Контрольные вопросы

1.Какие условия равновесия моста?

2. Почему есть 2 условия равновесия моста переменного тока?

3. Что такое раздельный отсчет?

4. Что такое чувствительность мостовой схемы?

5. Зачем в смежные плечи моста Соти включается емкость?

 

Работа № 7

Исследование измерительных выпрямителей.

Цель работы – построение вольтметров выпрямительной системы, расчет и исследование их характеристик.

Краткие пояснения. Для использования приборов магнитоэлектрической (МЭ) системы в цепях переменного тока применяют одно и двухполупериодные выпрямители (рисунки 7.1 и 7.2).

 

Рисунок 7.1 Однополупериодный   выпрямитель

                       с пропусканием обратного тока

 

 

Рисунок 7.2  Двухполупериодные выпрямители

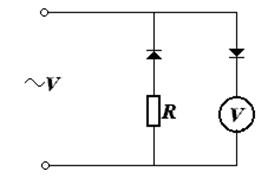
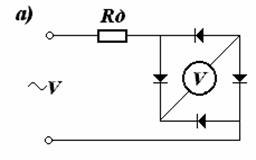
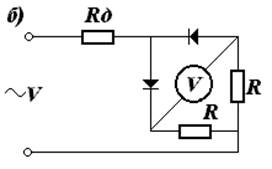
Вольтметр МЭ системы при этом покажет среднее значение напряжения, которое для одно и двухполупериодные схем соответственно равны:

 ;

 ,

где V_m -амплитуда переменного сигнала.

Резистор R  в однополупериодном выпрямителе ограничивает ток через диод. В двухполупериодном выпрямителе резисторы R применяют для уменьшения влияния температурной нестабильности диодов. Но при этом уменьшается чувствительность схемы. Добавочное сопротивление Rд  применяют для расширения пределов измерения вольтметров. Значение Rд для схем  7.2-а и 7.2-б соответственно  определяется по формулам:

где   V_пр  -предел измерения напряжения (среднеквадратичное значение);

I_m -максимальный  ток отклонения вольтметра (справочные данные);

R_v  -внутреннее сопротивление вольтметра;

r_¶ - прямые сопротивления диода.

Для уменьшения пульсации на приборе параллельно ему включается конденсатор.

Если прибор следует проградуировать в действующих или амплитудных значениях напряжения, то используют соотношения, связывающие среднеквадратическое V_ср.кв. , среднее (средневыпрямленное) V_ср , амплитудное V_м значения напряжения, коэффициенты формы К_ф и амплитуды К_а сигналов:

_,

.

Для синусоидального сигнала К_ф =1,1, К_а =1,41.

Практическая работа №7

1. Что покажет вольтметр выпрямительной системы в случаях одно и двухполупериодных выпрямителей (рисунки 7.1 и  7.2-а, если на вход подается синусоидальный сигнал с амплитудой V_m  из таблицы 1 (по номеру варианта №), а шкала вольтметра проградуирована с среднеквадратических значениях? Полученные значения (V_v ) теор. занести в таблицу 7.1.

Таблица 7.1

№ варианта	Vm,B	(Vv)теор.,В	(Vv)эксп., В
			f1=50Гц	f2=1кГц
№	10№

 

2. Собрать схемы  7.1 и  7.2 в среде “Electronics Workbench” на ЭВМ, с вольтметром постоянного тока. Для параметров входного сигнала п.1. снять показания вольтметра (V_v) эксп. для двух значениях частот f₁ и f₂ входного сигнала.

3. Какое добавочное сопротивление R¶ требуется подключить (см.  7.2-а и 7.2-б) для измерения переменного напряжения с амплитудой V_m? Характеристики напряжения и элементов схем взять по номеру варианта из таблицы 7.2 Полученное значение (R¶) теор занести в таблицу 7.2.

  Таблица 7.2

Вариант	Vm,B	Rv, Ом	R¶ , Ом	R, Ом	Im,A	(R¶)теор Ом	VV ,B
№	10№	103№	10№	10№	10-3№

 

4. Собрать схемы рисунков 2-А и 2-б на ЭВМ. Задавая такие же параметры элементов схем, входных сигналов, и R¶, полученное в п.3., снять показания вольтметра V_v.  Какое значение напряжения переменного тока покажет при этом вольтметр?

5. Определить чувствительность схем рисунков 7.2-а и 7.2-б, используя формулу . Для этого задавая небольшое приращение входного напряжения DV, измерить соответствующее ему изменение показаний вольтметра DV_v . Сравнить результаты.

 

Лабораторная работа №7

1. Ознакомиться с макетами и приборами, необходимыми для выполнения работы: вольтметром постоянного тока, универсальным вольтметром В7-16; осциллографом; источником переменного низкого напряжения (6-36 В, f=50 Гц).

2. Записать паспортные данные вольтметра постоянного тока, необходимые для расчета добавочного сопротивления R¶ при построении вольтметра переменного тока заданного предела измерения.

3. Собрать схему вольтметров выпрямительной системы (рисунки 7.1, 7.2). Источник регулируемого переменного напряжения  строится с помощью источника 6-36 В и реостатного макета (рисунок 7.3). Вольтметром В7-16 и осциллографом контролируются параметры переменного напряжения ~V.

 

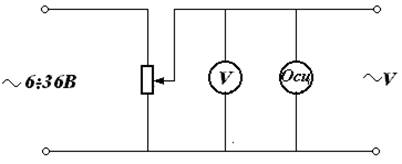
Рисунок 7.3 Источник регулируемого переменного напряжения~V.

 

4. Для одного значения переменного напряжения ~V на выходе источника измерить значение ~V вольтметрами одно и двухполупериодных выпрямительных систем . Для этого собрать схемы 7.1, 7.2-а, 5.2-б на стенде УС-1 и подать на их входы переменное напряжение с источника. Регулировкой потенциометра задать ~V по варианту V₀ таблицы 7.3. Снять показания вольтметра В7-16 (V₀ ), вольтметра постоянного тока  в этих случаях (V₁ , V₂ , V₃ ). Данные занести в таблицу 7.3.

Таблица 7.3

№ варианта	V0 , B	V1 , B	V2 , B	V3 , B	S1, град/В	S2, град/В	S3, град/В	V`0 , B	R¶, Ом	V`2 , B	V`3 , B
1 2 3 4	7 8,5 9 10							16 18 20 22

 

5.Зарисовать осциллограммы переменного напряжения ~V и напряжений на вольтметре постоянного тока.

6. Определить чувствительность вольтметров выпрямительных систем п.4 S₁, S_2, S_3,  задавая небольшие приращения DV потенциометром (DV  с В7-16) и измеряя изменения показаний вольтметров постоянного тока DV_V  в градусах угла поворота стрелки прибора. При этом учесть, что максимальный угол отклонения стрелки  a_мах=p /2 рад.

7. Снять градуировочную  характеристику вольтметров п. 4, изменяя ~V потенциометром от максимального значения вблизи предела шкалы вольтметра постоянного тока до нуля (снять 6¸8 точек). Построить график зависимости показаний вольтметра выпрямительной системы от показаний вольтметра В7-16 V_V=F(V₀). Определить, какое значение показывает вольтметр выпрямительной системы (амплитудное, среднее, действующее).

 

Обработка результатов

1. Рассчитать значение добавочного сопротивления R¶ (7.2-a, 7.2-б), которое необходимо для того, чтобы вольтметр выпрямительной системы показывал действующее значение напряжения ~V₀^’.  По варианту  с помощью вольтметра В7-16 в режиме омметра установить значение переменного сопротивления, равное рассчитанному R¶ и подключить его последовательно схемам 7.2-а, 7.2-б. Снять градуировочную характеристику     в этом случае. Построить ее график вместе с графиком п.7.

2.     Рассчитать абсолютную и приведенную погрешности: ,  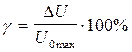во всех измеренных точках градуировочной характеристики. Нарисовать графики , .

 

Контрольные вопросы

1.    Что показывает вольтметр МЭ системы на переменном сигнале?

2.    Можно ли его применять для измерения синусоидального сигнала?

3.    Почему мостовой выпрямительный вольтметр имеет большую чувствительность?

4.    Для чего необходимо добавочное сопротивление R¶?

5.    Из-за чего возникает температурная погрешность выпрямителя?

6.    Когда больше среднее значение сигнала: с одно или двухполупериодным выпрямителем?

7.    Что покажет вольтметр действующих значений, если на входе постоянное напряжение, например, 1В?

 

Библиографический список

1.     Сергеев А.Г. и др. Метрология, стандартизация, сертификация:  учебное пособие.-М: Логос, 2003.

2.     Шакурский А. В. Основы метрологии, стандартизации и сертификации. Учебное пособие ПТИ, 2000 г.

3.     Усманов В.В., Шакурский А.В., Прошин А.И. Измерение электрических величин: Учебно-метод.разраб.-Пенза, ПТИ, 2007г.

Содержание

Работа №1. Виды измерений…………………………………………………..3

Работа № 2. Виды измерительных сигналов……………………………….11

Работа №3. Измерение токов и напряжений в цепях постоянного тока..17

Работа №4. Расширение пределов измерения

электроизмерительных приборов постоянного тока……………………...24

Работа №5. Измерение сопротивлений постоянному току……………….32

Работа №6. Измерение сопротивлений переменному току……………….39

Работа №7. Исследование измерительных выпрямителей……………….47