Министерство образования и науки Луганской Народной Республики

Индустриальный техникум ДонГТУ

 

 

 

 

 

 

 

 

Методические рекомендации

для самостоятельной работы

студентов

по дисциплине «Численные методы»

 

для студентов специальности

09.02.03 «Программирование в компьютерных системах»

 

 

 

 

 

Алчевск

2016

 

 

Разработала	_____________	Л.Л. Кузьмина  – преподаватель высшей категории, старший преподаватель
Рецензент	_____________	Л.С. Филоненко – преподаватель высшей категории

 

 

 

     

Утверждено на заседании Методического совета

__________Л.Л. Кузьмина  председатель Методического совета ИТ ДонГТУ

                 

 

 

 

 

 

Рассмотрено и одобрено на заседании цикловой комиссии

«Информатики и компьютерной техники»

Протокол от «___» ________  2016 г. № __

Председатель комиссии

_____________О.Ю. Ленкова

 

 

Содержание

 

Введение	4
Инструкция о модульно-рейтинговой системе текущего и итогового контроля уровня знаний студентов	7
Оценка элементов модулей дисциплины «Численные методы»	9
Модуль № 1	10
Модуль № 2	20
Модуль № 3	28
Варианты семестрового задания	36
Литература	37

 

 

 

 

 

 

 

 

 

 

 

 

 

Введение

Для современных инженерно-технических задач необходимо использовать сложный математический аппарат и разные методы их решения. При этом часто приходиться встречаться с задачами, для которых аналитическое решение или вообще невозможно, или выражается такими громоздкими формулами, что использовать их для практических целей нецелесообразно.

В таком случае используют численные методы решения, которые позволяют достаточно просто решить поставленную задачу. Широкое применение таких методов стало возможным с использованием электронно-вычислительной техники. С другой стороны, развитие ЭВМ нуждалось в разработках эффективных, надежных алгоритмов и применении их для решения таких задач.

Целью изучения курса «Численные методы» являются изучение алгоритмов ряда методов, которые позволяют решать прикладные задачи. Программой дисциплины не предусматривается рассмотрение всех разновидностей существующих методов, главной целью является достижение понимания основных методов, особенностей и областей их приложения.

Все знания и навыки, которые были получены при изучении дисциплины, могут быть использованы в процессе изучения специальных дисциплин, при выполнении курсового проекта, а также в практической работе на производстве.

На изучение дисциплина отводится 81 час, из них 52 – аудиторных занятий и 29 – на самостоятельную работу студента. Изучать материал следует систематически и в той последовательности, которая предусмотрена программой дисциплины.

Для полного и успешного изучения дисциплины запланированы следующие виды занятий:

1. Изучение материала по основным вопросам курса на лекционных занятиях

2.  Выполнения практических работ и расчетных заданий.

3. Самостоятельное изучение отдельных вопросов с использованием этих методических рекомендаций и литературы, которую необходимо использовать для изучения дисциплины. Самостоятельная работа предусматривает подготовку студентов к практическим работам, практическим занятиям, контрольным работам, выполнению расчетных заданий, семестрового задания и тому подобное.

Организация самостоятельной работы студентов предполагает внедрение в деятельность таких приемов работы: смысловой переработки текстов, закрепления учебного материала, усвоения обобщенных способов решения заданий, приемы краткой, самой рациональной записи (выписывание, планы, тезисы, конспекты, общие приемы работ с книгой); общие приемы запоминания; концентрирование внимания на использовании студентами разных видов самоконтроля, поэтапную проверку своей работы, общие приемы поиска дополнительной информации (работы с библиографическими справками, каталогами, словарями).

Методические рекомендации к самостоятельной работе студентов содержат три модуля, оценку каждого его элемента. Первый модуль содержит материал по теории погрешностей, алгебре матриц и методов решения систем линейных уравнений, второй модуль – методы решения нелинейных уравнений, а третий модуль содержит задачи интерполяции и экстраполяции функций. Каждый модуль заканчивается защитой данного модуля по контрольным вопросам.

При проработке лекции необходимо прочитать ее, выучить основные определения, термины и формулы, ответить на контрольные вопросы, которые есть после каждой лекции. Если возникли вопросы, то более детально разобрать вопрос по литературе, указанной в данной методике, или обратиться за консультацией к преподавателю.

Правила выполнения и оформления

семестрового задания:

-        студент должен выполнить семестровое задание согласно своего варианта;

-        семестровое задание следует выполнять в отдельной тетради чернилами любого цвета, кроме красного, оставляя поля для замечаний преподавателя;

-        решение задач следует располагать в порядке номеров, указанных в заданиях, сохраняя номера задач;

-        перед решением каждой задачи нужно выписать полностью условие;

-        решение задач оформлять обстоятельно и аккуратно, объясняя все действия;

-        семестровое задание, выполненное не по своему варианту, не засчитываются;

-        по получении проверенной работы студент должен исправить в ней все отмеченные ошибки и недостатки.

 

 

 

 

Инструкция

по модульной – рейтинговой системе

текущего и итогового контроля уровня знаний студентов

по дисциплине «Численные методы»

для специальности  «Разработка программного обеспечения»

 

Общее количество часов на дисциплина - 81; аудиторных – 52;

самостоятельных – 29 часов.  Дисциплина изучается один семестр.

Теоретический материал разбит на три модуля. Каждый модуль – это завершенный раздел дисциплины.

Модуль 1 – Теория погрешностей. Методы решения систем линейных уравнений

Модуль 2 – Методы решения нелинейных уравнений

Модуль 3 – Интерполяция и экстраполирование

Модульно-рейтинговая система предусматривает оценку знаний студентов по дисциплине

«5» – 90 - 100 баллов

«4» – 74 -  89 баллов

«3» – 60 – 73 баллов

Студенты, которые своевременно выполнили график учебного процесса и набрали 60 баллов и выше в течение семестра считаются успевающими.

Присутствие студента необходимо для сообщения ему суммарной оценки и занесения ее в зачетную книжку и ведомость.

К сдаче экзамена допускаются студенты, которые выполнили график самостоятельной работы и набрали определенное количество необходимых баллов, из возможных 50, но не менее 25. Такого количества достаточно для допуска к экзамену, согласно решения дисциплинарной комиссии.

Студенты, которые в течение семестра работали не ритмично, нарушали график учебного процесса и не набрали необходимого количества баллов, считаются неуспевающими. Такие студенты имеют возможность получить зачетные 60–100 баллов во время сессии. Для сдачи экзамена студент должен получить допуск.

Когда студент набирает 60 (и более) баллов по результатам работы в семестре, но не полностью выполнил график самостоятельной работы, то есть не отработал практическую работу или расчетное задание, то такому студенту не засчитывается весь модуль и он считается должником. Об этом предупреждается студент. Такой студент имеет право сдавать не весь материал дисциплины, а лишь ее часть, то есть задолженности по модулю. Для студента, который выполнил график самостоятельной работы, но не получил необходимое количество зачетных баллов по одному из модулей дисциплины, предоставляется возможность, во время сессии добрать это количество баллов, чтобы считаться успевающим.

 

 

 

 

 

 

 

Оценка элементов модулей дисциплины

«Численные методы»

 

Модуль №1

1.      Проработка  лекций  № 1 - 4

2.      Подготовка к выполнению практической работы № 1

3.      Подготовка к выполнению практической работы № 2

4.      Подготовка к выполнению практической работы № 3

5.      Подготовка к защите модуля № 1 по лекциями № 1 - 4

6.      Выдача семестрового задания, с. 36

 

1.      Проработать лекции № 1 - 4 по плану лекции.

При проработке лекции необходимо прочитать ее, выучить основные определения,  термины и формулы, ответить на контрольные вопросы, которые есть после каждой лекции. Если возникли вопросы, более плотно разобрать вопрос по литературе, указанной в действующей методике, или обратиться за консультацией к преподавателю.

[3] с. 3 - 29

2. Практическая работа № 1 по теме «Обращение матрицы методом разбиения ее на клетки»

Для данной работы нужно выполнить расчетное задание по литературе [2] c.13-15, где дано объяснение выполнения работы и варианты индивидуального задания, дать ответы на контрольные вопросы, которые есть после лекции к этой практической работе.

3. Практическая работа № 2 по теме «Решение систем линейных уравнений методом итераций»

Для данной работы нужно выполнить расчетное задание по литературе [2] c.49-54, где дано объяснение выполнения работы и варианты индивидуального задания, дать ответы на контрольные вопросы, которые есть после лекции к этой практической работе.

4. Практическая работа № 3 по теме «Решения систем линейных уравнений методом Зейделя»

Для данной работы нужно выполнить расчетное задание по литературе [2] c.49-54, где дано объяснение выполнения работы и варианты индивидуального задания, дать ответы на контрольные вопросы, которые есть после лекции к этой практической работе.

5. Защита модуля № 1

Контрольные вопросы модуля № 1

Защита модуля проводится тестовым контролем согласно лекциям № 1 – 4

1. В каких утверждениях говориться о приближенных числах? Выберите все правильные ответы

1. В книге 582 страницы

2. Вес коробки 50 г

3. В лесу около 50000 деревьев

4. Ширина дома 14,25

2. Что называется приближенным числом?

1. Число, незначительно отличающееся от точного числа и заменяющее его в вычислениях

2. Число, округленное до трех знаков после запятой

3. Число, не дающее истинного значения величины числа

4. Число, полученное в результате действий над числами

3. На какие группы можно подразделить погрешности? Выберите все правильные ответы

1. Исходные

2. Относительные

3. Погрешности округления

4. Остаточные

4. Абсолютной погрешностью приближенного числа а называют:

1.

2.

3.

4.

5. Предельной абсолютной погрешностью приближенного числа а называют:

1.

2.

3.

4.

6. Относительной погрешностью δ_а  приближенного числа а называют:

1.

2.

3.

4.

7. Предельной относительной погрешностью δ^*_а  приближенного числа а называют:

1.

2.

3.

4.

8. Чему равен определитель второго порядка матрицы А? Выберите все правильные ответы

1. Произведению элементов главной диагонали минус произведение элементов побочной диагонали

2.

3. Произведению элементов побочной диагонали минус произведение элементов главной диагонали

4.

9. Что называют рангом матрицы

1. Рангом матрицы называют наибольший порядок миноров данной матрицы, отличных от нуля

2. Рангом матрицы называют наименьший порядок миноров данной матрицы, отличных от нуля

3. Определитель матрицы отличный от нуля

4. Определитель обратной матрицы

10. Матрица называется обратной по отношению к данной, если:

1. А × А^-1 = 0

2. А × А^-1 = А^-1 × А = Е

3. А - А^-1 = 0

4. Нет ни одного правильного ответа

11. Под абсолютной величиной матрицы А понимают:

1. Определитель матрицы А

2. Матрица, где все элементы записаны с противоположным знаком

3. Матрица, где все элементы есть модули элементов матрицы А

4. Число, равное произведению всех элементов матрицы А

12. Первой нормой матрицы А является:

1. Максимальная сумма модулей элементов матрицы по столбцам

2. Максимальная сумма модулей элементов матрицы по строкам

3. Корень квадратный из суммы квадратов модулей всех элементов матрицы

4. Сумма квадратов модулей всех элементов матрицы

13. Второй нормой матрицы А является:

1. Максимальная сумма модулей элементов матрицы по столбцам

2. Максимальная сумма модулей элементов матрицы по строкам

3. Корень квадратный из суммы квадратов модулей всех элементов матрицы

4. Сумма квадратов модулей всех элементов матрицы

14. Третьей нормой матрицы А является:

1. Максимальная сумма модулей элементов матрицы по столбцам

2. Сумма квадратов модулей всех элементов матрицы

3. Максимальная сумма модулей элементов матрицы по строкам

4. Корень квадратный из суммы квадратов модулей всех элементов матрицы

15. Первой нормой вектора Х является:

1. Сумма модулей координат вектора

2. Максимальная из координат вектора, взятая по модулю

3. Корень квадратный из суммы квадратов модулей координат вектора

4. Сумма квадратов модулей всех элементов вектора

16. Второй нормой вектора Х является:

1. Сумма модулей координат вектора

2. Корень квадратный из суммы квадратов модулей координат вектора

3. Максимальная из координат вектора, взятая по модулю

4. Сумма квадратов модулей всех элементов вектора

17. Третьей нормой вектора Х является:

1. Сумма модулей координат вектора

2. Максимальная из координат вектора, взятая по модулю

3. Корень квадратный из суммы квадратов модулей координат вектора

4. Сумма квадратов модулей всех элементов вектора

18. Решением системы линейных уравнений называется:

1. Любая совокупность чисел, которая будучи подставленной на место неизвестных в уравнения данной системы, обращает все эти уравнения в нули

2. Любые числа, которые можно подставить в уравнения системы

3. Любая совокупность чисел, которая будучи подставленной на место неизвестных в уравнения данной системы, обращает все эти уравнения в тождества

4. Нет ни одного правильного ответа

19. В чем заключается метод Гаусса?

1. В элементарных преобразованиях системы уравнений

2. В последовательном исключении неизвестных

3. В прибавлении (вычитании) к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое отличное от нуля число

4. В выражении одних неизвестных через другие

20. Когда применим метод Гаусса?

1. При условии, что все ведущие коэффициенты системы отличны от нуля

2. При условии, что все ведущие коэффициенты системы равны нулю

3. При условии, что все ведущие коэффициенты системы равны единице

4. При условии, что все ведущие коэффициенты системы любые числа

21. Чему равен определитель системы линейных уравнений по схеме Гаусса?

1. Произведению первых коэффициентов системы

2. Произведению всех коэффициентов системы

3. Произведению коэффициентов побочной диагонали системы

4. Произведению ведущих элементов схемы единственного деления

22. Что позволяют получать приближенные методы решения систем линейных уравнений?

1. Значения корней системы с заданной точностью

2. Значения корней системы с заданной точностью в виде предела последовательности некоторых векторов

3. Значения корней системы с заданной точностью в виде последовательности некоторых векторов

4. Нет ни одного правильного ответа

23. Какие методы приближенных решений систем линейных уравнений вы знаете? Выберите все правильные ответы.

1. Метод итераций

2. Метод Гаусса

3. Метод Зейделя

4. Метод исключения неизвестных

24. Что принимают за нулевое приближение в методе итераций?

1. Столбец единиц

2. Столбец нулей

3. Столбец свободных членов

4. В этом методе нет нулевого приближения

25. Когда заканчивается процесс вычислений по методу итераций?

1. Этот процесс бесконечный

2. Когда получена заданная точность решения системы уравнений

3. Когда полученное решение системы уравнений имеет три знака после запятой

4. В любой момент

26.   Формула для вычисления приближений по методу итераций имеет вид:

1.

2.

3.

4.

27. Условия сходимости итерационного процесса. Выберите все правильные ответы:

1.

2.

3.

4.

28. Оценка погрешности метода итераций находится по формуле:

1.

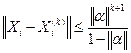
2.

3.

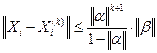
4. Нет ни одного правильного ответа

 

29. Условия сходимости метода Зейделя. Выберите все правильные ответы:

1.

2.

3.

4.

30. Оценка погрешности метода итераций находится по формуле:

1.

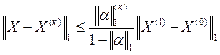
2.

3.

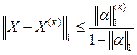
4. Нет ни одного правильного ответа

31. Чему равна абсолютная погрешность алгебраической суммы нескольких приближенных чисел? Выберите все правильные ответы

1. Абсолютная погрешность алгебраической суммы нескольких чисел не превышает суммы абсолютных погрешностей этих чисел.

2.

3. Абсолютная погрешность алгебраической суммы нескольких чисел равна сумме абсолютных погрешностей этих чисел.

4.

32. Чему равна предельная абсолютная погрешность алгебраической суммы нескольких приближенных чисел? Выберите все правильные ответы

1.

2.

3. Предельная абсолютная погрешность алгебраической суммы равна сумме предельных абсолютных погрешностей слагаемых.

4. Предельная абсолютная погрешность алгебраической суммы не превосходит суммы предельных абсолютных погрешностей слагаемых.

33. Чему равна относительная погрешность суммы нескольких приближенных чисел? Выберите все правильные ответы

1. Предельная относительная погрешность суммы слагаемых одного знака равна сумме предельных относительных погрешностей слагаемых.

2. Предельная относительная погрешность суммы слагаемых одного знака заключена между наименьшей и наибольшей предельными относительными погрешностями слагаемых.

3.

4.

34. Чему равна абсолютная погрешность произведения нескольких приближенных чисел? Выберите все правильные ответы

1.

2.

3.

4.

35. Чему равна относительная погрешность произведения нескольких приближенных чисел? Выберите все правильные ответы

1. Относительная погрешность произведения нескольких приближенных чисел, отличных от нуля,  не превышает суммы относительных погрешностей этих чисел.

2. Относительная погрешность произведения нескольких приближенных чисел, отличных от нуля,  равна сумме относительных погрешностей этих чисел.

3.

4.

36. Чему равна предельная относительная погрешность произведения нескольких приближенных чисел? Выберите все правильные ответы

1. Предельная относительная погрешность произведения не превосходит суммы предельных относительных погрешностей сомножителей

2.

3. Предельная относительная погрешность произведения равна сумме предельных относительных погрешностей сомножителей

4.

37. Чему равна абсолютная погрешность частного приближенных чисел? Выберите все правильные ответы

1.

2.

3.

4.

38. Чему равна относительная погрешность частного приближенных чисел? Выберите все правильные ответы

1. Относительная погрешность частного приближенных чисел не превышает суммы относительных погрешностей делимого и делителя.

2. Относительная погрешность частного приближенных чисел  равна сумме относительных погрешностей делимого и делителя

3.

4.

39. Чему равна предельная относительная погрешность частного приближенных чисел? Выберите все правильные ответы

1. Предельная относительная погрешность частного приближенных чисел не превосходит суммы предельных относительных погрешностей делимого и делителя

2.

3. Предельная относительная погрешность частного приближенных чисел равна сумме предельных относительных погрешностей делимого и делителя

4.

40. Чему равна абсолютная погрешность степени и корня приближенного числа? Выберите все правильные ответы

1.

2.

3.

4.

42. Чему равна предельная относительная погрешность m-й степени приближенного числа? Выберите все правильные ответы

1. Предельная относительная погрешность m-й степени  приближенного числа в m раз больше предельной относительной погрешности самого числа

2.

3. Предельная относительная погрешность m-й степени  приближенного числа в m раз меньше предельной относительной погрешности самого числа

4.

43. Чему равна предельная относительная погрешность корня m-й степени приближенного числа? Выберите все правильные ответы

1. Предельная относительная погрешность корня m-й степени приближенного числа в m раз больше предельной относительной погрешности подкоренного числа

2.

3. Предельная относительная погрешность корня m-й степени  приближенного числа в m раз меньше предельной относительной погрешности подкоренного числа

4.

Модуль №2

1.    Проработать лекции № 5 - 6

2.    Подготовка к выполнению практической работы № 4

3.    Подготовка к выполнению практической работы № 5

4.    Подготовка к выполнению практической работы № 6

5.    Подготовка к обязательной контрольной работе

6.    Подготовка к защите модуля № 2 по лекциям № 5 - 6

7.    Выполнение семестрового задания, с. 36

 

1.      Проработать лекции № 5 - 6 по плану лекции.

При проработке лекции необходимо прочитать ее, выучить основные определения, термины и формулы, ответить на контрольные вопросы, которые есть после каждой лекции. Если возникли вопросы, более плотно разобрать вопрос по литературе, указанной в действующей методике, или обратиться за консультацией к преподавателю.

[3] с. 29 - 43

2. Практическая работа № 4 по теме «Графическое отделение корней и уточнение их методом половинного деления»

В данной работе нужно выполнить расчетное задание, используя литературу [2] c.61-65, где дано объяснение  выполнения работы и варианты индивидуального задания, дать ответы на контрольные вопросы, которые есть после лекции к этой практической работе.

3. Практическая работа № 5 по теме «Графическое отделение корней и уточнение их методом хорд»

В данной работе нужно выполнить расчетное задание, используя литературу [2] c.65-68, где дано объяснение выполнения работы и варианты индивидуального задания, дать ответы на контрольные вопросы, которые есть после лекции к этой практической работе.

4. Практическая работа № 6 по теме «Графическое отделение корней и уточнение их методом касательных»

В данной работе нужно выполнить расчетное задание, используя литературу [2] c.68-69 где дано объяснение выполнения работы и варианты индивидуального задания, дать ответы на контрольные вопросы, которые есть после лекции к этой практической работе.

5. Обязательная контрольная работа

Контрольная работа состоит из трех задач и проводится в аудитории в течение двух академических часов. Работа выполняется на листах со штампом. Каждая задача обязательно должна иметь объяснение к решения. Перед контрольной работой студент должен повторить теоретический материал, рассмотреть примеры, которые приведены в учебниках и практических занятиях.

6. Защита модуля № 2

Контрольные вопросы к модулю № 2

Защита модуля проводится тестовым контролем согласно лекциям № 5 - 6

1. Что называется решением уравнения f(x) = 0?

1. Совокупность значений переменной х, при которых это уравнение превращается в верное равенство

2. Любые значения переменной х

3. Любые значения переменной х, которые можно подставить в уравнение

4. Нет ни одного правильного ответа

2. Для чего используется графический метод решения уравнений?

1. Для нахождения точного решения уравнения с помощью графика функции

2. Для выбора начального приближения корня уравнения и дальнейшего его уточнения

3. Чтобы научиться строить графики функций

4. Этот метод нигде не применяется

3. На какие этапы разбивается нахождение приближенных значений корней уравнения? Выберите все правильные ответы

1. Отделение корней

2. Решение уравнения

3. Уточнение корней до заданной степени точности

4. Построение графика функции

4. Что значит «отделить корни» уравнения?

         1. Написать все корни по порядку

         2. Нарисовать корни на числовой прямой

3. Разбить всю область допустимых значений на отрезки, в каждом из которых содержится один корень

4. Разбить всю область допустимых значений на отрезки, в каждом из которых могут находиться корни уравнения

5. Какие существуют способы отделения корней уравнения? Выберите все правильные ответы

1. Математический

2. Аналитический

3. Графический

4. Приближенный

6. Какие методы уточнения корней вы знаете? Выберите все правильные ответы

1. Метод проб

2. Метод касательных

3. Метод хорд

4. Метод итераций

7. В чем заключается метод проб?

1. В разбиении отрезка пополам и выборе того отрезка, на котором функция принимает значения одинаковых знаков

2. В разбиении отрезка и выборе того отрезка, на котором функция принимает значения одинаковых знаков

3. В разбиении отрезка и выборе того отрезка, на котором функция принимает значения разных знаков

4. В разбиении отрезка пополам и выборе того отрезка, на котором функция принимает значения разных знаков

8. До каких пор продолжается деление отрезка в методе проб?

1. До тех пор, пока левый край отрезка не будет корнем уравнения заданной точности

2. До тех пор, пока середина отрезка не будет корнем уравнения заданной точности

3. До тех пор, пока правый край отрезка не будет корнем уравнения заданной точности

4. Этот процесс продолжается бесконечно

9. Какое условие должно выполнятся для нахождения корня уравнения заданной точности методом проб?

1.

2.

3. Не проверяется ни какого условия

4.

10. В чем заключается метод хорд?

1. В замене на достаточно малом отрезке дуги кривой стягивающей ее хордой

2. В замене на достаточно малом отрезке дуги кривой стягивающей ее касательной

3. В замене каждого отрезка стягивающей его хордой

4. В замене каждого отрезка стягивающей его касательной

11. Каким правилом пользуются при выборе формул в методе хорд?

1. Неподвижным концом отрезка является тот, для которого знак функции отличается от знака второй производной

2. Неподвижным концом отрезка является тот, для которого знак функции совпадает со знаком второй производной

3. Неподвижным концом отрезка является тот, для которого знак функции совпадает со знаком первой производной

4. Неподвижным концом отрезка является тот, для которого знак функции отличается от знака первой производной

12. Какое условие должно выполнятся для нахождения корня уравнения заданной точности методом хорд?

1.

2.

3. Не проверяется ни какого условия

4.

13. Когда справедливы формулы оценки погрешности для метода хорд?

1. Если М = 2m, где ,

2. Если М > 2m, где ,

3. Если М ≤ 2m, где ,

4. Если М ≠ 2m, где ,

14.  В чем заключается метод касательных?

1. В замене на достаточно малом отрезке дуги кривой стягивающей ее хордой

2. В замене на достаточно малом отрезке дуги кривой касательной к этой кривой

3. В замене каждого отрезка стягивающей его хордой

4. В замене каждого отрезка стягивающей его касательной

15. Каким правилом пользуются при выборе формул в методе касательных?

1. Подвижным концом отрезка является тот, для которого знак функции отличается от знака второй производной

2. Подвижным концом отрезка является тот, для которого знак функции совпадает со знаком второй производной

3. Подвижным концом отрезка является тот, для которого знак функции совпадает со знаком первой производной

4. Подвижным концом отрезка является тот, для которого знак функции отличается от знака первой производной

16. Какое условие должно выполнятся для нахождения корня уравнения заданной точности методом касательных?

1.

2.

3. Не проверяется ни какого условия

4.

17. Какие используют формулы для оценки погрешности метода касательных?

1.

2.

3.

4.

18. Какая последовательность чисел называется сходящейся?

1. Если она стремиться к нулю

2. Если все ее члены отрицательные

3. Если все ее члены положительные

4. Если она имеет предел

19. В чем заключается метод итераций для решения уравнений?

1. Подвижным концом отрезка является тот, для которого знак функции отличается от знака второй производной

2. Неподвижным концом отрезка является тот, для которого знак функции совпадает со знаком второй производной

3. Привести уравнение к виду х = φ(х) и проверить условие для лучшей сходимости итерационного процесса

4. Подвижным концом отрезка является тот, для которого знак функции совпадает со знаком второй производной

20. Условия сходимости итерационного процесса?

1.

2.

3.

4.

21. Какое условие должно выполнятся для нахождения корня уравнения заданной точности методом итераций?

1.

2.

3.

4.

22. Для чего применяют метод Ньютона?

1. Для решения систем трех уравнений

2. Для решения систем двух уравнений

3. Для решения уравнений

4. Для решения неравенств

23. Как графически найти корни уравнения у = f(x)?

1. Построить график функции у = f(x)

2. Построить график функции f = у(x)

3. Найти точки пересечения кривой с осью ОУ

4. Найти точки пересечения кривой с осью ОХ

24. Что необходимо находить при отделении корней аналитическим методом?

1. Найти вторую производную, критические точки и определить интервалы, на которых функция принимает значения одинаковых знаков

2. Найти вторую производную, критические точки и определить интервалы, на которых функция принимает значения противоположных знаков

3. Найти первую производную, критические точки и определить интервалы, на которых функция принимает значения противоположных знаков

4. Найти первую производную, критические точки и определить интервалы, на которых функция принимает значения одинаковых знаков

25. По какой формуле находятся корни уравнения методом проб?

1.

2.

3.

4.

26. По каким формулам находятся корни уравнения методом хорд, если

f ^‘ (x) ∙ f ^‘’(x) >0? Выберите все правильные ответы

1.

2.

3.

4.

27. По каким формулам находятся корни уравнения методом хорд, если

f ^‘ (x) ∙ f ^‘’(x) <0? Выберите все правильные ответы

1.

2.

3.

4.

28.  По каким формулам находятся корни уравнения методом касательных, если f ^‘ (x) ∙ f ^‘’(x) >0? Выберите все правильные ответы

1.

2.

3.

4. Нет правильного ответа

29. По каким формулам находятся корни уравнения методом касательных, если f ^‘ (x) ∙ f ^‘’(x) <0? Выберите все правильные ответы

1.

2.

3.

4. Нет правильного ответа

30. Как графически решить систему двух уравнений?

1. На глаз определить точки пересечения графиков функций

2. Построить графики уравнений в одной плоскости и найти их точки пересечения

3. Построить графики уравнений на разных чертежах и наложить один на другой

4 . Нет правильного ответа

 

Модуль №3

                          1.  Проработать лекции № 7 - 8

                          2.  Подготовка к выполнению практической работы № 7

                          3.  Подготовка к выполнению практической работы № 8

                          4.  Подготовка к выполнению практической работы № 9

                          5.  Подготовка к выполнению практической работы № 10

                          6.  Подготовка к защите модуля № 3 по лекциям № 7 - 8

                          7.  Сдача семестрового задания, с. 36

 

1.      Проработать лекции № 7 - 8 по плану лекции.

При проработке лекции необходимо прочитать ее, выучить основные определения,  термины и формулы, ответить на контрольные вопросы, которые есть после каждой лекции. Если возникли вопросы, более плотно разобрать вопрос по литературе, указанной в действующей методике, или обратиться за консультацией к преподавателю.

[3] с. 43 - 57

2. Практическая работа № 7 по теме «Вычисления значений функции с помощью интерполяционного многочлена Лагранжа»

В данной работе нужно выполнить расчетное задание, используя литературу [2] c.109-111, где дано объяснение выполнения работы и варианты индивидуального задания, дать ответы на контрольные вопросы, которые есть после лекции к этой практической работе.

3. Практическая работа № 8 по теме «Вычисления значений функции с помощью первой и второй интерполяционных формул Ньютона»

В данной работе нужно выполнить расчетное задание, используя литературу [2] c.113-118, где дано объяснение выполнения работы и варианты индивидуального задания, дать ответы на контрольные вопросы, которые есть после лекции к этой практической работе.

4. Практическая работа № 9 по теме «Вычисления определенных интегралов по формуле прямоугольников»

В данной работе нужно выполнить расчетное задание, используя литературу [2] c.127-131, где дано объяснение выполнения работы и варианты индивидуального задания, дать ответы на контрольные вопросы, которые есть после лекции к этой практической работе.

6. Практическая работа № 10 по теме «Вычисления определенных интегралов по формулам трапеций и Симпсона»

В данной работе нужно выполнить расчетное задание, используя литературу [2] c.131-136, где дано объяснение выполнения работы и варианты индивидуального задания, дать ответы на контрольные вопросы, которые есть после лекции к этой практической работе.

7. Защита модуля № 3

 

Контрольные вопросы к модулю № 3

Защита модуля проводится тестовым контролем согласно лекций № 7 - 8

1. Какие задачи формулируются как задачи интерполирования?

1. Задачи, в которых необходимо найти значения функции в точках, отличных от табличных значений

2. Задачи, в которых необходимо найти значения функции в точках, которые даны в таблице

3. Любые математические задачи

4. Нет ни одного правильного ответа

2. Какой процесс называется интерполированием?

1. Процесс нахождения точного значения функции в точках, отличных от узлов интерполяции

2. Процесс нахождения точного значения функции в узлах интерполяции

3. Процесс нахождения приближенного значения функции в точках, отличных от узлов интерполяции

4. Нет ни одного правильного ответа

3. Какой процесс называется экстраполированием?

1. Процесс нахождения точного значения функции в точках, которые находятся за пределами отрезка интерполирования

2. Процесс нахождения точного значения функции в узлах интерполяции

3. Процесс нахождения приближенного значения функции в точках, которые находятся за пределами отрезка интерполирования

4. Процесс нахождения приближенного значения функции в точках, отличных от узлов интерполяции

4. В чем состоит геометрический смысл интерполирования?

1. В построении точек на плоскости

2. В построении кривой, проходящей через данные точки

3. В построении графика функции

4. В построении схемы

5. В чем заключается процесс интерполирования функции?

1. В нахождении аналитического выражения табулированной функции

2. В нахождении приближенного выражения функции

3. В выполнении шагов интерполяции

4. В выполнении определенного алгоритма

6. Что называют узлами интерполяции?

1. Любые точки из области определения

2. Любые точки, не принадлежащие области определения

3. Точки, в которых неизвестны значения функции

4. Точки, в которых известны значения функции

7. Какой многочлен называют интерполяционным?

1. Любой многочлен

2. Многочлен, взятый в качестве приближенной функции, для поиска аналитического выражения табулированной функции

3. Многочлен, выбранный в качестве точной функции

4. Нет ни одного правильного ответа

8. Какие узлы называют равноотстоящими?

1. Точки, которые располагаются через разный интервал друг от друга

2. Точки, произвольно отстоящие друг от друга

3. Точки, которые располагаются через одинаковый интервал друг от друга

4. Любые точки из области определения

9. Какие узлы называют неравноотстоящими?

1. Точки, которые располагаются через равный интервал друг от друга

2. Точки, произвольно отстоящие друг от друга

3. Точки, которые располагаются через одинаковый интервал друг от друга

4. Любые точки из области определения

10. Что называют шагом интерполяции?

1. Величина интервала, через который располагаются узлы интерполяции

2. Величина интервала, через который располагаются значения функции

3. Любой произвольный интервал расположения чисел

4. Длина узла интерполяции

 

11. Как записывается интерполяционный многочлен Лагранжа?

1.

2.

3.

4.

12. Как записывается интерполяционный многочлен Лагранжа для равноотстоящих узлов интерполяции?

1.

2.

3.

4.

13. Что обозначают буквой h в интерполяционных многочленах?

1. Расстояние

2. Высота интерполяции

3. Число шагов интерполяции

4. Шаг интерполяции

14. Что обозначают буквой q в интерполяционных многочленах?

1. Расстояние

2. Высота интерполяции

3. Число шагов интерполяции

4. Шаг интерполяции

15. Как записывается первая интерполяционная формула Ньютона для равноотстоящих узлов интерполяции?

1.

2.

3.

4.

16. Как записывается вторая интерполяционная формула Ньютона для равноотстоящих узлов интерполяции?

1.

2.

3.

4.

17. Как записывается интерполяционная формула Ньютона для неравноотстоящих узлов интерполяции?

1.

2.

3.

4.

18. В чем преимущество интерполяционной формулы Ньютона над интерполяционной формулой Лагранжа?

1. Добавление новых узлов интерполяции приводит к проведению расчетов заново

2. Нет преимуществ

3. Расчеты по этим формулам не отличаются, сколько бы узлов интерполяции не добавляли

4. Добавление новых узлов интерполяции не приводит к проведению расчетов заново

19. В каких случаях прибегают к численному дифференцированию?

1. Когда не хочется вычислять производную

2. Когда методы дифференциального исчисления к исследованию функции применить нельзя

3. Когда методы дифференциального исчисления к исследованию функции можно применить

4. Таких случаев нет

20. Что необходимо определить по задаче численного дифференцирования?

1. Аналитическое выражение производной

2. Аналитическое выражение функции

3. Вычислить интеграл

4. Вычислить производную

22. В каких случаях прибегают к численному интегрированию?

1. Когда не хочется вычислять интеграл

2. Когда первообразную F(х) не удается выразить через элементарные функции

3. Когда первообразную F(х) можно выразить через элементарные функции

4. Таких случаев нет

23. Что необходимо определить по задаче численного интегрирования?

1. Найти определенный интеграл на отрезке [a,b], если подынтегральная функция на отрезке [a,b] задана таблично.

2. Аналитическое выражение функции

3. Вычислить интеграл

4. Вычислить производную

24. Какие формулы называются квадратурными?

1. Формулы приближенного дифференцирования

2. Формулы приближенного интегрирования

3. Формулы приближенного вычисления

4. Формулы сокращенного умножения

25. Какие методы приближенного вычисления определенного интеграла вы использовали на практике? Выберите все правильные ответы

1. Метод прямоугольников

2. Метод квадратов

3. Метод трапеций

4. Метод парабол

26. Какой вид имеет формула левых прямоугольников?

1.

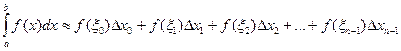
2.

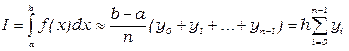
3.

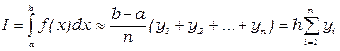
4.

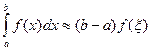
27. Какой вид имеет формула правых прямоугольников?

1.

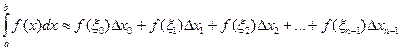
2.

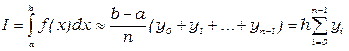
3.

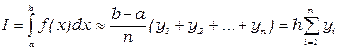
4.

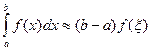
28. Какой вид имеет формула Симпсона?

1.

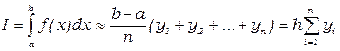
2.

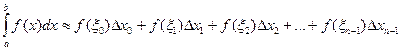
3.

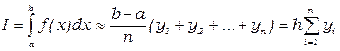
4.

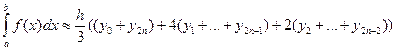
29. Какой из методов численного интегрирования наиболее точный?

1. Метод прямоугольников

2. Метод квадратов

3. Метод трапеций

4. Метод парабол

30. Чему равно h в методе прямоугольников?

1. h = 1

2. h = (b-a)/n

3. h = (b-a)

4. h = (b-a)/2n

 

31. Чему равно h в методе Симпсона?

1. h = 1

2. h = (b-a)/n

3. h = (b-a)

4. h = (b-a)/2n

 

8. Семестровое задание

Правила оформления семестрового задания даны в введении данного методического пособия. Согласно своего варианта выполните следующие задания:

1. Действия над приближенными числами. Оценка погрешностей результата, [ 1 ] с. 6

2. Обращение матрицы методом разбиения ее на клетки

(№ варианта + 4),  [ 1 ] с. 13

3. Решение систем линейных уравнений по формулам Крамера и с помощью обратной матрицы, [ 1 ] с. 22

4. Графическое и аналитическое отделение корней уравнения и уточнение любого из них методами проб, хорд и касательных, [ 1 ] с. 69

5. Вычислить определенный интеграл по формулам прямоугольников, трапеций и Симпсона, [ 1 ] с.136

 

 

Литература

Базовая

1. Н.И. Данилина, Н.С. Дубровская, О.П. Квашня. Численные методы. Учебник для техникумов. М., «Высш. школа». 1976. –  368 с.: ил.

2. Г.Н. Воробьева, А.Н. Данилова. Практикум по вычислительной математике: Учебн. пособие для техникумов. – 2-ое изд., перераб. и доп. – М.: Высш. школа, 1990. – 208 с.: ил.

Дополнительная

3. Б.П. Демидович, И.А. Марон. Основы вычислительной математики. – М.: Физматгиз, 1960. – 659с.

4. Н.В. Копченова, И.А. Марон. Вычислительная математика в примерах и задачах. М.: Наука, 1982. – 366 с.