Методические рекомендации к уроку №1 (1)

Методические рекомендации к проведению урока

Тема урока: Квадратный трехчлен

Тип урока: урок изучения новой темы

Цели обучения:

8.2.1.1 усвоить понятие корня квадратного трехчлена;

8.2.1.2 выделять полный квадрат двучлена из трехчлена;

Цели урока:

Учащиеся

• знают понятие корня квадратного трехчлена;
• умеют выделять полный квадрат двучлена из квадратного трехчлена в несложных случаях.

Структура урока

1.    Организационный момент.

2.    Актуализация пройденного материала.

3.    Целеполагание

4.    Объяснение новой темы

a.       Введение определения квадратного трехчлена

b.      Выделение полного квадрата двучлена из трехчлена

5.    Закрепление изученного

6.    Подведение итогов урока. Рефлексия

Теоретический материал к уроку, определения к понятиям и др.

Определение. Многочлен вида ax²+bx+c  называется трехчленом, где х- переменная; a,b,c – коэффициенты и а≠0. Как и в квадратном уравнении a называется первым коэффициентом, b - вторым коэффициентом, с – свободным членом.

Для нахождения наибольшего и наименьшего значения квадратного трехчлена из него необходимо выделить полный квадрат. Затем определить знак первого коэффициента квадратного трехчлена.

При а > 0 квадратный трехчлен обладает наименьшим значением, при а < 0 - наибольшим значением.

 Корнем квадратного трехчлена называется число, обращающее его в нуль.

Инструкции к демонстрациям и технике безопасности.

Демонстрация материала осуществляется с помощью презентации PowerPoint. Слайды презентации содержат анимации, которые позволяют поэтапно вывести на экран решения и ответы к предложенным заданиям. Поэтому при показе презентации следует делать паузы после демонстрации заданий и постановки вопросов, давая учащимся время на их выполнение и обдумывание ответов.

Дополнительные методические рекомендации по организации урока.

Данный урок основан на активных методах обучения, прежде чем ввести новое понятие учащимся предлагаются определенные вопросы и задания, затем на основании их ответов и решений учитель совместно с учащимися вводит новый материал. В ходе парной/ групповой/фронтальной работы необходимо способствовать тому, чтобы каждый учащийся смог прокомментировать свое решение. Уделяйте внимание паузам для обдумывания (1-2 мин) после того, как будет задан вопрос.

Дополнительные разноуровневые (на дифференциацию) задания.

Базовый уровень

Запишите квадратный трехчлен в виде

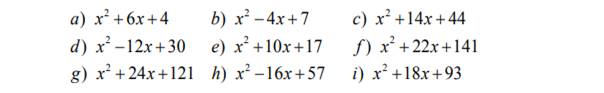
Продвинутый уровень

Известно, что стороны прямоугольника 5 см и 3 см. Если уменьшить его большую сторону на а см, а меньшую увеличить на а см, то при каком значении а площадь прямоугольника принимает наибольшее значение?

Рекомендации по формативному оцениванию.

Формативное оценивание производится на каждом этапе урока (самооценивание, оценивание учителем по критериям). Оценка путем наблюдения за вовлечением учеников в работу при выполнении заданий и за участием в диалогах. Прогресс, ответную реакцию на задания в парах, в группах необходимо отслеживать для того, чтобы оценить вклад каждого ученика и выявить наличие ошибок для их дальнейшей коррекции.

Ответы, критерии к заданиям, дополнительные материалы к уроку.

Ответы к заданиям будут полезны для организации самооценивания или взаимооценивания учащихся.

Ответы к приложению 1.

Ключевое слово: Ермеков

Ответы к приложению 2.

№1. а) 5 и 3;  б) 0 и 0,5; в) 2 и -2.

№2. а) ;   б) ;   в) .

№3. b=2

Критерии оценивания к каждому блоку заданий прописаны в приложениях к уроку, а также указаны в краткосрочном плане.

Список полезных ссылок и литературы.

Алгебра. 8-класс: Учебник для 8 класса общеобразовательной школы с русским языком обучения/ А.Н. Шыныбеков – 3-издание. – Алматы: «Атамұра», 2012. 288 с.

Алгебра. 8 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 10-е изд., испр. — М. : Мнемозина,

2010.

Лебединцева Е.А., Беленкова Е.Ю. Алгебра 8 класс. Задания для обучения и развития учащихся. Учебное пособие. М.: Интеллект-Центр, 2013. 108-бет.