Методические рекомендации по обучению решению нестандартных задач по математике в начальной школе

Методические рекомендации по обучению решению нестандартных задач по математике в начальной школе

Как показал школьный опыт, процесс обучения детей младших классов умению решать нестандартные арифметические задачи можно разделить на два этапа. На первом этапе необходимо провести специальную работу по выводу и осознанию общих методов к решению задач таких типов. Детям нужно заранее усвоить процесс решения любых арифметических задач (читает задачу; выделит, что известно и что необходимо узнать и т. д.); познакомиться со способами работы на каждой ступени решения задач (виды наглядной трактовки задач, поиск их решений, проверка решения задачи и др.). На следующем этапе ученики употребляют ранее сформулированные общие способы в процессе самостоятельной попытки решить конкретную задачу.

Рассмотрим методические предложения о том, как можно организовать работу по обучению решению нестандартных задач. В описании методических предложений можно выделить несколько типов задач. Задачи всех типов подчиняются определенной цели. Первая задача одного из типов решается совместно с учителем (по той причине, что она сложнее, чем остальные задачи), она помогает найти метод, с помощью которого можно будет решить задачу. На следующих задачах ученики практикуются применять метод, сформулированный ранее, и выделяют ориентиры, которые позволяют решить, в каких случаях лучше всего применять этот метод.

Задачи первого типа формулируют первую рекомендацию для учащихся младших классов при решении нестандартных задач: для решения задачи предлагается построить к ней чертеж или рисунок. Нужно начинать с этой рекомендации, потому что учащиеся уже поняли это во время решения стандартных задач. Однако в этом случае необходимо рассмотреть ряд особенностей использования графических изображений. Во-первых, использование графических изображений при решении нестандартных арифметических задач поможет найти ответ, а порой часть неизвестных находится из чертежа без совершения арифметических действий. Во-вторых, в некоторых случаях может понадобиться сделать вспомогательные построения, то есть при решении задачи нужен будет сделать новые рисунки, учитывая полученные данные. Чертеж будет применяться также при использовании других способов решения нестандартных задач.

Задача1. Веревку длиной 12 м разрезали на 6 равных частей. Сколько разрезов сделали?

Прочитав задачу, младшие школьники должны ответить на вопрос, встречались ли они с такими задачами и умеют ли они их решать?

Если учащиеся думают, что они могут найти решение задачи, учителю необходимо дать им возможность найти ответ, оценить и убедиться в ошибочности своего решения (Разделив 12 на 6, мы выясним, что длина одной части равна 2 м. Но в задаче нужно узнать не длину одной части, а число разрезов. Следовательно, что решение задачи неправильно). После этого ученики могут снова сделать ошибочное заключение: «Сколько частей, столько и разрезов». Учитель предлагает проверить найденный ответ, нарисовав чертеж. Учащиеся обозначают верёвку как отрезок длиной в 12 клеток, разделяют его вертикальными черточками на 6 одинаковых частей. Посчитав количество сделанных черточек (разрезов), они поймут, что их 5, а не 6, как они думали до этого. Эту задачу ученики решили без выполнения арифметических действий. Ответ был найден по чертежу. Под рисунком дети пишут ответ на вопрос в задаче. Так, ученики делают вывод, что при решении неизвестной задачи полезно сделать рисунок, поскольку с помощью него можно найти правильный ответ.

Решение таких задач способствуют подтверждению этого вывода, сделанного во время поиска решения первой задачи. Учитель предлагает ученикам научиться решать арифметические задачи с помощью построения чертежей.

Задача 2. Ширина шторы для окна составляет 2 м 10 см. Необходимо пришить 8 колец на одинаковом расстоянии (первое и последнее кольца должны быть на краях шторы). Сколько сантиметров нужно отставить между кольцами?

При решении задач подобного типа, можно объяснить детям что иногда часть данных лучше всего искать с помощью чертежей, а часть — с помощью арифметических действий.

Используя ранее сделанный вывод, дети выполняют схематический чертеж к этой задаче. Ученики отмечают засечкой первое кольцо, отмеряют отрезок любой длины, отмечают вторую засечку, и так действуют, пока не отметят 8 засечек. По выполненному схематическому чертежу считают число равных частей, на которые 8 колец разделят штору.

Чтобы дать ответ на вопрос задачи, детям будет необходимо только разделить всю ширину шторы на 7 одинаковых частей: 210:7=30 (см).

Задача 3 . В гараже стояло 6красных машин,а зелёных на7больше чем красных, а синих на 4 меньше, чем зелёных.

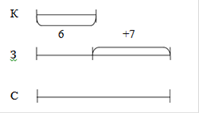Модели.

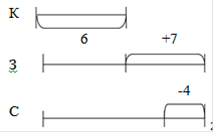Задание: определи, к каким машинам относятся чертежи?

Необходимо также познакомить детей, с тем что иногда при решении задачи надо делать дополнительные построения и перестраивать чертежи учитывая полученные данные при решении задачи.

С помощью задач второго типа можно вывести следующее предложение для учеников во время решения нестандартных задач: для нахождения ответа, бывает нужно определить дополнительный элемент или часть.

Задача1. Разложить 45 карандашей в 4 пенала так, что если число карандашей в 3-ем пенале увеличить в 2 раза, а в 4-ом уменьшить в 2 раза, а в первом и втором не менять их количество, то в каждом пенале будет одно и то же число карандашей.

Сначала школьники изображают первый схематический чертеж.

При анализе схематического чертежа, ученики могут обратить внимание на то, что на нём присутствуют одинаковые отрезки, но не все. Учитель советует доделать чертеж, чтобы все отрезки имели одинаковые части, а после говорит, что в данном случае будет разумно определить дополнительный элемент — часть. Ученики примут число карандашей в 3-ем пенале за 1 часть, тогда число карандашей в 4-ом пенале составит 4 части, в 1-ом — 2 части и во 2-ом — 2 части. После этого производится арифметическое решение:

•        2+2+1+4=9 (ч.) - составляют 45 карандашей.

•        45:9=5 (шт.) - содержится в 1 части или количество карандашей в 3 пенале.

•        5*2=10 (к.) - количество карандашей в первом или во втором пенале.

•        5*4=20 (к.) - количество карандашей в четвертом пенале.

При поиске решения этой задачи пользовались несколькими приемами: строили и достраивали чертеж, вводили вспомогательный элемент. Его лучше ввести, когда на схематическом чертеже получены одинаковые отрезки.

В последующих задачах ученики упражняются в решении задач с введением вспомогательного элемента.

Задачи третьего типа .При решении этих задач предлагается ещё одна рекомендация для учеников младшего школьного возраста, применяемая при решении нестандартных задач: при поиске ответа на вопрос задачи можно пользоваться способом подбора.

Задача1. Сумма четырех различных чисел равна 13. Наименьшее из этих чисел на 5 меньше наибольшего. Найдите эти числа.

Учащиеся делают вывод, что этого сделать невозможно, поскольку в условии задачи ничего не сказано о числовых отношениях между вторым и третьим числом. Появляется проблема: возможно ли найти решение этой задачи? Быть может, в ней недостаточно данных? Педагог выдвигает предположение о том, что нужно использовать для решения данной задачи способ подбора.

Удобнее начинать рассуждать с наименьшего из чисел.

- Возьмем число 0. Тогда у нас получится: 0+ _ + _ + 5= 13. Попробуем подобрать пропущенные числа. Их сумма равна 13-5-0=8. Данные числа должны быть различными и меньше 5, но больше 0. Между 0 и 5 идут числа 1, 2, 3, 4. Среди этих чисел выбираем два, которые дают в сумме 6. Это числа 2 и 4. Проведем проверку. Для этого складываем эти четыре числа: 1 + 2 + 4 + 6 = 13. Получили соответствующую сумму.

Проверяем наличие иных вариантов ответа на вопрос задачи. Пробуем число 2: 2 + _ + _ + _ + 7 = 13. Сумма пропущенных чисел равна 4. Среди чисел 3, 4, 5, 6 нельзя выбрать два числа, которые дают в сумме 4 (сумма любых двух перечисленных чисел больше 4). Также проверяем число 3. Числа, начиная с 4, не нуждаются в проверке. Получаем ответ задачи: числа 1, 2, 4, 6.

Таким образом, при последовательном рассмотрении различных возможных вариантов подобрали те, которые подходят под все условия данной задачи. Данный способ рационален в том случае, если количество возможных вариантов маленькое.

При решении подобных заданий младшие школьники тренируются в применении способа подбора.

Задачи четвертого типа. В задачах данного типа учащимся предлагается следующая рекомендация: полезно переформулировать задачу, то есть сказать ее другими словами, чтобы она стала знакомой и понятной. При этом в большинстве случаев будет происходить перевод текста задачи на язык математики.

Задача1. Число груш в ящике двузначное. Их можно раздать поровну 2, 3 или 5 мальчикам, но нельзя раздать поровну 4 ребятам. Сколько груш в ящике? (Нужно указать наименьшее двузначное число.)

Вначале младшие школьники пробуют моделировать условие задачи, но у них возникают трудности. Поскольку на схематическом чертеже сложно изобразить, что 4 ребятам невозможно поровну раздать груши. Вследствие этого школьники переходят к применению способа подбора. Педагог предлагает, в первую очередь, переформулировать содержание задачи, для облегчения выполнения перебора. Задачу формулируют так: «Найди наименьшее двузначное число, которое делится на 2, 3, 5 и не делится на 4». После этого выполняют способ перебора.

Задачи пятого типа. Детям предлагается следующая рекомендация: условие или вопрос задачи можно разделить на части и решить задачу по частям.

Задача1. В два трамвая сели 123 пассажира. Затем из одного трамвая вышли 6 человек. Трое из них сели в другой трамвай, а остальные поехали на автобусе. После этого в трамваях стало пассажиров поровну. Сколько пассажиров было в каждом трамвае изначально?

Предлагается решать эту задачу следующем образом: нужно разбить её на две части для облегчения решения. Дети изучают первые три предложения задачи и анализируют их.

1)      6-3=3 (п.) - поехали на автобусе.

2)      123-3=120 (п.) - остались в двух трамваях.

3)      120 : 2 = 60 (п.) — стало в каждом трамвае.

Чтобы облегчить формулировку последней части задачи, можно переделать чертеж с применением найденных данных: «Из одного трамвая вышло 6 человек, и в нем осталось 60 человек. В другой трамвай сели 3 человека, и в нем стало 60 человек. Сколько человек было в каждом трамвае изначально?» — и заканчивают решение:

4) 60 + 6 = 66 (п.) — было в первом трамвае.

5) 60 – 3 = 57 (п.) — было во втором трамвае.

Бывает полезно разделить на части не условие, а вопрос задачи. Данный прием используется в задачах с большим числом разных объектов или действий с ними, с несколькими вопроса ми. В следующих задачах также можно использовать прием разбиения задачи на части.

Задачи шестого типа .Задачи данного типа рекомендуется решать задачу «с конца».

Задача1. Бабушка троих внучек оставила утром чашку вишни. Первой проснулась Маша, съела третью часть вишни и ушла. Второй проснулась Катя, она съел третью часть того, что было в чашке, и ушла. Позднее всех встала Ксюша. Она съела также третью часть вишни. После этого в чашке осталось 8 вишен. Сколько вишен бабушка утром положила в чашку?

Учитель предлагает начать решать задачу «с конца», так как известно, сколько вишен осталось в конце, когда три внучки съели вишни. Из чертежа видно, что 8 вишен — это всех вишен, которые были в чашке, когда встала Ксюша. Найдем, сколько вишен было в чашке, когда встала Ксюша: 8 : 2 3 = 12 (в.).  

12 вишен — это всех вишен, которые были в чашке, когда встала Катя. Найдем, сколько вишен было в чашке, когда встала Катя: 12 : 2 3 = 27 (в.). Делается вывод о том, что, решая «с конца», последовательно пришли к тому, что было в самом начале. Прием используется, когда в задаче известно число, полученное в конце выполнения каких-либо действий.

Задачи седьмого типа. Задачи данного типа рекомендуется решать задачу с использованием таблицы.

 Задача1. Бабушка вручила Кате купить в магазине 300 грамм конфет по цене 420 рублей за 1 кг, 400 грамм печенья по 380 рублей за 1 кг и три пирожных по 25 рублей за штуку. Какую сдачу Катя получит в кассе, если бабушка дала ей 500 рублей?

Найди стоимость каждого продукта, заполни таблицу и запиши ответ:

Задача 2. Марина решила пообедать в столовой. Сколько рублей сдачи она должна получить с 500 рублей, если выбрала гороховый суп, мясной пирожок и компот?

Задача 3. Семья Каримовых в субботу выехала в цирк на автобусе. В семье –  папа, мама, сын — второклассник Иван, дочь — четырехлетняя Катя и дедушка. Сколько денег семья Каримовых потратит на билеты в цирк и оплату проезда в автобусе, если цена билета в автобусе 17 рублей, у дедушки имеется пенсионный проездной билет, у Кати проезд бесплатный, а цены билетов для входа в цирк указаны у кассы?

КАССА

Цена билетов в цирк «Империя»:

Для взрослых (от 16 лет) — 250 рублей

Для детей (от 7-16 лет) — 150 рублей

Для пенсионеров и инвалидов — 100 рублей

Для детей (до 7 лет) — бесплатно

Заполни таблицу данными, выполнив нужные вычисления, и запиши ответ:

Задачи восьмого типа. Задачи данного типа рекомендуется решать с помощью предположения.

Задача 1. В магазине «Незнайка» продавались двухколесные самокаты и трехколесные велосипеды. Вовочка посчитал, что всего колес 26, а рулей — 11. Сколько было самокатов и велосипедов в магазине «Незнайка»?

Запиши в «окошках», какому способу рассуждения соответствует способ решения.

•        Пусть все 26 колес были от самокатов

•        Пусть все 11 рулей были от велосипедов

•        Пусть все 11 рулей были от самокатов

 Задача 2. У бабушки Вали в деревне жили гусята и кутята. Бабушка посчитала, что у них у всех было 26 лап и 8 голов. Сколько гусят и кутят было у бабушки Вали?

Заполни таблицу:

Как изменится количество всех лап, если одного гусенка заменить на одного кутенка?

Рассмотри другое решение и объясни его:

Пусть все 8 питомцев бабушки Вали были ___, тогда:

•        8*2=16 -

•        26-16=10 -

•        10:2=5 -

•        8-5=3 -

 Задача 3. На весенних каникулах дедушка каждый день со своими внуками решала задачи на логику. Каждый день каждый из внуков решал либо две, либо три таких задачи. Дина решала 25 задач, а Коля — 19. сколько дней они гостили у дедушки?

•        На сколько задач меньше решил Коля, чем Дина?

•        На сколько задач Дина могла решить больше за один день, чем Коля?

•        Сколько дней Коля решал меньше задач, чем Дина?

•        Сколько задач Дина решила за это время? ______ А Коля? _______

•        Составь решение из предложенных действий, указав их порядок, и запиши:

Задача 4. Петя купил букет из трёх тюльпанов. Сколько рублей сдачи он получит с купюры в 500 рублей?

Стоимость ромашки — 90 рублей;

Стоимость тюльпана — 130 рублей;

Стоимость розы — 50 рублей.

На сколько рублей букет из 5 роз дешевле букета из трех тюльпанов?

Какое наибольшее число ромашек мог бы купить Петя на свои деньги?

Таким образом, нами были разработаны следующие методические рекомендации по организации работы при обучении решению нестандартных задач:

- рекомендуется построить к ней чертеж или рисунок;

- необходимо ввести вспомогательный элемент или часть;

- при поиске ответа на вопрос задачи можно пользоваться способом подбора;

 - полезно переформулировать задачу, то есть сказать ее другими словами, чтобы она стала знакомой и понятной;

- условие или вопрос задачи можно разделить на части и решить задачу по частям;

- рекомендуется решать задачу «с конца»;

- решать задачу с использованием таблицы;

 - решать с помощью предположения.