
Государственное бюджетное профессиональное образовательное учреждение
«Каслинский промышленно-гуманитарный техникум»
ВЕРХНЕУФАЛЕЙСКИЙ ФИЛИАЛ
Методические РЕКОМЕНДАЦИИ
по выполнению практических (лабораторных) работ
по дисциплине
по специальности СПО 15.02.08 « Технология машиностроения»
форма обучения: очная
2020г.
|
СОГЛАСОВАНО на заседании предметно-цикловой комиссии Протокол № _____ от «____»____________2020г. Председатель ПЦК ______________ Г.В. Хорошайло
|
УТВЕРЖДАЮ: Заместитель директора по УР ___________ Н.Н.Ефанова
|
Методические рекомендации по выполнению практических работ учебной дисциплины Е.Н.01. Математика разработаны на основе рабочей программы по дисциплине Математика, в соответствии с ФГОС по профессии СПО 15.02.08
«Технология машиностроения»
Организация разработчик : Верхнеуфалейский филиал ГБПОУ «КПГТ»
Разработчик: Хусаинов Варис Галимжанович, преподаватель Верхнеуфалейского филиала ГБПОУ «КПГТ»первой категории.
СОДЕРЖАНИЕ
1 |
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА |
3 |
2 |
ПРАКТИЧЕСКАЯ РАБОТА № 1ДЕЙСТВИЯ С МАТРИЦАМИ |
6 |
3 |
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ПРОВЕДЕНИЮПРАКТИЧЕСКОЙ РАБОТЫ № 2ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ |
13 |
4 |
ПРАКТИЧЕСКОЙ РАБОТЫ № 3,4РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ РАЗЛИЧНЫМИ СПОСОБАМИ |
20 |
5 |
ПРАКТИЧЕСКОЙ РАБОТЫ № 5ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ, ЗАДАННЫМИ В АЛГЕБРАИЧЕСКОЙ ФОРМЕ |
32 |
6 |
ПРАКТИЧЕСКОЙ РАБОТЫ № 6,7ТЕМА: «ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ В ТРИГОНОМЕТРИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФОРМЕ» |
37 |
7 |
ПРАКТИЧЕСКОЙ РАБОТЫ № 8,9РЕШЕНИЕ ПРОСТЕЙШИХ ЗАДАЧ ТЕОРИИ ВЕРОЯТНОСТЕЙ |
39 |
8 |
ПРАКТИЧЕСКОЙ РАБОТЫ №10ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ДИФФЕРЕНЦИАЛОВ ВЫСШИХ ПОРЯДКОВ |
58 |
9 |
ПРАКТИЧЕСКОЙ РАБОТЫ № 11,12ИССЛЕДОВАНИЕ ФУНКЦИИ ПРИ ПОМОЩИ ПРОИЗВОДНЫХИССЛЕДОВАНИЕ И ПОСТРОЕНИЕ ГРАФИКОВ СЛОЖНЫХ ФУНКЦИЙ |
65 |
10 |
ПРАКТИЧЕСКОЙ РАБОТЫ № 13,14ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ |
72 |
11 |
ПРАКТИЧЕСКОЙ РАБОТЫ № 15РЕШЕНИЕ ПРИКЛАДНЫХ ЗАДАЧ (ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА) |
80 |
Практическое занятие - это форма организации учебного процесса, предполагающая выполнение обучающимися по заданию и под руководством преподавателя одной или нескольких практических работ.
Дидактическая цель практических работ - формирование у обучающихся профессиональных умений, а также практических умений, необходимых для изучения последующих учебных дисциплин, а также подготовка к применению этих умений в профессиональной деятельности.
Так, на практических занятиях по математике у обучающихся формируется умение решать задачи, которое в дальнейшем должно быть использовано для решения профессиональных задач по специальным дисциплинам.
В ходе практических работ обучающиеся овладевают умениями пользоваться информационными источниками, работать с нормативными документами и инструктивными материалами, справочниками, выполнять чертежи, схемы, таблицы, решать разного рода задачи, делать вычисления.
Задачи, которые решаются в ходе практических занятий по математике:
1) расширение и закрепление теоретических знаний по математике, полученных в ходе лекционных занятий;
2) формирование у обучающихся практических умений и навыков, необходимых для успешного решения задач по математике;
3) развитие у обучающихся потребности в самообразовании и совершенствовании знаний и умений в процессе изучения математики;
4) формирование творческого отношения и исследовательского подхода в процессе изучения математики;
5) формирование профессионально-значимых качеств будущего специалиста и навыков приложения полученных знаний в профессиональной сфере.
Критерии оценки:
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможны некоторые неточности, описки, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка, или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущено не более двух ошибок или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Преподаватель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
Цель работы:
Используя теоретический материал и образцы решения задач, решить примеры по теме «Действия с матрицами»
Перечень справочной литературы :
1. Математика: учебник для студентов образовательных учреждений СПО/С.Г. Григорьев, С.В. Иволгина; под редакцией В.А. Гусева – 10-е изд., стер. – М.: Издательский центр «Академия». 2014. – 416 с.
2. Элементы высшей математики: учебник для студентов образовательных учреждений СПО/С.Г. Григорьев, Ю.А. Дубинский – 9-е изд., стер. – М.: Издательский центр «Академия». 2013. – 320 с.
3. Шипачев В.С. Основы высшей математика: учебник для вузов. -М. Высш.шк., 2010 г.
Краткие теоретические сведения:
Матрицей называется прямоугольная таблица чисел, состоящая из m строк и n столбцов, которую записывают в следующем виде:
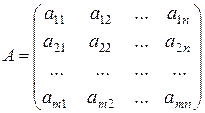 .
.
Для
обозначения матрицы используют прописные латинские буквы, для обозначения
элементов матрицы – строчные латинские буквы с указанием номера строки и
столбца, на пересечении которых стоит данный элемент. Запись « матрица B имеет размер mxn» означает, что речь идет о матрице, состоящей из m строк и n столбцов. Например, матрица 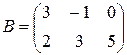 имеет размер 2x3. Далее, bij - обозначение элемента, стоящего
на пересечении i-й строки и j-го столбца данной матрицы (в примере b23=5).
имеет размер 2x3. Далее, bij - обозначение элемента, стоящего
на пересечении i-й строки и j-го столбца данной матрицы (в примере b23=5).
При ссылке на i-ю строку матрицы A используют обозначение Ai, при ссылке на j-й столбец – обозначение Aj.
Матрица, у которой число строк совпадает с числом столбцов, называется квадратной. Элементы a11 , a22 ,…, ann квадратной матрицы A (размера nxn) образуют главную диагональ. Квадратная матрица, у которой отличные от нуля элементы могут стоять только на главной диагонали, называется диагональной. Диагональная матрица, у которой все элементы (главной диагонали!) равны 1, называется единичной. Наконец, квадратная матрица, у которой ниже (выше) главной диагонали находятся только нули, называется верхней (нижней) треугольной матрицей. Например, среди квадратных матриц размера 3x3
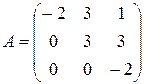 ,
,
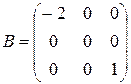 ,
, 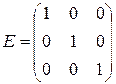 ,
,
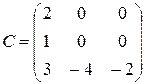
матрица A является верхней треугольной, B – диагональной, C – нижней треугольной, E – единичной.
Матрицы A, B называются равными (A=B), если они имеют одинаковый размер, и их элементы, стоящие на одинаковых позициях, совпадают.
Арифметические действия с матрицами.
Чтобы умножить матрицу A на отличное от нуля вещественное число k, необходимо каждый элемент матрицы умножить на это число:
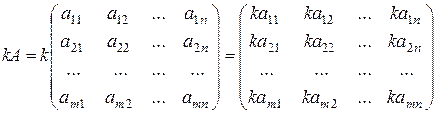 .
.
Чтобы найти сумму матриц A, B одной размерности, необходимо сложить элементы с одинаковыми индексами (стоящие на одинаковых местах):
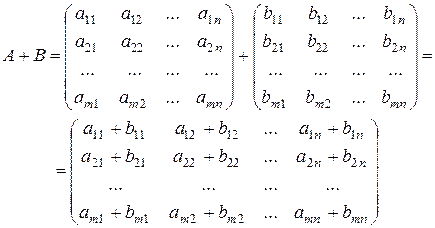 .
.
Пример 1. Найти 2A-B, если 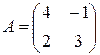 ,
, 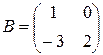 .
.
Решение. Сначала умножаем матрицу A на число «2», затем матрицу B на число «-1», и, наконец, находим сумму полученных матриц:
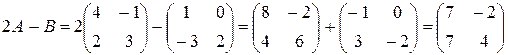
Имеем:
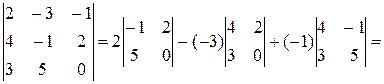
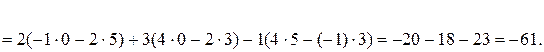
Произведение
AB можно определить только для матриц
A размера mxn и
B размера nxp, при этом AB=C, матрица C имеет размер mxp, и ее элемент cij находится как скалярное
произведение i-й строки матрицы A на j-й столбец матрицы B: ![]() (i=1,2,…,m; j=1,2,…,p). Фактически необходимо каждую строку матрицы A (стоящей слева) умножить скалярно
на каждый столбец матрицы B (стоящей справа).
(i=1,2,…,m; j=1,2,…,p). Фактически необходимо каждую строку матрицы A (стоящей слева) умножить скалярно
на каждый столбец матрицы B (стоящей справа).
Пример
2. Найти произведение матриц 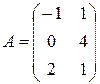 и
и 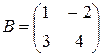 .
.
Решение. Размер матрицы A 3x2, матрицы В 2х2. Поэтому произведение АВ найти можно, произведение ВА – нет. Действуя по сформулированному выше правилу, получаем:
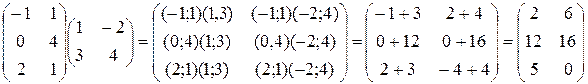
Матрицей, транспонированной к матрице A размера mxn, называется матрица AT размера nxm, строки которой являются столбцами исходной матрицы.
Например,
если 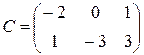 , то
, то 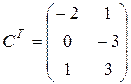 .
.
Пример 3. Найти 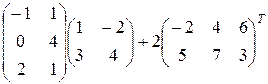 .
.
Решение. Воспользовавшись вычислениями, проведенными при решении примера, а также правилами умножения матрицы на число и сложения матриц, получим:
 .
.
Матрицы A, B называются эквивалентными, если одна получена из другой путем элементарных преобразований.
Рангом матрицы A в дальнейшем будем считать число строк эквивалентной
ей ступенчатой матрицы, используя обозначение r(A). Так, в рассмотренном выше
примере 3.4 r(A)=3, r(B)=2. Можно доказать, что ранг матрицы A (размера mxn) не может быть больше ![]() (например,
для матрицы А размера
2x3
(например,
для матрицы А размера
2x3 ![]() ).
Кроме того, ранг матрицы не зависит ни от выбора ведущих элементов, ни от
проводимых преобразований. Это свойство можно использовать при проверке. Так, в
примере 3.4 после перестановки первой и второй строки в матрице B можно в качестве ведущего сначала
рассмотреть элемент b12, а затем вычеркнуть третью строку,
пропорциональную второй (
).
Кроме того, ранг матрицы не зависит ни от выбора ведущих элементов, ни от
проводимых преобразований. Это свойство можно использовать при проверке. Так, в
примере 3.4 после перестановки первой и второй строки в матрице B можно в качестве ведущего сначала
рассмотреть элемент b12, а затем вычеркнуть третью строку,
пропорциональную второй (![]() ):
):
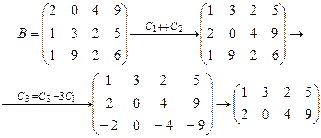
Вычисление определителей. Определитель матрицы A размера 2x2 (определитель 2-го порядка) – это число, которое можно найти по правилу:
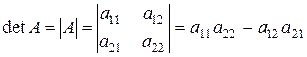
(произведение элементов, стоящих на главной диагонали матрицы, минус произведение элементов, стоящих на побочной диагонали).
Определитель матрицы A размера 3x3 (определитель 3-го порядка) – число, вычисляемое по правилу «раскрытие определителя по первой строке»:
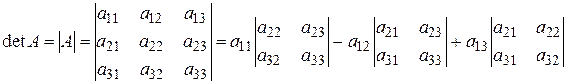
Пример 4. Найти: 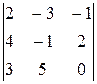
Решение.
При нахождении определителя воспользуемся сначала формулой 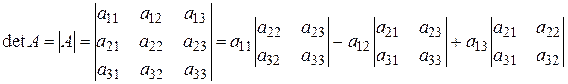 , а затем (для вычисления
определителей 2-го порядка) формулой
, а затем (для вычисления
определителей 2-го порядка) формулой 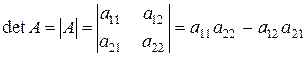 .
.
Порядок проведения работы:
Задания
Задание 1. Выполнить арифметические действия с матрицами:
1) ![]() ; 2)
; 2) 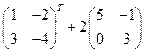 ;
;
3) 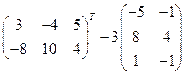 ; 4)
; 4)
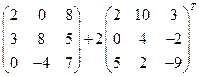 ;
;
5)
![]() ;
;
6)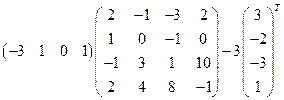 ;
;
7)
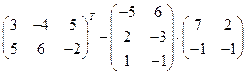
Задание 2. Доказать равенство (AB)C=A(BC) для матриц:
1) 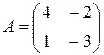 ,
,
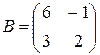 ,
, 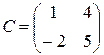 ;
;
2) 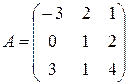 ,
,
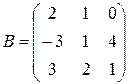 ,
, 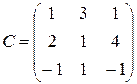 ;
;
3)
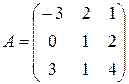 ,
, 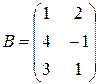 ,
,
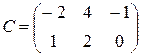 ;
;
Задание 3.
Найти: 1) 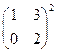 ; 2)
; 2) 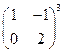 ; 3)
; 3) 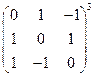 .
.
Задание 4. Вычислить определители:
|
1) |
2) |
3) |
|
4) |
5) |
6) |
|
7) |
|
|
Вычисление определителей
1. Если переставить две строки (или два столбца) определителя, то определитель изменит знак.
2. Если соответствующие элементы двух столбцов (или двух строк) определителя равны или пропорциональны, то определитель равен нулю.
3. Значение определителя не изменится, если поменять местами строки и столбцы, сохранив их порядок.
4. Если все элементы какой-либо строки (или столбца) имеют общий множитель, то его можно вынести за знак определителя.
5. Значение определителя не изменится, если к элементам одной строки (или столбца) прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число
6. Определитель второго порядка вычисляется по формуле
𝑎1 𝑎2
|𝑏1 𝑏2| = 𝑎1𝑏2 − 𝑎2𝑏1
3. Определитель третьего порядка вычисляется по формуле
𝑎1 𝑏1 𝑐1
|𝑎2 𝑏2 𝑐2| = 𝑎1𝑏2𝑐3 + 𝑎2𝑏3𝑐1 + 𝑎3𝑏1𝑐2 − 𝑎3𝑏2𝑐1 − 𝑎2𝑏1𝑐3 − 𝑎1𝑏3𝑐2
𝑎3 𝑏3 𝑐3
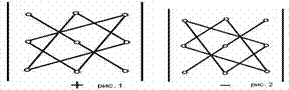
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком "плюс"; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком "минус":
|
𝑎11 |𝑎21 𝑎31 |
𝑎12 𝑎22 𝑎32 |
𝑎13 𝑎11 𝑎23| 𝑎21 𝑎33 𝑎31 |
𝑎12 𝑎22 = 𝑎32 |
= 𝑎11𝑎22𝑎33 + 𝑎12𝑎23𝑎31 + 𝑎13𝑎21𝑎32 − 𝑎13𝑎22𝑎31 − 𝑎32𝑎23𝑎11
− 𝑎33𝑎21𝑎12
1.Вычислить определитель по правилу треугольников
|3 4 1|
4 2 5
2. Вычислить определитель разложением по элементам второго столбца:
4 −1 4
|−2 3 1|
1 −2 3
3. Вычислить определитель используя свойства:
10 5 15
| 2 4 9 |
4 1 3
4. Вычислить определитель, разложив на сумму:
𝑎 + 5 10 𝑎
|𝑎 + 𝑏 2𝑏 𝑎| 3𝑏 4𝑏 𝑏
5. Вычислить определитель
1 2 1 3
2 1 1 2|
|
1.Вычислить определитель по правилу треугольников:
|2 3 5|
2.Вычислить определитель разложением по элементам третьей строки:
−1 2 −3
| 2 3 1 |
−2 2 −3
6 3 9
|8 4 2|
4. Вычислить определитель, разложив на сумму:
2𝑡 3𝑡 𝑡
|𝑛 + 𝑡 3𝑡 𝑛 |
3𝑟 3𝑟 2𝑟
5. Вычислить определитель
1 1 3 2
2 4 1 2
| |
1 2 3 2
2 2 1 4
ѣ
Вычислить определитель по правилу треугольников:
1 3 3
|2 2 5|
4 2 3
2. Вычислить определитель разложением по элементам третьей строки:
−1 2 4
| 2 −2 1 |
−3 2 −2
3. Вычислить определитель используя свойства:
6 3 12
|2 6 4 |
2 3 8
4. Вычислить определитель, разложив на сумму:
𝑛 + 3 6 𝑛
|𝑛 + 𝑚 2𝑚 𝑛 |
3𝑚 4𝑚 𝑚
5. Вычислить определитель
2 1 3 2
2 3 1 2
1 1 3 2
2 2 1
Вычислить определитель по правилу треугольников:
1 2 4
|2 3 5|
1 2 3
2. Вычислить определитель разложением по элементам третьей строки:
−1 2 4
| 3 −2 −4|
1 2 3
3. Вычислить определитель используя свойства:
4 8 6
|2 4 9|
2 6 3
4. Вычислить определитель, разложив на сумму:
𝑚 + 2 4 𝑚
|𝑛 + 𝑚 2𝑚 𝑛 |
4 4 2
5. Вычислить определитель
1 2 1 3
2 1 3 2
1 1 2 3
3 3 2
Вычислить определитель по правилу треугольников:
1 1 3
|2 2 5|
4 2 3
2. Вычислить определитель разложением по элементам третьей строки:
−1 2 4
|−2 3 −1|
1 2 −2
3. Вычислить определитель используя свойства:
6 3 6
|2 4 9|
2 1 3
4. Вычислить определитель, разложив на сумму:
𝑛 + 3 6 𝑛
|𝑛 + 𝑚 2𝑚 𝑛 |
3𝑚 4𝑚 𝑚
5. Вычислить определитель
2 1 3 2
2 3 1 2
1 1 3 2
2 2 1
Вычислить определитель по правилу треугольников:
2 1 1
|3 3 4|
1 3 3
2. Вычислить определитель разложением по элементам третьей строки:
2 −4 3
|−2 −1 2 |
1 −2 −3
3. Вычислить определитель используя свойства:
2 2 6
|8 6 9|
1 4 3
4. Вычислить определитель, разложив на сумму:
𝑘 + 3 6 𝑘
|𝑛 + 𝑘 2𝑘 𝑛|
6 12 6
5. Вычислить определитель
1 2 1 3
2 1 3 2
1 1 2 3
3 3 2
Цель работы:
Используя теоретический материал и образцы решения задач, решить примеры по теме «Решение систем линейных алгебраических уравнений различными способами»
Перечень справочной литературы :
1. Математика: учебник для студентов образовательных учреждений СПО/С.Г. Григорьев, С.В. Иволгина; под редакцией В.А. Гусева – 10-е изд., стер. – М.: Издательский центр «Академия». 2014. – 416 с.
2. Элементы высшей математики: учебник для студентов образовательных учреждений СПО/С.Г. Григорьев, Ю.А. Дубинский – 9-е изд., стер. – М.: Издательский центр «Академия». 2013. – 320 с.
3. Шипачев В.С. Основы высшей математика: учебник для вузов. -М. Высш.шк., 2010 г.
1.Пусть дана система линейных уравнений
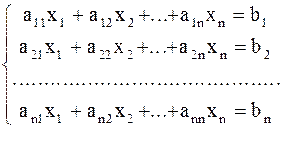 (1)
(1)
Коэффициенты a11,12,..., a1n, ... , an1 , b2 , ... , bn считаются заданными.
Вектор -строка íx1 , x2 , ... , xn ý - называется решением системы (1), если при подстановке этих чисел вместо переменных все уравнения системы (1) обращаются в верное равенство.
Определитель n-го порядка D=çAê=ça ij ç, составленный из коэффициентов при неизвестных, называется определителем системы (1). В зависимости от определителя системы (1) различают следующие случаи:
a)
Если D¹, то система (1) имеет единственное решение,
которое может быть найдено по формулам Крамера : x1=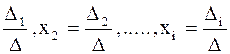 , где
, где
определитель n-го порядка Di ( i=1,2,...,n) получается из определителя системы путем замены i-го столбца свободными членами b1 , b2 ,..., bn.
б) Если D= , то система (1) либо имеет бесконечное множество решений , либо несовместна ,т.е. решений нет.
2. Рекомендации по выполнению заданий
1. Рассмотрим систему 3-х линейных уравнений с тремя неизвестными.
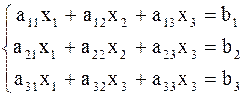 (2).
(2).
1. В данной системе составим определитель 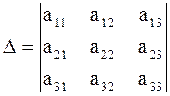 и вычислим.
и вычислим.
2. Составить и вычислить следующие определители:
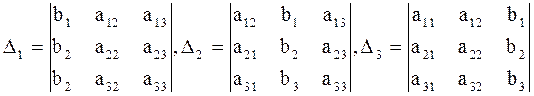 .
.
3. Воспользоваться формулами Крамера.
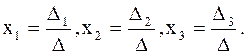
Практическое значение правила Крамера для решения системы n линейных уравнений с п неизвестными невелико, так как при его применении приходится вычислять п +1 определителей n-го порядка: D, Dx1, Dx2, …,Dxn. Более удобным является так называемый метод Гаусса. Он применим и в более общем случае системы линейных уравнений, т. е. когда число уравнений не совпадает с числом неизвестных.
Пример 1
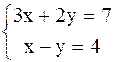
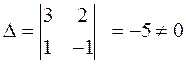
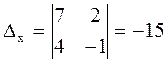
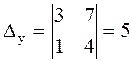
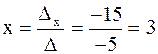
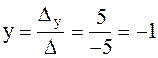 .
.
Проверка:
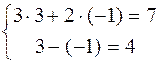 Ответ:
( 3 ; -1 ).
Ответ:
( 3 ; -1 ).
Пример 2
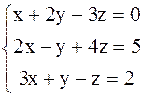
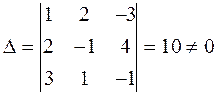
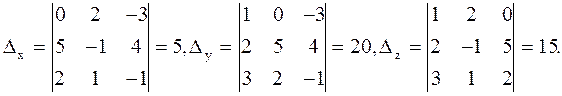
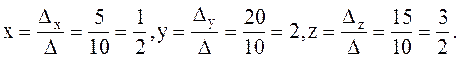
Проверка:
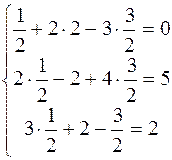 Ответ:
x=0,5; y=2; z=1,5 .
Ответ:
x=0,5; y=2; z=1,5 .
Более удобным является так называемый метод Гаусса. Он применим и в более общем случае системы линейных уравнений, т. е. когда число уравнений не совпадает с числом неизвестных.
![]() Итак,
пусть дана система, содержащая m линейных уравнений с п неизвестными:
Итак,
пусть дана система, содержащая m линейных уравнений с п неизвестными:
а11х1 + а12х2 + …+ а1nхn = b1;
а21х1 + а22х2 + …+ а2nхn = b2;
. ……………………………………
аm1х1 + аm2х2 + …+ аmnхn = bm
Метод Гаусса решения системы заключается в последовательном исключении переменных.
Схема единственного деления. Рассмотрим простейший вариант метода Гаусса, называемый схемой единственного деления.
Прямой ход состоит из n - 1 шагов исключения.
1-й шаг. Целью этого шага является исключение неизвестного x1 из уравнений с номерами i = 2, 3, …, n. Предположим, что коэффициент a11 ¹ 0. Будем называть его главным элементом 1-го шага.
Найдем величины
qi1 = ai1/a11 (i = 2, 3, …, n),
называемые множителями 1-го шага. Вычтем последовательно из второго, третьего, …, n-го уравнений системы первое уравнение, умноженное соответственно на q21, q31, …, qn1. Это позволит обратить в нуль коэффициенты при x1 во всех уравнениях, кроме первого. В результате получим эквивалентную систему
a11x1 + a12x2 + a13x3 + … + a1nxn = b1 ,
a22(1)x2 + a23(1)x3 + … + a2n(1)xn = b2(1) ,
a32(1)x2 + a33(1)x3 + … + a3n(1)xn = b3(1) ,
. . . . . . . . . . . . . . .
an2(1)x2 + an3(1)x3 + … + ann(1)xn = bn(1) .
в которой aij(1) и bij(1) вычисляются по формулам
aij(1) = aij − qi1a1j , bi(1) = bi − qi1b1.
2-й шаг. Целью этого шага является исключение неизвестного x2 из уравнений с номерами i = 3, 4, …, n. Пусть a22(1) ≠ 0, где a22(1) – коэффициент, называемый главным (или ведущим) элементом 2-го шага. Вычислим множители 2-го шага
qi2 = ai2(1) / a22(1) (i = 3, 4, …, n)
и вычтем последовательно из третьего, четвертого, …, n-ого уравнения системы второе уравнение, умноженное соответственно на q32, q42, …, qm2. В результате получим систему
a11x1 + a12x2 + a13x3 + … + a1nxn = b1 ,
a22(1)x2 + a23(1)x3 + … + a2n(1) = b2(1) ,
a33(2)x3 + … + a3n(2)xn = b3(2) ,
. . . . . . . . . . . . . . . . . . .
an3(2)x3 + … + ann(2)xn = bn(2) .
Здесь коэффициенты aij(2) и bij(2) вычисляются по формулам
aij(2) = aij(1) – qi2a2j(1) , bi(2) = bi(1) – qi2b2(1).
Аналогично проводятся остальные шаги. Опишем очередной k-й шаг.
k-й шаг. В предположении, что главный (ведущий) элемент k-ого шага akk(k–1) отличен от нуля, вычислим множители k-го шага
qik = aik(k–1) / akk(k–1) (i = k + 1, …, n)
и вычтем последовательно из (k + 1)-го, …, n-го уравнений полученной на предыдущем шаге системы k-e уравнение, умноженное соответственно на qk+1,k, qk+2,k, …, qnk.
После (n - 1)-го шага исключения получим систему уравнений
a11x1 + a12x2 + a13x3 + … + a1nxn = b1 ,
a22(1)x2 + a23(1)x3 + … + a2n(1)xn = b2(1) ,
a33(2)x3 + … + a3n(2)xn = b3(2) ,
. . . . . . . . . . . . . . . . . . . .
ann(n–1)xn = bn(n–1) .
матрица A(n-1) которой является верхней треугольной. На этом вычисления прямого хода заканчиваются.
Алгоритм для решения системы линейных уравнений методом Гаусса
Выражаем первое неизвестное из первого уравнения и подставляем его в остальные уравнения.
Для систем нелинейных уравнений этот метод не всегда применим уже в силу того, что из уравнений системы совсем не обязательно можно будет выразить одну неизвестную через остальные.
Примеры решения систем линейных уравнений методом Гаусса
Пример 1
Решить методом Гаусса систему уравнений
![]() x1
– 2x2 + x3 + x4 = –1;
x1
– 2x2 + x3 + x4 = –1;
3x1 + 2x2 – 3x3 – 4x4 = 2;
2x1 – x2 + 2x3 – 3x4 = 9;
x1 + 3x2 – 3x3 – x4 = –1.
![]() Решение: Составим матрицу В и преобразуем ее. Для удобства
вычислений отделим вертикальной чертой столбец, состоящий из свободных
членов:
Решение: Составим матрицу В и преобразуем ее. Для удобства
вычислений отделим вертикальной чертой столбец, состоящий из свободных
членов:
![]()
![]() 1 –2 1 1 –1
1 –2 1 1 –1
B = 3 2 –3 –4 2
2 –1 2 –3 9
1 3 –3 –1 –1
Умножим первую строку матрицы В последовательно на 3, 2 и 1 и вычтем соответственно из второй, третьей и четвертой строк. Получим матрицу, эквивалентную исходной:
![]()
![]()
![]() 1 –2 1 1 –1
1 –2 1 1 –1
0 8 –6 –7 5
0 3 0 –5 11
0 5 –4 –2 0
Третью строку матрицы умножим на 3 и вычтем ее из второй строки. Затем новую вторую строку умножим на 3 и на 5 и вычтем из третьей и четвертой строк. Получим матрицу, эквивалентную исходной:
![]()
![]() 1 –2 1 1 –1
1 –2 1 1 –1
0 –1 –6 8 –28
0 0 –1 0 –3
0 0 0 19 –19
Из коэффициентов последней матрицы составим систему, равносильную исходной:
![]() x1 – 2x2 + x3 + x4 = –1;
x1 – 2x2 + x3 + x4 = –1;
– X2 – 6x3 + 8x4 = –28;
– x3 = –3;
19x4 = –19.
Решим полученную систему методом подстановки, двигаясь последовательно от последнего уравнения к первому. Из четвертого уравнения x4 = –1, из третьего х3 = 3. Подставив значения х3 и x4 во второе уравнение, найдем x2 = 2. Подставив значения x2, x3, x4 в первое уравнение, найдем x1 = 1.
Ответ. (1; 2; 3;-1).
Пример 2
Решить систему уравнений
|
|
Решение:
|
Выразим из первого уравнения переменную x:
Выразим теперь из второго уравнения переменную
Теперь третье уравнение зависит только от y и мы можем его решить:
Итак, переменная y найдена. По уже полученным формулам
для x и z мы можем последовательно их найти:
Ответ. (2; –1; 1). |
Этот метод иногда можно применить и для решения нелинейных систем.
Пример 3
Решить систему уравнений
|
|
Решение:
|
Выразим z из второго уравнения: z = 1 + 2x – y и подставим его в первое и третье уравнения. Получим систему из двух уравнений с двумя неизвестными:
Опять из первого уравнения выражаем y (её легче
выразить, чем x):
Теперь по найденному x находим y и z:
Ответ. (1; 0; 3), (–1; –2; 1). |
Контрольные вопросы:
- понятие определителя n-ого порядка;
- методы решения систем линейных уравнений;
- решение систем линейных уравнений методом Крамера;
- формулы Крамера;
- решение систем линейных уравнений методом Гаусса.
Порядок выполнения работы:
Примеры по теме:
Решение систем линейных уравнений методом Крамера
ВАРИАНТ 1
Решить системы:
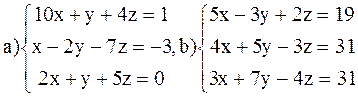
ВАРИАНТ 2
Решить системы:
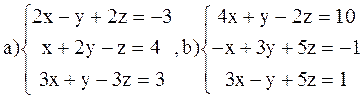
ВАРИАНТ 3
Решить системы:
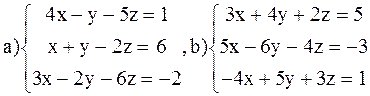
ВАРИАНТ 4
Решить системы:
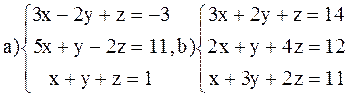
ВАРИАНТ 5
Решить системы:
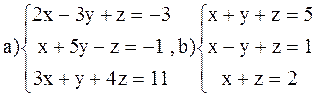
ВАРИАНТ 6
Решить системы:
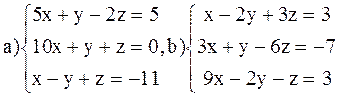
ВАРИАНТ 7
Решить системы:
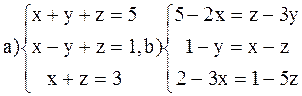
ВАРИАНТ 8
Решить системы:
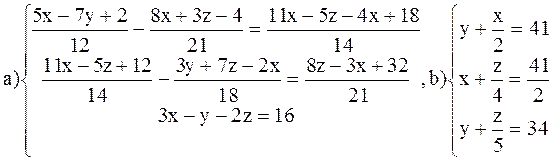
Примеры по теме:
Решение систем линейных уравнений методом Гаусса
ВАРИАНТ 1
Решить системы:
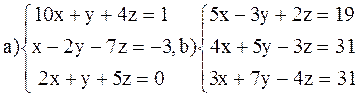
ВАРИАНТ 2
Решить системы:
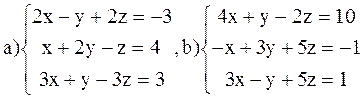
ВАРИАНТ 3
Решить системы:
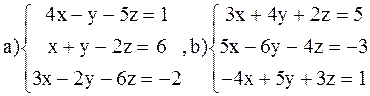
ВАРИАНТ 4
Решить системы:
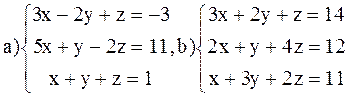
ВАРИАНТ 5
Решить системы:
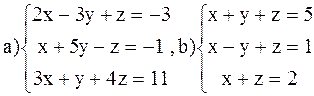
ВАРИАНТ 6
Решить системы:
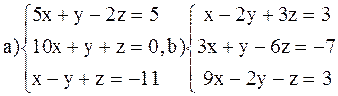
ВАРИАНТ 7
Решить системы:
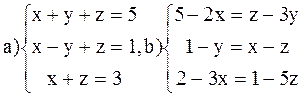
ВАРИАНТ 8
Решить системы:
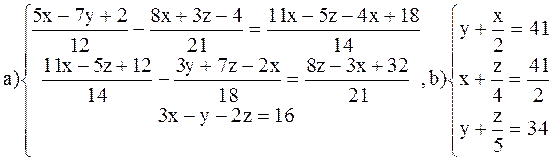
Цель работы:
Используя теоретический материал и образцы решения задач, решить примеры по теме «Действия над комплексными числами, заданными в алгебраической форме»
Перечень справочной литературы :
1. Математика: учебник для студентов образовательных учреждений СПО/С.Г. Григорьев, С.В. Иволгина; под редакцией В.А. Гусева – 10-е изд., стер. – М.: Издательский центр «Академия». 2014. – 416 с.
2. Элементы высшей математики: учебник для студентов образовательных учреждений СПО/С.Г. Григорьев, Ю.А. Дубинский – 9-е изд., стер. – М.: Издательский центр «Академия». 2013. – 320 с.
3. Шипачев В.С. Основы высшей математика: учебник для вузов. -М. Высш.шк., 2010 г.
Краткие теоретические сведения:
Квадратное уравнение с действительными коэффициентами и отрицательным дискриминантом не имеет действительных корней. Поэтому приходится расширять множество действительных чисел, добавляя к нему новые числа. Эти новые числа вместе с действительными числами образуют множество, которое называют множеством комплексных чисел.
Комплексным числом - называется выражение вида z = a+b i , где a и b действительные числа, число а называется действительной частью комплексного числа z = a+b·i, а число b – его мнимой частью, а i – мнимая единица, определяемая равенством i ² = -1.
Например, действительная часть комплексного числа z = 2+3·i равна a =2, а мнимая равна b = 3.
Действительные числа: z=a+0i=a, z=Re z.
Мнимые числа: z=0+bi=bi, z=Im z.
Равные комплексные числа: z1=a+bi, z2=c+di, z1=z2, если a=c, b=d.
Противоположные комплексные числа: z=a+bi, z=-a-bi.
Сопряженные комплексные числа: z=a+bi, z=a-bi.
Суммой двух комплексных чисел z1=a+b·i и z2= c+d·i называется комплексное число: z = z1 + z2 = (a+b·i ) + ( c+d·i ) = (a+c) + (b+d)·i,
Произведением двух комплексных чисел z1=a+b·i и z2= c+d·i называется комплексное число : z = z1 · z2 =( a+b·i )·( c+d·i )=(a·c – b·d) + (a·d + b·c)·i
Из формул вытекает, что сложение и умножение можно выполнять по правилам действий с многочленами, считая i2= –1. Операции сложения и умножения комплексных чисел обладают свойствами действительных чисел. Основные свойства:
Переместительное свойство:
Z1 +Z2=Z2+Z1, Z1·Z2=Z2·Z1
Сочетательное свойство:
(Z1+Z2)+Z3=Z1+(Z2+Z3), (Z1·Z2)·Z3=Z1·(Z2·Z3)
Распределительное свойство:
Z1·(Z2+Z3)=Z1·Z2+Z1·Z3
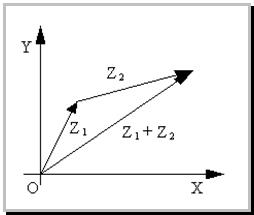
Рисунок 1.
Согласно определению сложения двух комплексных чисел, действительная часть суммы равна сумме действительных частей слагаемых, мнимая часть суммы равна сумме мнимых частей слагаемых. Точно также определяются координаты суммы векторов (Рис.1).
Вычитание комплексных чисел – это операция, обратная сложению: для любых комплексных чисел Z1 и Z2 существует, и притом только одно, число Z, такое, что: Z + Z2=Z1 Z = Z1 – Z2
Число Z=Z1+(-Z2 )называют разностью чисел Z1 и Z2.
Z= (a+b·i ) - ( c+d·i ) = (a-c) + (b-d)·i,
Деление вводится как операция, обратная умножению: Z×Z2=Z1
Разделив обе части на Z2
получим: Z=![]()
Из этого уравнения видно, что Z2![]() 0
0
Производится умножение делимого и
делителя на число, сопряженное делителю. Z=![]() =
= 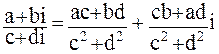
|
|
Геометрическое изображение разности комплексных чисел
|
Рисунок 2 |
Разности
Z2 – Z1 комплексных чисел Z1 и Z2,
соответствует разность векторов, соответствующих числам Z1 и Z2.
Модуль ![]() разности двух
комплексных чисел Z2 и Z1 по определению модуля
есть длина вектора Z2 – Z1. Построим этот вектор, как
сумму векторов Z2 и (–Z1) (рисунок 2). Таким
образом, модуль разности двух комплексных чисел есть расстояние между точками комплексной
плоскости, которые соответствуют этим числам.
разности двух
комплексных чисел Z2 и Z1 по определению модуля
есть длина вектора Z2 – Z1. Построим этот вектор, как
сумму векторов Z2 и (–Z1) (рисунок 2). Таким
образом, модуль разности двух комплексных чисел есть расстояние между точками комплексной
плоскости, которые соответствуют этим числам.
Пример 1: Найти сумму и произведение комплексных чисел Z1=2 – 3×i и
Z2= –7 + 8×i.
Z1 + Z2 = 2 – 7 + (–3 + 8)×i = –5 + 5×i
Z1×Z2 = (2 – 3×i)×(–7 + 8×i) = –14 + 16×i + 21×i + 24 = 10 + 37×i
|
|
Пример 2: Найти сумму и произведение комплексных чисел Z1=1 + 2×i и Z2= 2 - i.
Имеем
![]()
![]()
![]()
Пример 3:
Даны комплексные числа Z1=
4 + 5·i и Z2= 3 + 4·i. Найти разность Z2 –
Z1 и частное ![]()
Z2 – Z1 = (3 + 4·i) – (4 + 5·i) = –1 – i
![]() =
=![]() =
=![]()
Контрольные вопросы:
- понятие комплексного числа (К.Ч.);
- алгебраическая форма записи К.Ч;
- арифметические операции над К.Ч.
Порядок проведения работы:
Задания
Вариант № 1
1. Дано комплексное число
Z = 21 – 4 i
Записать число равное, противоположное, сопряженное исходному.
2. Выполнить действие
Z = ( 3 - 2 i + ( - 6 - 2 i )
3. Выполнить умножение
Z = ( 3 + 4 i ) ( 1 + 3 i )
4. Выполнить деление
Z = ( - 6 + 2 i )) : ( 3 - 4 i )
5. Выполнить действия
Z = ( 5 + 2 i ) : ( 2 - 5 i ) + (7 + 3 i ) : ( 1 - 2 i )
Вариант № 2
1 Дано комплексное число
Z = 3 + 9 i
Записать число равное, противоположное, сопряженное исходному.
2 Выполнить действие
Z = ( 5 + 3 i ) + ( - 2 - 5 i )
3 Выполнить умножение
Z = ( -2 + 3 i ) ( -1 - 6 i )
4 Выполнить деление
Z = ( 4 +- 3 i ) : ( -2 - 5 i )
5 Выполнить действия
Z = ( -1 + 3 i ) : ( 5 + i ) - ( 3 - 4 i ) : ( 4 + 3 i )
Тема: «Действия над комплексными числами в тригонометрической и показательной форме»
Цель работы: научиться переводить комплексные числа и выполнять действия над комплексными числами в тригонометрической и показательной формах.
Краткие теоретические сведения.
Для всякого комплексного числа z = a + ib справедливо равенство:
z=R(cosφ+ isinφ) называют тригонометрической формой комплексного числа,
z = – называют показательной формой комплексного числа
Здесь - модуль комплексного числа - расстояние от
начала координат до соответствующей точки комплексной плоскости. Попросту
говоря, модуль – это длина радиус-вектора.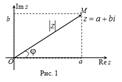
Угол φ между положительной полуосью действительной оси и радиус-вектором, проведенным из начала координат к соответствующей точке, называется аргументом комплексного числа - .
Действия над комплексными числами в тригонометрической форме.
В тригонометрической форме
z1 =R1(cosφ1 + isinφ1), z2 =R2(cosφ2 + isinφ2)
В показательной форме
Z1 = , Z2 =
Умножение
Z1 ∙ Z2 = R1∙R2(cos(φ1+φ2) + isin(φ1+φ2)).
Z1·Z2=
Деление
.
,
Возведение в степень
zn =Rn(cos nφ + isin nφ) - формула Муавра
.
Извлечение корня
, k = 0,1,2.....n-1
,
k = 0,1,2.....n-1
Примеры решения задач:
Пример. А) Представить числа z1 = , в тригонометрической и показательной форме,
Б) вычислить в тригонометрической форме: 1) z1∙z2; 2) ; 3) ; 4)
Решение: А). Получим тригонометрическую и показательную форму z1 = ,
1) Найдем модуль числа - , 2) Найдем аргумент числа - ,
3) запишем к.ч. в тригонометрической и показательной форме:
z1 = .
,
1) - модуль числа,
2) - аргумент числа
3) запишем к.ч. в тригонометрической и показательной форме:
.
Б) Произведение:
z1∙z2 =
.
Частное:
=
.
Возведение в степень:
.
Извлечение из под знака корня:
.
Пр k=0: ;
Пр k=1: .
Задания для самостоятельного решения
1. Изобразить комплексные числа на комплексной плоскости.
2. Определить длину и аргумент каждого комплексного числа.
3. Представить данные комплексные числа в тригонометрической и показательной форме.
4. Вычислить в тригонометрической и показательной формах:
1) z1∙z2; 2) ; 3) ; 4)
Z1= 2- 2i; Z2=
Z1= ; Z2=
Z1= ; Z2=
Z1= ; Z2=
Цель работы:
Используя теоретический материал и образцы решения задач, решить примеры по теме «Решение простейших задач теории вероятностей»
Перечень справочной литературы :
1. Математика: учебник для студентов образовательных учреждений СПО/С.Г. Григорьев, С.В. Иволгина; под редакцией В.А. Гусева – 10-е изд., стер. – М.: Издательский центр «Академия». 2014. – 416 с.
2. Элементы высшей математики: учебник для студентов образовательных учреждений СПО/С.Г. Григорьев, Ю.А. Дубинский – 9-е изд., стер. – М.: Издательский центр «Академия». 2013. – 320 с.
3. Шипачев В.С. Основы высшей математика: учебник для вузов. -М. Высш.шк., 2010 г.
Краткие теоретические сведения:
Теория вероятности
Случайные события. Частота. Вероятность
Теория вероятностей — математическая наука, изучающая закономерности массовых случайных явлений (событий).
Случайным событием (или просто событием) называется всякое явление, которое может произойти или не произойти при осуществлении определенной совокупности условий. Теория вероятностей имеет дело с такими событиями, которые имеют массовый характер. Это значит, что данная совокупность условий может быть воспроизведена неограниченное число раз. Каждое такое осуществление данной совокупности условий называют испытанием (или опытом).
Если, например, испытание состоит в бросании монеты, то выпадение герба является событием; если испытание — изготовление подшипника данного типа, то соответствие подшипника стандарту — событие; если испытание — бросание игральной кости, т. е. кубика, на гранях которого проставлены цифры (очки) от 1 до 6, то выпадение пятерки — событие.
События будем обозначать заглавными буквами латинского алфавита: A, В, С, ...
Пусть при n испытаниях событие A появилось m раз.
Отношение m/n называется частотой (относительной частотой) события A и обозначается Р*(А)=m/n
Опыт показывает, что при многократном повторении испытаний частота Р*(А) случайного события обладает устойчивостью.
Событие называется достоверным, если оно в данном опыте обязательно должно произойти; наоборот, событие называется невозможным, если оно в данном опыте не может произойти.
Пусть, например, из урны, содержащей только черные шары, вынимают шар. Тогда появление черного шара — достоверное событие; появление белого шара — невозможное событие.
Если событие достоверно, то оно произойдет при каждом испытании (m=n). Поэтому частота достоверного события всегда равна единице. Наоборот, если событие невозможно, то оно ни при одном испытании не осуществится (m=0). Следовательно, частота невозможного события в любой серии испытаний равна нулю. Поэтому вероятность достоверного события равна единице, а вероятность невозможного события равна нулю.
Если событие A не является ни достоверным, ни невозможным, то его частота m/n при большом числе испытаний будет мало отличаться от некоторого числа p (где 0 < p < 1 ) — вероятности события A.
Совмещением (или произведением) двух событий A и В называется событие, состоящее в совместном наступлении как события A, так и события В. Это событие будем обозначать АВ или ВА.
Аналогично, совмещением нескольких событий, например A, В и С, называется событие D=ABC, состоящее в совместном наступлении событий A, В и С.
Объединением (или суммой) двух событий A и В называется событие С, заключающееся в том, что произойдет по крайней мере одно из событий A или В. Это событие обозначается так: С=А+В.
Объединением нескольких событий называется событие, состоящее в появлении по крайней мере одного из них. Запись D=A+B+C означает, что событие D есть объединение событий A, В и С.
Два события A и В называются несовместными, если наступление события A исключает наступление события В. Отсюда следует, что если события A и В несовместны, то событие AB — невозможное.
Аксиомы вероятностей
Пусть A и B — два несовместных события, причем в n испытаниях событие A произошло m1 раз, а событие В произошло m2 раз. Тогда частоты событий A и В соответственно равны P*(A)=m1/n, P*(B)=m2/n. Так как события A и В несовместны, то событие A+B в данной серии опытов произошло m1+m2 раз. Следовательно,
![]()
Таким образом, частота события A+B равна сумме частот событий A и В. Но при больших n частоты P*(A), P*(B) и P*(A+B) мало отличаются от соответствующих вероятностей P(A), P(B) и P(A+B). Поэтому естественно принять, что если A и В — несовместные события, то P(A+B)=P(A)+P(B)
Изложенное позволяет высказать следующие свойства вероятностей, которые мы принимаем в качестве аксиом.
Аксиома 1. Каждому случайному событию A соответствует определенное
число Р(А), называемое его вероятностью и удовлетворяющее условию ![]() .
.
Аксиома 2. Вероятность достоверного события равна единице.
Аксиома 3 (аксиома сложения вероятностей). Пусть A и В — несовместные события. Тогда вероятность того, что произойдет хотя бы одно из этих двух событий, равна сумме их вероятностей:
|
P(A+B)=P(A)+P(B) |
(1) |
Аксиома 3 допускает обобщение на случай нескольких событий, а именно: если события A1, A2, ..., An, попарно несовместны, то
|
|
(2) |
Событием, противоположным событию ![]() ,
называется событие
,
называется событие ![]() , состоящее в ненаступлении
события
, состоящее в ненаступлении
события ![]() . Очевидно, события
. Очевидно, события ![]() и
и ![]() несовместны.
несовместны.
Пусть, например, событие ![]() состоит в
том, что изделие удовлетворяет стандарту; тогда противоположное событие
состоит в
том, что изделие удовлетворяет стандарту; тогда противоположное событие ![]() заключается в том, что
изделие стандарту не удовлетворяет. Пусть событие
заключается в том, что
изделие стандарту не удовлетворяет. Пусть событие ![]() —
выпадение четного числа очков при однократном бросании игральной кости; тогда
—
выпадение четного числа очков при однократном бросании игральной кости; тогда ![]() — выпадение нечетного числа
очков.
— выпадение нечетного числа
очков.
Теорема 1. Для любого события ![]() вероятность
противоположного события
вероятность
противоположного события ![]() выражается равенством
выражается равенством
|
|
(3) |
Доказательство. Событие ![]() +
+![]() , состоящее в наступлении
или события
, состоящее в наступлении
или события ![]() , или события
, или события ![]() , очевидно, является
достоверным. Поэтому на основании аксиомы 2 имеем Р(
, очевидно, является
достоверным. Поэтому на основании аксиомы 2 имеем Р(![]() +
+![]() )=1. Так как события
)=1. Так как события ![]() и
и ![]() несовместны, то используя аксиому 3, получим Р(
несовместны, то используя аксиому 3, получим Р(![]() +
+![]() )=Р(
)=Р(![]() )+P(
)+P(![]() ). Следовательно, Р(
). Следовательно, Р(![]() )+P(
)+P(![]() )=1, откуда
)=1, откуда ![]() .
.
Теорема 2. Вероятность невозможного события равна нулю.
Доказательство непосредственно следует из аксиомы 2 и теоремы 1, если заметить, что невозможное событие противоположно достоверному событию.
Классическое определение вероятности
Как было сказано выше, при большом числе n испытаний частота P*(A)=m/n
появления события A обладает устойчивостью и дает приближенное значение
вероятности события A, т.е. ![]() .
.
Это обстоятельство позволяет находить приближенно вероятность события опытным путем. Практически такой способ нахождения вероятности события не всегда удобен. В ряде случаев вероятность события удается определить до опыта с помощью понятия равновероятности событий (или равновозможности).
Два события называются равновероятными (или равновозможными), если нет никаких объективных причин считать, что одно из них может наступить чаще, чем другое.
Так, например, появления герба или надписи при бросании монеты представляют собой равновероятные события.
Рассмотрим другой пример. Пусть бросают игральную кость. В силу симметрии кубика можно считать, что появление любой из цифр 1, 2, 3, 4, 5 или 6 одинаково возможно (равновероятно).
События E1,E2, ..., EN в данном опыте образуют полную группу, если в результате опыта должно произойти хотя бы одно из них. Так, в последнем примере полная группа событий состоит из шести событий — появлений цифр 1, 2, 3, 4, 5 и 6.
Очевидно, любое событие A и противоположное ему событие ![]() образуют полную группу.
образуют полную группу.
Событие B называется благоприятствующим событию A, если наступление события B влечет за собой наступление события A.
Так, если A — появление четного числа очков при бросании игральной кости, то появление цифры 4 представляет собой событие, благоприятствующее событию A.
Пусть события E1,E2, ..., EN в данном опыте образуют полную группу равновероятных и попарно несовместных событий. Будем называть их исходами испытания. Предположим, что событию A благоприятствуют M исходов испытания. Тогда вероятностью события A в данном опыте называют отношение M/N. Итак, мы приходим к следующему определению.
Вероятностью P(A) события в данном опыте называется отношение числа M исходов опыта, благоприятствующих событию A, к общему числу N возможных исходов опыта, образующих полную группу равновероятных попарно несовместных событий:
![]()
Это определение вероятности часто называют классическим. Можно показать, что классическое определение удовлетворяет аксиомам вероятности.
Пример 1. На завод привезли партию из 1000 подшипников. Случайно в эту партию попало 30 подшипников, не удовлетворяющих стандарту. Определить вероятность P(A) того, что взятый наудачу подшипник окажется стандартным.
Решение: Число стандартных подшипников равно 1000—30=970. Будем считать, что каждый подшипник имеет одинаковую вероятность быть выбранным. Тогда полная группа событий состоит из N=1000 равновероятных исходов, из которых событию A благоприятствуют М=970 исходов. Поэтому P(A)=M/N=970/1000=0.97
Пример 2. В урне 10 шаров: 3 белых и 7 черных. Из урны вынимают сразу два шара. Какова вероятность р того, что оба шара окажутся белыми?
Решение: Число N всех равновероятных исходов испытания равно числу способов, которыми можно из 10 шаров вынуть два, т. е. числу сочетаний из 10 элементов по 2:
![]()
Число благоприятствующих исходов:
![]()
Следовательно, искомая вероятность
![]()
Пример 3. В урне 2 зеленых, 7 красных, 5 коричневых и 10 белых шаров. Какова вероятность появления цветного шара?
Решение: Находим соответственно вероятности появления зеленого,
красного и коричневого шаров:
Р(зел.)=2/24; Р(кр.)=7/24; Р(кор.)=5/24. Так как рассматриваемые события,
очевидно, несовместны, то, применяя аксиому сложения, найдем вероятность
появления цветного шара:
![]()
Условная вероятность. Теорема умножения вероятностей
Во многих задачах приходится находить вероятность совмещения событий А и В, если известны вероятности событий А и В.
Рассмотрим следующий пример. Пусть брошены две монеты. Найдем вероятность появления двух гербов. Мы имеем 4 равновероятных попарно несовместных исхода, образующих полную группу:
|
|
1-я монета |
2-я монета |
|
1-й исход |
герб |
герб |
|
2-й исход |
герб |
надпись |
|
3-й исход |
надпись |
герб |
|
4-й исход |
надпись |
надпись |
Таким образом, P(герб,герб)=1/4. Пусть теперь нам стало известно, что на первой монете выпал герб. Как изменится после этого вероятность того, что герб появится на обеих монетах? Так как на первой монете выпал герб, то теперь полная группа состоит из двух равновероятных несовместных исходов:
|
|
1-я монета |
2-я монета |
|
1-й исход |
герб |
герб |
|
2-й исход |
герб |
надпись |
При этом только один из исходов благоприятствует событию (герб, герб). Поэтому при сделанных предположениях Р(герб,герб)=1/2. Обозначим через А появление двух гербов, а через В — появление герба на первой монете. Мы видим, что вероятность события А изменилась, когда стало известно, что событие B произошло.
Новую вероятность события А, в предположении, что произошло событие B, будем обозначать PB(А).
Таким образом, Р(A)=1/4; PB(А)=1/2
Теорема умножения. Вероятность совмещения событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие осуществилось, т. е.
|
P(AB)=P(A)PA(B) |
(4) |
Доказательство. Докажем справедливость соотношения (4), опираясь на классическое определение вероятности. Пусть возможные исходы Е1, Е2, ..., ЕN данного опыта образуют полную группу равновероятных попарно несовместных событий, из которых событию A благоприятствуют M исходов, и пусть из этих M исходов L исходов благоприятствуют событию B. Очевидно, что совмещению событий A и B благоприятствуют L из N возможных результатов испытания. Это дает
![]() ;
; ![]() ;
; ![]()
Таким образом,
![]()
Поменяв местами A и B, аналогично получим
|
|
(5) |
Из формул (4) и (5) имеем
|
|
(6) |
Теорема умножения легко обобщается на любое , конечное число событий. Так, например, в случае трех событий A1, A2, A3 имеем *
![]()
В общем случае
|
|
(7) |
Введем теперь следующее определение. Два события A и B называются независимыми, если предположение о том, что произошло одно из них, не изменяет вероятность другого, т. е. если
|
|
(8) |
Из соотношения (6) вытекает, что из двух равенств (8) одно является следствием другого.
Пусть, например, событие A — появление герба при однократном брссании монеты, а событие B — появление карты бубновой масти при вынимании карты из колоды. Очевидно, что события A и B независимы. В случае независимости событий A к B формула (4) примет более простой вид:
|
|
(9) |
т. е. вероятность совмещения двух независимых событий равна произведению вероятностей этих событий.
События А1, А2, ..., Аn называются независимыми в совокупности, если вероятность наступления каждого из них не меняет своего значения после того, как одно или несколько из остальных событий осуществились.
Исходя из этого определения, в случае независимости событий А1, А2, ..., Аn между собой в совокупности на основании формулы (7) имеем
|
|
(10) |
Пример 1. Какова вероятность того, что при десятикратном бросании монеты герб выпадет 10 раз?
Решение: Пусть событие Ai — появление герба при i-м бросании. Искомая вероятность есть вероятность совмещения всех событий Ai (i=1,2,3,...,10), а так как они, очевидно, независимы в совокупности, то применяя формулу (10), имеем
![]()
Но P(Ai)=1/2 для любого i; поэтому
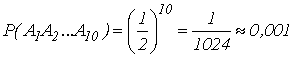
Пример 2. Рабочий обслуживает три станка, работающих независимо друг от друга. Вероятность того, что в течение часа станок не потребует внимания рабочего, для первого станка равна 0,9, для второго — 0,8, для третьего — 0,7. Найти: 1) вероятность р того, что в течение часа ни один из трех станков не потребует внимания рабочего; 2) вероятность того, что в течение часа по крайней мере один из станков не потребует внимания рабочего.
Решение:
1) Искомую вероятность р находим по формуле (10):
![]()
2) Вероятность того, что в течение часа станок потребует внимания рабочего для первого станка равна 1—0,9=0,1, для второго и для третьего станков она соответственно равна 1—0,8=0,2 и 1—0,7=0,3. Тогда вероятность того, что в течение часа все три станка потребуют внимания рабочего, на основании формулы (10) составляет
![]()
Событие A, заключающееся в том, что в течение часа все три станка
потребуют внимания рабочего, противоположно событию ![]() , состоящему в том, что по крайней мере один из станков не
потребует внимания рабочего. Поэтому по формуле (3) получаем
, состоящему в том, что по крайней мере один из станков не
потребует внимания рабочего. Поэтому по формуле (3) получаем
![]()
Пример 3. Из урны, содержащей 3 белых и 7 черных шаров, вынимают два шара. Какова вероятность того, что оба шара окажутся белыми ?
Решение: Эта задача уже была решена в п. 3 с помощью классического определения вероятности. Решим ее, применяя формулу (5). Извлечение двух шаров равносильно последовательному их извлечению. Обозначим через А появление белого шара при первом извлечении, а через В — при втором. Событие, состоящее в появлении двух белых шаров, является совмещением событий А и В. По формуле (5) имеем
![]()
Но Р(А)=3/10; РA(В)=2/9, поскольку после того, как был вынут первый белый
шар, в урне осталось 9 шаров, из которых 2 белых. Следовательно,
![]()
Формула полной вероятности
Пусть событие A может произойти только вместе с одним из попарно несовместных событий H1, H2, ..., Hn, образующих полную группу. Тогда, если произошло событие A, то это значит, что произошло одно из попарно несовместных событий H1A, H2A, ..., HnA. Следовательно,
![]()
Применяя аксиому сложения вероятностей, имеем
![]()
Но ![]() (i=1, 2, ..., n), поэтому
(i=1, 2, ..., n), поэтому
|
|
(11) |
Эта формула называется формулой полной вероятности. События H1, H2, ..., Hn часто называют «гипотезами».
Пример. В магазин поступили электрические лампочки одного типа, изготовленные на четырех ламповых заводах: с 1-го завода 250 шт., со 2-го — 525 шт., с 3-го — 275 шт. и с 4-го — 950 шт. Вероятность того, что лампочка прогорит более 1500 часов, для 1-го завода равна 0,15, для 2-го — 0,30, для 3-го — 0,20, для 4-го — 0,10. При раскладке по полкам магазина лампочки были перемешаны. Какова вероятность того, что купленная лампочка прогорит более 1500 часов?
Решение: Пусть A — событие, состоящее в том, что лампочка прогорит более 1500 часов, а Н1, Н2, Н3 и Н4 — гипотезы, что она изготовлена соответственно 1, 2, 3 или 4-м заводом. Так как всего лампочек 2000 шт., то вероятности гипотез соответственно равны
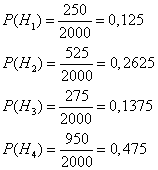
Далее, из условия задачи следует, что
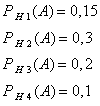
Используя формулу полной вероятности (11), имеем
![]()
Формула Бейеса
Предположим, что производится некоторый опыт, причем об условиях его
проведения можно высказать n единственно возможных и несовместных гипотез ![]() , имеющих вероятности
, имеющих вероятности ![]() . Пусть в результате опыта
может произойти или не произойти событие А, причем известно, что если опыт
происходит при выполнении гипотезы
. Пусть в результате опыта
может произойти или не произойти событие А, причем известно, что если опыт
происходит при выполнении гипотезы ![]() , то
, то ![]()
![]()
Спрашивается, как изменятся вероятности гипотез, если стало известным,
что событие А произошло? Иными словами, нас интересуют значения вероятностей ![]() На основании соотношений
(4) и (5) имеем
На основании соотношений
(4) и (5) имеем
![]()
![]()
откуда
![]()
Но по формуле полной вероятности
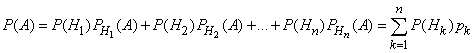
Поэтому
|
|
|
(12) |
Формула (12) называется формулой Бейеса*.
Пример. На склад поступило 1000 подшипников. Из них 200 изготовлены на 1-м заводе, 460—на 2-м и 340 - на 3-м. Вероятность того, что подшипник окажется нестандартным, для 1-го завода равна 0,03, для 2-го — 0,02, для 3-го — 0,01. Взятый наудачу подшипник оказался н естандартным. Какова вероятность того, что он изготовлен 1-м заводом?
Решение: Пусть A — событие, состоящее в том, что взятый Подшипник
нестандартный, а ![]() - гипотезы, что он
изготовлен соответственно 1-м, 2-м или 3-м заводом. Вероятности указанных
гипотез составляют
- гипотезы, что он
изготовлен соответственно 1-м, 2-м или 3-м заводом. Вероятности указанных
гипотез составляют
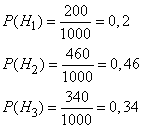
Из условия задачи следует, что
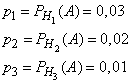
Найдем ![]() , т. е. вероятность того,
что подшипник, оказавшийся нестандартным, изготовлен 1-м заводом. По формуле
Бейеса имеем
, т. е. вероятность того,
что подшипник, оказавшийся нестандартным, изготовлен 1-м заводом. По формуле
Бейеса имеем
![]()
Таким образом, вероятность гипотезы, что подшипник изготовлен 1-м заводом, изменилась после того, как стало известно, что он нестандартен.
Последовательные испытания. Формула Бернули
Предположим, что производится n независимых испытаний, в результате
каждого из которых может наступить или не наступить некоторое событие A. Пусть
при каждом испытании вероятность наступления события А равна P(A)=p и,
следовательно, вероятность противоположного события (ненаступления А) равна ![]() . Определим вероятность Pn(m)
того, что событие А произойдет m раз при n испытаниях. При этом заметим, что
наступления или ненаступления события А могут чередоваться различным образом.
Условимся записывать возможные результаты испытаний в виде комбинаций букв А и
. Определим вероятность Pn(m)
того, что событие А произойдет m раз при n испытаниях. При этом заметим, что
наступления или ненаступления события А могут чередоваться различным образом.
Условимся записывать возможные результаты испытаний в виде комбинаций букв А и ![]() . Например, запись
. Например, запись ![]() означает, что в четырех
испытаниях событие осуществилось в 1-м и 4-м случаях и не осуществилось во 2-м
и 3-м случаях.
означает, что в четырех
испытаниях событие осуществилось в 1-м и 4-м случаях и не осуществилось во 2-м
и 3-м случаях.
Всякую комбинацию, в которую А входит m раз и ![]() входит n-m раз, назовем благоприятной. Количество благоприятных
комбинаций равно количеству k способов, которыми можно выбрать m чисел из
данных n; таким образом, оно равно числу сочетаний из n элементов по m, т.е.
входит n-m раз, назовем благоприятной. Количество благоприятных
комбинаций равно количеству k способов, которыми можно выбрать m чисел из
данных n; таким образом, оно равно числу сочетаний из n элементов по m, т.е.
![]()
Подсчитаем вероятности благоприятных комбинаций. Рассмотрим сначала случай, когда событие A происходит в первых m испытаниях и, следовательно, не происходит в остальных n-m испытаниях. Такая благоприятная комбинация имеет следующий вид:
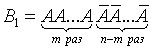
Вероятность этой комбинации в силу независимости испытаний (на основании теоремы умножения вероятностей) составляет
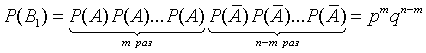
Так как в любой другой благоприятной комбинации Вi событие A встречается
также m раз, а событие ![]() происходит n-m раз, то
вероятность каждой из таких комбинаций также равна
происходит n-m раз, то
вероятность каждой из таких комбинаций также равна ![]() .
Итак
.
Итак
![]()
Все благоприятные комбинации являются, очевидно, несовместными. Поэтому (на основании аксиомы сложения вероятностей)
![]()
Следовательно,
|
|
(13) |
|
или, так как |
|
, то |
|
|
(13') |
Формула (13) называется формулой Бернулли *.
Пример 1. Вероятность попадания в цель при одном выстреле равна 0,6.
Какова вероятность того, что 8 выстрелов дадут 5 попаданий?
Решение: Здесь
n=8;
m=5;
p=0,6;
q=1-0,6=0,4.
Используя формулу (13'), имеем
![]()
Пример 3. Игральную кость бросают 80 раз. Определить вероятность того, что цифра 3 появится 20 раз.
Решение: Здесь
m=20;
n=80;
p=1/6;
q=1-1/6=5/6;
далее находим
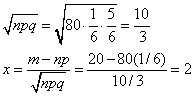
Используя формулу (15), получим
![]()
так как из табличного значения находим, что
![]()
1. Дано:
В партии из 23 деталей находятся 10 бракованных. Вынимают из
партии наудачу две детали. Используя классическое определение теории
вероятности определить, какова вероятность того, что обе детали окажутся
бракованными.
Решение:
Число N всех равновероятных исходов испытания равно
числу способов, которыми можно из 23 деталей вынуть две, т.е. числу сочетаний
из 23 элементов по 2:
![]()
Число благоприятных исходов
![]()
Cледовательно, искомая вероятность
![]()
2. Дано:
В ящике лежат шары: 4 белых, 10 красных, 8 зеленых, 9
коричневых. Из ящика вынимают один шар. Пользуясь теоремой сложения
вероятностей определить, какова вероятность, что шар окажется цветным (не
белым) ?
Решение:
Всего в ящике лежит N=4+10+8+9=31 шар.
Вероятность вытащить красный шар
![]()
Вероятность вытащить зеленый шар
![]()
Вероятность вытащить коричневый шар
![]()
Т.к. эти три события несовместны, то пользуясь теоремой
сложения вероятностей определим вероятность того, что шар окажется цветным (не
белым)
![]()
3. Дано:
В вопросах к зачету имеются 75% вопросов, на которые студенты
знают ответы. Преподаватель выбирает из них два вопроса и задает их студенту.
Определить вероятность того, что среди полученных студентом вопросов есть хотя
бы один, на который он знает ответ
Решение:
Вероятность вытащить знакомый вопрос p=0.75,
незнакомый q=1-p=1-0.75=0.25
Пусть H1 - гипотеза, что студент не знает ни одного из
2-х вопросов.
Вероятность этой гипотезы:
![]()
Искомая вероятность соответственно равна:
![]()
4. Дано:
На складе находятся 26 деталей из которых 13 стандартные.
Рабочий берет наугад две детали. Пользуясь теоремой умножения вероятностей
зависимых событий определить вероятность того, что обе детали окажутся
стандартными.
Решение:
Извлечение двух деталей равносильно последовательному их
извлечению. Обозначим через A - появление стандартной детали при первом
извлечении, а через B - при втором. Событие, состоящее в извлечении двух
стандартных деталей, является совмещением событий А и B.
Пользуясь теоремой умножения вероятностей имеем:
![]()
, где
![]()
Поскольку после того, как была вынута первая стандартная
деталь на складе осталось 25 деталей, из которых 12 стандартных, то
![]()
, тогда
![]()
5. Дано:
В сборочный цех поступили детали с трех станков. На первом
станке изготовлено 51% деталей от их общего количества, на втором станке 24% и
на третьем 25%. При этом на первом станке было изготовлено 90% деталей первого
сорта, на втором 80% и на третьем 70%. Используя формулу полной вероятности
определить, какова вероятность того, что взятая наугад деталь окажется первого
сорта ?
Решение:
Пусть A - cобытие, состоящее в том, что взятая деталь
окажется первого сорта, а H1, H2 и H3 - гипотезы, что она
изготовлена соответственно на 1, 2 и 3 станке.
Вероятности этих гипотез соответственно равны:
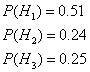
далее, из условия задачи следует, что:
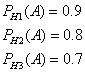
Используя формулу полной вероятности, получим искомую
вероятность
![]()
6. Дано:
Имеется три одинаковых по виду ящика. В первом ящике
находится 26 белых шаров, во втором 15 белых и 11 черных, в третьем ящике 26
черных шаров. Из выбранного наугад ящика вынули белый шар. Используя формулу
Байеса вычислить вероятность того, что белый шар вынут из первого ящика.
Решение:
Пусть A - cобытие, состоящее в том, что взятый шар
окажется белым, а H1 и H2 - гипотезы, что он был взят из 1-го и
2-го ящика. (Третий ящик рассматривать не будем, т.к. там только черные шары, а
из условий известно, что вынут именно белый шар.)
Вероятности указанных гипотез соответственно равны:
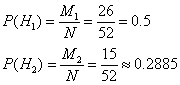
, здесь N=26+15+11=52 - количество шаров в 1-м и 2-м
ящиках
Из условия задачи следует, что:
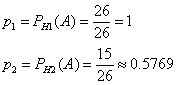
Найдем PA(H1), т.е. вероятность того, что вынутый
белый шар был взят из 1-го ящика.
![]()
7. Дано:
Вероятность изготовления нестандартной детали равна 0.11.
Пользуясь формулой Бернулли найти вероятность того, что из пяти наудачу взятых
деталей будут четыре стандартных.
Решение:
Формула Бернулли:
![]()
В соответствии с исходными данными, здесь:
q=0.11
p=1-q=1-0.11=0.89
n=5
m=4
Используя формулу Бернулли получим:
![]()
Варианты заданий
Вариант 1
1. Сколькими способами можно составить трехцветный
полосатый флаг, если имеется материал 5 различных цветов?
2. Сколько четырехзначных чисел можно составить из цифр 1,2,3,4
при условии, что каждая цифра может содержаться в записи числа лишь нечетное число раз?
3. Решите уравнение ![]() .
.
4. Из колоды в 36 карт вытаскивают две карты. Какова вероятность извлечь при этом 2 туза?
Вариант 2
1. В яхт-клубе состоит 9 человек. Из них надо выбрать председателя, заместителя, секретаря и казначея. Сколькими способами это можно сделать?
при условии, что каждая цифра может содержаться в записи числа лишь 1 раз?
4. Из колоды в 36 карт вытаскивают три карты. Какова вероятность того, что все они тузы?
Вариант 3
1. Из 30 членов спортивного клуба надо не только составить команду
из 4 человек для участия в четырехэтапной эстафете, но и определить порядок выхода спортсменов на этапы. Сколькими способами это можно сделать?
2. Сколько трехзначных чисел можно составить из цифр 1,2,3
при условии, что цифры могут повторяться?
3.
Решите уравнение ![]() .
.
4. В урне находится 3 белых и 4 черных шара. Какова вероятность того, что вынутые из нее наудачу два шара окажутся белыми?
Вариант 4
1. В городской думе 30 человек. Из них надо выбрать председателя и трех его заместителей. Сколькими способами это можно сделать?
2. Сколько трехзначных чисел можно составить из цифр 1,2,3,4,0 при условии, что каждая цифра может содержаться в записи числа лишь 1 раз?
4. В урне находится 2 белых, 3 красных и 16 черных шаров. Какова вероятность того, что из вынутых из нее наудачу двух шаров один окажется белым, а другой красным?
Вариант 5
1.Сколькими способами можно выбрать из полной колоды,
содержащей 36 карт, 4 карты разных мастей при условии, что среди вынутых карт нет ни одной пары карт одинакового достоинства?
при условии, что одна и только одна цифра содержится в записи числа четное число раз?
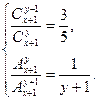
4. В лотерее 4 выигрышных билета и 96 пустых. Какова вероятность того, что на 10 купленных билетов выпадет хотя бы один выигрыш?
Вариант 6
1. В классе 15 девочек и 17 мальчиков. Для дежурства на избирательном участке надо выделить трех девочек и двух мальчиков. Сколькими способами это можно сделать?
при условии, что одна и только одна цифра содержится в записи числа четное число раз?
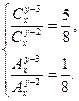
4. Из колоды в 36 карт наудачу вынимают 3 карты. Какова вероятность того, что среди них окажется хотя бы один туз?
Цель работы:
Используя теоретический материал и образцы решения задач, решить примеры по теме «Вычисление производных и дифференциалов высших порядков»
Перечень справочной литературы :
1. Математика: учебник для студентов образовательных учреждений СПО/С.Г. Григорьев, С.В. Иволгина; под редакцией В.А. Гусева – 10-е изд., стер. – М.: Издательский центр «Академия». 2014. – 416 с.
2. Элементы высшей математики: учебник для студентов образовательных учреждений СПО/С.Г. Григорьев, Ю.А. Дубинский – 9-е изд., стер. – М.: Издательский центр «Академия». 2013. – 320 с.
3. Шипачев В.С. Основы высшей математика: учебник для вузов. -М. Высш.шк., 2010 г.
Краткие теоретические сведения:
Правила дифференцирования
1) ![]() ;
;
2) ![]() , в частности
, в частности ![]() ;
;
3) ![]() ;
;
4) ![]() , если
, если![]() ;
;
5) ![]() , если
, если ![]() и
и ![]() .
.
Формулы дифференцирования
![]()
![]() в частности,
в частности, ![]()
![]() в частности,
в частности, ![]()
![]() в частности,
в частности, ![]()
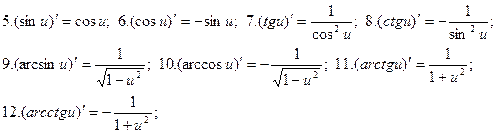
Примеры нахождения производной элементарных функций:
1) 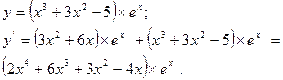
2) 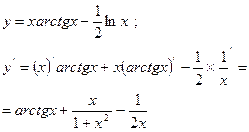
3) ![]()
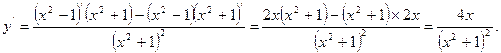
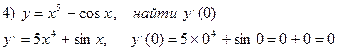
Производная сложной и обратной функций
Определение. Пусть ![]() и
и ![]() ,
тогда
,
тогда ![]() - сложная функция с
промежуточным аргументом
- сложная функция с
промежуточным аргументом ![]() и
независимым аргументом
и
независимым аргументом ![]() .
.
Теорема. Если функция ![]() имеет
производную
имеет
производную ![]() в точке
в точке ![]() , а функция
, а функция ![]() имеет производную
имеет производную ![]() в соответствующей точке
в соответствующей точке ![]() , то сложная функция
, то сложная функция ![]() имеет производную
имеет производную ![]() в точке
в точке ![]() которая находится по формуле
которая находится по формуле ![]() .
.
Правило нахождения производной сложной функции:
Для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу.
Это правило остается в силе, если промежуточных аргументов несколько.
Пример. Вычислить производную сложной функции:
1) ![]() .
.
Решение:
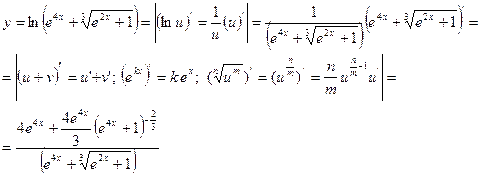
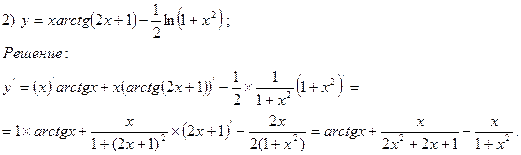
Обратная функция
Определение. Пусть задана функция ![]() с
областью определения D и множеством значений
с
областью определения D и множеством значений ![]() . Если каждому значению
. Если каждому значению ![]() соответствует единственное
значение
соответствует единственное
значение ![]() , то определена функция
, то определена функция ![]() с областью определения
с областью определения ![]() и множеством значений D (рис1). Такая функция
и множеством значений D (рис1). Такая функция ![]() называется
обратной к функции
называется
обратной к функции ![]() и записывается
в следующем виде:
и записывается
в следующем виде: ![]() . Про функции
. Про функции ![]() и
и ![]() говорят,
что они являются взаимно обратными.
говорят,
что они являются взаимно обратными.
![]()
![]()
![]() (рис
1)
(рис
1)
Примеры:
1) ![]() и
и ![]()
2) ![]() и
и ![]()
3) ![]() и
и ![]()
( Для того, чтобы для функции ![]() найти обратную функцию надо
переменную
найти обратную функцию надо
переменную ![]() выразить через
переменную у).
выразить через
переменную у).
Теорема.
Если функция ![]() строго монотонна на
интервале (а;b) и имеет не равную нулю производную
строго монотонна на
интервале (а;b) и имеет не равную нулю производную ![]() в производной точке этого
интервала, то обратная ей функция
в производной точке этого
интервала, то обратная ей функция ![]() также
имеет производную
также
имеет производную ![]() в
соответствующей точке, определяемую равенством
в
соответствующей точке, определяемую равенством ![]() .
.
Пример:
1. Пользуясь
правилом дифференцирования обратной функции, найти производную функции ![]()
Решение: Обратная функция ![]() имеет производную
имеет производную ![]() . Следовательно,
. Следовательно,
 .
.
Дифференциал функции
Определение. Если функция ![]() дифференцируема
в точке
дифференцируема
в точке ![]() , т.е. имеет в этой
точке конечную производную
, т.е. имеет в этой
точке конечную производную![]() , то ее
приращение
, то ее
приращение ![]() можно записать в виде
можно записать в виде ![]() , где
, где ![]() .
.
Главная, линейная относительно ![]() часть
часть ![]() приращения функции называется
дифференциалом функции и обозначается
приращения функции называется
дифференциалом функции и обозначается![]()
![]() :
:
![]() .
. ![]()
При достаточно малых ![]() приращение
функции приближенно равно ее дифференциалу т.е.
приращение
функции приближенно равно ее дифференциалу т.е. ![]() .
.
Примеры:
Решение:
Используя формулу, ![]() получаем dy
= (-sinx+10x)dx.
получаем dy
= (-sinx+10x)dx.
2. Для функции ![]() найти приращение
найти приращение![]() при
при ![]() и
и![]() .
.
Решение:
Используя формулу, ![]() получаем
получаем ![]() (
(![]() )
)![]()
![]() =
=
=(![]() )
)![]() . Выполняя подстановку
. Выполняя подстановку ![]() и
и![]() , находим
приращение
, находим
приращение![]() :
:
![]() =(3
=(3![]()
![]() )
)![]() =0,05
=0,05
Ответ: ![]() =0,05
=0,05
Перечень заданий.
Вариант 1
Найдите производную функции:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
Вариант 2
Найдите производную функции:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
Вариант 3
Найдите производную функции:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
Вариант 4
Найдите производную функции:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
Вариант 5
Найдите производную функции:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
Вариант 6
Найдите производную функции:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
|
Вариант 1 Найдите дифференциал функции: |
Вариант 2 Найдите дифференциал функции: |
|
Вариант 3 Найдите дифференциал функции: |
Вариант 4 Найдите дифференциал функции:
|
|
Вариант 5 Найдите дифференциал функции: |
Вариант 6 Найдите дифференциал функции:
|
Цель работы:
Используя теоретический материал и образцы решения задач, решить примеры по теме «Исследование функции при помощи производных. Исследование и построение графиков сложных функций»
Перечень справочной литературы :
1. Математика: учебник для студентов образовательных учреждений СПО/С.Г. Григорьев, С.В. Иволгина; под редакцией В.А. Гусева – 10-е изд., стер. – М.: Издательский центр «Академия». 2014. – 416 с.
2. Элементы высшей математики: учебник для студентов образовательных учреждений СПО/С.Г. Григорьев, Ю.А. Дубинский – 9-е изд., стер. – М.: Издательский центр «Академия». 2013. – 320 с.
3. Шипачев В.С. Основы высшей математика: учебник для вузов. -М. Высш.шк., 2010 г.
Краткие теоретические сведения:
Исследование функции при помощи производных
Некоторые теоремы о дифференцируемых
функциях
Теорема
Ролля. Если функция ![]() непрерывна
на отрезке
непрерывна
на отрезке ![]() , дифференцируема на
интервале (а;b) и на концах отрезка принимает
одинаковые значения
, дифференцируема на
интервале (а;b) и на концах отрезка принимает
одинаковые значения ![]() , то найдется
хотя бы одна точка
, то найдется
хотя бы одна точка ![]() (а;b), в которой производная
(а;b), в которой производная ![]() обращается
в нуль, т. е.
обращается
в нуль, т. е. ![]() .
.
Теорема Коши.
Если функции ![]() и
и ![]() непрерывны на отрезке
непрерывны на отрезке ![]() , дифференцируемы на интервале (а;b), причем
, дифференцируемы на интервале (а;b), причем ![]() для
для ![]() (а;b) то
найдется хотя бы одна точка
(а;b) то
найдется хотя бы одна точка ![]() (а;b) такая, что выполняется равенство
(а;b) такая, что выполняется равенство ![]() .
.
Теорема
Лагранжа. Если функция ![]() непрерывна
на отрезке
непрерывна
на отрезке ![]() , дифференцируема на
интервале (а;b) и на концах отрезка принимает
одинаковые значения
, дифференцируема на
интервале (а;b) и на концах отрезка принимает
одинаковые значения ![]() , то найдется
хотя бы одна точка
, то найдется
хотя бы одна точка ![]() (а;b) такая, что выполняется равенство
(а;b) такая, что выполняется равенство ![]() .
.
Следствие 1 Если производная некоторой функции на промежутке равна нулю, то функция постоянна на этом промежутке.
Следствие 2 Если две функции имеют равные производные на некотором промежутке, то они отличаются друг от друга на постоянное слагаемое.
Возрастание и убывание функций
Теорема 1. (необходимые условия). Если дифференцируемая на
интервале (а;b) функция ![]() возрастает
(убывает), то
возрастает
(убывает), то ![]()
![]() для любого
для любого ![]() .
.
Теорема 2. (достаточные условия). Если функция ![]() дифференцируема на интервале (a;b) и
дифференцируема на интервале (a;b) и ![]()
![]() для любого
для любого ![]() , то эта функция возрастает
(убывает) на интервале (a;b).
, то эта функция возрастает
(убывает) на интервале (a;b).
Теоремы 1 и 2 позволяют довольно просто исследовать функцию на монотонность (функция, убывающая или возрастающая, называется монотонной).
Пример. Исследовать функцию ![]() =x3-3x-4 на монотонность.
=x3-3x-4 на монотонность.
Решение:
![]()
![]()
![]()
![]() +
- +
+
- +
![]() Х
Х
-1 1
![]() при
при
![]()
![]() при
при
![]()
Ответ: данная функция возрастает при ![]() и убывает
и убывает ![]()
Максимум и минимум функций
Теорема (необходимое условие). Если дифференцируемая функция ![]() имеет экстремум в точке
имеет экстремум в точке ![]() , то ее
производная в этой точке равна нулю:
, то ее
производная в этой точке равна нулю: ![]() =0.
=0.
Теорема (достаточное условие экстремума). Если непрерывная функция
![]() дифференцируема в некоторой
дифференцируема в некоторой ![]() -окрестности критической точки
-окрестности критической точки ![]() и при переходе
через нее (слева на право) производная
и при переходе
через нее (слева на право) производная ![]() меняет
знак с плюса на минус, то
меняет
знак с плюса на минус, то ![]() есть точка максимума, с минуса на
плюс, то
есть точка максимума, с минуса на
плюс, то ![]() - точка минимума.
- точка минимума.
Удобно использовать другой достаточный признак существования экстремума основанный на определении знака второй производной.
Теорема. Если в точке ![]() первая производная функции
первая производная функции ![]() равна
нулю
равна
нулю ![]() , а вторая производная в
точке
, а вторая производная в
точке ![]() существует и отличная от нуля
существует и отличная от нуля ![]() , то при
, то при ![]() в точке
в точке ![]() функция имеет максимум и минимум - при
функция имеет максимум и минимум - при ![]() .
.
Выпуклость графика функции. Точки перегиба
Точка графика непрерывной функции ![]() ,
отделяющая его части разной выпуклости, называется точкой перегиба.
,
отделяющая его части разной выпуклости, называется точкой перегиба.
Теорема. Если функция ![]() во
всех точках интервала (a;b)
имеет отрицательную вторую производную, т.е.
во
всех точках интервала (a;b)
имеет отрицательную вторую производную, т.е. ![]() ,
то график функции в этом интервале выпуклый вверх.
,
то график функции в этом интервале выпуклый вверх.
Если же ![]() для любого
для любого ![]() - график выпуклый вниз.
- график выпуклый вниз.
Теорема (достаточное условие существования точек перегиба). Если
вторая производная ![]() при переходе
через точку
при переходе
через точку ![]() в
которой она равна нулю или не существует, меняет знак, то точка графика с
абсциссой
в
которой она равна нулю или не существует, меняет знак, то точка графика с
абсциссой ![]() есть
точка перегиба.
есть
точка перегиба.
Асимптоты графика функции
Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой.
Асимптоты бывают вертикальными, наклонными и горизонтальными.
Прямая х=а является вертикальной асимптотой графика функции ![]() , если
, если ![]() , или
, или ![]() , или
, или ![]() .
.
Если существует наклонная асимптота у=Rx+b, то R и b
находится по формуле: ![]() ,
, ![]() .
.
Если R=0, то у=b- уравнение горизонтальной асимптоты.
Общая схема исследования функции и построения
графика функции
Исследование функции целесообразно вести в определенной последовательности.
1. Найти область определения функции.
2. Найти (если это можно) точки пересечения графика с осями координат.
3. Найти интервалы знакопостоянства функции (промежутки, на которых ![]() >0 или
>0 или ![]() <0).
<0).
4. Выяснить, является ли функция четной, нечетной или общего вида.
5. Найти асимптоты графика функции.
6. Найти интервалы монотонности функции.
7. Найти экстремумы функции.
8. Найти интервалы выпуклости и точки перегиба графика функции.
Пример. Исследовать функцию ![]() и построить ее график.
и построить ее график.
1. ![]()
2. ![]()
Точка (0;0)- точка пересечения графика с осями ОХ и ОУ.
3. Функция знакоположительна (у>0) в интервалах ![]() и
и ![]() ,
знакоотрицательна – в
,
знакоотрицательна – в ![]() и
и ![]()
4. Функция ![]() является
нечетной т.к.
является
нечетной т.к. ![]() .
Следовательно, график ее симметричен относительно начала координат. Для
построения графика достаточно исследовать ее при
.
Следовательно, график ее симметричен относительно начала координат. Для
построения графика достаточно исследовать ее при ![]() .
.
5. Прямые х = 1 и х = -1 являются ее вертикальными асимптотами.
Выясним наличие наклонной асимптоты.

![]()
Следовательно, есть горизонтальная асимптота ее уравнение у=0. Наклонных асимптот нет.
Прямая у=0 является асимптотой и при ![]() ,
и при
,
и при ![]() .
.
6.![]()
![]() .
.
Так как у’>0 в области определения, то функции является возрастающей на каждом интервале области определения.
7. Т.к. ![]() , то
критическими точками является точки
, то
критическими точками является точки
х1 = -1 и х2 = 1.
Данные точки не принадлежат области определения функции, значит, функция экстремумов не имеет.
8. Найдем у”
![]()

Точка (0;0) – точка перегиба графика функции.
График выпуклый вверх на интервалах ![]() и
и
![]() ; выпуклый вниз на интервалах
; выпуклый вниз на интервалах ![]()
![]() и
и
![]()
![]()
«Исследование функции при помощи производных»
Задание Исследовать функцию на монотонность и экстремум:
|
Вариант №1
|
Вариант №2
|
|
Вариант №3 1. y = 2. y = |
Вариант №4 1. y = 2. y = |
|
Вариант №5 1. y = 2. y = |
Вариант №6 1. y = 2. y = |
|
Вариант №7 1. y= 2. y = |
Вариант №8 1. y = 2. y = |
|
Вариант №9 1. y = 2. y = |
Вариант №10 1. y= |
Цель работы:
Используя теоретический материал и образцы решения задач, решить примеры по теме «Основные методы интегрирования»»
Перечень справочной литературы :
1. Математика: учебник для студентов образовательных учреждений СПО/С.Г. Григорьев, С.В. Иволгина; под редакцией В.А. Гусева – 10-е изд., стер. – М.: Издательский центр «Академия». 2014. – 416 с.
2. Элементы высшей математики: учебник для студентов образовательных учреждений СПО/С.Г. Григорьев, Ю.А. Дубинский – 9-е изд., стер. – М.: Издательский центр «Академия». 2013. – 320 с.
3. Шипачев В.С. Основы высшей математика: учебник для вузов. -М. Высш.шк., 2010 г.
Краткие теоретические сведения:
Определенный интеграл
Определение. Пусть функция ![]() определена
на отрезке [a;b], a<b. Разобьем этот отрезок на n произвольных частей точками
определена
на отрезке [a;b], a<b. Разобьем этот отрезок на n произвольных частей точками ![]()
В каждом из полученных частичных отрезков ![]() выберем
произвольную точку Сi
выберем
произвольную точку Сi ![]() и составим сумму
и составим сумму ![]() (*)
(*)
где ![]() . Сумма вида (*) называется интегральной
суммой для функции
. Сумма вида (*) называется интегральной
суммой для функции ![]() на отрезке [a;b].
на отрезке [a;b].
Обозначим через ![]() длину
наибольшего частичного отрезка разбиения:
длину
наибольшего частичного отрезка разбиения: ![]()
Определение. Если существует конечный предел интегральной суммы ![]() , когда
, когда ![]() так, что
так, что ![]() , то этот предел называют
определенным интегралом от функции
, то этот предел называют
определенным интегралом от функции ![]() на
отрезке [a;b] и обозначают
следующим образом:
на
отрезке [a;b] и обозначают
следующим образом:  или
или  . В этом случае функция
. В этом случае функция ![]() называется интегрируемой на
отрезке [a;b] . Числа a и b называются соответственно
нижним и верхним пределами интегрирования,
называется интегрируемой на
отрезке [a;b] . Числа a и b называются соответственно
нижним и верхним пределами интегрирования, ![]() –
подынтегральной функцией,
–
подынтегральной функцией, ![]() –
переменной интегрирования.
–
переменной интегрирования.
Отметим, что непрерывность функции является достаточным условием ее интегрируемости.
Основные свойства определенного интеграла
 ;
;  ;
;
 ; где a,
b, c любые числа.
; где a,
b, c любые числа.
 ;
;  .
.
Формула Ньютона – Лейбница
Если функция ![]() непрерывна на
отрезке [a;b] и функция у = F(x) является некоторой ее
первообразной на этом отрезке, то имеет место формула Ньютона – Лейбница
непрерывна на
отрезке [a;b] и функция у = F(x) является некоторой ее
первообразной на этом отрезке, то имеет место формула Ньютона – Лейбница  .
.
Вычисление определенных интегралов
Простым и удобным методом вычисления определенного интеграла  от непрерывной функции является
формула Ньютона-Лейбница:
от непрерывной функции является
формула Ньютона-Лейбница:  .
.
При вычислении определенных интегралов широко используется метод замены переменной и метод интегрирования по частям.
Интегрирование подстановкой
Пусть для вычисления интеграла  от
непрерывной функции сделана подстановка
от
непрерывной функции сделана подстановка ![]() =
=![]() (t)
(t)
Теорема. Если:
1) функция ![]() и её
производная
и её
производная ![]() непрерывны при
непрерывны при ![]() ;
;
2) множеством значений функции ![]() при
при ![]() является отрезок [a;b];
является отрезок [a;b];
3) ![]() и
и ![]() то
то 
Интегрирование по частям
Теорема. Если функции ![]()
![]() и
и ![]() имеют
непрерывные производные на отрезке [a;b],
то имеет место формула
имеют
непрерывные производные на отрезке [a;b],
то имеет место формула  .
.
Пример.
Вычислить  .
.
Решение:


Ответ: 
Неопределенный интеграл
Основные свойства неопределенного интеграла
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
12.2. Таблица основных интегралов.
![]() в частности,
в частности, ![]()

![]()
Основные методы интегрирования
Метод непосредственного интегрирования
Определение. Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств неопределенного интегрирования приводится к одному или нескольким табличным интегралом, называется непосредственном интегрированием.
Примеры:
1) ![]()
2) 
Метод интегрирования подстановкой
Метод
подстановки (или замены переменной) заключается в том, что заменяют ![]() на
на ![]() ,
где
,
где ![]() - непрерывно дифференцируемая
функция, полагают
- непрерывно дифференцируемая
функция, полагают ![]() и получают
и получают ![]() .
.
Примеры:
1) 
2) 
3) 
4) 
13.3. Метод интегрирования по частям
![]()
|
Вид интеграла |
Подстановка |
|
|
|
|
P(x) – многочлен. |
|
|
|
Двукратное интегрирование Например:
|
Примеры:
1) 
2) 
Порядок проведения работы:
№ 1Вычислить определенный интегралы:
|
Вариант 1 |
Вариант 2 |
||
|
1. |
|
1. |
|
|
2. |
|
2. |
|
|
3. |
|
3. |
|
|
4. |
|
4. |
|
№2. Применяя метод непосредственного интегрирования, вычислить интегралы:
|
Вариант 1 |
Вариант 2 |
||
|
1. |
|
1. |
|
|
2. |
|
2. |
|
|
3. |
|
3. |
|
|
4. |
|
4. |
|
№3. Пользуясь методом подстановки вычислить интегралы:
Вариант 1 Вариант 2
1. ![]() 1.
1. ![]()
2. ![]() 2.
2. ![]()
3.  3.
3. ![]()
4. ![]() 4.
4. ![]()
№4. С помощью метода интегрирования по частям вычислить интегралы:
Вариант 1 Вариант 2
1. ![]() 1.
1. ![]()
2. ![]() 2.
2. ![]()
3. ![]() 3.
3. ![]()
4. ![]() 4.
4. ![]()
Цель работы:
Используя теоретический материал и образцы решения задач, решить примеры по теме «Решение прикладных задач (Приложения определенного интеграла)»
Перечень справочной литературы :
1. Математика: учебник для студентов образовательных учреждений СПО/С.Г. Григорьев, С.В. Иволгина; под редакцией В.А. Гусева – 10-е изд., стер. – М.: Издательский центр «Академия». 2014. – 416 с.
2. Элементы высшей математики: учебник для студентов образовательных учреждений СПО/С.Г. Григорьев, Ю.А. Дубинский – 9-е изд., стер. – М.: Издательский центр «Академия». 2013. – 320 с.
3. Шипачев В.С. Основы высшей математика: учебник для вузов. -М. Высш.шк., 2010 г.
Краткие теоретические сведения:
Вычисление площади плоской фигуры
Найдем
площадь S криволинейной трапеции, ограниченной кривой ![]() осью
осью ![]() и
двумя прямыми
и
двумя прямыми ![]() и
и ![]() , где
, где ![]() ,
,
![]() (рис. 1)
(рис. 1)
Так
дифференциал переменной площади S есть площадь прямоугольника
с основанием dx и высотой ![]() ,
т. е.
,
т. е. ![]() , то, интегрируя это
равенство в пределах от a до b, получим
, то, интегрируя это
равенство в пределах от a до b, получим
![]()
(1)
Если
криволинейная трапеция прилегает к оси ![]() так,
что
так,
что ![]() ,
, ![]() (рис.
2), то дифференциал переменной площади S равен
(рис.
2), то дифференциал переменной площади S равен ![]() откуда
откуда
![]()
(2)
В
том случае, когда криволинейная трапеция, ограниченная кривой ![]() , осью
, осью ![]() и
прямыми x=a и x=b, лежит под осью
и
прямыми x=a и x=b, лежит под осью ![]() (рис.
3), площадь находится по формуле
(рис.
3), площадь находится по формуле
![]()
(3)
Если
фигура, ограниченная кривой ![]() , осью
, осью ![]() и прямыми x=a и x=b, расположена по обе стороны
от оси
и прямыми x=a и x=b, расположена по обе стороны
от оси ![]() (рис. 4), то
(рис. 4), то
![]()
(4)
Пусть,
наконец, фигура S ограничена двумя пересекающимися кривыми ![]() и
и ![]() и
прямыми x=a и x=b, где
и
прямыми x=a и x=b, где ![]() и
и ![]() (рис. 5). Тогда ее площадь
находится по формуле
(рис. 5). Тогда ее площадь
находится по формуле
![]()
(5)
Пример. Вычислить
площадь фигуры, ограниченной указанными линиями ![]()
![]()
![]() и
и ![]()
Решение. Выполним
построение фигуры. Строим прямую ![]() по двум точкам А(4;0) и В(0;2) (рис.6). Выразив у
через х, получим
по двум точкам А(4;0) и В(0;2) (рис.6). Выразив у
через х, получим ![]() По формуле (1),
где
По формуле (1),
где ![]() ,
, ![]() и
и ![]() ,
находим
,
находим
 (кв.
ед.)
(кв.
ед.)
В
качестве проверки вычислим площадь трапеции ![]() обычным
путем. Находим:
обычным
путем. Находим: ![]() ,
, ![]() ,
, ![]() .
Следовательно,
.
Следовательно, ![]() (кв. ед.).
(кв. ед.). ![]()
Вычисление пути, пройденного точкой
Путь,
пройденный точкой при неравномерном движении по прямой с переменной скоростью ![]() за промежуток времени от
за промежуток времени от ![]() до
до ![]() ,
вычисляется по формуле
,
вычисляется по формуле
![]()
(6)
Пример. Скорость
движения точки изменяется по закону ![]() м/с.
Найти путь, пройденный точкой за 10 с от начала движения.
м/с.
Найти путь, пройденный точкой за 10 с от начала движения.
Решение. Согласно
условию, ![]() ,
, ![]() ,
, ![]() .
По формуле (6) находим
.
По формуле (6) находим
 (м).
(м).
Вычисление работы силы
Работа,
произведенная переменной силой ![]() при
перемещении по оси
при
перемещении по оси ![]() материальной
точки от
материальной
точки от ![]() до
до ![]() , находится по формуле
, находится по формуле
 (7)
(7)
При решении задач на вычисление работы силы часто используется закон Гука:
![]() ,
(8)
,
(8)
где F - сила, H; x - абсолютное удлинение пружины, м, вызванное силой F, а k - коэффициент пропорциональности, Н/м.
Пример. Сжатие х винтовой пружины пропорционально приложенной силе F. Вычислить работу силы F при сжатии пружины на 0,04 м, если для сжатия ее на 0,01 м нужна сила 10 Н.
Решение. Так как, ![]() м при
м при ![]() Н,
то, подставляя эти значения в равенство (8), получим
Н,
то, подставляя эти значения в равенство (8), получим ![]() откуда
откуда ![]() 1000
Н/м. Подставив теперь в это же равенство значение k,
находим
1000
Н/м. Подставив теперь в это же равенство значение k,
находим ![]() , т. е.
, т. е. ![]() Искомую работу найдем по формуле
(7), полагая
Искомую работу найдем по формуле
(7), полагая ![]() ,
, ![]() :
:
 (Дж).
(Дж).
Вычисление работы, производимой при поднятии груза
Пример. Цилиндрическая цистерна с радиусом основания 0,5 м и высотой 2 м заполнена водой. Вычислить работу, которую необходимо произвести, чтобы выкачать воду из цистерны.
Решение. Выделим на глубине х горизонтальный слой высотой
dx (рис. 7).
Работа
А, которую надо произвести, чтобы поднять слой воды весом Р на высоту х, равна
![]() .
.
Изменение
глубины х на малую величину dx вызовет изменение объема V на
величину ![]() и изменение веса Р на
величину
и изменение веса Р на
величину ![]() при этом совершаемая
работа А изменится на величину
при этом совершаемая
работа А изменится на величину ![]()
Проинтегрировав это равенство при изменении х от 0 до Н, получим
 (Дж).
(Дж).
Вычисление силы давления жидкости
Значение силы Р давления жидкости на горизонтальную площадку зависит от глубины погружения х этой площадки, т. е. от расстояния площадки до поверхности жидкости.
Сила давления (Н) на горизонтальную площадку вычисляется по формуле
![]()
где ![]() - плотность жидкости,
- плотность жидкости, ![]() ; S
площадь площадки,
; S
площадь площадки, ![]() ; х - глубина
погружения площадки, м.
; х - глубина
погружения площадки, м.
Если площадка, испытывающая давление жидкости, не горизонтальна, то давление на нее различно на разных глубинах, следовательно, сила давления на площадку есть функция глубины ее погружения Р(х).
Пример. Вычислить силу давления воды на вертикальный прямоугольный шлюз с основанием 20 м и высотой 5 м (уровень воды совпадает с верхним обрезом шлюза).
Решение. На глубине х
выделим горизонтальную полоску шириной dx (рис
8). Сила давления Р на стенку шлюза есть функция от х. Изменение глубины х на
малую величину dx вызовет изменение силы давления Р на малую
величину ![]() .
.
Продифференцировав
переменную Р, получим приближенное значение (главную часть) ![]() приращения
приращения ![]() .
.
Находим
приближенное значение силы давления воды на эту полоску: ![]() Но
Но ![]() Интегрируя
Интегрируя
![]() при изменении х от 0 до 5, получим
при изменении х от 0 до 5, получим
 (МН).
(МН).
Длина дуги плоской кривой
Пусть
плоская кривая АВ (рис. 9) задана уравнением ![]() причем
причем ![]() и
и
![]() - непрерывные функции в промежутке
- непрерывные функции в промежутке
![]() Тогда дифференциал
Тогда дифференциал ![]() длины дуги АВ выражается формулой
длины дуги АВ выражается формулой
 или
или ![]()
а длина дуги АВ вычисляется по формуле
 (9)
(9)
где ![]() и
и ![]() -
значения независимой переменной х в точках А и В.
-
значения независимой переменной х в точках А и В.
Если кривая задана
уравнением ![]() то длина дуги АВ
вычисляется по формуле
то длина дуги АВ
вычисляется по формуле
![]()
(10)
где c и d – значения независимой переменной у в точках А и В.
Пример. Найти длину
окружности ![]()
Решение. Дифференцируя уравнение окружности, имеем
![]()
![]()
По формуле (9) вычислим длину дуги четверти окружности, взяв пределы интегрирования от 0 до r:

Длина окружности равна ![]()
![]()
![]()
![]()
(рис. 1) (рис. 2) (рис. 3)
![]()
![]()
![]()
(рис. 4) (рис. 5) (рис. 6)
![]()
![]()
![]()
(рис. 7) (рис. 8) (рис. 9)
Порядок проведения работы:
|
Вариант 1 |
Вариант 2 |
||
|
1. |
Вычислить площадь плоской фигуры, ограниченной функциями: x-2y+4=0, x+y-5=0, y=0. |
1. |
Вычислить площадь плоской фигуры, ограниченной функциями: 2x-3y+6=0, y=0, x=3. |
|
2. |
При сжатии пружины на 0,05 м затрачивается работа 25 Дж. Какую работу необходимо совершить, чтобы сжать пружину на 0,1 м? |
2. |
Для растяжения пружины на 0,04 м необходимо совершить работу 20 Дж. На какую длину можно растянуть пружину, совершив работу 80 Дж? |
|
3. |
Цилиндрическая цистерна с радиусом основания 0,5 м и высотой 2 м заполнена водой. Вычислить работу, которую необходимо произвести, чтобы выкачать воду из цистерны.
|
3. |
Вычислить работу, которую надо произвести, чтобы выкачать из резервуара конической формы с вершиной, обращенной книзу. Резервуар наполнен доверху водой. Радиус основания конуса R=1м, высота конуса 2м. |
|
4. |
Вычислить силу давления воды на вертикальный прямоугольный шлюз с основанием 20м и высотой 5м (уровень воды совпадает с верхним обрезом шлюза).
|
4. |
Вычислить силу давления воды на вертикальную плотину, имеющую форму равнобедренной трапеции с основаниями a и b (a > b) и высотой h.
|
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.