Методические рекомендации по выполнению практический заданий

МР-23-08.02.09-ОП.03

комитет по науке и высшей школе

Санкт-Петербургское государственное

БЮДЖЕТНОЕ профессиональное образовательное учреждение

 «Санкт-Петербургский техникум отраслевых технологий,

финансов и права»

метоические рекомендации

по выполнению ПРАКТИЧЕСКИХ ЗАНЯТИЙ

ОП.03 Электротехника

Специальность 08.02.09

«Монтаж, наладка и эксплуатация электрооборудования промышленных и гражданских зданий и сооружений»

Методические рекомендации по выполнению практических занятий для студентов составлены в соответствии с рабочей программой учебной дисциплины ОП 03 «Электротехника» по специальности 08.02.09 и «Монтаж, наладка и эксплуатация электрооборудования промышленных и гражданских зданий».

 

Разработчик: преподаватель СПбТОТФиП					А.С. Савватеев
				(подпись)
СОГЛАСОВАНО
На заседании цикловой комиссии № 08.02.09
Протокол №	06	от	01.02.2023
Председатель ЦК № 08.02.09					А.В. Бычков
				(подпись)
УТВЕРЖДЕНА
Учебно-методический совет техникума
Протокол №	06	от	09.03.2023
Методист					О.В. Корнилова
				(подпись)

 

                                     

 

 

Оглавление

1. Пояснительная записка.. 4

2. ПЕРЕЧЕНЬ ПРАКТИЧЕСКИХ ЗАДАНИЙ.. 5

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №1 РАСЧЕТ И ВЫБОР ПРОВОДОВ ПО ДОПУСТИМОМУ НАГРЕВУ   6

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №2 РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ МЕТОДОМ УЗЛОВЫХ И КОНТУРНЫХ УРАВНЕНИЙ.. 10

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №3 Расчет сложных цепей с использованием уравнений Кирхгофа.. 14

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №4 Расчет смешанного соединения конденсаторов   18

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №5 Классификация магнитных материалов.. 23

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №6 Расчёт неразветвленной неоднородной магнитной цепи. 28

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №7 Преобразование энергии на основе электромагнитной индукции.. 33

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №8 Основные параметры и формы представления переменного тока.. 34

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №9 РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА С ПРИМЕНЕНИЕМ КОМПЛЕКСНЫХ ЧИСЕЛ.. 38

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №10 РАСЧЕТ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПРИ НЕСИНУСОИДАЛЬНОМ НАПРЯЖЕНИИ НА ВХОДЕ. 41

 

1. Пояснительная записка

 

Методические рекомендации к практическим занятиям предназначены в качестве методического пособия при проведении практических занятий по ОП.03 «Электротехника» для специальности 08.02.09 «Монтаж, наладка и эксплуатация электрооборудования промышленных и гражданских зданий»

Практические занятия проводятся после изучения соответствующих разделов и тем дисциплины. Выполнение обучающимися практических заданий позволяет им понять, где и когда изучаемые теоретические положения и практические умения могут быть использованы в будущей практической деятельности.  

Целью практических занятий является закрепление теоретических знаний и приобретение практических умений и навыков.

Методические рекомендации по каждому практическому занятию имеют теоретическую часть с необходимыми для выполнения работы формулами, пояснениями, таблицами; алгоритм выполнения заданий.

 

 

2. ПЕРЕЧЕНЬ ПРАКТИЧЕСКИХ ЗАНЯТИЙ

№ п/п	Наименование	Количество часов
1	Расчет и выбор проводов по допустимому нагреву	2
2	Расчет электрических цепей методом узловых и контурных уравнений	2
3	Расчет сложных цепей с использованием уравнений Кирхгофа	2
4	Расчет смешанного соединения конденсаторов	2
5	Классификация магнитных материалов	2
6	Расчёт неразветвленной неоднородной магнитной цепи.	2
7	Преобразование энергии на основе электромагнитной индукции	2
8	Основные параметры и формы представления переменного тока	2
9	Расчет электрических цепей переменного тока с применением комплексных чисел	2
10	Расчет электрической цепи при несинусоидальном напряжении на входе	2

 

 

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №1 РАСЧЕТ И ВЫБОР ПРОВОДОВ ПО ДОПУСТИМОМУ НАГРЕВУ

Цель:

1.      Изучить влияние силы тока на проводники.

2.      Рассмотреть, почему необходимо осуществлять выбор проводов по допустимому нагреву.

3.      Научиться пользоваться справочной литературой для определения допустимого сечения провода по нагреванию.

Необходимые материалы и оборудование:

1.      Методические указания по выполнению практических занятий;

2.      Индивидуальное задание;

3.      Конспект лекций по предмету;

Ход работы:

1.        Изучить теоретическую часть как зависит степень нагревания от силы тока и площади поверхности проводника.

2.        В практическом задании необходимо определить сечение провода электрической  цепи в зависимости от токовой нагрузки.

3.        По исходным данным (таблица 1), применяя данные формулы, определить ток установки. P_{установки} = n P; I = P/U.

4.        Определить сечение провода по таблице.   

Площадь сечения проводов в зависимости от токовой нагрузки для медных проводов с резиновой и полихлорвиниловой изоляцией, проложенных открыто.

5.      Ответить на контрольные вопросы

Поперечное сечение, мм2	Наибольший допустимый ток, А	Поперечное сечение, мм2	Наибольший допустимый ток, А
0,50	10	35	150
0,75	13	50	190
1,0	15	70	240
1,5	20	95	290
2,5	27	120	340
4,0	36	150	390
6,0	46	185	450
10	68	240	535
16	90	300	615
25	125	400	735

 

 

 

Пояснение к работе:

Электрический ток в проводниках представляет собой направленное движение свободных электронов. При столкновении движущихся электронов с молекулами вещества их кинетическая энергия преобразуется в тепловую энергию, вследствие чего происходит нагревание проводника. Скорость преобразования электрической энергии в тепловую характеризуется мощностью   P = U I = I²R, Вт. Количество электрической энергии W, преобразованной в тепло за время t,  W = Pt = I²Rt, Дж.                                             

    Количество тепла, выделенное током I в сопротивлении R, Q = I²Rt, Дж.

    Преобразование электрической энергии в тепло находит применение в разнообразных нагревательных приборах. В остальных приборах (электрических машинах, аппаратах, проводах) преобразование электрической энергии в тепловую является непроизводительным расходом энергии, то есть потерями энергии, снижающими их коэффициент полезного действия. Кроме того, тепло, вызывая нагревание этих устройств, ограничивает допустимый ток или, как говорят, их нагрузку: при перегрузке повышение температуры может привести к повреждению изоляции или сокращению срока службы установки.

      При нагревании провода приращение его температуры зависит от массы и материала провода и количества выделившегося в нем тепла. Скорость отдачи тепла в окружающую среду пропорциональна разности температур провода и среды. В первый момент, когда температура провода равна температуре окружающей среды, вся теплота, выделенная током, идет на нагрев провода. В результате его температура быстро повышается. По мере ее роста увеличивается количество теплоты, отдаваемой проводом среде, а количество теплоты, расходуемой на нагрев, уменьшается. Наконец наступает момент установления температурного баланса: количество отдаваемой энергии равно количеству полученной энергии и повышение температуры провода прекращается.

     Температуру провода, соответствующую моменту баланса, называют установившейся. Время, в течение которого провода нагреваются до установившейся температуры, зависит от их геометрических размеров и условий охлаждения. Нагрев провода допускается до температур порядка 600 – 800С. В соответствии с допустимой температурой существует понятие допустимого тока. Допустимым или номинальным называют ток, при котором устанавливается наибольшая допустимая температура.

     У изолированных проводов допустимый нагрев определяется видом и свойствами изоляции, у голых (неизолированных) проводов – изменением их механических свойств. Если ток, проходящий по проводу, больше номинального, то такую перегрузку можно допустить только кратковременно. Чем больше ток в проводе по сравнению с номинальным, тем кратковременной может быть перегрузка.

       Коротким замыканием называют соединение двух неизолированных проводов различного потенциала. Ток короткого замыкания может практически в десятки и сотни раз превышать номинальный ток цепи, что может вызвать тепловые механические повреждения ее отдельных элементов. Для защиты цепи от перегрузок служат плавкие предохранители, которые при определенном токе плавятся, разрывая электрическую цепь.

Таблица 1 - Исходные данные:

Исходные данные
№ варианта	1	2	3	4	5	6	7	8	9	10
Количество приемников эл. энергии, n	20	18	22	24	30	32	35	16	25	21
Напряжение цепи U, В	150	160	120	210	140	120	130	220	230	150
Мощность приемника Р, Вт	160	150	220	120	130	220	230	210	180	160
№ варианта	11	12	13	14	15	16	17	18	19	20
Количество приемников эл. энергии, n	17	23	26	31	27	33	28	34	29	36
Напряжение цепи U, В	180	220	120	160	180	130	200	140	150	120
Мощность приемника Р, Вт	200	120	210	200	140	120	110	100	180	150
№ варианта	21	22	23	24	25	26	27	28	29	30
Количество приемников эл. энергии, n	15	37	38	39	40	38	27	24	28	26
Напряжение цепи U, В	200	150	120	110	130	210	110	120	130	210
Мощность приемника Р, Вт	170	120	150	120	210	160	140	200	220	180

 

Пример выполнения задания

В цепь с напряжением 120 В включено 25 ламп. Мощность каждой из них 150 Вт.

Определить сечение медных проводов установки.

 

 

 

 

 

 

Дано:	Решение
U=120 B n = 25 Р = 150 Вт	1.      Определяем мощность установки. Pустановки = n P = 25*150 = 3750 Вт 2.      Определяем ток установки. I = P/U = 3750/ 120 = 31,25А ≈ 31А
Определить:  S	3.      Определяем по таблице сечение провода. Ближайшее сечение равно 4 мм2 с допустимым током 36 А.

Контрольные вопросы

1.  Какая температура называется установившейся?

2.  Какой ток называют допустимым?

3. Что такое короткое замыкание?

4. Каким образом защищают цепи от перегрузок?

5. Для чего необходимо знать количество теплоты выделяемое кабелей при прохождении электрического тока?

 

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №2 РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ МЕТОДОМ УЗЛОВЫХ И КОНТУРНЫХ УРАВНЕНИЙ

Цель работы:

1.      Научиться рассчитывать сложные электрические схемы постоянного тока методом узловых и контурных уравнений (МУКУр)

Необходимые материалы и оборудование:

1.      Методические указания по выполнению практических занятий;

2.      Индивидуальное задание;

3.      Конспект лекций по предмету;

Ход работы:

1.      Изучить теоретическую часть расчета сложных электрических схем постоянного тока методом узловых и контурных уравнений.

2.      Решить индивидуальное задание

3. В задаче обязательно вычертить электрическую схему, соответствующую условию задачи, и показать на ней заданные и искомые величины, а также направление токов. Привести данные своего варианта.
4. Решение задачи сопровождается краткими пояснениями.
5. Текст, формулы, числовые выкладки должны быть четкими без помарок. Цифровая подстановка в уравнении должна даваться один раз без промежуточных сокращений и расчетов. Численное значение каждого символа должно обязательно занимать то же место в формуле, что и сам символ. Все расчеты необходимо вести в системе СИ. Буквенные обозначения единиц измерения ставятся только возле окончательного результата и в скобки не заключаются, например, 120 В, 13 А, 100 Вт.

Пояснение к работе:

Данный метод является одним из самых простейших методов расчёта электрических цепей постоянного тока любой сложности. Основывается на составлении уравнений по I и II законам Кирхгофа. Алгоритм расчёта:

1. Определяем число ветвей m, узлов и контуров в электрической цепи. Число токов в цепи равно числу ветвей. Для каждой ветви выбираем условное направление тока и укажем их на схеме.

2. По первому закону Кирхгофа составляем уравнение для узлов в количе-стве n -1, где n – число узлов.

3. На основании II закона Кирхгофа составляем m – n + 1 уравнений, где m-число ветвей, n-число узлов. Для обхода выбираем контуры с меньшим числом ветвей и содержащих хотя бы одну новую ветвь. Контур обходим по часовой стрелке.

4. Полученные уравнения объединяем в систему и решаем любым способом, известным из математики.

Определить токи во всех ветвях цепи (рисунок 1), если Э.Д.С. источников энергии Е₁ = 150В, Е₂ = 80В, их внутренние сопротивления R₀₁ = 1 Ом, R₀₂=0.5 Ом; сопротивления резисторов R₁=9 Ом, R₂=19,5 Ом, R₃ = 25 Ом. Задачу решить методом узловых и контурных уравнений, составленных по законам Кирхгофа. Составить уравнение баланса мощностей.

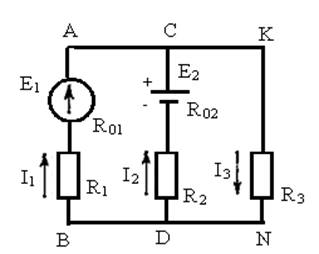
Рис. 1 – Электрическая схема

Решение

1. На схеме произвольно показываем направления токов ветвей.

2. В задаче три неизвестных тока, для их нахождения необходимо составить систему из трех уравнений.

Первое уравнение составим для узловой точки С по первому закону Кирхгофа:

I₁ +I₂ –I₃ =0

второе уравнение составим для контура АСDВА по второму закон Кирхгофа; направление обхода контура примем «по часовой стрелке»

Е₁—Е₂ =I₁ (R₁+R₀₁)—I₂(R₂+R₀₂);

третье уравнение составим для контура СКNDС но второму закону Кирхгофа; направление обхода контура примем «по часовой стрелке»:

Е₂=I₂(R₂+R₀₂) +I₃R₃.

3. Подставляем исходные данные в полученную систему из трех уравнений и находим значения токов ветвей:

I1 +I2 –I3 =0	(1)	I1 +I2 –I3 =0	(1)
Е1—Е2 =I1 (R1+R01)—I2(R2+R02)	(2)	150—80 =I1 (9+1)—I2(19.5+0.5)	(2)
Е2= I2(R2+R02) +I3R3	(3)	80=I2(19.5+0.5) +I325	(3)

 

Из второго уравнения получаем:

70=10 I₁ – 20 I₂;  

Из третьего уравнения получаем:

80=20I₂ +25I₃;

Подставляем выражения I₁ и I₃в первое уравнение и находим ток I₂:

I₂+7 + 2 I₂ - 3,2 + 0,8 I₂=0;  3,8 I₂=- 3,8; I₂ = -1А

Определяем токи I₁и I₃:

I₁ = 7+2 · (-1 )=5А;   I₃=3,2—0,8 (- 1) =4 А.

Проверка по первому закону Кирхгофа: I₁ + I₂ - I₃=0; 5-1-4 = 0.

Ток I₂ получился отрицательным, это значит, что первоначально произвольно принятое направление тока I₂от точки Dк точке С оказалось неверным и должно быть изменено на противоположное. При этом ток I₂ будет направлен против направления Э.Д.С. Е₂, следовательно, источник с Э.Д.С. Е₂ находится в режиме потребителя (например, заряд батареи аккумуляторов)

Индивидуальное задание

На рисунке 2 изображена схема сложной электрической цепи: Е₁, Е₂ – Э.Д.С. источников энергии; R₀₁, R₀₂ – их внутренние сопротивления; R₁, R₂, R₃ – сопротивления резисторов. 

Числовые значения этих параметров указаны в таблице 2

Начертить схему цепи; показать направление токов в ветвях. Определить токи ветвей I₁, I₂, I₃ методом узловых и контурных уравнений.

Составить уравнение баланса мощностей

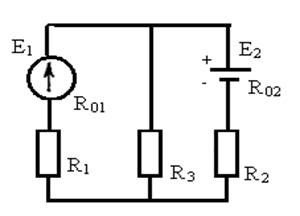
Рисунок 2 - Электрическая схема

 

 

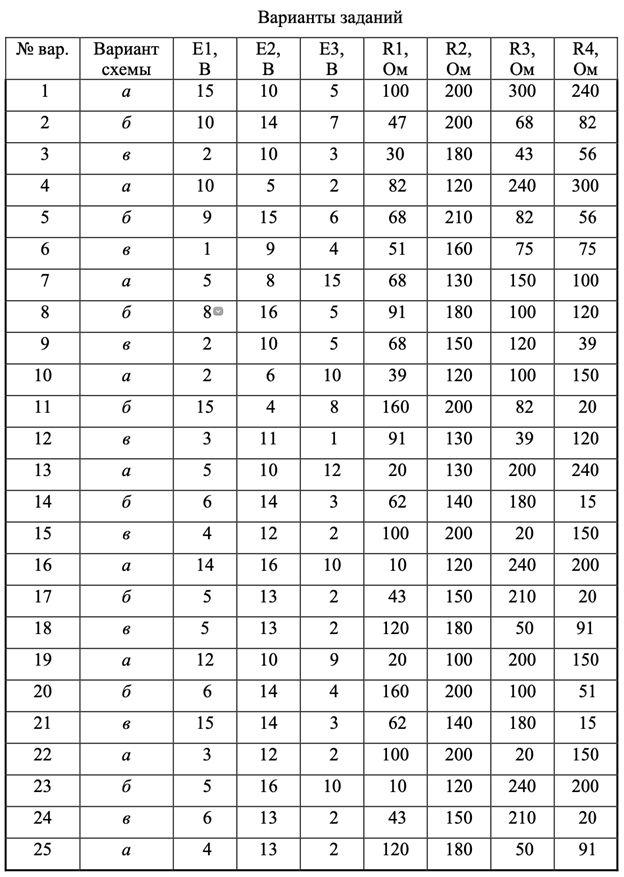
Таблица 2 - Исходные данные к практической работа № 2

Номер варианта – последняя цифра порядкового номера по журналу
№ варианта	Е1, В	Е2, В	R01, Ом	R02, Ом	R1, Ом	R2, Ом	R3, Ом	Метод расчета
0.	85	200	0,3	2,0	12,0	1,7	12,0	Метод узловых и контурных уравнений
1.	55	120	0,2	0,5	6,0	15,0	6,0
2.	105	146	2,0	2,0	50,0	4,5	50,0
3.	80	34	0,5	0,3	20,0	19,0	20,0
4.	55	120	0,2	0,5	6,0	15,0	6,0
5.	100	200	0,3	2,0	12,0	1,7	12,0
6.	80	120	0,2	0,5	60,0	15,0	6,0
7.	50	146	2,5	2,0	25,0	4,5	50,0
8.	10	34	1,5	0,35	10,0	19,0	20,0
9.	20	120	1,2	0,65	6,0	15,0	30,0

 

 

 

 

 

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №3 Расчет сложных цепей с использованием уравнений Кирхгофа

Цель:

Научиться рассчитывать электрическую цепь по уравнениям Кирхгофа.

Необходимые материалы и оборудование:

1.                                                       Методические рекомендации по выполнению практических занятий

Ход работы:

1.                         Вначале проводится опрос студентов с целью выявить их теоретические знания по теме, затем совместно решается задача и дается задание на самостоятельное решение.

Пояснения к работе:

1.                                     Для расчета схемы по уравнениям Кирхгофа предварительно необходимо задать направления токов в ветвях схемы и выбрать контуры и направления их обхода. Направления токов и обхода контуров выбираются произвольно. Если в результате расчета для какого-либо тока будет получено значение со знаком минус, то это означает, что фактическое направление противоположно выбранному.

2.                                     При записи очередного уравнения по первому закону Кирхгофа необходимо, чтобы хотя бы один ток в этом уравнении не входил ни в одно из ранее записанных уравнений. При выборе очередного контура для записи уравнений по второму закону Кирхгофа необходимо, чтобы в каждый очередной контур входила хотя бы одна ветвь, не вошедшая во все остальные контуры. Решение полученной системы уравнений позволяет определить токи во всех ветвях схемы.

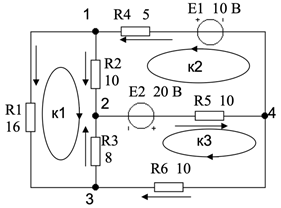
Рис. 2.1 – Электрическая схема

3.                  Схема имеет шесть ветвей (n=6) и четыре узла (n=4). Число уравнений по первому закону Кирхгофа k₁=nу-1=4 – 1 = 3. Число уравнений по второму закону Кирхгофа 2 =nв-(nу-1)=6–(4-1)=3. Номиналы резисторов и ЭДС источников напряжения приведены на схеме.

4.                  Для записи уравнений выберем узлы 1, 2 и 3, контуры к1, к2 и к3. На рисунке заданы направления токов в ветвях и направления обхода контуров. Выбор узлов и контуров произволен, так же как и направлений токов и обхода контуров. Контуры следует выбирать по возможности простой конфигурации.

5.                  Запишем уравнения по первому закону Кирхгофа.

узел 1 - I1 – I2 + I4 = 0

узел 2 I2 + I3 – I5 = 0

узел 3 I1 – I3 + I6 = 0
Далее запишем уравнения по второму закону Кирхгофа для выделенных

контуров и выбранных направлений обхода:

контур к1                   – I1·R1 + I2·R2 – I3·R3 = 0

контур к2                   I2·R2 – E2 + I5·R5 – E1 +I4·R4 = 0

контур к3                   – E2 + I5·R5 + I6·R6 + I3·R3 = 0

Уравнения  выше удобнее записать в форме

контур к1                   – I1·R1 + I2·R2 – I3·R3 = 0

контур к2                   I2·R2 + I5·R5 +I4·R4 = E1+E2

контур к3                   I5·R5 + I6·R6 + I3·R3 = E2

Подставим в уравнения численные значения сопротивлений резисторов и напряжений источников

Решая эту систему уравнений, получим значения токов

I1 = 0,333 А, I2 = 0,933 А, I3 = 0,500 А, I4 = 1,267 А, I5 = 1,433 А, I6 = 0,167 А.

Все значения токов имеют положительные знаки, что свидетельствует о совпадении реальных направлений токов с приведенными на рис. 2.1

Проверим результат решения, подставив значения токов в уравнения, составленные по первому закону Кирхгофа:

– I1 – I2 + I4 = - 0,333 - 0,933 + 1,267 = 0,

I2 + I3 – I5 = 0,933 + 0,500 - 1,433 = 0,

I1 – I3 + I6 = 0,333 - 0,500 + 0,167 = 0.

Студентам предлагается подставить значения в уравнения, составленные по второму закону, и убедиться в правильности решения.

Задание

Для заданной электрической цепи, в которой R5 = 75 Ом, R6 = 150 Ом, а остальные параметры указаны в таб. 1, требуется:

• определить все токи и напряжения в схеме по уравнениям Кирхгофа;

• определить все токи и напряжения в схеме методом контурных токов;

• определить все токи и напряжения в схеме методом узловых потенциалов;

• определить ток через резистор R6 методом эквивалентного генератора.

 

 

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №4 Расчет смешанного соединения конденсаторов

Цель работы:

1.      Закрепить знания методов расчета электрической емкости и зарядов конденсаторов при их смешанном соединении.

Необходимые материалы и оборудование:

1.      Методические указания по выполнению практических занятий;

2.      Индивидуальное задание;

3.      Конспект лекций по предмету;

Ход работы:

1.      Изучить теоретическую часть расчета смешанного соединения конденсаторов.

2.      Решить индивидуальное задание

3. Решение задачи сопровождается краткими пояснениями.

Пояснение к работе:

Электричес­кий конденсатор — это система из двух проводников (обкладок, пластин), разделенных диэлектриком.

Конденсаторы обладают свойством накапливать на своих обкладках электрические заряды, равные по величине и противоположные по знаку.

Электрический заряд q каждой из обкладок пропорционален напряжению U между ними: q= C*U

Величину С, равную отношению заряда одной из обкладок конденсатора к напряжению между ними, называют электрической емкостью конден­сатора и выражают в фарадах (Ф).

Емкость конденсатора зависит от геометрических размеров, формы, взаимного расположения и рас­стояния между обкладками, а также от свойств диэлектрика.

Конденсаторы могут быть соединены последова­тельно, параллельно и смешанно (последовательно-параллельно).

Последовательное соединение

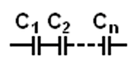
При таком на обкладках всех конденсаторов будут одинаковые по величине заряды: q=q₁=q₂=…=q_n

Напряжения на конденсаторах будут различны, так как они зависят от их емкостей:  

U₁=q₁/C₁ ; U₂=q₂/C₂ ; U_n=q_n/C_n ; 

Общее напряжение:

U=U₁+U₂+…U_n

 Общая, или эквивалентная, емкость

C=q/U или 1/C=1/C₁+1/C₂+…+1/C_n

 Параллельное соединение

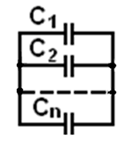
 При параллельном соединении напряжение на всех конденсаторах одинаковое.

Заряды на обкладках отдельных конденсаторов при различной их емкости:

q₁=C₁ * U ; q₂=C₂ * U ; q_n=C_n * U ;

Заряд, полученный всеми параллельно соединен­ными конденсаторами:

q=q₁+q₂+…+q_n

Общая (эквивалентная) емкость:

q=q₁+q₂+…+q_n

C=C₁+C₂+…+C_n

Задание:

1.      Определить эквивалентную емкость батареи конденсаторов, соединенных по схеме (рис. 3), при соответствующих положениях ключей.

Рис. 3 – Электрическая схема

 

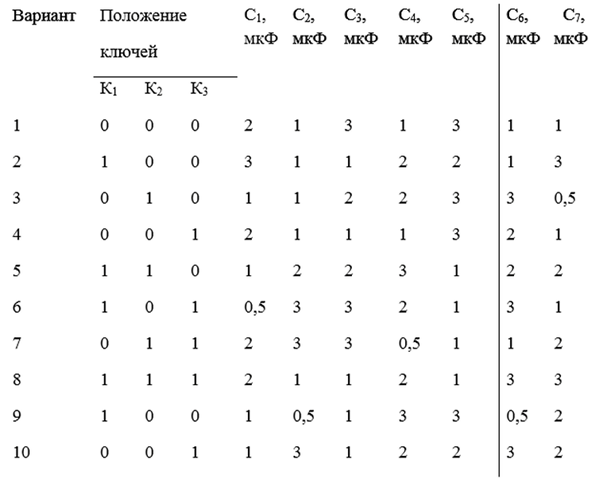
2. Для случая, когда ключи К1, К2 и К3 разомкнуты, найти заряды на каждом конденсаторе и общий заряд схемы.

 

 

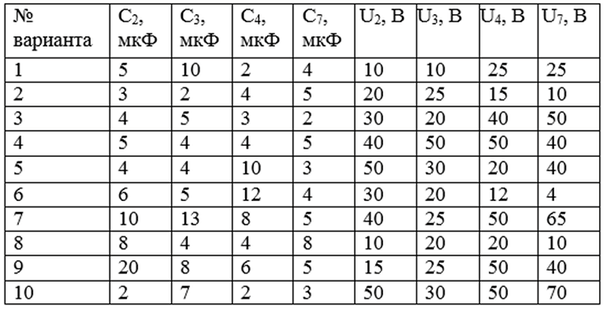
Пример решение:

Для своих данных начертить исходную схему.

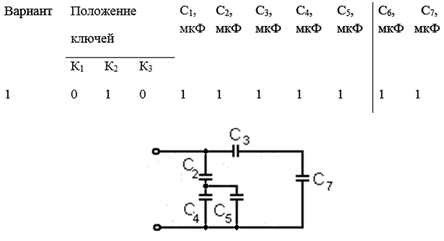
2. Рассчитать последовательное соединение С3-С7:

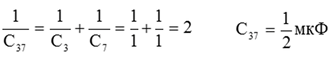
3. Рассчитать параллельное соединение С4-С5:

4. Рассчитать последовательное соединение С2-С45:

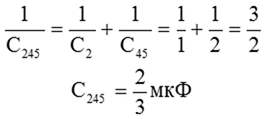
5. Найти эквивалентную емкость, рассчитав параллельное соединение С245-С37:

Задание 2

1. Для своих данных начертить исходную схему. 

2. Рассчитать заряды на каждом конденсаторе:

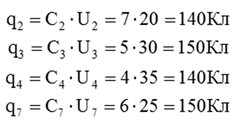
3. Рассчитать общий заряд схемы:

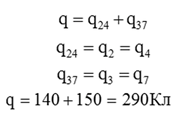
4. Проверка:

 

 

 

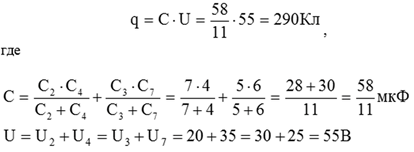
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №5 Классификация магнитных материалов

Цель работы:

1.      Изучить магнитные свойства различных материалов; явления намагничивания и перемагничивания ферромагнитных материалов

2.      Научиться определять величину магнитной индукции по кривой намагничивания

Необходимые материалы и оборудование:

1.      Методические указания по выполнению практических занятий;

Ход работы:

1.      Изучить теоретическую часть классификации магнитных материалов

2.      Ответить на контрольные вопросы

Пояснение к работе:

Все вещества в природе являются магнетиками в том понимании, что они обладают определенными магнитными свойствами и определенным образом взаимодействуют с внешним магнитным полем. Магнитными называют материалы, применяемые в технике с учетом их магнитных свойств. Магнитные свойства вещества зависят от магнитных свойств микрочастиц, структуры атомов и молекул.

Магнитные материалы делятся: магнитомягкие материалы; магнитотвердые материалы; магнитные материалы специального назначения.

I.Магнитомягкие материалы – это материалы, обладающие свойствами ферромагнетика.

Ферромагнетик  - это железо, никель, кобальт или другое вещество, которое имеет высокую магнитную проницаемость.

 Магнитная проницаемость  - это физическая величина, характеризующая связь между магнитной индукцией В и магнитным полем Н в веществе.

Магнитная индукция - это вектор магнитной индукции В, основная характеристика магнитного поля (рис 4.).

Рис. 4 - Линии магнитной индукции полей постоянного магнита.

 

Магнитомягкие материалы обладают высокой магнитной проницаемостью, небольшой коэрцитивной силой и малыми потерями на гистерезис.

Коэрцитивная сила - это напряженность магнитного поля, вызывающая магнитную индукцию ферромагнетика, равную нулю, в условиях циклического перемагничивания.

Гистерезис - это явление, которое состоит в том, что намагниченность тела зависит от магнитного поля (рис 5).

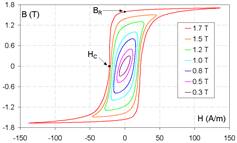
Рис 5.Петли магнитного гистерезиса.

 

К магнитомягким материалам относятся:

1.                  технически чистое железо (электротехническая низкоуглеродистая сталь);

2.                  электротехнические кремнистые стали;

3.                  железоникелевые и железокобальтовые сплавы;

4.                  магнитомягкие ферриты (ферритовые сердечники).

Магнитомягкие материалы используются в качестве сердечников трансформаторов, электромагнитов, в измерительных приборах генераторов, электродвигателей, дросселей, стабилизаторов, реле и т.д. Магнитомягкие, т.е. легко намагничивающиеся материалы имеют узкую петлю гистерезиса небольшой площади при высоких значениях индукции. Материалы этого типа с округлой петлей гистерезиса применяют для работы в низкочастотных магнитных полях. Магнитомягкие материалы с прямоугольной петлей гистерезиса используют в импульсных устройствах магнитной памяти.

Свойства магнитомягких материалов:

1. Малое значение коэрцитивной силы (то есть размагничивание происходит медленно).

2. Способность намагничиваться до насыщения даже в слабых полях. То есть там существует высокая магнитная проницаемость.

Магнитная проницаемость m - это величина, характеризующая магнитные свойства материала.

3. Малые потери на перемагничивание.

 Перемагничивание – это изменение направления намагниченности ферро или ферримагнитного образца на противоположное под действием внешнего магнитного поля.

II. Магнитотвердые материалы (магнитожесткие материалы) намагничиваются до насыщения и перемагничиваются в сравнительно сильных магнитных полях напряженностью в тысячи и десятки тысяч А/м. Характеризуются высокими значениями коэрцитивной силы.

 Магнитотвердые материалы – это материалы для постоянных магнитов, использующихся в электродвигателях и других электротехнических устройствах, в которых требуется постоянное магнитное поле.

 Магнитотвердые материалы  обладают большой удельной энергией. Эта энергия пропорциональна произведению остаточной индукции на величину коэрцитивной силы.

Магнитотвердые материалы намагничиваются с трудом, но способны длительное время сохранять сообщенную им энергию. Для них характерна широкая петля гистерезиса большой площади.

Классификация магнитотвердых материалов:

1. Литые магнитотвердые материалы на основе сплавов Fe-Ni-Al (используются для изготовления постоянных магнитов).

2. Порошковые магнитотвердые материалы, получаемые путем прессования порошков с последующей термообработкой (используются для изготовления постоянных магнитов сложной формы).

3. Магнитотвердые ферриты. Ферриты являются химическим соединением оксида железа Fe₂O₄ с оксидами двухвалентных металлов, например, Cu, Zn, Mg, Ni, Fe, Co и Mn.

Ферриты представляют собой магнитную керамику с большим удельным сопротивлением, в 1010 раз превышающим сопротивление железа. Ферриты применяют в высокочастотных цепях, так как их магнитная проницаемость практически не снижается с увеличением частоты. Недостатком ферритов является их низкая индукция насыщения и низкая механическая прочность. Поэтому ферриты применяют в низковольтной электронике.

Основными характеристиками магнитотвердых материалов являются:

- коэрцитивная сила Н_с;

-остаточная индукция В_r;

- максимальная удельная энергия, отдаваемая магнитом во внешнее пространство W_a^;

Магнитотвердые материалы перемагничиваются только в очень сильных магнитных полях и служат в основном для изготовления постоянных магнитов.

III.              Магнитные материалы специального назначения - это магнитные материалы, имеющие узкие области применения, благодаря высоким значениям одного, иногда двух параметров.

К магнитным материалам специального назначения относят:

- магнитные материалы с прямоугольной петлей гистерезиса;

- СВЧ- ферриты;

- магнитострикционные материалы.

1. Магнитные материалы с прямоугольной петлей гистерезиса. Сердечники из материала с прямоугольной петлей гистерезиса имеют два устойчивых магнитных состояния, которые соответствуют различным направлениям магнитной индукции. Это свойство используется для хранения и переработки двоичной информации. Магнитные материалы с прямоугольной петлей гистерезиса (ППГ) находят широкое применение в устройствах автоматики, вычислительной техники, в аппаратуре телеграфной связи.

2. СВЧ - ферриты - это неметаллические твёрдые магнитные материалы. Магнитными характеристиками ферритов можно управлять с помощью внешнего магнитного поля. В СВЧ-технике используют ряд эффектов, основанных на взаимодействии электромагнитной волны с магнитными моментами атомов (ионов) СВЧ ферритов.

Назначение. В качестве ферритов СВЧ используются магний-марганцевые ферриты с большим содержанием оксида магния, литий-цинковые ферриты, никель-цинковые ферриты и ферриты сложного состава.

 3. Магнитострикционные материалы – это ферромагнитные металлы и сплавы, а также ферриты, у которых происходит изменение формы и размеров при намагничивании.

Применение. Магнитострикционные материалы применяют:

- для изготовления сердечников электромеханических преобразователей в электроакустической и ультразвуковой технике;

-для сердечников электромеханических и магнитострикционных фильтров;

-для резонаторов и линий задержек.

 

Контрольные вопросы:

1.      Отчего зависят магнитные свойства вещества?

2.      На какие классы делятся магнитные материалы?

3.      Магнитомягкие материалы – это …?

4.      Ферромагнетик – это…?

5.      Магнитная проницаемость – это…?

6.      Коэрцитивная сила - это…?

7.      Гистерезис - это…?

8.      Свойства магнитомягких материалов?

9.      Как классифицируются магнитотвердые материалы?

10.  Основные характеристики магнитотвердых материалов?

11.  Как классифицируются магнитные материалы специального назначения?

 

 

 

 

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №6 Расчёт неразветвленной неоднородной магнитной цепи.  

Цель работы:

1.      Освоить прямую задачу расчета неразветвленной неоднородной магнитной цепи.

Необходимые материалы и оборудование:

1.      Методические указания по выполнению практических занятий;

2.      Индивидуальное задание;

3.      Конспект лекций по предмету;

Ход работы:

1.      В практическом задании необходимо определить число витков, которое необходимо намотать на сердечник из электротехнической стали Э-330, при заданном токе в обмотке, для получения заданной магнитной индукции в воздушном зазоре. Якорь выполнен из той же электротехнической стали.

2.      Размеры участков магнитной цепи l₁, l₂, l₀ и площадь поперечного сечения S задаются.

                                                                 l₁

 

                                                                l₀

                 l₂

 

3.      В четных вариантах напряженность магнитного поля Н определяется по графику зависимости магнитной индукции В от напряженности магнитного поля Н.

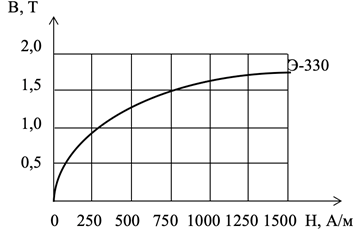
4.      В нечетных вариантах напряженность магнитного поля Н определяется по заданному значению относительной магнитной проницаемости m_r по формуле                         Н = В/m₀m_r

5.      Переписать из таблицы данные своего варианта.

6.      Выполнить расчет в соответствии с вариантом, применяя следующие формулы: Ф=BS,  B=Ф/S, U_m = Hl, Н₀ = В/m₀, Н = В/m₀m_r, F_m=IN,  F_m=Hl

7.      Исходные данные.

№ вар. Параметры	1 / 2	3 / 4	5 / 6	7 / 8	9 / 10	11 / 12	13 / 14
В, Т (нечет.вар.)	0,5	1,1	1,5	0,7	1,3	1,6	0,6
mr,    (нечет.вар.)	500	450	300	350	500	550	350
Ф, Вб  (чет.вар.)	2,1∙10-4	2,8∙10-4	3,0∙10-4	4,2∙10-4	5,1∙10-4	5,0∙10-4	2,4∙10-4
S, см2  (чет.вар.)	3,5	3,0	2,8	3,4	3,1	2,9	5,0
I, А	10	9	7	5	6	11	14
l1, м	0,5	0,2	0,1	0,4	0,3	0,6	0,7
l2, м	0,12	0,09	0,05	0,1	0,06	0,1	0,18
l0, м	0,002	0,001	0,003	0,004	0,001	0,002	0,003

 

№ вар. Параметры	15 / 16	17 / 18	19 / 20	21 / 22	23 / 24	25 / 26	27 / 28
В, Т (нечет.вар.)	1,2	0,7	1,4	0,8	1	1,1	0,5
mr,    (нечет.вар.)	450	400	500	300	400	450	350
Ф, Вб  (чет.вар.)	4,8∙10-4	5,2∙10-4	5,6∙10-4	6,0∙10-4	5,4∙10-4	3,5∙10-4	4,5∙10-4
S, см2  (чет.вар.)	4,8	4,6	4,2	4,7	3,6	2,5	3,2
I, А	12	13	4	3	6	10	9
l1, м	0,8	0,9	0,6	0,4	0,3	0,2	0,5
l2, м	0,2	0,3	0,14	0,1	0,05	0,03	0,1
l0, м	0,004	0,011	0,002	0,003	0,007	0,005	0,002

Пояснение к работе:

Магнитной цепью называют совокупность устройств, содержащих ферромагнитные материалы, вдоль которых замыкается поток магнитной индукции. Примерами магнитных цепей является сердечники электромагнитов, катушек магнитных усилителей, трансформаторов, электрических машин и т.д. Магнитные цепи бывают замкнутые, в которых магнитный поток полностью замыкается в ферромагнитных цепях, и разомкнутые, в которых имеются воздушные зазоры.

Магнитные цепи, у которых магнитная проницаемость везде одинакова, называются однородными. Магнитные цепи, у которых магнитная проницаемость отдельных участков различная, называются неоднородными.  Магнитные цепи могут быть неразветвленные и разветвленные.

Для расчета магнитных цепей используют закон Ома, первый и второй законы Кирхгофа.

Закон Ома - Ф=F_m/R_m  

F_m– намагничивающая или магнитодвижущая сила.

Это величина, характеризующая свойство тока возбуждать магнитное поле. Для проводника с током она численно равна величине этого тока - F_m = I [A]

F_m= IN, [A] – для катушки индуктивности, N – число витков. Магнитодвижущая сила создает магнитный поток в магнитной цепи.

Ф = BS, [Вб]– магнитный поток это величина, численно равная количеству линий магнитной индукции, пронизывающих данную площадь.

S – площадь сечения сердечника [м²]

В = m_аН, [T] – магнитная индукция это векторная величина, характеризующая интенсивность  магнитного поля в данной его точке с учётом влияния среды.

R_m= l/m_а∙S, [1/Гн] – магнитное сопротивление это сопротивление магнитной цепи потоку магнитной индукции.

l [м] – длина сердечника. 

m_а [Гн/м] – абсолютная магнитная проницаемость это величина, характеризующая свойство материала намагничиваться, то есть создавать собственное магнитное поле под действием намагничивающей силы внешнего магнитного поля.

Закон Ома формулируется следующим образом:

Величина магнитного потока в сечении магнитопровода прямо пропорциональна намагничивающей силе и обратно пропорциональна магнитному сопротивлению цепи магнитному потоку.

       Первый закон Кирхгофа - применяется для разветвленных магнитных цепей.

       Ток в катушке намотанный на средний стержень создает магнитный поток Ф, который разветвляется в боковые стержни на магнитные потоки Ф₁ и Ф₂.

Ф=Ф₁+Ф₂      Ф - Ф₁ - Ф₂ = 0

Алгебраическая сумма магнитных потоков в точке разветвления равна нулю.

        Второй закон Кирхгофа - алгебраическая сумма намагничивающих сил замкнутого контура равна  алгебраической сумме магнитных напряжений на всех участках магнитной цепи.

U_m = Hl, [A] – магнитное напряжение на участке это произведение напряженности поля на длину участка.

H = I / 2πa  = I / l, [A/м] – напряжённость магнитного поля это векторная величина, характеризующая интенсивность магнитного поля в данной его точке независимо от магнитных свойств среды.

       При решении магнитных цепей рассматривается прямая и обратная задачи.

Прямая задача – если известны сечение, материалы отдельных участков, а также магнитные потоки, то можно определить намагничивающую силу.

Обратная задача – если известны намагничивающая сила, сечение и материалы отдельных ветвей, то можно определить магнитные потоки в стержнях.

       Прямая задача при расчете неразветвленной однородной магнитной цепи

выполняется в следующем порядке:

По заданному магнитному потоку Ф и известной площади поперечного сечения

    сердечника S, определяется магнитная индукция B=Ф/S

2. Определяют напряженность магнитного поля H в сердечнике по характеристике    намагничивания.

3. Находят намагничивающую силу по закону полного тока или второму закону   Кирхгофа F_m=IN,  F_m=Hl

       Расчет неразветвленной неоднородной магнитной цепи - такая магнитная цепь состоит из нескольких участков, отличающихся длиной, материалом. При решении прямой задачи известны размеры и материал каждого участка цепи, а магнитный поток задан. Определяют намагничивающую силу. Порядок решения такой же, как и для однородной цепи, но магнитная индукция и напряженность магнитного поля определяются для каждого участка.

Пример решения:

Четный вариант

 Дано:  Ф = 3,8∙10^-4 Вб

             S = 3,1 см² = 3,1∙ 10^-4 м²

             I = 8 А

             l₁ = 0,5 м

             l₂ = 0,09 м

             l₀ = 0,003 м

  Определить N

1.    Определяем магнитную индукцию

     Ф = BS,  B=Ф/S   В = 3,8∙10^-4/ 3,1∙ 10^-4 = 1,2 Т

2.    На представленном графике по рассчитанному значению магнитной индукции определяем напряженность магнитного поля в сердечнике и якоре

Н₁ = Н₂ = 375 А/м

3.    Определяем магнитное напряжение на участке l₁

     U_m1 = H₁∙ l₁ = 375∙0,5 = 187,5 А

4.    Определяем магнитное напряжение на участке l₂

U_m2 = H₂∙ l₂ = 375∙0,09 = 33,75 А

5.    Определяем напряженность магнитного поля в воздушном зазоре l₀

 Н₀ = В/m₀m_r    m_r =1      Н₀ = В/m₀ = 1,2 / 4π∙10^-7 = 95,5∙10⁴ А/м

6.    Определяем магнитное напряжение в воздушном зазоре l₀

     U_m0 = H₀∙ 2l₀ = 95,5∙10⁴∙2∙0,003 = 5730 А    2l₀ – так как воздушных зазора два

7.    Определяем намагничивающую силу всей магнитной цепи

     F_m= U_m1 + U_m2 + U_m0 = 187,5 + 33,75 + 5730 = 5951,25 А

8.    Определяем необходимое число витков обмотки

 F_m=I∙N   N = F_m / I = 5951,25 / 8 = 743,9 ≈ 744 витка

Нечетный вариант

 Дано:  В = 1,2 Т

             m_r = 300

             I = 8 А

             l₁ = 0,5 м

             l₂ = 0,09 м

             l₀ = 0,003 м

  Определить N

1.    Определяем напряженность магнитного поля в сердечнике и якоре

 В = m_а∙Н = m₀∙m_r∙Н    Н₁ = Н₂ = В / m₀∙m_r = 1,2 / 4π∙10^-7∙300 = 3184,7 А/м

2.    Определяем магнитное напряжение на участке l₁

     U_m1 = H₁∙ l₁ = 3184,7∙0,5 = 1592,35 А

3.    Определяем магнитное напряжение на участке l₂

 U_m2 = H₂∙ l₂ = 3184,7∙0,09 = 286,6 А

4.    Определяем напряженность магнитного поля в воздушном зазоре l₀

 Н₀ = В/m₀m_r    m_r =1      Н₀ = В/m₀ = 1,2 / 4π∙10^-7 = 95,5∙10⁴ А/м

5.    Определяем магнитное напряжение в воздушном зазоре l₀

     U_m0 = H₀∙ 2l₀ = 95,5∙10⁴∙2∙0,003 = 5730 А    2l₀ – так как воздушных зазора два

6.    Определяем намагничивающую силу всей магнитной цепи

     F_m= U_m1 + U_m2 + U_m0 = 1592,35 + 286,6 + 5730 = 7608,95 А

7.    Определяем необходимое число витков обмотки

 F_m=I∙N   N = F_m / I = 7608,95 / 8 = 951 виток

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №7 Преобразование энергии на основе электромагнитной индукции

Цель работы:

1.      Изучить принцип действия преобразователей электрической энергии: генератора, двигателя и трансформатора

Необходимые материалы и оборудование:

1.      Методические указания по выполнению практических занятий;

2.      Индивидуальное задание;

3.      Конспект лекций по предмету;

Ход работы:

1.      Ознакомиться с теоретическим материалом

2.      Описать физические принципы работы:

a.       Генератора

b.      Двигателя

c.       Трансформатора

3.      Описать область применения каждого устройства

Варианты заданий:

№ Вариант
1,5,9,13,17,21,25,29	Асинхронный двигатель с короткозамкнутым ротором
2,6,10,14,18,22,26,30	Асинхронный двигатель с фазным ротором
3,7,11,15,19,23,27,31	Явнополюсный синхронный генератор
4,8,12,16,20,24,28,32	Неявнополюсный синхронный генератор

 

1.       

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №8 Основные параметры и формы представления переменного тока

Цель работы:

1.        Изучение графического изображения изменения переменного тока по заданному уравнению синусоидальной ЭДС.

2.        Определение начальной фазы и мгновенного значения  ЭДС.

3.        Определение сдвига фаз между ЭДС.

4.        Познакомиться с методами построения и анализа синусоидальных величин.

5.        Получение практических навыков построения графических изображений синусоидальных величин и чтения осциллограмм переменных величин.

6.        Научиться определять параметры синусоидальных величин

Необходимые материалы и оборудование:

1.      Методические указания по выполнению практических занятий;

2.      Индивидуальное задание;

3.      Калькулятор;

4.      Конспект лекций по предмету;

Ход работы:

1.      Ознакомиться с теоретическими положениями о синусоидальных величинах.

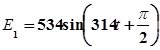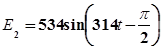2.      Построить в одной системе координат графики мгновенных значений переменных ЭДС:  и . Найти сумму указанных ЭДС.

Пояснение к работе:

Переменный электрический ток – это ток, изменяющийся с течением времени.

Значение этой величины в рассматриваемый момент времени называется мгновенным значением тока i.

Наиболее распространен переменный синусоидальный ток, являющийся синусоидальной функцией времени

Переменный синусоидальный сигнал характеризуется:

·         периодом Т, который выражается в секундах (с),

·         частотой f - величиной, обратной периоду, выражается в герцах (Гц).

·         Круговой (угловой) частотой ω = 2πf (1/с).

 

 

Мгновенное значение тока:

i = I_m sin (ωt + ψ_i),

где i – мгновенное значение тока, А;

I_m – амплитудное значение тока, А;

ω – круговая (угловая) частота, 1/с;

ψ_i – начальная фаза тока;

t – время, с.

Синусоидальные величины принято изображать графиками в виде зависимости от ωt. На данном графике ψ_i >0.

Аналогично выражаются мгновенные значения напряжения и ЭДС.

e = E_m sin (ωt + ψ_e)     u = U_m sin (ωt + ψ_u),                                                                                                         

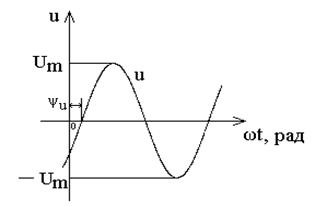
Начальная фаза тока (ЭДС, напряжения) ψ_i, ψ_e, ψ_u – это значение фазы в момент времени t = 0.

Разность начальных фаз двух синусоидальных величин одной и той же частоты называют сдвигом фаз.

Сдвиг фаз между напряжением и током определяется вычитанием начальной фазы тока из начальной фазы напряжения:

φ = ψ_u – ψ_i

Действующее значение переменного тока (ЭДС, напряжения) – это среднеквадратичное значение переменного тока (ЭДС, напряжения) за период Т.

Если ток, ЭДС или напряжение изменяются по синусоидальному закону, то  действующее значение составляет:

 

 

 

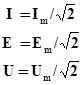Представление синусоидальных величин вращающимися векторами

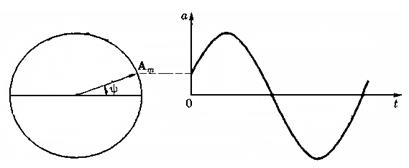
Для представления синусоидально изменяющейся величины a=Am sin(ωt+ψ) с начальной фазой ψ вращающимся вектором построим радиус-вектор Am этой величины длиной, равной амплитуде Am и под углом ψ к горизонтальной оси. Это будет его исходное положение в момент начала отсчета t = 0.

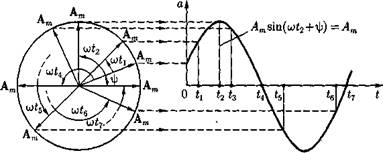
Если радиус-вектор вращать с постоянной угловой скоростью ω против направления движения часовой стрелки, то его проекция на вертикальную ось будет равна Am sin(ωt+ψ) .

Применение вращающихся векторов позволяет компактно представить на одном рисунке совокупность различных синусоидально изменяющихся величин одинаковой частоты.

 

 

Пример решения:

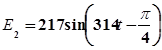Построить в одной системе координат графики мгновенных значений переменных ЭДС:  и . Найти сумму указанных ЭДС.

                                                       Решение.

 

 

 

 

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №9 РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА С ПРИМЕНЕНИЕМ КОМПЛЕКСНЫХ ЧИСЕЛ

Цель работы:

1.      Формирование практических навыков расчета электрической цепи переменного тока с применением комплексных чисел

Необходимые материалы и оборудование:

1.      Методические указания по выполнению практических занятий;

2.      Индивидуальное задание;

3.      Калькулятор;

4.      Конспект лекций по предмету;

5.      Канцелярские принадлежности.

Ход работы:

1.      Изучить метод расчета основанный на символическом изображении действительных синусоидальных функций времени комплексными числами.

2.      Начертите схему, согласно своему варианту (таблица 3 и рис.6).

3.      Используя значения таблицы 3, запишите исходные данные согласно своему варианту

4.      Рассчитайте напряжения во всех участках цепи, используя символический метод расчета.

5.      Рассчитайте силу тока I в цепи.

6.      Рассчитайте активную P, реактивную Q и полную S мощности цепи.

7.      Начертите в масштабе векторную диаграмму напряжений.

 

 

 

Таблица 3 - Исходные данные:

Вариант	R1	R2	R3	XC1	XC2	XC3	XL1	XL2	XL3	C1	C2	C3	L1	L2	L3	f	P	Q	S	I	U	№ Схемы
	Ом	Ом	Ом	Ом	Ом	Ом	Ом	Ом	Ом	мкФ	мкФ	мкФ	Гн	Гн	Гн	Гц	Вт	ВАр	ВА	А	В
1	5	4	6	2	-	-	7	-	-	-	500	-	-	0,03	-	50	-	-	-	-	100	1
2	15	20	-	-	15	-	8	-	-	35,38	-	450	-	0,02	-	450	-	-	-	-	150	2
3	10	15	4	12	-	-	10	-	-	-	500	-	-	0,02	-	350	-	-	-	-	200	3
4	5	3	6	-	-	-	4	3	-	79,6	900	-	-	-	0,007	250	-	-	-	-	100	4
5	2	3	-	7	-	-	6	8	-	-	600	-	-	-	0,02	150	-	-	-	-	140	5
6	4	-	-	5	8	-	8	10	-	-	-	350	-	-	0,01	100	-	-	-	-	100	6
7	4	3	-	8	-	7	6	-	-	-	1000	-	-	0,007	-	500	-	-	-	-	150	7
8	7	4	2	-	-	-	6	-	-	40	650	-	-	0,01	-	400	-	-	-	-	200	8
9	3	7	-	-	-	-	6	9	-	400	800	-	-		0,008	300	-	-	-	-	150	9
10	2	6	-	4	-	8	8	12	6,3	-	600	-	-		-	50	-	-	-	-	100	10

 

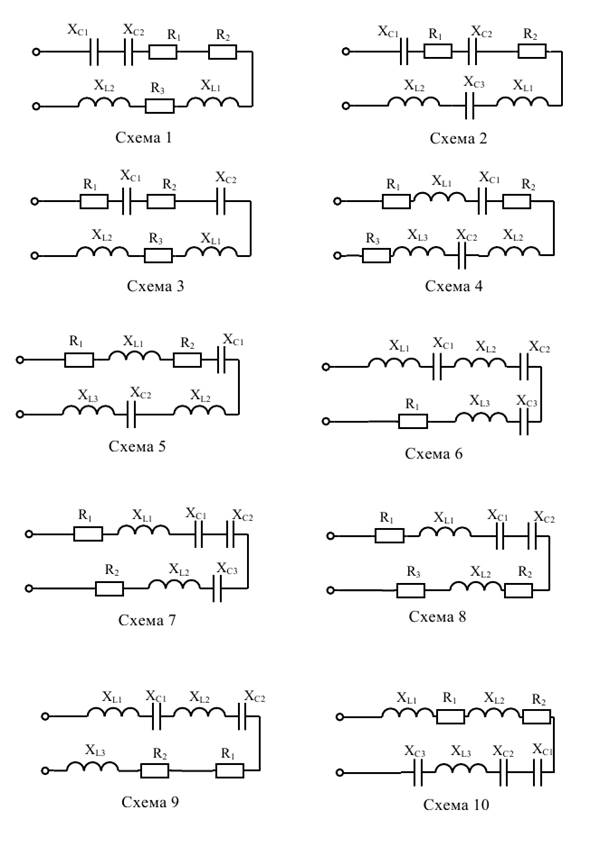
Рис.5 Схемы электрических цепей

 

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №10 РАСЧЕТ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПРИ НЕСИНУСОИДАЛЬНОМ НАПРЯЖЕНИИ НА ВХОДЕ

Цель работы:

1.      Научиться определять параметры несинусоидальных величин

-        частоту изменения;

-        максимальное значение

-        начальную фазу

-        реактивное и полное сопротивление для каждой гармонической составляющей

Необходимые материалы и оборудование:

1.      Методические указания по выполнению практических занятий;

2.      Индивидуальное задание;

3.      Калькулятор;

4.      Конспект лекций по предмету;

5.      Канцелярские принадлежности.

Ход работы:

1.      Ознакомиться с теорией о несинусоидальных величинах

2.      Выбрать из таблицы данные по номеру задания

3.      Рассчитать силу тока, мощности P, Q, S

4.      Формула напряжение

5.      Начертить в масштабе синусоиды напряжения и тока

6.      Дать определение несинусоидальной переменной кривой

7.      Дать определение «ряд Фурье»

8.     

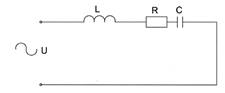
Рис.6 Схема электрической цепи

 

Параметры цепи :  

R=  10 Ом  ,   

L=   15,95 мГн ,     

C=70,77 мкФ.

 

Скачано с www.znanio.ru