Омский летно-технический колледж гражданской авиации имени А.В. Ляпидевского –

филиал федерального государственного бюджетного образовательного учреждения высшего образования «Ульяновский институт гражданской авиации имени Главного маршала авиации Б.П. Бугаева»

(ОЛТК ГА – филиал ФГБОУ ВО УИ ГА )

 

 

 

 

 

 

 

 

 

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО ВЫПОЛНЕНИЮ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

по  дисциплине

«Математика»

Специальности

25.02.01 Техническая эксплуатация летательных аппаратов и двигателей

25.02.04 Летная эксплуатация летательных аппаратов

 

 

 

 

Разработал:

Пищагина Е.С., преподаватель математики

           

                                              

                                          

Рассмотрено

на заседании ЦМК

от «_____»__________20__г.

Протокол №_________

 

 

 

 

 

 

 

 

 

 

 

Омск - 2021

АННОТАЦИЯ

        Методические рекомендации по выполнению самостоятельной работы по дисциплине «Математика», являющейся дисциплиной математического и общего естественнонаучного учебного цикла составлены в соответствии с требованиями Федерального государственного образовательного стандарта специальности и на основании  программы учебной дисциплины ЕН.01, Математика (рассмотрена и утверждена на заседании ЦМК ЕНД  «____» ___________20____г., протокол № ___)

Методические рекомендации по выполнению самостоятельных работ предназначены для курсантов 1 курса по специальностям:

25.02.01 Техническая эксплуатация летательных аппаратов и двигателей;

25.02.04 Летная эксплуатация летательных аппаратов.

Темы самостоятельных работ соответствует основным разделам программы, их выполнение обеспечивает более глубокое изучение материала, направлено на закрепление и систематизацию знаний, умений и формирование общих компетенций. Виды самостоятельных работ включают работу с понятийным аппаратом, вопросами по теме, подготовку докладов и рефератов, подборку материалов, составление презентаций и аннотаций, выполнение расчетно-графической работы.

 

 

Рецензент: ____________,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

СОДЕРЖАНИЕ

Пояснительная записка. 4

Тематическое  планирование  самостоятельной  работы курсантов. 6

Подготовка доклада. 7

Написание реферата на заданную тему. 11

Выполнение практических заданий (Решение задач) 18

Решение задач по теме «Применение систем линейных уравнений в экономике». 33

Проведение исследования. 41

Подготовка презентации на заданную тему. 44

Выполнение расчетно-графической работы.. 55

Библиографический список. 66

 

 

Пояснительная записка

Методические рекомендации по выполнению внеаудиторной самостоятельной  работы по естественно - научной  дисциплине «Математика»  предназначены для курсантов 1-го курса специальностей 25.02.01 Техническая эксплуатация летательных аппаратов и двигателей; 25.02.04 Летная эксплуатация летательных аппаратов.

Объем самостоятельной работы курсантов определяется федеральным государственным образовательным стандартом среднего профессионального образования (ФГОС СПО).

Выполнение внеаудиторной самостоятельной  работы является обязательной для каждого курсанта, её объём в часах определяется действующим рабочим учебным планом   ОЛТК ГА – филиал ФГБОУ ВО УИ ГА.

Самостоятельная внеаудиторная работа по математике проводится с целью:

-    формирования общих и профессиональных компетенций

-    систематизации и закрепления полученных теоретических знаний и практических умений курсантов;

-    углубления и расширения теоретических знаний;

-    развития познавательных способностей и активности курсантов, самостоятельности, ответственности и организованности;

-    развития исследовательских умений;

-    формирования самостоятельности мышления, способностей к саморазвитию, самосовершенствованию и самореализации.

Внеаудиторная самостоятельная работа выполняется курсантом по заданию преподавателя, но без его непосредственного участия.

Используются следующие виды заданий для внеаудиторной самостоятельной работы:

-    для овладения знаниями: чтение текста (учебника, дополнительной литературы), работа со словарями и справочниками, учебно-исследовательская работа, использование аудио- и видеозаписей, компьютерной техники и Интернета;

-    для закрепления и систематизации знаний: повторная работа над учебным материалом (учебника, дополнительной литературы, аудио- и видеозаписей), составление плана и алгоритма решения, составление таблиц для систематизации учебного материала, ответы на контрольные вопросы, подготовка сообщений к выступлению на уроке, конференции, подготовка сообщений, докладов, рефератов, тематических кроссвордов;

-    для формирования умений: решение задач повышенной сложности.

Самостоятельная работа представляет собой планируемую, организационно и методически направляемую преподавателем деятельность курсантов по освоению дисциплины «Прикладная математика» и приобретению профессиональных навыков, осуществляемую за рамками аудиторной учебной работы курсантов.

Перед выполнением внеаудиторной самостоятельной работы курсант должен внимательно выслушать инструктаж преподавателя по выполнению задания, который включает определение цели задания, его содержание, сроки выполнения, ориентировочный объем работы, основные требования к результатам работы, критерии оценки. В процессе инструктажа преподаватель предупреждает курсантов о возможных типичных ошибках, встречающихся при выполнении задания.

Критериями оценки результатов внеаудиторной самостоятельной работы курсанта являются:

-          уровень освоения курсантом  учебного материала;

-          умение курсанта использовать теоретические знания при выполнении практических задач;

-          сформированность общеучебных умений;

-          обоснованность и четкость изложения ответа;

-          оформление материала в соответствии с требованиями.

 

Тематическое  планирование  самостоятельной  работы курсантов   

Тема	Вид самостоятельной работы	Количество часов
		25.02.01	25.02.04
Раздел 1. Линейная алгебра
Тема 1.2. Системы линейных уравнений	Индивидуальные задания «Применение систем линейных уравнений в экономике»	4	4
Раздел 3. Основные понятия и методы математического анализа
Тема 3.1. Функции, их свойства и графики.	Рефераты «Использование метода трапеций, парабол для приближенных вычислений»	4	4
Тема 3.2. Основные понятия теории пределов и непрерывности  функции	Доклад: «История развития теории пределов».	2	2
Тема 3.3. Ряды	Исследовательская работа «Использование метода рядов Фурье при получении радиоволн высоких частот».	4	2
Раздел 4. Интегральное и дифференциальное исчисление
Тема 4.1. Производная и дифференциал функции	Индивидуальные задания «Решение задач повышенной сложности по вычислению дифференциала функции»	2	2
Тема 4.3. Определенный интеграл	Индивидуальные задания: ««Решение задач повышенной сложности по вычислению интегралов».	6	2
Тема 4.4. Дифференциальные уравнения	Доклад «Дифференциальные уравнения высшего порядка».	2	2
Тема 4.4. Дифференциальные уравнения	Доклад «Использование метода дифференциальных уравнений в автоматических системах управления воздушными судами».	2	2
Раздел 5. Теория вероятностей и математическая статистика
Тема 5.1. Теория вероятности	Доклад «Схемы Бернулли»	2	2
Тема 5.3. Математическое ожидание и дисперсия случайной величины	Презентация «Применение сложных расчетов в экономических процессах».	4	4
Тема 5.4. Предмет и основные понятия математической статистики	Расчетно-графическая работа «Графическое изображение статистических преобразований»	2	2

 

Вид работы: Подготовка доклада.

 

Курсант должен

знать:

-          композиционную структуру доклада

уметь:

-          сообщать новую информацию;

-          использовать технические средства;

-          хорошо ориентироваться в теме доклада;

-          дискутировать и быстро отвечать на заданные вопросы;

-          четко выполнять установленный регламент

 

Тема 3.2. Основные понятия теории пределов и непрерывности функции

Доклад: «История развития теории пределов».

Тема 4.4. Дифференциальные уравнения

Доклад «Дифференциальные уравнения высшего порядка».

Доклад «Использование метода дифференциальных уравнений в автоматических системах управления воздушными судами».

Тема 5.1. Теория вероятности

Доклад «Схемы Бернулли»

 

Инструкция по выполнению самостоятельной работы

Доклад – это устное выступление на заданную тему. В учебных заведениях время доклада, как правило, составляет 5-15 минут.

Цели доклада:

1. Научиться убедительно и кратко излагать свои мысли в устной форме. (Эффективно продавать свой интеллектуальный продукт).

2. Донести информацию до слушателя, установить контакт с аудиторией и получить обратную связь.

План и содержание доклада

Важно при подготовке доклада учитывать три его фазы: мотивацию, убеждение, побуждение. В первой фазе доклада рекомендуется использовать:

-          риторические вопросы;

-          актуальные местные события;

-          личные происшествия;

-          истории, вызывающие шок;

-          цитаты, пословицы;

-          возбуждение воображения;

-          оптический или акустический эффект;

-          неожиданное для слушателей начало доклада.

Как правило, используется один из перечисленных приёмов. Главная цель фазы открытия (мотивации) – привлечь внимание слушателей к докладчику, поэтому длительность её минимальна.

Ядром хорошего доклада является информация. Она должна быть новой и понятной. Важно в процессе доклада не только сообщить информацию, но и убедить слушателей в правильности своей точки зрения. Для убеждения следует использовать:

-          сообщение о себе кто?

-          обоснование необходимости доклада почему?

-          доказательство кто? когда? где? сколько?

-          пример берём пример с …

-          сравнение это так же, как…

-          проблемы что мешает?

Третья фаза доклада должна способствовать положительной реакции слушателей. В заключении могут быть использованы:

-          обобщение;

-          прогноз;

-          цитата;

-          пожелания;

-          объявление о продолжении дискуссии;

-          просьба о предложениях по улучшению;

-          благодарность за внимание.

Фазы доклада

-          ИНФОРМАЦИЯ

-          ОБЪЯСНЕНИЕ

-          ОБОСНОВАНИЕ

-          ДОКАЗАТЕЛЬСТВО

-          ПРИМЕР      

-          ПРОБЛЕМЫ

-          СРАВНЕНИЕ

-          ЗАКЛЮЧЕНИЕ

Открытие фазы

-          МОТИВАЦИЯ

-          УБЕЖДЕНИЕ

-          ПОБУЖДЕНИЕ

 

Обратная связь

При общении следует помнить о правильной реакции (реплике) на задаваемые вам вопросы. Правильная реакция на вопрос: ·

-               Да. ·

-               Хорошо. ·

-               Спасибо, что вы мне сказали. ·

-               Это является совсем новой точкой зрения. ·

-               Это можно реализовать. ·

-               Вы попали в точку. ·

-               Именно это я имею в виду. ·

-               Прекрасная идея. ·

-               Это можно делать и так. ·

-               Вы правы. ·

-               Спасибо за Ваши указания. ·

-               Это именно и является основным вопросом проблемы.

 

Составляющие воздействия докладчика на слушателей

Выделяют три составляющих воздействия докладчика на слушателей

1. Язык доклада Короткие предложения. Выделение главных предложений. Выбор слов. Иностранные слова и сокращения. Образность языка. 2. Голос Выразительность. Вариации громкости. Темп речи. 3. Внешнее общение Зрительный контакт. Обратная связь. Доверительность. Жестикуляция.

Составляющие воздействия	Средства достижения воздействия
1. Язык доклада	Короткие предложения. Выделение главных предложений. Выбор слов. Иностранные слова и сокращения. Образность языка.
2. Голос	Выразительность. Вариации громкости. Темп речи.
3. Внешнее общение	Зрительный контакт. Обратная связь. Доверительность. Жестикуляция.

Формы контроля и критерии оценок

Доклады выполняются на листах формата А4 в соответствии с представленными в методических рекомендациях требованиями.

«Отлично» ( 5 ) выставляется в случае, когда объем доклада составляет 5-6 страниц, текст напечатан аккуратно, в соответствии с требованиями, полностью раскрыта тема доклада, информация взята из нескольких источников, доклад написан грамотно, без ошибок. При защите доклада курсант продемонстрировал отличное знание материала работы, приводил соответствующие доводы, давал полные развернутые ответы на вопросы и аргументировал их.

«Хорошо»  ( 4 ) выставляется в случае, когда объем доклада составляет 4-5 страниц, текст напечатан аккуратно, в соответствии с требованиями, встречаются небольшие опечатки, полностью раскрыта тема доклада, информация взята из нескольких источников, реферат написан грамотно. При защите доклада курсант продемонстрировал хорошее знание материала работы, приводил соответствующие доводы, но не смог дать полные развернутые ответы на вопросы и привести соответствующие аргументы.

«Удовлетворительно»  ( 3 ) - в случае, когда объем доклада составляет менее 4 страниц, текст напечатан неаккуратно, много опечаток, тема доклада раскрыта не полностью, информация взята из одного источника, реферат написан с ошибками. При защите доклада курсант продемонстрировал слабое знание материала работы, не смог привести соответствующие доводы и аргументировать сои ответы.

«Неудовлетворительно»  ( 2 ) - в случае, когда объем доклада составляет менее 4 страниц, текст напечатан неаккуратно, много опечаток, тема доклада не раскрыта, информация взята из 1 источника, много ошибок в построении предложений. При защите доклада курсант продемонстрировал слабое знание материала работы, не смог раскрыть тему, не отвечал на вопросы.

 

 

Вид работы: Написание реферата на заданную тему

 

Тема 3.1. Функции, их свойства и графики

Реферат «Использование метода трапеций, парабол для приближенных вычислений»

Курсант должен

знать:

-          суть основных вопросов изложенных в реферате по выбранной теме;

-          основные понятия этой темы;

уметь:

-          работать с разнообразными источниками информации.

 

Инструкция по выполнению самостоятельной работы

Реферат – краткое изложение в письменном виде или в форме публичного доклада содержания научного труда или трудов, обзор литературы по теме. Изложение материала носит проблемно-тематический характер, показываются различные точки зрения, а также собственные взгляды на проблему. Содержание реферата должно быть логичным. Объём реферата, как правило, от 5 до 15 машинописных страниц. Перед началом работы над рефератом следует наметить план и подобрать литературу. Прежде всего, следует пользоваться литературой, рекомендованной учебной программой, а затем расширить список источников, включая и использование специальных журналов, где имеется новейшая научная информация.

Структура реферата:

-          Титульный лист.

-          Оглавление.

-          Введение (дается постановка вопроса, объясняется выбор темы, её значимость и актуальность, указываются цель и задачи реферата, даётся характеристика используемой литературы).

-          Основная часть (состоит из глав и подглав, которые раскрывают отдельную проблему или одну из её сторон и логически являются продолжением друг друга).

-          Заключение (подводятся итоги и даются обобщённые основные выводы по теме реферата, делаются рекомендации).

-          Список литературы. В списке литературы должно быть не менее 8–10 различных источников. Допускается включение таблиц, графиков, схем, как в основном тексте, так и в качестве приложений.

 

Критерии оценки реферата:

-          соответствие теме; глубина проработки материала;

-          правильность и полнота использования источников;

-          владение терминологией и культурой речи;

-          оформление реферата.

Рефераты могут быть представлены на теоретических занятиях в виде выступлений.

 

Работа над введением

Введение – одна из составных и важных частей реферата. При работе над введением необходимо опираться на навыки, приобретенные при написании изложений и сочинений. В объеме реферата введение, как правило, составляет 1-2 машинописные страницы. Введение обычно содержит вступление, обоснование актуальности выбранной темы, формулировку цели и задач реферата, краткий обзор литературы и источников по проблеме, историю вопроса и вывод.

 Вступление – это 1-2 абзаца, необходимые для начала. Желательно, чтобы вступление было ярким, интригующим, проблемным, а, возможно, тема реферата потребует того, чтобы начать, например, с изложения какого-то определения, типа «политические отношения – это…».

Обоснование актуальности выбранной темы - это, прежде всего, ответ на вопрос: «почему я выбрал(а) эту тему реферата, чем она меня заинтересовала?». Можно и нужно связать тему реферата с современностью.

Краткий обзор литературы и источников по проблеме – в этой части работы над введением необходимо охарактеризовать основные источники и литературу, с которой автор работал, оценить ее полезность, доступность, высказать отношение к этим книгам.

История вопроса – это краткое освещение того круга представлений, которые сложились в науке по данной проблеме и стали автору известны.

Вывод – это обобщение, которое необходимо делать при завершении работы над введением.

 

Требования к содержанию реферата

Содержание реферата должно соответствовать теме, полно ее раскрывать. Все рассуждения нужно аргументировать. Реферат показывает личное отношение автора к излагаемому. Следует стремиться к тому, чтобы изложение было ясным, простым, точным и при этом выразительным. При изложении материала необходимо соблюдать общепринятые правила: ─ не рекомендуется вести повествование от первого лица единственного числа (такие утверждения лучше выражать в безличной форме); ─ при упоминании в тексте фамилий обязательно ставить инициалы перед фамилией; ─ каждая глава (параграф) начинается с новой строки; ─ при изложении различных точек зрения и научных положений, цитат, выдержек из литературы, необходимо указывать источники, т.е. приводить ссылки.

Правила оформления ссылок

В реферате сведения об использованной литературе приводятся чаще всего в скобках после слов, к которым относятся. В скобках сначала указывается номер книги в списке литературы, а затем через запятую страница. Если ссылка оформляется на цитату из многотомного сочинения, то после номера книги римской цифрой указывается номер тома, а потом номер страницы. Примеры: (1,145); (4,II,38).

 

Работа над заключением

Заключение – самостоятельная часть реферата. Оно не должно быть переложением содержания работы. Заключение должно содержать:

-          основные выводы в сжатой форме;

-          оценку полноты и глубины решения тех вопросов, которые вставали в процессе изучения темы.

Объем 1-2 машинописных или компьютерных листа формата А4.

 

Оформление приложения

Приложение помещается после заключения и включает материалы, дополняющие основной текст реферата. Это могут быть таблицы, схемы, фрагменты источников, иллюстрации, фотоматериалы, словарь терминов, афоризмы, изречения, рисунки и т.д.

 

Примеры оформления:

Приложение 1. Терминологический словарь “Тригонометрические функции”.

Приложение 2. Алгоритм решения дифференциального уравнения.

Приложение 3. Инструкционная карта по правилам исследования функции.

В тексте реферата необходимо делать примечания. Пример: (см. приложение 1, С.21). Приложение является желательным, но не обязательным элементом реферата.

 

Правила оформления библиографических списков

Список литературы помещается в конце реферата и пронумеровывается. Сведения о книгах в списке литературы излагаются в алфавитном порядке. Сведения о книге даются в следующем порядке:

-          автор (фамилия, инициалы);

-          название, подзаголовок;

-          выходные данные (место издания, издательство и год издания).

Пример: Григорьев В.П., Дубинский Ю.А., Элементы высшей математики. Учебник для среднего профессионального образования. – М.: Академия, 2008.

Если речь идет о статье, напечатанной в сборнике, журнале или газете, то после автора и названия публикации указываются:

-          название сборника, журнала, газеты;

-          место издания и год издания (если сборник);

-          год, номер журнала или дата выхода газеты, страница.

Пример: Пленков О.Ю. Развитие математики в России // Математические ведомости. – 2012. - №1. – С.10- 16.

В библиографическом описании не разрешается сокращать фамилии авторов, а также заглавия книг и статей. Сокращаются только названия городов: Москва (М.), Санкт-Петербург (СПб.). Названия остальных городов пишутся без сокращений. Если книга издавалась параллельно в двух городах, названия их приводятся через точку с запятой.

 

Требования к оформлению реферата

Текст работы пишется разборчиво на одной стороне листа (формата А4) с широкими полями слева, страницы пронумеровываются. При изложении материала нужно четко выделять отдельные части (абзацы), главы и параграфы начинать с новой страницы, следует избегать сокращения слов. Если работа набирается на компьютере, следует придерживаться следующих правил (в дополнение к вышеуказанным): набор текста реферата необходимо осуществлять стандартным 12 шрифтом; заголовки следует набирать 14 шрифтом (выделять полужирным); межстрочный интервал полуторный; разрешается интервал между абзацами; отступ в абзацах 1-2 см.; поле левое 2,5 см., остальные 2 см.; нумерация страницы снизу или сверху посередине листа; объем реферата 20-24 страницы.

 

Подготовка к защите и порядок защиты реферата

Необходимо заранее подготовить тезисы выступления (план-конспект). Порядок защиты реферата:

1. Краткое сообщение, характеризующее задачи работы, ее актуальность, полученные результаты, вывод и предложения.

2. Ответы курсанта на вопросы преподавателя.

3. Отзыв руководителя-консультанта о ходе выполнения работы.

 

 

 

Советы курсанту при защите реферата:

На всю защиту реферата отводится чаще всего около 15 минут. При защите постарайтесь соблюсти приведенные ниже рекомендации. 

-          Вы должны вспомнить материал максимально подробно, и это должно найти отражение в схеме Вашего ответа. Но тут же необходимо выделить главное, что наиболее важно для понимания материала в целом, иначе Вы сможете проговорить все 15 минут и не раскрыть существа вопроса. Особенно строго следует отбирать примеры и иллюстрации. 

-          Вступление должно быть очень кратким. Строго следите за точностью своих выражений и правильностью употребления терминов. 

-          Не пытайтесь рассказать побольше за счет ускорения темпа, но и не мямлите. 

-          Не демонстрируйте излишнего волнения и не напрашивайтесь на сочувствие.

-          Будьте особенно внимательны ко всем вопросам преподавателя, не бойтесь дополнительных вопросов – чаще всего преподаватель использует их как один из способов помочь Вам или сэкономить время. 

-          Прежде чем отвечать на дополнительный вопрос, необходимо сначала правильно его понять. Для этого нужно хотя бы немного подумать, иногда переспросить, уточнить: правильно ли Вы поняли поставленный вопрос. И при ответе следует соблюдать тот же принцип экономности мышления, а не высказывать без разбора все, что Вы можете сказать. 

-          Будьте доброжелательны и тактичны.

План-график работы над рефератом

Этапы работы	Содержание работы курсанта	Форма отчетности курсанта	Содержание работы преподавателя
1. Вводный	Выбор темы реферата, поиск и ознакомление с литературой, формулирование цели и задач работы, составление плана	Вариант плана, цель и задачи работы, список литературы		Консультация, коррекция деятельности, проверка плана реферата и списка литературы
2.Основной	Работа над основным содержанием и заключением реферата	Краткие тезисы, подробный план работы, черновые записи		Устное собеседование, индивидуальная консультация,  коррекция
3. Заключительный	Оформление реферата	Завершенный реферат		Проверка, рецензирование работы, возврат реферата
4. Защита реферата	Подготовка к защите	Защита реферата		Принятие защиты реферата

 

Образец оформления содержания

Образец оформления титульного листа к реферату

Форма контроля и критерии оценки реферата.

Рефераты выполняются на листах формата А4 в соответствии с представленными в методических рекомендациях требованиями.

«Отлично»  ( 5 ) выставляется в случае, когда объем реферата составляет 10-12страниц, текст напечатан аккуратно, в соответствии с требованиями, полностью раскрыта тема реферата, отражена точка зрении автора на рассматриваемую проблему, реферат написан грамотно, без ошибок. При защите реферата курсант продемонстрировал отличное знание материала работы, приводил соответствующие доводы, давал полные развернутые ответы на вопросы и аргументировал их.

«Хорошо»  ( 4 ) выставляется в случае, когда объем реферата составляет 8- 10 страниц, текст напечатан аккуратно, в соответствии с требованиями, встречаются небольшие опечатки, полностью раскрыта тема реферата, отражена точка зрения автора на рассматриваемую проблему, реферат написан грамотно. При защите реферата курсант продемонстрировал хорошее знание материала работы, приводил соответствующие доводы, но не смог дать полные развернутые ответы на вопросы и привести соответствующие аргументы.

«Удовлетворительно»  ( 3 ) - в случае, когда объем реферата составляет менее 8 страниц, текст напечатан неаккуратно, много опечаток, тема реферата раскрыта неполностью, не отражена точка зрения автора на рассматриваемую проблему, реферат написан с ошибками. При защите реферата курсант продемонстрировал слабое знание материала работы, не смог привести соответствующие доводы и аргументировать на свои ответы.

«Неудовлетворительно»  ( 2 )- в случае, когда объем реферата составляет менее 5страниц, текст напечатан неаккуратно, много опечаток, тема реферата не раскрыта, не отражена точка зрения автора на рассматриваемую проблему, много ошибок в построении предложений. При защите реферата курсант продемонстрировал слабое знание материала работы, не смог раскрыть тему не отвечал на вопросы.

Вид работы: Выполнение практических заданий (Решение задач)

 

Курсант должен

знать:

-          основные формулы, необходимые для решения задач по предложенной теме;

-          основные методы решения задач;

-          правила оформления решения задачи;

уметь:

-          применять изученные методы для решения задач;

-          составлять и реализовывать алгоритм решения задачи.

 

Тема 1.2. Системы линейных уравнений

Решение задач по теме «Применение систем линейных уравнений в экономике»

Тема 4.1. Производная и дифференциал функции

Решение задач повышенной сложности по вычислению дифференциала функции

Тема 4.3. Определенный интеграл

Решение задач повышенной сложности по вычислению интегралов

 

Практическое задание — это одна из форм учебной работы, которая ориентирована на закрепление изученного теоретического материала, его более глубокое усвоение и формирование умения применять теоретические знания в практических, прикладных целях.

Особое внимание при выполнение практических заданий уделяется формированию общих учебных или профессиональных компетенций. Такие компетенции формируются в процессе выполнения конкретных заданий — упражнений, задач и т. п. — под руководством и контролем преподавателя.

Умение решать задачи является одним из основных показателей уровня математического развития, глубины усвоения математического материала.

 

Этапы подготовки к практическому занятию:

-          освежите в памяти теоретические сведения, полученные на занятиях  и в процессе самостоятельной работы,

-          подберите необходимую учебную и справочную литературу,

-          определитесь в целях и методах выполнения практического задания.

 

 

Тема 1.2. Системы линейных уравнений

Решение задач по теме «Применение систем линейных уравнений в экономике»

 

Математика интенсивно проникает в другие науки: во многом этот процесс происходит благодаря разделению математики на ряд самостоятельных областей. Язык математики универсален, что является объективным отражением универсальности законов окружающего нас мира.

Экономика как наука об объективных причинах функционирования и развития общества пользуется разнообразными количественными характеристиками, а потому вобрала в себя большое число математических методов.

Использование элементов алгебры матриц является одним из основных методов решения многих экономических задач. Этот вопрос стал особенно актуальным при разработке и использовании баз данных: при работе с ними почти вся информация хранится и обрабатывается в матричной форме.

Также существует ряд экономических задач, приводящих к составлению и решению систем линейных алгебраических уравнений на основе прогноза выпуска продукции по известным запасам сырья.

На основе алгебры матриц и аппарате матричного анализа американский экономист В.В. Леонтьев создал математическую модель, которая решает проблему баланса между отдельными отраслями мирового хозяйства.

Таким образом, применение элементов линейной алгебры в значительной степени упрощает способы решения многих задач экономики.

 

Инструкция по выполнению самостоятельной работы

1) Повторить теоретический материал  «Системы линейных алгебраических уравнений»: В.Т Лисичкин,  И.Л Соловейчик, Математика. Учебник для среднего профессионального образования. – М.: Высшая школа, 1991. – стр.81-91.

2) Рассмотреть решение экономических задач с помощью СЛАУ.

 

Системы линейных уравнений широко используются в задачах экономики. Рассмотрим их применение на примере.

 

Пример 1. Из некоторого листового материала необходимо выкроить 360 заготовок типа А, 300 заготовок типа Б и 675 заготовок типа В. При этом можно применять три способа раскроя. Количество заготовок, получаемых из каждого листа при каждом способе раскроя, указано в таблице:

Тип заготовки	Способ раскроя
	1	2	3
А	3	2	1
Б	1	6	2
В	4	1	5

 

Ход решения задачи:

Записать в математической форме условия выполнения задания.

Решение. Обозначим через  x, y,  z   количество листов материала, раскраиваемых соответственно первым, вторым и третьим способами. Тогда при первом способе раскроя   x  листов будет получено  3x  заготовок типа А, при втором - 2y, при третьем - z.

Для полного выполнения задания по заготовкам типа А сумма

 должна равняться 360, т.е.

Аналогично получаем уравнения

которым должны удовлетворять неизвестные  x, y, z   для того, чтобы выполнить задание по заготовкам Б и В. Полученная система линейных уравнений и выражает в математической форме условия выполнения всего задания по заготовкам А, Б и В. Решим систему методом исключения неизвестных. Запишем расширенную матрицу системы и приведем ее с помощью элементарных преобразований к треугольному виду.

 

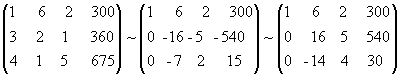
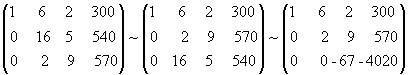
Следовательно, исходная система равносильна следующей:

 

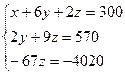
Из последнего уравнения находим z = 60; подставляя найденное значение  z   во второе уравнение, получаем y = 15 и, наконец, из первого имеем x = 90. Итак, вектор C (90, 15, 60) есть решение системы.

 

Пример 2.  Три судна доставили в порт 6000 т чугуна, 4000 т железной руды и 3000 т апатитов. Разгрузку можно производить как непосредственно в железнодорожные вагоны для последующей доставки потребителям, так и на портовые склады. В вагоны можно разгрузить 8000 т, а остаток груза придется направить на склады. Необходимо учесть, что поданные в порт вагоны не приспособлены для перевозки апатитов. Стоимость выгрузки 1 т в вагоны составляет соответственно 4, 30, 5,25 и 2,20  ден. ед.

Записать в математической форме условия полной разгрузки судов, если затраты на нее должны составить 58850  ден. ед.

Решение. По условию задачи, доставленные в порт чугун, железную руду и апатиты можно разгрузить двумя способами: либо в железнодорожные вагоны, либо в портовые склады. Обозначим через x _{i j} количество груза (в тоннах) i-го вида (i= 1,2,3), которое предполагается разгрузить j-м способом (j = 1, 2). Таким образом, задача содержит шесть неизвестных. Условие полной разгрузки чугуна можно записать в виде

                                                                                                                 (1)

где x ₁₁, x ₁₂ - части чугуна, разгружаемого соответственно в вагоны и на склады. Аналогичное условие должно выполняться и для железной руды:

                                                                                                                  (2)

Что же касается апатитов, то их можно разгружать только на склады, а поэтому неизвестное x ₃₁ = 0, и условие полной разгрузки апатитов принимает вид

                                                                .                                                           (3)

Условие полной загрузки всех поданных в порт вагонов запишется так:

                                                                                                                    (4)

Затраты на разгрузку, по условию, определены в 58850 ден. ед., что можно выразить записью:

                                                            (5)

Итак, с учетом сложившейся в порту ситуации условия полной разгрузки судов выражаются в математической форме системой линейных уравнений (1) - (5). С учетом (3) уравнение (5) перепишется в виде:

и теперь мы имеем систему из четырех уравнений с четырьмя неизвестными  x _11,  x ₁₂, x ₂₁,  x ₂₂,  расширенная матрица которой имеет вид:

.

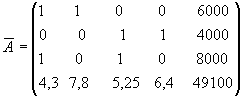Преобразуем ее к треугольному виду:

 

  .

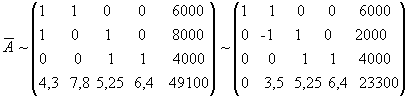
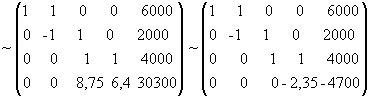Наша система равносильна следующей:

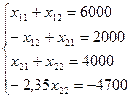
откуда x ₂₂ = 2000, x ₂₁ = 2000, x ₁₂ = 0, x ₁₁ = 6000.

 

Пример 3. На предприятии имеется четыре технологических способа изготовления изделий А и Б из некоторого сырья. В таблице указано количество изделий, которое может быть произведено из единицы сырья каждым из технологических способов.

Записать в математической форме условия выбора технологий при производстве из 94 ед. сырья 574 изделий А и 328 изделий Б.

Изделие	Выход из единицы сырья
	I	II	III	IV
А	2	1	7	4
Б	6	12	2	3

 

Ход решения задачи. Обозначим через x₁, x₂, x₃, x₄  количество сырья, которое следует переработать по каждой технологии, чтобы выполнить плановое задание. Получим систему трех линейных уравнений с четырьмя неизвестными:

 

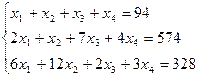
Решаем ее методом Гаусса:

 

.

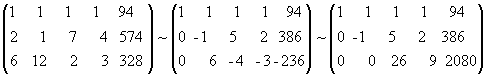
Имеем: r (А) = r (А) = 3, следовательно, число главных неизвестных равно трем, одно неизвестное  x₄  - свободное. Исходная система равносильна следующей:

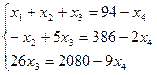
Из последнего уравнения находим , подставляя  во второе уравнение, будем иметь:  и, наконец, из первого уравнения получим: .. С математической точки зрения система имеет бесчисленное множество решений, т. е. неопределенна. С учетом реального экономического содержания величины  x₁  и  x₄  не могут быть отрицательными, тогда из соотношения  получим: .

 Тогда вектор (0, 14, 80, 0) является решением данной системы.

 

Пример 4: Оптимальный план перевозок.

С двух заводов поставляются автомобили для двух автохозяйств, потребности которых соответственно 200 и 300 машин. Первый завод выпустил 350 машин, а второй- 150 машин. Известны затраты на перевозку машин с завода в каждое автохозяйство (см. таблицу).

 

Минимальные затраты на перевозку равны 7950 ден.ед. Найти оптимальный план перевозок машин. 
Решение. Пусть x_ij- количество машин, поставляемых с i – го завода j-му автохозяйству (i,j=1,2). 
Получаем систему 

 

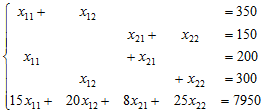
Решаем систему, например, методом Гаусса.

 Найдем x₁₁=50, x₁₂=300, x₂₁=150, x₂₂=0

 

3) Выполнить практические задания:

 

Задача 1.

 Предприятие выпускает ежесуточно четыре вида изделий, основные  производственно-экономические показатели которых приведены в таблице.

 

Требуется определить следующие ежесуточные показатели: расход сырья S, затраты рабочего времени T и стоимость Р выпускаемой продукции предприятия.

 

Задача 2.

 

Дана таблица, в которой приведены данные о дневной производительности 5 предприятий холдинга, выпускающих 4 вида продукции с потреблением трех видов сырья, а также продолжительность работы каждого предприятия за год и цена каждого вида сырья.

Вид изделия, №	Производительность предприятий, изд./ день					Затраты видов сырья, ед. веса/ изд.
	1	2	3	4	5	1	2	3
1	4	5	3	6	7	2	3	4
2	0	2	4	3	0	3	5	6
3	8	15	0	4	6	4	4	5
4	3	10	7	5	4	5	8	6
	Кол-во рабочих дней за год					Цены видов сырья, ден.ед./ед. веса
	1	2	3	4	5	1	2	3
	200	150	170	120	140	40	50	60

 

Требуется определить:

1)      годовую производительность каждого предприятия по каждому виду изделий;

2)      годовую потребность каждого предприятия в каждом виде сырья;

3)      годовую сумму финансирования каждого предприятия для закупки сырья, необходимого для выпуска продукции указанных видов и количеств.

 

Задача 3.

Обувная фабрика специализируется по выпуску изделий трех видов: сапог, кроссовок и ботинок; при этом используется сырье трех типов: S₁,S₂,S₃. Нормы расхода каждого из них на одну пару обуви и объем расхода сырья на один день заданы таблицей:

Найти ежедневный объем выпуска каждого вида обуви.

 

Задача 4.

С двух заводов поставляются автомобили для двух автохозяйств, потребности которых соответственно 200 и 300 машин. Первый завод выпустил 350 машин, а второй – 150 машин. В таблице приведены затраты на перевозку машин с завода в каждое автохозяйство.

Завод	Затраты на перевозку в автохозяйство, ден. ед.
	1	2
1	15	20
2	8	25

Минимальные затраты на перевозку равны 7950 ден.ед. Найти оптимальный план перевозок машин.

 

Задача 5.

Предприятие выпускает три вида продукции, используя сырье трех типов. Необходимые характеристики производства указаны в таблице. Требуется определить объем выпуска продукции каждого вида при заданных запасах сырья.

 

Форма контроля и критерии оценки выполнения практических заданий..

Задания выполняются в специальных тетрадях для самостоятельной работы.

«Отлично»  ( 5 ) выставляется в случае, когда правильно решены все 5 задач.

«Хорошо»  ( 4 ) выставляется в случае, когда правильно решены 4 задачи, или решено 5 задач, но есть неточности в вычислениях.

«Удовлетворительно»  ( 3 ) - в случае, когда правильно решены 3 задачи, или решено 4 задачи, но есть неточности или ошибки в вычислениях.

«Неудовлетворительно»  ( 2 ) - в случае, когда правильно решены менее 3 задач, или решено 3 задачи,  но есть неточности или ошибки в вычислениях.

Тема 4.1. Производная и дифференциал функции

Инструкция по выполнению самостоятельной работы

1)      Повторить теоретический материал: В.Т Лисичкин, И.Л Соловейчик, Математика. Учебник для среднего профессионального образования. – М.: Высшая школа, 1991. – стр.178, 215-216.

2)      Алгоритм дифференцирования сложной функции:

1.                 Чтобы найти производную сложной функции, надо ее правильно прочитать;

2.                 Чтобы правильно прочитать функцию, надо определить в ней порядок действий;

3.                 Функцию читаем в обратном порядку действий направлении;

4.                 Производную  находим по ходу чтения функции.

 

!!! Обратите внимание на приоритет (порядок) применения правил: правило дифференцирования сложной функции применяется в последнюю очередь

 

 

3)      Выполнить задания:

Продифференцировать сложную функцию

Пример 1

 

 

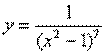
Пример 2

а) 

б)  

 

Пример 3

 

 

Пример 4

 

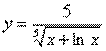
Пример 5

 

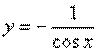
Пример 6

 

 

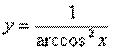
Пример 7

 

 

Пример 8

 

 

Пример 9

 

Пример 10

 

Примеры выполнения заданий:

 

Задание.1	Найти производную функции
Решение.	По свойству дифференцирования сложной функции вначале находим производную натурального логарифма и домножаем на производную подлогарифмической функции: Производная суммы равна сумме производных и константу можно выносить за знак производной, поэтому имеем: Знаменатель дроби можно свернуть по формуле квадрат разности, а в числителе двойку вынесем как общий множитель за скобки: сокращаем:
Ответ.

 

Задание.2	Найти производную функции
Решение.	По свойству дифференцирования сложной функции и используя формулы вычисления производной показательной и тригонометрических функций, получим: Производная суммы равна сумме производных: Для вычисления данной производной использовались правила дифференцирования и таблица производных сложных функций.
Ответ.

 

Задание.3.	Найти производную функции
Решение.	По свойству дифференцирования сложной функции производная от данной функции сначала берется как от арксинуса, а затем умножается на производную от корня: Производная  так же берется по правилам дифференцирования сложной функции, сначала производная от корня, а затем умножается на производную от подкоренного выражения: производная разности равна разности производных, тогда
Ответ.

 

 

Форма контроля и критерии оценки выполнения практических заданий.

Задания выполняются в специальных тетрадях для самостоятельной работы.

«Отлично»  ( 5 ) выставляется в случае, когда правильно решены все 10 примеров.

«Хорошо»  ( 4 ) выставляется в случае, когда правильно решены 8-9 примеров, или решено 10 примеров, но есть неточности в вычислениях.

«Удовлетворительно» ( 3 )  - в случае, когда правильно решены 6-7 примеров, или решено 8 примеров,  но есть неточности в вычислениях.

«Неудовлетворительно»  ( 2 ) - в случае, когда правильно решены менее 6 примеров, или решено 6 примеров,  но есть неточности в вычислениях.

 

Тема 4.3. Определенный интеграл

«Решение задач повышенной сложности по вычислению интегралов».

 

Инструкция по выполнению самостоятельной работы

1) Изучить теоретический материал:

Несобственные интегралы. Примеры решений

К изучению несобственных интегралов лучше приступать в последнюю очередь в ходе изучения интегрального исчисления функции одной переменной. Необходимо хорошо изучить материал о неопределенных интегралах,  определенных интегралах, уметь находить  площадь плоской фигуры с помощью определенного интеграла. Кроме того, потребуются  знания простейших пределов  и  графиков элементарных функций..

Образно говоря, несобственный интеграл – это «продвинутый» определенный интеграл, и на самом деле сложностей с ними не так уж и много, к тому же у несобственного  интеграла есть очень хороший геометрический смысл.

Что значит вычислить несобственный интеграл? Вычислить несобственный интеграл – это значит, найти ЧИСЛО (точно так же, как в определенном интеграле),  или доказать, что он расходится  (то есть, получить в итоге бесконечность вместо числа).

Несобственные интегралы бывают двух видов.

 

1. Несобственный интеграл с бесконечным пределом (ами) интегрирования

Иногда такой несобственный интеграл еще называют несобственным интегралом первого рода. В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так: 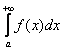. В чем его отличие от определенного интеграла? В верхнем пределе. Он бесконечный: .

Реже встречаются интегралы с бесконечным нижним пределом  или с двумя бесконечными пределами: .

Мы рассмотрим самый популярный случай 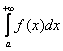. Техника работы с другими разновидностями – аналогична, и в конце параграфа будет ссылка на такие примеры.

Всегда ли существует несобственный интеграл 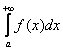? Нет, не всегда. Подынтегральная функция  должна быть непрерывной на промежутке 

Справка: строго говоря, утверждение неверно: если есть разрывы функции, то в ряде случаев можно разбить полуинтервал на несколько частей и вычислить несколько несобственных интегралов. Для простоты здесь и далее  будем  говорить, что несобственного интеграла не существует.

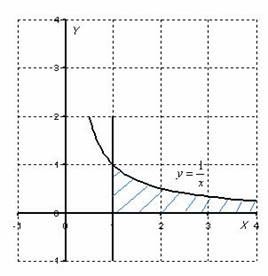
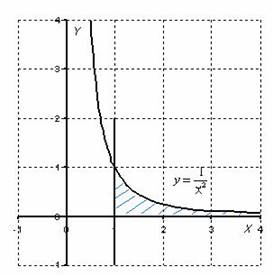
Изобразим на чертеже график подынтегральной функции . Типовой график и криволинейная трапеция для данного случая выглядит так:

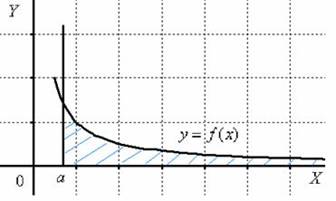В данном случае подынтегральная функция   непрерывна  на полуинтервале , а, значит, несобственный интеграл существует. Обратите внимание, что криволинейная трапеция у нас – бесконечная (не ограниченная справа) фигура.
Несобственный интеграл 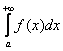 численно равен площади заштрихованной фигуры, при этом возможны два случая:

1) Первое, мысль, которая приходит в голову: «раз фигура бесконечная, то 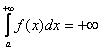», иными словами, площадь тоже бесконечна. Так быть может.  В этом случае говорят, что, что несобственный интеграл  расходится.

2) Но. Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: 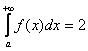. Может ли так быть? Да! Во втором случае несобственный интеграл сходится.

В каких случаях несобственный интеграл расходится, а в каком сходится? Это зависит от подынтегральной функции , и конкретные примеры мы очень скоро рассмотрим.

А что будет, если бесконечная криволинейная трапеция расположена ниже оси? В этом случае, несобственный интеграл 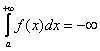 (расходится) либо равен конечному отрицательному числу.

 

Несобственный интеграл может быть отрицательным.

Важно!  Когда Вам для решения предложен ЛЮБОЙ несобственный интеграл, то, вообще говоря, ни о какой площади речи не идет и чертежа строить не нужно. Ваша задача найти ЧИСЛО либо доказать, что несобственный интеграл расходится. Геометрический смысл несобственного интеграла мы рассмотрели только для того, чтобы легче было понять материал.

Коль скоро, несобственный интеграл очень похож на определенный интеграл, то вспомним формулу Ньютона- Лейбница: 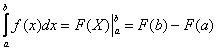. На самом деле формула применима и к несобственным интегралам, только ее нужно немного модифицировать. В чем отличие? В бесконечном верхнем пределе интегрирования: . Наверное, многие догадались, что это уже попахивает применением теории пределов, и формула запишется так: .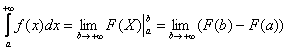

В чем отличие от определенного интеграла? Да ни в чем особенном! Как и в определенном интеграле, нужно уметь находить первообразную  функцию  (неопределенный интеграл), уметь применять формулу Ньютона-Лейбница. Единственное, что добавилось – это вычисление предела. Тем,  кто забыл этот материал, придется повторить материал занятия  «Пределы функций».

Рассмотрим два классических примера:

Пример 1

Вычислить несобственный интеграл или установить его расходимость.

Для наглядности построим чертеж.

 

Подынтегральная функция    непрерывна  на полуинтервале , значит, всё нормально и несобственный интеграл можно вычислить «штатным» методом.

Применение нашей формулы 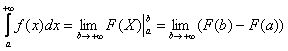  и решение задачи выглядит так:

То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.

В рассмотренном примере у нас простейший табличный интеграл и такая же техника применения формулы Ньютона-Лейбница, как в определенном интеграле. Но применятся эта формула под знаком предела. Вместо привычной буквы  «динамической» переменной выступает буква «бэ». Это не должно смущать или ставить в тупик, потому что любая буква ничем не хуже стандартного «икса».

Если Вам непонятно почему  при , то это очень плохо, либо Вы не понимаете простейшие пределы (и вообще не понимаете, что такое предел), либо не знаете, как выглядит график логарифмической функции. При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!

 

Чистовое оформление задания должно выглядеть примерно так:

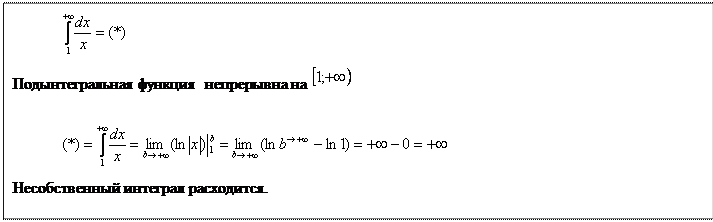
! При оформлении примера всегда прерываем решение, и указываем, что происходит с подынтегральной функцией. Этим мы идентифицируем тип несобственного интеграла.

Всегда смотрим и записываем, является ли подынтегральная функция  непрерывнойна интервале интегрирования.

Пример 2

Вычислить несобственный интеграл или установить его расходимость.

Выполним чертеж:

 

Во-первых, замечаем следующее: подынтегральная функция   непрерывна  на полуинтервале .

Решаем с помощью формулы :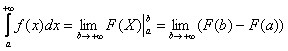

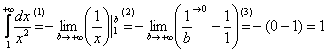
(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах). Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.

(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.

(3) Указываем, что  при  (Господа, это уже давно нужно  понимать) и упрощаем ответ.

Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.

Чистовое оформление примера должно выглядеть примерно так:

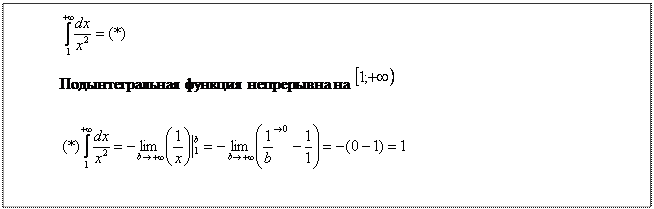
Пример 3

Вычислить несобственный интеграл или установить его расходимость.

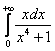
Подынтегральная функция  непрерывна  на .

Сначала попытаемся найти первообразную функцию  (неопределенный интеграл). Если нам не удастся этого сделать, то несобственный интеграл мы, естественно, тоже не решим.

На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс: . Из этих соображений напрашивается мысль, что неплохо бы в знаменателе получить квадрат. Делается это путем замены.

Проведем замену: 

Неопределенный интеграл найден, константу  в данном случае добавлять не имеет смысла.

На черновике всегда полезно выполнить проверку, то есть продифференцировать полученный результат:

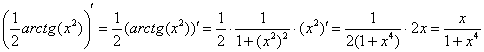
Получена исходная подынтегральная функция, значит, неопределенный интеграл найден правильно.

Теперь находим несобственный интеграл:

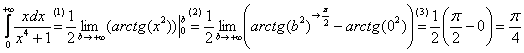
(1) Записываем решение в соответствии с формулой 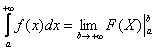. Константу лучше сразу вынести за знак предела, чтобы она не мешалась в дальнейших вычислениях.

(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница. Почему  при ? Смотрите график арктангенса в уже неоднократно рекомендованной статье.

(3) Получаем окончательный ответ. Тот факт, что  полезно знать наизусть.

Продвинутые курсанты могут не находить отдельно неопределенный интеграл, и не использовать метод замены, а использовать метод подведения функции под знак дифференциала и решать несобственный интеграл «сразу». В этом случае решение должно выглядеть примерно так:

2. Несобственные интегралы от неограниченных функций

Иногда такие несобственные интегралы называют несобственными интегралами второго рода. Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: 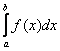. Но, в отличие от определенного интеграла, подынтегральная функция  терпит  бесконечный разрыв  (не существует): 1) в точке ,  2) или в точке , 3) или в обеих точках сразу, 4) или даже на отрезке интегрирования.

Если подынтегральной функции не существует в точке  

Сразу пример, чтобы было понятно: 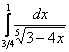. Вроде бы это определенный интеграл. Но на самом деле – это несобственный интеграл второго рода, если мы подставим в подынтегральную функцию значение нижнего предела , то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!

Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования. В этой связи проверим и верхний предел: . Здесь всё хорошо.

Криволинейная трапеция для рассматриваемой разновидности несобственного интеграла принципиально выглядит так:

 

Здесь почти всё так же, как в интеграле первого рода.
Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конченому числу (то есть, площадь бесконечной фигуры – конечна!).

Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а  к значению    справа. Легко проследить по чертежу: по оси  мы должны бесконечно близко приблизиться к  точке разрыва  справа.

Посмотрим, как это реализуется на практике.

 

Пример 6

Вычислить несобственный интеграл или установить его расходимость.

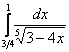
Подынтегральная функция терпит  бесконечный разрыв  в точке  (не забываем устно или на черновике проверить, всё ли нормально с верхним пределом!)

Сначала вычислим неопределенный интеграл:

Замена: 

Вычислим несобственный интеграл:

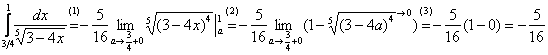
(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: . Добавка  обозначает, что мы стремимся к значению  справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом. В данном случае у нас правосторонний предел.

(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.

(3) Разбираемся с  при   . Как определить, куда стремиться выражение? Грубо говоря, в него нужно просто подставить значение  , подставляем три четверти и указываем, что . Причесываем ответ.

В данном случае несобственный интеграл равен отрицательному числу. В этом никакого криминала нет, просто соответствующая криволинейная трапеция расположена под осью .

 

Если подынтегральной функции не существует в точке 

Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит следующим образом:

 

Здесь всё абсолютно так же, за исключением того, что предел у нас стремится к значению  слева. По оси  мы должны бесконечно близко приблизиться к точке разрыва слева.

 

 

Пример 9

Вычислить несобственный интеграл или установить его расходимость.

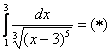
Подынтегральная функция терпит бесконечный разрыв в точке  (устно проверяем, что с другим пределом интегрирования всё нормально!).

Решим этот интеграл сразу – методом подведения функции под знак дифференциала. Те, кому трудно, могут сначала найти неопределенный интеграл по уже рассмотренной схеме.

 

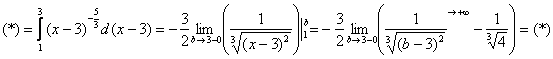
Добавка  обозначает, что предел у нас левосторонний, и к точке    мы приближаемся по оси    слева.

Разбираемся, почему дробь  (это лучше делать устно или на черновике).
Подставляем под корень предельное значение : 
 и тогда

Окончательно:
 

Несобственный интеграл расходится.

Знак минус обозначает, что соответствующая криволинейная трапеция расположена под осью. Будьте очень внимательны в знаках. Да, конечно, несобственный интеграл расходится, но  и  – это разные вещи, разные жанры, и если Вы недосмотрите за знаками, то, строго говоря, допустите серьезную ошибку.

 

2) Выполнить задание:

 

Вычислить несобственные интегралы или установить их расходимость.

 

Пример 1

 

Пример 2

 

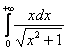
Пример 3

 

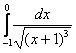
Пример 4

 

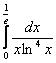
Пример 5

 

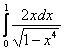
Пример 6

 

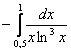
Форма контроля и критерии оценки выполнения практических заданий.

Задания выполняются в отдельных тетрадях для самостоятельной работы.

«Отлично»  ( 5 ) выставляется в случае, когда правильно решены все 6 примеров.

«Хорошо»  ( 4 ) выставляется в случае, когда правильно решены 4-5 примеров, или решено 6 примеров, но есть неточности в вычислениях.

«Удовлетворительно»  ( 3 ) - в случае, когда правильно решены 3 примера, или решено 4 примера,  но есть неточности в вычислениях.

«Неудовлетворительно»  ( 2 ) - в случае, когда правильно решены менее 3 примеров, или решено 3 примера,  но есть неточности в вычислениях.

 

 

 

Вид работы: Проведение исследования.

 

Тема 1.5. Последовательности и ряды

Исследовательская работа «Использование метода рядов Фурье при получении радиоволн высоких частот».

 

Курсант должен

знать:

-          основные принципы проведения исследования;

-          правила сбора и анализа информации;

уметь:

-          логически обрабатывать материал;

-          самостоятельно сравнивать, сопоставлять и обобщать материал;

-          классифицировать материал по тем или иным признакам;

-          высказывать свое отношение к описываемым явлениям и событиям.

 

Инструкция по выполнению самостоятельной работы

 

Исследовательская деятельность курсанта – этот вид деятельности предполагает самостоятельное формулирование проблемы и её решение, либо решение сложной предложенной проблемы с последующим контролем преподавателя, что обеспечит продуктивную творческую деятельность и формирование наиболее эффективных и прочных знаний (знаний-трансформаций). Этот вид задания может выполняться в ходе занятий курсанта в аудитории или планироваться.

Ряд Фурье — в математике — способ представления произвольной сложной функции суммой более простых. В общем случае количество таких функций может быть бесконечным, при этом чем больше таких функций учитывается при расчете, тем выше оказывается конечная точность представления исходной функции. В большинстве случаев в качестве простейших используются тригонометрические функции синуса и косинуса, в этом случае ряд Фурье называется тригонометрическим, а вычисление такого ряда часто называют разложением на гармоники.

Ряды Фурье от прочих рядов отличаются выбором базисных функций, по которым идёт разложение, - для них за базис приняты гармонические функции (sin, cos) кратных частот. Это особенно удобно для исследования поведения периодических функций, а это очень важный для практики класс функций (вся радиотехника имеет дело как раз с периодическими сигналами) . Так что зная реакцию системы на воздействие чистого синусоидального сигнала и зависимость такой реакции от частоты (частотную характеристику системы) , можно легко предсказать, что будет, если вместо синуса подать на неё прямоугольный импульс или ещё какой-то сигнал.

Преобразование Фурье вычисляется всякий раз, когда мы слышим звук. Ухо автоматически выполняет вычисление, проделать которое наш сознательный ум способен лишь после нескольких лет обучения математике. Наш орган слуха строит преобразование, представляя звук — колебательное движение частиц упругой среды, распространяющееся в виде волн в газообразной, жидкой или твёрдых средах — в виде спектра последовательных значений громкости для тонов различной высоты. Мозг превращает эту информацию в воспринимаемый звук.

Аналогичные операции можно производить с помощью математических методов над звуковыми волнами или практически над любыми другими колебательными процессами — от световых волн и океанских приливов до циклов солнечной активности. Пользуясь этими математическими приёмами, можно раскладывать функции, представляя колебательные процессы в виде набора синусоидальных составляющих — волнообразных кривых, переходящих от максимума к минимуму, затем опять к максимуму, подобно океанской волне.

Преобразование Фурье — это функция, описывающая амплитуду и фазу каждой синусоиды, соответствующей определённой частоте. (Амплитуда представляет высоту кривой, а фаза — начальную точку синусоиды.)

Преобразование Фурье стало мощным инструментом, применяемым в различных научных областях. В некоторых случаях его можно использовать как средство решения сложных уравнений, описывающих динамические процессы, которые возникают под воздействием электрической, тепловой или световой энергии. В других случаях оно позволяет выделять регулярные составляющие в сложном колебательном сигнале, благодаря чему можно правильно интерпретировать экспериментальные наблюдения в астрономии, медицине,  химии, радиоэлектронике.

Цель исследования –  углубление знаний и выработка навыков решения задач по теме «Ряды Фурье».

 

Задание – Изучив предложенную литературу и информацию с открытых Интернет-источников, доказать необходимость использования метода рядов Фурье при получении радиоволн высоких частот»

 

 

Список литературы:

1.            Баскаков С.И. Радиотехнические цепи и сигналы: Учебник для вузов.- М.: Высшая школа, 1988. -448с.

2.            Отнес Р., Эноксон Л. Прикладной анализ временных рядов. М.: Мир, 1982. -428с.

3.            Сергиенко А.Б. Цифровая обработка сигналов./ Учебник для вузов. - СПБ.: Питер, 2003.- 608с.

4.            Радиотехнические цепи и сигналы. Задачи и задания/ под ред. Проф. А.Н. Яковлева. - Новосибирск: Издательство НГТУ, 2002. - 348 с.

5.            Григорьев В.П., Дубинский Ю.А., Элементы высшей математики. Учебник для среднего профессионального образования. –М.: Академия, 2008.

6.            Кудрявцев В.А., Демидович Б.П., Краткий курс высшей математики – М., Наука, 2005.

7.            Дадаян А.А. Математика. Учебник для среднего профессионального образования. – М., Форум-Инфра,2003.

8.            www.allmath.ru

 

Форма контроля и критерии оценки выполнения расчетно-графической работы.

Отчет о работе выполняется в форме реферата. (См. правила оформления и оценивания рефератов, стр. 10). Оценка за работу выставляется в виде зачет/незачет.

 

 

Вид работы: Подготовка презентации на заданную тему

 

Курсант должен

знать:

-          основополагающие понятия теории вероятностей и математической статистики.

уметь:

-          составлять тезисный план презентации;

-          организовывать сбор и подготовку информации;

-          ориентироваться в выборы способов представления;

-          создавать презентации с помощью MSt Power Point;

-          проводить «репетиции» презентации

 

Тема 5.3. Математическое ожидание и дисперсия случайной величины

Презентация «Применение сложных расчетов в экономических процессах».

 

Задание – изучить предложенную тему по указанным литературным и Интернет источникам, подготовить презентацию по предложенной теме.

 

Основная литература

1.                  Туганбаев, А. А. Теория вероятностей и математическая статистика [Электронный ресурс] / А. А. Туганбаев, В. Г. Крупин. - Электрон. дан. - М. : Лань, 2011. - 320 с.

2.                  Гмурман В.Е. Теория вероятностей и математическая статистика 12-е изд. Учебное пособие для вузов. [Электронный ресурс] / Гмурман В.Е. - М. : Издательство Юрайт, 2010. - 479 с.

Дополнительная литература

1.    Болотюк, В.А. Практикум и индивидуальные задания по курсу теории вероятностей (типовые расчеты) / В.А. Болотюк, Л.А. Болотюк, А.Г. Гринь А.Г., И.П. Гринь И.П. и др. – «Лань», 2010 – 288 с. – Режим доступа: http://e.lanbook.com/books/element.php?pl1_cid=186&pl1_id=534

Интернет-ресурсы

1.                  http://www.mathcs.carleton.edu/probweb/probweb.

2.                  http://www.ruf.rice.edu/~lane/rvls.html

3.                  http://www.math.uah.edu/stat

4.                  http://www.statsoft.ru/home/textbook/default.htm

5.                  http://teorver-online.narod.ru/tvms-i.html

6.                  http://distance.ru/4stud/umk/stat/stat.html

 

Инструкция по выполнению самостоятельной работы

 

Правила оформления компьютерных презентаций

Общие правила дизайна

Многие дизайнеры утверждают, что законов и правил в дизайне нет. Есть советы, рекомендации, приемы. Дизайн, как всякий вид творчества, искусства, как всякий способ одних людей общаться с другими, как язык, как мысль — обойдет любые правила и законы. Однако, можно привести определенные рекомендации, которые следует соблюдать, во всяком случае, начинающим дизайнерам, до тех пор, пока они не почувствуют в себе силу и уверенность сочинять собственные правила и рекомендации.

Правила шрифтового оформления:

Шрифты с засечками читаются легче, чем гротески (шрифты без засечек); Для основного текста не рекомендуется использовать прописные буквы. Шрифтовой контраст можно создать посредством: размера шрифта, толщины шрифта, начертания, формы, направления и цвета.

Правила выбора цветовой гаммы.

Цветовая гамма должна состоять не более чем из двух-трех цветов. Существуют не сочетаемые комбинации цветов. Черный цвет имеет негативный (мрачный) подтекст. Белый текст на черном фоне читается плохо (инверсия плохо читается).

Правила общей композиции.

На полосе не должно быть больше семи значимых объектов, так как человек не в состоянии запомнить за один раз более семи пунктов чего-либо.

Логотип на полосе должен располагаться справа внизу (слева наверху и т. д.).

Логотип должен быть простой и лаконичной формы.

Дизайн должен быть простым, а текст — коротким.

Изображения домашних животных, детей, женщин и т.д. являются положительными образами.

Крупные объекты в составе любой композиции смотрятся довольно неважно. Аршинные буквы в заголовках, кнопки навигации высотой в 40 пикселей, верстка в одну колонку шириной в 600 точек, разделитель одного цвета, растянутый на весь экран — все это придает дизайну непрофессиональный вид.

Не стоит забывать, что на каждое подобное утверждение есть сотни примеров, доказывающих обратное. Поэтому приведенные утверждения нельзя назвать общими и универсальными правилами дизайна, они верны лишь в определенных случаях.

 

 

 

Рекомендации по дизайну презентации

Чтобы презентация хорошо воспринималась слушателями и не вызывала отрицательных эмоций (подсознательных или вполне осознанных), необходимо соблюдать правила ее оформления.

Презентация предполагает сочетание информации различных типов: текста, графических изображений, музыкальных и звуковых эффектов, анимации и видеофрагментов. Поэтому необходимо учитывать специфику комбинирования фрагментов информации различных типов. Кроме того, оформление и демонстрация каждого из перечисленных типов информации также 7 7 подчиняется определенным правилам. Так, например, для текстовой информации важен выбор шрифта, для графической — яркость и насыщенность цвета, для наилучшего их совместного восприятия необходимо оптимальное взаиморасположение на слайде.

Рекомендации по оформлению и представлению на экране материалов различного вида.

Текстовая информация

-          размер шрифта: 24–54 пункта (заголовок), 18–36 пунктов (обычный текст);

-          цвет шрифта и цвет фона должны контрастировать (текст должен хорошо читаться), но не резать глаза;

-          тип шрифта: для основного текста гладкий шрифт без засечек (Arial, Tahoma, Verdana), для заголовка можно использовать декоративный шрифт, если он хорошо читаем;

-          курсив, подчеркивание, жирный шрифт, прописные буквы рекомендуется использовать только для смыслового выделения фрагмента текста.

Графическая информация

-          рисунки, фотографии, диаграммы призваны дополнить текстовую информацию или передать ее в более наглядном виде;

-          желательно избегать в презентации рисунков, не несущих смысловой нагрузки, если они не являются частью стилевого оформления;

-          цвет графических изображений не должен резко контрастировать с общим стилевым оформлением слайда;

-          иллюстрации рекомендуется сопровождать пояснительным текстом;

-          если графическое изображение используется в качестве фона, то текст на этом фоне должен быть хорошо читаем.

Анимация

Анимационные эффекты используются для привлечения внимания слушателей или для демонстрации динамики развития какого-либо процесса. В этих случаях использование анимации оправдано, но не стоит чрезмерно насыщать презентацию такими эффектами, иначе это вызовет негативную реакцию аудитории.

Звук

-          звуковое сопровождение должно отражать суть или подчеркивать особенность темы слайда, презентации;

-          необходимо выбрать оптимальную громкость, чтобы звук был слышен всем слушателям, но не был оглушительным;

-          если это фоновая музыка, то она должна не отвлекать внимание слушателей и не заглушать слова докладчика. Чтобы все материалы слайда воспринимались целостно, и не возникало диссонанса между отдельными его фрагментами, необходимо учитывать общие правила оформления презентации.

Единое стилевое оформление

-          стиль может включать: определенный шрифт (гарнитура и цвет), цвет фона или фоновый рисунок, декоративный элемент небольшого размера и др.;

-          не рекомендуется использовать в стилевом оформлении презентации более 3 цветов и более 3 типов шрифта;

-          оформление слайда не должно отвлекать внимание слушателей от его содержательной части;

все слайды презентации должны быть выдержаны в одном стиле.

Содержание и расположение информационных блоков на слайде

-          информационных блоков не должно быть слишком много (3-6);

-          рекомендуемый размер одного информационного блока — не более 1/2 размера слайда;

-          желательно присутствие на странице блоков с разнотипной информацией (текст, графики, диаграммы, таблицы, рисунки), дополняющей друг друга;

-          ключевые слова в информационном блоке необходимо выделить;

-          информационные блоки лучше располагать горизонтально, связанные по смыслу блоки — слева направо;

-          наиболее важную информацию следует поместить в центр слайда;

-          логика предъявления информации на слайдах и в презентации должна соответствовать логике ее изложения.

Помимо правильного расположения текстовых блоков, нужно не забывать и об их содержании — тексте. В нем ни в коем случае не должно содержаться орфографических ошибок. Также следует учитывать общие правила оформления текста.

После создания презентации и ее оформления, необходимо отрепетировать ее показ и свое выступление, проверить, как будет выглядеть презентация в целом (на экране компьютера или проекционном экране), насколько скоро и адекватно она воспринимается из разных мест аудитории, при разном освещении, шумовом сопровождении, в обстановке, максимально приближенной к реальным условиям выступления.

 

Рекомендации к содержанию презентации.

По содержанию

На слайдах презентации не пишется весь тот текст, который произносит докладчик (во- первых, в этом случае сам факт произнесения доклада теряет смысл, так как аудитория обычно умеет читать, а во-вторых, длинный текст на слайде плохо воспринимается и только мешает слушанию и пониманию смысла).

Текст на слайде должен содержать только ключевые фразы (слова), которые докладчик развивает и комментирует устно.

Если презентация является основой устного доклада, то по европейским и американским правилам второй слайд должен содержать краткое перечисление всех основных вопросов, которые будут рассмотрены в докладе. Это нечасто встречается у нас даже на «взрослых» конференциях, но практика показывает, что правило – чрезвычайно полезное: дисциплинирует докладчика, концентрирует внимание слушателей, а, кроме того, во время создания такого слайда от автора требуется очень четко выделить и сформулировать ключевые проблемы доклада.

Если презентация имеет характер игры, викторины, или какой-либо другой, который требует активного участия аудитории, то на каждом слайде должен быть текст только одного шага, или эти «шаги» должны появляться на экране постепенно.

По оформлению

На первом слайде пишется не только название презентации, но и имена авторов (в ученическом случае – и руководителя проекта) и дата создания.

Каждая прямая цитата, которую комментирует или даже просто приводит докладчик (будь то эпиграф или цитаты по ходу доклада) размещается на отдельном слайде, обязательно с полной подписью автора (имя и фамилия, инициалы и фамилия, но ни в коем случае – одна фамилия, исключение – псевдонимы). Допустимый вариант – две небольшие цитаты на одну тему на одном слайде, но не больше.

Все схемы и графики должны иметь названия, отражающие их содержание.

Подбор шрифтов и художественное оформление слайдов должны не только соответствовать содержанию, но и учитывать восприятие аудитории. Например, сложные рисованные шрифты часто трудно читаются, тогда как содержание слайда должно восприниматься все сразу – одним взглядом.

На каждом слайде выставляется колонтитул, включающий фамилию автора и/или краткое название презентации и год создания (например, в презентации «Политическая история народов Дагестана и ее влияние на историю России» в колонтитуле стояло: «Иванова. Народы Дагестана. 2004»), номер слайда.

В конце презентации представляется список использованных источников, оформленный по правилам библиографического описания.

Правила хорошего тона требуют, чтобы последний слайд содержал выражение благодарности тем, кто прямо или косвенно помогал в работе над презентацией.

Кино и видеоматериалы оформляются титрами, в которых указываются:

-          название фильма (репортажа),

-          год и место выпуска,

-          авторы идеи и сценария,

-          руководитель проекта.

 

Правила компьютерного набора текста при создании презентаций

Общие правила оформления текста

Точка в конце заголовка и подзаголовках, выключенных отдельной строкой, не ставится. Если заголовок состоит из нескольких предложений, то точка не ставится после последнего из них. Порядковый номер всех видов заголовков, набираемый в одной строке с текстом, должен быть отделен пробелом независимо от того, есть ли после номера точка.

Точка не ставится в конце подрисуночной подписи, в заголовке таблицы и внутри нее. При отделении десятичных долей от целых чисел лучше ставить запятую (0,158), а не точку (0.158).

Перед знаком препинания пробел не ставится (исключение составляют открывающиеся парные знаки, например, скобки, кавычки). После знака препинания пробел обязателен (если этот знак не стоит в конце абзаца). Тире выделяется пробелами с двух сторон. Дефис пробелами не выделяется.

Числительные порядковые и количественные выражаются в простом тексте словами (обычно, однозначные при наличии сокращенных наименований), цифрами (многозначные и при наличии сокращенных обозначений) и смешанным способом (после десятков тысяч часто применяются выражения типа 25 тыс.), числительные в косвенных падежах набирают с так называемыми наращениями (6-го). В наборе встречаются арабские и римские цифры.

Индексы и показатели между собой и от предшествующих и последующих элементов набора не должны быть разделены пробелом (Н2О, м3/с)

Нельзя набирать в разных строках фамилии и инициалы, к ним относящиеся, а также отделять один инициал от другого.

Не следует оставлять в конце строки предлоги и союзы (из одной-трех букв), начинающие предложение, а также однобуквенные союзы и предлоги в середине предложений.

Последняя строка в абзаце не должна быть слишком короткой. Надо стараться избегать оставления в строке или переноса двух букв. Текст концевой строки должен быть в 1,5-2 раза больше размера абзацного отступа, т.е. содержать не менее 5-7 букв. Если этого не получается, необходимо вогнать остаток текста в предыдущие строки или выгнать из них часть текста. Это правило не относится к концевым строкам в математических рассуждениях, когда текст может быть совсем коротким, например "и", "или" и т.п.

Знаки процента (%) применяют только с относящимися к ним числами, от которых они не отделяются.

Знаки градуса (°), минуты ('), секунды ('') от предыдущих чисел не должны быть отделены пробелом, а от последующих чисел должны быть отделены пробелом (10° 15'). Формулы в текстовых строках набора научно-технических текстов должны быть отделены от текста на пробел или на двойной пробел.

Формулы, следующие в текстовой строке одна за другой, должны быть отделены друг от друга удвоенными пробелами.

Знаки номера (№) и параграфа (§) применяют только с относящимися к ним числами и отделяются пробелом от них и от остального текста с двух сторон. Сдвоенные знаки набираются вплотную друг к другу. Если к знаку относится несколько чисел, то между собой они отделяются пробелами. Нельзя в разных строках набирать знаки и относящиеся к ним цифры.

В русском языке различают следующие виды сокращений: буквенная аббревиатура — сокращенное слово, составленное из первых букв слов, входящих в полное название (СССР, НДР, РФ, вуз); сложносокращенные слова, составленные из частей сокращенных слов (колхоз) или усеченных и полных слов (Моссовет), и графические сокращения по начальным буквам (г. — год), по частям слов (см. — смотри), по характерным буквам (млрд — миллиард), а также по начальным и конечным буквам (ф-ка — фабрика). Кроме того, в текстах применяют буквенные обозначения единиц физических величин. Все буквенные аббревиатуры набирают прямым шрифтом без точек и без разбивки между буквами, сложносокращенные слова и графические сокращения набирают как обычный текст. В выделенных шрифтами текстах все эти сокращения набирают тем же, выделительным шрифтом.

 

Специфические требования при компьютерном наборе текста

При наборе текста одного абзаца клавиша «Перевод строки» («Enter») нажимается только в конце этого абзаца.

Между словами нужно ставить ровно один пробел. Равномерное распределение слов в строке текстовым процессором выполняется автоматически. Абзацный отступ (красную строку) устанавливать с помощью пробелов запрещено; для этого используются возможности текстового процессора (например, можно использовать бегунки на горизонтальной полосе прокрутки или табулятор).

Знак неразрывный пробел (Вставка → Символ, вкладка Специальные знаки или комбинация клавиш CTRL+SHIFT+пробел) препятствует символам, между которыми он поставлен, располагаться 10 10 на разных строчках, и сохраняется фиксированным при любом выравнивании абзаца (не может увеличиваться, в отличие от обычного пробела).

Выделением называют особое оформление отдельных слов или частей текста, которое подчеркивает их значение. Все виды выделений делят на три группы:

-          шрифтовые выделения, выполняемые путем замены характера или начертания шрифта, — набор курсивом, полужирным, жирным, полужирным курсивом, прописными или капительными буквами, шрифтами другого кегля или даже другой гарнитуры;

-          нешрифтовые выделения, выполняемые путем изменения расстояний между буквами (набор вразрядку) или между строками набора (дополнительные отбивки отдельных строк), изменения формата набора (набор «в красную строку», набор с одно- или двусторонними втяжками), подчеркивания текста тонкими или полужирными линейками или заключения отдельных частей текста в рамки и т. п.;

-          комбинированные выделения, выполняемые одновременно двумя способами, например, набор полужирным вразрядку, набор полужирным шрифтом увеличенного кегля с выключкой в «красную строку» и дополнительными отбивками, набор курсивом с заключением текста в рамку и т. п. Шрифтовые выделения (курсивом, полужирным, жирным) должны быть выполнены шрифтами той же гарнитуры и кегля, что и основной текст. Знаки препинания, следующие за выделенной частью текста, должны быть набраны шрифтом основного текста.

В текстовом наборе абзацные отступы должны быть строго одинаковыми во всем документе, независимо от кегля набора отдельных частей текста.

Знак тире, или длинное тире, может быть набрано с помощью одновременного нажатия комбинации клавиш CTRL+SHIFT+серый минус (серый минус располагается на цифровой клавиатуре, справа) или Вставка → Символ, вкладка Специальные знаки.

 

Общие правила оформления презентации

Дизайн

Выберите готовый дизайн или создайте свой так, чтобы он соответствовал Вашей теме, не отвлекал слушателей.

Титульный лист

1. Название презентации.

2. Автор: ФИО, студента, место учебы, год.

3. Логотип (по желанию).

Второй слайд «Содержание» – список основных вопросов, рассматриваемых в содержании. Лучше оформить в виде гиперссылок (для интерактивности презентации).

Заголовки

1. Все заголовки выполнены в едином стиле (цвет, шрифт, размер, начертание).

2. В конце точка НИКОГДА не ставится (наверное, можно сделать исключение только для учеников начальной школы).

3. Анимация, как правило, не применяется.

Текст

1. Форматируется по ширине.

2. Размер и цвет шрифта подбираются так, чтобы было хорошо видно.

3. Подчеркивание НЕ используется, т.к. оно в документе указывает на гиперссылку.

4. Элементы списка отделяются точкой с запятой. В конце обязательно ставится точка.

5. На схемах текст лучше форматировать по центру.

6. В таблицах – по усмотрению автора.

7. Обычный текст пишется без использования маркеров списка:

8. Выделяйте главное в тексте другим цветом (желательно все в едином стиле).

Графика

1. Используйте четкие изображения с хорошим качеством.

2. Лучше растровые изображения (в формате jpg) заранее обработать в любом графическом редакторе для уменьшения размера файла. Если такой возможности нет, используйте панель «Настройка изображения».

Анимация

Используйте только в том случае, когда это действительно необходимо. Лишняя анимация только отвлекает.

 

Список литературы

1. Сначала указывается фамилия (в алфавитном порядке) и инициалы.

2. Пишется название источника (без кавычек).

3. Ставится тире и указывается место издания.

4. Через двоеточие указывается издательство (без кавычек).

5. После запятой пишется год издания.

Пример: 1. Петров А.В. Экономика в школе. – М.: Просвещение, 2001.

2. Сидоров Т.В. Экономика транспорта. – Спб.: Аврора, 2000.

3. Щукина И.Г. Люди и машины. – Саратов: Лицей, 2006.

Интернет-ресурсы: указывается полный адрес в виде гиперссылки,  например: http://it-n.ru/board.aspx?cat_no=6361&tmpl=Thread&BoardId=6364&ThreadId=9887&page=0

 

Для правильной работы презентации все вложенные файлы (документы, видео, звук и пр.) размещайте в ту же папку, что и презентацию.

Правила оформления презентаций

Общие требования к смыслу и оформлению:

Всегда необходимо отталкиваться от целей презентации и от условий прочтения. Презентации должны быть разными — своя на каждую ситуацию. Презентация для выступления, презентация для отправки по почте или презентация для личной встречи значительно отличаются;

Представьте себя на месте просматривающего.

 Общий порядок слайдов:

-          Титульный;

-          План презентации (практика показывает, что 5-6 пунктов — это максимум, к которому не следует стремиться);

-          Основная часть;

-          Заключение (выводы);

-          Спасибо за внимание (подпись).

Требования к оформлению диаграмм:

-          У диаграммы должно быть название или таким названием может служить заголовок слайда;

-          Диаграмма должна занимать все место на слайде;

-          Линии и подписи должны быть хорошо видны.

 Требования к оформлению таблиц:

-          Название для таблицы;

-          Читаемость при невчитываемости;

-          Отличие шапки от основных данных.

Последний слайд (любое из перечисленного):

-          Спасибо за внимание;

-          Вопросы;

-          Подпись;

-          Контакты

 

Форма контроля и критерии оценки

Презентацию необходимо предоставить преподавателю для проверки в электронном виде.

«Отлично»  ( 5 ) выставляется в случае, если презентация выполнена аккуратно, примеры проиллюстрированы, полностью освещены все обозначенные вопросы.

«Хорошо»  ( 4 ) выставляется в случае, если работа содержит небольшие неточности .

«Удовлетворительно»  ( 3 ) - в случае, если презентация выполнена неаккуратно, не полностью освещены заданные вопросы.

«Неудовлетворительно»  ( 2 ) - работа выполнена небрежно, не соблюдена структура, отсутствуют иллюстрации.
Вид работы:  Выполнение расчетно-графической работы

 

Курсант должен

знать:

-          основные формулы, необходимые для выполнения расчетов;

-          основные методы выполнения расчетов;

-          правила оформления расчетно-графического задания;

уметь:

-          применять изученные методы для выполнения расчетов;

-          составлять и реализовывать алгоритм выполнения расчетов;

-          выполнять графические иллюстрации к полученным данным.

 

Тема 5.4. Предмет и основные понятия математической статистики

Расчетно-графическая работа «Графическое изображение статистических преобразований»

 

Расчетно-графическая работа – это самостоятельное исследование курсанта. Выполняя РГР курсант совершенствует знания и умения, полученные в процессе изучения дисциплины “Прикладная математика”, а именно: определять цель, выделять задачи, формулировать проблемы и находить способы их решения.  Работая над РГР курсант получает умения и навыки, которые будут полезными в будущем – при выполнении более сложных задач (курсовая работа, дипломная работа, научное исследование).

 

Целью написания РГР является:

-       систематизация, закрепление и расширение теоретических знаний и практических умений курсанта;

-       приобретение опыта работы с литературой и другими источниками информации, умение обобщать и анализировать научную информацию, вырабатывать собственное отношение к  проблеме;

-       выработка умения применять информационные и компьютерные технологии для решения прикладных математических задач;

-       проведение глубокого анализа результатов собственных исследований и формирование содержательных выводов относительно качества полученных результатов.

 

Этапы выполнения расчетно-графической работы:

Расчетно–графическая работа выполняется в два этапа.

Первый этап РГР выполняется  включает следующее:

-       определение актуальности и цели работы,

-       подбор литературы и источников информации согласно предложенной  теме,

-       сбор данных, необходимых для раскрытия избранной темы,

-       систематизацию и структурирование данных,

-       оформление результата выполнения первого этапа.

Второй этап РГР  включает следующее:

-       выбор метода обработки информации,

-       обоснование и описание избранного метода,

-       обработку информации,

-       получение результатов,

-       интерпретацию результатов,

-       формулирование выводов,

-       оформление отчета,

 

Отчет о выполнении РГР оформляется в специальной тетради для самостоятельной работы.

 

Инструкция по выполнению самостоятельной работы

1) Повторить  теоретический материал: В.Т Лисичкин,  И.Л Соловейчик, Математика. Учебник для среднего профессионального образования. – М.: Высшая школа, 1991. – стр.427-440.

2) Изучить примеры решения статистических задач.

 

Задача 1. Для выборки объёма N = 100 , представленной вариационным рядом 

xi	-1	0	1	2	3	4	5
ni	3	2	11	25	31	23	5

 

Построить полигон относительных частот и гистограмму накопленных частот. Найти выборочное среднее  и выборочное среднее квадратичное уклонение . Определить доверительный интервал с доверительной вероятностью  для оценки математического ожидания генеральной совокупности в предположении, что среднее квадратичное уклонение генеральной совокупности равно исправленному выборочному среднему S. Проверить гипотезу о нормальности закона распределения генеральной совокупности, используя критерий Пирсона с уровнем значимости .

 

 

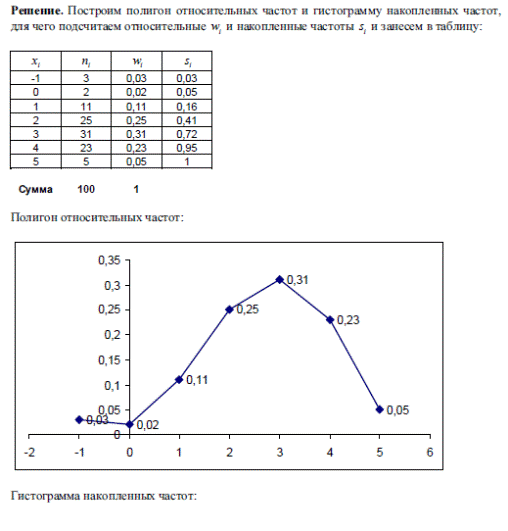
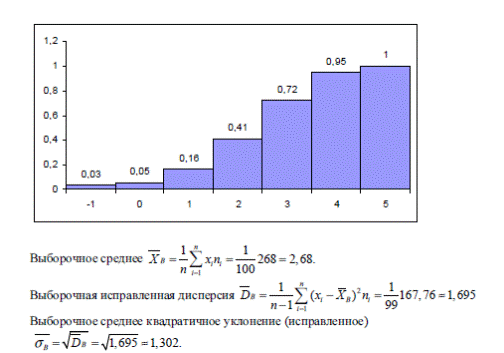
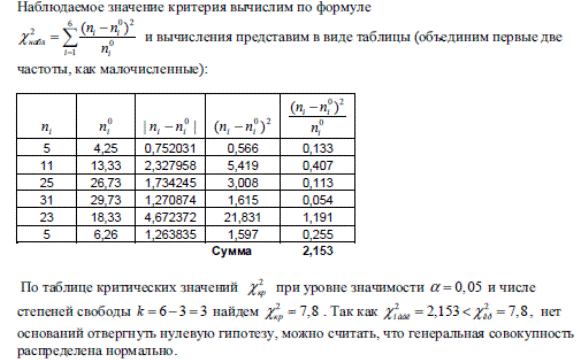
Задача 2. По выборке объёма N=100 двумерной генеральной совокупности, представленной таблицей

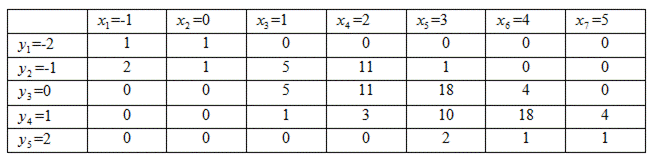
Написать уравнение линейной регрессии для условного математического ожидания  на X в ви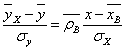де , где 
Сделать схематический чертёж.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

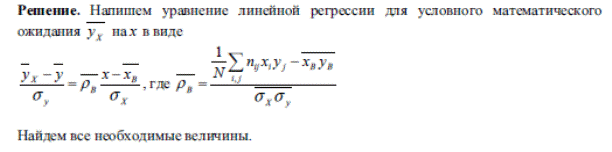
Задача 3. Дана выборка выручки магазина за 30 дней (тыс. руб.)

а) Составить группированный статистический ряд с числом интервалов k выбранных произвольно от 5 до 8.

б) Построить по статистическому ряду гистограмму, полигон, кумулятивную кривую.

в) Найти точечные оценки для математического ожидания, дисперсии и среднеквадратического отклонения.

Выборка
55	71	66	74	71	70	68	76	75	73	65	75	73	70	67
59	63	68	65	65	81	69	64	57	58	68	70	71	71	71

 

 

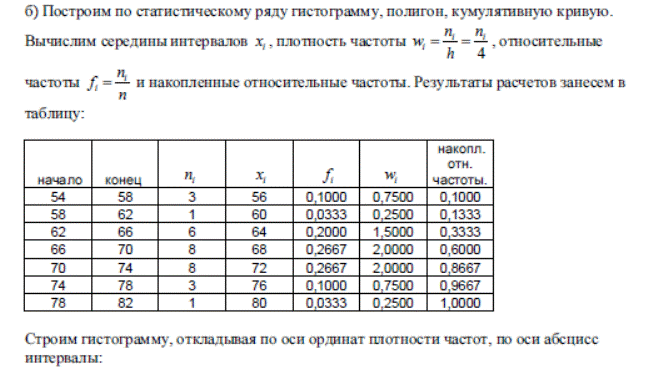
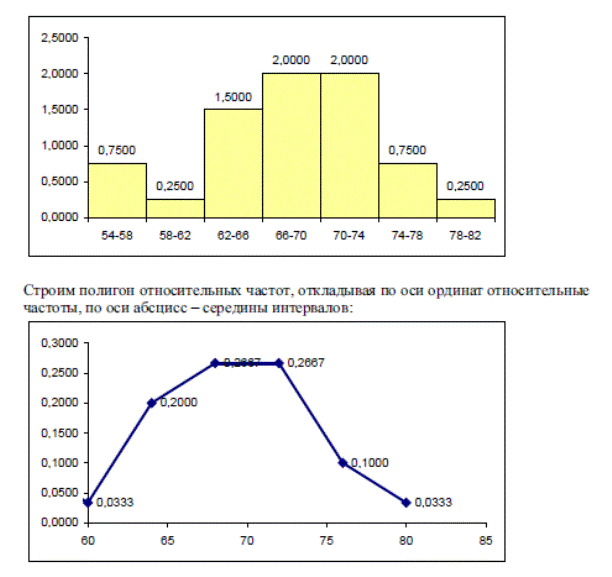
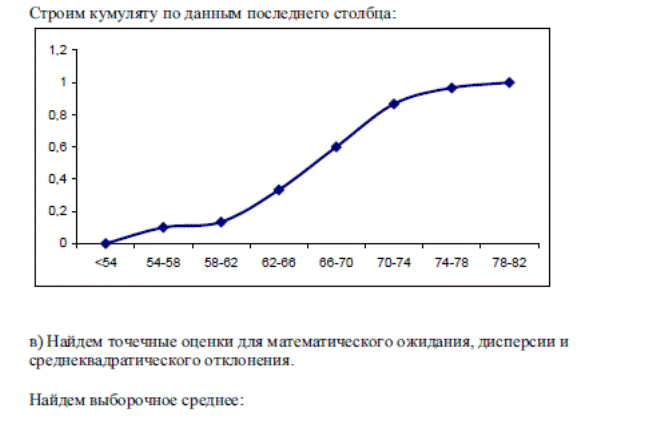
3) Выполнить расчетно-графическое задание

 

Задача 1. Имеются следующие данные о размерах основных фондов (в млн. руб.) 30 предприятий:

4,2; 2,4; 4,9; 6,7; 4,5; 2,7; 3,9; 2,1; 5,8; 4,0; 2,8; 7,3; 4,4; 6,6; 2,0; 6,2; 7,0; 8,1; 0,7; 6,8; 9,4; 7,6; 6,3; 8,8; 6,5; 1,4; 4,6; 2,0; 7,2; 9,1.

а) постройте интервальную таблицу частот с шириной интервала 2 (млн. руб.).

б) постройте гистограмму

 

Задача 2. Дан следующий вариационный ряд

 

Требуется 

1) Построить полигон распределения
2) Вычислить выборочную среднюю, дисперсию, моду, медиану
3) Построить выборочную функцию распределения
4) Найти несмещенные оценки математического ожидания и дисперсии.

 

Задача 3. В 100 частях воды растворяется следующее число условных частей азотнокислого натрия NaNO₃ (признак Y) при соответствующих температурах (X):

X	0	4	10	14	23	28	34	56	69
Y	63,4	72	73,3	81,3	83,7	91,3	97,6	105,4	114,1

На количество растворившегося NaNO₃ влияют случайные факторы. Предполагается наличие статистической линейной зависимости между температурой и количеством растворившегося NaNO₃. Найти МНК – оценку коэффициентов линейной модели.

 

Форма контроля и критерии оценки выполнения расчетно-графической работы.

Расчетно-графическая работа выполняются в специальных тетрадях для самостоятельной работы.

«Отлично»  ( 5 ) выставляется в случае, когда правильно решены все 3 задачи, верно выполнены расчеты и построены статистические кривые.

«Хорошо»  ( 4 ) выставляется в случае, когда правильно решены 2 задачи, или решено 3 задачи, но есть неточности в расчетах или построении статистических кривых.

«Удовлетворительно»  ( 3 ) - в случае, когда правильно решена только 1  задача, или решено 2 задачи . но есть неточности или ошибки в расчетах или построении статистических кривых.

«Неудовлетворительно»  ( 2 ) - в случае, не решено ни одной задачи, или решена 1 задача, . но есть неточности или ошибки в расчетах или построении статистических кривых.

 

Библиографический список

 

1.                  Григорьев В.П., Дубинский Ю.А., Элементы высшей математики. Учебник для среднего профессионального образования. –М.: Академия, 2008.

2.                  Гмурман В.Е., Теория вероятностей и математическая статистика.- М., Высшая школа, 2006.

3.                  Гмурман В.Е., Руководство по решению задач по теории вероятностей и математической статистики. – М., Высшая школа, 2006.

4.                  Шипачев В.С., Сборник задач по высшей математике, М., Высшая школа, 2006.

5.                  Дадаян А.А. Сборник задач по математике. Учебное пособие для среднего профессионального образования. – М., Форум-Инфра,2003.

6.                  Кудрявцев В.А., Демидович Б.П., Краткий курс высшей математики – М., Наука, 2005.

7.                  Дадаян А.А. Математика. Учебник для среднего профессионального образования. – М., Форум-Инфра,2003.

8.                  Гончаренко, В.М. Элементы высшей математики : учебник / Гончаренко В.М., Липагина Л.В., Рылов А.А. - Москва: КноРус, 2020. — 363 с. — ISBN 978-5-406-01472-1. — URL: https://book.ru/book/935921— Текст: электронный.

9.                  Гулиян, Б.Ш. Элементы высшей математики : учебное пособие / Гулиян Б.Ш., Гулиян Г.Б. — Москва : КноРус, 2021. — 436 с. — ISBN 978-5-406-06303-3. — URL: https://book.ru/book/939826 — Текст: электронный.

10.              Бахтина, Е.В. Комплект контрольно-измерительных материалов составлен для текущего контроля по дисциплине «Математика : монография / Бахтина Е.В., Корякина М.Л., Киселева И.И., Шулятьева Н.Н. — Москва : Русайнс, 2019. — 77 с. — ISBN 978-5-4365-3744-3. — URL: https://book.ru/book/934593). — Текст : электронный.

 

Скачано с www.znanio.ru