Методические указания для проведения практических работ по дисциплине «Информатика» по теме «Основы логики»

Тема: Основы Логики.

Цель занятия: Изучить основные логические конструкции и их описание  Необходимое оборудование: сеть Интернет, ПК. 

Теоретическая часть

Логика (др.-греч. Λογική — «наука о правильном мышлении», «способность к рассуждению» от др.-греч. Λόγος –«рассуждение», «мысль», «разум») раздел философии, нормативная наука о формах, методах и законах интеллектуальной познавательной деятельности, формализуемых с помощью логического языка. Поскольку это знание получено разумом, логика также определяется как наука о формах и законах правильного мышления. Так как мышление оформляется в языке в виде рассуждения, частными случаями которого являются доказательство и опровержение, логика иногда определяется как наука о способах рассуждения или наука о способах доказательств и опровержений. 

Логика как наука изучает методы достижения истины в процессе познания опосредованным путём, не из чувственного опыта, а из знаний, полученных ранее, поэтому её также можно определить как науку о способах получения выводного знания.

Одна из главных задач логики – определить, как прийти к выводу из предпосылок (правильное рассуждение) и получить истинное знание о предмете размышления, чтобы глубже разобраться в нюансах изучаемого предмета мысли и его соотношениях с другими аспектами рассматриваемого явления.

В любой науке логика служит одним из основных инструментов. Кроме философии,логика также является подразделом математики, а булева алгебра одной из основ информатики.

Математическая логика (теоретическая логика, символическая логика) раздел математики, изучающий математические обозначения, формальные системы, доказуемость математических суждений, природу математического доказательства в целом, вычислимость и прочие аспекты оснований математики. В более широком смысле рассматривается как математизированная ветвь формальной логики – «логика по предмету, математика по методу», «логика, развиваемая с помощью математических методов».

Алгебра логики (алгебра высказываний) — раздел математической логики, в котором изучаются логические операции над высказываниями. Чаще всего предполагается, что высказывания могут быть только истинными или ложными, то есть используется такназываемая бинарная или двоичная логика, в отличие от, например, троичной логики. Базовыми элементами, которыми оперирует алгебра логики, являются высказывания.

Глоссарий, определения логики

Высказывание - это повествовательное предложение, про которое можно определенно сказать истинно оно или ложно (истина (логическая 1), ложь (логический 0)).

Логические операции - мыслительные действия, результатом которых является изменение содержания или объема понятий, а также образование новых понятий.

Логическое выражение - устное утверждение или запись, в которое, наряду с постоянными величинами, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных величин (объектов) логическое выражение может принимать одно из двух возможных значений: истина (логическая 1) или ложь (логический 0).

Сложное логическое выражение - логическое выражение, состоящее из одного или нескольких простых логических выражений (или сложных логических выражений), соединенных с помощью логических операций. Логические операции и таблицы истинности 1) Логическое умножение или конъюнкция:

Конъюнкция - это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложеное выражение ложно.

Обозначение: F = A & B.

Таблица истинности для конъюнкции

2)   Логическое сложение или дизъюнкция:

Дизъюнкция - это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженныя ложны.

Обозначение: F = A + B.

Таблица истинности для дизъюнкции

3)   Логическое отрицание или инверсия:

Инверсия - это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.

Таблица истинности для инверсии

4)   Логическое следование или импликация:

Импликация - это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. Тоесть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием. Таблица истинности для импликации

5)   Логическая равнозначность или эквивалентность:

Эквивалентность - это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.

Таблица истинности для эквивалентности

Порядок выполнения логических операций в сложном логическом выражении

1.   Инверсия;

2.   Конъюнкция;

3.   Дизъюнкция;

4.   Импликация;

5.   Эквивалентность.

Для изменения указанного порядка выполнения логических операций используются скобки.

Практическая работа №1

Доказательство логических тождеств

Используя таблицы истинности, докажите или опровергните тождества: Вариант 1

₃₎ AB AC  B C  AB B C

Ответы:

Построение логического выражения

Способ 1

До этого момента мы считали, что логическое выражение уже задано и нам надо что-то с ним сделать (построить таблицу истинности, упростить и т.

п.). Такие задачи называются задачами анализа (от греческого — разложение), в них требуется исследовать заданное выражение. При проектировании различных логических устройств, в том числе и устройств компьютеров, приходится решать обратную задачу — строить логическое выражение по готовой таблице истинности, которая описывает нужное правило обработки данных. Эта задача называется задачей синтеза (от греческого — совмещение).

В качестве простейшего примера построим логическое выражение, тождественное операции импликации X = А —> В, по её таблице истинности

(рис. 1).

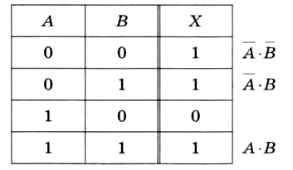
Рис. 1

 Способ 1. В таблице истинности мы выделяем все строки, где логическое выражение равно единице. Тогда искомое выражение может быть записано как логическая сумма выражений, каждое из которых истинно только^ одном случае.

Например, выражение А • B истинно только при А = 0 и В = 0, т. е.

только в первой строке таблицы. Выражение А • В истинно только во второй строке, а А • В — только в последней.

Существует простое правило: если в некоторой строке переменная равна нулю, она входит в произведение с отрицанием, а если равна 1, то без отрицания.

Складывая выражения для всех отмеченных строк (кроме третьей, где функция равна нулю), получаем:

Х = А • B + А • В + А • В.

Упрощаем это выражение:

X = А • (B + В) + А • В = А + А • В = (А + А) • (А + В) = А + В.

Таким образом, мы вывели формулу, которая позволяет заменить импликацию через операции «НЕ» и «ИЛИ».

Способ 2

 Способ 2. Если в таблице истинности нулей меньше, чем единиц, удобнее сначала найти формулу для обратного выражения, X, а потом применить операцию «НЕ». В данном случае выражение равно нулю в единственной строке, при А =1 и В =0, только в этой строке X = 1, поэтому, используя предыдущий способ, получаем X = А • В. Теперь остаётся применить операцию «НЕ» и закон де Моргана:

Х = А • B = A + В.

Рассмотрим более сложный пример, когда выражение зависит от трёх переменных. В этом случае в таблице истинности будет 8 строк (рис. 2).

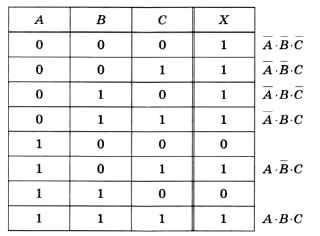
Рис. 2

Отметим все строки, где X = 1, и для каждой из них построим выражение, истинное только для этой комбинации переменных (см. рис. 3.20).

Теперь выполним логическое сложение:

Х = А • B • C + А • B • C + А • B • C + А • B • C + А • B • C + А • B • C.

Упрощение этого выражения даёт:

X = А • B • (C + С) + А • В (C + С) + А • С • (B + В) = А • B + А • B + А •

С = А • (B + В) + А • С = А + А • С = (А + А) • (А +С) = А + С.

Используя второй способ, получаем:

X = А • B • (C + А • В • C = А • C • (B + В) = А • C.

Тогда X = А • C = А + С. В данном случае второй способ оказался проще, потому что в столбце X таблицы истинности меньше нулей, чем единиц.

Способ 3

 Способ 3. При небольшом количестве нулей можно использовать ещё один метод. Попробуем применить операцию «НЕ» к исходному выражению для X, без предварительного упрощения: X = А • B • C + A • B • C

Применяя закон де Моргана, получим: X = (А • B • C) + (A • B • C).

Используя закон де Моргана для обеих скобок, находим:

X =(А + В + С) • (А + B + С).

Заметим, что выражение в каждой скобке ложно только для одной комбинации исходных данных, при которых Х = 0.

Таким образом, третий способ заключается в том, чтобы для каждой строки в таблице истинности, где выражение равно 0, построить логическую сумму, в которую переменные, равные в этой строке единице, входят с инверсией, а равные нулю — без инверсии. Выражение для X — это произведение полученных сумм.

В нашем примере выражение упрощается с помощью распределительного закона для «И» и закона исключённого третьего:

Х = (А + В + С) • (А + В + С) = (А + С) + В • B = А + С.

Неудивительно, что мы получили тот же ответ, что и раньше.

Иногда при упрощении выражений может потребоваться искусственный приём, который сначала вроде бы усложняет запись, но затем позволяет получить более простую форму. Например, рассмотрим выражение

Х = А • В + А • С + B • С.

Учитывая, что В + B = 1, можно представить второе слагаемое в виде:

А • С = А • (В + B) • С = А • В • С + (А • (B • С.

Тогда получаем:

Х = А • В + А • В • С + B • С = А • В • (1 + С)+ (А + 1) • В • С = А • В + В • С.

Практическая работа №2

 Синтез логических выражений

Постройте и упростите логические выражения, соответствующие приведённым таблицам истинности. В каждом случае выбирайте наиболее простой способ синтеза. В вашем решении опишите все шаги алгоритма. Вариант 1     

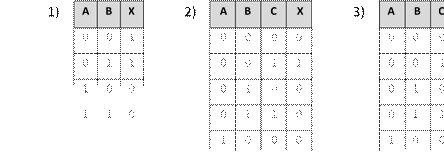
                                                               1 0 1 1                 1 0 1 1

Вариант 2           

                                                               1 1 0 1                 1 1 0 1

                                                               1 0 1 1                 1 0 1 1

Вариант 3           

                                                               1 1 0 1                 1 1 0 0

1 0 1 1

1 1 0 1

1 1 1 1

                                                               1 0 1 0                 1 0 1 1

Вариант 5           

                                                               1 1 0 1                 1 1 0 0

                                                               1 0 1 0                 1 0 1 0

Вариант 6           

                                                               1 1 0 1                 1 1 0 1

Ваpиант 3               A 

AB  B C AC

Ваpиант 6             

AB AB 

AB AB A C

Контрольные вопросы 1) Что такое логика?

2)  Что изучает логика?

3)  Задачи логики

4)  Что изучает математическая логика?

5)  Что такое алгебра логики? 6) Элементы алгебры логики

7)       Операции высказываний

8)       Что такое дизъюнкция, как записывается?

9)       Что такое конъюнкция, как записывается?

10)   Что такое отрицание, как записывается?

11)   Что такое эквиваленция, как записывается?

12)   Что такое импликация, как записывается