
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ ДНР
ГПОУ «Донецкий политехнический колледж»
Высшая
Математика
Методические указания и контрольные задания
для студентов специальностей:
38.02.01 Экономика и бухгалтерский учет (по отраслям);
09.02.03 Программирование в компьютерных системах;
08.02.04 Водоснабжение и водоотведение;
08.02.09 Монтаж, наладка эксплуатация электрооборудования промышленных и гражданских зданий;
23.02.03 Техническое обслуживание и ремонт автомобильного транспорта.
(заочной
формы обучения)
2019
|
|
Высшая математика: метод. указания и контрольные задания : для студентов всех специалностей заоч. формы обучения / сост. И.С.Орлова- 2019. – 32 с.
Учебно-методические материалы составлены в соответствии с требованиями государственного образовательного стандарта и рабочими программами по дисциплине. Они содержат методические рекомендации по изучению дисциплины, выполнению контрольной работы, варианты заданий к контрольным работам, список рекомендуемой литературы.
|
Одобрена и рекомендована
с целью практического применения
методической комиссией математических дисциплин
протокол № ___ от «___»_________2019 г.
Председатель МК__________ И.С.Орлова
ВВЕДЕНИЕ
Учебные дисциплины «Математика» и «Элементы высшей математики» являются естественнонаучными дисциплинами, формулирующей базовые знания для освоения общепрофессиональных и специальных дисциплин.
Основные задачи математики в средних специальных учебных заведениях на базе основной средней школы:
– математическое обеспечение специальной подготовки, т. е. вооружение студентов математическими знаниями и умениями, необходимыми для изучения специальных дисциплин, разработки курсовых и дипломных проектов;
– подготовка студентов к плодотворной практической профессиональной деятельности и продолжения образования;
– дальнейшее повышение квалификации путем самообразования.
В процессе изучения программного материала проводится тематический контроль знаний студентов, по окончании курса в установленную сессию – зачет.
Общие методические указания
по выполнению контрольной работы
В соответствии с учебным планом по дисциплине «Математика» предусмотрено выполнение одной контрольной работы. Вариант контрольной работы определяется по номеру студенческого билета (зачетной книжки) и соответствует последней цифре. Если последней цифрой является ноль, то это соответствует десятому варианту. Контрольная работа содержит 9 заданий.
Контрольная работа должна быть выполнена в срок в соответствии с учебным планом и сдана за две недели до сессии. В период сессии работа на проверку не принимается.
Работа, выполненная не по своему варианту, возвращается без проверки и зачета.
Студенты, не имеющие зачета по контрольной работе, к зачету по дисциплине не допускаются.
Во время зачета зачтенные контрольные работы представляются преподавателю.
Содержание тем контрольных работ
1. Теория определителей.
2. Аналитическая геометрия.
3. Теория пределов функции.
4. Дифференциальное исчисление.
5. Интегральное исчисление.
6. Основные понятия теории вероятностей.
7. Теория комплексных чисел.
8. Дифференциальные уравнения.
9. Математическая статистика.
Требования к выполнению и оформлению контрольной работы
1. Контрольная работа выполняется в тетради школьного формата в клетку. Следует пронумеровать страницы и оставить на них поля 3 см для замечаний преподавателя.
2. На обложке тетради должен быть приклеен титульный лист утвержденного образца. На нем надо указать наименование предмета, номер контрольной работы, номер варианта, фамилию, имя, отчество, адрес студента, шифр, специальность, учебную группу, а также название учебного заведения.
3. Работа должна быть выполнена чернилами одного цвета, аккуратно, разборчиво.
4. Каждую задачу необходимо начинать с новой страницы.
5. Решение задач нужно располагать в порядке номеров, указанных в задании. Номера задач следует указывать перед условием.
6. Условия всех задач необходимо записывать полностью.
7. При оформлении записей в тетради необходимо выполнять общие требования к культуре их ведения. Перечислим важнейшие из этих требований:
а) студенты должны
соблюдать абзацы, всякую новую мысль следует начинать
с красной строки;
б) важные формулы, равенства, определения нужно выделять в отдельные строки, чтобы сделать их более обозримыми;
в) при описании решения задачи краткая запись условия определяется от решения, в конце решения ставится ответ;
г) серьезное внимание следует уделять правильному написанию сокращенных единиц величин по Международной системе единиц (СИ);
д) необходимо правильно употреблять математические символы.
8. Решения задач
должны сопровождаться краткими, но достаточно обоснованными пояснениями,
используемые формулы нужно вписывать и сопровождать
всеми вычислениями.
9. Чертежи и графики должны быть построены карандашом с использованием чертежных инструментов (циркуля, линейки, угольника), соблюдая масштаб.
10. В конце работы следует указать литературу, которая использовалась, проставить дату выполнения работы и подпись.
11. Если в работе допущены недочеты и ошибки, то студент должен выполнить все указания преподавателя, сделанные в рецензии.
Вопросы для контроля теоретических знаний
1. Теория определителей. Метод Крамера.
а) Определители второго и третьего порядка.
б) Свойства определителей.
в) Решение систем линейных уравнений методом Крамера.
2. Аналитическая геометрия.
а) Понятие вектора в пространстве.
б) Формула длины вектора.
в) Действия над векторами.
г) Скалярное произведение векторов. Угол между векторами.
3. Теория пределов функции.
а) Понятие предела функции.
б) Основные свойства пределов.
в) Методы нахождения пределов функций.
4. Дифференциальное исчисление.
а) Понятие производной функции.
б) Правила дифференцирования.
в) Таблица производных функций.
г) Производная сложной функции.
5. Интегральное исчисление.
а) Понятие определенного интеграла.
б) Свойства определенного интеграла.
в) Таблица основных интегралов.
г) Формула Ньютона — Лейбница.
д) Методы интегрирования.
6. Элементы теории вероятностей.
а) Элементы комбинаторики.
б) Основные понятия теории вероятностей.
в) Операции над событиями и вероятностями событий.
7. Элементы теории комплексных чисел.
а) действия над комплексными числами в алгебраической форме.
б) действия над комплексными числами в тригонометрической форме.
действия над комплексными числами в показательной форме.
8. Дифференциальные уравнения.
9. Математическая статистика.
Методические указания
к выполнению контрольной работы
I. Теория определителей
1.1. Определители второго и третьего порядка
Определителем
второго порядка
называется число 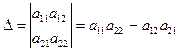 .
.
Определителем третьего порядка называется число
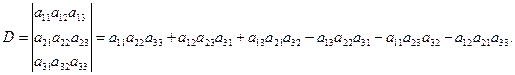
Основные свойства определителей:
1. Если строки или столбцы определителя поменять местами, то значение определителя не изменится.
2. Если переставить две строки (столбца) определителя местами, то значение определителя изменится на противоположное.
3. Если элементы строки (столбца) определителя содержат общий множитель, то его можно вынести за знак определителя.
4. Если две строки (столбца) определителя содержат соответственно пропорциональные элементы, то значение определителя равно нулю.
5. Если к элементам какой-либо строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число, то значение определителя не изменится.
Пример.
Вычислить
определитель: 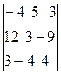 .
.
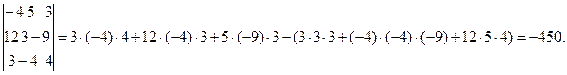
1.2. Решение систем линейных уравнений
методом Крамера
Рассмотрим систему трех линейных уравнений с тремя неизвестными: x1, x2, x3:
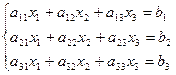
(коэффициенты aij и свободные члены bi считаются заданными).
Решение: составим
определители ![]()
![]() :
:
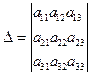 ,
, 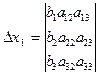 ,
,
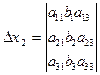 ,
, 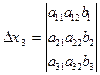 ,
,
где D называют определителем системы, а определители Dxi получены из основного определителя D заменой свободными членами bi элементов соответствующего столбца.
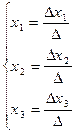
Правила Крамера:
1) если D ¹ 0, то система имеет единственное решение;
2) если D = 0, Dxi ¹ 0, то система несовместна;
3) если D = Dxi = 0, то система имеет бесконечное множество решений.
Пример.
Решить систему
линейных уравнений: 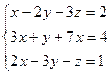 .
.
Решение: составим определители D, Dx, Dy, Dz и найдем их значения.
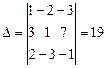 (D ¹
0, следовательно, система имеет единственное решение).
(D ¹
0, следовательно, система имеет единственное решение).
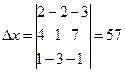 ,
,
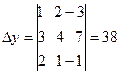 ,
,
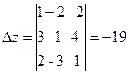 .
.
Найдем решение
системы: 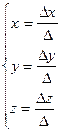 ,
, 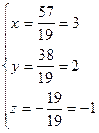 .
.
Ответ: (3; 2; –1).
II. Аналитическая геометрия
2.1. Координаты вектора в пространстве.
Действия над векторами в координатной форме
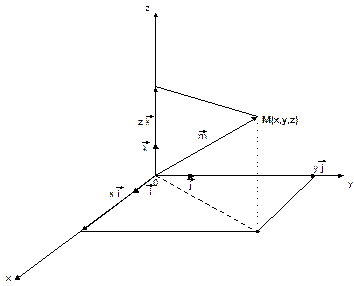
Пусть M(x; у; z) – координаты точки в пространстве.
Выберем: ![]() – единичные векторы на
соответствующих осях координат:
– единичные векторы на
соответствующих осях координат:
![]()
Всякий вектор
пространства можно представить в виде линейной комбинации единичных векторов![]() :
:
![]() ,
,
где ![]() –
координаты вектора в пространстве.
–
координаты вектора в пространстве.
Длина вектора ![]() вычисляется по формуле
вычисляется по формуле ![]() .
.
Рассмотрим две
точки пространства: ![]() и
и ![]() .
.
Найдем координаты вектора![]() :
:
![]()
Таким образом, ![]() – координаты вектора
– координаты вектора![]()
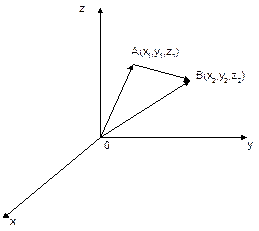 Длина
вектора
Длина
вектора ![]() определяется по формуле
определяется по формуле ![]() .
.
Справедливо следующее утверждение:
пусть ![]() и
и ![]() тогда
тогда
![]() ,
,
![]() ,
,
![]() .
.
Пример 1.
Найти расстояние между точками А и В, если известно, что А(–2;3;1) и В(2;1;5).
Решение:
1. Найдем
координаты вектора ![]() :
:
![]()
2. Вычислим длину
вектора ![]() :
: ![]()
Ответ: 6.
Пример 2.
Найти длину
вектора ![]() если
если ![]() .
.
Решение:
1. Обозначим: ![]()
2. Найдем
координаты вектора ![]()
![]()
3. Найдем
координаты вектора ![]()
![]()
4. Вычислим длину
вектора ![]()
![]()
Ответ: 3.
2.2. Скалярное произведение векторов. Угол между векторами
Скалярным
произведением
двух векторов ![]() и
и ![]() называется произведение модулей
этих векторов на косинус угла между ними.
называется произведение модулей
этих векторов на косинус угла между ними.
Обозначение: ![]()
Особые случаи:
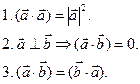
Если векторы ![]() и
и ![]() заданы
своими координатами:
заданы
своими координатами: ![]() и
и ![]() то
скалярное произведение вычисляется по формуле
то
скалярное произведение вычисляется по формуле ![]()
Угол между
векторами выражается следующим образом: 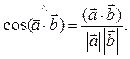
В координатной
форме 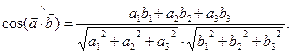
Пример 3.
Найти угол между
векторами ![]() и
и ![]() ,
если
,
если ![]() и
и ![]()
Решение:
Обозначим: ![]() .
.
Ответ: ![]()
III. Введение в теорию пределов функций
Определение: число А
называется пределом функции y = f(x) при ![]() , если для любого числа
, если для любого числа ![]() , существует
, существует ![]() такое, что при
такое, что при ![]() выполняется неравенство
выполняется неравенство ![]() .
.
Обозначение: ![]() .
.
Основные свойства пределов:
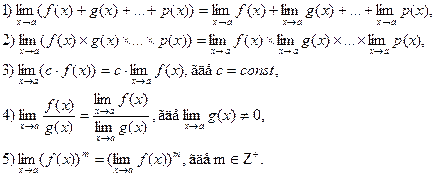
Функция f(x) называется непрерывной
в данной точке a, если выполняется равенство ![]()
Замечательные пределы:
1. ![]() – первый замечательный предел.
– первый замечательный предел.
2. ![]() – второй замечательный
предел.
– второй замечательный
предел.
3. ![]() – третий замечательный предел.
– третий замечательный предел.
Техника вычисления пределов
Пример 1.
Найти ![]() .
.
Решение.
Функция ![]() – непрерывная, графиком ее является
парабола. Следовательно, заменяя ее аргумент предельным значением, найдем
значение предела:
– непрерывная, графиком ее является
парабола. Следовательно, заменяя ее аргумент предельным значением, найдем
значение предела:
![]() .
.
Ответ: –8.
Пример 2.
Найти 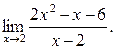
При
непосредственном нахождении предела и числитель и знаменатель обращаются в
нуль, таким образом, получается неопределенность вида![]() .
.
Чтобы раскрыть
неопределенность ![]() , разложим числитель на
множители:
, разложим числитель на
множители:
![]() ,
,
и сократим дробь на выражение (х – 2),
предел которого при ![]() равен 0.
равен 0.
Тогда
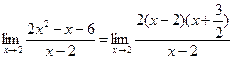 .
.
Ответ: 7.
Пример 3.
Найти ![]() .
.
Решение:
Непосредственно
подстановкой убеждаемся, что выражение обращается в неопределенность вида ![]() .
.
Разложим числитель и знаменатель на множители:
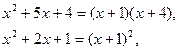
и сократим дробь на выражение (х + 1). Таким образом
![]() .
.
Ответ: ¥.
Пример 4.
Найти: ![]() .
.
Решение:
При ![]() непосредственно подстановкой имеем
неопределенность вида
непосредственно подстановкой имеем
неопределенность вида ![]() .
.
Чтобы раскрыть
неопределенность, разделим числитель и знаменатель дроби на наивысшую степень
переменной – ![]() . Тогда
. Тогда
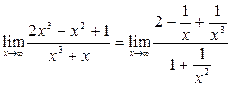 .
.
Поскольку ![]() , то
, то 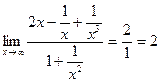 .
.
Ответ: 2.
Пример 5.
Найти: 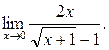
Решение.
Непосредственно
подстановкой имеем неопределенность ![]() .
.
Раскроем
неопределенность, умножив числитель и знаменатель на число, сопряженное к
знаменателю дроби: ![]()
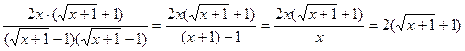 .
.
Тогда
![]()
Ответ: 4.
Пример 6.
Найти:
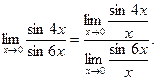
Решение:
Найдем
пределы, используя первый замечательный предел ![]()
![]()
![]()
Таким
образом: ![]() .
.
Замечание:
![]() , так как если
, так как если ![]() , то
, то ![]() .
.
Значит
![]()
Ответ: ![]()
Пример 7.
Найти:
![]() .
.
Решение:
Преобразуем
выражение, стоящее под знаком предела, к виду 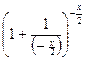 ,
,
и используем второй замечательный предел ![]()
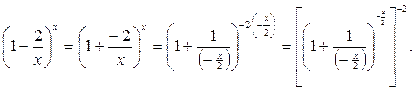
Если
![]() , то
, то ![]() .
Значит:
.
Значит:
![]()
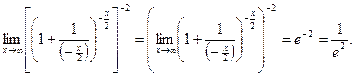
Ответ: ![]() .
.
IV. Дифференциальное исчисление
4.1. Производная функции
Производной функции f(x) в точке x0 называется предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю, если этот предел существует и конечен.
![]()
![]()
Справедливы следующие правила:
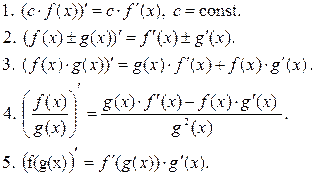
Нахождение производной называется дифференцированием функции.
Основные формулы дифференцирования:
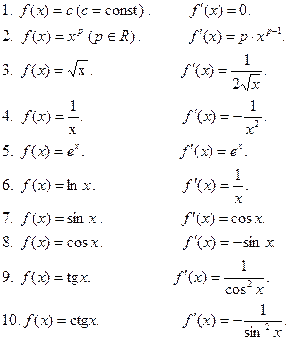
Пример 1. Найти значение производной функции f(x)
в точке ![]() ,
,
если ![]() .
.
Решение.
Функция f(x) представляет собой алгебраическую сумму двух функций:
![]()
Следовательно: ![]() по правилу 2.
по правилу 2.
Функция p(x)
есть композиция логарифмической и тригонометрической функций, а значит, по правилу
5 ![]()
Функция q(x) есть композиция степенной и тригонометрической функций, следовательно, по правилам 1, 5
![]()
Таким образом:
![]()
при 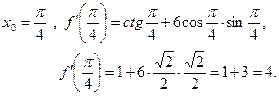
Ответ: ![]() .
.
Пример 2. Найти значение производной функции f(x)
в точке x0 = 2, если ![]() .
.
Решение:
Функция f(x)
представляет собой произведение двух функций: ![]() .
.
Следовательно, по
правилу 3 ![]() .
.
Согласно правилу 2,
![]() .
.
Функция q(x) есть композиция функций: логарифмической и линейной, так как
![]()
При преобразовании функции q(x) были использованы свойства степени и свойства логарифма.
Таким образом:
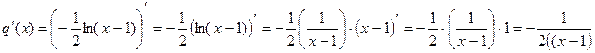
по правилам 1, 5.
Найдем ![]() :
:
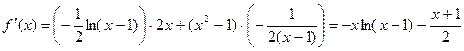 .
.
При x0 = 2
![]()
Ответ: ![]()
4.2. Производные высших порядков функции
Производная f'(x) называется производной первого порядка от функции f(x).
Производная (f'(x))' называется производной второго порядка от функции f(x).
Обозначение: f II(x).
(f II(x))' = f III(x) – производная третьего порядка от f(x).
(f III(x))' = f IV(x) – производная четвертого порядка от f(x) и т. д.
Если f(n–1)(x) – производная (n – 1) порядка функции от f(x), то (f(n–1)(x))' = f(n)(x) – производная n-го порядка от f(x).
Пример 3. Найти производную третьего порядка от функции f(x) = cos2x.
Решение:
![]() (правило 5).
(правило 5).
![]() (правило 5).
(правило 5).
![]()
Ответ: ![]()
V. Интегральное исчисление
5.1. Понятие неопределенного интеграла и его свойства
Функция F(x) называется первообразной для функции f(x) на заданном промежутке, если для всех точек этого промежутка выполняется равенство F'(x) = f(x).
Если F(x) – первообразная для функции f(x) и С – некоторая постоянная, то (F(x) + C) также есть первообразная для f(x).
Неопределенным интегралом от функции f(x) называется множество функций (F(x) + C), являющихся первообразными для f(x).
Обозначение: ![]()
Основные свойства определенного интеграла:
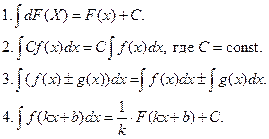
5.2. Таблица основных интегралов
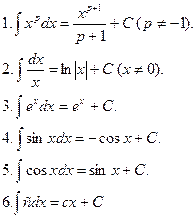
5.3. Методы интегрирования
5.3.1. Непосредственное интегрирование. Нахождение интегралов
с помощью таблицы интегралов и основных свойств интеграла
Пример 1. Найти интеграл: ![]() .
.
Решение:
Согласно свойствам 1, 2, 3 интеграл примет вид:
![]()
По таблице интегралов находим:
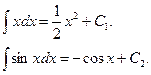
Следовательно,
![]()
Обычно сумму всех
неопределенных постоянных обозначают одной буквой:
С = С1 + С2 + С3.
Пример 2.
Найти интеграл ![]() .
.
Решение:
Рассмотрим подынтегральную
функцию ![]() .
.
Представим ее в
виде композиции двух функций: степенной и линейной ![]() .
.
Согласно свойству 4 и формуле (1) таблицы интегралов, определяется интеграл:
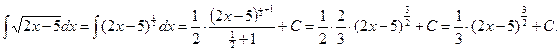
5.4. Определенный интеграл и его свойства
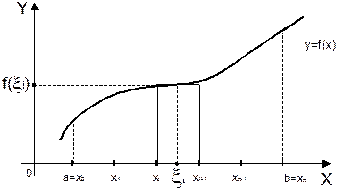 Пусть функция y = f(x) определена на
отрезке [a; b].
Пусть функция y = f(x) определена на
отрезке [a; b].
Разобьем [a; b] на n равных частей точками: a = x0 < x1 < x2 <…< xn–1 < xn = b.
На каждом элементарном отрезке
[xi; xi + 1] выберем
произвольную точку xi
и обозначим ![]() .
.
Тогда ![]() называется интегральной суммой для
функции f(x) на отрезке
называется интегральной суммой для
функции f(x) на отрезке
[a; b].
Определенным
интегралом
от функции f(x) на отрезке [a; b] называется предел
интегральной суммы функции при ![]() , стремящемся к
нулю.
, стремящемся к
нулю.
Обозначение: 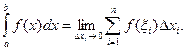
Основные свойства:
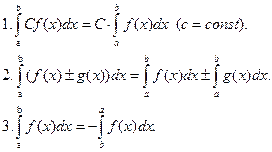
4. Если a < c < b, то 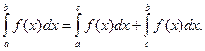
5.5. Методы вычисления определенного интеграла
1. Формула Ньютона — Лейбница:
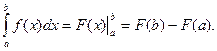
Пример 4.
Вычислить интеграл
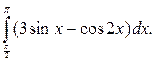
Решение:
Согласно свойствам 1, 2, интеграл запишем в виде
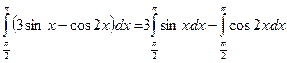
Применив формулу Ньютона — Лейбница, вычислим интегралы:
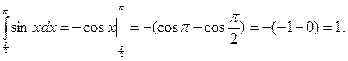
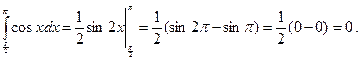
Следовательно, окончательно имеем
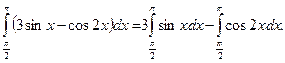
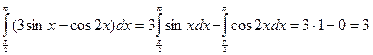 .
.
Ответ:3.
VI. Введение в теорию вероятностей
6.1. Элементы комбинаторики
Раздел математики, в котором решаются задачи на составление различных комбинаций из конечного множества элементов, удовлетворяющих заданным начальным условиям, и подсчет числа всех таких комбинаций, называют комбинаторикой.
В зависимости от правил составления комбинаций выделяют три типа:
1) размещения ![]() , где n!=1×2×3´…´(n – 1)×n, 0! = 1
, где n!=1×2×3´…´(n – 1)×n, 0! = 1 ![]() – число размещений из n элементов по k элементов;
– число размещений из n элементов по k элементов;
2) перестановки Pn = n!, где Pn – число перестановок из n элементов;
3) сочетания ![]() , где
, где
![]() – число сочетаний из n элементов по k элементов.
– число сочетаний из n элементов по k элементов.
Пример 1.
Из предлагаемого набора цифр 1, 2, 3, 4, 5, 6 найти:
1) количество комбинаций всех двузначных чисел;
2) количество комбинаций всех шестизначных чисел, кратных 5.
Решение:
1. Согласно условию задачи, каждая комбинация включает две цифры из данного набора: комбинации 12 и 21 различны, потому что являются различными двузначными числами. Следовательно, комбинации относятся к типу размещений. Найдем число таких комбинаций.
![]()
Ответ: 30.
2. По признаку делимости чисел на 5 все шестизначные числа комбинации по условию задачи оканчиваются цифрой 5. Следовательно, вычислив количество перестановок цифр 1, 2, 3, 4, 6, найдем число всех комбинаций.
![]()
Ответ: 120.
Пример 2.
Найти, сколько диагоналей имеет выпуклый десятиугольник.
Решение:
Количество всех
прямых, которые можно провести через вершины десятиугольника, есть число
сочетаний из 10 точек по 2: ![]()
Исключив из общего числа прямых количество сторон десятиугольника, найдем число его диагоналей: 45 – 10 = 35.
Ответ: 35.
6.2. Основные понятия теории вероятностей
Раздел математики, в котором изучаются случайные события и выявляются закономерности при их массовом повторении, называется теорией вероятности.
События, связанные с некоторым испытанием, при осуществлении которого либо происходят, либо не происходят, называются случайными.
Всякое действие, явление, наблюдение с несколькими различными исходами, реализуемое при данном комплексе условий, называется испытанием.
События, которые имеют равные возможности произойти при испытании в данном комплексе условий, называются равновозможными.
Обозначение: А, В, С, Д,… – случайные события.
События называются
несовместными, если никакие два из них не могут произойти при данном
испытании вместе. В противном случае события называются
совместными.
Полной системой событий (А1 А2 А3…) называется совокупность несовместных событий, наступление хотя бы одного из них при данном испытании обязательно.
Два события
называются противоположными, если они образуют полную систему событий. Обозначения: А – случайное событие, ![]() – событие, противоположное к
случайному событию А.
– событие, противоположное к
случайному событию А.
Событие называют достоверным, если при испытании его наступление обязательно. Обозначение: U.
Событие называют невозможным, если при испытании его наступление невозможно. Обозначение: V.
Пример 1.
При стрельбе по мишени возможны следующие события:
А – поражение мишени,
В – промах по мишени,
С – выбито наибольшее число очков.
События А, В и С являются равновозможными;
события А и В – несовместными, противоположными, образующие полную систему событий: (А, В);
события А и С – совместными.
Число, которое выражает меру объективной возможности наступления случайного события, называется вероятностью этого события. Обозначение: P(A).
![]() , где m – число исходов
испытания, благоприятствующих наступлению события А; n – число всех
равновозможных и несовместных исходов.
, где m – число исходов
испытания, благоприятствующих наступлению события А; n – число всех
равновозможных и несовместных исходов.
Основные свойства:
1. ![]()
2. ![]()
3. ![]()
Пример 2.
В группе студентов 16 девушек и 14 юношей.
Определить вероятность того, что оба вызванных наугад студента окажутся юношами.
Решение:
Обозначим А событие, которое состоит в том, что вызванные наугад студенты – юноши.
Тогда ![]()
Следовательно: ![]()
Ответ: ![]() .
.
6.3. Операции над событиями и вероятностями событий
Суммой событий (А1 + А2 + А3 +…+ Аn) называется событие, наступающее только тогда, когда происходит хотя бы одно из данных событий А1, А2, А3,… Аn.
Произведением событий (А1 ´ А2 ´ А3 ´ …´ Аn) называется событие, наступающее только тогда, когда данные события А1, А2, А3,… Аn происходят одновременно.
Особые случаи:
1. ![]()
2. ![]()
Если события А1
и А2 – несовместные, то ![]() .
.
Если события А1
и А2 – совместные, то ![]() .
.
Пример 3.
Из 30 студентов в группе 8 из них занимаются волейболом, 12 – теннисом, 6 – посещают занятия и по волейболу и по теннису.
1. Какова вероятность того, что выбранный наудачу студент либо занимается двумя видами спорта, либо не занимается ни одним из них?
2. Какова вероятность того, что выбранный наудачу студент занимается либо волейболом, либо теннисом?
Решение:
1. Обозначим:
А – событие, состоящее в том, что выбранный наудачу студент занимается двумя видами спорта;
В – событие, состоящее в том, что студент ничем не занимается.
Тогда (А + В) – событие, состоящее в том, что студент либо занимается двумя видами спорта, либо не занимается ни одним из них.
События А и В – несовместные, а значит, P(A + B) = P(A) + P(B).
Найдем вероятности
событий А и В: ![]() .
.
Следовательно, ![]() .
.
Ответ: ![]() .
.
2. Обозначим:
С – событие, состоящее в том, что студент занимается волейболом;
D – событие, состоящее в том, что студент занимается теннисом;
(С + D) – событие,
состоящее в том, что студент занимается либо волейболом,
либо теннисом;
(С×D) – событие, состоящее в том, что студент занимается и волейболом и теннисом.
События С и D – совместные, а значит,
![]()
![]() .
.
Таким образом, ![]() .
.
Ответ: ![]() .
.
Если А и В
– два случайных события одного испытания, то условной вероятностью события А
при условии, что наступило событие В называют такое число, что ![]() .
.
Обозначение: ![]() .
.
Если события А и В – независимые, т. е. наступление одного из них не оказывает никакого влияния на наступление другого, то выполняются следующие условия:
![]()
Пример 4.
Какова вероятность того, что выбранная наугад карта из колоды в 36 листов окажется тузом, если известно, что она пиковой масти?
Решение:
Обозначим:
А – событие, состоящее в том, что выбранная карта является тузом;
В – событие, состоящее в том, что взятая карта масти пик.
События А и В совместные, а значит, (А×В) – событие, которое состоит в том, что взятая карта оказалась тузом пик. Вычислим вероятности событий В и (АВ).
![]() , следовательно,
, следовательно, ![]() .
.
Ответ: ![]() .
.
Пример 5.
Имеется три партии электроламп, в каждой из которых соответственно 20, 30 и 50 штук. Какова вероятность того, что выбранная наугад лампа из ста данных проработает заданное время, если вероятность того, что лампы проработают заданное время для каждой партии, соответственно равна 0,7; 0,8 и 0,9?
Решение:
Обозначим:
Н1, Н2, и Н3 – события, состоящие в том, что выбранная лампа принадлежит соответственно 1-й, 2-й, 3-й партии;
А – событие состоит в том, что взятая лампа проработает заданное время.
Тогда
![]() по определению вероятности
события.
по определению вероятности
события.
![]() по условию задачи.
по условию задачи.
Согласно формуле полной вероятности события, имеем:
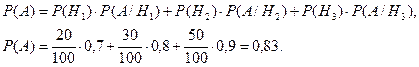
Ответ: 0,83.
Если Н1, Н2, Н3,…, Нi,…, Нn – полная система попарно несовместных событий, связанных с некоторым испытанием, а А – произвольное событие, наступившее в ходе того же испытания вместе с одним из событий Нi, то сумма произведений вероятностей P(Нi) и P(A/Нi):
![]() – определяет формулу полной
вероятности события А.
– определяет формулу полной
вероятности события А.
Алгебраическая
форма:
![]()
Модуль комплексного числа: ![]()
Аргумент комплексного числа: 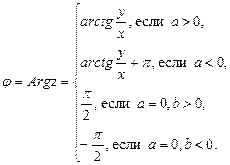
Действия над комплексными числами в алгебраической форме:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
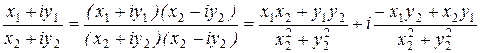 , при условии, что
, при условии, что ![]() .
.
Тригонометрическая
форма:
![]()
Действия над комплексными числами в тригонометрической:
1)
![]() ;
;
2)
![]() ;
;
3)
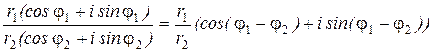 ;
;
4)
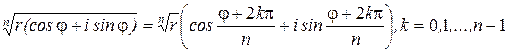 .
.
Показательная
форма:
![]()
Действия над комплексными числами в показательной форме:
1)
![]() ;
;
2)
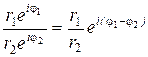 ;
;
Задание 1 Записать в
тригонометрической и показательной формах комплексные числа ![]() і
і ![]() .
Вычислить
.
Вычислить ![]() и
и ![]() .
.
![]() ,
,
![]() ,
,![]() ,
,
![]()
Используем приложение А.
Чтобы
записать комплексное число ![]() в
тригонометричкской форме
в
тригонометричкской форме ![]() =r(cosj+isinj), найдем его
модуль r и аргумент j:
=r(cosj+isinj), найдем его
модуль r и аргумент j:
![]()
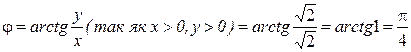
Тепер запишемо
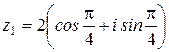 .
.
Таким же
образом запишем в тригонометрической форме комплексное число ![]() :
:
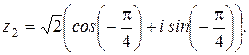
В
показательной форме ![]() ,
, ![]()
Вычислим ![]() .в тригонометрической форме:
.в тригонометрической форме:
![]()
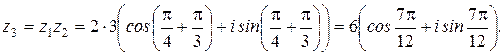
Вычислим ![]() в алгебраической форме:
в алгебраической форме:
![]() .
.
Задание 9
Дискретная случайная величина задана рядом распределения. Необходимо:
а) записать пропущенную вероятность;
б) вычислить вероятность попаданий в указанные интервалы;
в) вычислить числовые характеристики случайной величины M x , Dx ,s x .
|
x i |
1 |
4 |
7 |
9 |
12 |
14 |
|
p i |
0,1 |
0,15 |
|
0,4 |
0,05 |
0,15 |
P(X=1); P(X=8); P(X<5); P(X>8); P(4<X<13); P(10<X<20).
Так
как ![]() , то пропущенная вероятность равна
1-(0,1+0,15+0,4+0,05+0,15)=0,15.
, то пропущенная вероятность равна
1-(0,1+0,15+0,4+0,05+0,15)=0,15.
Р(Х=1)=0,1; Р(Х=8)=0; Р(Х<5)=P(X=1)+P(X=4)=0,25; P(X>8)=P(X=9)+P(X=12)+P(X=14)=0,4+0,05+0,15=0,6
P(4<X<13)=P(X=7)+P(X=9)+P(X=12)=0,15+0,4+0,05=0,6
P(10<X<20)=P(X=12)+P(X=14)=0,05+0,15=0,2.
![]() .
.
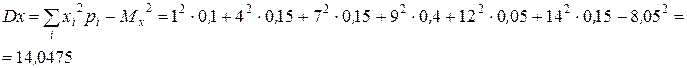
sx=![]() .
.
задания для контрольной работы
Вариант № 1
I. Теория определителей
1. Решить систему линейных уравнений:
а) 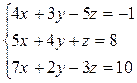 , б)
, б)
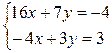 .
.
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
Найти:
а) координаты векторов![]() и
и ![]() ;
;
б) скалярное произведение векторов![]() и
и ![]() ;
;
в) угол между векторами ![]() и
и ![]() ;
;
A(3; –1; 2), B(1; 1; 1), C(–5; 3; 1).
III. Теория пределов функции
3. Найти указанные пределы функций.
а) 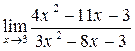 ; б)
; б) 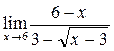 ; в)
; в) 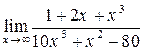 ;
г)
;
г) 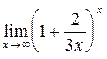 .
.
IV. Дифференциальное исчисление
4. Найти производные функций при заданном значении аргумента
а) 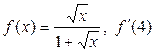 ; б)
; б)
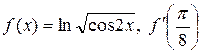 .
.
V. Интегральное исчисление
5. Вычислить определенный интеграл:
а) 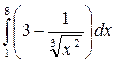 ; б)
; б)
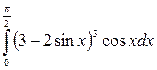 .
.
VI. Элементы теории вероятностей
В группе студентов 10 девушек и 15 юношей. Определить вероятность того, что оба вызванных наугад студента окажутся девушками.
VII.Элементы теории комплексных чисел
Записать в
тригонометрической и показательной формах комплексные числа ![]() и
и ![]() .
Вычислить
.
Вычислить ![]() ,z4/
,z4/
|
№ |
|
|
|
|
|
7. |
|
|
|
|
Вариант № 2
I. Теория определителей
1. Решить систему линейных уравнений:
a) 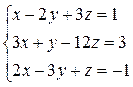 , б)
, б)
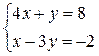 .
.
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
Найти:
а) координаты векторов![]() и
и ![]() ;
;
б) скалярное произведение векторов![]() и
и ![]() ;
;
в) угол между векторами ![]() и
и ![]() ;
;
A(1; 8; –3), B(3; 2; 6), C(2; 6; –1).
III. Теория пределов функции
3. Найти указанные пределы функций.
а) 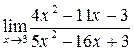 ;
б)
;
б) 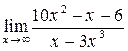 ; в)
; в) 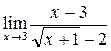 ;
г)
;
г) ![]() .
.
IV. Дифференциальное исчисление
4. Найти производные функций при заданном значении аргумента
а) 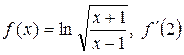 ; б)
; б)
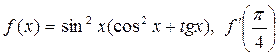 .
.
V. Интегральное исчисление
5. Вычислить определенный интеграл:
а) 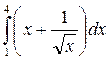 ; б)
; б)
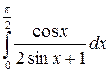 .
.
VI. Элементы теории вероятностей
Из 20 студентов в группе 4 из них занимаются рисованием, 10 – поют в хоре, 2 – посещают занятия и по рисованию и поют в хоре.
Какова вероятность того, что выбранный наудачу студент посещает оба кружка?
VII.Элементы теории комплексных чисел
Записать в
тригонометрической и показательной формах комплексные числа ![]() и
и ![]() .
Вычислить z3
;z4
.
Вычислить z3
;z4
|
№ |
|
|
|
|
|
7. |
|
|
|
|
Вариант № 3
I. Теория определителей
1. Решить систему линейных уравнений:
a) 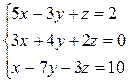 ; б)
; б)
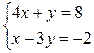 .
.
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
Найти:
а) координаты векторов![]() и
и ![]() ;
;
б) скалярное произведение векторов![]() и
и ![]() ;
;
в) угол между векторами ![]() и
и ![]() ;
;
A(4; –2; 5), B(2; 2; 1), C(3; 6; 1).
III. Теория пределов функции
3. Найти указанные пределы функций.
а) 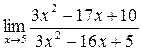 ;
б)
;
б)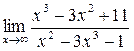 ; в)
; в) 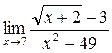 ;
г)
;
г) ![]() .
.
IV. Дифференциальное исчисление
4. Найти производные функций при заданном значении аргумента
а) ![]() ; б)
; б)
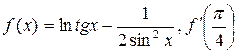 .
.
V. Интегральное исчисление
5. Вычислить определенный интеграл:
а) 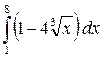 ; б)
; б)
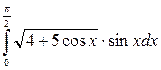 .
.
VI. Элементы теории вероятностей
Из 24 студентов в группе 6 из них занимаются легкой атлетикой, 10 – боксом, 4 – посещают занятия и по легкой атлетике и по боксу.
Какова вероятность того, что выбранный наудачу студент занимается либо легкой атлетикой, либо боксом?
VII.Элементы теории комплексных чисел
Записать в
тригонометрической и показательной формах комплексные числа ![]() и
и ![]() .
Вычислить z3;z4/
.
Вычислить z3;z4/
|
№ |
|
|
|
|
|
7. |
|
|
|
|
Вариант № 4
I. Теория определителей
1. Решить систему линейных уравнений:
а)
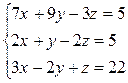 ; б)
; б)
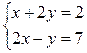 .
.
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
Найти:
а) координаты векторов![]() и
и ![]() ;
;
б) скалярное произведение векторов![]() и
и ![]() ;
;
в) угол между векторами ![]() и
и ![]() ;
;
A(–3; 7; 1), B(1; 5; 3), C(2; –7; 3).
III. Теория пределов функции
3. Найти указанные пределы функций.
а) 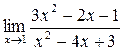 ;
б)
;
б) 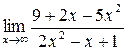 ; в)
; в) 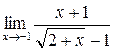 ;
г)
;
г) ![]() .
.
IV. Дифференциальное исчисление
4. Найти производные функций при заданном значении аргумента
а) ![]() ; б)
; б)
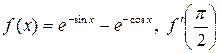 .
.
V. Интегральное исчисление
5. Вычислить определенный интеграл:
а) 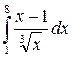 ; б)
; б)
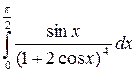 .
.
VI. Элементы теории вероятностей
Какова вероятность того, что выбранная наугад карта из колоды в 36 листов окажется дамой, если известно, что она бубновой масти?
VII.Элементы теории комплексных чисел
Записать в
тригонометрической и показательной формах комплексные числа ![]() и
и ![]() .
Вычислить
z3;z4/ .
.
Вычислить
z3;z4/ .
|
№ |
|
|
|
|
|
7. |
|
|
|
|
Вариант № 5
I. Теория определителей
1. Решить систему линейных уравнений:
а)
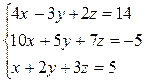 ; б)
; б)
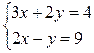 .
.
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
Найти:
а) координаты векторов![]() и
и ![]() ;
;
б) скалярное произведение векторов![]() и
и ![]() ;
;
в) угол между векторами ![]() и
и ![]() ;
;
A(2; 3; –6), B(5; –1; 6), C(4; 1; 3).
III. Теория пределов функции
3. Найти указанные пределы функций.
а) 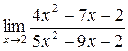 ;
б)
;
б)![]() ; в)
; в) 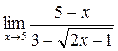 ;
г)
;
г) ![]() .
.
IV. Дифференциальное исчисление
4. Найти производные функций при заданном значении аргумента
а) 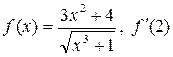 ; б)
; б)
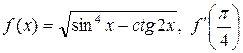 .
.
V. Интегральное исчисление
5. Вычислить определенный интеграл:
а) 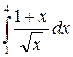 ; б)
; б)
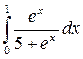 .
.
VI. Элементы теории вероятностей
В группе студентов 12девушек и 18 юношей.
Определить
вероятность того, что оба вызванных наугад студента окажутся
девушками.
VII.Элементы теории комплексных чисел
Записать в
тригонометрической и показательной формах комплексные числа ![]() и
и ![]() .
Вычислить
z3;z4/.
.
Вычислить
z3;z4/.
|
№ |
|
|
|
|
|
7. |
|
|
|
|
Вариант № 6
I. Теория определителей
1. Решить систему линейных уравнений:
а)
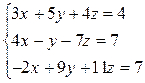 ; б)
; б)
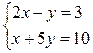 .
.
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
Найти:
а) координаты векторов![]() и
и ![]() ;
;
б) скалярное произведение векторов![]() и
и ![]() ;
;
в) угол между векторами ![]() и
и ![]() ;
;
A(–1; 5; 4), B(5; –4; 2), C(1; 3; 3).
III. Теория пределов функции
3. Найти указанные пределы функций.
а) 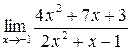 ;
б)
;
б) 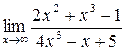 ; в)
; в) 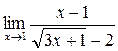 ;..г)
;..г)
![]() .
.
IV. Дифференциальное исчисление
4. Найти производные функций при заданном значении аргумента
а) 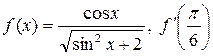 ; б)
; б)![]()
![]() .
.
V. Интегральное исчисление
5. Вычислить определенный интеграл:
а) 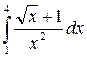 ; б)
; б)
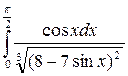 .
.
VI. Элементы теории вероятностей
В коробке 10 шоколадных конфет и 16 карамельных конфет. Определить вероятность того, что обе взятых из коробки наугад конфет – шоколадные.
VII.Элементы теории комплексных чисел
Записать в
тригонометрической и показательной формах комплексные числа ![]() и
и ![]() .
Вычислить
z3;z4/ .
.
Вычислить
z3;z4/ .
|
№ |
|
|
|
|
|
7. |
|
|
|
|
Вариант № 7
I. Теория определителей
1. Решить систему линейных уравнений:
а) 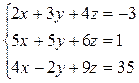 ; б)
; б)
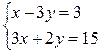 .
.
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
Найти:
а) координаты векторов![]() и
и ![]() ;
;
б) скалярное произведение векторов![]() и
и ![]() ;
;
в) угол между векторами ![]() и
и ![]() ;
;
A(5; –2; 3), B(4; 6; –1), C(1; 2; 1).
III. Теория пределов функции
3. Найти указанные пределы функций.
а) 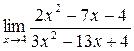 ;
б)
;
б) 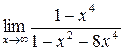 ; в)
; в) 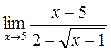 ;
г)
;
г)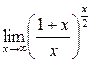 .
.
IV. Дифференциальное исчисление
4. Найти производные функций при заданном значении аргумента
а) 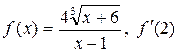 ; б)
; б)
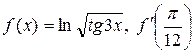 .
.
V. Интегральное исчисление
5. Вычислить определенный интеграл:
а) 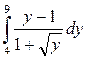 ; б)
; б)
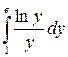 .
.
VI. Элементы теории вероятностей
Из 16 школьников в классе 6 из них коллекционируют марки, 8 – открытки, а 4 – коллекционируют и марки и открытки. Какова вероятность того, что выбранный наудачу школьник коллекционирует и марки и открытки?
VII.Элементы теории комплексных чисел
Записать в
тригонометрической и показательной формах комплексные числа ![]() и
и ![]() .
Вычислить
z3;z4 .
.
Вычислить
z3;z4 .
|
№ |
|
|
|
|
|
7. |
|
|
|
|
Вариант № 8
I. Теория определителей
1. Решить систему линейных уравнений:
а)
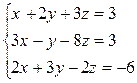 ; б)
; б)
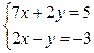 .
.
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
Найти:
а) координаты векторов![]() и
и ![]() ;
;
б) скалярное произведение векторов![]() и
и ![]() ;
;
в) угол между векторами ![]() и
и ![]() ;
;
A(8; –3; –1), B(4; –1; 3), C(–1; 3; 1).
III. Теория пределов функции
3. Найти указанные пределы функций.
а) 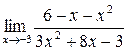 ;
б)
;
б) 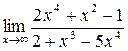 ; в)
; в) 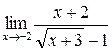 ;
г)
;
г) ![]() .
.
IV. Дифференциальное исчисление
4. Найти производные функций при заданном значении аргумента
а) ![]() ; б)
; б)
![]() .
.
V. Интегральное исчисление
5. Вычислить определенный интеграл:
а) 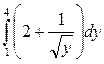 ; б)
; б)
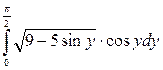 .
.
VI. Элементы теории вероятностей
В вазе находятся 12 груш и 10 яблок. Определить вероятность того, что оба взятых из вазы наугад фрукта – груши.
VII.Элементы теории комплексных чисел
Записать в
тригонометрической и показательной формах комплексные числа ![]() и
и ![]() .
Вычислить
.
Вычислить ![]() , z4
.
, z4
.
|
№ |
|
|
|
|
|
7. |
|
|
|
|
Вариант № 9
I. Теория определителей
1. Решить систему линейных уравнений:
а) 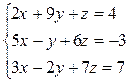 ; б)
; б)
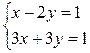 .
.
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
Найти:
а) координаты векторов![]() и
и ![]() ;
;
б) скалярное произведение векторов![]() и
и ![]() ;
;
в) угол между векторами ![]() и
и ![]() ;
;
A(–6; 1; 4), B(8; 3; –1), C(2; 5; 3).
III. Теория пределов функции
3. Найти указанные пределы функций.
а) 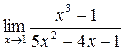 ;
б)
;
б) 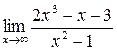 ; в)
; в) 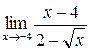 ;
г)
;
г) 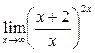 .
.
IV. Дифференциальное исчисление
4. Найти производные функций при заданном значении аргумента
а) 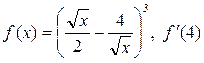 ; б)
; б)
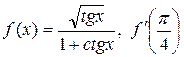 .
.
V. Интегральное исчисление
5. Вычислить определенный интеграл:
а) 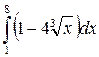 ; б)
; б)
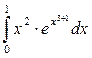 .
.
VI. Элементы теории вероятностей
Какова вероятность того, что выбранная наугад карта из колоды в 36 листов окажется королем, если известно, что она имеет масть «черви»?
VII.Элементы теории комплексных чисел
Записать в
тригонометрической и показательной формах комплексные числа ![]() и
и ![]() .
Вычислить z3;z4/.
.
Вычислить z3;z4/.
|
№ |
|
|
|
|
|
7. |
|
|
|
|
Вариант № 10
I. Теория определителей
1. Решить систему линейных уравнений:
а) 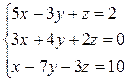 ; б)
; б)
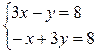 .
.
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
Найти:
а) координаты векторов![]() и
и ![]() ;
;
б) скалярное произведение векторов![]() и
и ![]() ;
;
в) угол между векторами ![]() и
и ![]() ;
;
A(–2; –4; 1), B(4; 5; 3), C(1; 8; 5).
III. Теория пределов функции
3. Найти указанные пределы функций.
а) 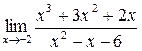 ;
б)
;
б) 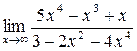 ; в)
; в) 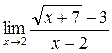 ;
г)
;
г) ![]() .
.
IV. Дифференциальное исчисление
4. Найти производные функций при заданном значении аргумента
а) 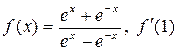 ; б)
; б)
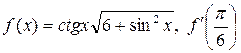 .
.
V. Интегральное исчисление
5. Вычислить определенный интеграл:
а) 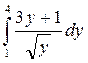 ; б)
; б)
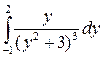 .
.
VI. Элементы теории вероятностей
В урне находятся 15 белых и 25 черных шаров. Определить вероятность того, что оба выбранных наугад шара окажутся белыми.
VII.Элементы теории комплексных чисел
Записать в
тригонометрической и показательной формах комплексные числа ![]() и
и ![]() .
Вычислить z3;z4/.
.
Вычислить z3;z4/.
|
№ |
|
|
|
|
|
7. |
|
|
|
|
Задание VIII Дифференциальные уравнения
8.Найти общее решение дифференциальных уравнений.
|
1.а) б) в)
|
2.а) б) |
|
3.а) б) в) |
4. а) б) в) |
|
5. а) б) в) |
6.а) б) в |
|
7.а) б) в) |
8. а) б) в)
|
|
9.а) б) в) |
10.а) б) в)
|
Задание IX Математическая статистика
Дискретная случайная величина задана рядом распределения. Необходимо: а) записать пропущенную вероятность;
б) вычислить вероятность попаданий в указанные интервалы;
в) вычислить числовые характеристики случайной величины M x , Dx ,s x .
1.
|
x i |
1 |
3 |
7 |
9 |
12 |
14 |
|
p i |
0,1 |
0,2 |
|
0,4 |
0,05 |
0,15 |
P(X=2); P(X=9); P(X<5); P(X>8); P(4<X<13); P(10<X<20);
2.
|
x i |
3 |
4 |
6 |
8 |
13 |
18 |
|
p i |
0,15 |
0,20 |
0,10 |
0,35 |
|
0,05 |
P(X=9); P(X=4); P(X<8); P(X>2); P(5<X<11); P(70<X<40)
3.
|
x i |
1 |
4 |
5 |
8 |
11 |
14 |
|
p i |
0,10 |
0,10 |
0,25 |
|
0,10 |
0,05 |
P(X=11); P(X=0); P(X<10); P(X>4); P(5<X<13); P(3<X<30)
4.
|
x i |
3 |
5 |
7 |
9 |
13 |
14 |
|
p i |
0,05 |
0,05 |
0,25 |
0,35 |
|
0,10 |
P(X=1); P(X=7); P(X<8); P(X>5); P(6<X<15); P(10<X<30)
5.
|
x i |
6 |
7 |
9 |
11 |
14 |
17 |
|
p i |
0,35 |
|
0,15 |
0,05 |
0,10 |
0,10 |
P(X=4); P(X=9); P(X<10); P(X>7) P(2<X<9); P(6<X<26)
6.
|
x i |
0 |
5 |
7 |
8 |
11 |
15 |
|
p i |
|
0,05 |
0,10 |
0,10 |
0,35 |
0,10 |
P(X=3); P(X=15); P(X<6); P(X>9); P(2<X<12); P(7<X<25)
7.
|
x i |
2 |
6 |
9 |
12 |
14 |
16 |
|
p i |
0,25 |
0,15 |
0,10 |
|
0,05 |
0,05 |
P(X=1); P(X=12); P(X<6); P(X>7); P(3<X<15); P(8<X<80)
8.
|
x i |
1 |
3 |
5 |
12 |
14 |
16 |
|
p i |
0,25 |
0,15 |
|
0,10 |
0,05 |
0,05 |
P(X=1); P(X=12); P(X<6); P(X>7); P(3<X<15); P(8<X<20)
9.
|
x i |
2 |
4 |
6 |
10 |
14 |
16 |
|
p i |
|
0,15 |
0,10 |
0,20 |
0,05 |
0,05 |
P(X=1); P(X=12); P(X<6); P(X>7); P(3<X<15); P(8<X<80)
10.
|
x i |
2 |
6 |
9 |
12 |
14 |
16 |
|
p i |
|
0,15 |
0,10 |
0,3 |
0,05 |
0,05 |
P(X=1); P(X=12); P(X<6); P(X>7); P(3<X<15); P(9<X<20)
Список рекомендуемой литературы
Основная литература
Математика : учеб. пособие для техникумов / под ред. В.П. Омельченко. – Ростов н/Д : Феникс, 2005.
Математика для техникумов. Алгебра и начала анализа. Ч. 1 и 2 / под ред. Г.Н. Яковлева, – М. : Наука, 1988.
Математика для техникумов. Геометрия / под ред. Г.Н. Яковлева. – М. : Наука, 1982.
Математика : учеб. пособие для техникумов / под ред. В.Т. Лисичкина, И.Л. Соловейчик. – М. : Высш. шк., 1991.
Дополнительная литература
Практические занятия по математике / под ред. Н.В. Богомолова. – М. : Высш. шк., 1990.
Сборник задач по математике для
техникумов / под ред. О.Н. Афанасьевой. –
М. : Наука, 1987.
Математика для техникумов / под ред. И.И. Валуце, Г.Д. Дилигул. – М. : Наука, 1990.
Высшая математика / под ред. В.С. Щипачева. – М. : Высш. шк., 1996.
Высшая математика в упражнениях и задачах. Ч. 1 / под ред. П.Е. Данко, А.Г. Попова, Т.Я. Кожевниковой. – М. : Высш. шк., 1997.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.