
1 2
![]() (№ 324468) Решите
уравнение x2 x 3 0.
(№ 324468) Решите
уравнение x2 x 3 0.
(№ 324469) Решите уравнение x x 2 2x 1 2x1.
(№ 324470) Решите уравнение x 24 4x 22 5 0.
12 (№ 324471)
Решите неравенство ![]() x2 7x 8
0.
x2 7x 8
0.
12 (№ 324472)
Решите неравенство ![]() x2 7x 8
0.
x2 7x 8
0.
12 (№ 324473)
Решите неравенство ![]() 2
0.
2
0.
x 1 2
![]() (№ 324474) Решите
неравенство x
42 3x
4.
(№ 324474) Решите
неравенство x
42 3x
4.
![]() 2
x 0, (№ 324475)
Решите систему неравенств 2
3
x2 .
2
x 0, (№ 324475)
Решите систему неравенств 2
3
x2 .
6 9x 31 4x
(№ 324476) Решите неравенство 3x 72 7x 32.
(№ 324477) Решите неравенство x2 x2 9 9 x2 9.
7 3 x 2 3 7 x 2 2x,
(№ 324478) Решите систему неравенств
x 4x 8 0.
![]() (№ 324479) Найдите значение
выражения a3 16a
a 1
4 a 1 4
при a
45.
(№ 324479) Найдите значение
выражения a3 16a
a 1
4 a 1 4
при a
45.
4x9y
![]() (№ 324480) Найдите значение
выражения y
, если 2 x3
y
(№ 324480) Найдите значение
выражения y
, если 2 x3
y
![]() x y7.
x y7.
3x3 x9 .
(№ 324481) Сократите дробь ![]() x 10 2x4
x 10 2x4
(№ 324482) Найдите значение выражения ![]() p a
, если p b
p a
, если p b ![]() b6b
.
b6b
.
p6 a b 3
p a , если (№ 324483) Найдите значение выражения
![]() p 1a
p 1a
p b
b
![]() b33b
b33b
![]() b1.
b1.
(№ 324484) Найдите значение выражения 61a 11b50, если ![]() 9.
9.
(№ 324485) Найдите f 3, если f x 1 76x.
(№ 324486) Решите уравнение x 73 49x 7.
(№ 324487) Решите уравнение x3 4x2 5x.
(№ 324489) Решите уравнение x3 3x2 x 3 0.
(№ 324490) Решите уравнение x 22x 3 12x 2.
(№ 324491) Решите уравнение x 2x 3x 4 x 2x 3x 5.
(№ 324492) Решите уравнение 2x 32x 3 2x 3x 32.
(№ 324493) Решите уравнение x4 x 202.
(№ 324494) Решите уравнение x6 x 53.
2x2 7x 3 (№ 324495)
Решите уравнение ![]() x2 9 1.
x2 9 1.
![]() (№ 324496) Решите уравнение x2
6x 6 x 6 x 7.
(№ 324496) Решите уравнение x2
6x 6 x 6 x 7.
(№ 324497) Решите уравнение x2 252 x2 3x 102 0.
3x2 y 4, (№ 324498) Решите систему уравнений 2x2 y 1.
2x2 3y2 11,
(№ 324499) Решите систему уравнений 2 6y2 11 .x
4x
x 6y2 7y, (№ 324500) Решите систему уравнений 2 x 6y 7 .x
2x 32 5y, (№ 324501) Решите систему уравнений 2
3x 2 5 .y
x2 y2 37,
(№ 324502) Решите систему уравнений xy 6. x2 4y 1, (№ 324503) Решите систему уравнений 2 3 4y y2.
x
x6y 7 0,
(№ 324504) Решите систему уравнений y 4
![]()
x y 10 3.
(№ 324505) Три бригады изготовили вместе 173 детали. Известно, что вторая бригада изготовила деталей в 3 раза больше, чем первая и на 12 деталей меньше, чем третья. На сколько деталей больше изготовила третья бригада, чем первая.
(№ 324506) Свежие фрукты содержат 80% воды, а высушенные — 4%. Сколько требуется свежих фруктов для приготовления 2 кг высушенных фруктов?
(№ 324507) Свежие фрукты содержат 72% воды, а высушенные — 20%. Сколько сухих фруктов получится из 100 кг свежих фруктов?
(№ 324508) Имеются два сосуда, содержащие 20 и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 41% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 43% кислоты. Сколько килограммов кислоты содержится в первом растворе?
(№ 324509) Два человека отправляются из одного и того же места на прогулку до опушки леса, находящейся в 3,5 км от места отправления. Один идет со скоростью 2,7 км/ч, а другой — со скоростью 3,6 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?
(№ 324510) Дорога между пунктами A и B состоит из подъёма и спуска, а её длина равна 19 км. Турист прошёл путь из A в B за 5 часов, из которых спуск занял 4 часа. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 1 км/ч?
(№ 324511) Из двух городов одновременно навстречу друг другу отправляются два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 6 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 162 км, скорость первого велосипедиста равна 15 км/ч, скорость второго — 30 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
(№ 324512) Два автомобиля отправляются в 340-километровый пробег. Первый едет со скоростью на 17 км/ч большей, чем второй, и прибывает к финишу на 1 ч раньше второго. Найдите скорость первого автомобиля. (№ 324513) Из A в B одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого автомобилиста на 11 км/ч, а вторую половину пути проехал со скоростью 66 км/ч, в результате чего прибыл в B одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 40 км/ч.
(№ 324514) Велосипедист выехал с постоянной скоростью из города А в город B, расстояние между которыми равно 60 км. Отдохнув, он отправился обратно в A, увеличив скорость на 10 км/ч. По пути он сделал остановку на 3 часа, в результате чего затратил на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость велосипедиста на пути из A в B.
(№ 324515) Два велосипедиста одновременно отправляются в 60километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым.
(№ 324516) Моторная лодка прошла против течения реки 77 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения равна 4 км/ч.
(№ 324517) Теплоход проходит по течению реки до пункта назначения 165 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 5 часов, а в пункт отправления теплоход возвращается через 18 часов после отплытия из него.
(№ 324518) От пристани A к пристани B, расстояние между которым равно 70 км, отправился с постоянной скоростью первый теплоход, а через 1 час после этого следом за ним со скоростью на 8 км/ч большей, отправился второй. Найдите скорость первого теплохода, если в пункт B оба теплохода прибыли одновременно.
(№ 324519) Первый рабочий за час делает на 10 деталей больше, чем второй, и заканчивает работу над заказом, состоящим из 60 деталей, на 3 часа раньше, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
(№ 324520) Первая труба пропускает на 10 литров воды в минуту меньше, чем вторая труба. Сколько литров воды в минуту пропускает первая труба, если резервуар объёмом 60 литров она заполняет на 3 минуты раньше, чем вторая труба?
(№ 324521) Из городов A и B навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 2 часа раньше, чем велосипедист приехал в A, а встретились они через 45 минут после выезда. Сколько часов затратил на путь из B в A велосипедист?
(№ 324522) Расстояние между городами A и B равно 80 км. Из города A в город B выехал автомобиль, а через 20 минут следом за ним со скоростью 90 км/ч выехал мотоциклист. Мотоциклист догнал автомобиль в городе C и повернул обратно. Когда он проехал половину пути из C в A, автомобиль прибыл в B. Найдите расстояние от A до C.
(№ 324523) Первый велосипедист выехал из посёлка по шоссе со скоростью 12 км/ч. Через час после него со скоростью 10 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа после этого догнал первого.
(№ 324524) Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 1 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 5 минут назад. Найдите скорость первого бегуна, если известно, что она на 2 км/ч меньше скорости второго.
(№ 324525) Расстояние между пристанями A и B равно 60 км. Из A в B по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот прошёл 36 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 4 км/ч.
(№ 324526) Баржа проплыла по течению реки 60 км и, повернув обратно, проплыла ещё 20 км, затратив на весь путь 7 часов. Найдите собственную скорость баржи, если скорость течения равна 1 км/ч.
(№ 324527) Игорь и Паша красят забор за 3 часа. Паша и Володя красят этот же забор за 6 часов, а Володя и Игорь — за 4 часа. За какое время мальчики покрасят забор, работая втроём?
(№ 324528) Смешали некоторое количество 11%-го раствора некоторого вещества с таким же количеством 21%-го раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
(№ 324529) Первую половину трассы автомобиль проехал со скоростью 56 км/ч, а вторую — со скоростью 84 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
(№ 324530) Первые 2 часа автомобиль ехал со скоростью 55 км/ч, следующий час — со скоростью 70 км/ч, а последние 3 часа — со скоростью 90 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
(№ 324531) Первые 100 км автомобиль ехал со скоростью 50 км/ч, следующие 240 км — со скоростью 60 км/ч, а последние 200 км — со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
(№ 324532) Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо придорожного столба за 30 секунд. Найдите длину поезда в метрах.
(№ 324533) Поезд, двигаясь равномерно со скоростью 54 км/ч, проезжает мимо идущего параллельно путям со скоростью 6 км/ч навстречу ему пешехода за 30 секунд. Найдите длину поезда в метрах.
(№ 324534) Поезд, двигаясь равномерно со скоростью 65 км/ч, проезжает мимо идущего в том же направлении параллельно путям со скоростью 5 км/ч пешехода за 30 секунд. Найдите длину поезда в метрах.
(№ 324535) По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 70 км/ч и 30 км/ч. Длина товарного поезда равна 1400 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 3 минутам.
(№ 324536) Постройте график функции y 1 ![]() xx2 22x
и определите, при каких значениях m прямая y m не
имеет с графиком ни одной общей точки.
xx2 22x
и определите, при каких значениях m прямая y m не
имеет с графиком ни одной общей точки.
x4 x3
(№ 324537)
Постройте график функции y
1 ![]() x
x2 и определите, при
каких значениях m прямая y m
имеет с графиком две общие точки.
x
x2 и определите, при
каких значениях m прямая y m
имеет с графиком две общие точки.
x 5x2 5x 4
(№ 324538) Постройте
график функции y
![]() и
определите, x
4
и
определите, x
4
при каких значениях m прямая y m имеет с графиком ровно одну общую точку.
![]() (№ 324539) Постройте график
функции y x
2 x
2
(№ 324539) Постройте график
функции y x
2 x
2![]() . Какое наибольшее число общих точек график данной функции может иметь с
прямой, параллельной оси абсцисс?
. Какое наибольшее число общих точек график данной функции может иметь с
прямой, параллельной оси абсцисс?
![]() (№ 324540) Постройте график
функции y x
2 6
x 8.
Какое наибольшее число общих точек график данной функции может иметь с прямой,
параллельной оси абсцисс?
(№ 324540) Постройте график
функции y x
2 6
x 8.
Какое наибольшее число общих точек график данной функции может иметь с прямой,
параллельной оси абсцисс?
x2 x 6x2 4x 5
(№ 324541) Постройте график функции y ![]() x2 2x 3
и определите, при каких значениях m прямая y m имеет
с графиком ровно одну общую точку.
x2 2x 3
и определите, при каких значениях m прямая y m имеет
с графиком ровно одну общую точку.
x2 4x 6, если x 1,
(№ 324542) Постройте график функции y
3x, если x 1
и определите, при каких значениях m прямая y m имеет с графиком ровно две общие точки.
(№ 324543) Найдите все значения k , при каждом из которых прямая y kxимеет с графиком функции y x2 4 ровно одну общую точку.
Постройте этот график и все такие прямые.
(№ 324544) Найдите все значения k , при каждом из которых прямая y kxимеет с графиком функции y x2 1 ровно одну общую точку. Постройте этот график и все такие прямые.
(№ 324545) Найдите p и постройте график функции y x2 p , если известно, что прямая y 6x имеет с этим графиком ровно одну общую точку.
![]() x2 x x (№
324546) Постройте график функции y
и определите, при x 1
x2 x x (№
324546) Постройте график функции y
и определите, при x 1
каких значениях m прямая y m не имеет с графиком ни одной общей точки.
![]() x2 2x x
x2 2x x
(№ 324547) Постройте график функции y и определите, при x 2
каких значениях m прямая y m не имеет с графиком ни одной общей точки.
x2 4x, если x 1,
(№ 324548) Постройте график функции y
x 6, если x 1
и определите, при каких значениях m прямая y m имеет с графиком ровно две общие точки.
6x x2, если x 1,
(№ 324549) Постройте график функции y
x 8, если x 1
и определите, при каких значениях m прямая y m имеет с графиком ровно две общие точки.
x2 9x 1
(№ 324550) Постройте
график функции y
![]() и
определите, при 1
x
и
определите, при 1
x
каких значениях k прямая y kx имеет с графиком ровно одну общую точку.
x3, если x 1,
(№ 324551) Постройте график функции y 1,5x 4,5, если 3 x 4, 1,5x7,5, если x 4
и определите, при каких значениях m прямая y m имеет с графиком ровно две общие точки.
x2 4x 4, если x 4,
(№ 324552) Постройте график функции y 16
![]() x
, если x 4
x
, если x 4
и определите, при каких значениях m прямая y m имеет с графиком одну или две общие точки.
4 x 1
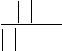
![]() (№
324553) Постройте график функции y
x
4x2
и определите, при каких значениях k прямая y kx не
имеет с графиком ни одной общей точки. (№ 324554) Постройте график функции y
12
x
1x
x
(№
324553) Постройте график функции y
x
4x2
и определите, при каких значениях k прямая y kx не
имеет с графиком ни одной общей точки. (№ 324554) Постройте график функции y
12
x
1x
x
![]() 1x
и определите,
1x
и определите,
при каких значениях m прямая y m имеет с графиком ровно одну общую точку.
(№ 324555) Постройте график функции y x 2 ![]() 4x5
4x5![]() и определите, при каких значениях m прямая y m имеет
с графиком ровно три общие точки.
и определите, при каких значениях m прямая y m имеет
с графиком ровно три общие точки.
![]() (№ 324556) Постройте график
функции y
x2 5x 3 x
2 6 и определите, при каких значениях m прямая y m имеет
с графиком ровно три общие точки.
(№ 324556) Постройте график
функции y
x2 5x 3 x
2 6 и определите, при каких значениях m прямая y m имеет
с графиком ровно три общие точки.
![]() (№ 324557) Постройте график
функции y
4 x
1 x2 4x 3 и определите, при каких значениях m
прямая y m
имеет с графиком ровно три общие точки.
(№ 324557) Постройте график
функции y
4 x
1 x2 4x 3 и определите, при каких значениях m
прямая y m
имеет с графиком ровно три общие точки.
![]() (№ 324558) Постройте график
функции y
x x 24x и
определите, при каких значениях m прямая y m имеет
с графиком ровно две общие точки.
(№ 324558) Постройте график
функции y
x x 24x и
определите, при каких значениях m прямая y m имеет
с графиком ровно две общие точки.
![]() (№ 324559) Постройте график
функции y
x x 3
x x
и определите, при каких значениях m прямая y m имеет
с графиком ровно две общие точки.
(№ 324559) Постройте график
функции y
x x 3
x x
и определите, при каких значениях m прямая y m имеет
с графиком ровно две общие точки.
(№ 324560)
Постройте график функции y
![]() 22xx21x и определите,
при каких значениях k прямая y
kx имеет с графиком ровно одну общую точку.
22xx21x и определите,
при каких значениях k прямая y
kx имеет с графиком ровно одну общую точку.
![]() (№ 324561) Постройте график
функции y x
2 4
x 2x
и определите, при каких значениях m прямая y m имеет
с графиком не менее одной, но не более трёх общих точек.
(№ 324561) Постройте график
функции y x
2 4
x 2x
и определите, при каких значениях m прямая y m имеет
с графиком не менее одной, но не более трёх общих точек.
(№ 324562) Отрезки ![]() лежат на параллельных прямых, а
отрезки
лежат на параллельных прямых, а
отрезки ![]() и
и ![]() пересекаются в точке
пересекаются в точке ![]() .
Найдите
.
Найдите ![]() , если
, если ![]() .
.
(№ 324563) Прямая, параллельная
стороне ![]() треугольника
треугольника ![]() , пересекает стороны
, пересекает стороны ![]() в точках
в точках ![]() соответственно.
Найдите
соответственно.
Найдите ![]() , если
, если
![]() .
.
![]() (№ 324564)
Прямая, параллельная стороне
(№ 324564)
Прямая, параллельная стороне ![]() треугольника
треугольника ![]() , пересекает стороны и
в точках и соответственно. Найдите
, пересекает стороны и
в точках и соответственно. Найдите ![]() , если
, если
![]() .
.
(№ 324565) Катеты прямоугольного треугольника равны 18 и 24. Найдите высоту, проведѐнную к гипотенузе.
(№ 324566) Точка ![]() является основанием высоты,
проведѐнной из вершины прямого угла
является основанием высоты,
проведѐнной из вершины прямого угла ![]() треугольника
треугольника ![]() к
гипотенузе
к
гипотенузе ![]() . Найдите
. Найдите ![]() , если
, если
![]() .
.
![]() (№ 324567)
Прямая, параллельная основаниям трапеции
(№ 324567)
Прямая, параллельная основаниям трапеции ![]() , пересекает еѐ
боковые стороны и в точках и соответственно. Найдите длину отрезка
, пересекает еѐ
боковые стороны и в точках и соответственно. Найдите длину отрезка ![]() ,
если
,
если ![]() .
.
![]() (№
324568) Найдите боковую сторону трапеции , если углы
(№
324568) Найдите боковую сторону трапеции , если углы ![]() и
и ![]() равны
соответственно
равны
соответственно ![]() .
.
![]() (№
324569) Биссектриса угла параллелограмма пересекает сторону
(№
324569) Биссектриса угла параллелограмма пересекает сторону ![]() в точке
в точке ![]() .
Найдите периметр параллелограмма, если
.
Найдите периметр параллелограмма, если ![]() .
.
![]()
![]() (№ 324570) Биссектрисы углов и
параллелограмма
(№ 324570) Биссектрисы углов и
параллелограмма ![]() пересекаются в точке, лежащей на стороне
. Найдите , если
пересекаются в точке, лежащей на стороне
. Найдите , если ![]() .
.
(№ 324571) Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 15, а одна из диагоналей ромба равна 60. Найдите углы ромба.
(№ 324572) Высота ![]() ромба
ромба ![]() делит сторону
делит сторону ![]() на
отрезки
на
отрезки ![]() и
и
![]() . Найдите высоту ромба.
. Найдите высоту ромба.
![]() (№ 324573)
Биссектрисы углов
(№ 324573)
Биссектрисы углов ![]() при боковой стороне
при боковой стороне ![]() трапеции
трапеции ![]() пересекаются
в точке . Найдите , если
пересекаются
в точке . Найдите , если ![]() .
.
1
(№ 324574) Отрезки ![]() являются хордами окружности.
Найдите длину хорды
являются хордами окружности.
Найдите длину хорды ![]() , если
, если ![]() , а расстояния от центра
окружности до хорд
, а расстояния от центра
окружности до хорд ![]() и
и ![]() равны соответственно 12
и 5.
равны соответственно 12
и 5.
(№ 324575) В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 5.
(№ 324576) В трапецию, сумма длин боковых сторон которой равна 16, вписана окружность. Найдите длину средней линии трапеции.
![]() (№
324577) Углы и треугольника
(№
324577) Углы и треугольника ![]() равны соответственно
равны соответственно ![]() . Найдите
. Найдите ![]() ,
если радиус окружности, описанной около треугольника
,
если радиус окружности, описанной около треугольника ![]() , равен 8.
, равен 8.
(№ 324578) Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся, как 6:7:23. Найдите радиус окружности, если меньшая из сторон треугольника равна 12.
![]()
![]() (№ 324579) Окружность, вписанная в
треугольник
(№ 324579) Окружность, вписанная в
треугольник ![]() , касается его сторон в точках , и .
Найдите углы треугольника
, касается его сторон в точках , и .
Найдите углы треугольника ![]() , если углы треугольника равны , и .
, если углы треугольника равны , и .
![]()
![]() (№ 324580) Точка
(№ 324580) Точка ![]() является
основанием высоты
является
основанием высоты ![]() , проведенной из вершины прямого угла
, проведенной из вершины прямого угла ![]() прямоугольного
треугольника
прямоугольного
треугольника ![]() . Окружность с диаметром
. Окружность с диаметром ![]() пересекает
стороны
пересекает
стороны ![]() в точках и
соответственно. Найдите , если .
в точках и
соответственно. Найдите , если .
(№ 324581) Окружность с центром на стороне ![]() треугольника
треугольника
![]() проходит
через вершину
проходит
через вершину ![]() и касается прямой
и касается прямой ![]() в точке
в точке ![]() .
Найдите диаметр окружности, если
.
Найдите диаметр окружности, если ![]() .
.
![]()
![]()
![]()
![]() (№ 324582) Окружность пересекает
стороны и треугольника в точках и соответственно и проходит через вершины
и . Найдите длину отрезка
(№ 324582) Окружность пересекает
стороны и треугольника в точках и соответственно и проходит через вершины
и . Найдите длину отрезка ![]() , если
, если ![]() , а сторона в 1,5 раза
больше стороны .
, а сторона в 1,5 раза
больше стороны .
2
1. Основания BC и AD трапеции ABCD равны соответственно 5 и 20,
BD 10. Докажите,
что треугольники ![]() подобны.
подобны.
2. В выпуклом четырёхугольнике ABCD углы BCA и BDA равны. Докажите, что углы ABD и ACD также равны.
3. Докажите, что отрезок, соединяющий середины оснований трапеции, делит её на две равные по площади части.
4. На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади трапеции.
5. Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AB и CD четырёхугольника пересекаются в точке M . Докажите, что треугольники MBC и MDAподобны.
6. Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.
7. Точка E — середина боковой стороны AB трапеции ABCD. Докажите, что площадь треугольника ECD равна половине площади трапеции.
8. Высоты AA1 и BB1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы AAB1 1 и ABB1 равны.
9. Биссектрисы
углов ![]() параллелограмма ABCD
пересекаются в точке E стороны BC . Докажите, что E —
середина BC .
параллелограмма ABCD
пересекаются в точке E стороны BC . Докажите, что E —
середина BC .
10. В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке O . Докажите, что площади треугольников AOB и COD равны.
11. В треугольнике ABC с тупым углом ACB проведены высоты AA1 и BB1. Докажите, что треугольники ACB1 1 и ACB подобны.
12.
Через точку ![]() пересечения диагоналей параллелограмма
ABCDпроведена прямая, пересекающая стороны AB и CD в
точках P и T соответственно. Докажите, что BP DT .
пересечения диагоналей параллелограмма
ABCDпроведена прямая, пересекающая стороны AB и CD в
точках P и T соответственно. Докажите, что BP DT .
13. Биссектрисы углов B и C трапеции ABCD пересекаются в точке O , лежащей на стороне AD. Докажите, что точка O равноудалена от прямых AB, BC и CD.
14. Окружности с центрами в точках I и J пересекаются в точках A и B, причём точки I и J лежат по одну стороны от прямой AB. Докажите, что AB IJ .
1
15. Окружности с центрами в точках I и J не имеют общих точек. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении m n: . Докажите, что диаметры этих окружностей относятся также m n: .
16. Докажите, что медиана треугольника делит его на два треугольника, площади которых равны между собой.
2
 В выпуклом
четырёхугольнике
В выпуклом
четырёхугольнике ![]() диагональ является биссектрисой угла
диагональ является биссектрисой угла ![]() и
пересекается с диагональю в точке
и
пересекается с диагональю в точке ![]() . Найдите
. Найдите ![]() , если известно, что
около четырёхугольника можно описать окружность,
, если известно, что
около четырёхугольника можно описать окружность, ![]() .
.
В равнобедренную трапецию, периметр которой равен 120, а площадь равна 540, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
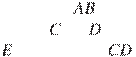
![]()
![]() В трапеции
В трапеции ![]() боковая
сторона перпендикулярна основанию . Окружность проходит через точки и и
касается прямой в точке . Найдите расстояние от точки до прямой , если , .
боковая
сторона перпендикулярна основанию . Окружность проходит через точки и и
касается прямой в точке . Найдите расстояние от точки до прямой , если , .
Биссектриса ![]() треугольника
треугольника ![]() делит сторону
делит сторону ![]() на
отрезки, и
на
отрезки, и

![]() . Касательная
к описанной окружности треугольника , проходящая
через точку
. Касательная
к описанной окружности треугольника , проходящая
через точку ![]() , пересекает прямую
, пересекает прямую ![]() в точке
в точке ![]() .
Найдите
.
Найдите
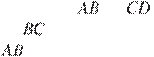
![]() Боковые стороны и
трапеции равны соответственно 8 и 10, а основание равно 2. Биссектриса угла
проходит через середину стороны . Найдите площадь трапеции.
Боковые стороны и
трапеции равны соответственно 8 и 10, а основание равно 2. Биссектриса угла
проходит через середину стороны . Найдите площадь трапеции.
В треугольнике ![]() биссектриса
биссектриса ![]() и медиана
и медиана ![]() перпендикулярны
и имеют одинаковую длину, равную 4. Найдите стороны треугольника
перпендикулярны
и имеют одинаковую длину, равную 4. Найдите стороны треугольника ![]() .
.
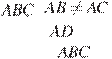 На стороне
На стороне ![]() остроугольного
треугольника ( ) как на диаметре построена полуокружность, пересекающая высоту
в точке ,
остроугольного
треугольника ( ) как на диаметре построена полуокружность, пересекающая высоту
в точке ,
![]()
![]() — точка
пересечения высот треугольника . Найдите
— точка
пересечения высот треугольника . Найдите
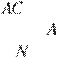 Точки
Точки ![]() лежат на
стороне треугольника
лежат на
стороне треугольника ![]() на расстояниях соответственно 4 и 15 от
вершины . Найдите радиус окружности, проходящей через точки
на расстояниях соответственно 4 и 15 от
вершины . Найдите радиус окружности, проходящей через точки ![]() и и
касающейся луча
и и
касающейся луча ![]() , если
, если
![]() .
.
Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 12, а площадь равна 18.
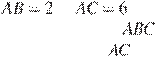 В треугольнике
В треугольнике ![]() известно,
что , , точка
известно,
что , , точка ![]() — центр окружности, описанной около
треугольника . Прямая
— центр окружности, описанной около
треугольника . Прямая ![]() , перпендикулярная прямой
, перпендикулярная прямой ![]() , пересекает
сторону в точке
, пересекает
сторону в точке ![]() . Найдите
. Найдите
![]() .
.
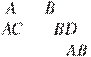 Окружности радиусов 1 и 4
касаются внешним образом. Точки и лежат на первой окружности, точки
Окружности радиусов 1 и 4
касаются внешним образом. Точки и лежат на первой окружности, точки ![]() — на второй. При
этом и — общие касательные окружностей. Найдите расстояние между прямыми и
— на второй. При
этом и — общие касательные окружностей. Найдите расстояние между прямыми и
![]() .
.
![]()
![]() Четырёхугольник со
сторонами и вписан в окружность. Диагонали и пересекаются
в точке , причём . Найдите радиус окружности, описанной около этого
четырёхугольника.
Четырёхугольник со
сторонами и вписан в окружность. Диагонали и пересекаются
в точке , причём . Найдите радиус окружности, описанной около этого
четырёхугольника.
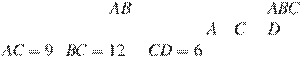
![]() На стороне треугольника
взята точка так, что окружность, проходящая через точки , и , касается прямой .
Найдите
На стороне треугольника
взята точка так, что окружность, проходящая через точки , и , касается прямой .
Найдите ![]() , если
, если
, и .
![]() В параллелограмме
В параллелограмме ![]() проведена
диагональ . Точка
проведена
диагональ . Точка ![]() является центром окружности, вписанной в
треугольник . Расстояния от точки
является центром окружности, вписанной в
треугольник . Расстояния от точки ![]() до точки
до точки ![]() и прямых
соответственно равны 10, 8 и 6. Найдите
и прямых
соответственно равны 10, 8 и 6. Найдите
![]() площадь параллелограмма
площадь параллелограмма
Основания трапеции относятся как 1:3. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. В каком отношении эта прямая делит площадь трапеции?
Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 2.
Углы при одном из оснований трапеции равны ![]() , а отрезки,
соединяющие середины противоположных сторон трапеции равны 11 и 10. Найдите
основания трапеции.
, а отрезки,
соединяющие середины противоположных сторон трапеции равны 11 и 10. Найдите
основания трапеции.
Найдите площадь трапеции, диагонали которой равны 3 и 4, а средняя линия равна 2,5.
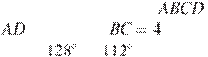 Середина
Середина ![]() стороны
стороны ![]() выпуклого
четырехугольника равноудалена от всех его вершин. Найдите , если
, а углы
выпуклого
четырехугольника равноудалена от всех его вершин. Найдите , если
, а углы ![]() и
и ![]() четырёхугольника равны
соответственно и .
четырёхугольника равны
соответственно и .
![]()
![]() В
треугольнике биссектриса угла
В
треугольнике биссектриса угла ![]() делит высоту, проведённую из вершины , в
отношении 5:4, считая от точки . Найдите радиус окружности, описанной около
треугольника
делит высоту, проведённую из вершины , в
отношении 5:4, считая от точки . Найдите радиус окружности, описанной около
треугольника ![]() , если .
, если .
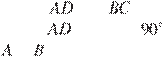 В
трапеции
В
трапеции ![]() основания и равны соответственно 36 и
12, а сумма углов при основании равна . Найдите радиус окружности, проходящей
через точки и и касающейся прямой
основания и равны соответственно 36 и
12, а сумма углов при основании равна . Найдите радиус окружности, проходящей
через точки и и касающейся прямой ![]() , если
, если ![]() .
.
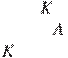 Две касающиеся внешним
образом в точке окружности, радиусы которых равны 5 и 15, вписаны в угол с
вершиной . Общая касательная к этим окружностям, проходящая через точку ,
пересекает стороны угла в точках
Две касающиеся внешним
образом в точке окружности, радиусы которых равны 5 и 15, вписаны в угол с
вершиной . Общая касательная к этим окружностям, проходящая через точку ,
пересекает стороны угла в точках
![]()
![]()
![]()
![]() и
. Найдите радиус окружности, описанной около треугольника
и
. Найдите радиус окружности, описанной около треугольника ![]() . (№
324621) Биссектрисы углов и параллелограмма пересекаются в точке .
Найдите площадь параллелограмма, если , а расстояние от точки до стороны
. (№
324621) Биссектрисы углов и параллелограмма пересекаются в точке .
Найдите площадь параллелограмма, если , а расстояние от точки до стороны ![]() равно
4.
равно
4.
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 40:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 12.
![]() В
треугольнике на его медиане
В
треугольнике на его медиане ![]() отмечена точка так,
что
отмечена точка так,
что
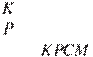 .
Прямая пересекает сторону
.
Прямая пересекает сторону ![]() в точке . Найдите
в точке . Найдите
отношение
площади треугольника ![]() к площади четырёхугольника .
к площади четырёхугольника .
![]()
![]() Из вершины прямого угла
Из вершины прямого угла ![]() треугольника
проведена высота . Радиус окружности, вписанной в треугольник , равен 8,
тангенс угла равен
треугольника
проведена высота . Радиус окружности, вписанной в треугольник , равен 8,
тангенс угла равен ![]() . Найдите радиус вписанной окружности
треугольника
. Найдите радиус вписанной окружности
треугольника ![]() .
.
![]()
![]() Медиана и биссектриса
Медиана и биссектриса ![]() треугольника
пересекаются в точке
треугольника
пересекаются в точке ![]() , длина стороны относится к длине
стороны как 9:7. Найдите отношение площади треугольника
, длина стороны относится к длине
стороны как 9:7. Найдите отношение площади треугольника ![]() к площади
четырёхугольника
к площади
четырёхугольника ![]() .
.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.