МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ - Тема: Составление интерполяционных формул Лагранжа, Ньютона, нахождение интерполяционных многочленов сплайнами.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Тема:

Составление интерполяционных формул Лагранжа, Ньютона, нахождение интерполяционных многочленов сплайнами.

Цель работы:

-          применить теоретический материал по данной теме через решение упражнений;

-          применить умения составлять интерполяционные формулы Лагранжа, Ньютона.

Оборудование:

1. Рабочая тетрадь в клетку.

2. Раздаточный материал: инструкционные карты-20шт.

3. Калькулятор простой.

Задание:

Вариант 1

1. Построить по имеющимся данным интерполяционный многочлен Лагранжа и естественные кубические сплайны.

Вычислить значения интерполяционного многочлена Лагранжа и естественных кубических сплайнов в точках . Оценить погрешность вычислений.

2. Вычислить значения функции в точках  , используя интерполяционную формулу Ньютона. Оценить погрешность вычислений.

3. Постройте кубический сплайн для функции  заданной таблицей

Вариант 2

1. Построить по имеющимся данным интерполяционный многочлен Лагранжа и естественные кубические сплайны.

Вычислить значения интерполяционного многочлена Лагранжа и естественных кубических сплайнов в точках . Оценить погрешность вычислений.

2. Вычислить значения функции в точках  , используя интерполяционную формулу Ньютона. Оценить погрешность вычислений.

3. Постройте кубический сплайн для функции  заданной таблицей

Порядок выполнения:

1.      Внимательно прочитать тему и цель практической работы.

2.      Изучить учебный материал по теме.

3.      Ответить на вопросы.

4.      Выполнить задания.

5.      Подготовить отчет.

Пояснения к работе (учебный материал):

Постановка задач интерполирования функции.

            Предположим, что в результате некоторого эксперимента для конечного набора значений  величины  из отрезка

получаем набор значений  величины y (табл. 1). Точки  в этом случае называются узлами. Если расстояние  является постоянным (т.е. не зависящем от i), то сетка значений, представленная табл. 1, называется равномерной.

            Если допустить, что между x и y существует функциональная зависимость , можно поставить вопрос о поиске аналитического представления функции F. Подобная задача может возникнуть даже тогда, когда аналитическое выражение для некоторой функции y=F(x), имеется, однако оно оказывается малопригодным для решения задачи, потому что операция, которую требуют осуществить над этой функцией, трудновыполнима. Задачу построения приближающей функции в общем смысле называют аппроксимацией.

            Классический подход к численному решению задачи аппроксимации заключается в том, чтобы опираясь на информацию о функции F, по некоторому алгоритму подобрать функцию G, в определённом смысле «близкую» к F. Чаще всего эта задача решается с помощью многочленов. Вычисления значений многочлена легко автоматизировать, производная и интеграл от многочлена в свою очередь так же являются многочленами, что упрощает работу.

            Простейший способ оценки «близости»  и  основывается на требовании строгого совпадения их значений в точках , т.е. . В этом случае способ аппроксимации функций называют интерполяцией, а процедуру вычисления значений

Таблица 1.

 с помощью  в точках, не являющихся узлами сетки, называется интерполированием.

Пусть известные значения некоторой функции  образуют таблицу вида табл. 1. Будем решать задачу интерполирования этой функции с помощью построения интерполяционного многочлена n-й степени:

                                                                                              (1)

который в узлах  принимает табличные значения :

                                                                                        (2)

Условия интерполяции (4.2) приводят к системе из  линейных алгебраических уравнений с  неизвестными – коэффициентами многочлена:

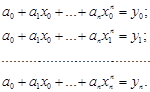                                                                                                               (3)

            Решая эту систему относительно неизвестных , мы получим аналитическое выражение полинома (1). Система (3) всегда будет иметь единственное решение, поскольку её определитель, известный в алгебре как определитель Вандермонда:

,

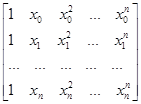составленный из попарно различных значений элементов  (различными они в данной ситуации будут всегда), не равен нулю. Отсюда и вытекают существование и единственность решения системы (3) и, следовательно, существование и единственность многочлена (1).

            Совершенно очевидно, что интерполяционный многочлен меньшей степени не существует, а большей существует, но не единственен. Поэтому интерполяция стандартно производится многочленами, степень которых на единицу меньше числа узлов. Описанный приём можно использовать и для практического решения задачи построения интерполяционного многочлена.

Интерполяционный многочлен Лагранжа.

Организация вычислений по формуле Лагранжа.

Пусть функция  задана табл. 1. Построим многочлен , степень которого не выше, чем n, и для которого выполнены условия интерполяции:

                                                                          (4)

Будем искать  в виде

                                                                                       (5)

где   - многочлен степени n, причем

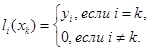                                                                                                               (6)

            Очевидно, что требование (6) с учетом (5) вполне обеспечивает выполнение условий (4).

            Многочлены  составим следующим образом:

                                                    (7)

где  - коэффициент, значение которого найдём из первой части условия (6):

(заметим, что ни один множитель в знаменателе не равен нулю). Подставим  в (7) и далее с учетом (5) окончательно имеем

                                                        (8)

            Это и есть интерполяционный многочлен Лагранжа. По таблице исходной функции F формула (8) позволяет довольно просто составить «внешний вид» многочлена.

Интерполяционные формулы Ньютона.

Рассмотрим другой способ построения интерполяционного многочлена. При этом, однако, не следует забывать, что по заданной таблице, содержащей значения функции в  узлов, интерполяционный многочлен n-й степени единственен и поэтому «новые» интерполяционный многочлены отличаются от многочлена Лагранжа, построенного по той же таблице, лишь внешним видом. Тем не менее они представляют ценность, поскольку вид (т.е. форма записи) многочлена определяет порядок и объем вычислений, что в численных методах существенно.

Часто интерполирование ведётся для функций, заданных равномерными сетками, когда шаг таблицы  является величиной постоянной. Для таких таблиц построение интерполяционных формул заметно упрощается, и мы ограничиваемся получением интерполяционных формул Ньютона лишь эля этого случая.

Конечные разности.

Пусть функция задана таблицей вида табл.1 с постоянным шагом. Разности между значениями функций в соседних узлах интерполяции называется конечными разновидностями первого порядка:

Из конечных разностей первого порядка образуются конечные разновидности второго порядка:

Таблица 4.

Продолжая этот процесс, можно по заданной таблице функций составить таблицу конечных разностей (табл. 4).

Конечные разности любого порядка могут быть представлены через значения функций. Действительно, для разностей первого порядка это следует из определения. Для разностей второго порядка имеем

Аналогично для разностей третьего порядка:

Методом математической индукции можно доказать, что

                                                        (10)

Первая интерполяционная формула Ньютона

Пусть для функции, заданной таблицей с постоянным шагом, составлена таблица конечных разностей (см. табл. 4). Будем искать интерполяционный многочлен в виде:

                  (11)

Это многочлен n-й степени. Значения коэффициентов  найдем из условия совпадения значений исходной функции и многочлена в узлах.

Полагая  из (11) находим , откуда . Далее, полагая , получаем , откуда .

При имеем  т.е. , или , откуда .

Проведя аналогичные выкладки, можно получить

Методом полной математической индукции можно доказать, что в общем случае выражение для  будет иметь следующий вид:

                                                                                                                        (12)

Подставим теперь (12) в выражение для многочлена (11):

           (13)

Часто эта формула записывается в несколько ином виде. Введем вместо переменной x новую переменную l:  или . Тогда ,

и т.д. После этого формула (13) принимает вид

             (14)

Формула (14) называется первой интерполяционной формулой Ньютона. Эта формула традиционно применяется для интерполирования в начале отрезка интерполяции, для значений t в интервале (0, 1). Первую интерполяционную формулу Ньютона называют по этой причине формулой для интерполирования вперёд. Заметим, что путём переопределения узлов за начальное значение  можно принимать любое табличное значение аргумента x (отбросив «лишние» узлы слева).

Вторая интерполяционная формула Ньютона

Когда значение аргумента находится ближе к концу отрезка интерполяции, применять первую интерполяционную формулу становится невыгодно. В этом случае применяется формула для интерполирования назад – вторая интерполяционная формула Ньютона:

                 (15)

Как и для первой формулы Ньютона, коэффициенты  находятся из условия совпадения значений функций и интерполяционного многочлена в узлах:

                                                                                                                  (16)

Подставляя (16) в (15) и переходя к переменной , получим окончательный вид второй интерполяционной формулы Ньютона:

         (17)

Функция  называется интерполяционным сплайном порядка  для функции  заданной таблицей

если:

1) на каждом отрезке       является многочленом порядка      

2)  и её производные до -го порядка включительно непрерывны на  

3)   , -непосредственно условие интерполяции.

Можно доказать, что эти условия достаточны для существования сплайна порядка  но не гарантируют его единственности.

Остановимся на построении наиболее популярных в практике аппроксимации функций кубических сплайнах. Согласно определению кубический сплайн  можно представить в виде

                                                                                                             (18)

где каждый из – многочлен третьей степени:

                              (19)

Привязку номера многочлена к узлам интерполяции помогает проследить следующая схема:

Последний пункт определения сплайна в сочетании с формулой (2) позволяет немедленно найти коэффициенты  или

                                                                                                                                 (20)

Условие непрерывности  в каждом узле приводит к равенствам  В развернутом виде с учетом (19) эти равенства примут вид

                     (21)

Введем обозначение  Понижая в равенствах (4) индекс на единицу (т.е. заменяя  на  что по существу ровно ничего не значит кроме изменения диапазона значений величины ) и учитывая (20), получим:

                                                      (22)

Условие непрерывности первой производной кубического сплайна, входящее в его определение, сводится к требованию  Дифференцируя формулу (2) и пользуясь введенными раннее обозначениями, получим

                                        (23)

Осталось использовать непрерывность второй производной сплайн-функции, т.е. условие  Оно порождает равенства

                                                   (24)

Совокупность равенств (22) – (24) образует систему  линейных алгебраических уравнений относительно  неизвестных  Для однозначной разрешимости её следует доопределить. Наиболее распространённый способ доопределения – потребность «гладкости» второй производной сплайна на концах отрезка:  что в принятых обозначениях сводится к равенствам  или с учетом (21),

                                                                                                                      (25)

Отметим, что первое из уравнений (25) совпадает формально с (24) при  если ввести коэффициент  (которого нет на самом деле в наборе ) и положить его равным нулю.

На практике удобно не решать непосредственно систему (22) – (25), а предварительно исключить из нее все неизвестные каких-либо двух групп. Начнем с исключения совокупности переменных  Для этого выразим  из (22):

                                            (26)

Перепишем (26), понизив индекс на единицу:

                                       (27)

Вычтем (26) из (27) и подставим полученную разность  в (23). После простых преобразований получим

                   (28)

Теперь исключим из (28) величины  Для этого выразим  из (24)

                                               (29)

Подставим это в (28) (понизив там, где это необходимо, индекс). Получим

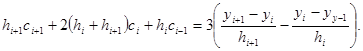                     (30)

Система (30) содержит лишь неизвестные  и является системой линейных алгебраических уравнений с трехдиагональной матрицей. При этом необходимое для вычислений значение величины  уже известно – см. (25).

Найдя неизвестные  по формулам (29) и первого из уравнений (25) найдем неизвестные  а затем с помощью (29) неизвестные  На этом построение кубического сплайна завершится.

При выполнении практической работы рассмотрите следующие примеры:

Пример 1.

Построим интерполяционный многочлен Лагранжа для функции, заданной таблицей значений:

            Из таблицы следует, что  (т.е. степень многочлена будет не выше 2); здесь . Используя формулу (8), получаем

.

            Используя обозначение , формуле (8) можно придать более сжатый вид. Продифференцируем  по x:

            При  имеем

            Тогда формула Лагранжа (8) принимает вид

                                                                                                   (9)

            Непосредственное применение формулы Лагранжа приводит к большому числу однотипных вычислений. Организация вычислений существенно улучшается, если пользоваться специальной вычислительной схемой.

            В табл. 2 показано построение такой схемы для 4-ч узлов . Таблица составляется заново для каждого нового значения аргумента x.

            Заполнение таблицы начинается с того, что вычисляются и заносятся в соответствующие клетки все элементарные разности (см. табл. 2). Вслед за этим вычисляются произведения  разностей по строкам:

 и т.д.

Таблица 2.

            Использованное в табл. 2 обозначение  - это знаменатель в формуле Лагранжа (9), т.е.

С учетом этого обозначения формула Лангранжа имеет вид

Все необходимые значения последовательно получаются в таблице. Сумма S образуется сложением элементов последнего столбца. Для получения окончательного значения  достаточно умножить S  на произведение  (произведение диагональных разностей таблицы).

Пример 2.

Имеется таблица значений некоторой функции:

Требуется получить значение этой функции в точке , пользуясь интерполяционным многочленом Лагранжа.

Вычисления приведённые в табл. 3. Для нахождения окончательного результата сумма значений последнего столбца умножается на произведение диагональных разностей: .

Таблица 3.

Пример 3.

Функция y(x) задана равномерной сеткой, для которой вычислена таблица конечных разновидностей (при вычислении ограничились разностями второго порядка, поскольку они не только малы, но и практически постоянны):

Вычислим значение .

Поскольку значение  находится в начале таблицы, применим интерполирование вперёд, при этом воспользуемся первой интерполяционной формулой Ньютона в форме (14). Вычислим в начале  Далее в соответствии с формулой (14) получим

Пример 4.

Для таблично заданной функции y(x) из примера 3 вычислим значение

Поскольку значение x находится в конце таблицы, воспользуемся вторым интерполяционным многочленом Ньютона, приняв . Вычислим в начале . Далее в соответствии с формулой (17) получим

Пример 5.

Построить по имеющимся данным интерполяционный многочлен Лагранжа и естественные кубические сплайны.

Вычислить значения интерполяционного многочлена Лагранжа и естественных кубических сплайнов в точках . Оценить погрешность вычислений.

Общий вид многочлена Лагранжа, использующегося для целей глобальной полиномиальной интерполяции, следующий:

На отыскание коэффициентов данного полинома таким способом связано с вычислением определителя Вандермонда, что представляет крайне плохо обусловленную задачу.

Поэтому интерполяционный многочлен Лагранжа выражают так:

,

где  выглядит следующим образом:

В нашем случае таблично заданной функции  (нумерация начинается с нуля). Следовательно:

где

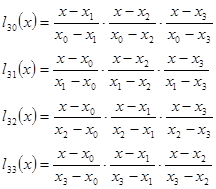
Теперь конструируем многочлен Лагранжа и убедимся, что сделали это правильно.

Для этого просчитаем значения  и убедимся, что они совпадают с табличными.

Проделав эту процедуру, и, убедившись, что всё считается верно найдем значения .

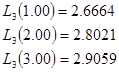
Далее найдём значения в этих же точках, но используя при этом естественные кубические сплайны. Естественные кубические сплайны – это тип сплайнов, которые получаются в предположении (добавка к системе уравнений для наклонов сплайна), что вторая производная в крайних точках таблицы  заданной функции обращается в ноль.

Общий вид системы для получения наклонов кубических сплайнов имеет вид:

Данная система для нашей таблично заданной функции состоит из двух уравнений: при.

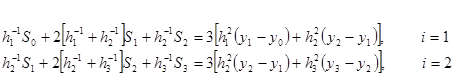
Поскольку неизвестных в системе – четыре , а уравнений – два, то систему нужно доопределить ещё двумя уравнениями. Эти добавочные два уравнения берутся из граничных условий соответствующего типа .

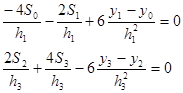
Стало быть, наша полная система для нахождения наклонов сплайнов имеет вид:

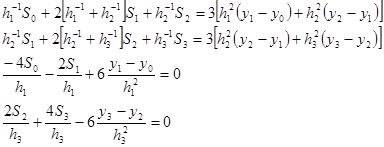
Инициализируя  соответствующими числовыми значениями и решая систему получившихся линейных уравнений, находим:

Общий вид сплайна совпадает с интерполяционным кубическим многочленом Эрмита.

Для того, чтобы рассчитать какого-либо значение, необходимо определить номер частичного отрезка, которому принадлежит это значение.

Сначала проверим, правильно ли мы нашли коэффициенты сплайна. Для этого просчитаем значения сплайна в табличных точках:

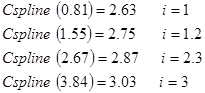
Убедившись, что коэффициенты найдены правильно, найдём значения в интересующих нас точках:

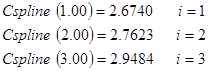
Сравним полученные результаты с результатами глобальной интерполяции при помощи полинома Лагранжа:

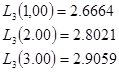
Поскольку точная аналитическая зависимость для таблично заданной функции неизвестна (вообще говоря, её может и не быть), то оценить  погрешность интерполяции с применением стандартных формул не удаётся.

Но, тем не менее, разность соответствующих значений, даваемых полиномом Лагранжа и сплайнами, найти возможно.

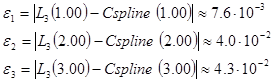
Как видно, наименьшая разница в рассчитываемых значениях наблюдается при .

Пример 6.

Вычислить значения функции в точке , используя интерполяционную формулу Ньютона для интерполяции вперёд. Оценить погрешность вычислений.

Сначала строим таблицу конечных разностей.

Поскольку у нас имеется пять таблично заданных точек, то последней и единственной в этой таблице будет- конечная разность четвертого порядка в точке .

Таблица конечных разностей записывается следующим образом:

Тем самым, общий вид многочлена Ньютона для интерполяции вперёд следующий:

Убедимся, что интерполяционный многочлен Ньютона построен правильно.

Для этого подсчитаем его значения во всех таблично заданных точках. Например, если .

И так для всех таблично заданных точек.

Теперь найдем значение при помощи многочлена Ньютона в интересующей нас точке .

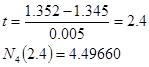
Для того, чтобы оценить погрешность этого результата, построим многочлен , содержащий на одну конечную разность меньше, чем , и найдём значение .

Погрешность приближения составляет:

Проверив, какие цифры ответа  с учетом погрешности  являются верными в строгом смысле, запишем ответ:

Используя МНК, найти приближающую линейную и квадратичную зависимость для набора экспериментальных значений x и y.

Пусть у нас имеется таблично заданная функция.

Подсчитаем суммы, которые нам потребуются для того, чтобы составить системы линейных уравнений, из которых мы сможем найти коэффициенты аппроксимирующей линейной и квадратичной зависимости.

Для многочлена первой степени система имеет вид:

Откуда  и .

Для многочлена второй степени система имеет вид:

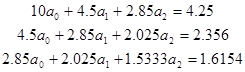
Откуда, .

Пример 7.

Построить кубический сплайн для функции  заданной таблицей

с дополнительными условиями:  Найти с помощью  значение функции  при  (заметим, что в основу таблицы положена функция ).

Учитывая, что  система (12) сведется всего к двум уравнениям:

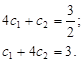
Ее решение (будем в этом простейшем примере вести решение в простых дробях):

Далее находим по (11) значение коэффициентов

Теперь по формулам (9) находим коэффициенты

Поскольку значения коэффициентов   – значения функции из таблицы (см. (3)), то сплайн построен:

Несложно проверить, что условия непрерывности  в точках  и  выполнены.

Для нахождения значения интерполирующей функции в заданной точке  заметим, что  и поэтому используем многочлен  Отметим для сопоставления с той же точностью значение функции, положенной в основу данного примера:

Вопросы для закрепления теоретического материала к практическому занятию:

1. Что такое интерполяция?

2. Каков общий вид обобщённого многочлена?

3. Записать общий вид многочлена Лагранжа.

4. Что такое интерполяция с кратными узлами?

5. Как рассчитать погрешность интерполяции?

6. Что такое конечная разность?

7. Что такое разделенная разность?

8. Записать интерполяционный полином Ньютона с конечными разностями.

9. Записать интерполяционный полином Ньютона с разделенными разностями.

10. Какая функция называется интерполяционным сплайном?

Содержание отчета:

Название практической работы.

Учебная цель.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

Литература:

- Численные методы и программирование: Учебное пособие / В.Д. Колдаев; Под ред. Л.Г. Гагариной. - М.: ИД ФОРУМ: НИЦ Инфра-М, 2016. - 336 с…

- Гателюк, О. В. Численные методы : учеб. пособие для СПО / О. В. Гателюк, Ш. К. Исмаилов, Н. В. Манюкова. — М. : Издательство Юрайт, 2018. — 140 с. — (Серия : Профессиональное образование)

- Бахвалов Н.С., Лапин А.В., Чижонков Е.В. «Численные методы в задачах и упражнениях»/ Под ред. В.А.Садовничего – М.:Высш.шк.,2016

-  Вержбицкий В.М. «Численные методы. Математический анализ и обыкновенные дифференциальные уравнения» - М.: Высшая школа, 2017

- Волков Е.А. «Численные методы» - СПб.: Издательство «Лань», 2015

- Исаков В.Н. «Элементы численных методов» - М.: Издательский центр «Академия», 2016.

- Бахвалов Н.С., Лапин А.В., Чижонков Е.В.; Под ред. Садовничий В.А Численные методы в задачах и упражнениях: Учебное пособие /., - 4-е изд., (эл.) - М.:БИНОМ. Лаб. знаний, 2015. - 243 с.: ISBN 978-5-9963-2980-9 - Режим доступа: http://znanium.com/

- А.В. Гулин, О.С. Мажорова, В.А. Морозова Введение в численные методы в задачах и упражнениях : учеб. пособие /. — М. : ИНФРА-М, 2017. — 368 с. — (Высшее образование: Бакалавриат). - Режим доступа: http://znanium.com/

- Калиткин Н.Н., Численные методы: Учебное пособие / - 2-е изд., исправленное. - СПб:БХВ-Петербург, 2015. - 587 с. ISBN 978-5-9775-2575-6 - Режим доступа: http://znanium.com/catalog/product/94450.

Скачано с www.znanio.ru