Поделиться
Публикация является частью публикации:
методичка Теория вероятностей Документ Microsoft Office Word.docx
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«КЕРЧЕНСКИЙ ГОСУДАРСТВЕННЫЙ МОРСКОЙ
ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ»
Филиал ФГБОУ ВО «КГМТУ» в г. Феодосия
Цикловая комиссия технологии сварки и кораблестроения
МАТЕМАТИКА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ИЗУЧЕНИЮ ТЕМЫ «ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»
для специалистов среднего звена по специальности
22.02.06 Сварочное производство
26.02.02 Судостроение
Профиль: технический
Форма обучения: очная
Сидорова Людмила Валентиновна
Феодосия, 2017 г.
Составитель: Сидорова Л.В., преподаватель высшей категории дисциплины «МАТЕМАТИКА», председатель цикловой комиссии технологии сварки и кораблестроения филиала ФГБОУ ВО «КГМТУ» в г.Феодосия _
____________________
_________________________-----------------------____________
Рецензент: Зубрилин К.М. канд. физико - математических наук, доцент кафедры математических и естественно-научных дисциплин филиала ФГБОУ ВО «КГМТУ» в г.Феодосия
____________________
Методические указания рассмотрены и одобрены на заседании цикловой комиссии технологии сварки и кораблестроения филиала ФГБОУ ВО «КГМТУ» в г.Феодосия,
протокол № ____ от ____20 г.
Председатель цикловой комиссии ______________ Сидорова Л.В.
Методические указания утверждены на заседании методической комиссии СПО филиала ФГБОУ ВО «КГМТУ» в г.Феодосия,
протокол № ____ от_________20______г.
СОДЕРЖАНИЕ
1. Введение 4 стр.
2. Теоретическая часть 7 стр.
3. Примеры решения прикладных задач 32 стр.
4. Задания для самостоятельного решения 35 стр.
5. Литература 38 стр.
Необходимостью в наши дни становится непрерывное образование, что требует полноценной подготовки. Всё больше специальностей связаны с непосредственным применением математики и ее подразделов, в частности, теории вероятностей и математической статистики.
Содержание темы «Теория вероятностей и математическая статистика» способствует развитию математического кругозора, специально подобранные задачи обеспечивают развитие математического мышления.
Цели изучения темы:
· формирование у студентов интереса к математике;
· выявление и развитие математических способностей;
· интеллектуальное развитие студентов;
· формирование понимания основ теории вероятностей и математической статистики
Задачи:
В результате обучения студенты должны:
План изучения темы «Теория вероятностей и математическая статистика»:
- изучение теории - 6 часов;
- практические занятия - 10 часов;
- самостоятельная работа студентов - 6 часов.
Развитие теории вероятностей, а с нею и развитие понятия вероятности можно разбить на несколько периодов.
|
|
В этот период, начало которого
теряется в веках, ставились и решались элементарные задачи, которые позже
будут отнесены к теории вероятностей. Никаких специальных методов в этот
период не возникает. Этот период кончается работами Кардано, Пачоли, Тарталья
и др. С вероятностными представлениями мы встречаемся еще в античности. У
Демокрита, Лукреция Кара и других античных ученых и мыслителей мы находим
глубокие предвидения о строении материи с беспорядочным движением мелких
частиц (молекул), мы встречаем рассуждения о равновозможных исходах
(равновероятных) и т. п. |
|
|
Возникновение теории вероятностей как науки. К середине, XVII в.
вероятностные вопросы и проблемы, возникающие в статистической практике, в
практике страховых обществ, при обработке результатов наблюдений и в других
областях, привлекли внимание ученых, так как они стали актуальными
вопросами. В первую очередь это относится к
Б. Паскалю, П. Ферма и X. Гюйгенсу. В этот период вырабатываются первые
специфические понятия, такие, как математическое ожидание и вероятность (в
форме отношения шансов), устанавливаются и используются первые свойства
вероятности: теоремы сложения и умножения вероятностей. В это время теория
вероятностей находит свои первые применения в демографии, страховом деле, в
оценке ошибок наблюдения, широко используя при этом понятие вероятности.
Следующий период начинается с появления работы Я. Бернулли "Искусство предположений"
(1713), в которой впервые была строго доказана первая предельная
теорема — простейший случай закона больших чисел. . К этому периоду, который
продолжался до середины XIX в., относятся работы Муавра, Лапласа, Гаусса и др.
В центре внимания в это время стоят предельные теоремы. Теория вероятностей
начинает широко применяться в различных областях естествознания. И хотя в этот
период начинают применяться различные понятия вероятности (геометрическая
вероятность, статистическая вероятность), господствующее положение занимает, в
особенности после работ Лапласа, так называемое классическое определение
вероятности.
Следующий период развития теории вероятностей связан прежде всего с
Петербургской математической школой. За два столетия развития теории
вероятностей главными ее достижениями были предельные теоремы. Но не были
выяснены границы их применимости и возможности дальнейшего обобщения. Наряду с
огромными успехами, достигнутыми теорией вероятностей в предыдущий
период, были выявлены и существенные недостатки в ее обосновании, это в большой
мере относится к недостаточно четким представлениям о вероятности.
В теории вероятностей создалось положение, когда дальнейшее ее развитие
требовало уточнения основных положений, усиления самих методов исследования.
Это было осуществлено русской математической школой во главе с П. Л. Чебышевым.
Среди ее крупнейших представителей мы видим А. А. Маркова и А. М. Ляпунова. В
этот период в теорию вероятностей входят оценки приближений предельных теорем,
а также происходит расширение класса случайных величин, подчиняющихся
предельным теоремам. В это время в теории вероятностей начинают рассматривать
некоторые зависимые случайные величины (цепи Маркова).
Понятие вероятности получило большое распространение в естественных
науках, в первую очередь это относится к физике. Появляются работы Максвелла, а
затем Больцмана и Д. Гиббса. Их трудами создается статистическая физика. Но это
внедрение вероятностных методов и понятий в физику шло в довольно большом
отрыве от достижений теории вероятностей.
Развитие теории вероятностей в начале ХХ в. привело к необходимости пересмотра
и уточнения ее логических основ, в первую очередь понятия вероятности.
Следует иметь в виду и то, что к началу ХХ в. аксиоматический метод стал проникать
во многие области математики (работы Д. Гильберта, Пеано и др.), что также
оказало влияние на теорию вероятностей. В результате всего этого возникла
необходимость аксиоматизации теории вероятностей и ее основного понятия —
вероятности.
Современный период развития теории вероятностей начался с установления
аксиоматики. Этого, прежде всего, требовала практика, так как для успешного
применения теории вероятностей в физике, биологии и других областях науки, а
также в технике и военном деле необходимо было уточнить и привести в стройную
систему ее основные понятия. Благодаря аксиоматике теория вероятностей стала
абстрактно-дедуктивной математической дисциплиной, тесно связанной с другими
математическими дисциплинами. Это обусловило небывалую широту исследований по
теории вероятностей и ее применениям, начиная от хозяйственно-прикладных
вопросов и кончая самыми тонкими теоретическими вопросами теории информации и
теории случайных процессов.
Первые работы этого периода связаны с именами С. Н, Бернштейна, Р. Мизеса, Э.
Бореля. Окончательное установление аксиоматики произошло в 30-е годы ХХ в.
Анализ тенденций развития теории вероятностей позволил А. Н. Колмогорову
создать общепринятую аксиоматику.
В этот период понятие вероятности проникает почти во все сферы человеческой
деятельности, становясь одним из основных понятий современной науки. Возникают
самые различные определения вероятности, несводимые друг к другу. Многообразие
определений основных понятий — существенная черта современной науки, и понятие
вероятности не исключение.
§1. Комбинаторика
При решении задач из различных областей науки и практики часто приходится отвечать на вопрос: сколькими способами можно выполнить то, что требуется? Например, способами можно составить расписание на день из пяти различных предметов, если в классе изучается 14 предметов, или сколько различных трёхзначных чисел можно составить из трёх различных заданных цифр, не повторяя их, или сколько различных связей существует между атомами и молекулами определённого вещества, или сколько диагоналей имеет выпуклый десятиугольник?
В этих задачах речь идёт о тех или иных комбинациях объектов. Такие задачи получили название КОМБИНАТОРНЫЕ и для их решения существуют общие методы решения.
Раздел математики, в котором рассматриваются методы решения комбинаторных задач, называется КОМБИНАТОРИКА.
1.1 Основные понятия комбинаторики
Выбранные (или выбранные и размещённые) группы элементов называются соединениями.
Если все элементы, полученного множества разные - получаем множество без повторений, а если в полученном множестве элементы могут повторятся, то получаем множества с повторениями.
Решение комбинаторных задач базируется на двух основных правилах: правило суммы и правило произведения.
Правило суммы. Если на тарелке лежит 5 груш и 4 яблока, то выбрать один фрукт (то есть яблоко или грушу) можно 9 способами (5+4=9). В общем виде имеет место утверждение:
если элемент А можно выбрать m способами, а элемент В - n способами, то А или В можно выбрать m+n способами.
Правило произведения. Если в киоске продают ручки 5 видов и тетради 4 видов, то выбрать набор из ручки и тетради (то есть пару - ручка и тетрадь) можно 5 ∙ 4 = 20 способами, так как с каждой из 5 ручек можно взять одну из 4 тетрадей. В общем виде имеет место утверждение:
если элемент А можно выбрать m способами, а после этого элемент В - n способами, то А и В можно выбрать m∙n способами.
Это утверждение означает, что если для каждого из m элементов A можно выбрать в пару любой из n элементов B , то количество пар равно произведению m ∙ n.
Следовательно, если приходится выбирать или первый, или второй, или третий и т. д. элемент, количества способов выбора каждого элемента складываются, а когда приходится выбирать набор, в который входят и первый, и второй, и третий, и т. д. элементы, количества способов выбора каждого элемента перемножаются
1.2 Формулы перестановок, размещений и сочетаний.
Введём понятие УПОРЯДОЧЕННОГО МНОЖЕСТВА. Рассмотрим задачи:
1) Из тридцати учащихся класса нужно избрать секретаря и председателя классного собрания. Сколькими способами это можно сделать?
2) Из тридцати учащихся класса нужно выделить двух учащихся для дежурства в столовой. Сколькими способами это можно сделать?
Обе задачи комбинаторные. Однако, они различны по содержанию условия. Во второй задаче не имеет значения, в каком порядке будут названы дежурные, тогда как в первой задаче это существенно. Действительно из двух избранных учащихся один может быть председателем, а другой секретарём, или наоборот.
Следовательно, при решении комбинаторных задач приходится иметь дело с конечными множествами, для которых существенен порядок элементов. Такие множества называются упорядоченными.
Указать порядок размещения элементов в конечном множестве из n элементов означает поставить в соответствие каждому элементу данного множества определённое натуральное число от 1 до n.
Известные числовые последовательности
являются упорядоченными. Например, множества А=
и
В = 
такие, что А=В, если множества не упорядоченные, А
В,
если множества упорядоченные.
ПЕРЕСТАНОВКОЙ из n элементов называют любое упорядоченное множество из n элементов.
Упорядоченное множество - это такое множество, для которого указано, какой элемент находится на первом месте, какой - на втором месте, … , какой на n – ом месте.
Пример. Дано число 236. Множество
цифр 
-
уже упорядоченное. Можно составить перестановки без повторений: (2, 3,
6), (2, 6, 3), (3, 2, 6), (3, 6, 2), (6, 2, 3), (6, 3, 2) - всего
6 перестановок.
Количество перестановок без
повторений из n элементов обозначают 
(Р – первая буква французского слова permutation
–перестановка).
Значит Р3 = 6.
Формула числа перестановок без повторений из n элементов:
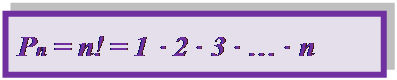
Задача. Сколькими способами 8 учащихся можно построить в колонну по одному?
Решение. Количество способов равно количеству перестановок из 8 элементов, так как учитывается порядок следования элементов и все 8 элементов выбираются.
Р8 = 8! = 1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 ∙ 7 ∙ 8 = 40 320 (способов).
Ответ: 40 320 способов построения.
РАЗМЕЩЕНИЕМ из n элементов по k без повторений называется любое упорядоченное множество из k элементов, состоящее из элементов n – элементного множества.
Например, из множества,
содержащего три цифры 
можно составить следующие размещения из двух элементов
без повторений: (1, 5), (1, 7), (5, 7), (5, 1), (7, 1), (7,
5).
Количество размещений из
n по k обозначается 
(читается «A из n по k», A - первая буква французского слова arrangement, что означает «размещение,
приведение в порядок»). Значит 
= 6.
Количество размещений из n по k без повторений вычисляется по формуле:
Задача. На соревнования
по лёгкой атлетике приехала команда из 12 спортсменок. Сколькими
способами тренер может определить, кто из них побежит в эстафете 4 
100 м на первом, на втором, на
третьем и четвёртом этапах?
Решение. Для спортсменок важно, в каком порядке они будут бежать, то есть учитывается порядок. В полученное соединение входят не все 12 заданных элементов. Следовательно, соответствующее соединение - размещение из 12 элементов по 4 без повторений, так как каждая спортсменка может бежать только на одном этапе.
= 12 ∙ (12-1) ∙(12-2) ∙ (12-3) = 12 ∙ 11
∙ 10 ∙ 9 = 11 880.
Ответ: 11 880 способов.
Если k = n имеем перестановки 
= 
. Поэтому формула числа размещений из n по k без
повторений может быть записана так:
Например, 
= 
= 
= 6! = 1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 = 720.
СОЧЕТАНИЕМ без повторений из n элементов по k называется любое k-элементное подмножество n-элементного множества.
Например, из множества 
можно составить следующие сочетания без повторений из трёх элементов:
,
,
,
.
Количество сочетаний без
повторений из n по k обозначается 
(читается «С из n по k», С - первая буква французского
слова combinaison, что означает сочетание. Значит 
= 4.
Количество сочетаний из n по k без повторений вычисляется по формуле:
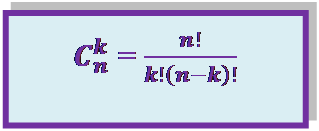
Свойства числа сочетаний без повторений.
1. 
= 
2.
= 1 
= 1
1.3 Вычисление числа сочетаний без повторения с помощью треугольника Паскаля.
Для вычисления числа сочетаний можно
применять формулу 
= 
, а можно
последовательно вычислять соответствующие значения, пользуясь свойством 
+ 
= 
.
Это равенство позволяет вычислять 
с помощью
специальной таблицы, которая называется треугольником Паскаля. Если
считать, что 
= 1, таблица будет
иметь следующий вид:
|
Значение
|
|
|
|
|
|
0 |
1 |
|
1 |
1 1 |
|
2 |
1 2 1 |
|
3 |
|
|
4 |
|
|
5 |
1 5 10 10 5 1 |
|
6 |
1 6 15 20 15 6 1 |
|
… |
. . . |
|
n |
|
Принцип составления треугольника Паскаля.
1. Каждая строка начинается с единицы и заканчивается единицей.
2. Если какая-нибудь строка уже заполнена, например третья, то в четвёртой строке надо записать:
ü На первом месте 1;
ü На втором запишем число, равное сумме двух чисел третьей строки стоящих над ним левее и правее.
ü ………. ;
ü На последнем месте пишем 1.
1.4 Формула Ньютона. Свойства биномиальных коэффициентов
Двучлен вида а + х называется БИНОМОМ.
Из курса алгебры известно
(а + х)1 = 1∙ а + 1 ∙ х;
(а+х)2 = а2 +2ах + х2 = 1 ∙ а2 +2 ∙ ах + 1 ∙ х2;
(а + х)3 = а3 + 3а2х + 3ах2 + х3 = 1 ∙ а3 + 3 ∙ а2х + 3 ∙ ах2 + 1 ∙ х3.
Можно заметить, что коэффициенты разложения степени бинома (а + х)n при n = 1, 2, 3, совпадают с числами в соответствующей строке треугольника Паскаля. Это свойство выполняется для любого натурального n, то есть справедлива формула
(a +x)n = 
an + 
an-1x + 
an-2x2 + 
an-3x3 + … + 
an-kxk + … + 
xn
Формулу называют биномом Ньютона.
Правая часть этого равенства называется разложением степени бинома (а +
х)n, а числа 
(при
k = 0, 1, 2, … ,n) называются биномиальными
коэффициентами.
Общий член разложения степени бинома имеет вид
T k+1
= 
an-kxk .
Записывая степень двучлена по формуле бинома Ньютона для небольших значений n, биномиальные коэффициенты можно записывать по треугольнику Паскаля.
|
Степень |
Значение
|
|
|
n |
|
|
|
(а + х)0 |
0 |
1 |
|
(а + х)1 |
1 |
1 1 |
|
(а + х)2 |
2 |
|
|
(а + х)3 |
3 |
|
|
(а + х)4 |
4 |
|
|
(а + х)5 |
5 |
1 5 10 10 5 1 |
|
(а + х)6 |
6 |
1 6 15 20 15 6 1 |
|
… |
… |
. . . |
|
|
n |
|
Например, (a +b)5 = a5 +5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5.
Если в формуле бинома Ньютона заменить х на -х, то получим формулу возведения в степень разности а –х, при этом в разложении перед нечётными степенями х будет стоять минус.
Например, (a -b)5 = a5 -5a4b + 10a3b2 - 10a2b3 + 5ab4 - b5.
Свойства биномиальных коэффициентов.
1. Число биномиальных коэффициентов (а следовательно и число слагаемых) в разложении n-ой степени бинома равно n+1.
2. Коэффициенты членов равноудалённых от концов разложения равны между собой.
3. Сумма всех биномиальных коэффициентов равна 2n.
4. Сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме биномиальных коэффициентов, стоящих на нечётных местах.
Например, (a -b)5 = a5 -5a4b + 10a3b2 - 10a2b3 + 5ab4 - b5.
1. Количество членов разложения 5+1=6.
2. Биномиальные коэффициенты первого и последнего равны 1; второго и предпоследнего равны 5; третьего от начала и третьего от конца равны 10.
3. 1 + 5 +10+5+1=32 = 25 - сумма всех биномиальных коэффициентов.
4. 1+10+5 = 16 – сумма всех биномиальных коэффициентов, стоящих на нечётных местах, 5+10+1 = 16 – сумма всех биномиальных коэффициентов, стоящих на чётных местах.
Вопросы для повторения.
1. Какие бывают множества по количеству элементов? Как они обозначаются?
2. Какими способами задаются множества?
3. Какие множества называются равными? К
4. Какое множество называется подмножеством данного множества?
5. Что называют пересечением двух множеств?
6. Что называют объединением двух множеств?
7. Что называют разностью двух множеств?
8. Какие задачи называют комбинаторными?
9. Что называют перестановкой из n элементов?
10. По какой формуле вычисляют число перестановок?
11. Что называют размещением из n элементов по m?
12. По какой формуле вычисляют число размещений из n элементов по m?
13. Что называют сочетанием из n элементов по m?
14. По какой формуле вычисляют число сочетаний из n элементов по m?
15. Что такое формула бинома Ньютона?
16. Назовите свойства биномиальных коэффициентов.
17. Как найти n- й член разложения Бинома Ньютона?
§ 2 Элементы теории вероятностей.
|
|
|
2.1 Понятие случайного события
В жизни и трудовой деятельности приходится иметь дело с событиями реального мира, зависящими от обстоятельств, которые либо неизвестны, либо не подлежат учёту. Например, нельзя предусмотреть, на какой билет выпадет выигрыш в будущем тираже лотереи, сколько зёрен даст определённый колос от посеянного зерна пшеницы, сколько выпускников школ города подадут заявления в наш филиал, будут ли среди деталей, изготовленных слесарем за смену бракованные и сколько.
События такого характера называются СЛУЧАЙНЫМИ. Теория вероятности занимается изучением случайных событий.
В природе нет ни одного физического явления, в котором бы не проявлялись явления случайности. Но в массовых однородных случайных событиях, то есть таких, которые могут неоднократно повторяться при выполнении одинаковых условий, независимо от человека, существуют закономерности, поддающиеся учёту.
|
Одновременно с массовыми случайными событиями существуют и единичные случайные события. Например, падение Тунгусского метеорита. Рассмотрим примеры, подтверждающие существование закономерностей в случайных массовых событиях Пример 1. Если бросить монету один раз, то нельзя предвидеть, какой стороной она выпадет - «гербом» или «числом». Нельзя увидеть никакой закономерности, если бросить монету 10 раз.
Ещё в XVIII веке известный французский естествоиспытатель Жорж Луи де БЮФФОН (1707 - 1782), бросив монету 4040 раз, получил 2048 выпадений «герба», английский математик и биолог Карл ПИРСОН (1857 – 1936), бросив монету 1 200 раз, получил 602 выпадения «герба» , а бросив 24 000 раз получил 12 120 выпадений «герба».
|
Примерами массовых событий является серия выстрелов одного стрелка из одной и той же винтовки, серийный выпуск ламп электроламповым заводом, а массовых случайных событий - попадание или промах в серии выстрелов, появление бракованных ламп в серийном выпуске электроламповым заводом.
|
Имя испытателя |
Количество бросков |
Количество выпадения «герба» |
|
Ж. БЮФФОН |
4040 |
2048 |
|
Ч. ПИРСОН |
1 200 |
602 |
|
24 000 |
12 120 |
С помощью проведения опыта, возможно предусмотреть его результат.
Умение предусмотреть ход опыта, в котором присутствуют элементы случайности, даёт возможность влиять на его результаты. Примером такого предвидения может быть история азартных игр, распространённых уже в семнадцатом веке.
Одна из них - игра в кости - состояла в том, что в стакан бросали два или три кубика, на гранях которых были нанесены от одной до шести точек. Каждый игрок бросал кости и подсчитывали количество очков. Условия игры могли быть разными и определялись заранее.
Для определения шансов на выигрыш важно знать как часто выпадает то или иное количество очков. Опытные игроки заметили, что при большем количестве бросков двух костей чаще выпадает 7, а реже 2 или 12, учитывая это, они принимали такие условия игры, которые обеспечивали им выигрыш.
Теория вероятности - математическая наука, изучающая закономерности массовых случайных событий.
Теория вероятности, как любой раздел математики, оперирует определённым кругом понятий. Большинству понятий теории вероятности даются определения, но некоторые принимаются как первичные, неопределяемые, как в геометрии точка, прямая и плоскость.
Первичным понятием теории вероятности является СОБЫТИЕ. Под событием понимают любое явление, про которое можно сказать, что оно происходит или не происходит, причём абстрагируясь от конкретной природы события.
Любое событие происходит вследствие ИСПЫТАНИЯ (или ОПЫТА). Под испытанием или опытом понимают те условия, в результате которых происходит событие. Например, подбрасывание монеты - испытание (опыт), а появление на ней «герба". Выпуск билетов лотереи - испытание, а появление выигрыша на определённый билет - событие. События обозначают большими буквами латинского алфавита А, В, С и т. д.
Экспериментами со случайными результатами, или случайными экспериментами, называют различные эксперименты, опыты, испытания, наблюдения, измерения, результаты которых зависят от случая и которые можно повторить многократно в одинаковых условиях.
Например, выстрелы по мишени, участие в лотереи, многолетнее наблюдение за погодой в один и тот же день в одном и том же месте, опыты с рулеткой, бросание игрального кубика, подбрасывание монеты и т. д.
Теория вероятности изучает массовые случайные события.
Событие, которое может произойти, а может и не произойти в процессе наблюдения или эксперимента в одних и тех же условиях называется случайным событием. Вы покупаете лотерейный билет и можете выиграть, а можете и не выиграть; на выборах может победить один кандидат, а может и другой; автобус может подойти во время, а может опоздать - всё это случайные события.
Например:
|
Испытание |
Случайное событие |
|
1. Бросание игрального кубика |
Появление трёх очков на верхней грани. |
|
2. Игра в шахматы |
Выигрыш у соперника |
|
3. Подбрасывание монеты |
Выпадение «герба» |
|
4. Выпуск ламп электроламповым заводом |
Появление бракованных ламп |
|
5. Выстрелы по мишени спортсменом |
Попадание в десятку. |
|
6. Участие в лотереи |
Выигрыш |
Массовыми называются события, наблюдаемые в определённых условиях, которые могут быть произведены неограниченное количество раз.
Массовыми считаются и те события, для которых соответствующие испытания нельзя воспроизвести, но есть возможность наблюдать аналогичные испытания в большом количестве. Например, вызов скорой помощи - испытание, а ложный из них - случайное событие.
Множество событий образует полную группу событий, если вследствие каждого испытания хотя бы одно событие произойдёт наверняка.
Например, появление 1, 2, 3, 4, 5, 6 очков при бросании игральной кости - полная группа событий.
События А1, А2, А3, .. , Аn называются попарно несовместными в данном испытании, если никакие два из них не могут произойти вместе.
Например, при выстреле по мишени попадание и промах не могут произойти вместе.
События А1, А2, А3, .. , Аn могут быть равновозможными или равновероятными (каждое из которых не имеет никаких преимуществ в появлении чаще другого при многократных испытаниях, проводимых в одинаковых условиях).
Например, появление 1, 2, 3, 4, 5, 6 очков при бросании игральной кости являются равновозможными или равновероятными.
Однако, не все события могут быть равновозможными или равновероятными. Может не прозвенеть будильник, перегореть лампочка, сломаться автобус, но в обычных условиях такие события маловероятны.
Важнейшими понятиями теории вероятности являются понятия достоверного и невозможного события.
Достоверные события - это события, которые в обычных условиях обязательно происходят.
Например, при давлении 101 325 Па (нормальное атмосферное давление) и 0 ̊ вода замерзает, а при температуре 100 ̊закипает; если перевернуть чашку с чаем, то он обязательно выльется.
Невозможные события - это события, которые в данных условиях никогда не происходят.
Невозможно не вылить воду из банки опрокинув её вверх дном.
Достоверные и невозможные события встречаются в жизни сравнительно редко, можно сказать, что мы живём в мире случайных событий. Поэтому важно понять: можно ли какими-то способами оценить шансы появления случайного события, которое нас интересует?
Ответ на эти вопросы даёт раздел математики, который называется теория вероятностей.
Одним из важных понятий , которые рассматриваются в теории вероятностей, является понятие эксперимента со случайными результатами.
Перед началом футбольного матча судья подбрасывает монету, чтобы определить, какая команда начинает матч с центра поля. У команд равные шансы начать игру. А имеет ли право судья вместо монеты подбросить кнопку?
Подбрасывание кнопки, как и подбрасывание монеты, - это эксперимент со случайными результатами.
Кнопка может упасть как на остриё так т на шляпку. Но можно ли эти события считать равновозможными или одно из них более вероятно. Чтобы ответить на этот вопрос надо опыт с кнопкой повторить много раз. Такое исследование провела группа студентов из 20 человек одного из харьковских лицеев в 2000 году. Каждый из студентов подбросил кнопку 100 раз, то есть было проведено 2000 экспериментов. В результате кнопка упала на остриё 909 раз, на шляпку 1091 раз. Этот эксперимент показывает, что кнопка чаще падает на шляпку. Следовательно, судья не имеет права для жеребьёвки использовать кнопку, так как у команд в такой ситуации были неравные шансы начать игру.
Экспериментами со случайными результатами (или коротко случайными экспериментами) называют различные эксперименты, опыты, испытания, наблюдения и измерения, результаты которых зависят от случая и которые можно повторить много раз в одинаковых условиях.
Например, это серия выстрелов одного и того же стрелка по одной и той же мишени, участие в лотереи, вынимание пронумерованных шаров из коробки, многочисленные наблюдения за погодой в один и тот же день в одном и том же месте, опыты с рулеткой, с бросанием игрального кубика, подбрасыванием монеты, кнопки.
Любой результат случайного эксперимента является случайным событием. Вследствие такого эксперимента это событие может произойти, или не произойти. Случайные события обозначают большими буквами латинского алфавита A, B, C, D, … .
2.2 Частота и относительная частота случайного события.
Одним из важных понятий, используемых в теории вероятностей, является понятие частоты случайного события.
Если при неизменных условиях случайный эксперимент проведён n раз и в n(A) случаях произошло событие А, то число n(A) называется частотой события А.
Например, учащиеся одной из школ провели 8 000 экспериментов с подбрасыванием монеты, каждый раз записывая результат - выпал «герб» (событие А) или «число» (событие В). В их экспериментах «герб» выпал 3692 раза. Следовательно, частота события А (выпал «герб») равна 3 692.
В опытах Бюффона «герб» выпал 2048 раз, следовательно частота события А (выпал «герб») равна 2 048. У Карла Пирсона «герб» выпал 12 012 раз, следовательно частота события А (выпал «герб») равна 12 012.
Для каждой серии рассмотренных экспериментов вычислим, какую часть число событий А, состоящих в том, выпал «герб», составляет от общего числа подбрасываний монеты, или, как говорят, подсчитаем относительную частоту выпадения «герба» (появления события А).
Относительной частотой случайного события называют отношение появления этого события к общему числу проведённых экспериментов.
Например, в приведённых экспериментах событие А (выпал «герб») :
0,4953 (у школьников);
0,5069 (у Бюффона);
0,5005 (у Пирсона).
2.3
Статистическое определение вероятности.
Серии экспериментов, проведённые
в разные эпохи и в разных странах дали похожие результаты: при
многократном подбрасывании монеты относительная частота появления
случайного события А (выпал
«герб») с точность до десятых равна 0,5. Следовательно, хотя каждый
результат подбрасывания монеты - случайное событие, при многократном
повторении эксперимента видна закономерность.
Число 0,5 - это вероятность случайного события выпал «герб».
Если при проведении большого количества случайных экспериментов, в каждом из которых может произойти или не произойти событие А, значение относительной частоты события А близко к некоторому определённому числу, то это число называется вероятностью случайного события А.
Это определение называют статистическим определением вероятности.
Вероятность события обозначается буквой Р латинского алфавита (первой буквой латинского слова probabilitas, что в переводе обозначает «вероятность»).
Если обозначить событие - «выпал герб» - буквой А, а выпало число - буквой В, то утверждение о том, что вероятности выпадения «герба» или «числа» равны 0,5, можно записать так:
Р(А) = 0,5; Р(В) = 0,5.
Иногда вероятность выражают в процентах:
Р(А) = 50%, Р(В) = 50%.
2.4
Классическое определение вероятности.
В случае,
когда элементарные события не являются равновероятными приходится
использовать статистическое определение вероятности. Но для того чтобы
найти вероятность интересующего нас события при статистическом
определении необходимо провести достаточно большое количество
экспериментов или наблюдений. Когда рассматриваются эксперименты со
случайными результатами и все эти результаты равновозможны, то
вероятность случайного события удаётся найти путём рассуждений, не
выполняя экспериментов.
При этом пользуются статистическим определением вероятности.
Вероятность события А
- это отношение числа благоприятствующих ему элементарных событий к
числу всех равновозможных элементарных событий в данном эксперименте.
В этом случае вероятность
события А вычисляется по формуле
Р(А) = 
,
где m - число благоприятствующих элементарных
событий; n - число равновозможных элементарных событий.
Пример. Из 15 изготовленных
велосипедов 3 оказались с дефектами. Какова вероятность того, что 2
выбранных наугад велосипедов будут без дефектов?
Решение.
Пусть событие А состоит в том, что 2 выбранных наугад велосипеда
будут без дефектов (благоприятствующие элементарные события). Из 15
велосипедов выбрать 2 можно 
способами. Эти выборы будут равновозможными
элементарными событиями.
n = 
= 
=
105;
m = 
=
=
66;
Р(А) = 
=
.
Ответ: вероятность 
.
2.5 Операции над событиями.
Суммой (объединением) событий А и В называется событие С (А + В = С; А
)
которое происходит, когда наступает событие А или событие В, или
оба одновременно.
Произведением (пересечением) событий А и В называется событие С, которое наступает, когда
происходят оба события А и В (А ∙ В = С; А 
В = С)
Разностью событий А и В (А/В = С) называется событие С, наступающее когда происходит событие А и не происходит событие В.
Пусть события А и В зависимы. Вероятность события В, вычисленная в предположении, что событие А произошло, называется условной вероятностью события В и обозначается Р (В/А).
Вероятность произведения событий равна произведению вероятностей событий.
Р(А ∙ В) = Р(А) + Р(В)
Вероятность суммы событий равна сумме событий или сумме событий без вероятности их совместного наступления для несовместных событий.
Р(А + В) = Р(А) + Р(В)
Р(А + В) = Р(А) + Р(В) – Р(АВ) (для несовместных событий).
2.4 Формула полной вероятности.
Пусть событие В может наступать только с одним из событий А1, А2, , …, Аn. Например, в магазин поступает одна и та же продукция с трёх разных предприятий в разном количестве. Существует разная вероятность выпуска некачественной продукции на разных предприятиях. Случайным образом отбирается одно изделие. Требуется определить вероятность того, что это изделие не качественное (событие В). А1, А2, А3 - это выбор изделия из продукции каждого предприятия. Вероятность события В можно рассчитать как сумму событий А1, А2, А3 :
Р(В) = Р(А1) + Р(А2) + Р(А3).
По теореме умножения вероятностей находим
Р(В) = Р(А1) ∙ Р(В/А1) + Р(А2) ∙ Р(В/А2) + Р(А3) ∙ Р(В/А3) (1).
Формула (1) называется формулой полной вероятности.
Рассмотрим пример.
В магазин поступила продукция с трёх различных предприятий: с первого - 20, со второго - 10, с третьего - 70 изделий. Известно, что вероятность некачественного изделия на первом предприятии Р(В) = 0,02, на втором - 0,03, на третьем - 0,05. Определим вероятность взятого некачественного товара в магазине.
Решение.
Вычислим вероятность выбора некачественного товара в магазине каждого предприятия:
Р(А1) = 20 : (20+010+70)= 0,2. Соответственно, Р(А2) = 0,1 и Р(А3) = 0,7. Используя формулу (1), находим Р(В) = 0,2 ∙ 0,02 + 0,1 ∙ 0,03 + 0,7 ∙ ,005 = 0,042.
2.5 Формула Байеса.
Пусть событие В происходит с одним из
несовместных событий А1, А2, , …, Аn.
Требуется найти вероятность события 
, если известно, что событие В произошло. На
основании теоремы о вероятности произведения двух событий можно
записать
Р(АiВ) = Р(В) ∙ Р(Аi/В) = Р(Аi) ∙ Р(В/Аi).
Откуда Р(Аi/В) = 
или
Р(Аi/В) = 
(2).
Формула (2) носит название - формула Байеса.
Рассмотрим пример.
Три различные организации представили в контролирующее управление счета для выборочной проверки. Первая организация представила 15 счетов, вторая 10, а третья =- 25. Вероятности правильного оформления счетов у этих организаций известны и составляют у первой организации - 0,9, у второй - 0,8 и у третьей - 0,85. Был выбран один счёт, и он оказался правильным. Определить вероятность того, что это был счёт второй организации.
Решение.
Пусть А1, А2, А3 - события выбора счёта у организаций.
Соответствующие вероятности Р(А1) = 15/50, Р(А2) = 10/50, Р(А3) = 25/50. По формуле полной вероятности Р(В) = 0,9 ∙ (15/50) + 0,8 ∙ (10/50) + 0,85 ∙ (25/50) = 0,855.
По форму Байеса Р(А2/В) = 
=
0,19.
§ 3. Схема Бернулли.
Пусть проводится несколько экспериментов, результатом каждого из которых может быть одно и тоже событие А.
Если вероятность появления события А в каждом из экспериментов не зависит от результатов других экспериментов, то такие эксперименты называются независимыми относительно события А.
Например, независимыми являются несколько
экспериментов по бросанию одного и того же игрального кубика в
одинаковых условиях. Пусть событие А - выпало 1 очко. Если кубик
правильной геометрической формы и однородный, то в каждом из этих
экспериментов вероятность р появления события А одинакова и равна 
(р
= 
). Тогда вероятность q непоявления события А в каждом из этих
экспериментов так же одинакова (это вероятность появления события 
,
поэтому q = 1 – р = 
).
Некоторые практические задачи сводятся к построению математической модели проведения независимых экспериментов с двумя результатами, вероятности которых p и q не изменяются от эксперимента к эксперименту.
Совокупность условий для построения модели называется схемой Бернулли.
Пусть проводится n независимых
экспериментов, в каждом из которых может произойти событие А, а
может и не произойти. Вероятность того, что произойдёт событие А в
каждом из экспериментов одинакова и равна р, а вероятность того, что
событие А не произойдёт ( то есть произойдёт событие 
)
равна q = 1 – р. найдём вероятность 
того,
что в n независимых экспериментах событие А произойдёт
точно m раз.
Искомую вероятность можно вычислить по формуле Бернулли:
= 
Задача. Найдите вероятность того, что при 10 бросаниях игрального кубика 3 очка выпадет ровно 2 раза.
Решение. условия схемы Бернулли:
событие А - выпало 3 очка при бросании игрального кубика; при всех
бросаниях кубика вероятность появления события А р = 
; вероятность события 
q
= 1 – р = 1 - 
= 
; по условию n = 10 и m = 2.
По формуле Бернулли: 
= 
= 
· 
=
0.291
§ 3. Понятие случайной величины и закон её распределения.
Случайной величиной называют переменную величину, которая в данном случайном эксперименте может принимать те или иные числовые значения с определённой вероятностью.
Случайная величина Х приняла значение х. Записывают это так: Х = х. В опыте с бросанием двух игральных костей были найдены вероятности появления той или иной суммы очков. Появление суммы очков - случайная величина. Обозначим её за Х. Тогда х1 = 2, х2 = 3, х3 = 4, …, х10 = 11, х11 = 12 - значения случайной величины Х. Значения случайной величины Х и соответствующая вероятность её появления (р1, р2, …, р10, р11) можно записать в виде таблицы:
|
Х |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Р |
|
|
|
|
|
|
|
|
|
|
|
С помощью этой таблицы можно увидеть, какие значения величина Х принимает с одинаковыми вероятностями, какое значение величины Х появляется с большей вероятностью и т. д. Такую таблицу называют таблицей распределения случайной величины по их вероятностям или говорят, что эта таблица задаёт закон распределения рассмотренной случайной величины.
Законом распределения случайной величины называется всякое соотношение устанавливающее связь между возможным значениями случайных величин и соответствующими им вероятностями.
Случайную величину можно задать в любом случайном эксперименте. Для этого достаточно каждому элементарному событию из пространства элементарных событий эксперимента поставить в соответствие некоторое число ( в этом случае говорят, что задана числовая функция, областью определения которой является пространство элементарных событий).
Случайной величиной называется числовая функция, областью определения которой является пространство элементарных событий.
Например, в эксперименте по подбрасыванию монеты пространство элементарных событий состоит из двух событий: u1 - выпал «герб», u2 - выпало «число». Эти события несовместны, и в результате эксперимента обязательно произойдёт только одно из них. Поставим в соответствие событию u1 число 1, а событию u2 число 0. Тогда получим случайную величину Х, которая принимает только два значения: х1 = 1, х2 = 0, то есть Х(u1) = х1 = 1, а Х(u2) = х2 = 0. Рассмотренную функцию - случайную величину Х - можно задать так же с помощью таблицы
|
Результат эксперимента |
u1 - выпал «герб» |
u2 - выпало «число». |
|
Значение Х |
1 |
0 |
Закон распределения этой случайной величины задаётся таблицей:
|
Х |
1 |
0 |
|
Р |
|
|
Закон распределения каждой случайной величины устанавливает соответствие между значениями случайной величины и их вероятностями, то есть является функцией, область определения которой - все значения случайной величины.
Законом распределения случайной величины Х называется функция, которая каждому значению х случайной величины Х ставит в соответствие число Р(Х=х) (вероятность события, состоящего в том, случайная величина Х приняла значение х)
В этом случае закон распределения случайной величины, принимающей только n значений, можно записать в виде таблицы:
|
Х |
х1 |
х2 |
… |
хn |
|
Р |
p1 |
p2 |
… |
pn |
Здесь х1, х2, …, хn - разные случайные величины Х, а рi= Р(Х-хi), где i = 1, 2, 3, …, n - вероятности, с которыми Х принимает эти значения.
События (Х=х1), (Х=х2, …, (Х=хn) попарно несовместны, и их сумма является достоверным событием. Поэтому сумма вероятностей этих событий является достоверным событием. Поэтому сумма вероятностей этих событий равна 1, следовательно,
Р1 + р2 + р3 + … + рn = 1.
Это равенство часто используют для проверки правильности задания закона распределения случайной величины, особенно в тех случаях, когда он задаётся не в результате теоретического расчёта вероятности событий с использованием классического определения вероятности, а в результате использования статистического определения вероятности.
Например, в экспериментах в экспериментах с подбрасыванием кнопки, падение кнопки на остриё или кружок может быть рассмотрено как случайная величина Y с условными значениями y1 = 1 (падение на остриё) и y2 = 0 (падение на кружок). Результаты серии экспериментов с некоторой кнопкой представлены в таблице, задающей закон распределения случайной величины.
|
Y |
1 |
0 |
|
P |
0,45 |
0,55 |
Проверка: 0,45 + 0,55 = 1.
В случае, когда приходится находить сумму всех значений некоторой величины, можно использовать знак ∑ (сигма, читается «сумма»), введённый Л. Эйлером (1707 – 1783). Например, если вероятность Р принимает значения Р1 + р2 + р3 + … + рn, то введём обозначение:
Р1 + р2 + р3 + … + рn
= 
.
Используя это обозначение, проверку правильности
составления последней таблицы можно записать: 
.=
0,45 + 0,55 = 1.
Рассмотренные случайные величины принимают изолированные друг от друга значения. Такие величины называются дискретными (от латинского слова discretus - раздельный, прерывистый).
Случайная величина называется дискретной, если множество её значений конечно или счётно.
Счётность означает, что мы можем установить взаимно однозначное соответствие между элементами заданного множества и натуральными числами, то есть можем указать, как можно пронумеровать все элементы множества.
Распределение вероятностей такой величины называется дискретным распределением вероятностей.
Если случайная величина может принимать любое значение на некотором промежутке, то такая величина называется непрерывной.
Например, время Т ожидания на
остановке троллейбуса является непрерывной случайной величиной в
случае, если пассажир знает, что автобусы ходят через 10 минут, и
приходит на остановку случайным образом. Эта случайная величина
принимает любое числовое значение Т 
.
Очевидно, что число значений непрерывной случайной величины бесконечно независимо от того , является ли промежуток значений ограниченным (отрезком) или неограниченным. Поэтому мы не можем для этой величины задать закон распределения так, как это задаётся для дискретной величины.
Вопросы для повторения.
1. Чем занимается теория вероятности как математическая наука?
2. Привести примеры случайных событий, массовых случайных событий.
3. Какие примеры подтверждают существование закономерностей в массовых случайных событиях?
4. Как возникла теория вероятностей? Где применяется?
5. Какие события называются случайными?
6. Какие события называются попарно несовместными
7. Какие события называются элементарными? Сформулировать классическое определение вероятности.
8. Чему равна вероятность достоверного события? Чему равна вероятность невозможного события?
9. Записать формулу Бернулли.
10. Записать формулу Байеса.
11.
§4. Понятие о статистике.
«Статистика знает всё», утверждали И.Ильф и Е. Петров в своём знаменитом романе «Двенадцать стульев» и продолжали: «Известно, сколько какой пищи съедает в год средний гражданин республики … известно, сколько в стране охотников, балерин, станков, собак всех пород, велосипедов, памятников, девушек, маяков и швейных машинок ... как много жизни, полной пыла, страстей и мысли, глядит на нас из статистических таблиц!»
Это ироническое описание даёт достаточно точное представление о СТАТИСТИКЕ (от латинского слова status - состояние).
СТАТИСТИКА - наука, изучающая, обрабатывающая и анализирующая количественные данные о разнообразнейших массовых явлениях в жизни.
ЭКОНОМИЧЕСКАЯ СТАТИСТИКА изучает изменение цен, спроса и предложения товаров, прогнозирует рост и падение производства и потребления.
МЕДИЦИНСКАЯ СТАТИСТИКА изучает эффективность разных лекарств и методов лечения, вероятность возникновения некоторых заболеваний в зависимости от возраста, пола, наследственности, условий жизни, вредных привычек, прогнозирует распространение эпидемий.
ДЕМОГРАФИЧЕСКАЯ СТАТИСТИКА изучает рождаемость, численность населения, его состав (возрастной, национальный, профессиональный).
Есть ещё статистика ФИНАНСОВАЯ, НАЛОГОВАЯ БИОЛОГИЧЕСКАЯ МЕТЕОРОЛОГИЧЕСКАЯ и т. д.
Статистика имеет многовековую историю. Уже в Древнем мире статистический учёт населения. Однако случайное толкование статистических данных, отсутствие строгой научной базы статистических прогнозов даже в середине XIX века ещё не позволяли говорить о статистике как науке. Только в XX веке появилась математическая статистика - наука, опирающаяся на законы теории вероятности.
Выяснилось, что статистические методы обработки данных из самых разных областей жизни имеют много общего. Это позволило создать универсальные научно обоснованные методы статистических исследований и проверки статистических гипотез.
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА - это раздел математики, изучающий математические методы обработки и использования статистических данных для научных и практических выводов.
В математической статистике рассматриваются методы, которые дают возможность по результатам экспериментов (статистическим данным) делать определённые выводы вероятностного характера.
Основными задачами математической статистики являются:
Ø Оценка вероятности. Пусть некоторое случайное событие имеет вероятность Р>0, но её значение нам не известно. Требуется оценить эту вероятность по результатам экспериментов, то есть решить задачу об оценке вероятности через частоту.
Ø Оценка закона распределения. Исследуется некоторая случайная величина, точное выражение для закона распределения которой нам неизвестно. Необходимо по результатам экспериментов найти приближённое выражение для функции, задающей закон распределения.
Ø Оценка числовых характеристик случайной величины (математическое ожидание, дисперсия).
Ø Проверка статистических гипотез (предположений). Исследуется некоторая случайная величина. Исходя из определённых рассуждений, выдвигается, например, гипотеза, что распределение этой случайной величины близко к нормальному. Необходимо по результатам экспериментов принять или отклонить эту гипотезу.
Результаты исследований, проводимых методами математической статистики, применяются для принятия решений. Например, при планировании и организации производства, при контроле качества продукции, при выборе оптимального времени наладки или замены действующей аппаратуры ( например, при определении времени замены двигателя самолёта, отдельных частей станков и т. д.).
Как в каждой науке, в статистике используются свои специфические термины и понятия.
|
Часто употребляемый термин |
Смысл термина |
Научный термин |
Определение |
|
Общий ряд данных |
То, откуда выбирают |
Генеральная совокупность |
Множество всех возможных результатов наблюдения (измерения) |
|
Выборка |
То, что выбирают |
Статистическая выборка, статистический ряд |
Множество результатов, реально полученных, в данном наблюдении (измерении) |
|
Варианта |
Значение одного из результатов наблюдения (измерения) |
Варианта |
Одно из значений элементов выборки |
|
Ряд данных |
Значения всех результатов наблюдения (измерения) |
Вариационный ряд |
Упорядоченное множество всех вариантов |
4.1 Генеральная совокупность и выборка.
Для изучения различных массовых явлений проводятся специальные статистические исследования.
Первый этап статистических наблюдений - целенаправленный сбор информации об изучаемом явлении. При изучении реальных явлений часто бывает невозможно обследовать все элементы совокупности. Например, практически невозможно выяснить размер обуви у всех людей планеты. Проверить наличие некачественных листов фотобумаги в небольшой партии хотя и реально, но бессмысленно, так как это приведёт к уничтожению всей партии бумаги. Бессмысленно проверить качество спичек в коробке и т. д. В подобных случаях вместо изучения всех элементов совокупности, называемой ГЕНЕРАЛЬНОЙ СОВОКУПНОСТЬЮ, обследуют её значительную часть, выбранную случайным образом. Эту часть называют ВЫБОРКОЙ.
Если в выборке присутствуют все значения случайной величины в тех же пропорциях, что и в генеральной совокупности, то эту выборку называют РЕПРЕЗЕНТАТИВНОЙ ( от французского слова - показательный).
Например, менеджер швейной фабрики большого города хочет выяснить, в каком количестве необходимо сшить одежду тех или иных размеров, он должен составить репрезентативную выборку из людей этого города. Объём её может быть не очень большим (например, 1000 человек), но в такую выборку нельзя брать только детей детского сада или только рабочих завода. Очевидно, что микромоделью города может служить совокупность жителей многоквартирного дома (или нескольких домов).
S - объём генеральной совокупности;
n - объём репрезентативной совокупности;
k - значений исследуемых признаков распределения по
частотам M1, M2, M3, …, Mk , где 
= n.
Тогда в генеральной
совокупности частотам M1, M2, M3, …, Mk будут соответствовать частоты s1,
s2, s3, … , sk тех же значений признака, что и в выборке ( 
= S ), По определению репрезентативной выборки получаем
= 
= 
Где I - порядковый номер значения признака (1
. Из этого соотношения находим
= S
или 
= S
, где 1
Пример. Обувной цех должен выпустить 1 000 пар кроссовок молодёжного фасона. Для определения того, сколько кроссовок и какого размера необходимо выпустить были выявлены размеры обуви у 50 наугад выбранных подростков.
Распределение размеров обуви по частотам представлены в таблице:
|
Размер (Х) |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
|
Частота (М) |
2 |
5 |
6 |
12 |
11 |
7 |
4 |
2 |
1 |
Сколько кроссовок разного размера будет изготавливать фабрика?
Решение.
|
Размер (Х) |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
|
Частота (М) |
2 |
5 |
6 |
12 |
11 |
7 |
4 |
2 |
1 |
|
Относительная частота (W) |
|
|
|
|
|
|
|
|
|
|
Количество кроссовок (SW) |
40 |
100 |
120 |
240 |
220 |
140 |
80 |
40 |
20 |
Относительная частота кроссовок 36
размера 
= 
. Количество кроссовок 36 размера, которые надо
выпустить 
∙ 1 000 = 40 (пар).
4.2 Статистические характеристики
рядов данных.
Ранжирование ряда данных. Под ранжированием ряда данных понимают расположение элементов этого ряда в порядке возрастания. Если ряд данных выборки имеет вид 5, 3, 7, 4, 6, 4, 6, 9, 4, то после ранжирования он примет вид 3, 4, 4, 4, 5, 6, 6, 7, 9 (*).
Размах выборки - это разность между наибольшим и наименьшим значениями случайных величин в выборке. Для ряда (*) размах выборки: R = 9-3=6.
Мода (от латинского слова modus - мера, правило) - это значение случайной величины, встречающейся чаще остальных. Для ряда (*) значение 4 встречается чаще все, поэтому М0 = 4.
Медиана - это так
называемое серединное значение упорядоченного ряда значений случайной
величины. Если количество чисел, записанное в ряду нечётное, то
медиана это число, записанное посередине; если количество чисел,
записанное в ряду чётное, то медиана - это среднее арифметическое
двух чисел, записанных посередине. Для ряда (*), в котором 9
членов, медиана это среднее (пятое) число 5: Ме = 5. Если рассмотреть ряд 3, 3, 4, 4, 4,
5, 6, 6, 7, 9, в котором 10 членов, то Ме = 
= 4,5.
Пример. После летних каникул провели опрос 10 девочек и 9 мальчиков одного класса о количестве книг, прочитанных ими за летние каникулы. Результаты были записаны в порядке опроса. Получили следующие ряды:
для девочек: 4, 3, 5, 3, 8, 3, 12, 4, 5, 5;
для мальчиков: 5, 3, 3, 4, 6, 4, 4, 7, 4.
Чтобы удобнее было анализировать информацию, в подобных случаях числовые ряды ранжируют. В результате ранжирования получают следующие ряды: для девочек: 3, 3, 3, 4, 4, 5, 5, 5, 8, 12;
для мальчиков: 3, 3, 4, 4, 4, 4, 5, 6, 7.
Тогда распределение по частотам М случайных величин: Х - число книг, прочитанных за каникулы девочками , и Y - число книг, прочитанных за каникулы мальчиками, можно задать таблицами:
|
Х |
3 |
4 |
5 |
8 |
|
||
|
М |
3 |
2 |
3 |
1 |
1 |
= n = 9
|
Y |
3 |
4 |
5 |
6 |
7 |
|
М |
2 |
4 |
1 |
1 |
1 |
Эти распределения можно также проиллюстрировать графически с помощью полигона частот.
Y
Размах в первом ряду (для девочек) R = 12-3=9, во втором ряду (для мальчиков) R = 7-3=4.
В первом ряду (для девочек) две моды - число «3» и число «5» (оба повторяются по три раза), а во втором ряду (для мальчиков) одна мода - число «4». На графике мода - это значение абсциссы точки, в которой достигается максимум полигона частот. Моды может и не быть, если все значения случайной величины встречаются одинаково часто.
4.3 Среднее
значение (
случайной
величины.
Средним значением случайной величины Х называется среднее арифметическое всех её значений
= 
(**)
Если случайная величина Х принимает значения х1, х2, .. , хk соответственно с частотами m1, m 2, … , mk, то среднее арифметическое можно вычислить по формуле
= 
Рассмотренном примере (для девочек) 
= 
=
5,2;
(для мальчиков) 
= 
= 
.
4.5 Математическое ожидание (МХ) случайной величины Х.
Пусть случайная величина Х принимает значения х1, х2, .. , хk соответственно с вероятностями р1, р 2, … , рk, то есть имеет закон распределения
|
Х |
х1 |
х2 |
… |
хk |
|
Р |
р1 |
р 2 |
… |
рk |
Сумма произведений всех значений случайной величины на соответствующие вероятности называется математическим ожиданием величины Х:
МХ = х1∙ р1 + х2∙ р 2 + … + хk ∙ рk.
Пусть закон распределения случайной величины Х задан таблицей:
|
Х |
2 |
5 |
6 |
7 |
|
Р |
0,3 |
0,1 |
0,2 |
0,4 |
Тогда МХ = 2 ∙ 0,3 + 5 ∙ 0,1 + 6 ∙ 0,2 + 7 ∙ 0,4 = 5,1.
Математическое ожидание показывает, какое среднее значение случайной величины Х можно ожидать в результате эксперимента ( при значительном количестве повторении эксперимента).
Например, пусть количество очков, выбиваемых при одном выстреле каждым из двух стрелков , имеют следующие законы распределения:
|
Х |
8 |
9 |
10 |
|
Р |
0,4 |
0,1 |
0,5 |
|
Х |
8 |
9 |
10 |
|
Р |
0,1 |
0,6 |
0,3 |
Чтобы выяснить, какой из стрелков стреляет более метко, находят математическое ожидание для каждой случайной величины:
МХ = 8 ∙ 0,4 + 9 ∙ 0,1 + 10 ∙ 0,5 = 9,1;
МХ = 8 ∙ 0,1 + 9 ∙ 0,6 + 10 ∙ 0,3 = 9,2.
Следовательно, среднее количество очков, выбиваемое при одном выстреле, у второго стрелка несколько выше, чем у первого. Это даёт основание сделать вывод о том, что второй стрелок стреляет несколько лучше, чем первый.
Практическая часть.
Пример. Найдите размах, моду, медиану и среднее значение совокупности значений случайной величины Х:
|
Х |
2 |
3 |
4 |
5 |
|
М |
3 |
4 |
1 |
3 |
Постройте полигон частот значений величины Х. Укажите на рисунке размах, моду, медиану заданной совокупности.
Решение. 2, 2, 2, 3, 3, 3, 3,4, 5, 5, 5.
1. R = 5-3=2;
2. М0 = 3;
3. Ме = 3;
4.
= 
= 
;
 |
4
3
 |
1
 |
2 3 4 5
Пример 2.
Девочки 11 класса на уроке физкультуры при прыжпрыжках в высоту показали следующие результаты (в см):
90, 125, 125, 130, 130, 135, 135, 135, 140, 140, 140.
Найдите моду, медиану и среднее значение совокупности данных.
Решение.
1. М0 = 135; М0 = 140;
2. Ме = 135;
3.
= 
= 
= 129
. лучше всего характеризует
спортивную подготовку девочек этого класса число 130 см.
Вопросы для контроля.
1. Чем занимается наука «Статистика»?
2. Какие вы знаете элементы статистического метода исследования?
3. Перечислите виды статистических наблюдений.
4. Что такое генеральная совокупность? Что такое выборка?
5. По какому плану проводится статистическое исследование?
6. Как построить гистограмму и полигон?
7. Что такое мода и медиана?
8. Какие виды средних значений применяются в статистике?
9. Что такое среднее арифметическое чисел?
10. Написать формулу среднего геометрического данных чисел.
11. Написать формулу среднего квадратичного данных чисел.
12. Что такое вариационный ряд?
13. Какие статистические таблицы вы знаете?
14. В чём состоит основная задача математической статистики?
§ 5 Примеры прикладных задач.
Задача 1. В магазин привезли электрические лампочки с трёх предприятий6 с первого - 200 штук, со второго - 100 штук, с третьего - 700 штук. Известно, что вероятность бракованных лампочек на первом предприятии 0,01. На втором - 0,02, на третьем - 0,04. Какова вероятность покупки бракованной лампочки в магазине?
Решение.
В1 случайное событие - бракованная лампочка первого предприятия;
В2 случайное событие - бракованная лампочка второго предприятия;
В3 случайное событие - бракованная лампочка третьего предприятия;
По условию задачи Р(В1) = 0,01, Р(В2) = 0,02, Р(В3) = 0,04.
Пусть А1 - случайное событие - куплена лампочка первого предприятия, тогда вероятность того, что куплена лампочка первого предприятия Р(А1) = 200 : (200+100+700) = 0,2.
Пусть А2 - случайное событие - куплена лампочка второго предприятия, тогда вероятность того, что куплена лампочка второго предприятия Р(А2) = 100 : (200+100+700) = 0,1.
Пусть А3 - случайное событие - куплена лампочка третьего предприятия, тогда вероятность того, что куплена лампочка третьего предприятия Р(А3) = 700 : (200+100+700) = 0,7.
В – случайное событие - куплена бракованная лампочка
Р(В) = Р(А1) · Р(В1) + Р(А2) · Р(В2) + Р(А3) · Р(В3)
Р(В) = 0,2 · 0,01 + 0,1 ·
0,02 + 0,7 · 0,04 0,032 
3,2%
Ответ вероятность того,
что купленная лампочка окажется бракованной 
3,2%.
Задача 2. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристреленного револьвера, если Джон стреляет из не пристреленного револьвера, то он попадает в муху с вероятностью 0,4. На столе лежит 10 револьверов, из которых только 2 пристрелены. Ковбой Джон видит на стене муху, хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, Джон не попадёт в муху.
Решение.
А – случайное событие: Джон не попадает в муху;
В1 - случайное
событие - Джон взял наугад пристреленный револьвер, тогда вероятность
того, что он взял наугад пристреленный пистолет Р(В1)= 2 : 10
= 0,2; вероятность того, что Джон промахнулся 
= 1
- 0,9 = 0,1.
В2 - случайное
событие - Джон взял наугад не пристреленный револьвер, тогда
вероятность того, что он взял наугад не пристреленный пистолет Р(В2)=
8 : 10 = 0,0,8; вероятность того, что Джон промахнулся 
(А)
= 1 - 0,4 = 0,6.
Тогда по формуле полной
вероятности Р(А) = Р(В1) · 
+
Р(В2) · 
.
Р(А) = 0,2 · 0,1 + 0,8 · 0,6 = 0,02 + 0,48 = 0,5.
Ответ: 50% -вероятность того, что Джон промахнётся.
Задача 3. Три цеха представили на заводской контроль изделия для выборочной проверки. Первый цех представил 30 изделий, второй - 20 изделий, третий - 50 изделий. Вероятность качественных изделий в первом цеху составляет 0,95, во втором цеху - 0,9, в третьем цеху - 0,85. Было выбрано одно изделие. Какова вероятность того, что это изделие второго цеха?
Решение.
А – событие –взято качественной изделие
А1 - случайное событие - взято изделие первого цеха, вероятность этого события 30 : (30 + 20 + 50) = 0,3. По условию вероятность качественных изделий в первом цеху составляет 0,95.
А2 - случайное событие - взято изделие второго цеха, вероятность этого события 20 : (30 + 20 + 50) = 0,2. По условию вероятность качественных изделий во втором цеху составляет 0,9.
А3 - случайное событие - взято изделие третьего цеха, вероятность этого события 50 : (30 + 20 + 50) = 0,5. По условию вероятность качественных изделий в первом цеху составляет 0,85.
По формуле полной вероятности
0,3 · 0,95 + 0,2 · 0,9 + 0,5 · 0,85 = 0,285 + 0,18 + 0,425 = 0,89
Вычислим по формуле Байеса вероятность того, что это изделие второго цеха
(А)
= 
=
0,20 = 20 %.
Ответ: 20 % вероятность того, что это изделие второго цеха.
Задача 4. Найдите количество трехзначных чисел, которые можно составить из цифр 1, 2, 3, 4, 5, 6, 7, если эти цифры не повторяются.
Решение.
В
данном множестве 7 элементов, из которых составляются подмножества из
3 элементов. Порядок следования элементов в подмножествах учитывается
и не все элементы данного множества входят в подмножество.
Следовательно, соответствующее соединение будет размещением из 7
элементов по 3 элемента без повторений.
=
7 · 6 · 5 = 210.
Задача 4. Из колоды в 36 карт наудачу вынимается одна. Какова вероятность того, что будет вынута пика или туз?
Решение.
События А (выбрана пика) и событие В (появился туз) не являются
несовместными - выбрана пика и она же является тузом. Поэтому для
вычисления искомой вероятности события А
В пользуются формулой
Р(А
В) = Р(А) + Р(В) – Р(А
В).
Вероятность
событий Р(А), Р(В) и Р(А
В)
вычисляются:
- Р(А)
= 
= 
;
- Р(В)
= 
= 
;
- Р(А
В)
= 
.
Тогда Р(А
В)
= 
+ 
- 
= 
+ 
- 
= 
= 
,
§6. Задачи для самостоятельного решения.
Для выбора формулы при решении комбинаторных задач достаточно выяснить следующее:
- Учитывается ли порядок следования элементов в соединении? (если нет , то это сочетания)
- Все ли заданные элементы входят в соединение? ( порядок важен и входят все элементы, то это перестановки; если в соединение входят не все элементы и важен порядок, то это размещения).
Задача 1. Найдите количество трехзначных чисел, которые можно составить из цифр 1, 2, 3, 4, 5, 6, 0, если эти цифры не повторяются.
(Ответ: 180).
Задача 2. На соревнование по лёгкой атлетике приехало 12 спортсменов. Сколькими способами тренер может определить, кто из них побежит в эстафете 4 по 100 метров на первом, втором, третьем и четвёртом месте?
(Ответ: 11 880).
Задача 3. Есть 10 книг, из которых 4 учебника. Сколькими способами можно поставить эти книги на полку так, чтобы все учебники стояли рядом?
(Ответ: 120 960)
Задача 4. Найдите сколькими способами 5 мальчиков и 5 девочек могут занять в театре в одном ряду места с 1-го по 10-е , если мальчики будут сидеть на нечётных местах, а девочки на чётных?
(Ответ: 14 400).
Задача 5. В классе 12 учащихся успешно занимаются математикой. Сколькими способами можно выбрать из них троих для участия в математической олимпиаде?
(Ответ: 220).
Задача 6. Три цеха представили на заводской контроль изделия для выборочной проверки. Первый цех представил 30 изделий, второй - 20 изделий, третий - 50 изделий. Вероятность качественных изделий в первом цеху составляет 0,95, во втором цеху - 0,9, в третьем цеху - 0,85. Было выбрано одно изделие. Какова вероятность того, что это изделие первого цеха?
(Ответ: 32%).
Задача 7. На сборку телевизоров поступают микросхемы от двух поставщиков, причём 70% от первого поставщика и 30% от второго. Брак микросхем первого поставщика составляет 2%, а второго - 3%. Какова вероятность того, что взятая микросхема окажется бракованной?
(ответ: 2,3%).
Задача 8. Три цеха представили на заводской контроль изделия для выборочной проверки. Первый цех представил 30 изделий, второй - 20 изделий, третий - 50 изделий. Вероятность качественных изделий в первом цеху составляет 0,95, во втором цеху - 0,9, в третьем цеху - 0,85. Было выбрано одно изделие. Какова вероятность того, что это изделие третьего цеха?
(Ответ: 48%).
Задача 9. На сборку телевизоров поступают микросхемы от двух поставщиков, причём 70% от первого поставщика и 30% от второго. Брак микросхем первого поставщика составляет 2%, а второго - 3%. Какова вероятность того, что взятая микросхема окажется качественной?
(ответ: 97,7%).
Задача 10. Набирая номер телефона, абонент забыл две последние цифры и , помня лишь, что они различны, набрал их наугад. Какова вероятность того, что номер был набран правильно?
(ответ: 
).
Задача 11. В чемпионате страны по футболу участвуют 18 команд, причём каждые две команды встречаются между собой два раза. Сколько матчей играется в течение сезона?
(Ответ: 306).
Задача 12. Из 1 000 произвольно выбранных деталей приблизительно 4 бракованных. Сколько приблизительно бракованных деталей будет среди 2 400 деталей?
(Ответ: 10).
Задача 13. Среди 100 электроламп 5 с браком. Какова вероятность того, что выбранные наудачу 3 лампы окажутся исправными?
(Ответ: 0,86)
Задача 14. Из 50 деталей 18 изготовлены в первом цехе, 20 - во втором, а остальные - в третьем. Первый и третий цеха дают продукцию отличного качества с вероятность 0,9, а второй цех - с вероятностью 0,6. Какова вероятность того, что наудачу взятая деталь будет отличного качества?
(Ответ: 0,78)
Литература.
1. Башмаков Н.И. Математика: учебник для студентов учреждений среднего проф. образования - М, 2014;
2. Башмаков Н.И. Математика: (базовый уровень) 10 класс,- М, 2014;
3. Башмаков Н.И. Математика: (базовый уровень) 11 класс,- М, 2014;
4. Практусевич М.Я. Математика Алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа 10 класс: учебник для общеобразовательных учреждений(углублённый уровень), М, Просвещение, 2014;
5. Практусевич М.Я. Математика Алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа 11класс: учебник для общеобразовательных учреждений(углублённый уровень), М, Просвещение, 2014;
Дополнительная литература:
1. Н.В. Богомолов. Практические занятия по математике. Учебное пособие для средних специальных учебных заведений - 6-е издание, стер. - М, высшая школа, 2013
2. В.Н. Калинина. Математическая статистика: Учебное пособие для средних специальных учебных заведений. Панкин В.Ф. - 4 – е издание, исп. - М. Дрофа, 2012
3. Спирина М.С., Спирин П.А. Дискретная математика: учебник для студентов УСПО - М: издательство «Академия», 2012.
4. Спирина М.С., Теория вероятностей и математическая статистика: учебник для студентов УСПО - М: издательство «Академия», 2012.
5. Е.В. Филимонова «Математика» Учебное пособие для средних специальных учебных заведений. - Ростов на Дону, издательство «Феникс», 2013
Электронные ресурсы.
1. [Электронный ресурс] // единая коллекция цифровых образовательных ресурсов - Режим доступа: http – http://school-cjllection.edu.ru
2. [Электронный ресурс] // Федеральный центр информационно-образовательных ресурсов - Режим доступа: http://foior.cdu.ru
3. [Электронный ресурс] // Единое окно доступа к образовательным ресурсам - Режим доступа: http://window.edu.ru
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
