Методический материал для проведения итоговой аттестации по математики 10 класса профильного уровня

Итоговая проверочная работа по МАТЕМАТИКЕ (Профильный уровень) 10 класс

Вариант 1

1.   Решите уравнениеЕсли уравнение имеет более одного корня, в ответе запишите больший из корней.

2. На конференцию приехали 5 ученых из Швеции, 7 из Италии и 4 из Чехии. Каждый из них делает на конференции один доклад. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что двенадцатым окажется доклад ученого из Чехии.

3. В треугольнике ABC AC = 4, BC = 3, угол C равен 90°. Найдите радиус описанной окружности этого треугольника.

4. Найдите значение выражения

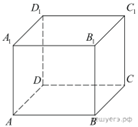
5. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известны длины рёбер: AB = 9, AD = 12, AA₁ = 18. Найдите синус угла между прямыми A₁D₁ и AC.

6. Небольшой мячик бросают под острым углом α к плоской горизонтальной поверхности земли. Максимальная высота полeта мячика, выраженная в метрах, определяется формулой  где  м/с — начальная скорость мячика, а g — ускорение свободного падения (считайте, что g=10 м/с). При каком наименьшем значении угла α (в градусах) мячик пролетит над стеной высотой 13,4 м на расстоянии 1 м?

7. Первая труба пропускает на 4 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 192 литра она заполняет на 4 минуты дольше, чем вторая труба?

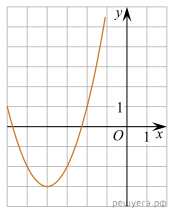
8. На рисунке изображён график функции вида , где числа a, b и c — целые. Найдите f(-12)

9. Вероятность того, что на тестировании по биологии учащийся О. верно решит больше 11 задач, равна 0,67. Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач.

Часть 2

10. а) Решите уравнение.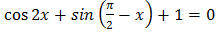

б) Найдите его корни, принадлежащие отрезку.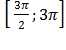

11. В правильной четырёхугольной призме ABCDA₁B₁C₁D₁ сторона основания AB равна 3, а боковое ребро. На рёбрах AB, A₁D₁ и C₁D₁ отмечены точки M, N и K соответственно, причём AM = A₁N = C₁K = 1.

а) Пусть L — точка пересечения плоскости MNK с ребром BC. Докажите, что MNKL — квадрат.

б) Найдите площадь сечения призмы плоскостью MNK.

12. Решите неравенство

13. Окружность проходит через вершины A, B и D параллелограмма ABCD, пересекает вторичную сторону BC в точке M и пересекает продолжение стороны CD за точку D в точке N.

а) Докажите, что AM=AN.

б) Найдите отношение CD:DN, если AB:BC=1:2, а

Итоговая проверочная работа по МАТЕМАТИКЕ (Профильный уровень) 10 класс

Вариант 2

1. Решите уравнениеЕсли уравнение имеет более одного корня, в ответе запишите меньший из корней.

2. В сборнике билетов по философии всего 45 билетов, в 18 из них встречается вопрос по теме "Пифагор". Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по теме "Пифагор".

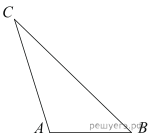
3. Найдите площадь треугольника, две стороны которого равны 21 и 2, а угол между ними равен 30°.

4. Найдите значение выражения

5. В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SO = 4, AC = 6. Найдите боковое ребро SC.

6. Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону  где t – время в секундах, амплитуда  В, частота /с, фаза  Датчик настроен так, что если напряжение в нeм не ниже чем  В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?

7. Первый час автомобиль ехал со скоростью 115 км/ч, следующие три часа — со скоростью 45 км/ч, а затем два часа — со скоростью 40 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

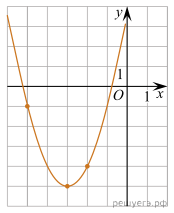
8. На рисунке изображён график функции  Найдите f(-9)

9. По отзывам покупателей Иван Иванович оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,8. Вероятность того, что этот товар доставят из магазина Б, равна 0,9. Иван Иванович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.

Часть 2

10. . а) Решите уравнение:

б) Найдите его корни, принадлежащие отрезку.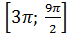

11. В правильной четырехугольной призме ABCDA₁B₁C₁D₁ точка K делит боковое ребро AA₁ в отношении AK : KA₁ = 1 : 2. Через точки B и K проведена плоскость α, параллельная прямой AC и пересекающая ребро DD₁ в точке M.

а) Докажите, что плоскость α делит ребро DD₁ в отношении DM : MD₁ = 2 : 1.

б) Найдите площадь сечения, если известно, что AB = 4, AA₁ = 6.

12. Решите неравенство

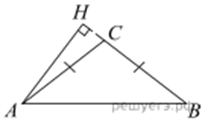
13. В треугольнике ABC стороны АB, BС и АС соответственно равны 9, 10 и 11. Высоты АН и BК пересекаются в точке О.

а) Докажите, что в треугольнике ABC угол B - острый.

б) Найдите площадь треугольника КОН.

Итоговая проверочная работа по МАТЕМАТИКЕ (Профильный уровень) 10 класс

Вариант 3

1.   Решите уравнениеЕсли уравнение имеет более одного корня, в ответе запишите больший из корней.

2. В классе 16 учащихся, среди них два друга — Вадим и Сергей. Учащихся случайным образом разбивают на 4 равные группы. Найдите вероятность того, что Вадим и Сергей окажутся в одной группе.

3. В треугольнике ABC  AC = BC, AB = 10, высота AH равна 3. Найдите синус угла BAC.

4. Найдите значение выражения

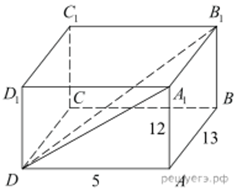5. Найдите угол DB₁A₁ прямоугольного параллелепипеда ABCDA₁B₁C₁D₁, в котором AB = 13, AD = 5, AA₁ = 12. Ответ дайте в градусах.

6. Деталью некоторого прибора является квадратная рамка с намотанным на неe проводом, через который пропущен постоянный ток. Рамка помещена в однородное магнитное поле так, что она может вращаться. Момент силы Ампера, стремящейся повернуть рамку, (в Нм) определяется формулой , где I=8A — сила тока в рамке, B=7∙10^-3  Тл — значение индукции магнитного поля, l=0,3 м — размер рамки,  — число витков провода в рамке,  — острый угол между перпендикуляром к рамке и вектором индукции. При каком наименьшем значении угла  (в градусах) рамка может начать вращаться, если для этого нужно, чтобы раскручивающий момент M был не меньше 0,63 Н  м?

7. Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

8. На рисунке изображён график функции вида  где числа a, b и c — целые. Найдите значение дискриминанта уравнения f(x)=0.

9. Вероятность того, что на тестировании по биологии учащийся П. верно решит больше 9 задач, равна 0,59. Вероятность того, что П. верно решит больше 8 задач, равна 0,65. Найдите вероятность того, что П. верно решит ровно 9 задач.

Часть 2

10. а) Решите уравнение.

б) Найдите его корни, принадлежащие отрезку.

11. В основании четырёхугольной пирамиды SKLMN лежит прямоугольник КLMN со сторонами КN=12, К L = 5. Длины боковых рёбер равны
 ,; SL = 9.

а) Докажите, что ребро SК является высотой пирамиды.

б) Найдите угол между прямыми SM и LN

12. Решите неравенство

13. Большее основание AD трапеции ABCD равно 8. Углы при этом основании равны по 75° . Угол между меньшим основанием и одной из диагоналей равен 45°.

а) Докажите, что АВ² = АО² + ОВ², где О - точка пересечения диагоналей.

б) Найдите площадь трапеции АВСD.

Итоговая проверочная работа по МАТЕМАТИКЕ (Профильный уровень) 10 класс

Вариант 4

1. Найдите корень уравнения . Если уравнение имеет более одного корня, то в ответе запишите больший из корней.

2. На чемпионате по прыжкам в воду выступают 20 спортсменов, среди них 3 прыгуна из Чехии и 2 прыгуна из Боливии. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что двенадцатым будет выступать прыгун из Чехии.

3. В треугольнике ABC AC=BC высота AH равна 20, AB=25 Найдите

4.Найдите значение выражения

5. В прямоугольном параллелепипеде  известны длины рёбер:AB=24, AD=10, AA₁=22  Найдите площадь сечения, проходящего через вершины A, A₁  и C

6. Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому   , где P — мощность излучения звезды (в ваттах), — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T — температура (в кельвинах). Известно, что площадь поверхности некоторой звезды равна  м² а мощность её излучения равна  Вт. Найдите температуру этой звезды в кельвинах.

7. Теплоход проходит по течению реки до пункта назначения 399 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 20 км/ч, стоянка длится 2 часа, а в пункт отправления теплоход возвращается через 42 часа после отплытия из него. Ответ дайте в км/ч.

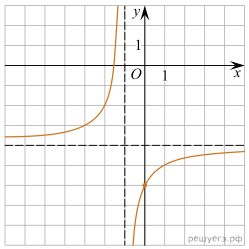
8. На рисунке изображён график функции вида  где числа a, b и c — целые. Найдите

9. Вероятность того, что на тестировании по математике учащийся П. верно решит больше 12 задач, равна 0,7. Вероятность того, что П. верно решит больше 11 задач, равна 0,79. Найдите вероятность того, что П. верно решит ровно 12 задач.

 Часть 2

11. а) Решите уравнение .

б) Найдите его корни, принадлежащие отрезку.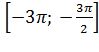

12. В прямом круговом цилиндре проведена образующая NN₁, точка N лежит в нижнем основании. Отрезок КМ₁ пересекает ось цилиндра, а точки К и М₁ лежат на окружностях нижнего и верхнего оснований соответственно.

а) Докажите, чтоявляется прямоугольным.

б) Найдите расстояние от точки N до прямой КМ₁ , если КN = 9,, N₁M₁ = 20.

13. Решите неравенство

14. Около окружности радиусом 3 описана равнобедренная трапеция ABCD (AD - большее основание), площадь которой равна 39.

а) Докажите, что синус угла при большем основании равен;.

б) Найдите площадь трапеции AMND, где Ми N - точки касания окружности с боковыми сторонами трапеции.