Лабораторные работы

по дисциплине

«Информационные технологии в профессиональной деятельности»

раздел «Электронные таблицы Excel»

Лабораторная работа № 1.

“Основы работы в программе Excel.”

I.ЦЕЛЬ: 1. Научиться вводить информацию в лист в программе Excel,

форматировать информацию, копировать информацию и

удалять её.

2. Научиться заполнять ячейку информацией в программе Excel,

форматировать ячейку и текст в ней и манипулировать

ячейками.

II.ОБОРУДОВАНИЕ: класс ПК

III.ХОД РАБОТЫ:

1.Изучить теоретический материал

2. Выполнить практическое задание.

Теоретическая часть.

Структура окна Excel.

Программа Excel предназначена для расчётов электронных таблиц. Файлом в программе Excel является Рабочая книга. Окно программы Microsoft Excel имеет все элементы присущие окну Word: заголовок окна, строку горизонтального меню, панель инструментов, три кнопки управления окном, две полосы прокрутки. Кроме того, окно Excel имеет и индивидуальные элементы: - это строка заголовков столбцов, обозначенных, латинскими буквами.

- это поле имени.

Указатель мышки имеет форму белого креста. Рабочая область электронных таблиц разбита на ячейки. Щелчком мышки по любой ячейке таблицы можно выделить ячейку. Адрес выделенной ячейки отражается в поле имени.

- это строка формул. В этой строке отражаются

формулы, которые набирают в ячейках. Кроме того, эта строка используется для редактирования старых записей в ячейках. Редактируют в строке формул, а результат редактирования будет в той ячейке, которая в момент редактирования была выделена.

- это строка с ярлычками листов рабочей

книги и кнопками прокрутки этих листов. Количество листов рабочей книги Excel, а так же имя листов можно менять. Для этого надо щёлкнуть правой кнопкой по ярлычку нужного вам листа и выбрать в ниспадающем меню один из пунктов: Добавить, Удалить, Переименовать и т. д. Кроме того, можно менять длину ячеек, если указатель мышки завести между заголовков столбцов, то появится чёрный крест в виде двойной стрелки.

Надо нажать левую кнопку мышки, и не отнимая пальца от кнопки, потянуть мышкой в сторону увеличения или уменьшения длины ячеек. Формулы в ячейки вводят только на английском языке, и только начиная со знака =. Например:=G6*10 или =200/F3 То есть, знаки математических операций такие же как и в языке Basic. Желательно их вводить с цифровой клавиатуры, её включают клавишей Num Lock.

Формат ячеек в Excel можно менять. Для этого нужно зайти в пункт Формат горизонтального меню. Если в ячейке после ввода информации появился знак [~~//////////~~], это значит изменён формат ячейки, иначе говоря информация в ячейке не соответствует её формату.

Любая функция, например: y = Cos x, состоит из имени функции (Cos), аргумента (х), результата (y).

Если в готовой таблице Excel произошло изменение каких-либо данных, то после ввода этих новых данных в таблицу, происходит автоматический пересчёт формул. Если на базе старых данных была построена диаграмма, то после ввода новых данных диаграмма тоже изменяется, приходя в соответствие с новыми данными. Это значит, готовую таблицу или диаграмму при необходимости можно редактировать.

Задание для практической работы.

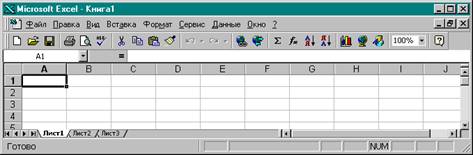
1. Создать файл на рабочем столе. (Имя файла «Лабраб7»). Выбрать в меню мышью “Файл” и нажать левую кнопку мыши.

2. Выйдет заставка с меню, спуститься мышью на слово “Создать” и нажать кнопку мыши.

3. Выйдет ниспадающее меню, передвигаться по нему мышью до слов “ Лист Microsoft Excel ”, нажать на кнопку мыши.

4. Выйдет пиктограмма листа с курсором, нажать Backspace, т.е .стереть всё перед курсором.

5. В чистом квадрате где находится курсор набрать имя файла (Лабраб7), нажать Enter, картинка изменит свой цвет.

6. Мышью вновь выбрать из верхнего меню слово “ Файл”, нажать кнопку мыши.

7. Выйдет меню, выбрать в нём мышью слово “Открыть”, нажать кнопку мыши, ждать пока машина не откроет лист на экране перед вами.

Свернуть, Развернуть, Закрыть

Меню

Заголовок

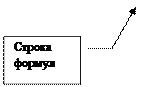8. Изучите панель инструментов данной программы. Поле листа разбито на ячейки. Каждая ячейка имеет свой адрес, например – А3,D5,F7 и т.д. Курсор на поле в виде белого креста.

9. Если курсор поместить между буквами в нумерации ячеек (верхняя строка), то курсор приобретает форму чёрного креста с поперечной двойной стрелкой.

10. Увеличить ширину столбца А.

11. Щёлкнуть мышью по ячейке Е10, она выделится, написать в ней свои фамилию, имя, отчество. Обратите внимание, что ваше Ф.И.О. появилось ещё и в строке формул после знака « = » . Щёлкнуть мышью по любой ячейке, Ваше Ф.И.О. из строки формул исчезнет, а в ячейке Е10 останется, явно выходя за её границы.

12. Увеличить длину ячейки до необходимых размеров, чтобы в неё входили Ваше Ф.И.О.

13. Щёлкнуть мышью по ячейке Е10, она выделится, но в ней нет курсора, т.е. запись непосредственно в ней нельзя откорректировать, но её можно поправить в строке формул, щёлкнув мышью в строке формул в то место записи, где необходимы исправления. Там появится курсор и можно удалять знаки и добавлять их.

14. Добавить перед своей фамилией номер группы. Затем щёлкнуть мышью по любой ячейке, вы увидите, что изменения сохранились в ячейке Е10.

15. Щёлкнуть мышью по ячейке Е10, она выделится. Выбрать в меню команду

Правка→Копировать , щёлкнуть по ней мышью и ячейка Е10 начнёт переливаться по периметру.

16. Щёлкнуть мышью по ячейке В5, она выделится. Нажать правую кнопку мышки, выйдет ниспадающее меню, в нём выбрать функцию «Вставить», в ячейке В5 появится та же информация, что и в Е10.

17. Щёлкнуть мышью по ячейке С8, она выделится. Нажать правую кнопку мышки, выйдет ниспадающее меню, в нём выбрать функцию «Вставить», в ячейке С8 появится та же информация, что и в Е10. Таким образом, вы произвели копирование информации из ячейки Е10 в ячейки В5 и С8.

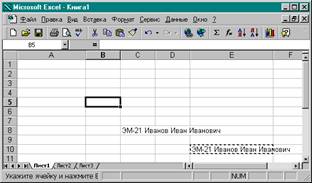18. Щёлкнуть мышью по ячейке В5, она выделится. Нажать кнопку Delete на клавиатуре. Информация из ячейки В5 исчезла, вы её удалили.

19. Таким образом, вы можете вводить информацию на лист построчно, менять длину ячеек под информацией, копировать из одной ячейки в другую, (аналогично можно копировать целую группу ячеек), можете корректировать информацию в ячейках и также удалять всю информацию из ячеек.

20. Перейти на Лист 2. Щелкнуть мышью на закладку «Лист 2».

21. Панель инструментов данного файла отличается от предыдущих, изучите её. Поле листа разбито на ячейки. Каждая ячейка имеет свой адрес, например – А3,D5,F7 и т.д.

22. Щёлкнуть мышью по ячейке А1, она выделится, написать в ней слово понедельник, щёлкнуть мышью по любой ячейке, а затем вновь по ячейке А1, появится чёрный квадратик в правом нижнем углу ячейки. Если подвести к нему стрелку мышки, то появится крест - это маркер заполнения. Если маркер заполнения потянуть мышью вниз, то все ячейки колонки под буквой А будут заполняться названиями дней недели в правильной последовательности. Проделайте это до ячейки А15 включительно.

23. Щёлкнуть мышью по ячейке В1, она выделится, написать в ней цифру 1, щёлкнуть мышью по ячейке В2, она выделится, написать в ней цифру 2, щёлкнуть мышью по любой ячейке, затем выделить две ячейки одновременно В1 и В2. Потянуть мышкой за маркер заполнения вниз до В15 включительно, все ячейки колонки В заполнит ряд натуральных чисел.

24. Аналогично заполни колонку С рядом из чётных чисел.

25. Выдели одновременно ячейки D1,С1,В1 и нажми мышью знак суммы

на панели инструментов. В ячейке D1 появится численное значение этой суммы. Аналогично заполни всю колонку D до ячейки D15 включительно. Затем по этой системе просуммируй все числа в колонке В, затем в колонке С и затем в D. То есть

данная программа может складывать числа как построчно так и по столбцам, это выгодная операция при бухгалтерских расчетах. В ячейке Е1 напиши слово март и постарайся при помощи маркера заполнения, заполнить всю колонку Е правильной последовательностью названий месяцев в году до ячейки Е15 включительно. После всех манипуляций лист должен иметь вид:

26. По окончанию работы необходимо всё напечатанное сохранить.

27. Выбрать мышью в верхнем меню слово “Файл”, нажать кнопку мыши.

28. Выйдет меню в котором надо выбрать слово “Сохранить”, и нажать кнопку мыши, машина будет сохранять при этом горит сигнал на дисководе и пока он не погаснет работу не начинать.

29. Закрыть файл..

Лабораторная работа № 2.

“Составление документов в программе Excel.”

I.ЦЕЛЬ: 1. Научиться вводить данные в ячейку в программе Excel,

редактировать их.

2. Научиться вводить формулы в ячейку в программе Excel,

редактировать их.

II.ОБОРУДОВАНИЕ: класс ПК

III.ХОД РАБОТЫ:

1.Изучить теоретический материал

2. Выполнить практическое задание.

Теоретическая часть.

а) Ввод формулы в ячейку.

Формула в ячейке начинается со знака «=» и может содержать следующие операторы ( табл.1 ), пары круглых скобок, числа, адреса ячеек, а также рабочего листа, вводимые в формулу командой Вставка à Функция или нажатием кнопки Мастер функция.

Таблица 1.

Оператор	Название
+	Сложение
-	Вычитание
*	Умножение
/	Деление
^	Возведение в степень
&	Конкатенация
=	Логическое сравнение
>	Логическое сравнение на больше
<	Логическое сравнение на меньше

Например: = ( А1 + А2 ) ^ 2 - возведение в квадрат суммы содержимого двух ячеек.

По умолчанию Excel создает в формулах относительные ссылки на адреса ячеек. Это означает, что Excel при копировании изменяет ссылки на ячейки в соответствии с новым положением формулы.

Например: пусть в ячейки А1,В1,А2 и В2 введены числа 1, 2, 3 и 5 соответственно; а в ячейку С1 введена формула =А1+В1.

Скопируем эту формулу в ячейку С. Для этого выделим ячейку С1, расположим указатель мыши на его маркере заполнения и протащим его вниз так, чтобы заполнить ячейку С2, после чего отпустим мышь. (Маркер заполнения - это черный квадрат в нижнем правом углу выделенной ячейки или диапазона ячеек. При расположении мыши на маркере заполнения он принимает вид черного креста.) После копирования в ячейку С2 будет введена формула =А2+В2 .

Для того чтобы скопировать формулу без изменения адресации - абсолютная ссылка - необходимо в формуле перед буквой и цифрой адреса ввести знак $, например $А$1. Это можно сделать нажав клавишу <F4>.

б) Форматы данных.

Форматирование производится для более наглядного представления результатов ввода или вывода числовых результатов. Форматирование данных в выделенной ячейке можно осуществить следующими способами:

1) выбрать пункт меню Формат, в нем выбрать команду Ячейки, затем выбрать вкладку Число;

2) щелчком правой кнопки мыши на ячейке вызвать контекстное меню и выбрать команду Формат ячеек.

Основные типы числовых форматов:

1) общий - принят по умолчанию;

2) числовой - позволяет определить число выводимых знаков после десятичной точки;

3) денежный - позволяет разделять тысячи и отобразить число с точностью до двух знаков после запятой;

4) процентный - позволяет вывести число, умноженное на 100, со знаком % и определить число выводимых знаков после десятичной точки;

5) дробный - при вводе в ячейку чисел в этом формате целую часть от дробной отделяют пробелом;

6) экспоненциальный - аЕв, а - мантисса, в - порядок, Е - 10. Например: число 0.0123 записывается как 1.23Е-2

7) текстовый - позволяет рассматривать числовые значения как текст.

в) Диапазон ячеек.

Форматировать данные можно как в одной ячейке, так и в диапазоне ячеек или группе несмежных диапазонов ячеек. Для адресации диапазона необходимо указать адреса верхней левой и нижней правой ячеек, разделив их двоеточием, например А1:С3 и С7:Е10.

Выделение диапазона ячеек производится следующим способом - щелкнуть угловую ячейку диапазона и перетащить указатель мыши на диагонально противоположную ячейку диапазона.

г) Выравнивание текста.

По умолчанию текст, введенный в ячейку выравнивается по ее левому краю, а числа - по правому. Изменить способ выравнивания в ячейке можно нажатием кнопок панели инструментов Форматирование (По левому краю, По центру, По правому краю).

Кроме того, вкладка Выравнивание диалогового окна Формат ячеек открываемого командой Формат®Ячейки, позволяет дополнительно изменять ориентацию текста в ячейке; выравнивать тест по вертикали и размещать перенос текста по словам внутри ячейки.

Если при расчетах в ячейке вместо числа появляется ########, это означает, что результат не помещается в ячейку и ее ширину необходимо увеличить.

Задание для практической работы.

Построить таблицу значений функции Z = 3X+Y ² .

Х изменяется на отрезке от 1 до 4 с шагом 0,5, Y - на отрезке от 4 до 10 с шагом 1.

1. На диске Рабочем столе создать “ Лист Microsoft Excel ”, документ назвать "Формула".

2. Открыть файл "Формула".

3. В ячейку А1 записать "Х", в ячейку А 2- " Y", в А3 - " Z".

4. Заполнить ячейки В1 - Н1 и В2 - Н2 значениями Х и Y соответственно.

5.
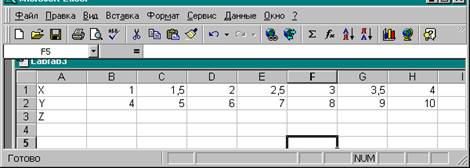
Таблица примет вид:

6. В ячейку В3 ввести формулу =3*В1+ В2^2.

7.
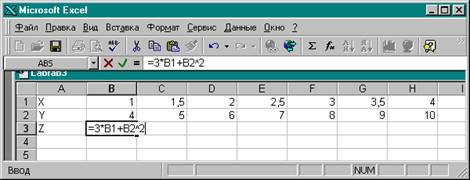
Таблица примет следующий вид:

8. Нажать клавишу <Enter>.

9. Таблица изменится:

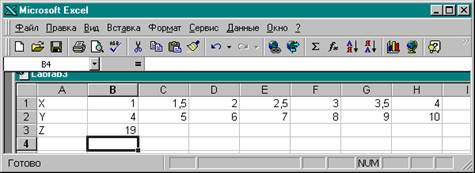
10. Выделить ячейку В3 и , используя маркер заполнения, скопировать формулу в ячейки С3 - Н3. Таблица значений функции Z = 3X+Y ² готова. Она имеет следующий вид:

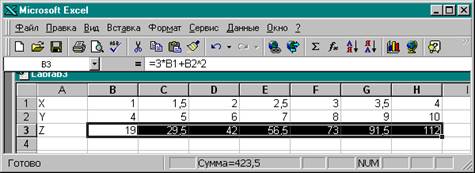
11. Самостоятельно построить таблицу значений функции F= (2A+B)/(C-4).

А изменяется на отрезке от 5 до 8,5 с шагом 0,5;

В изменяется на отрезке от 0 до 7 с шагом 1;

C изменяется на отрезке от 6 до 7,4 с шагом 0,2.

Для построения таблицы использовать ячейки А6 - I9.

12. Сохранить построенные таблицы.

â Дополнительное задание для практической работы.

На листе 3 построить таблицу значений функции:

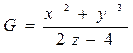для

Лабораторная работа №3.

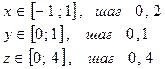
“Построение графиков функций в программе Excel.”

I.ЦЕЛЬ: Научиться использовать Мастер диаграмм и Мастер

функций для построения графиков в программе Excel.

II.ОБОРУДОВАНИЕ: класс ПК

III.ХОД РАБОТЫ:

1.Изучить теоретический материал

2. Выполнить практическое задание.

Теоретическая часть.

а) Работа с мастером функций.

Excel позволяет наглядно представлять результаты вычислений в виде графиков и гистограмм.. В качестве примера рассмотрим построение графика функции Y= cos²(px) на отрезке [ 0; 1 ].

При построении графика необходимо сначала построить таблицу ее значений при различных значениях аргумента, причем обычно аргумент изменяется с фиксированным шагом. Выберем шаг изменения аргумента 0.1.

1. Ввести в ячейки А1:А11 значения х: 0, 0.1, 0.2, … , 1. ( при заполнении ячеек можно использовать маркер заполнения (см. лаб. работу №7.1)).

2. Ввести в ячейку В2 формулу = cos(пи()*А1)^2.

Ввод формулы можно производить с клавиатуры или с помощью горизонтального меню : Вставка → Функция . Для ввода формулы можно также использовать кнопку Мастер функция на панели инструментов.

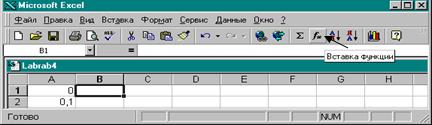В нашем случае выделим ячейку В1 и нажмем кнопку Мастер функций.

На появившемся диалоговом окне Мастер функций увидим два списка: Категория - список , включающий 11 категорий функций, и Функция - список имен функций, входящих в выбранную категорию.

3. Функция cos относится к категории Математические. Выберем эту функцию cos и нажмем кнопку ОК.

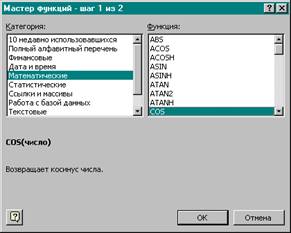4. На экране появится второе диалоговое окно Мастер функций.

5. В поле число вводим аргумент функции. В рассматриваемом примере это пи( )*А1. Нажав кнопку Мастер функция, расположенную перед полем Число, выберем функцию ПИ() и, нажав кнопку ОК, и вернемся в диалоговое окно функции cos.

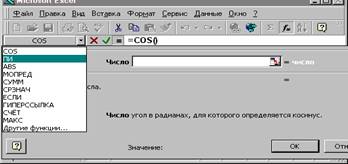6. С помощью клавиатуры введем знак *.

7. Щелкнув в ячейку А1 рабочего листа, введем А1.

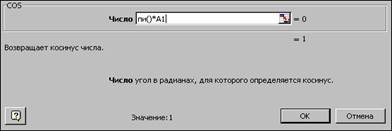8. Нажмем кнопку ОК .

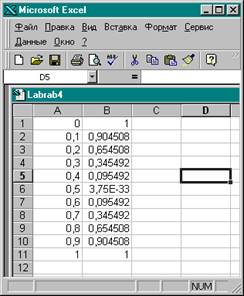
9. В ячейку В1 будет введена формула cos(пи()*А1). Ввод формулы можно производить и в ручную с клавиатуры.

10. Добавим с помощью клавиатуры в эту формулу операцию возведения в степень, получим cos(пи()*А1)^2. Нажмем кнопку ОК.

11.

Выделим ячейку В1, установим указатель мыши на маркере заполнения и протащим его вниз до ячейки В11. Таблица значений создана.

б) Работа с мастером диаграмм.

Excel предоставляет большой набор возможностей по графическому представлению данных. Имеется возможность выбора из 14 различных типов диаграмм, причем каждый вид диаграмм имеет несколько разновидностей. Создать диаграмму в Excel можно с помощью Мастера диаграмм, вызов которого осуществляется через горизонтальное меню (Вставка→ Диаграмма) или с панели инструментов нажатием соответствующей кнопки.

1. Выделим диапазон ячеек А1:В11, содержащий таблицу значений функции и ее аргумента.

2. Вызовем Мастер диаграмм.

На первом шаге выберем тип диаграммы - Точечная.

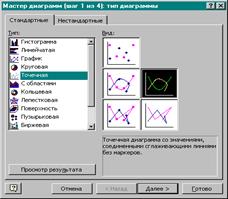4. Выберем вид графика - Сглаженный график.

5. Нажмем кнопку Далее.

Окно Мастера диаграмм изменить вид.

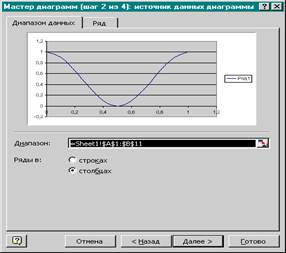7. На втором шаге в группе Ряды данных щелкнуть мышью в окно В столбцах.

8. Нажать кнопку Далее.

9. Окно Мастера диаграмм снова изменит свой вид.

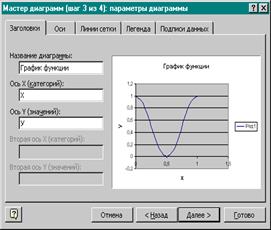10. На третьем шаге в поле Название диаграммы введем График функции.

11. В группу Название по осям в поля Категория (Х) и Категория (У) введем Х и У соответственно.

12.

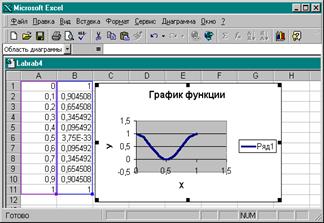Нажатием кнопки Готово завершим построение графика.

Задание для практической работы.

1.Построить таблицу значений и график функции Y = 4Sin²(3πX ) на отрезке [0; 2] с шагом 0,2.

2. Сохранить построенные таблицу и график.

â Дополнительное задание для практической работы.

На листе 3 построить таблицу значений и график функции:

для

Лабораторная работа № 4

“Построение графиков функций с одним условием.”

I.ЦЕЛЬ: Научиться строить графики функций с одним условием

в программе Excel.

II.ОБОРУДОВАНИЕ: класс ПК.

III.ХОД РАБОТЫ:

1.Изучить теоретический материал

2. Выполнить практическое задание.

Теоретическая часть.

Excel позволяет наглядно представлять результаты вычислений в виде графиков не только простых функций, но и функций с условием. В качестве примера рассмотрим построение графика функции

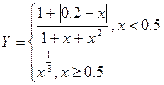
на отрезке [ 0; 1 ].

Выберем шаг изменения аргумента 0.1. Этот график строится так же, как и в лабораторной работе №4, за исключением - в ячейку В1 вводится формула:

=ЕСЛИ(А1<0,5;(1+АВS(0,2-А1))/(1+А1+А1^2);А1^(1/3)).

Синтаксис логической функции ЕСЛИ:

ЕСЛИ(лог._ выражение; ; значение_ если_ ложь)

Функция ЕСЛИ возвращает значение_ если_ истина в случае когда лог._ выражение имеет значение Истина, и значение значение_ если_ ложь - в противном случае. Функция ЕСЛИ возвращает значение_ если_ истина в случае когда лог._ выражение имеет значение Истина, и значение значение_ если_ ложь - в противном случае. Функция ЕСЛИ используется для организации переходов в зависимости от значения лог._ выражение. Логическое выражение строится из логических отношений (т.е. знаков <, >, =, ≤, ≥) и логических функций и логических функций И, ИЛИ, НЕ.

Синтаксис логической функции И:

И(лог._ значение1; лог._ значение2;…)

Функция И возвращает значение Истина в случае когда все аргументы имеет значение Истина, и значение Ложь, если хотя бы один аргумент имеет значение Ложь.

Синтаксис логической функции И:

ИЛИ(лог._ значение1; лог._ значение2;…)

Функция ИЛИ возвращает значение Истина в случае когда хотя бы один из аргументов имеет значение Истина, и значение Ложь, когда все аргументы имеют значение Ложь.

Синтаксис логической функции НЕ:

НЕ(лог._ значение)

Функция НЕ меняет на противоположное логическое значение своего аргумента.

Построение графика функции.

1. Ввести в ячейки А1:А11 значения х: 0, 0.1, 0.2, … , 1. ( при заполнении ячеек можно использовать маркер заполнения (см. лаб. работу №2)).

2. Ввести в ячейку В2 формулу

=ЕСЛИ(А1<0,5;(1+АВS(0,2-А1))/(1+А1+А1^2);А1^(1/3))

В нашем случае выделим ячейку В1 и нажмем кнопку Мастер функций.

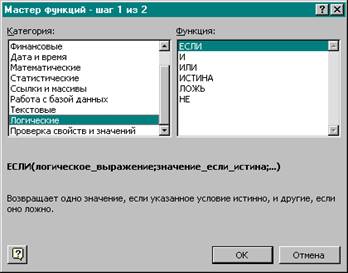
На появившемся диалоговом окне Мастер функций увидим два списка: Категория - список , включающий 11 категорий функций, и Функция - список имен функций, входящих в выбранную категорию.

Функция ЕСЛИ относится к категории Логические. Выберем функцию ЕСЛИ и нажмем кнопку ОК.

4. На экране появится второе диалоговое окно Мастер функций.

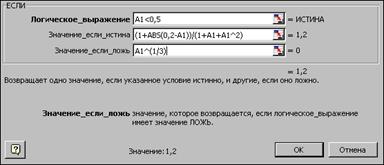
5. С помощью клавиатуры в поля Логическое выражение, Значение_если_истина и Значение_если_ложь вводим соответствующие значения.

6. Нажмем кнопку ОК .

7. Выделим ячейку В1, установим указатель мыши на маркере заполнения и протащим его вниз до ячейки В11. Таблица значений создана.

8. 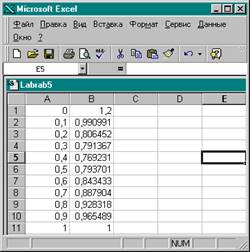Выделим диапазон ячеек А1:В11, содержащий таблицу значений функции и ее аргумента.

9. Вызовем Мастер диаграмм.

10. На первом шаге выберем тип диаграммы - Точечная.

11. Выберем вид графика - Сглаженный график.

12. Нажмем кнопку Далее.

13. Окно Мастера диаграмм

изменить вид.

На втором шаге в группе Ряды данных щелкнуть мышью в окно

В столбцах.

14. Нажать кнопку Далее.

15. Окно Мастера диаграмм снова изменит свой вид.

16. На третьем шаге в поле Название диаграммы введем График функции.

17. В группу Название по осям в поля Категория (Х) и Категория (У) введем Х и У соответственно.

18. Нажатием кнопки Готово завершим построение графика.

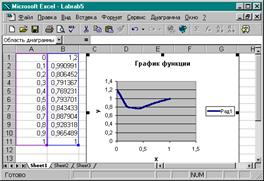Задания для практической работы.

1.Построить таблицу значений и график функции

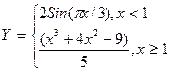на отрезке [0; 2] с шагом 0,2.

2. Сохранить построенные таблицу и график.

3. Закрыть программу Excel.

Дополнительное задание для практической работы.

На листе 3 построить таблицу значений и график функции:

для

ЛАБОРАТОРНАЯ РАБОТА № 5.

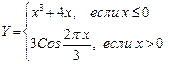
“Построение графиков функций с двумя условиями.”

I.ЦЕЛЬ: Научиться строить графики функций с двумя условиями

в программе Excel.

II.ОБОРУДОВАНИЕ: класс ПК.

III.ХОД РАБОТЫ:

1.Изучить теоретический материал

2. Выполнить практическое задание.

Теоретическая часть.

Excel позволяет наглядно представлять результаты вычислений в виде графиков не только простых функций, но и функций с двумя условием. Сначала вспомним правила записи основных логических функций.

Построение графика функции.

В качестве примера рассмотрим построение графика функции

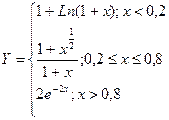на отрезке [ 0; 1 ].

Выберем шаг изменения аргумента 0.1. Этот график строится так же, как и в лабораторных работах №4 и №5, за исключением того, что в ячейку В1 вводится формула:

=ЕСЛИ(А1<0,2;1+Ln(1+А1);

ЕСЛИ(И(А1>=0,2;A1<=0.8);(1+A1^0.5)/(1+A1);2*EXP(-2*A1)))

Заметим, что в ячейку В1 можно ввести и более простую формулу, которая приведет к тому же результату:

=ЕСЛИ(А1<0,2;1+Ln(1+А1);

ЕСЛИ(A1<=0.8;(1+A1^0.5)/(1+A1);2*EXP(-2*A1)))

1. Ввести в ячейки А1:А11 значения х: 0, 0.1, 0.2, … , 1. ( при заполнении ячеек можно использовать маркер заполнения (см. лаб. работу №7.1.)).

2. Ввести в ячейку В2 формулу

=ЕСЛИ(А1<0,2;1+Ln(1+А1);

ЕСЛИ(И(А1>=0,2;A1<=0.8);(1+A1^0.5)/(1+A1);2*EXP(-2*A1)))

или

=ЕСЛИ(А1<0,2;1+Ln(1+А1);

ЕСЛИ(A1<=0.8;(1+A1^0.5)/(1+A1);2*EXP(-2*A1)))

В нашем случае выделим ячейку В1 и нажмем кнопку Мастер функций.

3. Функция ЕСЛИ относится к категории Логические. Выберем функцию ЕСЛИ и нажмем кнопку ОК.

4. На экране появится второе диалоговое окно Мастер функций.

5. С помощью клавиатуры в поля Логическое выражение, Значение_если_истина вводим соответствующие значения.

6. Для заполнения поля и Значение_если_ложь, во втором окне Мастера функций выберем еще раз функцию ЕСЛИ и заполним все необходимые поля параметрами второй функции ЕСЛИ.

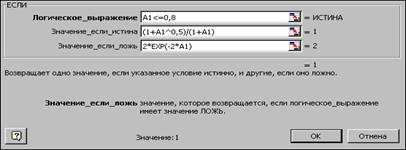7. Нажмем кнопку ОК .

8. Выделим ячейку В1, установим указатель мыши на маркере заполнения и протащим его вниз до ячейки В11. Таблица значений создана.

9. Выделим диапазон ячеек А1:В11, содержащий таблицу значений функции и ее аргумента.

10. Вызовем Мастер диаграмм.

11. На первом шаге выберем тип диаграммы - Точечная.

12. Выберем вид графика - Сглаженный график.

13. Нажмем кнопку Далее.

14. Окно Мастера диаграмм изменить вид.

15. На втором шаге в группе Ряды данных щелкнуть мышью в окно В столбцах.

16. Нажать кнопку Далее.

17. Окно Мастера диаграмм снова изменит свой вид.

18. На третьем шаге в поле Название диаграммы

введем График функции.

19. В группу Название по осям в поля Категория (Х) и Категория (У) введем Х и У соответственно.

20.

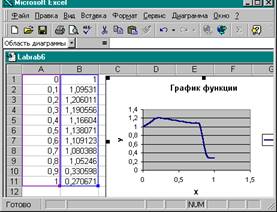Нажатием кнопки Готово завершим построение графика.

Задания для практической работы.

1.Построить таблицу значений и график функции

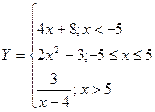на отрезке [-10; 10] с шагом 1.

2. Сохранить построенные таблицу и график.

3. Закрыть программу Excel.

â Дополнительное задание для практической работы.

На листе 3 построить таблицу значений и график функции:

для
Лабораторная работа № 6.

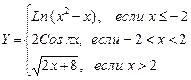
“Решение системы двух уравнений графическим

способом в программе Excel.”

I.ЦЕЛЬ: Научиться строить несколько графиков функций в одной

системе координат в программе Excel.

II.ОБОРУДОВАНИЕ: класс ПК

III.ХОД РАБОТЫ:

1.Изучить теоретический материал

2. Выполнить практическое задание.

Теоретическая часть.

а) Построение двух графиков функций в одной системе координат.

Рассмотрим пример построения в одной системе координат графиков следующих двух функций:

Y=2Sin(x) и Z=3Cоs(2x)-Sin(x) на отрезке [-3;0]

1. Ввести в ячейки А2:А17 значения переменной х от -3 до 0 с шагом 0,2

( при заполнении ячеек можно использовать маркер заполнения

(см. лаб. работу № 7.2)).

2. В ячейки В1 и С1 ввести Y и Z соответственно.

3. В ячейки В2 и С2 ввести формулы

=2*Sin(А2) и =3*Cos(2*А2)-Sin(А2)

Ввод формулы можно производить с клавиатуры или с помощью горизонтального меню : Вставка → Функция . Для ввода формулы можно также использовать кнопку Мастер функция на панели инструментов.

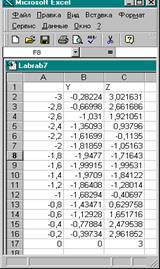( См. лабораторные работы №7.2 - №9.2).

4. Выделить диапазон ячеек В2:С2, установить указатель мыши на маркере заполнения этого диапазона ячеек и протащить его вниз так, чтобы заполнить диапазон В2:С17.

5. Выделить диапазон А1:С17, в который внесены таблицы значений двух функций, их общий аргумент и заголовки столбцов В и С.

6. Вызвать Мастер диаграмм. (См. лабораторные работы № 8 - №9.2.).

7. На первом шаге выбрать тип диаграммы - Точечная.

8. Выбрать вид графика - Сглаженный график.

9. Нажать кнопку Далее.

10. Окно Мастера диаграмм изменить вид.

11. На втором шаге в группе Ряды данных щелкнуть мышью в окно В столбцах.

12. Нажать кнопку Далее. Окно Мастера диаграмм снова изменит свой вид.

13. На третьем шаге в поле Название диаграммы ввести Графики функций.

14. В группу Название по осям в поля Категория (Х) и Категория (У) ввести Х и У соответственно.

15. 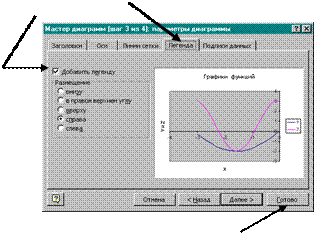Щелкнуть мышью по вкладке Легенда и в открывшейся вкладке щелкнуть мышью в окне Добавить легенду.

16. Нажатием кнопки Готово завершить построение графика.

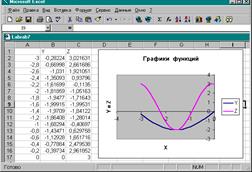
б) Решение системы двух уравнений графическим способом.

В математике одним из способов решения системы двух уравнений является графический способ. Для графического решения системы двух уравнений с двумя переменными надо построить в одной системе координат графики обоих уравнений и найти координаты точек пересечения этих графиков.

Рассмотрим следующий пример: Решить графически систему уравнений

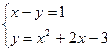
Для того, что бы решить систему уравнений графически необходимо:

1. Выразить значения У через Х

2. Построить в одной системе координат графики функций:

У1= Х+1 и У2=Х²+2Х-3

Для построения графиков выберем интервал [-5;5] и шаг 0,5.

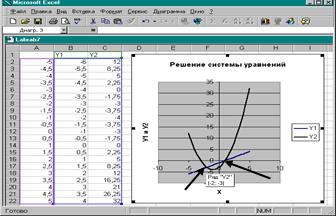
Графики будут иметь вид:

3. Подведем указатель мыши к местам пересечения графиков функций и считаем значения координат точек пересечения. Значения координат точек пересечения и будут решением системы уравнений. В нашем примере это точки с координатами (-2;-3) и (1;0). Таким образом, система уравнений имеет следующие решения :

Х= -2; У= -3 и Х= 1; У= 0.

Задания для практической работы.

1. Решить систему уравнений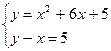

Для построения графиков выбрать интервал [-6; 6] и шаг 0,5.

2. Записать полученные значения корней в ячейки E2 и E3.

3. Сохранить построенные таблицу и график.

4. Закрыть программу Excel.

â Дополнительное задание для практической работы.

На листе 3 решить систему уравнений графическим способом:

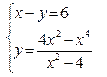
Для построения графиков выбрать интервал [-10;10] с шагом 1.
Лабораторная работа № 7

“Построение поверхности в программе Excel.”

I.ЦЕЛЬ: Научиться использовать Мастер диаграмм и Мастер

функций для построения поверхности в программе Excel.

II.ОБОРУДОВАНИЕ: класс ПК.

III.ХОД РАБОТЫ:

1.Изучить теоретический материал

2. Выполнить практическое задание.

Теоретическая часть.

Excel позволяет строить не только графики функций с одной переменной, но и поверхности, которые описываются функциями с двумя переменными.. В качестве примера рассмотрим построение поверхности Z= X²- Y² при изменении X и Y на отрезке [ -1; 1 ] с шагом 0.2

При построении поверхности необходимо сначала построить таблицу ее значений при различных значениях аргумента.

1. Ввести в ячейки B1:L12 значения X: -1;-0.8; … ; 1, а в диапазон ячеек А2:А12 - такую же последовательность значений переменной Y ( при заполнении ячеек можно использовать маркер заполнения (см. лаб. работу №7.2)).

2. Ввести в ячейку В2 формулу = $А2^2-B$1^2.

3. Выделить ячейку В2, установить указатель мыши на ее маркере заполнения и

протащить его так, чтобы заполнить диапазон B2:L12. Знак $, стоящий перед буквой в имени ячейки дает абсолютную ссылку на столбец с данным именем, а

знак $, стоящий перед цифрой - абсолютную ссылку на строку с этим именем. Поэтому при протаскивании (копировании) формулы из ячейки В2 в ячейки диапазона B2:L12 в них будет найдено значение Z при соответствующих значениях X и Y.

4. Выделить диапазон ячеек А1:L12, содержащий таблицу значений функции и ее

аргументов.

5. Вызвать Мастер диаграмм.

6. На первом шаге выберем тип диаграммы - Поверхность.

Выберем вид поверхности, например 1.

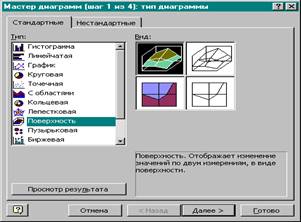8. Нажмем кнопку Далее.

9. Окно Мастера диаграмм изменить вид.

10. На втором шаге Мастера диаграмм заполняем диалоговое окно следующим образом. В группе Ряды данных находятся щелкнуть мышью в окно В строках.

11.Нажать кнопку Далее.

12. Окно Мастера диаграмм снова изменит свой вид.

13. На третьем шаге в поле Название диаграммы введем Поверхность.

14. В группу Название по осям в поля Категория (Х) ,Категория (У) и

Категория (Z) введем Х , У и Z. соответственно.

15. Щелкнуть мышью по вкладке Легенда и в открывшейся вкладке щелчком мыши

установить переключатель Добавить легенду в положение Нет.

16.
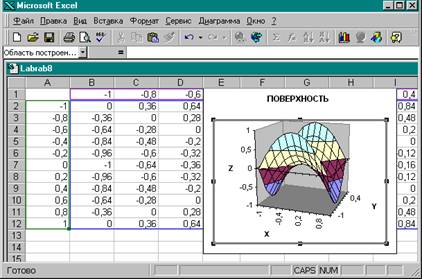
Нажатием кнопки Готово завершим построение поверхности.

Задание для практической работы.

1.Построить поверхность Z = 3x²- 2Sin²(y )y² , изменяя х и у на отрезке [-1; 1]

с шагом 0,2.

2. Сохранить построенную поверхность.

3. Закрыть программу Excel.

â Дополнительное задание для практической работы.

№ 1. На листе 3 построить поверхность:

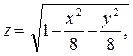изменяя x и y на отрезке [-2;2] с шагом 0,2.

№ 2. На листе 3 построить поверхность:

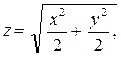изменяя x и y на отрезке [-4; 4] с шагом 0,4

Лабораторная работа № 8

“Решение нелинейных уравнений в программе Excel.”

I.ЦЕЛЬ: Научиться использовать графики функций для нахождения

корней нелинейных уравнений в программе Excel.

II.ОБОРУДОВАНИЕ: класс ПК.

III.ХОД РАБОТЫ:

1.Изучить теоретический материал

2. Выполнить практическое задание.

Теоретическая часть.

Программа Excel позволяет находить корни нелинейных уравнений. Рассмотрим пример нахождения всех корней уравнения:

х³+ 0,01х²- 0,7044х + 0,139104 = 0

Известно, что у полинома третьей степени имеется не более трех вещественных корней. Для нахождения корней их предварительно нужно локализовать, а затем уточнить с заданной погрешностью. С этой целью необходимо

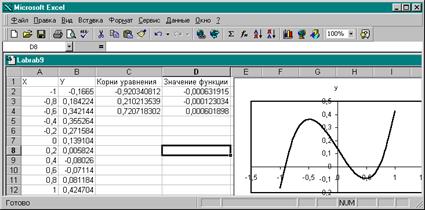
1. Построить график функции или ее протабулировать, например, на отрезке [-1;1] с шагом 0,2. Таблица значений и график функции

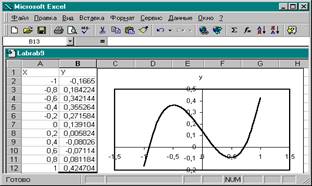у = х³+ 0,01х²- 0,7044х + 0,139104 будут следующими:

Корнями уравнения будут такие значения х, при которых значение у равно 0.

2. Из таблицы и графика видно, что нам удалось локализовать все корни уравнения, причем они находятся на интервалах [-1;-0,8], [0,2;0,4], [0,6;0,8], так как именно здесь полином меняет знак.

Найдем корни полинома методом последовательного приближений с помощью команды горизонтального меню Сервис → Подбор параметра. Относительная погрешность вычислений и предельное число итераций задаются на вкладке Вычисления диалогового окна Параметры, открываемого командой горизонтального меню Сервис → Параметры. Зададим относительную погрешность вычислений равной 0,00001, а предельное число итераций равной 1000. В качестве начальных значений приближений корням можно взять любые точки из отрезков локализации корней, например -0,9; 0,3 и 0,7.

3. Ввести в ячейку С1 название столбца "Приближение", а в ячейку D1 - "Значение функции".

4. В ячейку С2 ввести значение начального приближения -0,9, в ячейку С3 ввести 0,3 и в ячейку С4 ввести 0,7.

5. В ячейку D2 ввести формулу: =С2^3-0,01*C2^2-0,7044*C2+0,139104.

Выделить ячейку D2 и скопировать на диапазон D2:D4. Таким образом, в ячейках D2:D4 вычисляются значения полинома при значениях аргумента, введенного в ячейках С2:С4 соответственно .

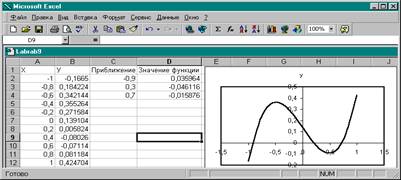7. В горизонтальном меню выбрать команду Сервис → Подбор параметра.

8. В поле Установить в ячейке диалогового окна ввести D2.

9. В поле Значение ввести 0.

10.

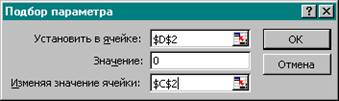В поле Изменяя значение ячейки ввести С2.

Вводить ссылки на ячейки в поля диалогового окна Подбор параметра удобнее не с клавиатуры, а щелчком мыши на соответствующей ячейке. При этом Excel автоматически будет превращать их в абсолютные ссылки (в нашем примере $C$2 и $D$2.

11. Нажать кнопку ОК.

12.

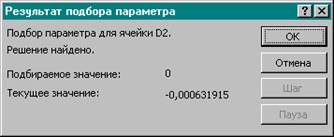Средство подбора параметров находит приближенное значение корня, которое помещает в ячейку С2. В данном случае оно равно -0,9203408.

13. Нажать кнопку ОК.

14. Аналогично в ячейки С3 и С4 поместить два оставшихся корня. Они равны 0,2102135 и 0,720718.

15. Изменить содержимое ячейки С1 на Корни уравнения.

Задания для практической работы.

1. Найти все корни уравнения х³ - 2,56х² - 1,3251х + 4,395006 = 0

Для построения таблицы табуляции и графика выбрать интервал [-5; 5] и шаг 0,5.

2. Записать полученные значения корней в ячейки С2:С4.

3. Сохранить полученные данные.

4. Закрыть программу Excel.

â Дополнительное задание для практической работы.

№ 1. На листе 2 решить нелинейное уравнение:

Для построения таблицы табуляции и графика выбрать интервал [-3; 3] с шагом 0,2.

№ 2. На листе 3 решить нелинейное уравнение:

Для построения таблицы табуляции и графика выбрать интервал [-2; 2] с шагом 0,2.

Лабораторная работа № 9

“Работа с массивами данных в программе Excel.”

I.ЦЕЛЬ: Научиться выполнять простейшие операции над массивами

данных в программе Excel.

II.ОБОРУДОВАНИЕ: класс ПК.

III.ХОД РАБОТЫ:

1.Изучить теоретический материал

2. Выполнить практическое задание.

Теоретическая часть.

Excel позволяет обрабатывать большой объем информации. Очень часто данные удобно представлять в виде таблиц. При работе с таблицами часто возникает необходимость применить одну и ту же операцию к целому диапазону ячеек или провести расчеты по формулам, зависящим от большого массива данных.

а) Простейшие операции над массивами.

В качестве первого примера простой операции над массивами рассмотрим умножение массива А1:В2, в который введены четыре любых числа, на число 5. Для выполнения операции умножения массива на число необходимо:

1. Выделить на рабочем листе область, например D1:E2, того же размера, как и массив - множимое.

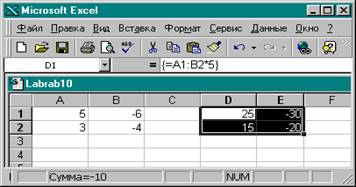
2. Теперь установим курсор в строке формул и введем формулу =А1:В2*5.

3. Закончить ввод необходимо не как обычно нажатием клавиши <Enter>, а нажатием клавиш <Ctrl> + <Shift> + <Enter>.

4. После выполнения этих действий Excel заключит формулу в строке формул в фигурные скобки:{ =А1:В2*5}, в ячейках D1:E2 появятся значения массива-произведения.

5. При работе с массивами формула действует на все ячейки диапазона. Нельзя изменять отдельные ячейки в операндах формулы.

6. Аналогично можно вычислить:

а) сумму ( разность) массивов { =А1:В2 + D1:E2 },

б) поэлементное произведение (деление) массивов { =А1:В2*D1:E2 },

в) массив, каждый элемент которого связан посредством некоторой функции с соответствующим элементом первоначального массива { = Sin (А1:В2)}.

7. Вычислить произведение массивов А1:В2 и D1:E2.

8. Результат вычислений поместить в ячейки А4:В5.

9. Для этого выделить диапазон ячеек А4:В5.

10. В строку формул ввести =А1:В2*D1:E2.

11. Нажать комбинацию клавиш <Ctrl> + <Shift> + <Enter>.

12.

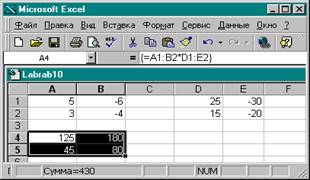В ячейках А4:В5 появится результат вычислений:

б) Встроенные функции для работы с массивами.

В Excel имеются следующие специальные функции для работы с матрицами:

Категория "Математические":

МОБР - Обратная матрица;

МОПРЕД - Определитель матрицы;

МУМНОЖ - Матричное произведение двух матриц;

Категория "Ссылки и массивы":

ТРАНСП - Транспонированная матрица.

Во всех случаях при работе с матрицами перед вводом формулы надо выделить область на рабочем листе, куда будет выведен результат вычислений.

Рассмотрим следующий пример: Вычислить значение У по формуле У=В^ТАВ,

где А- квадратная матрица, В - вектор, символ (^Т) обозначает операцию транспонирования матрицы. (Операцией транспонирования матрицы называется замена строк матрицы ее столбцами и наоборот.)

Таким образом, если задана матрица 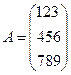, то транспонированная матрица будет иметь вид: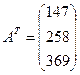

В нашем примере матрицы А и В заданы в следующем виде:

, .

1. Ввести квадратичную матрицу А в диапазон ячеек А1:В2.

2. Ввести вектор В в диапазон ячеек D1:D2.

3. Для вычисления У ввести в ячейку F1 формулу:

{=МУМНОЖ(МУМНОЖ(ТРАНСП(D1:D2);А1:В2);D1:D2)}

Формулу можно вводить как вручную с клавиатуры, так и использовать

Мастер функций.

Не забудьте, что для ввода формулы необходимо нажать клавиши

<Ctrl> + <Shift> + <Enter>.

4. После выполненных действий в ячейке F1 появится значение У=24.

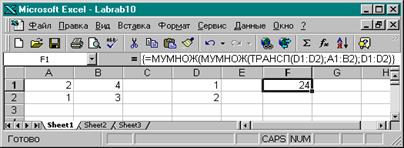Задание для практической работы.

№1.Вычислить значение квадратичной формы Z=Y^TA^TAY, где А - квадратная матрица,

Y - вектор-столбец. Результат записать в ячейку F1. Если выделить для А и У диапазоны ячеек А1:В2 и D1:D2 соответственно, то формула ввода будет следующей:

{=МУМНОЖ (ТРАНСП(D1:D2); МУМНОЖ (ТРАНСП (А1:В2); МУМНОЖ (А1:В2;D1:D2)))}.

Данные для ввода:

, .

Сохранить на Листе 1.

№2. Найти разность и сумму матриц: , .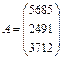

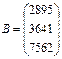Результат поместить в ячейки А5:D7 и А9:D11.

Сохранить на Листе2.

№3. Вычислить значение квадратичной формы Z=Y^TA³Y, где ,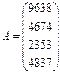

Результат поместить в ячейку Н1.

Сохранить на Листе 3.

По окончанию работы: Закрыть программу Excel.

â Дополнительное задание для практической работы.

Создать Лист Microsoft Excel. Назвать его «Дополнение».

№1. На листе 1 выполнить задание: Найти сумму и матричное произведение матриц:

C = 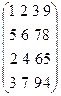и D =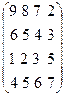

Результат поместить в ячейки A7 : D10 и A12 : D15.

№2. На листе 2 выполнить задание: Вычислить значение квадратичной формы

Z = X^T B² X , где

B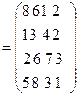 X= Результат поместить в ячейку H1.

Лабораторная работа № 10.

“Решение систем линейных уравнений методом

Крамера в программе Excel.”

I.ЦЕЛЬ: Научиться находить корни системы линейных

уравнений в программе Excel, используя функции

для работы с матрицами.

II.ОБОРУДОВАНИЕ: класс ПК.

III.ХОД РАБОТЫ:

1.Изучить теоретический материал

2. Выполнить практическое задание.

Теоретическая часть.

Вначале вспомним встроенные функции Excel для работы с матрицами:

Категория "Математические":

МОБР - Обратная матрица;

МОПРЕД - Определитель матрицы;

МУМНОЖ - Матричное произведение двух матриц;

Категория "Ссылки и массивы":

ТРАНСП - Транспонированная матрица.

Во всех случаях при работе с матрицами перед вводом формулы надо выделить область на рабочем листе, куда будет выведен результат вычислений. Формулы можно вводить вручную с клавиатуры, а также использовать Мастер функций.

Не забудьте, что для ввода формулы необходимо нажать клавиши

<Ctrl> + <Shift> + <Enter>.

Функции работы с матрицами могут также использоваться для нахождения корней системы линейных уравнений.

Рассмотрим следующий пример:

Решить систему линейных уравнений с двумя неизвестными

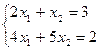
Данную систему можно записать в матричном виде следующим образом: АХ=В,

- матрица коэффициентов, - матрица свободных членов,

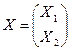- матрица неизвестных.

Решение линейной системы АХ=В имеет вид: Х=А^-1В. Здесь А^-1 - матрица, обратная по отношению к матрице А.

1. Запишем матрицу А в диапазон ячеек А1:В2.

2. Запишем матрицу В в диапазон ячеек D1:D2.

3. Под запись решения системы выделим диапазон ячеек А4:А5.

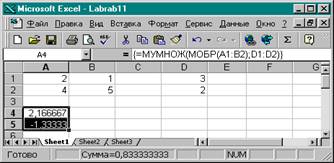
4. Введем в диапазон ячеек А4:В5 формулу =МУМНОЖ(МОБР(А1:В2);D1:D2).

5. Нажать клавиши <Ctrl> + <Shift> + <Enter>.

6. В ячейки А4:А5 запишутся значения корней системы (2,166667 и -1,33333)

7. Лист Excel будет иметь вид:

Задание для практической работы.

№1. Решить систему линейных уравнений:

Результат поместить в ячейки А5:А6. Сохранить на Листе1.

№2. Решить систему линейных уравнений:

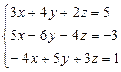
Результат поместить в ячейки А5:С5. Сохранить на Листе2.

№3. Решить систему линейных уравнений:

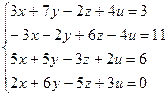
Результат поместить в ячейки В6:Е6. Сохранить на Листе 3.

По окончанию работы: Закрыть программу Excel.

â Дополнительное задание для практической работы.

Создать Лист Microsoft Excel. Назвать его «Дополнение».

№1. На листе 1 выполнить задание: Решить систему линейных уравнений:

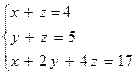
Результат поместить в ячейки A7 : A9.

№2. На листе 2 выполнить задание: Решить систему линейных уравнений:

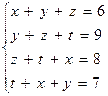
Результат поместить в ячейки A7 : A10.
Лабораторная работа 11.

“Решение обратной задачи в программе Excel.”

I.ЦЕЛЬ: Научиться находить аналитическую запись функции по

заданной таблице ее значений в программе Excel.

II.ОБОРУДОВАНИЕ: класс ПК

III.ХОД РАБОТЫ:

1.Изучить теоретический материал

2. Выполнить практическое задание.

Теоретическая часть.

Очень часто необходимо по набору значений функции записать формулу, которая эту функцию описывает. Любая обратная задача в своей постановке является некорректной и в связи с этим не имеет единственного решения без каких-либо допущений (ограничений).

Рассмотрим задачу аппроксимации.

Постановка: пусть функция y = f(x) задана таблично. Требуется найти ее аналитическое выражение.

Ограничение: предположительно известен общий вид этой функциональной зависимости.

Пусть имеются две наблюдаемые величины х и у, например, объем реализации фирмы, торгующей подержанными автомобилями, за шесть недель ее работы.

Х_i	1	2	3	4	5	6
У_i	7	9	12	13	14	17

Здесь Х_i - отчетная неделя, а У_i - объем реализации за эту неделю. Необходимо создать математическую модель, позволяющую сделать прогноз на следующую неделю.

1. Введем в ячейки А1:А6 значения Х_i, а в ячейки В1:В6 значения У_i.

Построим точечный график этой функции.

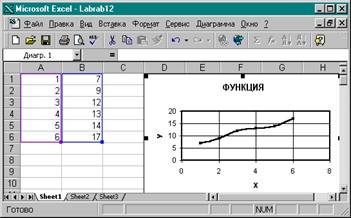3. Из графика видно, что экспериментальная зависимость монотонно возрастает и должна быть непрерывна. Следовательно, ее можно аппроксимировать (представить) каким-либо видом монотонно возрастающих функций.

4. Выделим точки графика щелчком мыши.

5. Щелкнем их правой кнопкой мыши.

6. В раскрывшемся контекстном меню выберем команду Добавить линии

тренда.

В раскрывшемся диалоговом окне Линии тренда на вкладке Тип в группе Построении линии тренда (аппроксимация и сглаживание)

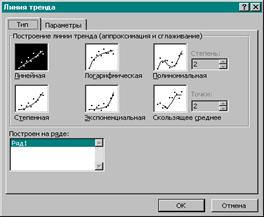выберем Линейная.

8. На вкладке Параметры установим флажки Показать уравнение на диаграмме и Поместить на диаграмму величину достоверности аппроксимации. Это значит, что на диаграмму будет помещен квадрат коэффициента корреляции.

9. Нажать кнопку ОК.

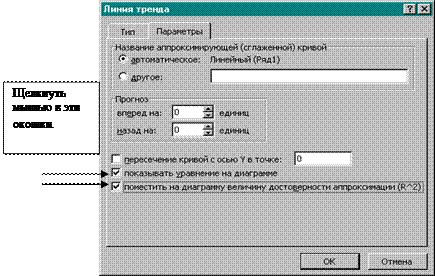- 3 -

10. На диаграмме получим график линейного тренда.

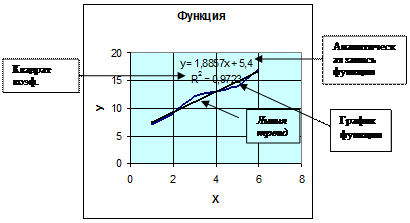11. По коэффициенту корреляции можно судить о правомерности использования линейного уравнения для описания заданной функции. Если он лежит в диапазоне от 0,9 до 1, то данную зависимость можно использовать для предсказания результата. Причем, чем ближе коэффициент корреляции к единице, тем точнее прогноз.

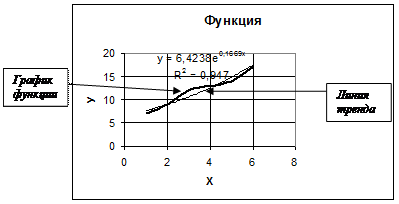
12. Предположим, что данные помещенные в таблице могут быть представлены в виде экспоненциальной зависимости.

13. В диалоговом окне Линии тренда на вкладке Тип в группе Построении линии тренда (аппроксимация и сглаживание) выберем Экспоненциальная.

14. Получим экспоненциальную линию тренда.

15. Из полученных графиков видно, что квадрат коэффициента корреляции экспоненциальной модели равен 0,947 и меньше квадрата коэффициента корреляции линейной модели 0,9723. Таким образом, в данном примере линейная модель более достоверно описывает зависимость между данными, приведенными в таблице.

16. Уравнение, описывающее заданную в таблице функцию, будет следующим:

У=1,8857Х+5,4

- 4 -

Задание для практической работы.

Найти эмпирические зависимости:

№1.

Х	1	2	3	4	5	6	7
У	13	19	29	30	37	44	49

Итоговую формулу, описывающею функцию поместить в ячейки С2.

Сохранить на Листе1.

№2.

Х	1	2	3	4	5	6	7	8	9
У	7	17	19	28	35	42	47	52	57

Итоговую формулу, описывающею функцию поместить в ячейки С2.

Сохранить на Листе2.

По окончанию работы: Закрыть программу Excel.

â Дополнительное задание для практической работы.

Найти эмпирические зависимости:

№1.

1563

1029

648

375

192

№2.

2,53

2,60

2,67

2,74

2,80

2,86

2,92

2,97

3,02

Скачано с www.znanio.ru