Методика обучения математики одаренных детей

1. Охарактеризуйте программу курса «Математическое развитие дошкольников». Составьте конспект одного занятия по развитию математических способностей детей 4-5 (6) лет.

Целью освоения дисциплины «Математическое развитие дошкольников» является формирование профессиональной компетентности обучающихся в области проектирования и организации работы с детьми дошкольного возраста по математическому развитию в соответствии с требованиями ФГОС.

Задачи освоения дисциплины

• вооружать обучающихся научно-методическими знаниями о процессе математического развития детей;
• учить определять содержание с группой детей и отдельными детьми, правильно выбирать наиболее эффективный путь воздействия на математическое развитие, анализировать полученный результат;
• обеспечить усвоение обобщенных представлений о построении педагогического процесса математического развития дошкольников, знаний конкретных способов формирования математических представлений детей и умений применять их в образовательной практике

Содержание курса (программа) представляет собой перечень математических понятий и видов моделирующих (конструк­тивных) действий, в процессе выполнения которых дети ус­ваивают эти понятия.

Младшая группа (от 3 до 4 лет) Примерный перечень представлений и моделирующих действий, которыми овладевают дети в процессе обучения математике

Геометрические понятия и отношения

Первичные представления о форме геометрических фигур (круглые треугольные, четырехугольные). Фигуры и тела (плоские и объемные) Простые задания на распознавание (выбор нужной фигуры из нескольких различных) и сравнение (выбор фигуры из похожих фигур). Выделение признаков цвета и формы фигур. Поиск одинаковых и похожих. Сериаций с геометрическими телами и фигурами. Конструирование геометрических фигур из различных материалов. Часть и целое: конструирование геомет­рических фигур из отдельных частей. Ориентировка в пространстве и на плоскости: ориентировка относительно себя, своего тела и другого объ­екта. Взаимное расположение фигур и предметов (над, под, за, перед, выше, ниже, внутри и снаружи).

Подготовка к формированию понятия числа

Сравнение предметов по различным признакам с постепенным выде­лением количественных характеристик. Сравнение множеств предметов способом установления взаимно однозначного соответствия. Знакомст­во с отношениями: больше, меньше, равно. Выделение одного, двух, трех предметов из группы по принципу числовой фигуры. Соотнесение слов числительных с соответствующими группами предметов (один, два, три...). Знакомство с количественным и порядковым счетом (до 5).

Символ числа — цифра.

Формирование представлений о величинах

Сравнение предметов по величине: длине и массе на основе сенсор­ных и кинестезических ощущений (прикладывание, визуальная прикидка на руке), по площади и емкости (наложением и экспериментально: нали­ванием, насыпанием). Формирование представления о значимости этих признаков для объекта.

Формирование конструктивных умений

Конструирование тел и фигур из отдельных частей, из палочек и спе­циальных наборов (мозаик). Конструирование сюжетных композиций и ор­наментов из произвольных и оформленных деталей (конструктивные аппликации). Конструктивное рисование (дорисовка и штриховка по кон­турной рамке).

 Средняя группа (от 4 до 5 лет)

Примерный перечень понятий и моделирующих действий, которыми овладевают дети в процессе обучения математике

Геометрические понятия

Уточнение представлений о форме геометрических фигур: простые за­дания на распознавание, на сравнение, на сериацию, на классификацию (по размеру, по форме, по цвету). Выполнение сюжетных рисунков и ор­наментов из геометрических форм, их закрашивание с использованием контурной рамки. Конструирование геометрических фигур из отдельных частей (геометрические мозаики, наборы «Сложи фигуру», палочки).

Конструирование предметных и сюжетных композиций из геомет­рических мозаик и палочек.

Круг и овал. Треугольник и четырехугольник. Квадрат. Прямоугольник. Объемные тела (шар, куб, прямая призма типа «кирпич», конус, цилиндр). Элементы проективного обследования этих фигур в практической деятель­ности.

Подготовка к формированию понятия числа

Сравнение предметов по различным признакам со словесным описа­нием сравнения. Сравнение групп предметов. Выделение одного, двух, трех предметов из группы по заданному признаку. Понятия: много—мало, столько же, несколько, одинаково, поровну.

Сравнение множеств предметов способом установления взаимно од­нозначного соответствия: больше, меньше, равно; больше на, меньше на. Способ сравнения путем пересчета элементов множества. Различные спо­собы уравнивания множеств.

Предметная модель натурального числа. Количественная характера стика множеств. Счет предметов в различном направлении и пространст венном расположении. Понимание того, что последнее числительно относится ко всей группе предметов, а не только к последнему из них. Понимание того, что общее количество предметов в группе не зависит от размера, цвета, формы, расстояния между предметами.

Счет на слух, по осязанию, счет движений. Присчитывание и отсчиты-вание предметов по одному с называнием итога: «Сколько всего?», «Сколь­ко осталось?»

Соотнесение числа с количеством предметов. Знакомство с цифра­ми. Соотнесение цифры, числа и количества.

Количественный и порядковый счет (до 10). Умение правильно отве тить на вопрос: «Который по счету?» Представление об упорядочении мно­жества путем нумерации его элементов (правила счета).

Формирование динамичной модели состава чисел (в виде соотноше­ния: целое — часть) для чисел 2, 3, 4, 5.

Подготовка к формированию представления об арифметическом действии

Связь между изменением количественной характеристики множества и предметным действием (изменением): объединение и добавление ве­дет к увеличению количества, выделение и изъятие части — к уменьше­нию количества. Способы уравнивания групп предметов путем увеличения количества предметов в меньшей группе или уменьшения их количества в большей группе. Сопровождение практических действий словами: до­бавил, стало больше, стало поровну, убавил, стало меньше.

Формирование представлений о величинах и их измерении Размер предметов. Понятия: большой — маленький, больше — мень­ше, одинаковые по размеру; высокий — низкий, выше — ниже, равные по высоте; длинный — короткий, длиннее — короче, равные по длине — на основе сравнения двух (нескольких) предметов, отличающихся одним или несколькими параметрами.

Способы сравнения (приложение, наложение, прикидка на руке). Пони­мание сходства и различия предметов по их размерам. Умение правильно использовать термины для обозначения размера предметов при их срав­нении. Составление групп предметов с заданными свойствами.

Сравнение предметов по длине и массе на основе сенсорных и кине-стезических ощущений (прикладыванием, визуально, наложением, при­кидкой на руке).

При сравнении свойств, поддающихся измерению (длина, масса, ем­кость), использование моделей-заместителей (меток) и различных мерок.

Сравнение длин прикладыванием и с помощью естественной мерки (шаг, локоть, ладонь) и условной мерки.

Формирование пространственных представлений

Ориентировка в окружающем пространстве: впереди, позади, перед, над, под, за и т. д. Установление отношений: выше — ниже, ближе —даль­ше, сбоку, на, следом и умение смоделировать эти отношения между объ­ектами, используя заместители.

Ориентировка на плоскости листа.

Работа с объемными формами. Плоский рисунок объемного тела (фронтальный вид) и композиции объемных тел. Формирование временных представлений

Времена года. Названия сезонов и порядок их следования. Сутки. Вре­мя суток (утро, день, вечер, ночь). Наглядная модель времен года. Формирование умения решать конструкторские задачи

Конструирование по образцу, по заданию, по контуру, по модели и по рисунку из различных материалов. Конструирование предметных и сю­жетных рисунков, аппликаций, орнаментов. Конструирование рисунков и аппликаций с опорой на контурную рамку.

Конспект НОД по ФЭМП «Поможем Незнайке»

Цели: способствовать формированию у детей элементарных математических представлений

Задачи:

• закрепить навыки счета в пределах 5;
• закрепить называния основных цветов;
• учить отвечать на вопросы: «какой по счету?»
• развивать внимание, память, учить ориентироваться в пространстве, развивать слуховое внимание;
• способствовать развитию умения различать и называть геометрические фигуры;
• воспитывать уважение друг к другу, желание прийти на помощь;
• активизация словаря;

Оборудование: проектор, пять шаров разного цвета, 4 обруча, большие геометрические фигуры из картона, маленькие геометрические фигуры по количеству детей, набор для аппликации, мяч.

Ход образовательной деятельности:

1. Организационный момент.

Ребята, сегодня я пришла в детский сад, и получила очень интересное видеописьмо. Давайте его посмотрим!

Видеообращение от Незнайки. 

«Дорогие ребята! Здравствуйте! Вы, конечно же, узнали меня, я - Незнайка! И мне очень нужна ваша помощь. Мы с друзьями сделали большой воздушный шар и полетели на нем в путешествие, но вдруг подул сильный ветер, он подхватил наш воздушный шар и понес его далеко-далеко, все мои друзья успели выпрыгнуть из него с парашютом, а я остался и попал в незнакомую мне страну Волшебных фигур! Чтобы найти дорогу домой, нужно выполнить задания, а я не знаю цифр и не умею считать. Поможете мне? Спасибо, друзья!»

     2. Математическая разминка «Воздушный шар Незнайки»

Ну что же, ребята, нужно выручать Незнайку. Согласны? Давайте вспомним, на чем Незнайка полетел в путешествие? (На воздушном шаре) А какая это геометрическая фигура? (Круг). Посмотрите, пожалуйста, на доску (или настоящие воздушные шары?) перед вами развешены разноцветные воздушные шары. Посчитайте по порядку воздушные шары (первый, второй).

- Сколько всего воздушных шаров вы видите? (5)

- Одинаковые ли шары? (Нет)

- Скажите, чем отличаются шары? (Шары отличаются цветом).

- Что у шаров одинаковое? (У шаров одинаковая форма и размер). Какого цвета первый, третий, пятый шарик?

- Который по счёту стоит красный шар? Жёлтый? Синий? И т. д.

- Вдруг подул ветер, и один воздушный шар улетел.

- Которого по счёту шара нет?

(Педагог убирает по одному воздушному шарику, и дети называют, которого по счёту шара нет).

Молодцы, справились с заданием!

3. Подвижная игра «Найди свой домик». 

Ребята, а какие еще геометрические фигуры, кроме круга, вы знаете?

А сейчас геометрические фигуры предлагают поиграть вам в игру «Найди свой домик».

«Жили-были в своих домиках геометрические фигуры. Как они называются? Круг, квадрат, треугольник и прямоугольник (показывает и раскладывает в обручи большие фигуры).

В математику играю,

Вас в фигуры превращаю!

Ты фигуру получи, и ее ты назови!

(Педагог  раздает всем детям по одной геометрической фигуре, а они называют фигуру).

Затем воспитатель объясняет правила игры, которые заключаются в том, что ребята бегают по комнате, а когда он ударит в бубен, должны найти свои домики. Те, у кого круг, бегут к обручу, где лежит круг, а те, у кого квадрат, - к обручу с квадратом  и т.д.  Когда дети разбегутся по местам, воспитатель проверяет, какие фигуры у детей, правильно ли они выбрали домик, уточняет, как называются фигуры и сколько их. При повторном проведении игры надо поменять местами фигуры, лежащие внутри обручей.

Молодцы ребята! Справились!

4. Домики страны Волшебных фигур (аппликация).

Ребята, а как вы думаете, какие домики у жителей страны Считалово? Правильно, разной формы, а порой и очень необычные, состоящие из нескольких геометрических фигур: показ слайдов/картинок.

Сейчас я предлагаю вам сделать аппликация одного такого домика. Посмотрите, пожалуйста, на образец:

- Сколько этажей в домике? (Считаем снизу вверх)

- А крыша какой геометрической фигуры? Сколько у нее углов?

- Какой формы труба у домика?

- Что нарисовано справа от домика? (Дерево)

- А что нарисовано слева от домика? (Собачка)

Дети выполняют аппликацию.

Молодцы, очень красивые домики у вас получились!

     5. Физкультминутка.

Раз, два, три, четыре, пять –

Все умеем мы считать.

Раз! Подняться, потянуться,

Два! Согнуться, разогнуться.

Три! В ладоши три хлопка,

Головою три кивка.

На четыре руки шире.

Пять – руками помахать.

6. Дидактическая игра с мячом «Скажи наоборот».

Дети становятся в круг.

Большой – маленький, длинный – короткий, высокий – низкий, широкий – узкий, толстый – тонкий, пустой-полный, мягкий-твердый.

Молодцы, ребята, Вы выполнили все задания и теперь Незнайка сможет вернуться обратно в свой Цветочный город!

Видеообращение Незнайки (стоит с воздушным шариком)

«Друзья, спасибо за помощь, вы все большие молодцы, справились со всеми заданиями, и я приготовил вам маленькие подарочки»

(Подарки (математические раскраски) находим в раздевалке, привязаны к воздушным шарам).

     6. Рефлексия.

Вот и подошло к концу наше путешествие, вам понравилось помогать Незнайке?

Какое задание понравилось больше всего?

Какие показались трудными?

Какие самыми легкими?

2. Разработайте методику ознакомления учащихся, проявивших выдающиеся математические способности, с одной из тем начального курса математики. Составьте план-конспект одного урока.

Начальный курс математики имеет свои особенности построения. Арифметический материал составляет главное содержание курса. Основой начального курса является арифметика натуральных чисел и основных величин. Кроме того, в него входят элементы геометрии и алгебраической пропедевтики, которые по возможности включаются в систему арифметических знаний, способствуя более высокому уровню усвоения понятий о числе, арифметических действиях и математических отношениях, т. е. элементы алгебры и геометрии не составляют особых разделов курса математики, а органически связываются с арифметическим материалом. Такая связь дает возможность, с одной стороны, раньше приобщить детей к идеям алгебры и геометрии и с другой – достичь более высокого уровня усвоения младшими школьниками арифметических знаний.

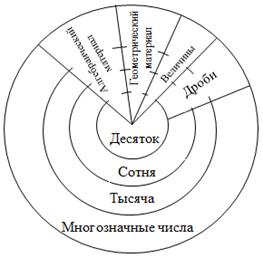
Арифметический материал вводится концентрически. Сначала изучается нумерация чисел первого десятка, которые не подлежат десятичному расчленению, вводятся цифры для записи этих чисел, изучаются действия сложения и вычитания. Затем рассматривается нумерация чисел в пределах 100, раскрывается понятие разряда, позиционный принцип записи чисел, которые подлежат десятичному расчленению, изучается сложение и вычитание двузначных чисел, вводятся два новых арифметических действия: умножение и деление. После этого изучается нумерация чисел в пределах 1000. Здесь рассматриваются три разряда (единицы, десятки, сотни), составляющие основу нумерации многозначных чисел, обобщаются знания об арифметических действиях, вводятся приемы письменного сложения и вычитания. Наконец, изучается нумерация многозначных чисел, рассматривается понятие класса, обобщается знание принципа поместного значения цифр, изучаются приемы письменных вычислений. Таким образом, в курсе выделены четыре концентра: десяток, сотня, тысяча, многозначные числа. Одновременно и в тесной связи с рассмотрением нумерации и арифметических действий изучаются другие вопросы: величины, дроби, алгебраический и геометрический материал. Схема материала изображено на рисунке I.

Выделение именно таких концентров объясняется особенностями десятичной системы счисления и вычислительными приемами: в каждом концентре раскрываются новые вопросы, связанные с системой счисления и арифметическими действиями.

Следует заметить, концентрическое расположение материала соответствует возможностям младших школьников: обучение математике на рис. 1 начинается с небольшой области чисел, доступной детям и известной им до школы; эта область чисел постепенно расширяется, и постепенно вводятся новые понятия; при таком построении курса обеспечивается систематическое повторение и вместе с тем углубление изученного, так как полученные ранее знания, умения и навыки находят применение в новой области чисел. Все это способствует лучшему усвоению курса.

Вопросы теории и вопросы практического характера органически связываются между собой. Многие вопросы теории вводятся индуктивно, а на их основе раскрываются вопросы практического характера. Например, распределительное свойство умножения вводится на основе обобщения частных фактов, после этого, используя это свойство, раскрывается прием умножения двузначного числа на однозначное.

При такой взаимосвязи хорошо усваиваются теоретические вопросы и формируются осознанные практические умения.

12· 3= (10+2)·3 =10·3+ 2· 3=36

Математические понятия, свойства, закономерности раскрываются в курсе в их взаимосвязи. Это не только связь между арифметическим, алгебраическим и геометрическим материалом, но и так называемые внутренние связи между различными понятиями курса, свойствами, закономерностями. Так, при изучении арифметических действий раскрываются их свойства, связи и зависимости между их компонентами и результатами.

Это дает возможность глубже раскрыть понятие арифметических действий, обогатить детей функциональными представлениями. Такое построение обеспечивает более глубокое усвоение курса, так как учащиеся будут овладевать не только отдельными вопросами курса, но одновременно и связями между ними.

Тема урока: «Пересечение множеств» 3 класс

Цель урока: сформировать представление о понятии «пересечение» множеств.

Задачи урока:

• узнать какую часть множеств называют «пересечением»;
• узнать какие элементы множеств входят в пересечение»;
• научиться понимать, читать и составлять данные высказывания;
• научиться изображать пересечение множеств при помощи графической модели.

Ход урока:

I.                   Орг. момент.

Учитель

Вот и солнышко с утра,

И в душе у нас весна!

Мы начнем урок с улыбок.

Выполним всё без ошибок

Учащиеся

Мы пришли сюда учиться,

Не лениться, а трудиться.

Слушаем внимательно,

Работаем старательно.

- Я рада, что у Вас хорошее настроение. Улыбнитесь друг другу. Я надеюсь, что такое настроение у Вас останется до конца урока и вы будете старательны и внимательны.

- Сейчас урок математики.

- Давайте повторим то, что мы уже знаем.

II.                Актуализация знаний учащихся.

- Какой раздел мы начали изучать? (Мы начали изучать  раздел «Множества»)

-  Что такое множества? (Множество – это группа предметов, объектов или живых существ, собранных вместе)

-  Можно ли назвать предметы, на данном рисунке, множеством? (Да, это группа живых существ собранных вместе.)

- Назовите это множество. (Множество бабочек.)

- Дайте общее название данным множествам.

- Из чего состоят множества? (Множества состоят из элементов)

- Что можно сделать с элементами множества? (Посчитать и перечислить их.)

- Посчитайте и перечислите элементы множества «Посуда».

- Что означает: «задал это множество перечислением»? (Значит, перечислил все элементы данного множества)

- А что значит: задать множество? (Это значит назвать общее свойство или признак всех его элементов.)

- Приведите свои примеры, назовите общее свойство каких-либо объектов.

III.             Постановка проблемы и поиск решения.

- Сегодня на уроке мы познакомимся ещё с одним понятием, связанным с множеством предметов.

- Какое множество вы видите? (Множество домов)

- На какие две группы можно поделить множества домов на доске? (Красные дома и желтые дома.)

- Какой основной признак у домов в первом множестве? (Красный цвет.)

- У домов второго множества? (Желтый цвет.)

- В нашем необычном городе живет странный архитектор. Кто такой архитектор? Ответы детей.

- Верно. Архитектор – человек проектирующий здания, создающий внешний вид городов.

-  В нашем городе он разрешает строить на одной улице только красные дома, а на другой только желтые дома. И живет в нашем городе веселый художник, он захотел построить дом красно-желтого цвета. Давайте поможем нашему художнику. Поставим дом на одну из улиц.

- Можем ли мы поставить этот домик на первую улицу? (Нет, потому, что их общий признак жёлтый цвет, а он желто-красный)

- Можем ли мы поставить этот домик на вторую улицу? (Нет.)

(Дети пытаются выполнить задание сами.)

- Смогли вы выполнить мое задание? (Нет.)

- Почему?  (Потому что на одной улице можно строить только желтые дома, а на другой только красные дома.)

- Какой у нас возникает вопрос? (Куда поставить красно-желтый дом?)

- Давайте вместе будем решать данную проблему.

- Какие признаки имеет наш дом? (Он желтого и красного цвета.)

- На каких улицах он может находится, благодаря своим признакам? (Он должен стоять на красной улице, потому что он красный и на желтой улице, потому что он желтый.)

- То есть он должен находится на обеих улицах одновременно

- А  как должны располагаться улицы, чтобы, находясь на одной улице, мы одновременно стояли и на другой улице. В таких местах обычно ставят светофоры. (Улицы должны пересекаться.)

-  Итак, какая гипотеза оказалась верной. (Поставить дом на пересечение двух дорог.)

-  Каждая улица это множество домов, значит, куда мы поставили наш дом.

(На пересечение множеств.)

- Предположите, какова будет тема нашего урока. (Пересечение множеств)

- Цель нашего урока: сформировать представление о понятии «пересечение» множеств.

- А вот задачи урока давайте попробуем сформулировать вместе. На какие вопросы по данной теме вы бы хотели получить ответы? Ответы детей.

- Задачи урока:

• узнать какую часть множеств называют «пересечением»;
• узнать какие элементы множеств входят в пересечение»;
• научиться понимать, читать и составлять данные высказывания;
• научиться изображать пересечение множеств при помощи графической модели;

- Оценивать свою работу на уроке вы будете при помощи оценочных листов. Посмотрите на вопросы в них. Они соответствуют задачам нашего урока. Если вы будите внимательны и старательны на уроке, то и оцените себя по достоинству.

- К нашим домикам мы вернёмся в конце урока и проверим, смогли ли мы решить поставленные перед собой задачи.

ФИЗМИНУТКА ДЛЯ ГЛАЗ.

- Давайте приготовим наши глазки для дальнейшей работа, проведём физминутку для глаз.

IV.              «Открытие» новых знаний.

1. Работа с множествами

- Приступаем к открытию новых знаний.

- Перед вами два множества и элементы множества. Посмотрите внимательно на элементы множества.

- Дайте названия данным множествам по цвету и материалу изготовления. (Множество зелёных объектов  и множество деревянных объектов)

- Давайте распределим данные объекты по множествам.

- Что вы заметили? (Что некоторые объекты, а именно карандаш и кубик вошли и в первое и во второе множество.)

- По свойствам эти предметы подходят И к множеству деревянных предметов И к множеству зелёных предметов. Они являются общими для этих двух множеств.

- Посмотрите, как это можно показать по другому .

- Эти элементы являются общими и для первого и для второго множества.

- Поэтому они находятся в пересечении множеств.

- Дайте названия данным множествам.

(1 – зеленые объекты; 2 – деревянные объекты.)

 - Попробуйте дать общее название элементам находящимся в пересечении. (зелёные И деревянные объекты)

2. Вывод.

- Так какую часть множеств называют пересечением? (Общую часть множеств называют пересечением.)

- Это мы с вами пришли к такому выводу.

Работа с учебником с.50

- Давайте проверим верно ли наше предположение. Прочитаем в учебнике сообщение с зелёным восклицательным знаком. (Учащиеся читают)

- Совпало ли наше предположение с выводами в учебнике? (Да.)

- Давайте ещё раз проговорим, что называют пересечением? (Общую часть множеств называют пересечением.)

Сообщение учителя со слайда

Если в названии множества есть слово «И», то каждый его элемент должен находиться на ПЕРЕСЕЧЕНИИ двух множеств – жить одновременно в двух странах.

3. Знакомство с графическим обозначением.

- Обратите внимание, что графически принято изображать отношения между множествами  с помощью кругов. Математики называют их кругами Эйлера, т.к. они изобретены Леонардом Эйлером.

- Леонард Эйлер швейцарский, немецкий и российский математик, внёсший значительный вклад в развитие математики. Он почти полжизни провёл в России, где внёс существенный вклад в становление российской науки.

ФИЗМИНУТКА

V.                Первичное закрепление нового материала .

1. Игра «Найди пересечение множеств»

- Какие множества вы видите?

- Какие объекты должны лежать в пересечении множеств?

- Покажите графически.

- Дайте название пересечению множеств.

- Что мы называем пересечением множеств? (Общую часть множеств называют пересечением.)

2. Работа в парах.

- Возьмите конверты. Прочитайте задание и выполните его.

- Распределите элементы множеств. Назовите каждое множество.

- Посмотрите на слайд, сравните со своей работой.

(Проверка с помощью сигнальных карточек)

3. Работа в группе.

- А сейчас вы будете работать в группе. У вас на столе лежит карточка с заданием. Вы должны будете показать отношения между множествами, данными в задании. А элементами множеств будут члены вашей команды. Старший группы должен будет объяснить, как группа выполняла задание.

(Ребята распределяют роли в группе.)

- Вы готовы. Сейчас каждая группа будет защищать свою работу, а учащиеся других групп должны будут просигнализировать, согласны ли они с тем, что представляют выступающие. Зелёный сигнал согласны, красный – не согласны.

1 группа

  Покажите отношение между множеством девочек и множеством учащихся в брюках. Элементами этих множеств являются учащиеся вашей группы.

   Какие элементы множеств находятся в пересечении и почему?

   Старший группы поясняет, как выполнили задание.

2 группа

    Покажите отношение между множеством мальчиков и множеством блондинов. Элементами этих множеств являются учащиеся вашей группы.

   Какие элементы множеств находятся в пересечении и почему?

   Старший группы поясняет, как выполнили задание.

3 группа

  Покажите отношение между множеством мальчиков и множеством учащихся в белом. Элементами этих множеств являются учащиеся вашей группы.

   Какие элементы множеств находятся в пересечении и почему?

   Старший группы поясняет, как выполнили задание.

4 группа

  Покажите отношение между множеством девочек и множеством учащихся имя которых начинается на букву «Д». Элементами этих множеств являются учащиеся вашей группы.

   Какие элементы множеств находятся в пересечении и почему?

   Старший группы поясняет, как выполнили задание.

4. Индивидуальная дифференцированная работа. (Выбор учащихся по степени сложности)

- У Вас на столах лежат карточки с заданием с  красной, зелёной и жёлтой полосой. Эти задания разного уровня сложности. С красной полосой - самое сложное. С зелёной - немного легче. С жёлтой - самое легкое. Выберите каждый для себя конверт и выполните задание. Пишите названия элементов словами.

(Проверка с помощью сигнальных карточек)

- Поднимите красный сигнал, кто выбрал, карточку с красной полосой. Расскажите, как выполняли.

- Поднимите зелёныё сигнал, кто выбрал, карточку с зелёной полосой. Расскажите, как выполняли. Согласны ли с выполнением? Кто взял другие элементы множеств.

- Поднимите жёлтый сигнал, кто выбрал, карточку с жёлтой полосой. Расскажите, как выполняли. Согласны ли с выполнением?

VI.             Домашнее задание.

- Решите примеры № 9, с. 51 – в соответствии с заданием.
- А еще у вас на столах есть карточки с синей полосой, в них задание связанное с темой нашего сегодняшнего урока.  Вы по желанию, можете взять конверт с заданием и выполнить его дома. Данная работа будет оценена.

VII.          Итог урока.

- Какая была тема урока? (Пересечение множеств.)

- Давайте вспомним, какие  задачи мы ставили перед собой в начале урока.

- Давайте проверим, смогли ли мы решить поставленные перед нами задачи.

(Дети дают ответы по каждому пункту.)

- А сейчас вернёмся к домикам, с которыми мы работали в начале урока.

- Изобразите пересечение множеств при помощи графической модели.

- Распределите элементы множества в данную модель.

- Дайте название каждому из множеств.

VIII.       Оценивание.

Листы самооценивания.

IX.             Рефлексия.

- Давайте подведём итог нашего урока. В этом вам помогут наши предложения (Высказывания детей)

3. Ознакомьтесь с материалами статьи Л.В. Лысогоровой «Педагогические условия развития математических способностей младших школьников» [3]. Каково ваше мнение?

В состав каждого из указанных качеств, входит некоторый набор профессионально значимых свойств личности: аккуратность, благородство, вежливость, выдержка и самообладание, деловитость, доброжелательность, добросовестность, критичность, логичность, любовь к детям, любознательность, наблюдательность, настойчивость, находчивость, обаяние, общительность, обязательность, организованность, ответственность, педагогическое воображение, потребность в передаче знаний, правдивость, принципиальность, решительность, распределение внимания, развитая речь, самокритичность, самостоятельность, скромность, сообразительность, способность видеть мир глазами ребенка, справедливость, тактичность, требовательность к себе и ученикам, трудолюбие, творческое воображение, уверенность в себе, умение выделять главное, целеустремленность, чувство юмора, чувство собственного достоинства, чуткость, эстетический вкус, эрудированность, эмпатия, фантазия и выдумка.

Создание таких условий позволяет развивать у учащихся способность обобщать математический материал, вычленять главное, выявлять общее в разных примерах и задачах, способность сокращать процесс рассуждения.

4. Ознакомьтесь с материалами статьи Н.Х. Агаханова «Средовый подход как условие развития математически одаренных школьников» [4]. Какова целесообразность использования  предложенного автором подхода в начальной школе? детском саду? Сделайте выводы.

В последнее время во многих странах мира, в том числе и в России, осознается необходимость совершенствования математического образования. Прежде всего это связано с тем, что математика становится все более востребованной в различных сферах деятельности, а применение математических методов и моделей стремительно распространяется не только на технические, но и на такие науки, как биология, медицина, метеорология, экономика, лингвистика и др. Как указывал академик А. Н. Колмогоров, принципиально область применения математики не ограничена.

Общеизвестно, что в развитие науки вносят вклад люди, которые обладают более высоким уровнем способностей к определенному виду деятельности, что в значительной степени объясняет тот общественный резонанс, который вызывает проблема одаренности в современном обществе.

Следует отметить, что описанная система работы с математически одаренными школьниками доказала свою эффективность многолетними впечатляющими успехами школьников из России на международных олимпиадах по математике и признанием отечественной математической школы во всем мире.

5. Ознакомьтесь с материалами статьи А.А. Афанасьевой [5]. Статья посвящена организации дистанционных факультативных занятий по математике для учащихся 3–6-х классов с целью расширения математического кругозора и способностей, развития интереса к предмету, формирования устойчивой мотивации к регулярным занятиям. В статье рассматриваются уже существующие проекты проведения дистанционных факультативных занятий по математике, даются рекомендации по выбору информационных и коммуникационных технологий, а также предлагается общая концепция занятий. Как вы считаете, будут ли полезны предложенные автором мероприятия математически одарённым детям?

Статья посвящена организации дистанционных факультативных занятий по математике для учащихся 3–6-х классов с целью расширения математического кругозора и творческих способностей, развития интереса к предмету, формирования устойчивой мотивации к регулярным занятиям. В статье рассматриваются уже существующие проекты проведения дистанционных факультативных занятий по математике, даются рекомендации по выбору информационных и коммуникационных технологий и, в частности, системы дистанционного обучения, а также предлагается общая концепция занятий, которая в дальнейшем может быть использована для создания рабочей программы.

Интерес учащихся к изучению математики, базируясь на занимательности должен поддерживаться и другими средствами: привлечения историко-математического (для показа прошлого и настоящего науки, а также перспектива ее будущего развития), решением жизненных задач, связью с потребностями, выдвигаемыми практической деятельностью человека. Естественно также при проведении факультативных занятий в основном использовать методы  изучения (а не обучения) математики, а также проблемную форму обучения. Факультативные занятия играют большую роль в совершенствовании школьного образования. Они позволяют производить поиск и экспериментальную проверку нового содержания, новых методов обучения, в широких пределах варьировать объем и сложность изучаемого материала.

6. Ознакомьтесь с педагогической технологией А.И. Савенкова проведения учебных исследований с дошкольниками [6] и младшими школьниками [7]. Разработайте по одной игре-исследованию для дошкольников и младших школьников.

«ДОРИСУЙ КАРТИНКУ»  

Цель: развитие у детей творческого воображения, мышления

Материал: листок бумаги с незаконченным изображением любого предмета, цветные карандаши или фломастеры

Ход: ребенку предлагается рассмотреть изображение, назвать предмет, изображение которого на листочке бумаги незакончено. Если ребенок затрудняется назвать предмет, используются наво­дящие вопросы, загадки. После того, как ребенок узнает предмет ему предлагается закончить изображение (дорисовать картинку) и раскрасить ее в середине.

 Игра – исследование «Числа вокруг нас».

Этап I. Организационный момент. (5 мин)

Добрый день дорогие ребята!

Сегодня учащиеся шестых классов выступят в роли исследователей. Ну а для того, чтобы познакомиться с объектом нашего исследования нужно разгадать загадки. Из начальных букв разгаданных слов и будет составлено новое слово - объект нашего исследования.

А) Ног нет, а хожу,

     Рта нет, а скажу,

     Когда спать, когда вставать,

     Когда работу начинать.   (Часы)

Б) Я одноухая старуха,

     Я прыгаю по полотну

     И нитку длинную из уха,

     Как паутину, я тяну. (Игла)

В) Растет она вниз головою,

     Не летом растет, а зимою,

     Но солнце ее припечет-

     Заплачет она и умрет. (Сосулька)

Г)  В одежде летом,

      А зимой – раздетый.  (Лес)

Д) Без окон, без дверей

     Полна горница людей.  (Огурец)

Получили слово число.

Исследованием в области чисел занимались и занимаются люди разных профессий.

Наверное, вы все обратили внимание, на то, что классная комната пестрит изречениями великих людей, и все они посвящены числу.

Итак, объектом нашего исследования будет число.

И мы начинаем игру-исследование «Числа вокруг нас».

Помните, ребята, дисциплина, сплоченность и дружба – залог вашего успеха!

А сейчас позвольте представить наше уважаемое жюри - главных экспертов в области чисел…

Этап II.Актуализация знаний.

Итак, группам приготовиться к блиц-опросу. (5 мин.)

Исследователи в группах обсуждают ответ на вопрос, право голоса имеет только ведущий специалист группы.

 Вопросы для 1 группы.

1)Числа, употребляемые при счете, называются… (натуральными)

2) Сколько простых чисел в первом десятке?  (4)

3) На уроке ученики выстроились в линейку на расстоянии одного метра друг от друга. Вся линейка растянулась на 25 метров? Сколько было учеников? (26)

4) Сколько сейчас времени, если оставшаяся часть суток в два раза больше прошедшей? (8 часов)

5) Кто окажется тяжелее первый людоед, который весил 48 кг и на ужин съел второго или второй, который весил 52 кг и съел первого? (одинаково)

Вопросы для 2 группы.

1)Если наибольший делитель натуральных чисел равен 1, то числа называют ….

( взаимно простыми)

2) Какую долю составляют сутки от года? ( или )

3) Угол в 1 ^° рассматривается в лупу, дающую четырехкратное увеличение. Какой величины покажется угол?    (1°)

4) Во сколько раз длина километра больше длины миллиметра? (в 1 млн. раз)

5)  Петух, стоя на одной ноге, весит 5 кг. Сколько он будет весить, если встанет на обе.  (5 кг)

Я, думаю, что исследователи готовы к более серьезным испытаниям.

Следующее задание, требует от вас точности в расчетах и быстроты выполнения. (4мин)

Выполните действия по порядку и расшифруйте фамилию известной детской писательницы. 1)2+3

2) 5-2

3)  ·

4) 2,4 ׃

5) 6 · 1

6) 1· 2

7) 2·

8) 1: 16

Ответ: Линдгрен

Астрид Линдгрен известная шведская писательница.

Расположите дроби в порядке возрастания, и вы узнаете имя одного из героев сказки. (4мин.)

Ответ: Карлсон

Найдите корень уравнения 0,2: (х-53)=: 2 и вы узнаете, какой возраст у мужчины в самом расцвете сил. (4мин.) Задание с решением сдается жюри на проверку. Ответ: х=54

Действительно, шведская писательница Астрид Линдгрен написала сказку «Малыш и Карлсон» в 1955 году. Поэтому в меру упитанному и в меру воспитанному Карлсону в этом году исполнилось 54 года. Сказка стала популярна не только в Швеции, но и во всем мире.

На русский язык сказка была переведена в 1957 году.

Поднимите руки, кто знаком с произведениями этой писательницы и может вспомнить героев ее других сказок?

7. Познакомьтесь с опытом организации и подробными сценариями занятий по формированию математических представлений дошкольников 4-7 лет (программа «Гармония», г. Воронеж) [8]. Каковы основные цели и математическое содержание занятий? Какие виды игровой и учебной деятельности используются? 

«В книге представлены подробные сценарии курсов занятий основного развивающего цикла для дошкольников — по формированию математических представлений (три года обучения). Данный курс рассчитан на реализацию в учреждениях дополнительного образования и создан на основе комплексной программы развития дошкольников. Эта программа реализована в студии развития для дошкольников «Гармония» Центра развития творчества детей и юношества Ленинского района г. Воронежа. Цель программы — расширение форм дополнительного образования для детей, не посещающих детский сад. Программа «Гармония» опирается в своих принципиальных моментах на новые наиболее актуальные программы по дошкольному образованию, получившие гриф Минобразования России. Книга адресована преподавателям учреждений дополнительного образования, дошкольных гимназий. Полезные материалы в ней также найдут воспитатели и методисты ДОУ, домашние воспитатели (гувернеры). Издание выходит в комплекте с книгой «Развитие речи, подготовка к освоению письма: занятия для дошкольников в учреждениях дополнительного образования» (сценарии занятий, три года обучения).»

8. Познакомьтесь с опытом организации образовательной работы с детьми дошкольного возраста, имеющими склонность к математике (детский сад № 30 «Гвоздичка», г. Саров) [9]. Законспектируйте основные положения системы работы авторов статьи.

Выявление детей, имеющих склонность к математике, началось с наблюдения за воспитанниками во всех видах деятельности, это позволило получить первичную информацию о характере и направленности интересов, склонности детей. Однако в ходе наблюдения за детьми трудно избежать субъективных оценок, и можно упустить из виду скрытые, нереализованные задатки и способности. Поэтому совместно с педагогом-психологом было проведено анкетирование родителей и индивидуальное обследование детей при помощи методики Дж. Равена.

Полученная информация помогла наметить систему предстоящей работы с детьми по следующим направлениям:

1. Определение форм и методов образовательной работы;
2. Пополнение развивающей предметно-пространственной среды группы;
3. Взаимодействие с семьей.

В организации образовательного процесса мы используем принцип индивидуально-дифференцированного подхода. Детям, имеющим высокий уровень развития интеллектуальных способностей, предлагаем усложненные варианты заданий, слуховые диктанты, логические ситуации (требующие умозаключений, построенные на основе логических схем), задачи (на поиск недостающей фигуры, логические), игры с блоками Дьенеша, палочками Кюизенера.

Перспективным и важным направлением в работе с детьми является развитие логического мышления, формирование приемов мыслительной деятельности, а также умений понимать и прослеживать причинно-следственные связи, выстраивать простейшие умозаключения, делать выводы. Для этого применяем различные виды занимательного материала:

1. Игры на моделирование плоских или объемных фигур;
2. Наглядные логические задачи;
3. Занимательные вопросы, задачи-шутки;
4. Задачи-головоломки.

9.  Ознакомьтесь с материалами статьи Л.Н. Галкиной [10]. В статье рассматриваются положения, связанные с развитием математических способностей детей дошкольного возраста; особенности развития математических способностей у детей в процессе конструирования; современные аспекты развития математических способностей детей в процессе логико-математических игр. Прокомментируйте.

В статье рассматриваются положения, связанные с развитием математических способностей детей дошкольного возраста. Особенности развития математических способностей у детей в процессе конструирования. Современные аспекты развития математических способностей детей в процессе логико-математических игр.

Уникальность дидактических материалов заключается в универсальности его применения в разных видах детской деятельности (игре, экспериментировании, конструировании, рисовании, аппликации) и возможностях развития математических способностей у детей с трех лет.

Таким образом, современные подходы к математическому образованию детей должны быть связаны с развитием сенсорных и интеллектуальных способностей в процессе познания окружающих предметов, действительности, а также в процессе организации разных видов детской деятельности (прежде всего в конструировании), в использовании проблемно-игровой технологии в обучении детей, что в полной мере обеспечивает развитие математических способностей уже в дошкольном возрасте.

Тема 3.2.

1. Ознакомьтесь с результатами диссертации Г.И. Сулкарнаевой «Методика развития одаренных учащихся при обучении математике в 5-6 классах» [1]. В теоретической части исследовании: разработаны теоретические основания развития одаренных детей в процессе обучения математике в общеобразовательной школе; спроектированы и обоснованы цели развития одаренных детей в  процессе обучения математике в общеобразовательной школе; обоснованы: построение системы математических и учебных задач, адекват­ной системе спроектированных целей, и выбор методов их использования в процессе обучения математике. Практическая значимость исследования состоит в разработке методического обеспечения развития одаренных детей в процессе обучения математике  в 5-6 классах общеобразовательной школы. Законспектируйте основные результаты работы.

В данной работе нашли решение задачи, выдвинутые в связи с проблемой и гипотезой исследования, и получены следующие основные результаты и выводы:

1. Выявлены теоретические основания методики развития одаренных учащихся в процессе обучения:

1.1. Показано, что понятия «одаренность» и «способность» можно считать синонимами, означающими индивидуальную меру выраженности свойств функциональных систем, которая позволяет успешно осуществлять какую-либо деятельность на высоком уровне.

1.2. Специальные способности есть общие способности, приобретшие черты оперативности под влиянием требований деятельности, и поэтому их необходимо развивать на фоне развития общих способностей и познавательных процессов средствами математики.

1.3. В психолого-педагогических исследованиях разработаны определенные методы диагностики и развития одаренных (способных) детей.

1.4. В то же время программы «Одаренные дети», а также специализированные школы и классы, конкурсы и олимпиады по предметам, получившие большое распространение в нашей стране, как показывают исследования, не решают всех проблем развития одаренных детей. Решение проблем таких детей - задача общеобразовательной школы. 

1.5. Методические исследования проблем развивающего обучения в настоящее время не образуют целостной системы развития одаренных (способных) учащихся в процессе обучения математике в общеобразовательной школе, в образовательных стандартах, программах и учебниках по математике для 5-6 классов не выделены элементы учебного материала и задач, цель которых - развитие одаренных (способных) детей средствами математики.

1.6. Для работы с одаренными (способными) учащимися, по мнению самих учителей, необходимо специальное методическое и диагностическое обеспечение, которое помогло бы учителю организовать эту работу непосредственно на уроке.

2. В настоящем исследовании впервые в теории и методике обучения математике спроектированы цели обучения математике в общеобразовательной школе, направленные на развитие одаренных (способных) детей в процессе обучения математики на основе соотнесения развивающих целей обучения математике высокого уровня, компонентов математических способностей и качеств математического мышления. На этой же основе выделены и соответствующие им типы математических и учебных задач.

3. Построена система математических и учебных задач, направленных на достижение поставленных целей, и выбраны методы включения таких задач в учебный процесс обучения математике в 5-6 классах. Система задач построена на основе классификации по нескольким основаниям: 1) по категориям целей; 2) по типам задач; 3) по темам школьной программы; 4) по уровням обученности и развития.

4. Экспериментальная проверка элементов разработанной методики обучения математике показывает повышение уровня успеваемости, уровня надежности по математике и общего развития детей (в том числе, одаренных), а также выявляет скрытую одаренность некоторых учащихся. В результате теоретического и экспериментального исследования была подтверждена правомерность гипотезы о том, что развитие одаренных (способных) детей в процессе обучения математике в школе лежит в плоскости дифференциации целей обучения математике по уровням обученности и развития учащихся; в выделении учебных и развивающих целей высокого уровня и соотнесении их с компонентами математических способностей и качествами математического мышления, что в совокупности можно представить как цели развития одаренных (способных) учащихся, а также в выделении адекватной целям системы основных типов математических и учебных задач. Представляется необходимым дальнейшее изучение и экспериментальное исследование проблемы развития одаренных детей в процессе обучения. Выводы по результатам настоящего исследования показывают, что оно не исчерпывает всех аспектов развития учащегося; представляется необходимым дальнейшее изучение и экспериментальное исследование проблемы по следующим направлениям: реализация задачи повышения уровня развития одаренности (способностей) учащихся наиболее эффективна тогда, когда предложенная методика используется как целостная система во всех классах и ступенях обучения и по другим предметам: эффективность подготовки учащихся к развитию одаренности существенно зависит от осведомленности и психологического настроя всех участников этого процесса.

2. Ознакомьтесь с материалами статьи Л.В. Хамидуллиной [2]. В статье предложен комплекс педагогических условий развития математической одаренности в процессе изучения математических дисциплин в 5-7 классах. Ваше мнение?

В статье представлен анализ отечественных и зарубежных исследований одаренности, рассмотрены различные подходы к этому феномену. Автором представлены несколько определений одаренности, рассмотрены ее типы у детей среднего школьного возраста. На основе теоретического анализа литературы предложен комплекс педагогических условий развития одаренности на уроках математики в условиях личностно-ориентированного обучения. Итак, нами определены следующие педагогические условия развития одаренных детей среднего школьного возраста на уроках математики: осуществление преемственности процесса выявления одаренности школьников с использованием разработанной комплексной методики диагностики, учитывающей дифференциацию признаков одаренности, и дальнейшего процесса избирательного развития выявленных компонентов одаренности; введение в содержание учебного процесса гибкой образовательной программы, имеющей в основе двуединую модель деятельности ученика и учителя по формированию специальных математических способностей и детской одаренности у детей младшего подросткового возраста с учетом гендерных особенностей; нацеленность разработанной личностноориентированной технологии обучения, ключевым компонентом которой является комплекс разноуровневых развивающих заданий, на самоанализ и самооценку познавательных возможностей и развитие индивидуальных познавательных стратегий учащихся; формирование компонентов одаренности детей по принципу интегративного нарастания составляющих; адаптация детей младшего школьного возраста при переходе в среднее звено общеобразовательной школы.

Таким образом, в ходе организации опытно-экспериментального исследования реализована цель развития одаренности младших подростков на уроках математики в условиях личностно-ориентированного обучения.

3. Разработайте методику ознакомления  учащихся 5 (6) класса, проявивших выдающие математические способности, с одной из тем курса математики. Составьте план-конспект одного урока.

Изучение процентов в 5 классе.

Проценты – одна из самых трудных тем для пятиклассников. Это можно объяснить, в частности, тем, что понятие процента не является чисто математическим, а относится к терминам экономистов. Например, в учебнике Виленкина Н.Я., Чеснокова А.С., Шварцбурда С.И. и Жохова В.И.  дается следующее определение процента: «Процентом называют одну сотую часть числа».  

В этом разделе программы 5 класса хорошо рассказать учащимся об истории возникновения процентов, а также об истории появления знака процента.

В названном учебнике содержатся также достаточно полезные с точки зрения общего развития дополнительные сведения, касающиеся промилле (от латинского «с тысячи») – десятой части процента. Сказать учащимся об этом нужно, указав при этом его обозначения %_0. 

Вообще, изобретение математических знаков и символов значительно облегчило изучение математики и способствовало дальнейшему ее развитию.

В этой теме можно использовать старинные задачи и задачи с историческими сюжетами, которые при необходимости учитель с легкостью может составить и сам, например, путем переформулировки некоторых задач, изложенных в учебнике 5-ого класса (следует ввести в такие задачи старинный сюжет). Разумеется, главное в составлении таких задач – фантазия, эрудиция и понимание цели образовательных задач.

Приведем примеры двух задач  исторического содержания, которые были составления для работы в 5-м классе по теме «Проценты».

Задача 1. Один небогатый римлянин взял в долг у заимодавца 50 сестерциев. Заимодавец поставил условие: «Ты вернешь мне в установленный срок 50 сестерциев и еще 20 % от этой суммы». Сколько сестерциев должен отдать небогатый римлянин заимодавцу, возвращая долг?

Ответ: 60 сестерциев.

Задача 2.  Некий человек взял в долг у ростовщика 100 рублей.  Между ними было заключено соглашение о том, что должник обязан вернуть деньги ровно через год, доплатив еще 80 % от суммы долга. Но через 6 месяцев должник решил вернуть свой долг.  Сколько рублей он вернет ростовщику?

Ответ: 140 рублей.

Теоретический исторический материал по теме «Проценты» можно найти в книге Депмана И. Я. И Виленкина Н. Я. «За страницами учебника математики».

План-конспект урока математики в 5 классе по теме:

«Проценты. Нахождение процентов от числа »
Цель урока: сформировать понятие процента, умение записывать в процентах десятичные дроби и проценты в виде десятичных дробей; совершенствовать вычислительные навыки

Задачи урока:

Образовательная: ознакомить учащихся с понятием “процент”; научить записывать в процентах десятичные дроби и проценты в виде десятичных дробей; научить учащихся находить 1% от числа; совершенствовать вычислительные навыки.

Развивающая: развивать умение осмысленного быстрого чтения информации, её группировки по заданному основанию; формировать самостоятельность в мышлении и учебной деятельности.

Воспитательная: воспитывать способность к взаимопониманию, навыки сотрудничества и коммуникативные умения при работе в группах.

Ход урока

1. Организационный момент.

Здравствуйте, ребята! Садитесь. Сегодня у нас необычный урок. Надеюсь, он будет для нас с вами плодотворным. Желаю вам успешной работы!

2. Актуализация опорных  знаний.

Задание 1. Выполните действия:

1)                        4)             7) 0,2+0,8;

                    5)                 8)

3)                   6) 333:1000;              9)

Задание 2. Найдите  часть числа: 1) 300;  2) 70;  3) 9;  4) 54,2;  5) 6,39.

Задание 3. В саду росло 400 деревьев, из которых  составляли  яблони. Сколько яблоневых деревьев росло в саду?

3. Мотивация. Изучение новой темы.

– Сегодня мы с вами будем учиться экономить.

– Кто помогает родителям ходить по магазинам? На чем обычно экономят ваши родители?

– Конечно, покупая вещи и продукты по акции! Что значит по акции? Со скидкой.

– Давайте вспомним ценники в магазинах, в чем измеряется скидка?

– Она измеряется в процентах!

Вывести на слайд различные продукты с ценниками и скидками.

– Маша и ее мама пошли в магазин и купили следующий набор продуктов по акции. Сколько денег смогли сэкономить Маша и ее мама, если купили товары со скидкой?

– Можем мы с вами найти, какова сэкономленная сумма? Нет, так как мы не знаем, как находить проценты от числа.

– Итак, давайте подумаем, какова тема нашего урока?

 Тема урока: «Проценты»

– Записываем в тетрадь  сегодняшнее число, классная работа и тему урока.

– Давайте определимся с целями нашего урока. (изучить понятие процента, научиться находить процент от числа …)

– Если вы вспомните ценники в магазине, то узнаете обозначение процента % (Вывести на слайд пример ценника с обозначением процента)

Сотая часть любой величины называется процентом.

– Давайте разберемся,  почему для процента берут именно сотую часть. Мы помним, что сотую часть метра называют сантиметром,  сотую часть гектара аром,  удобно выделять сотую часть.

– Давайте же попробуем подсчитать, какую же выгоду получит Маша и ее мама от скидок:

– Обратим внимание, что некоторые товары Маша и мама купили без скидки, т.е. заплатили всю стоимость – это 100%. Иногда говорят,  «выполнил на 100%» значит,  выполнил полностью.

– Как вы поняли проценты, тесно связаны с дробями (десятичными и обыкновенными).

– Любое количество процентов можно записать в виде десятичной дроби или натурального числа. Для этого нужно число, стоящее перед знаком %, разделить на 100.

– Так же можно выполнить обратное преобразование, т.е. записать десятичную дробь или натуральное число в %. Для этого нужно число умножить на 100 и к результату приписать знак %.

Физкультминутка.

4. Закрепление изученного материала.

– Давайте проверим, как вы усвоили новый материал. Выполним задание №1056 из учебника.

1)  8;

2) 0,04;

3)5,4;

4) 9;

5) 117,6;

6) 60.

Задача №1. Швейная фабрика выпустила 1200 костюмов. Из них 25% костюмы нового фасона. Сколько костюмов нового фасона выпустила фабрика?
Решение: Так как 1200 костюмов - это 100% выпуска, то, чтобы найти 1% выпуска, надо 1200 разделить на 100. Получим, что 1200 / 100 = 12, значит, 1% выпуска равен 12 костюмам. Чтобы найти, чему равны 25% выпуска, надо умножить 12 на 25. Так как 12 * 25 = 300, то фабрика выпустила 300 костюмов нового фасона.

Задача №2. Организм взрослого человека на 70% состоит из воды. Какова масса воды в теле человека, который весит 76 кг?

Решение: 1) 76 : 100 = 0,76 (кг) 1% от массы человека;

2) 0,76 * 70 = 53,2(кг).

Ответ: масса воды 53,2 кг.

Задача 3.  В магазин завезли 600 кг конфет, печенья и мармелада. 40% составляли конфеты, 25% – печенье. Сколько килограммов мармелада завезли в магазин?

Решение:

1)40+25=65 (%)- конфеты и печенья.

2) 100–65=35(%)- мармелад.

3) 600:100=6(кг) – 1%

4) 635=210 (кг)

Ответ: в магазин завезли 210 кг мармелада.

5. Самостоятельная работа.

Каждому варианту дается скидочная карта  магазина «Спортмастер». Необходимо подсчитать, какую скидку получит каждый вариант на определенный набор товаров.

1 вариант – 15% скидка.

2 вариант – 17% скидка.

Набор товаров и цена:

Ролики – 3500 рублей;

Шлем – 1400 рублей;

Защитные перчатки ­– 800 рублей.

6. Рефлексия

Подведем итог работы на уроке. Какую цель мы ставили? Достигли ли цели?

Назовите тему урока.

Что называется процентом?

Как перевести проценты в десятичную дробь?

Как перевести десятичную дробь в проценты?

Как найти процент от числа?

Оцените свою деятельность на уроке…

– Мне всё удалось

 –У меня остались вопросы

– Мне было интересно

– Мне было скучно

Поблагодарим, друг друга за урок! (все дружно похлопайте в ладоши)

Всем спасибо! До новых встреч!

4. Предложите тематику исследовательских работ (проектных работ) по одному из разделов курса математики 5 (6) класса.

Оригами и математика
Орнамент — отпечаток души народа.
Орнаменты и узоры
Ох уж эти дроби
Ох, уж эти проценты!
Понятие "дроби". История изучения.
Появление и развитие числа
Практическое применение процентов в нашей жизни.
Приемы решений задач на проценты.
Применение процентов в жизни.
Простые числа. Так ли проста их история.
Процентные вычисления и расчеты.
Процентные расчеты на каждый день.
Проценты в нашей жизни.
Проценты в современном мире.
Проценты вокруг нас
Проценты и дроби.
Числа Мерсенна.

Тема 3.3.

1. Какова специфика методики обучения алгебре учащихся, проявивших выдающиеся математические способности?

Методами и формами работы с одаренными учащимися на уроках математики являются методы творческого характера - проблемные, поисковые, эвристические, исследовательские, проектные - на основе форм индивидуальной и групповой работы. Наиболее эффективными являются технологии, которые реализуют идею индивидуализации обучения и дают простор для творческого самовыражения и самореализации учащихся. Это, прежде всего, технология проектного обучения, которая сочетается с технологией проблемного обучения, и методика обучения в «малых группах».

Важным элементом при работе с одаренными детьми является внеурочная деятельность. Потому как она активизирует познавательную деятельность учащихся и развивает их математические способности. Можно использовать во внеурочной работе с одаренными детьми следующие формы: групповые занятия, факультативы, конкурсы и викторины, курсы по выбору, элективные курсы, предметные олимпиады, работа по индивидуальным планам, интеллектуальные марафоны, индивидуальные творческие задания, проекты по различной тематике.

Таким образом, важной задачей современного общества является создание условий, обеспечивающих выявление и развитие одаренных детей, а так же реализацию их потенциальных возможностей. Работа с одаренными детьми своими специфическими средствами способствует решению целого комплекса гуманитарных задач и имеет большое значение в жизни общества. Нет сомнений, что математика и математический стиль мышления совершают сейчас триумфальный марш, как в науке, так и во многих науках. Учащиеся в школе должны относиться к математике с большим интересом, увлечением и пониманием необходимости математических знаний, как для будущей их деятельности, так и для жизни общества.

   Задачи полезные для развития способностей учащихся

  I. Задачи с не сформулированным вопросом. В этих задачах нарочито не     формулируется вопрос, но этот вопрос логически вытекает из данных в задаче    математических отношений. Учащиеся упражняются в осмысливании логики    данных в задаче отношений и зависимостей. Задача решается после того, как   ученик сформулирует вопрос (иногда к задаче можно поставить несколько    вопросов). В скобках указывается пропущенный вопрос.

Задача.  До конца суток осталось 4/5 того, что уже протекло от начала суток.       (Который сейчас час?)

II. Задачи с недостающими данными. В задачах этого типа отсутствуют    некоторые данные, вследствие чего дать точный ответ на вопрос задачи не    представляется возможным. Школьник должен проанализировать задачу и    доказать, почему нельзя дать точного ответа на вопрос задачи, чего не   хватает, что надо добавить. В скобках указываются пропущенные данные.

Задача. Даны две окружности, радиус одной из них - 3 см, расстояние между их  центрами - 10 см. Пересекаются ли эти окружности? (Требуется знать радиус   другой окружности.)

III. Задачи с излишними данными. В эти задачи нарочито введены       дополнительные ненужные данные, до известной степени маскирующие       необходимые для решения показатели. Ученики должны выделить те данные,       которые необходимы, для решения, и указать на лишние, ненужные (ненужные       данные выделены курсивом).

Задача. Четыре гири разного веса весят вместе 40 кг. Определить вес самой     тяжелой гири, если известно, что каждая из них втрое тяжелее другой, более    легкой, и что самая легкая весит в 12 раз меньше, чем весят вместе две    средних.

IV. Задачи на доказательство. Сущность этих задач в доказательстве   определенных положений. Учащиеся упражняются в построении правильного,    обоснованного, последовательного рассуждения.

Задача. Доказать, что выражение 5(х+4)-5х не может быть отрицательным числом при    любом значении х.

V. Задачи на рассуждение (или составление уравнений).

Задача. Я загадал число. Сумма половины и трети его на 7 единиц больше четверти    его. Что это за число?

VI. Задачи с несколькими решениями. Для упражнения гибкости мышления       важно, чтобы школьник умел находить несколько решений одной и той же     задачи. Если эти решения неравноценны с точки зрения экономичности и     рациональности, то ученик должен дать с этой точки зрения оценку каждому    решению.     Надо побуждать школьника найти наиболее рациональное, ясное, простое,   изящное решение.

Задача. Найти сумму всех целых чисел от 1 до 50.

VII. Задачи на соображение.

Для решения указанных задач не требуется никаких специальных знаний,       однако в ряде случаев необходимо проявить известную изобретательность.

Задача. Все целые числа, начиная с единицы, выписаны подряд. Какая цифра стоит    на 1955 месте?

VIII. Задачи на логическое рассуждение.

 На задачах этой серии тренируется способность логически рассуждать,       смекалка и сообразительность. Не все эти задачи являются математическими в    узком смысле слова, некоторые из них являются логическими задачами.

 Задача. Из 9 совершенно одинаковых по внешнему виду подшипников один       бракованный - он несколько легче остальных. Как найти его не более чем      двумя взвешиваниями на обычных весах без гирь?

 IX. Задачи с наглядным решением.

 Эти задачи сравнительно легко решаются с применением наглядно-образных    средств (рисунков, схем, чертежей). Тренируется способность наглядно     выражать математические соотношения задачи. Сначала ученика просят решить   указанные задачи рассуждением, без опоры на наглядные образы.

Задача. Сколько весит кирпич, если он весит килограмм плюс полкирпича?

 X. Задачи, требующие наглядных представлений.

Задачи этого типа учащиеся должны решать в уме, без помощи карандаша и       бумаги, без опоры на соответствующие фигуры или тела. Решение подобных     задач тренирует пространственные представления, способность мысленно    «видеть» соответствующие фигуры, тела, пространственные соотношения.

Задача. Какой угол опишет часовая стрелка за 2 часа? за 20 мин? а минутная    стрелка - за 10 мин? за 25 мин?

4. Выберите конкретную тему курса алгебры. Изучите соответствующие разделы программы и учебника. Выявите методические особенности изучения темы. Разработайте фрагменты методики обучения теме математически одаренных учащихся.

«Степень с натуральным показателем». Основной целью изучения данного пункта является накопление знаний о степенях, то есть создание своего рода фундамента для последующего изучения широкого круга тождественных преобразований различного вида и разделов: квадратный корень, степень с целым показателем, корень n-й степени. В связи с этим «степени с натуральным показателем» необходимо уделить особое внимание; добиться того, чтобы данная тема была усвоена всеми учащимися. Определение степени числа a с натуральным показателем n учащиеся должны хорошо усвоить, так как на его основе этого определения строится алгоритм вычисления степени. Для лучшего запоминания определения целесообразно использовать наглядный материал, представленный в таблице. Необходимо требовать от учащихся грамотного прочтения выражения вида при конкретных значениях a и n.

Степень с натуральным показателем

Внимание учащихся следует обратить на свойство степени с отрицательным основанием с четным и нечетным показателем, а также на справедливость неравенства        при любых значениях  . Таким образом, ученик в первую очередь должен привыкнуть определять знак получаемого значения степени.

Большое количество упражнений уделяется вычислению значений выражений. Для их выполнения учитель должен ознакомить учеников с принятым порядком выполняемых действий: при отсутствии скобок сначала выполняется возведение в степень, затем умножение и деление, и сложение и вычитание.

Некоторые   учащиеся   считают,   что                            . Во избежание ошибки, следует уделить внимание следующему упражнению.

Пример [1, с. 156].                                .

При изучении свойств степеней с натуральным показателем, учащиеся сталкиваются с теоремами и их доказательствами. На этом этапе важно объяснить, что равенство                                                            является основным свойством степени. Так как из него следуют правила деления степеней и возведения степени в степень. Уместно рекомендовать учащимся изучить доказательства свойств степеней по учебнику, либо попробовать доказать их самостоятельно. Требовать воспроизводить доказательства в дальнейшем – не рекомендуется.

Тема 3.4.

1. В чем особенности методики обучения геометрии учащихся, проявивших выдающиеся математические способности?

Изложение материала на уроках геометрии основывается на размышлении, выдвижении гипотез, анализе поставленных задач, здесь нужно уметь доказывать не только данную теорему, но и правильность своего творческого и логического мышления. Одаренные дети могут на этих уроках проявлять себя и показывать пример остальным ученикам класса к чему надо стремиться. Для поддержки интереса к урокам математики нужно использовать не только задания из учебника, но и занимательные задачи, позволяющие ученикам проявить смекалку и использовать свои неординарные способности. Одаренному ребенку, решающему предложенные на уроке задания намного быстрее остальных, нужно подобрать дополнительные задания более высокого уровня сложности, требующие от ученика нестандартного мышления. Организация дифференцированного подхода обучения на уроках математики поможет лучше реализовать свои индивидуальные способности учеников класса.

В наше время хорошее знание геометрии, это залог того, что в дальнейшем этот ученик может проявить свои способности в различных отраслях профессиональной деятельности, они пригодятся и математику, и экономисту, и дизайнеру.

Наличие в классе одаренного ребенка ставит перед педагогом определенные задачи. Очень важно, чтобы на уроке были заняты все ученики, значит нужно подбирать задания, которые заинтересуют и будут интересны всем ученикам класса. Однако, работая с одаренными детьми, педагог должен предусматривать не только урочную форму, но и внеурочную форму общения и работы. Эти формы помогут такому ученику лучше адаптироваться в школе, классе и лучше развить свои способности. На внеурочных занятиях, учитель, работая с заинтересованными детьми, уделяет время для разбора и решения нестандартных задач, привлекает учеников к исследовательской работе, может помочь подготовить презентации, которые в дальнейшем будут использоваться для объяснения нового материала.

Работа с одаренными детьми направлена на развитие интеллектуальных и творческих возможностей. Подбор задач осуществляется для различных уровней подготовки учеников. Одаренный ребенок в классе – это дополнительная ответственность для учителя, проверка на его профессиональную пригодность и способность к внедрению на уроках современных технологий, которые дают дополнительные возможности индивидуальные работы с каждым учеником. В условиях современного образования учитель должен увидеть и развить в ученике всестороннюю личность, и, учитывая его индивидуальные способности, дать обучающемуся самореализоваться, удовлетворить его познавательные интересы.

5. Выберите конкретную тему курса геометрии. Изучите соответствующие разделы программы и учебника. Выявите методические особенности изучения темы. Разработайте фрагменты методики обучения теме.

Центральное место в изучении равных треугольников занимают признаки равенства треугольников.

Прежде, чем, приступить к ознакомлению учащихся с этими признаками, ггадо пояеггить термины «угол, прилежащий к стороне», «угол, противолежащий стороне», «сторона, противолежащая углу», «угол, заключенный между сторонами» и т.д.. Учащиеся не всегда могут указать угол, противолежащий меньшей стороггс тупоугольного треугольника (рис. 57).

Полезно на чертеже продолжить стороны треугольника, заключающие некоторый угол, и выяснить, что прилежащие стороны лежат на сторонах угла (лучах), а противолежащая углу сторона расположена внутри угла (рис. 58).

Ознакомление с признаками равенства треугольников можно осуществить посредством упражнения.

Рис.57                                 Рис. 58

Например, перед введением признака равенства треугольников по двум сторонам и углу между ними выполняется упражнение.

1. Постройте два треугольника АВС и АВС, У которых А В = АВ = 6 см, АС = АС = 5 см, ZA = ZA 1 = 50°. Равны ли треугольники АВС и АВС!

Для того чтобы ответить на вопрос задачи, учащиеся должны (в рамках учебника А.В. Погорелова) измерить стороны ВС и ВС, углы В, В, С, Ci и сравнить результаты.

Упражнение приведет таким образом к выводу, что указанные треугольники АВС и АВС равны. Так как выполнение этого упражнения требует проведения различных измерений, а значит, и времени, то целесообразнее предложить его в качестве домашнего задания, а на уроке обсудить результаты его выполнения. Можно использовать для ознакомления с признаком и специальные модели.

По учебнику Л. С. Атанасяна и др. введение признаков равенства треугольников можно осуществить другим способом. Взять две каркасные модели треугольника, удовлетворяющие изучаемому признаку (равные элементы можно как-то выделить, например, окрасить одинаковым цветом), и наложить одну из них на другую (аналогичную операцию можно также выполнить с помощью компьютера). В результате этой операции треугольники совпадут, откуда и будет следовать их равенство.

Тема урока: «Первый признак равенства треугольников»

Цель урока:

Образовательная: сформировать представление о первом признаке равенства треугольников и о способе его доказательства; формировать навыки применения первого признака равенства треугольников при решении задач.

Развивающая: формировать умения анализировать, сопоставлять данные, выводить логические следствия из данных предпосылок, умение делать выводы, оценивать влияние условий на результат, развивать логическое мышление учащихся.

Воспитательная: формировать умение концентрировать внимание, сосредотачиваться.

Методы обучения: индуктивно-эвристический, дедуктивно-репродуктивный.

Тип урока: изучение новых знаний.

ХОД УРОКА

1. Организационный момент.

Приветствие учеников, проверка готовности кабинета и учащихся к уроку, проверка отсутствующих.

2. Актуализация знаний.

Учитель: на предыдущем уроке мы приступили к изучению главы «Треугольники». Выяснили, какие две фигуры, в частности, два треугольника называются равными. Сегодня мы выясним, можно ли установить равенство двух фигур, не проводя фактического наложения одной на другую, а сравнивая только некоторые элементы этих фигур, в частности, как сравнить треугольники.

Учитель: вспомните, какая фигура называется треугольником?

Ученик: треугольником называется фигура, образованная тремя точками, не лежащими на одной прямой и соединяющими их отрезками.

Учитель: начертите треугольник и покажите его стороны вершины и углы.

Ученик выходит к доске, чертит на ней треугольник с помощью линейки и мела, показывает вершины, углы и стороны треугольника.

Учитель: что такое периметр треугольника?

Ученик: периметр треугольника – это сумма длин трех его сторон.

Учитель: какие треугольники называются равными?

Ученик: две фигуры, в частности два треугольника называются равными, если их можно совместить наложением.

Учитель: верно. Теперь посмотрите на слайд. Там изображены треугольники ∆DEK, ∆MNP.

На слайде изображены треугольники (слайд 2)

Учитель: назовите углы ∆DEK, прилежащие к стороне ЕК.

Ученик: это углы Е и К.

Учитель: назовите углы ∆MNP, прилежащие к стороне MN.

Ученик: это углы М и N.

Учитель: назовите угол ∆DEK, заключенный между сторонами DE и DК.

Ученик: это угол D.

Учитель:  назовите угол ∆MNP, заключенный между сторонами NP и РМ.

Ученик: это угол P.

Учитель: между какими сторонами ∆DEK заключен угол К?

Ученик: между сторонами EK и DK.

Учитель: между какими сторонами ∆MNP заключен угол N?

Ученик: между сторонами MN и PN.

3. Изучение нового материала.

Учитель: откройте свои тетради и запишите число, классную работу и тему урока «Первый признак равенства треугольников».

Запись на слайде (слайд1) и в тетрадях:

Число.

Классная работа.

Первый признак равенства треугольников.

Учитель: Чтобы установить равенство двух треугольников, надо их совмещать или проверить равенство соответствующих сторон и соответствующих углов. Но иногда ни совместить, ни проверить все равенства нет возможности. Оказывается, достаточно установить лишь часть из них.

Посмотрите на слайд. Там изображены два треугольника АВС и АСD.

На слайде изображены треугольники (слайд 3)

Учитель: скажите, равны ли данные треугольники.

Ученик: нет.

Учитель: объясните почему.

Ученик: потому что при наложении они не совпадут.

Учитель: верно, теперь рассмотрим на слайде треугольники АВD и АСD. Какие стороны и углы у них равны или являются общими?

На слайде изображены треугольники (слайд 4)

Ученик: угол А  - общий и сторона АD общая.

Учитель: верно, а равны ли стороны AB и BC?

Ученик: они не равны.

Учитель: какой же мы можем сделать вывод?

Ученик: данные треугольники не равны.

Учитель: итак, у двух треугольников угол общий и общая сторона, но этого недостаточно, чтобы они были равны. Подумайте, если бы нам было известно, что две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, можно ли утверждать, что такие треугольники равны?

Ученик: нет, так как другие стороны не равны.

Учитель: о двух других сторонах ничего не известно, что нужно сделать в такой ситуации?

Ученик: нужно выяснить, являются ли эти стороны равными.

Учитель: для того, чтобы установить равенство двух треугольников, не обязательно выяснять, являются ли эти стороны равными, так как справедливо утверждение: «Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны». Это утверждение называется «Первый признак равенства треугольников». Посмотрите на слайд, там записано это утверждение, запишите его себе в тетрадь.

Учащиеся переписывают со слайда первый признак равенства треугольников (слайд 5).

Учитель: в математике каждое утверждение, справедливость которого устанавливается путем рассуждений, называется теоремой, а сами рассуждения называются доказательством теоремы.

Учитель: какие теоремы нам уже известны?

Ученик: свойство смежных углов и свойство вертикальных углов.

Учитель: Признак (по В.Далю) – это знак, отличие, все, почему узнают что–либо. Увидев морозный узор на окне, можно, не выходя из дома, сказать, что на улице холодно. Признак дает возможность устанавливать равенство двух треугольников, не проводя фактического наложения одного из них на другой, а сравнивая только некоторые элементы треугольников.

Учитель: любая теорема состоит из условия и заключения. Как вы понимаете, что может означать словосочетание «условие теоремы»,  а что – «заключение теоремы»?

Ученик: условие - это уже известные факты, о которых говорится в теореме, а заключение – это то, что нужно доказать.

Учитель: выделите условие теоремы «Первого признака равенства треугольников».

Ученик: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника.

Учитель: выделите  заключение теоремы.

Ученик: то такие треугольники равны.

Учитель: итак, докажем первый признак равенства треугольников. Посмотрите на слайд, там изображены равные треугольники.

На слайде изображены треугольники (слайд 6)

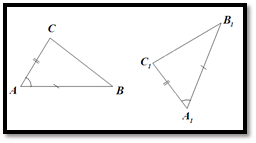
Учитель: опираясь на данные рисунка, скажите, что нам дано?

Ученик: ∆ АВС, ∆ А₁В₁С₁,  АВ = А₁В₁,  АС = А₁С₁, А = А_1.

Учитель: верно, что нужно доказать?

Ученик: ∆ АВС =  ∆ А₁В₁С_1.

Учитель: хорошо. Запишите это себе в тетрадь.

Запись на слайде (слайд 7) и в тетрадях:

Дано: ∆ АВС, ∆ А₁В₁С₁,  АВ = А₁В₁,

АС = А₁С₁, А = А₁.

Доказать: ∆ АВС =  ∆ А₁В₁С_1.

Учитель: наложим ∆ АВС на  ∆ А₁В₁С_1. так, чтобы 1) точка А совместилась с точкой А₁; 2) сторона АС совпала со стороной А₁С₁. Что можно сказать про точку С?

Ученик: так как  АС = А₁С₁, то точка С совпадает с точкой С_1.

Учитель: правильно. Так как А = А₁ по условию, то мы можем наложить ∆ АВС на  ∆ А₁В₁С₁ Так, чтобы: 3) сторона АВ совпала со стороной А₁В₁. Что нужно сделать дальше?

Ученик: так как АВ = А₁В₁, то точка В совпадет с точкой В₁. И сторона ВС совпадет со стороной В₁С_1.

Учитель: точка В совпала сточкой В₁, точка С совпала сточкой С₁, а через две точки можно провести только одну прямую – есть такое утверждение. Треугольники  АВС и   А₁В₁С₁ полностью совместились, значит, они равны по определению равных треугольников. Теорема доказана. Запишите доказательство себе в тетрадь.

Учащиеся записывают доказательство, при необходимости, сверяясь с записью на слайде (слайд 8)

Доказательство:

При наложении АС = А₁С_1.  Так как А = А₁ по условию, то АВ = А₁В_1.  Точка В совпадет с точкой В_1, а следовательно, ВС = В₁С_1. Точка В совпала сточкой В₁, точка С совпала сточкой С₁, а через две точки можно провести только одну прямую. Следовательно, ∆ АВС =  ∆ А₁В₁С_1.

Учитель: рассмотрим еще одну пару треугольников ∆ АВС и  ∆АDС, изображенных на слайде.

На слайде изображены треугольники (слайд 9)

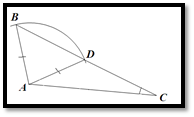
Учитель: внимательно выслушайте формулировку и ответьте мне на вопрос: если две стороны и угол одного треугольника соответственно равны двум сторонам и углу  другого треугольника, то такие треугольники равны. Как вы думаете, верно ли это утверждение?

Мнения учащихся могут разделиться.

Учитель: сторона АВ треугольника АВС равна стороне АD треугольника АDС, сторона АС – общая, иС – общий. Но треугольники не равны. Итак, условие утверждения выполнено, а заключение – нет. Значит утверждение не верно. Обратите особое внимание, на то, что условие «угол между сторонами» необходимо!

4. Закрепление изученного материала. 

Учитель: перейдем к решению задач.

Ученик выходит к доске, решает задачу у доски, комментируя свои действия; остальные учащиеся решают на местах, делают записи в своих тетрадях (рисунок и требование к задаче на слайде 10).

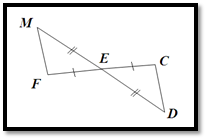
Доказать: ∆МЕF = ∆DЕС

Ученик: по рисунку, ME=DE, CE=EF, углы CED и FEM – вертикальные, значит они равны. Следовательно ∆МЕF = ∆DЕС по первому признаку равенства треугольников.

Ученик записывает доказательство на доске, а все остальные – в тетрадях:

Дано: ∆МЕF, ∆DЕС, ME=DE, CE=EF.

Доказать: ∆МЕF = ∆DЕС.

Доказательство: по условию ME=DE, CE=EF, углы CED и FEM равны (вертикальные), значит ∆МЕF = ∆DЕС.

Учитель: давайте проверим, верно ли вы доказали, посмотрите доказательство, которое приведено на слайде (слайд 11).

Дано: ∆МЕF, ∆DЕС, ME=DE, CE=EF.

Доказать: ∆МЕF = ∆DЕС.

Доказательство: по условию ME=DE, CE=EF, углы CED и FEM равны (вертикальные), значит ∆МЕF = ∆DЕС.

Учитель: следующая задача.

Ученик выходит к доске, решает задачу у доски, комментируя свои действия; остальные учащиеся решают на местах, делают записи в своих тетрадях (рисунок и требование к задаче на слайде 12).

Ученик записывает доказательство на доске, а все остальные – в тетрадях, затем все сверяются с доказательством, приведенным на слайде (слайд 13)

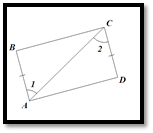
BC||AD. Доказать: ∆ABC= ∆ADC.

Дано: ∆ABC, ∆ADC, AB=CD, AC-общая.

Доказать: ∆ABC= ∆ADC.

Доказательство: по условию AB=CD, AC-общая, углы BAC и DCA равны (накрест лежащие), значит ∆ABC= ∆ADC.

5. Подведение итогов.

Учитель: сегодня на уроке вы в целом хорошо поработали; те учащиеся, которые работали у доски, получают соответствующие отметки. Итак, давайте повторим, какие треугольники называются равными?

Ученик: два треугольника называются равными, если их можно совместить наложением.

то называется теоремой?

Учитель: какую теорему мы сегодня доказали?

Ученик: первый признак равенства треугольников.

Учитель: сформулируйте ее.

Ученик: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Учитель: почему данная теорема называется признаком?

Ученик: потому что это теорема дает возможность устанавливать равенство двух треугольников, не проводя фактического наложения одного из них на другой, а сравнивая только некоторые элементы треугольников.

Учитель выставляет отметки за урок.

6. Домашнее задание. 

Учитель: записываем домашнее задание:

Запись в дневниках и на слайде (слайд 14):

П 14,15. Вопросы 1 -4 стр. 49. №93,95.

Учитель: на этом  урок окончен, можете быть свободны.