
À. Â. Ìîãèëåâ
Ë. Â. Ëèñòðîâà

Ñàíêò-Ïåòåðáóðã
«ÁÕÂ-Ïåòåðáóðã»
2008
УДК 681.3.06(075.3)
ББК 32.973.26-018.2я721
М74
Могилев, А. В.
М74 Методы программирования. Компьютерные вычисления /
А. В. Могилев, Л. В. Листрова. — СПб.: БХВ-Петербург, 2008. —
320 с.: ил. — (ИиИКТ)
ISBN 978-5-9775-0151-4
Книга является частью комплекта учебников по курсу информатики и информационно-коммуникационных технологий (ИКТ) в старших классах общеобразовательной школы на профильном уровне. Она охватывает 5-й и 6-й из 10-ти модулей курса и является продолжением пособий "Информация и информационные процессы. Социальная информатика", "Средства информатизации. Телекоммуникационные технологии".
В книге рассмотрены история развития языков программирования и парадигмы программирования, языки программирования высокого уровня, метаязыки для описания синтаксических конструкций языка высокого уровня, структурно-ориентированное программирование и язык Паскаль, введение в язык Си, элементы объектного программирования, основы логического программирования на языке Пролог, вычислительные методы, дано понятие о компьютерном моделировании.
По каждой рассматриваемой теме есть контрольные вопросы, темы для рефератов и докладов, вопросы для обсуждения, задачи и упражнения, лабораторные работы.
Для учащихся старших классов физико-математического, информационно-технологического и других профилей
УДК 681.3.06(075.3)
ББК 32.973.26-018.2я721 Группа подготовки издания:
|
Главный редактор |
Екатерина Кондукова |
|
Зам. главного редактора |
Антонина Панюшева |
|
Зав. редакцией |
Григорий Добин |
|
Редактор |
Екатерина Капалыгина |
|
Компьютерная верстка |
Ольги Сергиенко |
|
Корректор |
Людмила Минина |
|
Дизайн серии |
Инны Тачиной |
|
Оформление обложки |
Елены Беляевой |
|
Зав. производством |
Николай Тверских |
Ëèöåíçèÿ ÈÄ ¹ 02429 îò 24.07.00. Ïîäïèñàíî â ïå÷àòü 22.07.08.
Ôîðìàò 70×1001/16. Ïå÷àòü îôñåòíàÿ. Óñë. ïå÷. ë. 25,8.
Òèðàæ 1500 ýêç. Çàêàç ¹
"ÁÕÂ-Ïåòåðáóðã", 194354, Ñàíêò-Ïåòåðáóðã, óë. Åñåíèíà, 5Á.
Ñàíèòàðíî-ýïèäåìèîëîãè÷åñêîå çàêëþ÷åíèå íà ïðîäóêöèþ
¹ 77.99.60.953.Ä.003650.04.08 îò 14.04.2008 ã. âûäàíî Ôåäåðàëüíîé ñëóæáîé ïî íàäçîðó â ñôåðå çàùèòû ïðàâ ïîòðåáèòåëåé è áëàãîïîëó÷èÿ ÷åëîâåêà.
Îòïå÷àòàíî ñ ãîòîâûõ äèàïîçèòèâîâ â ÃÓÏ "Òèïîãðàôèÿ "Íàóêà"
199034, Ñàíêò-Ïåòåðáóðã, 9 ëèíèÿ, 12
ISBN 978-5-9775-0151-4 © Могилев А. В., Листрова Л. В., 2008
© Оформление, издательство "БХВ-Петербург", 2008
Оглавление
Предисловие ........................................................................................................... 7
МОДУЛЬ 5. ЯЗЫКИ И МЕТОДЫ ПРОГРАММИРОВАНИЯ ..................... 9 5.1. История развития языков программирования и парадигмы
программирования ............................................................................................. 11
Учебный материал ............................................................................................................. 11 Контрольные вопросы ....................................................................................................... 17 Темы для рефератов и докладов ....................................................................................... 17 Вопросы для обсуждения .................................................................................................. 18 Задачи и упражнения ......................................................................................................... 18
Лабораторные работы ........................................................................................................ 18
5.2. Языки программирования высокого уровня. Метаязыки для описания синтаксических конструкций языка высокого уровня ..... 19
Учебный материал ............................................................................................................. 19 Контрольные вопросы ....................................................................................................... 27 Темы для рефератов и докладов ....................................................................................... 28 Вопросы для обсуждения .................................................................................................. 28 Задачи и упражнения ......................................................................................................... 28
Лабораторные работы ........................................................................................................ 29
5.3. Паскаль как язык структурно-ориентированного
программирования ............................................................................................. 30
Учебный материал ............................................................................................................. 30 Введение в Паскаль .................................................................................................... 30 Основные конструкции языка Паскаль .................................................................... 37 Структуры данных ..................................................................................................... 42 Процедуры и функции ............................................................................................... 53 Обработка файлов ...................................................................................................... 58 Динамические информационные структуры ........................................................... 64
Оглавление
Работа с графикой ...................................................................................................... 69
Система программирования на Паскале .................................................................. 77 Контрольные вопросы ....................................................................................................... 78 Темы для рефератов и докладов ....................................................................................... 79 Вопросы для обсуждения .................................................................................................. 79 Задачи и упражнения ......................................................................................................... 79
Лабораторные работы ........................................................................................................ 81
5.4. Методы и искусство программирования ................................................. 83
Учебный материал ............................................................................................................. 83 Основные принципы разработки и анализа алгоритмов ........................................ 92 Методы построения алгоритмов, ориентированные на структуры данных ......... 99
Рекурсивные алгоритмы .......................................................................................... 103
Алгоритмы поиска и сортировки ............................................................................ 105 Контрольные вопросы ..................................................................................................... 120 Темы для рефератов и докладов ..................................................................................... 121 Вопросы для обсуждения ................................................................................................ 122 Задачи и упражнения ....................................................................................................... 122
Лабораторные работы ...................................................................................................... 123
5.5. Введение в язык программирования Си ............................................... 124
Учебный материал ........................................................................................................... 124
Общая характеристика языка и пример программы на Си .................................. 124 Элементы Си: алфавит, идентификаторы, литералы, служебные слова ............. 129 Типы данных и операции в языке Си. Выражения ............................................... 132
Операторы. Управляющие конструкции языка ..................................................... 141 Оператор присваивания ...................................................................................... 141
Оператор if/else .................................................................................................... 142
Оператор-переключатель switch ......................................................................... 144
Оператор цикла for .............................................................................................. 146
Оператор цикла while .......................................................................................... 149
Оператор цикла do/while ..................................................................................... 150
Оператор break ..................................................................................................... 150
Оператор продолжения continue ........................................................................ 151
Оператор безусловного перехода goto ............................................................... 152
Составные операторы и блоки ........................................................................... 152 Структура программы на Си. Понятие о функциях .............................................. 153
Классы памяти .......................................................................................................... 160 Функции ввода/вывода ............................................................................................ 165 Директивы препроцессора ...................................................................................... 171
Сравнение языков программирования Си и Паскаль ........................................... 174
Контрольные вопросы ..................................................................................................... 175 Темы для рефератов и докладов ..................................................................................... 176 Вопросы для обсуждения ................................................................................................ 176 Задачи и упражнения ....................................................................................................... 177 Лабораторные работы ...................................................................................................... 184
Оглавление 5
5.6. Элементы объектного программирования ........................................... 186
Учебный материал ........................................................................................................... 186 Контрольные вопросы ..................................................................................................... 204 Темы для рефератов и докладов ..................................................................................... 205 Вопросы для обсуждения ................................................................................................ 205 Задачи и упражнения ....................................................................................................... 205
Лабораторные работы ...................................................................................................... 206
5.7. Основы логического программирования на языке Пролог .............. 207
Учебный материал ........................................................................................................... 207 Общие сведения ....................................................................................................... 207 Алгоритм выполнения программ на Прологе........................................................ 213
Рекурсия .................................................................................................................... 217
Предикат отсечения и управление логическим выводом в программах ............. 220
Обработка списков ................................................................................................... 222
Решение логических задач на Прологе .................................................................. 226 Контрольные вопросы ..................................................................................................... 229 Темы для рефератов и докладов ..................................................................................... 230 Вопросы для обсуждения ................................................................................................ 230 Задачи и упражнения ....................................................................................................... 230
Лабораторные работы ...................................................................................................... 232
МОДУЛЬ 6. КОМПЬЮТЕРНЫЕ ВЫЧИСЛЕНИЯ ................................... 233
6.1. Вычислительные методы ......................................................................... 235
Учебный материал ........................................................................................................... 235 Вычисление значений функций. Интерполяция.................................................... 235 Решение нелинейных уравнений с одной переменной ......................................... 245 Решение систем линейных уравнений ................................................................... 257
Численное интегрирование ..................................................................................... 261 Контрольные вопросы ..................................................................................................... 267 Темы для рефератов и докладов ..................................................................................... 268 Вопросы для обсуждения ................................................................................................ 269 Задачи и упражнения ....................................................................................................... 270 Лабораторные работы ...................................................................................................... 274 Задания для самостоятельных и контрольных работ .................................................... 280
6.2. Понятие о компьютерном моделировании ............................................ 281
Учебный материал ........................................................................................................... 281 Моделирование как метод познания ...................................................................... 281 Этапы и цели компьютерного моделирования ...................................................... 284 Классификация информационных моделей ........................................................... 289
Построение компьютерной модели. Моделирование ........................................... 295 Информационные модели баз данных ............................................................... 297
Информационное моделирование в электронных таблицах ............................ 300
Оглавление
Контрольные вопросы ..................................................................................................... 303 Темы для рефератов и докладов ..................................................................................... 304 Вопросы для обсуждения ................................................................................................ 305 Задачи и упражнения ....................................................................................................... 305 Лабораторные работы ...................................................................................................... 308
Литература ........................................................................................................................ 316
Предметный указатель ..................................................................................... 317
Несмотря на значительные усилия, направленные на становление профильного образования, изменения в российской школе еще далеки от ожиданий. Одна из причин связана с недостаточностью учебно-методического обеспечения обучения на профильном уровне во многих образовательных областях, к которым относятся также информатика и информационные технологии.
Данный цикл пособий призван хотя бы отчасти снизить остроту этой проблемы и ликвидировать пробел в учебной литературе, предназначенной для обучения старшеклассников по профилям, включающим курс информатики и информационно-коммуникационных технологий профильного уровня: физико-математическом, информационно-технологическом и др.
Мы предлагаем модульный вариант как самого курса информатики и информационно-коммуникационных технологий, так и его учебного обеспечения. Значительный объем всего профильного курса (280 часов), разнородность его содержательных компонент (как с точки зрения соотношения теоретических и практических вопросов, так и сложности и трудоемкости деятельности учащихся), быстрое и неоднородное их развитие диктуют именно модульное построение данного курса, позволяющее выбирать, использовать и развивать модули учебного пособия независимо друг от друга. Кроме того, модульная структура курса обеспечивает большую гибкость и эффективность в достижении качества обучения, поскольку оно гарантируется качеством освоения каждого модуля в отдельности.
Согласно авторской учебной программе данный профильный учебный курс состоит из следующих 10 модулей:
1. Информация и информационные процессы.
2. Социальная информатика.
3. Средства информатизации.
4. Телекоммуникационные технологии.
5. Методы программирования.
6. Компьютерные вычисления.
Предисловие
![]()
7. Технологии обработки текстовой информации.
8. Технологии обработки графической и мультимедийной информации.
9. Технологии поиска и хранения информации.
10. Технологии автоматизации управления.
Настоящее пособие охватывает 5-й и 6-й модули курса и является продолжением пособий "Информация и информационные процессы. Социальная информатика", "Средства информатизации. Телекоммуникационные технологии" тех же авторов.
Пособия содержат учебный материал и различного рода задания и вопросы: тексты для чтения и изучения, контрольные вопросы, темы рефератов, вопросы для обдумывания и обсуждения, задания и упражнения, а также описание лабораторных работ. Это позволяет организовать занятия различного типа и реализовывать различные методы обучения от лекций и семинарских занятий до учебных проектов.
Для того чтобы облегчить ориентацию в пособии и придать ему структуру, мы используем следующие обозначения:
![]() — Учебный
материал;
— Учебный
материал;
— Контрольные вопросы;
— Темы для рефератов и докладов;
— Вопросы для обсуждения;
— Задачи и упражнения;
— Лабораторные работы.
МОДУЛЬ 5
Языки и методы
5.1. История развития языков программирования и парадигмы программирования
5.2. Языки программирования высокого уровня. Метаязыки для описания синтаксических конструкций языка высокого уровня
5.3. Паскаль как язык структурно-ориентированного программирования
5.4. Методы и искусство программирования
5.5. Введение в язык программирования Си
5.6. Элементы объектного программирования
5.7. Основы логического программирования на языке Пролог
2 Модуль 1. Информация и информационные процессы
5.1. История развития языков программирования и парадигмы программирования
 Учебный материал
Учебный материал
Основоположником программирования можно считать английского математика Чарлза Бэббиджа (1791—1871 гг.). В 20-х годах XIX века ему пришла идея создать такую механическую машину для вычислений, что порядок ее действий можно было предварительно записывать и впоследствии выполнять эти действия на машине автоматически. Это была идея, положившая начало программированию. Ч. Бэббидж посвятил реализации этой идеи всю жизнь. Он не добился успеха и признания современников при жизни, но оказал огромное влияние на современное развитие информатики.
Хотя использованный Бэббиджем способ записи программы на перфокартах, придуманный для управления ткацкими станками французским изобретателем Жозефом Мари Жаккаром, не имеет ничего общего с современными технологиями хранения и выполнения программ компьютерами, принцип остался тем же.
Рядом с Ч. Бэббиджем у истоков программирования стояла Ада Лавлейс, дочь английского поэта Чарлза Гордона Байрона. Она оказалась одним из немногих современников Чарлза Бэббиджа, кто сумел по достоинству оценить идею "аналитической машины". Она стала ближайшей помощницей и сподвижницей Бэббиджа, разработала некоторые приемы управления последовательностью вычислений, которые используются в программировании и по сей день, описала одну из важнейших конструкций практически любого современного языка программирования — цикл. Аду Лавлейс по праву считают первым в мире программистом.
Дальнейшего прогресса в программировании пришлось ждать почти 100 лет, и связан он был с появлением в середине 1940-х годов электромеханических и электронных вычислительных машин — родителей современных компьютеров.
Для программирования этих машин использовались машинные коды — цифровые комбинации, "понятные" только данной машине. Такое программирование было чрезвычайно трудоемким и сложным делом, доступным лишь небольшому кругу специалистов.
Первым шагом в развитии современных языков программирования стало создание в конце 1940-х годов Джоном Моучли, сотрудником Пенсильванского университета (США), системы кодирования машинных команд этих компьютеров с помощью специальных символов. Достижением создателей языков программирования было то, что они сумели заставить сам компьютер работать переводчиком с этих языков на машинный код. Описываемая система, которую назвали "Short Code", была по существу одним из первых примитивных интерпретаторов. Она использовала примитивный язык программирования высокого уровня. На нем программист записывал решаемую задачу в виде математических формул, а затем сам, используя специальную таблицу, переводил символ за символом, преобразовывая эти формулы в двухлитерные коды. В дальнейшем специальная программа компьютера превращала эти коды в двоичный машинный код.
Система кодирования, предложенная Моучли, увлекла одну из сотрудниц его группы — Грейс Мюррей Хоппер, которая стала третьим в мире програм- мистом.
В 1951 г. Хоппер создала первый в мире компилятор. Именно она ввела сам этот термин. Компилятор Хоппер осуществлял функцию объединения команд и в ходе трансляции производил организацию подпрограмм, выделение памяти компьютера, преобразование команд высокого уровня (в то время псевдокодов) в машинные команды. "Подпрограммы находятся в библиотеке (компьютера), а когда вы подбираете материал из библиотеки — это называется компиляцией", — так она объясняла происхождение введенного ею термина.
В 1954 г. группа под руководством Г. Хоппер разработала систему, включающую язык программирования и компилятор, которая в дальнейшем получила название MATH-MATIC. После удачного завершения работ по созданию MATH-MATIC Г. Хоппер и ее группа принялись за разработку нового языка и компилятора, который позволил бы пользователям программировать на языке, близком к обычному английскому. В 1958 г. появился компилятор FLOW-MATIC. FLOW-MATIC был первым языком для задач обработки коммерческих данных. Работы в этом направлении привели к созданию языка КОБОЛ (COBOL — Common Business Oriented Language). Одним из основных консультантов при его создании была Грейс Мюррей Хоппер.
При работе на компьютере "Maрк-I" Г. Хоппер и ее группе пришлось стать первопроходцами программирования. Они первыми придумали подпрограммы. Сейчас любой программист не задумываясь использует подпрограммы в любом языке программирования. Еще одно фундаментальное понятие техники программирования этой группы — "отладка". Однажды жарким летним днем 1945 г. неожиданно произошла остановка компьютера "Марк-I". Обнаружилась неисправность одного реле, контакты которого были заблокированы мотыльком, залетевшим в помещение вычислительного центра. Г. Хоппер вспоминала: "Когда к нам зашел офицер, чтобы узнать, чем мы занимаемся, мы ответили, что удаляем из компьютера насекомых (debuging)". С тех пор термин "debuging" (отладка) используется в технических процессах тестирования неисправностей в компьютере, а также в системах программирования.
Середина 50-х годов XX века характеризуется стремительным прогрессом в области программирования. Программирование в машинных командах стало вытесняться программированием на языках, выступавших в роли посредника между машинами и программистами. Первым и одним из наиболее распространенных стал Фортран (FORTRAN, от FORmula TRANslator — пере- водчик формул), разработанный группой программистов фирмы IBM в 1954 г. Этот язык получил большое распространение, стал основным языком для научных и технических расчетов, несколько раз усовершенствовался и широко используется до сих пор.
В конце 50-х годов плодом международного сотрудничества в области программирования явился Алгол-60 (ALGOL, от ALGOrithmic Language — алгоритмический язык, версия 1960 г.). Алгол предназначен для записи алгоритмов, которые строятся в виде последовательности процедур, применяемых для решения поставленных задач. Специалисты-практики восприняли этот язык далеко не однозначно, но, тем не менее, его влияние на развитие других языков и теорию программирования оказалось весьма значительным.
Развитие идеи Алгола о структуризации разработки алгоритмов нашло наивысшее отражение при создании в начале 1970-х годов языка Паскаль швейцарским ученым Никлаусом Виртом. Язык Паскаль первоначально разрабатывался как учебный, и, действительно, сейчас он является одним из основных языков обучения программированию в школах и вузах. Однако качества его в совокупности оказались столь высоки, что им охотно пользуются и профессиональные программисты.
В середине 1960-х годов сотрудники математического факультета Дартмутского колледжа Томас Курц и Джон Кемени создали специализированный язык программирования, который состоял из простых слов английского языка. Новый язык назвали "универсальным символическим кодом для начинающих" (Beginners All Purpose Symbolic Instruction Code, или, сокращенно, BASIC, а по-русски — Бейсик). Годом рождения нового языка можно считать 1964 г.
Долгое время универсальный язык Бейсик (имеющий множество версий) имел большую популярность и широкое распространение среди пользователей ЭВМ различных категорий во всем мире. В значительной мере этому способствовало то, что Бейсик начали использовать как встроенный язык персональных компьютеров, широкое распространение которых началось в конце 1970-х годов.
Большой отпечаток на современное программирование наложил язык Си (первая версия — 1972 г.), являющийся очень популярным в среде разработчиков систем программного обеспечения (включая операционные системы). Си сочетает в себе черты как языка высокого уровня, так и машинноориентированного языка, допуская программиста ко всем машинным ресурсам, чего не позволяют такие языки, как Бейсик и Паскаль.
Более специализированным языком является язык ЛОГО (от греческого logos — слово), созданный для обучения программированию школьников профессором математики и педагогики Сеймуром Пейпертом из Массачусетского технологического института. Обучаясь программированию на ЛОГО, дети задают простые команды и составляют из них программы, которые управляют условной "черепашкой" — объектом, оставляющем при перемещении след на экране монитора.
Отметим язык LISP (LISt Processing — обработка списков), появившийся в США в конце 1950-х годов, и еще один специализированный язык — Пролог (Prolog — PROgramming in LOGic), разработанный в 1970-е годы, как языки программирования для создания систем искусственного интеллекта.
В начале 1960-х годов все существующие языки программирования высокого уровня можно было пересчитать по пальцам, однако впоследствии их число достигло трех тысяч. Однако в практической деятельности используется не более двух десятков из них.
Разработчики ориентировали языки на разные классы задач, в той или иной мере привязывали их к конкретным архитектурам компьютеров, воплощали в них личные вкусы и идеи.
В конце 1960-х годов были сделаны попытки преодолеть эту "разноголосицу" путем создания универсального языка программирования. Первым детищем этого направления стал PL/1 (Programm Language One), 1967 г. Затем на эту роль претендовал Алгол-68 (1968 г.). Предполагалось, что подобные языки будут развиваться и усовершенствоваться и вытеснят все остальные. Однако ни одна из этих попыток на сегодняшний день не увенчалась успехом (хотя PL/1 в усеченных версиях использовали многие программисты). Стремление к универсальности языка приводило к неоправданной сложности конструкций программы, неэффективности получаемых исполняемых кодов.
Бурный рост числа различных языков программирования в период с конца 1960-х и до начала 1980-х годов сопровождался, как это ни странно, кризисом программного обеспечения. Остро не хватало программ для решения самых разных задач и программистов для их разработки, а написанные программы часто содержали ошибки и работали неустойчиво. Этот кризис особо остро переживало военное ведомство США. В январе 1975 г. Пентагон решил навести порядок в хаосе трансляторов и учредил комитет, которому было предписано разработать один универсальный язык. На конкурсной основе комитет проработал сотни проектов, и когда стало ясно, что ни один из существующих языков не может их удовлетворить, принял два проекта для окончательного рассмотрения. В мае 1979 г. был объявлен победитель — группа ученых во главе с Жаном Ихбиа. Победивший язык окрестили АДА, в честь Ады Лавлейс. Язык АДА — прямой наследник языка Паскаль. Этот язык предназначен для создания и длительного (многолетнего) сопровождения больших программных систем, допускает возможность параллельной обработки, управления процессами в реальном времени и многое другое, чего трудно или невозможно достичь средствами более простых языков.
Следует отметить, что многие языки, первоначально разработанные для больших и малых вычислительных машин, в дальнейшем были приспособлены к персональным компьютерам.
Языки программирования сохраняют свое предназначение для решения задач определенных типов. Выбор языка определяется удобствами для программистов, их предпочтениями в силу опыта и образования, а также пригодностью для данного компьютера и данной задачи. А задачи, решаемые с помощью компьютера, бывают самые разнообразные: вычислительные, экономические, графические, экспертные, создание системного программного обеспечения и т. д. Такая разнотипность решаемых компьютером задач и приводит к многообразию языков программирования.
Наилучший результат в программировании достигается при индивидуальном выборе языка программирования на основе класса задачи, уровня и интересов программиста. Например, Бейсик широко употребляется при обучении и написании простейших программ; Фортран является классическим языком программирования при решении математических и инженерных задач; Кобол используется как основной язык для массовой обработки данных в сферах управления и бизнеса.
Несмотря на многообразие языков программирования, каждый из них можно отнести к одной из всего трех парадигм. Парадигмой в науковедении называется набор теорий, гипотез, взглядов и подходов, относящихся к одному течению, в основе которых лежит общий принцип. В программировании известны три парадигмы: процедурная, функциональная и логическая. Большинство языков программирования, доминирующих при создании системного и прикладного программного обеспечения, таких как Фортран, Бейсик, Паскаль, Ада, Си, Модула, Форт, относятся к процедурной парадигме.
Однако по мере эволюции языков программирования получили широкое распространение и другие, принципиально иные, подходы к созданию программ.
Сущность процедурного программирования (его также называют операциональным, классическим) состоит в детальном описании шагов, действий, которые должен выполнить компьютер для того, чтобы решить задачу. Другими словами, процедурное программирование — это запись алгоритма средствами языка программирования. При этом ожидаемые свойства результата обычно не указываются. Основные понятия языков этих групп — оператор и данные. При процедурном подходе операторы объединяются в процедуры.
Внутри процедурной парадигмы можно выделить структурное программирование, которое не выходит за рамки этого направления, оно лишь использует полезные приемы программирования (структурная запись программы, отказ от оператора перехода, составные операторы или блоки), что делает программистскую деятельность более производительной и защищенной от ошибок и путаницы в программах.
Принципиально иные направления в программировании относятся к непроцедурным парадигмам. К ним можно отнести объектно-ориентированное и декларативное программирование. Из языков объектного программирования, имеющих популярность, следует назвать Си++, среды типа Delphi и Visual
Basic.
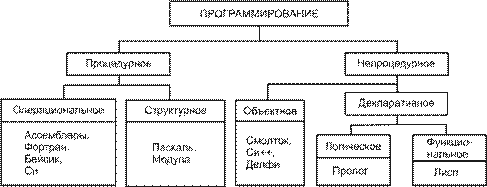
Рис. 5.1. Классификация языков программирования
При использовании декларативного языка программист задает исходные информационные структуры, взаимосвязи между ними и то, какими свойствами должен обладать результат. При этом процедуру его получения ("алгоритм") программист не описывает. В такого рода языках отсутствует понятие "оператор" ("команда"). Декларативные языки можно подразделить на два се- мейства: логические (типичный представитель — Пролог) и функциональные (Лисп).
По всей видимости, непроцедурные языки имеют большое будущее.
Общая классификация языков программирования в соответствии с парадигмами программирования приведена на рис. 5.1. Изучая этот курс, вы познакомитесь с несколькими языками программирования, относящимися к разным парадигмам.
 Контрольные вопросы
Контрольные вопросы
1. Как зарождалось программирование в докомпьютерную эпоху?
2. Каков вклад в появление первых языков программирования высокого уровня Дж. Моучли и Г. Хоппер?
3. Охарактеризуйте назначение языков Фортран, Алгол, Си, Паскаль.
4. В чем причина неудач универсальных языков PL/1 и Алгол-68?
5. Какие языки используются для разработки систем искусственного интеллекта?
6. Какие языки ориентированы на задачи обучения программированию?
7. Что называется парадигмой программирования?
8. Приведите примеры языков программирования, относящихся к различным парадигмам.
 Темы для рефератов и докладов
Темы для рефератов и докладов 1. Технологии программирования первых компьютеров.
2. Развитие машинных языков программирования.
3. Языки для научных вычислений.
4. Языки обработки символьной информации.
5. Языки разработки систем искусственного интеллекта.
6. Языки для начального обучения программированию.
7. Языки объектного программирования.
 Вопросы для
обсуждения
Вопросы для
обсуждения
1. Почему количество языков программирования так велико?
2. Может ли программирование стать ненужным?
3. Почему изучение языков программирования вызывает затруднения?
 Задачи и упражнения
Задачи и упражнения
1. Составьте сводную справочную таблицу языков программирования. Отразите в ней название языка (или его версии), год создания, назначение, парадигму, к которой язык относится.
 Лабораторные работы
Лабораторные работы
1. Выясните, какие книги имеются в библиотеке вашего учебного заведения (и других доступных библиотеках), посвященные языкам и технологиям программирования. Какие это языки? Составьте сводную таблицу-каталог.
2. Выполните поиск в Интернете ресурсов, посвященных языкам и технологиям программирования. Постарайтесь оценить эти ресурсы на предмет доступности. Составьте каталог этих ресурсов.
3. Выясните, какие системы программирования и на каких языках доступны в вашем учебном заведении.
 Учебный материал
Учебный материал
Языки программирования — это формальные языки, специально созданные для общения человека с компьютером.
Языками высокого уровня называют языки программирования, универсальные по отношению к архитектуре компьютеров и использующие обозначения, близкие к принятым в математике и других видах деятельности человека. На таких языках удобно писать прикладные программы, решающие какието научные, технические, управленческие задачи. Программы на языках высокого уровня содержат служебные слова естественного (английского) языка, состоят из легко читаемых и понимаемых команд. Это отличает такие языки от языков низкого уровня (машинно-ориентированных).
Машинно-ориентированные языки содержат примитивные команды, соответствующие особенностям данной архитектуры компьютера (в этом и состоит их машинная ориентированность), и к тому же записываемые машинными кодами, обычно в шестнадцатеричной форме, типа: переслать число в ячейку; считать число из ячейки; увеличить содержимое ячейки на +1 и т. п. Команда на машинном языке обычно описывает простейший обмен содержимого ячеек памяти, элементарные арифметические и логические операции. Команда содержит код и адреса ячеек, с содержимым которых выполняется закодированное действие.
С машинно-ориентированными языками трудно работать, но созданные с их помощью квалифицированным программистом программы занимают меньше места в памяти и работают быстрее. С помощью этих языков удобнее разрабатывать системные утилиты, антивирусные программы, драйверы (программы для управления устройствами компьютера), некоторые другие виды программ.
Языки программирования высокого уровня имеют следующие достоинства:
алфавит языка значительно шире машинного, что делает его гораздо бо- лее выразительным и существенно повышает наглядность и понятность текста;
набор операций, допустимых для использования, не зависит от набора машинных команд, а выбирается из соображений удобства записи алгоритмов решения задач определенного класса;
конструкции команд (операторов) отражают привычные человеку приемы обработки данных и задаются в удобном для чтения и понимания виде; используется аппарат переменных и действия с ними; поддерживается широкий набор типов данных.
Языки программирования высокого уровня являются машиннонезависимыми и требуют использования соответствующих программпереводчиков (трансляторов) для перевода программы на язык компьютера, на котором она будет исполняться.
Каждый язык программирования, равно как и "естественный" язык (русский, английский и т. д.), имеет алфавит, словарный запас, свои грамматику и синтаксис, а также семантику.
Алфавит — фиксированный для данного языка набор основных символов, допускаемых для составления текста программы на этом языке.
Синтаксис — система правил, определяющих допустимые конструкции языка программирования из букв алфавита.
Семантика — система правил однозначного толкования отдельных языковых конструкций, позволяющих воспроизвести процесс обработки данных.
Понятие подразумевает некоторую синтаксическую конструкцию и определяемые ею свойства программных объектов или процесса обработки данных.
Взаимодействие синтаксических и семантических правил определяют те или иные понятия языка, например операторы, идентификаторы, переменные, функции и процедуры, модули и т. д. В отличие от естественных языков, правила грамматики и семантики для языков программирования, как и для всех формальных языков, должны быть явно, однозначно и четко сформулиро- ваны.
Для строгого и точного описания синтаксиса языка программирования, как правило, используют специальные метаязыки (языки для описания других языков). Наиболее распространенными метаязыками являются металингвистические формулы Бэкуса — Наура (язык БНФ) и синтаксические диаграммы Вирта.
Язык БНФ (называемый также языком нормальных форм) представляет собой способ записи конструкций языка программирования с помощью формул, похожих на математические. Для каждого понятия языка существует единственная метаформула (нормальная форма). Она состоит из левой и правой частей. В левой части указывается определяемое понятие, а в правой — задается множество допустимых конструкций языка, которые объединяются в это понятие. В формуле используют специальные метасимволы в виде угловых скобок, которые обозначают определяемое понятие (в левой части формулы) или ранее определенное понятие (в ее правой части). Левая и правая части формулы разделяются метасимволом "::=", имеющим смысл "по определению есть". Знак "|" следует читать "или". Например, метаформулы
<переменная>::=А|В
<выражение>::=<переменная>|<переменная>+<переменная>|<переменная>–
<переменная>
означают, что <переменная> это одна из букв, А или В, а <выражение> — любая из следующих десяти записей: А; В; А+А; А+В; В+А; В+В; А–А; А–В; В–А; В–В.
Правая часть метаформулы может содержать правило построения допустимых последовательностей. Допускаются рекурсивные определения терминов и понятий, т. е. когда в правой части формулы участвует понятие, определяемое левой частью. Например, пусть необходимо ввести понятие <двоичный код>, под которым понимается любая непустая последовательность цифр 0 и 1. Тогда простое и компактное рекурсивное определение с помощью метаформул выглядит так:
<двоичная цифра>::= 0 | 1
<двоичный код>::=<двоичная цифра>|<двоичная цифра><двоичный код>
Данное определение позволяет определить, является ли некая конструкция определяемым понятием.
Так, для нашего примера метаформулы двоичного кода конструкция 001101 является двоичным кодом, поскольку, последовательно применяя рекурсию, мы имеем следующие 5 шагов рекурсии:
1. 0 — двоичная цифра, а 01101 — двоичный код, поскольку
2. 1 — двоичная цифра, а 1101 — двоичный код, поскольку
3. 1 — двоичная цифра, а 101 — двоичный код, поскольку
4. 1 — двоичная цифра, а 01 — двоичный код, поскольку
5. 0 — двоичная цифра, а 1 — также двоичная цифра, рекурсия завершена.
Если же взять конструкцию 1021, то она не является двоичным кодом, поскольку:
1. 1 — двоичная цифра, а 021 — не двоичный код, поскольку
2. 0 — двоичная цифра, а 21 — не двоичный код, поскольку
3. 2 — не двоичная цифра.
Для задания синтаксических конструкций произвольной длины часто используют фигурные скобки как метасимволы. Фигурные скобки означают, что конструкция может повторяться нуль или более раз. В частности, термин <двоичный код> можно определить по-другому, а именно:
<двоичный код>::=<двоичная цифра>{<двоичная цифра>}
И еще, для полноты множества синтаксических конструкций, необходимо определить конструкцию <пусто>:
<пусто>::= .
В большинстве учебных пособий по программированию, технических описаний языков, метаформулы рассматриваемого языка представлены полностью.
Синтаксические диаграммы позволяют графически отобразить значения метапеременных метаязыка. Диаграмма состоит из основных символов или понятий языка.
Каждая диаграмма имеет входящую и выходящую стрелки, означающие начало и конец синтаксической конструкции и отражающие процесс ее чтения и анализа. Из каждого элемента выходит одна или несколько стрелок, указывающих на те элементы, которые могут следовать непосредственно за данным элементом.
Для сравнения с метаформулами приведем несколько примеров. Синтаксическая диаграмма
![]() <переменная>
<переменная>
эквивалентна метаформуле <переменная>::= А|В.
Еще примеры:
<двоичная цифра> ::= <двоичный код ::=>
![]() <двоичная цифра>
<двоичная цифра>![]()
<двоичная цифра>
Металингвистические формулы заложены в трансляторы; с их помощью ведется проверка используемых программистом конструкций на формальное соответствие какой-нибудь из конструкций, синтаксически допустимых в этом языке (синтаксический контроль).
Пользуясь средствами форм Бэкуса — Наура и синтаксическими диаграммами, опишем грамматику языков программирования.
Алфавиты большинства языков программирования близки друг другу и основываются на буквах латинского алфавита, арабских цифрах и общепринятых спецсимволах, таких как знаки препинания, математических операций, сравнений и обозначений. Большинство популярных языков программирования в своем алфавите содержат следующие элементы:
<буква> : : = A|a|B|b|C|c|D|d|E|e|F|f и т. д.
<цифра> : : = 0|1|2|3|4|5|6|7|8|9
<знак арифметической операции > : : = *|/|+|–
<разделитель> : : = . | , | ; | : | ( | ) | [ | ] |{ | }| ' | : =
<служебное слово> : : = begin | end | if | then | else| for | next и т. д.
<спецсимвол> :: = <знак арифметической операции> | <разделитель> |
<служебное слово>
<основной символ>::=<буква> | <цифра> | <спецсимвол>
<комментарий>::= {любая последовательность символов}
Несмотря на значительные различия между языками программирования, ряд фундаментальных понятий в большинстве из них схожи.
Оператор — одно из главных понятий всех языков программирования. Каждый оператор представляет собой законченную фразу языка и однозначно определяет некоторое действие над данными. В соответствии с теорией алгоритмов выделяют основные (базовые) операторы языка:
присвоения;
условного и безусловного перехода; пустой оператор.
К производным операторам относят:
составной оператор;
оператор выбора;
оператор цикла;
оператор присоединения.
Все операторы языка в тексте программы отделяются друг от друга явными или неявными разделителями, например:
S1; S2; ...; Sn
Операторы выполняются в порядке их следования в тексте программы. Лишь с помощью операторов перехода этот естественный порядок может быть нарушен.
Большая часть операторов ведет обработку величин.
Величины могут быть постоянными и переменными. Значения постоянных величин не изменяются в ходе выполнения программы. Величина характеризуется типом, именем и значением. Наиболее распространенные типы величин — числовые (целые и вещественные), символьные, логические. Тип величины определяется ее значением.
Другая важная классификация величин — простые и составные. Простая величина имеет одно значение. Ей соответствует одна ячейка памяти (точнее, "машинное слово") или ее эквивалент во внешней памяти компьютера.
Составной величине может соответствовать сразу много значений, объединенных под одним именем. Эти значения представляют собой элементы (компоненты) величины. Самый широко известный пример — массив, у которого элементы различаются по индексам (номерам).
Вопрос о выборе и описании структур данных — входных, выходных и промежуточных — не менее важен для успеха решения прикладной задачи, чем вопрос о правильности последовательности операторов программы.
Важнейшие характеристики структурированной величины таковы: упорядоченность (да или нет), однородность (да или нет), способ доступа к элементам, постоянство числа элементов (да или нет). Так, массив является упорядоченной однородной структурой с прямым доступом к элементам и постоянным их количеством.
Всем объектам данных в языках программирования даются индивидуальные имена. Имя программного объекта называют идентификатором (от слова "идентифицировать"). Чаще всего идентификатором является любая конечная последовательность букв и цифр, начинающаяся с буквы:
<идентификатор>::=<буква>
<идентификатор> ::= <идентификатор>(<буква>| <цифра>)
Как правило, в качестве идентификатора запрещается использовать служебные слова языка.
Многим слово "идентификатор" не нравится, и в настоящее время чаще употребляют слово "имя", поскольку
<имя>::=<идентификатор>
Программисты выбирают имена по своему усмотрению. Принципы выбора и назначения имен объектам данных естественны. Следует избегать мало выразительных обозначений, а также кратких имен. Имена должны быть понятны, наглядны, отражать суть обозначаемого объекта. Например:
Summa, Time, i, j, Radius, init
Некоторым идентификаторам заранее предписан определенный смысл и их называют стандартными, например Sin — это имя известной математической функции.
Описания объектов данных связаны с правилами обработки данных. Данные бывают разные и необходимо для каждого из них определить его свойства. Например, если в качестве данных выступает массив, следует задать его размерность, границы индексов, тип элементов массива. Описательная часть языка программирования является необходимой как для системных программистов — разработчиков трансляторов, которые должны, в частности, проводить синтаксическую и семантическую диагностику программ, — так и для "прикладного" программиста, которому объявления объектов данных облегчают процесс разработки и отладки программ.
В некоторых языках широко применяются описания данных по умолчанию для стандартных числовых и символьных данных. В этом случае тип данных задается с помощью имени объекта данных. Например, в Фортране переменные, имена которых начинаются с букв I, J, K, L, M, N, по умолчанию принимают целые значения (при отсутствии явного описания типа, которое также возможно), т. е. определены как числовые данные целого типа. В Бейсике данные строкового типа присваиваются переменным, имена которых заканчиваются специальным символом $: A$, S1$, а просто имена без $ и специального описания получают действительный тип значений двойной точности.
Особый интерес в языках программирования представляют описания нестандартных структур данных, таких как запись, файл, объект, список, дерево и т. п.
Приведем список наиболее употребительных обозначений типов данных, используемых в описаниях:
Целый — Integer
Вещественный — Real
Логический — Boolean
|
Символьный |
— Char |
|
Строковый |
— String |
|
Массив |
— Array |
|
Множество |
— Set |
|
Файл |
— File |
|
Запись |
— Record |
|
Объект |
— Object |
Переменные играют важнейшую роль в системах программирования. Понятие "переменная" в языках программирования отличается от общепринятого в математике. Переменная — это программный объект, способный принимать некоторое значение с помощью оператора присваивания. В ходе выполнения программы значения переменной могут неоднократно изменяться. Каждая переменная после ее описания связывается с некоторым значением. Синтаксически переменная представляется своим идентификатором (или именем).
Семантический смысл переменной заключается в хранении некоторого значения, соответствующего ее типу (например, переменная целого типа может принимать значение произвольного целого числа), а также в выполнении с ней операций пересылки в нее и извлечения из нее этого значения.
Функция — программный объект, задающий вычислительную процедуру определения значения, зависимого от некоторых аргументов. Вводится в языки программирования для задания программистом необходимых ему функциональных зависимостей. В каждом языке высокого уровня имеется в наличии библиотека стандартных функций: арифметических, логических, символьных, файловых и т. п. Функции — стандартные и задаваемые программистом — используются в составе выражений.
Выражения строятся из постоянных величин, имен переменных, функций, скобок, знаков операций и т. д. Выражение имеет определенный тип, определяемый типом принимаемых в итоге его вычисления значений. Возможны выражения арифметические, принимающие числовые значения, логические, символьные, строковые и т. д. Выражение 5 + 7 является, несомненно, арифметическим, выражение A + B может иметь самый разный смысл — в зависимости от типа данных, которые стоят за идентификаторами A и B.
Процедура — программный объект, представляющий некоторый самостоятельный этап обработки данных. По сути, процедуры явились преемниками подпрограмм, которые были введены для облегчения разработки программ еще на самых ранних стадиях развития программирования. При своем описании процедура имеет входные и выходные параметры, называемые формальными. При использовании процедуры ее параметры, получившие конкретные значения, становятся фактическими.
Модуль (Unit) — это специальная программная единица, предназначенная для создания библиотек и разделения больших программ на логически связанные блоки.
По сути, модуль — набор констант, типов данных, переменных, процедур и функций. В состав модуля входят разделы: заголовок, интерфейс, реализация, инициализация.
Заголовок необходим для ссылок на модуль.
Интерфейс содержит объявления, включая процедуры и функции.
Раздел реализация содержит тела процедур и функций, перечисленных в интерфейсной части.
Раздел инициализация содержит операторы, необходимые для инициализации модуля.
Каждый модуль компилируется отдельно, и каждый элемент модуля можно использовать в программе без дополнительного объявления.
 Контрольные вопросы
Контрольные вопросы
1. Какие преимущества имеют языки программирования высокого уровня по сравнению с машинно-ориентированными языками?
2. Каковы основные составляющие языка программирования высокого уровня?
3. В чем отличие понятий языков программирования от аналогичных понятий естественного языка?
4. С какой целью используются и что представляют собой металингвистические формулы Бэкуса — Наура?
5. Что представляет собой синтаксическая диаграмма Вирта?
6. В чем различие между постоянными и переменными величинами? Чем характеризуется величина?
7. В чем отличие между величинами простыми и структурированными?
8. Для чего служит описание величин в программах? Какие стандартные типы данных используют языки высокого уровня?
9. Для чего служат операторы?
10. В чем состоит назначение функций? процедур? модулей?
 Темы для рефератов и докладов
Темы для рефератов и докладов 1. Проблемы изучения естественных и формальных языков.
2. Базовые понятия математической лингвистики.
3. Метаязыки для описания формальных языков.
4. Тенденции развития языков программирования высокого уровня.
5. Развитие описания данных в языках программирования.
6. Развитие декларативных языков программирования.
 Вопросы для
обсуждения
Вопросы для
обсуждения
1. Какими могут быть языки "сверхвысокого" уровня, делающие ненужным программирование?
2. Кому больше нужны БНФ и диаграммы Вирта: программистам или разработчикам компиляторов?
 Задачи и упражнения
Задачи и упражнения
1. Запишите на основе алфавита, включающего русские и английские буквы, цифры и специальные знаки (по своему усмотрению), несколько цепочек символов. Опишите эти цепочки на метаязыках БНФ и диаграмм Вирта.
2. Опишите известные вам конструкции языков программированиия с помощью БНФ.
3. Опишите известные вам операторы языков программированиия с помощью диаграмм Вирта.
 Лабораторные работы
Лабораторные работы
1. Найдите в литературе и интернет-источниках описание синтаксиса языков высокого уровня. С помощью каких метаязыков оно выполнено? Составьте справочную таблицу, которая помогла бы быстро найти нужное описание конструкции языка программирования.
 Учебный материал
Учебный материал
Язык Паскаль был создан Н. Виртом в 1971 г. как язык обучения программированию и записи алгоритмов в статьях и книгах. Паскаль стал первым языком, с которым знакомится большинство будущих программистов в мире.
Он оказался настолько удачным, что до сих пор играет особую роль и в практическом программировании, и в его изучении. В нем реализованы принципы структурного программирования и полного описания данных, повышающие устойчивость программного кода, позволяющие найти и устранить большинство ошибок еще на стадии трансляции программы.
Трансляторы для программ, написанных на Паскале, разработаны для различных компьютеров и в настоящее время имеют множество разновидностей.
Существует много версий языка Паскаль. Различия между ними порой весьма велики. Базовая версия языка, созданная Виртом, в этих версиях значительно расширена и дополнена, для того чтобы дать/получить из языка обучения инструмент профессиональных разработчиков прикладного программного обеспечения.
Тем не менее это версии одного языка, что, в частности, подтверждается их совместимостью "сверху вниз", т. е. любая программа, написанная на "младшей" версии языка, останется работоспособной и при переходе к "старшей" версии. Приведенные далее тексты программ и примеры соответствуют (если нет специальных оговорок) практически всем версиям Паскаля.
Любая программа на Паскале является текстовым файлом с собственным именем и с расширением pas. Рассмотрим в качестве примера текст программы 1 решения квадратного уравнения. Эта программа имеет вид последовательности символов латинских и русских букв, арабских цифр, знаков операций, скобок, знаков препинания и некоторых дополнительных символов. В ней можно выделить описания данных и операторы, описывающие действия, которые надо выполнить компьютеру над этими данными.
![]()
|
program SquareEqRoots; |
|
|
{заголовок программы} |
|
var |
|
|
{список переменных} |
|
a,b,c: real; |
|
|
{коэффициенты уравнения} |
|
d,x1, x2: real; |
|
|
{вспомогательные переменные} |
|
begin |
|
|
{начало программы} |
|
writeln; |
|
|
{пропуск строки на экране} |
writeln('введи a,b,c'); read(a,b,c); {запрос и ввод данных}
|
d:=b*b–4*a*c; |
{дискриминант} |
|
if d<0 then |
{если d<0, то} |
|
write('корней нет') |
{печатать} |
|
else |
{иначе} |
|
begin x1:=(–b+sqrt(d))/(2*a); |
{начало серии команд} |
|
x2:=(–b–sqrt(d))/(2*a); |
{вычисляем корни} |
|
write('x1=',x1,' x2=',x2) |
{печать корней} |
|
end |
{конец серии} |
|
end. |
{конец программы} |
Схематически программа представляется в виде последовательности восьми разделов:
1. Заголовок программы.
2. Описание внешних модулей, процедур и функций.
3. Описание меток.
4. Описание констант.
5. Описание типов переменных.
6. Описание переменных.
7. Описание функций и процедур.
8. Раздел операторов.
Не в каждой программе обязательно присутствуют все восемь разделов, в простейшей программе, например, могут быть только 5-й и 8-й разделы.
Каждый раздел начинается со служебного слова, назначение которого зафиксировано в Паскале так, что его нельзя употреблять для других целей
(табл. 5.1).
Таблица 5.1. Список зарезервированных слов языка Паскаль в версии для ПК
|
absolute |
абсолютный |
label |
метка |
|
and |
логическое И |
library |
библиотека |
|
array |
массив |
mod |
остаток от деления |
|
asm |
ассемблер |
nil |
отсутствие |
|
begin |
начало блока |
not |
логическое НЕ |
|
case |
вариант |
or |
логическое ИЛИ |
|
const |
константа |
of |
из |
|
constructor |
конструктор |
object |
объект |
|
div |
деление нацело |
packed |
упакованный |
|
goto |
переход на |
procedure |
процедура |
|
do |
выполнять |
program |
программа |
|
downto |
уменьшить до |
record |
запись |
|
destructor |
деструктор (разрушитель) |
repeat |
повторять |
|
else |
иначе |
set |
множество |
|
end |
конец блока |
shl |
сдвиг битов влево |
|
exports |
экспорт |
shr |
сдвиг битов вправо |
|
external |
внешний |
string |
строка |
|
file |
файл |
then |
то |
|
for |
для |
to |
увеличивая |
|
forward |
опережающий |
type |
тип |
|
function |
функция |
unit |
модуль |
|
if |
если |
until |
до |
|
implementation |
реализация |
uses |
использовать |
|
in |
в (входит в ...) |
var |
переменная |
|
inline |
основной |
while |
пока |
|
interrupt |
прерывание |
with |
с |
|
interface |
интерфейс |
xor |
исключающее ИЛИ |
|
inherited |
наследование |
|
|
Рассмотрим пример программы 2, вычисляющей длину окружности и площадь круга по заданному радиусу.
![]()
program circle; const pi=3.14159; var
r,s,l : real; begin
writeln('введите радиус'); readln(r); s:=pi*r*r; l:=2*pi*r;
writeln('площадь круга=',s:8:4); writeln('длина окружности=',l:8:4) end.
В этой программе можно выделить четыре раздела. Описание заголовка начинается со служебного слова program, описание констант — const, описание переменных — var, раздел операторов начинается с begin. Программа заканчивается служебным словом end, после которого ставится точка. Описания величин и операторы друг от друга отделяются знаком "точка с запятой".
Для обозначения величин используются имена. Они составляются из латинских букв и цифр, причем первым символом должна быть буква. В примере использованы имена величин — pi, r, s и l.
Имя программы (в примере — circle) выбирается автором и составляется по такому же правилу.
Постоянные величины (константы) чаще всего бывают числовыми или символьными (но могут быть и других типов, о которых речь пойдет далее). Значения символьных констант заключаются в апострофы.
Постоянные величины описываются в разделе констант по схеме: const <имя> = <константа>
В разделе констант может быть описано несколько постоянных величин, например:
const
pi=3.14159; k=–15; s='площадь';
Данные, обрабатываемые программой, могут быть разных типов (числа, символы, строки, массивы и т. д.). Тип определяет область допустимых значений, а также операции и функции, применяемые к величинам этого типа. В Паскале имеется несколько встроенных простых типов со стандартными именами integer (для целых величин), real (для вещественных величин), char (для литерных величин), boolean (для логических величин) и byte (для коротких целых величин).
Группа типов, значения каждого из которых можно перечислить в некотором списке, — ординарные типы. Для них определена порядковая функция ord(x) — номер значения x в списке (для целочисленного х: ord(x)=x); функции pred(x) — значение в списке, предшествующее х, и succ(x) — значение в списке, следующее за x). Из простых типов данных ординарным не является только тип real.
Переменные описываются в разделе описания переменных следующим образом: var <список имен переменных>: <тип>
Имена в списке разделяются запятой. В этом разделе может быть описано несколько переменных разного типа, например: var a,b,c:real; k,l:integer; p:boolean;
Над целыми величинами определены арифметические операции : * (умножение), div (деление нацело), mod (вычисление остатка от деления), +, — (сложение и вычитание); операции перечислены в порядке старшинства.
Например:
25 div 4 = 6
25 mod 4 = 1
Целый результат дают некоторые стандартные функции (аргумент функции заключается в круглые скобки):
abs(x) — абсолютная величина целого x;
sqr(x) — квадрат значения x;
trunc(x) — целая часть вещественной величины x;
round(x) — целое число, полученное из вещественного x по правилу округления;
random(x) — случайное целое число из интервала от 0 до x.
Например: trunc(4.7)=4; round(4.7)=5; sqr(3)=9
Для данных типа byte определены те же операции и функции, что и для данных типа integer.
Над вещественными величинами определены операции: *, +, –, /, а также стандартные функции при вещественном или целом аргументе: abs(x), sqr(x), sin(x), cos(x), arctan(x), ln(x), exp(x), sqrt(x) — квадратный корень из x, int(x) — целая часть из x, random — случайное число из интервала от 0 до 1. Указанные операции и функции дают вещественный результат.
Над логическими величинами определены операции: not — отрицание, and — конъюнкция, or — дизъюнкция. Логическая функция odd(x) принимает значение true, если целочисленное x является нечетным, и false, если четным.
Множество всех символов образуют символьные величины (тип char), которые являются упорядоченными, причем 'A'<'B'<'C'<...<'Z',
'a'<'b'<...<'z', '0'<'1'<...<'9'.
Основной "строительный материал" программы на Паскале — выражения и оператор присваивания.
Выражения — это конструкции, задающие правила вычисления значений переменных. В общем случае выражения строятся из переменных, констант, функций с помощью знаков операций и скобок.
Оператор присваивания — основной оператор языка. Он имеет следующий
вид:
<имя переменной> := <выражение> и определяет действие компьютера по помещению результатов вычисления <выражения>, записанного справа от знака присваивания :=, в область оперативной памяти, обозначенной <именем переменой>. Отметим, что присваивание :=, это совсем не то, что равенство =. Равенство — это операция сравнения двух величин, результатом которой является логическое значение true или false.
Тип переменной и тип выражения должны быть согласованы (величины принадлежат одному и тому же типу). Есть исключение: имя переменной может относиться к типу real, а значение выражения — к типу integer.
Примеры: l:=2*pi*r; p:=(a+b+c)/2; z:=sqrt(sqr(x)+sqr(y))
В Паскале можно вводить с клавиатуры числовые и символьные данные.
Имеются две встроенные процедуры (подпрограммы) ввода:
read(<список переменных>);
readln(<список переменных>).
При выполнении процедуры read(x1,x2,...,xN) программа прерывается и компьютер ждет ввода с клавиатуры N значений переменных из списка x1, x2, ..., xN. Эти значения — константы соответствующих типов — должны при вводе разделяться пробелами. Набор данных завершается клавишей ввода.
Процедура readln отличается от read только тем, что при завершении ввода курсор перемещается в начало следующей строки.
Пример:
var a,b:real; c:char; d:integer; ...
read(a,c,d,b); ...
Допустимый ввод: 83.14 k 200 –7.15
Программа на Паскале может выводить на экран или на принтер значения числовых или символьных выражений. Имеются две процедуры вывода на экран:
write(<список выражений>);
writeln(<список выражений>).
Процедура write(x1,x2,...,xN) печатает на экране значения выражений из списка x1, x2, ..., xN. Процедура writeln отличается от write тем, что переводит курсор в начало следующей строки.
Для управления печатью используются форматы данных. Пусть x — переменная типа real. Если не использовать форматы, то значение x будет выводиться в "плавающей" форме (например, 1.654887892Е–04). Форматы позволяют напечатать вещественное число в естественной форме. Пусть m, n — целые числа. Процедура write(x:m:n) выводит на экран значение переменной x в виде десятичной дроби, причем m определяет общее число выводимых символов, включая цифры, точку и знак числа, n — количество цифр после точки. Если количество выводимых символов меньше m, то перед числом добавляются пробелы.
Пусть, например, x=387.26. Табл. 5.2 демонстрирует влияние форматов на вывод значения x.
Таблица 5.2
|
Оператор |
Строка вывода |
|
writeln('*',x) |
* 3.8726000000E+02 |
|
writeln('*',x:8:3) |
* 387.260 |
|
writeln('*',x:8:1) |
* 387.3 |
Один формат — ширину поля вывода — можно использовать и для вывода значений выражений типов integer, boolean, char.
Конструкции языка Паскаль разрабатывались с учетом принципов структурного программирования и ориентированы на высокую дисциплину программирования. Это означает, что программист должен использовать небольшое число конструкций, применяя как чередование, так и вложение их друг в друга. Не рекомендуется (хотя и возможно) использовать оператор перехода go to.
Реализация последовательности действий (т. е. структуры следования) выполняется с помощью составного оператора:
begin <последовательность операторов> end
Операторы в последовательности операторов разделяются ";". Отметим, что ";" является разделителем и не относится к операторам.
Раздел операторов в программе всегда является составным оператором. Служебные слова begin и end часто называют операторными скобками.
В целях повышения удобочитаемости и понятности в структурном программировании рекомендуется записывать end под соответствующим ему begin, а все вложенные операторы записывать с одной позиции в строке с отступом вправо. В результате получается характерная "лесенная" запись программы на Паскале.
Для реализации ветвления в Паскале предусмотрены два оператора: условный оператор и оператор выбора. Они предназначены для выделения из составляющих их операторов одного, который и выполняется.
Структура и действие условного оператора таковы:
if <логическое выражение> then <оператор 1> else <оператор 2>
Условный оператор может не содержать часть else <оператор 2>, т. е. может быть неполным:
if <логическое выражение> then <оператор 1>
В этом случае, если значение логического выражения равно false, условный оператор не вызывает никаких действий.
Пример: составим программу, которая определяет длину общей части двух отрезков числовой оси, заданных координатами своих концов соответственно a, b и c, d (a<b, c<d). Если отрезки имеют общую часть, то левая координата общей части отрезков m равна максимальному из чисел a и c, а правая n — минимальному из чисел b и d.
![]()
program cross; var a,b,c,d,m,n,l:real; begin writeln('введите координаты концов отрезков'); read(a,b,c,d); writeln; if a<c then m:=c else m:=a; if b<d then n:=b else n:=d; if m<n then l:=n–m else l:=0; writeln('длина общей части отрезков=',l:6:2) end.
Оператор выбора имеет следующую форму:
case <выражение> of
<список констант 1> : <оператор 1>;
<список констант 2> : <оператор 2>; ................................... <список констант N> : <оператор N> end.
Выражение, стоящее между служебными словами case и of, должно иметь значение одного из ординарных типов. Список констант может состоять из одной константы.
Оператор варианта вычисляет значение выражения, записанного после case. Если его значение совпадает с одной из констант в некотором списке, то выполняется оператор, стоящий после этого списка. Если значение выражения не совпало ни с одной константой во всех вариантах, то оператор варианта ничего не делает.
В качестве примера приведем программу, которая в зависимости от номера месяца выдает сообщение о времени года.
![]()
program seasons; var k:integer; begin writeln('введите номер месяца'); readln(k); case k of
1,2,12:writeln('зима');
3,4,5:writeln('весна');
6,7,8:writeln('лето'); 9,10,11:writeln('осень') end end.
Для реализации циклов в Паскале имеются три оператора: оператор цикла с предусловием, оператор цикла с постусловием и оператор цикла с параметром.
Если число повторений оператора цикла (тела цикла) известно заранее, то удобно воспользоваться оператором цикла с параметром. В других случаях следует использовать операторы цикла с предусловием (цикл "пока") или с постусловием (цикл "до"). Форма цикла с предусловием такова: while <логическое выражение> do <оператор>
Исполняется этот цикл следующим образом. Сначала вычисляется значение логического выражения. Если оно имеет значение true, то выполняется оператор тела цикла, после чего снова вычисляется значение логического выражения. Если же логическое выражение имеет значение false, оператор тела цикла не выполняется и производится переход на следующий после цикла оператор.
В качестве примера использования такого цикла решим следующую задачу. Необходимо подсчитать число действительных слагаемых, пока их сумма не превысит 100.
Введем обозначения: sum — сумма; num — число слагаемых; w — значение очередного слагаемого. Вначале величины sum и num равны нулю. Цикл продолжается, пока выполняется неравенство sum<100.
![]()
program store; var sum,w:real; num:integer; begin num:=0;sum:=0; while sum<100 do begin writeln('введите слагаемое'); readln(w); sum:=sum+w; if sum<=100 then num:=num+1 else writeln('сумма превысила 100') end; writeln('число слагаемых =',num:3) end.
Оператор цикла с постусловием имеет форму:
repeat <последовательность операторов> until <логическое выражение>
Он исполняется следующим образом. Выполняется последовательность операторов. Далее вычисляется значение логического выражения. Если это значение true, то происходит переход на следующий после цикла оператор, в противном случае снова выполняется последовательность операторов и т. д.
Решим предыдущую задачу, применяя цикл с постусловием. Цикл заканчивается, если выполняется условие: sum>100.
![]()
program store2; var sum,w:real; num:integer; begin num:=0;sum:=0; repeat writeln('слагаемое'); readln(w); sum:=sum+w; if sum<=100 then num:=num+1 else writeln('сумма превысила 100') until sum>=100; writeln('количество слагаемых =',num:3) end.
Оператор цикла с параметром предусматривает вычисление выражений 1 и 2, присвоение параметру цикла значения выражения 1, проверку, что оно не превышает значения выражения 2, и, если это так, выполнение оператора тела цикла, после чего параметр изменяется на 1 и все повторяется. Если же параметр при проверке оказывается больше значения выражения 2, оператор тела цикла не выполняется и происходит переход на оператор, следующий после цикла.
Оператор цикла с параметром имеет две формы:
for <параметр>:= <выражение 1> to <выражение 2> do <оператор>
<Параметр>, <выражение 1>, <выражение 2> должны быть одного типа, относящегося к ординарным типам. <Параметр> в этом цикле возрастает. Действие эквивалентно действию следующего составного оператора:
begin
<параметр>:=<выражение 1>; while <параметр> <= <выражение 2> do begin
<oператор>;
<параметр>:=succ(<параметр>) end end.
for <параметр>:=<выражение 1> downto <выражение 2> do <оператор> Этот цикл эквивалентен следующему:
begin
<параметр>:=<выражение 1>; while <параметр> >= <выражение 2> do begin
<oператор>;
<параметр>:=pred(<параметр>) end end.
Пример: составим программу, по которой будет напечатана таблица перевода километров в мили (1 миля = 1,603 км). Параметром цикла можно считать целую величину k — количество километров. Пусть эта величина изменяется от 1 до 10 (с шагом 1, разумеется).
![]()
program mili;
const a=1.603; b='км'; c='мили'; var k:integer; m:real; begin
writeln(b:5,c:7); writeln; for k:=1 to 10 do
begin
m:=k/a; writeln(k:5,m:6:3) end end.
Запишем в этой программе цикл с параметром по второй форме:
for k:=10 downto 1 do begin
m:=k/a; writeln(k:5,m:6:3) end.
Тогда значения k в таблице будут убывать от 10 до 1 с шагом 1.
Особую роль в структурном программировании играет определение и описание данных и их структур. Как уже говорилось, от удачного выбора типов и структур данных зависит эффективность, понятность, устойчивость программы к ошибкам программиста, возможность ее сопровождать и развивать длительное время.
Помимо простых предопределенных типов real, integer, boolean, byte, char, программист по своему желанию может определить новые типы.
Еще один ординарный тип данных — перечисляемый тип, он задается путем перечисления его элементов.
Описание перечисляемого типа выполняется в разделе типов следующим образом: type <имя типа> = <список имен> Примеры:
type operator = (plus,minus,multi,divide); color = (white,red,blue,yelow,purple,green); В списке должно быть не более 256 имен.
К элементам перечисляемого типа можно применять функции ord(x), pred(x), succ(x) и операции отношения. Отметим, что данные этого типа не подлежат вводу и выводу с помощью функций ввода/вывода и могут использоваться внутри программы для повышения ее читабельности и понятности.
Для иллюстрации работы с перечисляемыми типами приведем программу 8, переводящую английские названия дней недели на русский язык.
![]()
program week; type days=(mon,tue,wed,thu,fri,sat,sun); var d:days; begin for d:=mon to sun do case d of mon:writeln('понедельник'); tue:writeln('вторник'); wed:writeln('среда'); thu:writeln('четверг'); fri:writeln('пятница'); sat:writeln('суббота'); sun:writeln('воскресенье') end end.
Интервальный тип (или тип диапазона) — это подмножество другого уже определенного типа, называемого базовым. В качестве базового может выступать один из ординарных типов. Интервал можно задать в разделе типов указанием наименьшего и наибольшего значений, входящих в него и разделяющихся двумя последовательными точками, например:
type days=(mon,tue,wed,thu,fri,sat,sun); workdays=mon..fri; index=1..30; letter='a'..'z';
Можно задать интервал и в разделе переменных: var a:1..100; b:–25..25;
Операции и функции — те же, что и для базового типа. Использование интервальных типов в программе позволяет экономить память и избегать выхода значения переменной интервального типа за границы интервала. Пример: если k — номер месяца в году, то вместо описания var k:integer; можно написать var k:1..12;
Рассмотренные к настоящему моменту типы можно было назвать простыми. Для решения ложных задач их оказывается недостаточно. В этом случае используются составные структуры данных.
Часто используемый составной тип — массив. Массив — это последовательность, состоящая из заранее задаваемого числа элементов одного типа. Массивы необходимы для решения таких задач, когда требуется одновременно иметь в памяти набор однотипных данных и выполнять их преобразования, т. е. использовать прямой доступ к этим данным с помощью вычисляемых значений индексов.
Все элементы массива имеют общее имя (имя массива) и различаются индексами. Индексы можно вычислять, их тип должен быть ординарным. При описании массивов используются служебные слова array и of. В описании массива указывается тип его элементов и типы их индексов.
Форма описания такова: type <имя типа> = array [<список типов индексов>] of <тип элементов>
Тип элементов — произвольный, он также может быть составным. Число индексов называется размерностью массива. После описания типа массива конкретные массивы можно задать в разделе описания переменных.
Например:
type vector = array [1..10] of real; table = array ['A'..'Z',1..5] of integer; var a,b : vector; c : table;
Отметим, что тип массива table — двухмерный, это таблица, положение элемента в которой задается двумя индексами — латинской буквой и цифрой от 1 до 5. Обращение к элементу массива осуществляется с помощью задания имени переменной, за которым следует заключенный в квадратные скобки список индексов элемента.
Например: а[7]:=3.1; b[k*k+1]:=0; c['M',3]:=–14;
Если массивы имеют одно и то же описание, то во многих версиях Паскаля допустимо их копирование, например: b:=a;.
Описание массива можно совместить с описанием соответствующих переменных:
var a,b : array [1..10] of real; d : array [byte] of char;
В версиях Паскаля, предназначенных для практического программирования, предусмотрен полезный прием: инициализация начальных значений составных переменных с помощью типизированных констант. Типизированные константы используются как переменные того же типа.
Форма описания начальных значений элементов массива: const <имя массива>: <тип массива> = (<список значений элементов>) Тип массива может быть описан ранее:
type digits = array [1..5] of char; const a : digits =('0','2','4','6','8');
Рассмотрим часто встречающуюся задачу упорядочения членов числовой последовательности по какому-либо признаку.
Пример: упорядочить члены числовой последовательности по возрастанию.
Используем метод упорядочения, носящий имя метод "пузырька". Здесь имеет место аналогия с "всплыванием" пузырька в жидкости под действием силы Архимеда. Будем сравнивать пары соседних элементов последовательно справа налево и переставлять элементы в паре, если они стоят в порядке, не соответствующем требуемому:
5,3,2,4,1 → 5,3,2,1,4 → 5,3,1,2,4 → 5,1,3,2,4 → 1,5,3,2,4
В начале просмотра присвоим некоторой логической переменной значение true: p:=true;
Если при просмотре пар была совершена хотя бы одна перестановка, изменим значение логической переменной на противоположное:
p:=false;
Это означает, что последовательность еще не была упорядочена и просмотр пар надо повторить. Цикл просмотров заканчивается, если после очередного просмотра выполняется условие:
p=true;
Последовательность зададим в программе как массив типизированных констант из 10 элементов — целых чисел.
![]()
program bubble; const a:array[1..10] of integer=(19,8,17,6,15,4,13,2,11,0); var b,i:integer; p :boolean; begin clrscr;
for i:=1 to 10 do write(a[i]:3); writeln; writeln; repeat p:=true;
for i:=10 downto 2 do if a[i]<a[i–1] then begin b:=a[i];a[i]:=a[i–1]; a[i–1]:=b; p:=false end until p=true; for i:=1 to 10 do write(a[i]:3); writeln end.
Обработка элементов двумерных массивов (матриц) обычно выполняется с помощью двойного цикла. Один цикл задает индекс строки, другой — индекс столбца.
При решении различных задач обработки информации часто возникает необходимость в использовании последовательностей символов. Такую последовательность можно описать как массив символов, однако в Паскале для таких целей имеется более удобный тип данных string[n] строка из n символов, где n<=255. Отметим, что элемент строки с индексом 0 хранит заданную при описании длину строки n, а элементы строки индексируются целыми числами от 1 до n. Способы описания переменных — строк — аналогичны описанию массивов.
Строковый тип определяется в разделе описания типов, переменные этого типа — в разделе описания переменных:
type word : string[20]; var a,b,c : word;
Можно совместить описание строкового типа и соответствующих переменных в разделе описания переменных:
var a,b,c : string[20]; d : string[30];
Можно определить строковую переменную и ее начальное значение как констант-строку: const l:string[11]='информатика';
Символы, составляющие строку, занумерованы слева направо; к ним можно обращаться с помощью индексов, как к элементам одномерного массива.
Для переменных одного строкового типа определен лексикографический порядок, являющийся следствием упорядоченности символьного типа:
'fife'<'tree' (т. к. 'f'<'t'); '4'>'237' (т. к. '4'>'2').
Кроме логических операций <, >, =, для величин строкового типа определена некоммутативная операция соединения (конкатенации), обозначаемая знаком плюс: a:='кол'+'о'+'кол'; (в результате a='колокол').
Для строковых величин определены следующие четыре стандартные функции:
Функция соединения — concat(s1,s2,...,sk), аналогичная конкатенации с помощью операции "+". Значение функции — результат соединения строк s1, s2, ..., sk, если он содержит не более 255 символов.
Функция выделения — copy(s,i,k). Выделяет k символов из строки s, начиная с i-того символа: a:=copy('крокодил',4,3); В результате a='код'.
Функция определения длины строки — length(s). Возвращает количество символов, имеющихся в строке s:
b:=length('каникулы'); В результате b=8.
Функция определения позиции — pos(s,t). Определяет номер позиции, начиная с которого строка s входит первый раз в строку t; результат равен 0, если строка s не входит в t:
c:=pos('ом','компьютер'); В результате c=2.
В Паскале определены также четыре стандартные процедуры для обработки строковых величин:
Процедура удаления — delete(s,i,k). Удаляет k символов из строки s, начиная с i-того символа. s:='таракан'; delete(s,5,2);
В результате s='таран'.
Процедура вставки — insert(s,t,i). Вставляет в строку t строку s, начиная с позиции i:
t:='таран'; insert('ка',t,5); В результате t='таракан'.
Процедура преобразования числа в строку символов — str(k,s). Превращает число k в строку s, каждый элемент которой — цифра числа k: str(564,s);
В результате s='564'.
Процедура преобразования строки из цифр в число — val(s,k,i), кроме формирования числа k из цифр строки s определяет значение i=0, если
в строке s нет символов, отличных от цифр, в противном случае i равно позиции первого символа, отличного от цифры:
val('780',k,i);
В результате k=780, i=0.
Рассмотрим несколько программ, в которых используются строковые величины.
1. Составить программу, определяющую количество гласных в русском тексте, содержащем не более 100 символов.
Здесь удобно определить констант-строку, состоящую из всех 18 строчных и заглавных русских букв, и в цикле проверить, будет ли очередной символ заданного текста элементом констант-строки.
![]()
program vowel; const c:string[18]='аеиоуыэюяАЕИОУЫЭЮЯ'; var a :string[100]; k,n:integer; begin writeln('введите текст'); readln(a);n:=0; for k:=1 to length(a) do if pos(a[k],c)>0 then n:=n+1; writeln('кол. гласных=',n) end.
Отметим, что данную задачу удобнее и рациональнее решать с использованием другого составного типа данных — множества, который будет описан далее.
2. Заменить в арифметическом выражении функцию sqr на exp. Замена выражения sqr на exp достигается последовательным применением процедур delete и insert.
![]()
program stroka; var a,b:string[40]; k:integer; begin writeln('введите строку <= 40 символов'); readln(a);b:=a; repeat k:=pos('sqr',b); if k>0 then
begin delete(b,k,3);insert('exp',b,k); end until k=0; writeln('старая строка=',a); writeln('новая строка=',b); end.
3. Ввести и упорядочить по алфавиту 10 латинских слов. В программе определим массив из 10 элементов-строк и упорядочим его элементы методом пузырька.
![]()
program order; const s=10; type word=string[20]; var i,j,k :1..s; b:word; p:boolean; list :array[1..s] of word; begin clrscr;writeln('введите список слов'); for i:=1 to s do readln(list[i]); repeat p:=true; for i:=s downto 2 do if list[i]<list[i–1] then begin b:=list[i]; list[i]:=list[i–1]; list[i–1]:=b; p:=false end until p=true; writeln('упорядоченный список слов:'); for i:=1 to s do writeln(list[i]) end.
Множество в Паскале позволяет решать задачи, требующие сравнения значений ординальных величин и имеет такой же смысл, как и в алгебре, — это неупорядоченная совокупность отличных друг от друга однотипных элементов. Число элементов множества не должно превышать 255. В качестве типа элементов может быть любой ординарный тип, кроме типа integer и его интервалов, содержащих числа >255. Тип элементов множества называется базовым. При описании множественного типа используются служебные слова set и of. Задание конкретного множества определяется правилом (конструктором) — списком элементов или интервалов, заключенным в квадратные скобки. Пустое множество обозначается двумя символами [].
Множественный тип можно определить в разделе описания типов по схеме: type <имя> = set of <тип элементов>; Например:
type t=set of byte; var a:t;
Можно совместить описание множественного типа и соответствующих переменных:
var code : set of 0..7; digits : set of '0' . . '9';
Можно описать переменную множественного типа и задать ее первоначальное значение в разделе описания констант, как множество констант. Тип множества следует описать ранее, например:
type up=set of 'A' . . 'Z'; low=set of 'a' . . 'z'; const upcase : up=['A' . . 'Z']; vocals : low=['a', 'e', 'i', 'o', 'u', 'y'];
delimiter : set of char=[' ' . . ' / ' , ' : ' . . ' ? '];
Для данных множественного типа определены операции объединения, пересечения и дополнения множеств, обозначаемые в Паскале соответственно знаками +, * и –, а также отношения равенства множеств (A=B), неравенства (A<>B), включения (A<=B, A>=B).
Логическая операция проверки принадлежности элемента x множеству A
(x in A) принимает значение true, если элемент x принадлежит множеству A, и false в противном случае. Так как к элементам множества прямого доступа нет, то операция in часто используется для этой цели.
Заметим, что операции отношения на множествах выполняются быстрее, чем соответствующие операции на числах, поэтому их выгодно применять в программах. Переменные множественного типа также удобно применять в задачах, где порядок данных не имеет значения, например при моделировании случайных событий.
Пример: составить программу, анализирующую латинский текст и печатающую в алфавитном порядке все найденные в нем буквы, а затем все ненайденные.
Пусть alfa — множество всех букв латинского алфавита. Будем вводить заданный текст с клавиатуры символ за символом, одновременно формируя множество E — множество латинских букв текста. В конце текста введем символ *. Затем с помощью операции in будем проверять, какие буквы алфавита имеются во множестве E. Множество N — множество ненайденных букв в тексте — определяется оператором: N:=alfa–E.
![]()
program search; const alfa:set of char=['a' ..'z']; var c:char;E,N:set of char; begin clrscr; E:=[]; writeln('введите текст, конец ввода -*');read(c); while c<> '*' do begin if c in alfa then E:=E+[c]; read(c) end; writeln; if E=alfa then writeln('найдены все латинские буквы') else begin
N:=alfa–E; writeln('найдены:'); for c:='a' to 'z' do if c in E then write(c); writeln; writeln('не найдены:'); for c:='a' to 'z' do if c in N then write(c); writeln end end.
Комбинированный тип (записи) — одна из наиболее гибких и удобных структур данных, применяющихся при описании сложных объектов, которые характеризуются различными свойствами, а также при создании различных информационных систем. Запись — это последовательность, состоящая из фиксированного числа величин разных типов, называемых полями или компонентами записи. Так же, как и массив, запись содержит ряд отдельных компонентов, однако компоненты могут быть различных типов. В отличие от массива, указание на компоненту производится с помощью явно указанного имени поля. Неявное указание, вычисление значения имени поля невозможно. Например, адресные данные (индекс, город, улица, номер дома, квартиры) можно представить как запись (record):
type address = record index : string[6]; city : string[20]; street : string[20]; haus,flat : integer end;
Из примера видно, что тип "запись" описывается по схеме
type <имя типа записи> = record <имя поля 1> : <тип>;
<имя поля 2> : <тип>; ..................... <имя поля N> : <тип> end;
Как и при описании массивов, можно совместить описание типа записи и соответствующих переменных. Например, данные о двух книгах можно описать так:
var book1,book2 : record authors : string[20]; title : string[40]; pages : integer; publisher : string[20]; year : integer end;
Переменную типа "запись" и ее первоначальное значение можно определить в разделе констант в следующем виде:
const <имя>: <имя типа> = <константное значение>
<Константное значение> — это список имен полей и соответствующих значений, заключенный в круглые скобки. Элементы списка разделяются знаком "точка с запятой". Например, запись о начале координат можно определить так:
type point = record x, y, z : integer end;
const o: point = (x:0; y:0; z:0);
С компонентами записи можно обращаться как с переменными соответствующего типа. Обращение к компонентам записи осуществляется с помощью указания имени поля через точку. Пусть, например, переменная х имеет тип address, т. е. в программе имеется описание var x: address. Тогда допустимы следующие присваивания:
x.haus:=52; x.street:='пр.Героев'; x.city:='Москва';
x.flat:=135; x.index:='129113'
Для того чтобы облегчить запись операций над полями записи, служит опeрaтор with do. Предыдущий пример с использованием этого оператора можно переписать так:
with x do begin haus:=52; street:='пр.Героев'; city:='Москва'; flat:=135; index:='129113' end
В операторах присваивания разрешается использовать не только имена полей, но и имена записей.
Тип поля также может быть записью.
В качестве примера опишем структурированный тип записи, позволяющий хранить данные о человеке: его фамилию, имя, отчество, день, месяц, год рождения, пол, домашний и рабочий телефоны.
man = record fio : record fam, im, otch : string[10]; end; data : record day : 1..31; mes : 1..12; god : integer end; pol : char; telef : record dom,rab : string[10]; end; end;
В Паскале разрешается использовать тип "запись" при описании других составных типов данных, например можно построить массив записей.
Важное значение в Паскале имеют процедуры и функции, определяемые программистом. Эти конструкции позволяют разрабатывать и отлаживать модульные программы, содержащие десятки и сотни тысяч команд. Создание таких программ без аппарата процедур и функций было бы невозможным, поскольку работа с такими программами превосходит по своей сложности возможности человека и не обеспечивает разделения труда в программистских коллективах. Использование процедур и функций, напротив, позволяет "разбить" исходную задачу на набор взаимосвязанных подзадач, для решения каждой из них независимо друг от друга разработать и отладить силами многих программистов подпрограммы и функции размером 15—20 строк и таким образом по принципу "разделяй и властвуй" решить сложную задачу.
Необходимо различать описание и вызов процедур и функций.
Процедуры и функции описываются в разделе программы, следующем за разделом описания переменных, непосредственно перед телом основной программы. При описании процедур и функций необходимо следить, чтобы функции и процедуры, используемые другими функциями и процедурами, были определены раньше. Исключение составляет описание рекурсивных функций и процедур, обращающихся к самим себе. Этот случай требует специального обозначения.
Процедура имеет такую же структуру, как и программа, но с двумя отли-
чиями:
описание процедуры заканчивается точкой с запятой (а не точкой);
заголовок процедуры начинается со служебного слова procedure, за которым следует список формальных параметров — аргументов в следующей форме:
procedure <имя> (<список описаний формальных параметров>);
Все имена, описанные в программе до процедуры, действуют во всей программе и в любой ее подпрограмме (если они там не описаны заново). Они называются глобальными, в отличие от локальных имен, описанных в процедуре и действующих лишь в ней.
Данные для обработки могут передаваться процедуре через глобальные имена или через параметры процедуры. Описание формальных параметров может иметь вид:
<список имен>: <тип> или var <список имен>: <тип>
В первом случае говорят о параметрах-значениях, во втором — о параметрах-переменных. Отличие параметров-значений от параметров-переменных состоит в том, что изменения параметров-значений, произошедшие в процедуре, не передаются из процедуры в основную программу (или вызвавшую ее процедуру или функцию). Это важно для того, чтобы избежать ошибок, связанных с незаметным для программиста изменением переменных, используемых процедурой. Кроме того, параметры-значения могут быть выражениями, вычисляемыми при входе в процедуру. Такие параметры используются лишь для передачи данных в процедуру. Параметры-переменные используются как для передачи значений в процедуру, так и при выводе результатов в программу или вызвавшую ее процедуру или функцию. В простейшем случае заголовок процедуры может содержать только имя процедуры (если для передачи данных в процедуру и обратно используются глобальные переменные).
Оператор вызова процедуры имеет вид:
<имя процедуры> (<список выражений и переменных>);
Указанные при вызове процедуры выражения и переменные называют фактическими параметрами. Их список должен точно соответствовать списку описаний формальных параметров процедуры. Во время вызова процедуры каждому параметру присваивается значение соответствующего фактического параметра. По завершению процедуры параметры-значения не изменятся, а параметры-переменные получат значения, вычисленные процедурой.
Пример: составим программу, которая с помощью строки символов разделит экран на части, где напечатает таблицу квадратных корней для чисел 1, 2,..., 10 и таблицу кубов чисел 1, 2,..., 5.
Печать строки символов оформим как процедуру. Так как никакую информацию передавать из процедуры в программу не надо, то аргументы процедуры (вид и количество символов) будут описаны как параметры-значения.
Заметим, что процедура в программе выполняется пять раз.
![]()
program section; var x:integer;
procedure line(a:integer;c:char); var j:integer; begin
for j:=1 to a do write(c); writeln end; begin
line(35,'–'); writeln('таблица квадратных корней'); line(35,'–');
for x:=1 to 10 do writeln(x:8,sqrt(x):8,4); line (35,'–'); writeln('таблица кубов чисел'); line(35,'–');
for x:=1 to 5 do writeln(x:8,x*x*x:8:4); line(35,'*') end.
Функции, определяемые в Паскале программистом, аналогичны процедурам с тем отличием, что идентификатор (имя) функции служит для возврата в вызвавшую ее программу, процедуру или функцию скалярного, вещественного или строкового значения.
Отличия функции от процедуры:
заголовок функции начинается со служебного слова function и заканчивается указанием типа значения функции:
function <имя> (<список описаний формальных параметров>): <тип>;
раздел операторов функции должен содержать хотя бы один оператор присваивания имени функции;
обращение к функции — не оператор, а выражение вида:
<имя функции> (<список фактических параметров>);
Функции (и процедуры) могут использовать свое имя в собственном описании, т. е. могут быть рекурсивными.
Пример: составим программу, которая для заданных четырех натуральных чисел a, b, c, d напечатает наибольшие общие делители первой и второй пар чисел и сравнит их по величине.
Определим рекурсивную функцию nod(x,y) с помощью формул:
x, если y=0
![]() nod(x,y) nod(y,x), если x<y
nod(x mod y,y), если x>y
nod(x,y) nod(y,x), если x<y
nod(x mod y,y), если x>y
Применяя эти формулы к числам 21 и 15, последовательно находим: nod(21,15) = nod(6,15) = nod(15,6) = nod(3,6) = nod(6,3) = nod(0,3) = nod(3,0) = 3.
![]()
program four; var a,b,c,d,m,n:integer; function nod(x,y:integer):integer; var h:integer; begin if y=0 then h:=x else if x<y then h:=nod(y,x) else h:=nod(x mod y, y); nod:=h end; begin writeln('введите 4 натуральных числа'); read(a,b,c,d); writeln; m:=nod(a,b); n:=nod(c,d); writeln('нод(',a,',',b,')=',m); writeln('нод(',c,',',d,')=',n); if m>n then writeln('первый > второго') else if m<n then writeln(' первый < второго') else writeln('нод пар равны') end.
При разработке больших программных комплексов целесообразно создавать личные библиотеки процедур и функций, специализированные библиотеки коллективного пользования и др. С одной из таких библиотек — встроенной библиотекой стандартных процедур и функций — программисты имеют дело практически всегда. В состав этой библиотеки входят процедуры и функции вычисления значений ряда элементарных функций: синуса, косинуса, экспоненты и т. д., процедуры и функции обработки символьных величин, процедуры ввода-вывода и др.
Встроенная библиотека подключается к любой программе автоматически при компиляции.
В промышленных версиях Паскаля для создания библиотек и разделения больших программ на логически связанные независимые друг от друга составные части используют модули. В состав модуля входят следующие разделы: заголовок, интерфейс, реализация, инициализация. Заголовок необходим для ссылок на модуль. Интерфейс содержит объявления, включая процедуры и функции, представленные списком заголовков и доступные пользователям в теле основной программы. Раздел "реализация" содержит тела процедур и функций, перечисленных в интерфейсной части модуля. Раздел "инициализация" содержит операторы, необходимые для инициализации модуля. Таким образом, модуль — это набор констант, типов данных, переменных, процедур и функций. Каждый модуль компилируется отдельно; результат компиляции сохраняется как библиотека процедур и функций. Каждый элемент модуля можно использовать в программе пользователя без дополнительного объявления, для чего достаточно записать имя используемого модуля в директиве uses в начале программы после ее заголовка.
Известны стандартные модули Crt, Graph и др., применяемые в Турбо Паскале (Turbo Pascal) — одной из версий Паскаля. В этих модулях содержатся сервисные процедуры и функции по работе с экраном дисплея, клавиатурой, графическими примитивами и т. п. Модули подключаются к программе специальной командой, размещаемой сразу после заголовка: uses <имя модуля>;
Программист может сам создать модуль.
Этот модуль может быть отдельно откомпилирован. После этого любая программа, написанная на Паскале, может получить доступ к интерфейсным объектам (в данном случае — процедурам) этого модуля с помощью директивы uses <имя модуля>. При описании модуля в интерфейсной части модуля от процедур присутствуют лишь заголовки, а в части "реализация" от заголовков процедур остаются лишь их имена.
Одна из наиболее фундаментальных структур данных — файл (последовательность). Программная организация компьютеров, их связь с внешними устройствами основаны на файловой структуре.
Файлы позволяют решить две проблемы:
возможность формирования и сохранения значений для последующего использования другими программами (например, в программах многократной обработки информационных систем, таких как платежные ведомости, различные АСУ, базы данных, необходимость длительного хранения информации очевидна);
взаимодействие программ с внешними устройствами ввода/вывода: дисплеем, принтером, АСП и т. п.
В Паскале эти проблемы снимаются с помощью структурированных данных файлового типа.
Файловый тип данных в программе задается следующим образом: type <имя файлового типа> = file of <тип компонентов>;
В качестве типа компонентов файла разрешается использовать любой тип данных, кроме файлового.
Например:
type
intfile = file of integer; refile = file of real; chfile = file of char; ran = 1 . . 10; st = set of ran; vector = array[ran] of real; compl = record re,im : integer; end;
setfile = file of st; vecfile = file of vector; compfile= file of compl;
Описание файловой переменной задается обычным способом в разделе описаний. Например: var f: intfile; или var f : file of integer;
Файловая переменная является буфером между Паскаль-программой и внешним устройством и должна быть логически с ним связана. Связь осуществляется оператором языка Паскаль: assign (<имя файловой переменной>,'<имя устройства>');
Как правило, файлы для хранения данных связаны с устройством внешней памяти на магнитных носителях (дисковод) и носят название внешние файлы. Если, например, файл с именем primer.dat логически связан с дисководом A:, то все данные, помещаемые в файл, будут храниться на этом дисковом накопителе, а установка "окна" между программой и файлом будет определяться через файловую переменную f оператором: assign (f, 'primer.dat');
Если внешним устройством является принтер, то связь осуществляется оператором:
assign(f, 'lst:');
Здесь lst — логическое имя печатающего устройства. Далее приведены логические имена внешних устройств ввода/вывода: con — консоль; trm — терминал; kbd — клавиатура; lst — принтер; aux — буфер сети; usr — драйвер пользователя.
После осуществления связи файловая переменная f отождествляется с соответствующим файлом.
Для работы с файлом его необходимо открыть, а по окончании работы — закрыть. Файл открывается для чтения оператором reset(f), для записи — оператором rewrite(f).
Чтение и запись данных осуществляются известными командами read/write, только в начале списка помещается имя файловой переменной:
read (f, <список ввода>); readln (f, <список ввода>); write(f, <список вывода>); writeln(f, <список вывода>);
Закрытие файла осуществляется командой close(f).
Условно файл можно представить в виде ленты, у которой есть начало, а конец не фиксируется. Компоненты файла записываются на эту ленту последовательно, друг за другом:
|
f 0 |
f 1 |
f 2 |
f 3 |
... |
м.к. |
|
^ т.м.
Здесь т.м. — текущий маркер, указывающий на рабочую позицию (окно) файла; м.к. (маркер конца файла) — специальный код, автоматически формируемый вслед за последним элементом файла.
Такого рода файлы называются файлами последовательного доступа. В исходной версии Паскаля файлов прямого доступа, для которых можно непосредственно "достать" любую компоненту, не предусмотрено; однако в Турбо Паскале элементы прямого доступа есть (например, через функцию seek, см. далее).
Команда rewrite(f) — открыть файл для записи — устанавливает файл в начальное состояние режима записи; текущий маркер устанавливается на маркер конца файла. Если в файле f до этого была информация, то она уничтожается.
В открытом для чтения командой reset(f) файле текущий маркер устанавливается на нулевое состояние, однако содержимое файла не утрачивается.
rewrite(f)
|
м.к. |
|
|
^
reset(f)
|
f0 |
f1 |
f2 |
f3 |
... |
м.к. |
|
^
Команда закрытия файла close(f) обязательна, поскольку эта команда формирует маркер конца файла, что в большинстве случаев является необходимым (например, для работы с функцией eof(f), см. далее).
В системе Турбо Паскаль предусмотрены встроенные функции по работе с файлами:
filesize(f) — текущее количество компонент открытого файла;
filepos(f) — номер текущей позиции маркера;
rename(f,имя) — переименование файла, связанного с f;
erase(f) — уничтожение файла;
execute(f) — выполнение COM-файла;
chain(f) — выполнение CHN-файла;
seek(f,N) — устанавливает маркер на позицию N; eof(f) — возвращает true, если найден конец файла;
ealn(f) — возвращает true, если найден конец строки.
На практике широко используются текстовые файлы, которые состоят из литерных (логических) строк. Поэтому в языке Паскаль предусмотрен стандартный файловый тип text (он не является file of char, скорее всего, это — file of string[n]). Логические строки бывают разной длины, в том числе и нулевой. В конец каждой строки помещается специальный символ "конец строки" (eoln — "end of line"). В качестве печатного символа конца строки используют литеру #. Текстовый файл (text) является строго последовательным, к нему не применимы некоторые встроенные функции, в частности, seek. В отличие от типизированных файлов, с текстовым файлом нельзя одновременно проводить операции чтения (read) и записи (write). Однако допустимы операторы writeln и readln. Числовые данные, целые и вещественные, в текстовом файле должны записываться через пробел.
Далее приведены несколько примеров, иллюстрирующих работу с файлами.
Пример 1. Вывод данных на печатающее устройство — принтер (lst:).
![]()
program print; var fal :text; x :real; name :string[25]; begin assign(fal,'lst:'); rewrite(fal); x:=2.5; name:='Слава'; writeln(fal,x:8:2); writeln(fal,'Привет, ',name); close(fal) end. {Здесь файловая переменная fal связывается с принтером lst:, и запись в файл fal практически означает вывод на печать}
Пример 2. Создание и сохранение в файле xxx.dat последовательности целых чисел от 10 до 20.
![]()
program zapis; var f: file of integer; i: integer; begin assign(f,'xxx.dat'); rewrite(f); for i:=10 to 20 do write(f,i); close (f); end. {После выполнения программы формируется внешний файл xxx.dat}
Пример 3. Считывание первых пяти компонент из существующего файла xxx.dat и вывод на дисплей квадратов этих значений.
![]()
program read; var ff: file of integer; j,i : integer; begin assign(ff,'xxx.dat'); reset(ff); for j:=1 to 5 do begin read(ff,i); writeln(i*i); end; close(ff); end.
Пример 4. В текстовом файле (text) slov.txt содержится русский текст. Определить, сколько гласных букв в тексте.
![]()
program text; var ft : text; n : integer; ch : char; st : set of char; begin assign (ft,'slov.txt'); reset(ft); st := ['А','Е','И','О','У','Ы','Э','Ю','Я']; st := st+['а','е','и','о','у','ы','э','ю','я']; n:=0; while not eof(ft) do begin read(ft, ch); if ch in st then n:=n+1; end; close(ft);
writeln; write('кол-во гласных букв =',n); end.
Поскольку длина текста (файла) неизвестна, то в цикле "пока" используется логическая функция eof(f), которая возвращает значение true, если найден конец файла.
Пример 5. Шифрование и дешифрование текста.
Программа шифрования заданного текста (sekret) использует следующее правило шифровки: каждая буква в тексте заменяется на букву, расположенную на n позиций вправо от искомой в русском алфавите. Причем последним символом алфавита является пробел ' ', далее алфавит продолжается циклически.
Значение смещения n находится вo внешнем файле n.key, который формируется программой key. Зашифрованный текст выводится во внешний файл с именем шифр.txt, а также на дисплей.
Программа дешифровки (retsek) считывает шифрованный текст из файла шифр.txt и выводит на экран дисплея искомый текст.
![]()
program key; var n : integer; f : file of integer; begin assign (f,'n.key'); rewrite(f); write('введи ключ(смещение): '); readln(n); write(f,n); close(f); end.
![]()
program sekret; var slovo,anslovo: string[100]; alfavit : string[33]; n, i, k, p : integer; fkl : file of integer; fs : text; begin alfavit:='абвгдежзийклмнопрстуфхцчшщъыьэюя '; assign(fkl,'n.key'); reset(fkl); read(fkl,n); close(fkl); writeln; write('введи текст: '); readln(slovo); anslovo:=''; for k:=1 to length(slovo) do begin for i:=1 to 33 do
if slovo[k]=alfavit[i] then begin p:=i+n; if p >33 then p:=p mod 33; anslovo:=anslovo+alfavit[p];
end; end; assign(fs,'шифр.txt'); rewrite(fs); write(fs,anslovo);close(fs); writeln; write(anslovo); end.
![]()
program retsek; var slovo, anslovo : string[100]; alfavit : string[33]; n, i, k, p : integer; fi : file of integer; f : text; begin alfavit:='абвгдежзийклмнопрстуфхцчшщъыьэюя '; assign(fi,'n.key'); reset(fi); read(fi,n); close(fi); assign(f,'шифр.txt'); reset(f); read(f,anslovo); close(f) slovo:=''; for k:=1 to length(anslovo) do begin for i:=1 to 33 do if anslovo[k]=alfavit[i] then begin p:=i–n; if p < 1 then p:=33–p mod 33; slovo:=slovo+alfavit[p]; end; end; writeln; write('текст шифровки: ',slovo); end.
До сих пор мы рассматривали статические переменные. Такие переменные автоматически порождаются при входе в программу, процедуру или функцию, в которых они описываются, существуют на протяжении работы программы, процедуры или функции и уничтожаются при выходе из них.
Обращение к статическим переменным производится по их именам, а тип определяется их описанием. Вся работа по размещению статических объектов в памяти машины выполняется на этапе трансляции. Однако использование только статических переменных может вызвать трудности при составлении эффективной машинной программы. Во многих случаях заранее неизвестен размер той или иной структуры данных, или структура может изменяться в процессе выполнения программы. Одна из подобных структур — последовательный файл — уже ранее рассматривалась.
В языке Паскаль предусмотрена возможность использования динамических величин. Для них выделение и очистка памяти происходят не на этапе трансляции, а в ходе выполнения самой программы. Для работы с динамическими величинами в Паскале предусмотрен специальный тип значений — ссылочный. Этот тип не относится ни к простым, ни к составным. Переменные ссылочного типа, или указатели, являются статическими переменными. Значением переменной ссылочного типа является адрес ячейки — места в памяти соответствующей динамической величины. Свое значение ссылочная переменная получает в процессе выполнения программы, в момент появления соответствующей динамической величины.
Переменные ссылочного типа (указатели) вводятся в употребление обычным путем с помощью их описания в разделе переменных, а их тип, указывающий на тип создаваемых в программе соответствующих динамических величин, тоже определяется либо путем задания типа в описании переменных, либо путем указания имени ранее описанного типа.
Значением указателя является адрес ячейки, начиная с которой будет размещена в памяти соответствующая динамическая величина. Задание ссылочного типа выполняется по схеме: type <имя ссылочного типа> = ^ <имя типа динамической величины> Значок ^ указывает на то, что величина является динамической.
Например:
type
p = ^ integer; q = ^ record x: integer; y: string [20] end;
Объявлены два ссылочных типа — p и q. Первый — указатель на целочисленные значения, второй — на запись из двух полей.
Связь указателя с динамическим объектом можно изобразить следующим образом:
![]() p
p
На этой схеме р — имя указателя; звездочкой изображено значение указателя, а стрелка отражает тот факт, что значением указателя является адрес объекта (ссылка на объект), посредством которого объект и доступен в программе.
В некоторых случаях возникает необходимость в качестве значения указателя принять "пустую" ссылку, которая не связывает с указателем никакого объекта. Такое значение в Паскале задается служебным словом nil и принадлежит любому ссылочному типу. Результаты выполнения оператора p:=nil; можно изобразить следующим образом:
![]() p
p
Имея объявленные типы, можно обычным образом описывать переменные этих типов. Например: var i: p; zap: q;
Динамические переменные базовых типов можно вводить прямо в разделе описания переменных: var i: ^integer;
Описание указателя еще не резервирует память для значения соответствующего динамического объекта. Так, каждое приведенное ранее описание выделяет в памяти два байта для записи адреса * — значения указателя, но никакой величины типа p или q в памяти не образуется, и даже адреса * еще нет.
Для порождения динамического объекта, на который указывает ссылочная переменная i, служит стандартная процедура new(i), где new — "новый" — имя процедуры, i — имя указателя.
Процедура new(i) выполняет две функции:
резервирует место в памяти для размещения динамического объекта соответствующего типа с именем i;
указателю i присваивает адрес динамического объекта i.
Однако узнать адрес динамической переменной с помощью процедуры writeln(i) нельзя.
Динамические объекты размещаются по типу стека в специальной области памяти — так называемой "куче", свободной от программ и статических переменных. Как уже было отмечено, символ ^ после имени указателя означает, что речь идет не о значении ссылочной переменной, а о значении того динамического объекта, на который указывает эта ссылочная переменная. Так, если в программе имеется описание переменной var i:^integer;
то при выполнении процедуры new(i) порождается динамическая переменная типа integer. Если затем будет выполнен оператор присваивания i^:= 58; то этой динамической переменной будет присвоено значение 58.
Имя ссылочной переменной с последующим символом ^ называют переменной с указателем. Именно она синтаксически выполняет роль динамической переменной и может быть использована в любых конструкциях языка, где допустимо использование переменных того типа, что и тип динамической переменной.
Так, если j — статическая переменная типа integer, то допустимы операторы присваивания j:=j+i^+2; i^:=i^ div 3+7; i^:=sqr(i^) и т. д. Если ссылочная переменная b указывает на массив
type mas = array[1...100] of integer; var b:^mas то в этом случае переменные с указателем могут выглядеть, например, так: b^[2], b^[k+5].
Если в процессе выполнения программы некоторый динамический объект p^, созданный в результате выполнения оператора new(p), становится ненужным, то его можно уничтожить (очистить выделенное ему место в памяти) с помощью стандартной процедуры dispose(p). В результате выполнения оператора вида dispose(p) динамический объект, на который указывает ссылочная переменная p, прекращает свое существование, занимаемое им место в памяти становится свободным, а значение указателя р становится неопределенным (но не равным nil).
Если p имел пустое значение nil до вызова процедуры dispose(p), то это приведет к "зависанию" программы.
Если же до вызова этой процедуры указатель p не был определен, то это может привести к выходу из строя операционной системы.
Значение одного указателя можно присвоить другому указателю того же типа. Можно также указатели одинакового типа сравнивать друг с другом, используя отношения "=" или "<>".
Стандартные процедуры new и dispose позволяют динамически порождать программные объекты и уничтожать их, что дает возможность использовать память машины более эффективно.
Связанные списки данных. Несмотря на богатый набор типов данных в Паскале, он не исчерпывает всего практически необходимого для разработки многих классов программ. В частности, из разнообразных связанных структур данных в языке стандартизированы массивы и файлы, а кроме них могут потребоваться и схожие с ними, но иные структуры. Для них характерны, в частности, следующие признаки:
не определенное заранее число элементов;
необходимость хранения в оперативной памяти.
Средство для реализации таких структур дает аппарат динамических переменных.
Простейшей из динамических структур является однонаправленный список. Он строится подобно очереди на прием к врачу: пациенты сидят на любых свободных местах, но каждый из них знает, за кем он в очереди (т. е. данные размещаются на свободных местах в памяти, но каждый элемент содержит ссылку на предыдущий или следующий элемент). Поскольку количество пациентов заранее не задано, они могут уходить из очереди и появляться в ней, причем не только в начале или конце очереди, но и в ее середине (если они приходят по предварительной записи или направлениям других врачей), структура является динамической.
Другая подобная структура — стек. Его моделью может служить закрытая с одного конца трубка, в которую через открытый конец помещают шарики. При этом реализуется принцип "последним вошел — первым вышел". Возможное количество элементов в стеке не фиксировано.
Остановимся на примере стека и покажем его программную реализацию. Технически при этом следует решить ряд задач, из которых наиболее специфическими являются:
связывание последующих компонентов стека;
смещение ссылок при каждом движении по стеку.
Из-за необходимости хранить не только значение каждого элемента, но и соответствующую ссылку на последующий элемент, каждый из элементов будем хранить в виде двухполевой записи, в которой первое поле — значение элемента, а второе — ссылка на следующий элемент. Схематически эту структуру можно описать следующим образом:
![]() a
a ![]() a . . .
a . . . ![]() a
a ![]() a nil
a nil
(элементу, который пришел первым, ссылаться не на что, о чем свидетельствует "пустая ссылка" nil).
Пусть для конкретности элементы стека — действительные числа, и при последовательном заполнении состояния стека будут:
1,75
35,7 1,75
–6,94 35,7 1,75
Приведенная далее программа включает две процедуры: добавления очередной компоненты к стеку и изъятия ее. Программа формирует указанный стек и производит контрольное извлечение из него. Каждое действие снабжено комментарием, который поможет разобраться в программе. Следует обратить особое внимание на организацию смещения ссылок.
![]()
program stack; {формирование динамической структуры — стека} type s=^StackComp; StackComp=record b:real; p:s; end; var a:s; k:real; procedure Dobavl(k:real); {процедура добавления к стеку числа k} var j:s; begin new(j); {создание новой динамической записи} j^.b:=k; {внесение следующей компоненты стека} j^.p:=a; {смещение указателя} a:=j {формирование новой записи} end; procedure Vzjat(var k:real); {процедура чтения из стека} var j:s; begin j:=a; k:=j^.b; {k–значение последней компоненты} a:=j^.p; {перенастройка указателя} dispose(j) {ликвидация использованной записи} end; begin {пример записи и чтения} a:=nil; Dobavl(1.75);
Dobavl(35.7);
Dobavl(–6.94); {сформирован стек: –6.94, 35.7, 1.75}
Vzjat(k); writeln(k); {контрольное взятие из стека}
Vzjat(k); writeln(k); {еще одно взятие из стека} Vzjat(k); writeln(k) {еще одно взятие из стека} end. {результат работы программы: –6.94 35.7 1.75}
Машинная (компьютерная) графика — одно из важных направлений в современной прикладной информатике. В отличие от базового Паскаля, современные версии содержат мощные средства разработки графических программ. Рассмотрим часть соответствующих возможностей Турбо Паскаля, в котором они реализованы с помощью стандартного модуля Graph.
Модуль представляет собой мощную библиотеку графических подпрограмм универсального назначения, рассчитанную на работу с наиболее распространенными графическими адаптерами SVGA IBM-совместимых персональных
компьютеров.
Подключение модуля Graph.tpu к программе выполняется директивой uses graph;
Инициализация графического экрана осуществляется с помощью процедуры Initgraph. Процедура инициализации в Турбо Паскале имеет три аргумента:
Initgraph(<драйвер>, <режим>, '<путь к драйверу>') Она может быть выполнена так:
uses graph; var gd, gm: integer; {переменные gd и gm определяют драйвер и режим} begin gd:=vga; gm:=vgahi; initgraph(gd,gm,'d:\tp55'); ...
Первые две команды можно заменить одной: gd:=detect;
Целая константа detect=0 в модуле Graph автоматически распознает драйвер и устанавливает режим максимального разрешения для данной машины.
Процедура closegraph освобождает память от драйвера и устанавливает режим работы экрана, который был до инициализации графики.
Для обнаружения ошибок в графике применяются функции graphresult и grapherrormsg (код ошибки). Последняя выдает строку сообщения о характере ошибки, соответствующей коду. Инициализация графического режима с проверкой ошибок может быть выполнена в программе следующим образом:
uses graph; var gd, gm, errorcod: integer; begin gd:=detect; initgraph(gd,gm,''); errorcod:=graphresult; if errorcod<>grok then begin writeln('ошибка графики'); writeln(grapherrormsg(errorcod)); halt end;
Процедура Halt останавливает выполнение программы и возвращает управление операционной системе.
Для формирования палитры используется система смешения красного, зеленого и синего цветов и изменения яркости луча. Цвет задается номером из списка цветов палитры в интервале 0 .. 15.
Процедуры setcolor(<цвет>) и setbkcolor(<цвет>) устанавливают текущий цвет рисунка и цвет фона. При инициализации графики по умолчанию устанавливается черный фон и белый цвет рисунка.
В табл. 5.3 указаны основные процедуры модуля Graph, применяющиеся для построения простейших геометрических примитивов.
Координаты точек воспринимаются в "экранной" системе координат, в которой начало — верхний левый угол экрана, ось X направлена вниз, ось Y — направо. Максимальные значения координат определяются разрешением.
В процедуре setlinestyle(a,b,t) первый аргумент а — стиль линии, второй параметр b — "образец" — имеет значение 4, если a=4, в остальных случаях b=0; третий параметр t — толщина линии — может иметь значение 1 (нормальная толщина) или 3 (жирная линия).
Таблица 5.3. Основные процедуры модуля Graph
|
Заголовок процедуры |
Геометрический смысл |
|
putpixel(x,y,c) |
Построить точку (х,у) цветом с |
|
setlinestyle(a,b,t) |
Установить стиль, образец и толщину линий |
|
line(x1,y1,x2,y2) |
Соединить две точки отрезком |
|
rectangle(x1,y1,x2,y2) |
Построить прямоугольник с заданными концами диагонали и сторонами, параллельными осям координат |
|
circle(x,y,r) |
Построить окружность с центром (х,у) и радиусом r |
|
arc(x,y,a,b,r) |
Построить дугу окружности: а, b — начальный и конечный угол в градусах |
|
ellipse(x,y,a,b,rx,ry) |
Построить эллиптическую дугу: rx, ry — полуоси эллипса |
|
setfillstyle(t,c) |
Установить стиль закраски и ее цвет |
|
fillellipse(x,y,rx,ry) |
Построить закрашенный эллипс, используя цвет рисунка |
|
floodfill(x,y,cg) |
Закрасить фигуру до границы с цветом cg; (х,у) — внутренняя точка фигуры |
|
bar(x1,y1,x2,y2) |
Построить столбец, используя тип и цвет закраски |
|
pieslice(x,y,a,b,r) |
Построить и закрасить сектор круга |
|
sector(x,y,a,b,rx,ry) |
Построить и закрасить эллиптический сектор |
|
settextstyle(f,n,d) |
Установить шрифт, направление вывода и размер символа текста |
|
outtextxy(x,y,st) |
Вывести строку st, начиная с точки (х,у) |
Таблица 5.3 (окончание)
|
Заголовок процедуры |
Геометрический смысл |
|
outtext(st) |
Вывести строку, начиная с точки расположения текущего указателя |
Первый аргумент процедуры setfillstyle(t,c) — тип закраски t — принимает значения из интервала 0..12. Наиболее употребителен тип t=1 — заполнение фигуры текущим цветом.
Для вывода текста на графический экран сначала выполняется процедура settextstyle(f,n,d), устанавливающая шрифт f, направление вывода n и размер символов (параметр d). При f=0 используется стандартный точечный шрифт, встроенный в систему Турбо Паскаль. С использованием других шрифтов познакомимся позже. Направление вывода n принимает значения 0 (горизонтальный вывод) и 1 (вертикальный вывод).
Размер букв определяется параметром d, принимающим значения из интервала 1..10. Если d=1 и f=0, то каждый символ занимает квадрат 8*8 точек, при d>1 сторона квадрата умножается на d.
Далее с помощью процедуры outtextxy(x,y,st) строка st выводится на экран, начиная с точки (x,y). Например:
settextstyle(0,0,2); outtextxy(100,200,'горизонтальная строка'); outtextxy(100,230,'размер увеличен вдвое');
Пример 1. Программа рисует звездное небо с 400 звездами, вспыхивающими постепенно, и полную желтую луну.
![]()
program sky; uses crt,graph; var k,gd,gm:integer; begin gd:=detect; initgraph(gd,gm,''); randomize; for k:=1 to 400 do begin putpixel(random(640),random(480),random(15)+1); delay(10); end; setfillstyle(1,14); setcolor(14); circle(550,80,30); floodfill(550,80,14); repeat until keypressed; closegraph end.
Пример 2. Узор. Используя простейшие геометрические образы, строят замечательные графические изображения. Далее приведена программа изображения муарового узора, полученного пересечением двух семейств расходящихся отрезков прямых. Качество и изображение получаемого узора зависит в основном от трех параметров: k1, k2 — расстояний между отрезками слева и справа; h — смещения вниз (вверх) всего семейства.
![]()
program uzor; uses crt, graph; var gd,gm,errCode,i,k1,k2,h: integer; begin k1:=8; k2:=3; h:=110; gd:=Detect; InitGraph(gd,gm,''); errCode:=GraphResult; if errCode = grOk then begin setcolor(green); for i:=1 to (420 div k1) do begin line(0,i*k1,640,i*k2+h); line(0,i*k2+h,640,i*k1); end; repeat until keypressed; CloseGraph; end else writeln('errCode=',errCode) end.
Процедуры построения прямоугольных фигур удобно использовать, в частности, при построении схем, диаграмм.
Пример 3. Программа 25 строит столбчатую диаграмму, наглядно отражающую числовую информацию о населении 6 крупных городов мира: Токио, Гамбурга, Москвы, Бангкока, Мехико и Парижа.
![]()
program colon; uses crt,graph; const m:array[1..6] of real=(11500,2300,9700,5100,12400,8200); name:array[1..6] of string=('Токио','Гамбург','Москва','Бангкок','Мехико','Париж'); var gd,gm,k,n,s:integer; st:string[6]; begin
gd:=detect; initgraph(gd,gm,' '); setcolor(15); setlinestyle(0,0,1); line(60,400,620,400); line(60,400,60,100);
settextstyle(0,0,1); for k:=1 to 12 do
begin n:=1000*k; str(n,st); outtextxy(10,400–20*k–4,st); line(60,400–k*20,65,400–k*20) end;
setcolor(14); settextstyle(0,0,2);
outtextxy(120,20,'Население городов (тысяч)'); settextstyle(0,0,1); for k:=1 to 6 do begin setfillstyle(1,k+2);
bar(100+(k–1)*70,400,100+k*70,round(400–m[k]/1000*20)); outtextxy(100+(k–1)*70+4,450,name[k]); end;
repeat until keypressed; closegraph end.
Процедура bar3d(x1,y1,x2,y2,d,top) рисует трехмерный столбец, глубина которого определяется параметром d. Последний параметр процедуры top — логического типа. Если top=true, рисуется верхнее основание столбика, в противном случае оно не изображается, что позволяет рисовать столбики один над другим. Диаграммы с трехмерными столбиками красивы, но их труднее создавать.
Построение графиков функций. Построение графиков функций — неотъемлемая часть большинства программ, предназначенных для обучения математике, физике. Далее представлен пример программы построения графика функции y=x*x*sin(1/x) на произвольном отрезке [a,b]. Количество точек графика (параметр n) также задается произвольно (точка x=0 исключается, т. к. в ней функция не определена). В программе определяются величины t1=(x1–x0)/(b–a) и t2=(y1–y0)/(2m), которые означают масштабы по осям X и Y соответственно.
График рассматриваемой функции представлен на двух отрезках [a,b] и [–0.1,0.1]. Чтобы построить график другой функции, достаточно задать ее аналитический вид в описании функции (function f).
![]()
program grafik; uses crt, graph;
var gd,gm, errCode : integer; a,b : real; n : integer; function f(x:real):real; begin if x<>0 then f:=x*x*sin(1/x); end;
procedure grafun(x0,x1,y0,y1,n :word;a,b:real); var h,m,x, t1,t2 : real; i, u,v,xv,yv : word; begin
h:=(b–a)/n; {поиск максимума f(x)} m:=abs(f(a));
for i:=1 to n do if m<abs(f(a+i*h)) then m:=abs(f(a+i*h)); t1:=(x1–x0)/(b–a);
t2:=(y1–y0)/(2*m); {построение координатных осей} setfillstyle(1,15); bar(x0–5,y0–5,x1+5,y1+5); xv:=round(x0–a*t1); yv:=round((y0+y1)/2); setcolor(1); line(xv,y0,xv,y1); line(x0,yv,x1,yv);
Moveto(x0,yv–round(f(a)*t2)); {установка курсора в начало графика} setcolor(3); {построение графика} for i:=1 to n do begin
x:=a+i*h; u:=x0+round((x–a)*t1); v:=yv–round(f(x)*t2); lineto(u,v); end;
end; {конец процедуры } begin
clrscr; write ('введи a,b и n : '); readln(a,b,n); gd:=Detect; InitGraph(gd,gm,''); errCode:=GraphResult; if errCode = grOk then begin grafun(100,500,50,300,n,a,b); grafun(550,620,10,100,200,–0.1,0.1); repeat until keypressed; CloseGraph; end
else writeln('errCode=',errCode); end.
Для изображения поверхностей, определяемых функцией двух переменных z=f(x,y), можно использовать разные способы. Одним из них является метод построения семейства одномерных графиков функции z=f(x,y) от одной переменной x или y различных фиксированных значениях другой. Это может быть хорошей тренировкой для самостоятельной работы по освоению гра- фики.
Построение движущихся изображений. Особую ценность в графике представляет организация движения фрагментов рисунка.
Наиболее просто это сделать по следующему плану:
1. Нарисовать фрагмент в нужном месте экрана.
2. Стереть фрагмент, рисуя его цветом фона или используя процедуру cleardevice.
3. Снова нарисовать фрагмент в другом месте экрана.
Такой способ осуществлен в программе billiard, где два шарика радиусом 5 пикселов разных цветов двигаются с одинаковой скоростью внутри зеленого прямоугольника, построенного с помощью процедуры bar.
Процедура blou измеряет смещение центра шарика от сторон прямоугольника по каждой оси и, если это смещение на следующем шаге цикла станет меньше радиуса, изменяет направление движения, моделируя поведение упругого шара при ударе о стенку.
В программе также рассмотрена ситуация соприкосновения шариков во время их движения. Она решается примитивно просто: каждый шарик меняет направление своего движения на противоположное.
![]()
program billiard; uses crt,graph; var x,y,dx,dy,gd,gm:integer; x1,y1,dx1,dy1:integer; procedure blow(a,b:integer; var c,d:integer); begin if (a<107) or (a>523) then c:=–c; if (b<107) or (b>363) then d:=–d; end; begin gd:=detect; initgraph(gd,gm,''); setcolor(14); setlinestyle(0,0,1); rectangle(99,99,531,371); setfillstyle(1,3); bar(100,100,530,370); x:=320; y:=240; dx:=2; dy:=2; x1:=320; y1:=200; dx1:=–2; dy1:=–2; repeat circle(x,y,5); setcolor(4); circle(x1,y1,5); blow(x,y,dx,dy); blow(x1,y1,dx1,dy1); delay(10); if (abs(x–x1)<=10) and (abs(y–y1)<=10) then begin dx:=–dx; dy:=–dy; dx1:=–dx1; dy1:=–dy1; delay(300) end;
setcolor(3); circle(x,y,5); x:=x+dx; y:=y+dy; setcolor(3); circle(x1,y1,5); x1:=x1+dx1; y1:=y1+dy1; setcolor(14) until keypressed; closegraph end.
Система программирования Турбо Паскаль. Главное меню интегрированной среды содержит следующие пункты:
E — системное меню;
File — работа с файлами (сохранение, загрузка, связь с операционной системой);
Edit — редактирование текущего файла (стандартные возможности встроенного текстового редактора);
Search — поиск и замена фрагментов текста;
Run — запуск программы на выполнение;
Compile — компиляция программы;
Options — установка опций интегрированной среды;
Debug — установка параметров отладки программы;
Window — работа с окнами;
Tools — инструментальные программные средства; Help — система помощи и подсказок.
Интегрированная среда пользователя позволяет работать в многооконном режиме, редактируя несколько файлов одновременно. Допускается работа с мышью. Очень удобен сервис для работы с окнами и системой помощи Help, которая контекстно вызывается из любого окна, а в окне Help допустимы некоторые команды редактирования. Имеется возможность менять цветовую палитру самой интегрированной среды.
Компилятор может работать в трех режимах: обычном режиме MS DOS (Real), защищенном режиме (Protected) и в режиме операционной среды Windows (Windows). Синтаксическая подсветка обеспечивает цветовое выделение управляющих структур, зарезервированных слов, идентификаторов, строк и т. п. Секция меню Tools предназначена для передачи управления внешним программам и создания собственных инструментальных программных средств. Нажатие клавиш <Alt>+<F10> (или правый щелчок мыши) активизирует локальные меню, чувствительные к контексту (Browse, Edit, Help, Message, Watch).
Библиотека стандартных модулей включает модули: Crt, Graph, Graph3,
Overlay, String, System, Turbo3, WinAPI, WinCrt, WinDos, WinPrn, WinTypes, WinProcs.
1. Назовите разделы программы на Паскале. Какова их последовательность?
2. Какие типы данных относят к ординарным?
3. Какие операции допустимы над величинами целого типа? Вещественного типа?
4. Как в Паскале осуществляется ввод и вывод данных?
5. Как в Паскале реализуется ветвление?
6. В чем различие оператора ветвления и оператора выбора? Как реализуется оператор выбора?
7. Какие виды оператора цикла имеются в языке Паскаль? Как эти операторы выполняются?
8. Для чего служит и как определяется перечислимый тип данных?
9. Для чего может понадобиться интервальный тип данных?
10. Как описываются и используются в программах массивы?
11. Какие действия возможны над величинами строкового типа?
12. Какие операции допустимы над множествами?
13. В чем различия между одномерными массивами и записями?
14. Для чего служат и в каких случаях используются в программах процедуры и функции?
15. По каким правилам описывают процедуры и функции и как их вызы- вают?
16. Какие параметры называют формальными и какие — фактическими?
17. В чем различие между локальными и глобальными переменными?
18. Для чего служат модули?
19. Для чего при программировании на Паскале используются файлы?
20. Какие операции и функции используются при работе с файлами?
21. В чем различие статических и динамических переменных?
22. Как реализуется связь указателя с динамическим объектом?
23. Что такое "связанный список данных"?
24. Какими графическими процедурами располагает система программирования Турбо Паскаль?
25. Как можно создать движущееся изображение?
 Темы для рефератов и докладов
Темы для рефератов и докладов 1. Развитие Паскаля от разработки Вирта до современных систем программирования.
2. Принципы работы компилятора с языка Паскаль.
3. Компьютерное представление данных различных типов.
4. Использование динамических структур данных для решения задач обработки информации.
5. Рекурсивное программирование на Паскале.
6. Перспективы развития языка Паскаль.
1. Правда ли, что на Паскале можно запрограммировать решение любой задачи?
2. Какой язык программирования самый лучший?
3. Чем полезно и чем мешает требование описания данных в Паскале?
Для выполнения следующих заданий необходимо написать, отладить и исполнить программу на Паскале.
1. Упорядочите числа a, b, c в порядке возрастания.
2. Определите все пары двузначных чисел, обладающих свойством:
(20+25)^2 = = 2025.
3. Вычислите в числовом массиве а1, а2, ..., аn суммы положительных и отрицательных элементов, подсчитайте разность и тех, и других чисел.
4. Вычислите сумму произведений элементов двух десятимерных векторов
X и Y.
5. Упорядочите массив х1, х2, ..., хn по неубыванию, используя метод сортировки вставками: пусть первые k элементов уже упорядочены по неубыванию; берется (k+1)-й элемент и размещается среди первых k элементов так, чтобы упорядоченными оказались уже (k+1) первых элементов.
6. Решите систему n линейных уравнений методом Гаусса.
7. Замените в заданном арифметическом выражении все вхождения sin на cos и sqrt на abs.
8. Для заданного текста определите длину содержащейся в нем максимальной последовательности цифр 0, 1, 2, ..., 9.
9. Дан текст из латинских букв и знаков препинания. Составьте программу частотного анализа букв этого текста, т. е. напечатайте каждую букву с указанием количества ее вхождений и процента вхождений.
10. Найдите и выведите в порядке убывания все простые числа из диапазо- на [2..201].
11. Создайте программу, которая выполняет поиск адреса по фамилии ученика вашего класса, используя представление данных в массиве, состоящем из записей.
12. Заданы N точек на плоскости. Найдите точку, ближайшую к началу координат. Используйте тип "запись".
13. Найдите площадь выпуклого четырехугольника со сторонами x, y, z, t и одной из диагоналей d.
14. Разработайте программу, которая вычислит 500!=1*2*3*...*500. Поскольку такое большое число само по себе не может храниться в памяти компьютера, для хранения значащих цифр результата используйте массив целого типа.
15. Имеется внешний файл записей lab.zap, содержащий сведения об учениках школы. Файл формируется приведенной далее программой. Составьте программу, в которой необходимо сделать следующее:
• упорядочить файл по признаку class в порядке возрастания;
• упорядочить файл по признаку god в порядке убывания;
• упорядочить файл в алфавитном порядке.
program lab; type shcool = record fio : string[20]; class : 1 . . 11; god : integer; pol : char; end; var x:array[1..100] of shcool; n,i:integer; f:file of school; begin write('введите кол-во учеников:'); readln(n); assign(f,'lab.zap'); rewrite(f); for i:=1 to n do with x[i] do begin write('введи Ф.И.О.',i,'–ого ученика:'); readln(fio); write('класс:'); readln(class); write('год рождения:–'); readln(god); write('пол(м/ж):–'); readln(pol); write(f,x[i]); end; close(f); end.
16. Напишите программы, одна из которых выполняет "сжатие" текста (если подряд идет более 4 одинаковых символов, она должна заменить их на этот символ, разделитель # и число повторений символа) и обратное преобразование.
17. Постройте трехмерные столбчатую и круговую диаграммы для различных числовых таблиц.
18. Напишите программу, строящую графики заданных функций.
19. Создайте демонстрационную модель идеального газа в замкнутом объеме.
Лабораторная работа 1. Простые типы данных. Символьный тип. Перечисляемые и интервальные типы.
1. Дано натуральное число:
• найти сумму цифр этого числа;
• верно ли, что число начинается и заканчивается одной и той же цифрой.
2. Найти все трехзначные числа, такие что сумма цифр равна А, а само число делится на В (А и В вводятся с клавиатуры).
3. Найти количество делителей натурального числа. Сколько из них четных?
Лабораторная работа 2. Одномерные массивы.
1. Заменить максимальный по модулю отрицательный элемент нулем.
2. Заменить первые k элементов массива на противоположные по знаку.
3. Вставить в массив число k после всех элементов, кратных своему номеру (k вводить с клавиатуры).
Лабораторная работа 3. Двухмерные массивы.
1. Дан двухмерный массив размерностью 5*6, заполненный целыми числами с клавиатуры. Сформировать одномерный массив, каждый элемент которого равен произведению четных положительных элементов соответствующего столбца.
2. Дан двухмерный массив размером n*m, заполненный случайным образом. Определить, есть ли в данном массиве строка, в которой ровно два отрицательных элемента.
3. В двухмерном массиве удалить строку, содержащую наибольший элемент массива, и строку, содержащую наименьший элемент массива.
Лабораторная работа № 4. Строковый и множественный типы данных.
1. Дана последовательность слов. Напечатать все слова, предварительно выполнив преобразования их по правилу: заменить во всех словах первую букву заглавной.
2. Вывести общие русские буквы трех предложений.
3. Решить ребус:
VOLVO
![]()
F I AT
MOTOR
Лабораторная работа № 5. Комбинированный тип данных (записи).
1. Дан текстовый файл, в котором хранятся данные об учениках класса: фамилия, имя, отчество, адрес (улица, дом, квартира) и домашний телефон (если есть). Вывести на экран фамилию, имя и адрес тех учеников, до кого нельзя дозвониться.
2. Дан массив данных о работающих в фирме: фамилия, имя, отчество, адрес (улица, дом, квартира) и дата поступления на работу (месяц, год). Во второй массив записать только данные тех из них, кто на сегодняшний день проработал уже не менее 5 лет.
В предыдущем разделе, посвященном языку Паскаль, приведено немало примеров программ. Однако при анализе готовой программы чаще всего не ясно, как разработчики к ней пришли. В этой главе рассказывается об общих моментах в технологии программирования. Конечно, при разработке небольших учебных программ не все элементы данной технологии можно применить. Однако в тех случаях, когда это делается, польза от применения знаний о методах программирования несомненна.
Современный подход к проектированию программ основан на декомпозиции задачи, которая в свою очередь основана на использовании абстракций. Целью при декомпозиции является создание модулей, которые представляют собой небольшие, относительно самостоятельные программы, взаимодействующие друг с другом по хорошо определенным и простым правилам. Если эта цель достигнута, то разработка отдельных модулей может осуществляться различными людьми независимо друг от друга, при этом объединенная программа будет функционировать правильно.
Различают абстракцию через параметризацию и через спецификацию. Смысл абстракции через параметризацию в том, что одним алгоритмом можно решать задачи, отличающиеся различными исходными данными, задаваемыми как параметры. Смысл абстракции через спецификацию в том, что разными алгоритмами можно получить один и тот же искомый результат. При этом описываются результаты работы программы. Смысл обращения к программе становится ясным через анализ ее спецификации, а не самого текста программы.
Разработка любой программы или программной системы начинается с определения требований к ней для конкретного набора пользователей и заканчивается эксплуатацией системы этими пользователями.
Существуют различные подходы и технологии разработки алгоритмов и программ. Хотя программирование в значительной степени искусство, тем не менее можно систематизировать и обобщить накопленный профессиональный опыт. По современным взглядам проектирование и разработку программ целесообразно разбить на ряд последовательных этапов:
1. Постановка задачи.
2. Проектирование программы.
3. Построение модели.
4. Разработка алгоритма.
5. Реализация алгоритма.
6. Анализ алгоритма и его сложности.
7. Тестирование программы.
8. Документирование.
Кратко остановимся на каждом из этих этапов.
При постановке задачи для крупных компьютерных программ необходимо выполнить следующее:
выработать требования (свойства, качества и возможности), необходимые для решения проблемы или достижения цели (как правило, эта деятельность носит экспертный характер);
разработать спецификации, включающие:
• цель программы;
• граничные условия;
• описание функций системы;
• спецификации входных и выходных данных;
• верификационные требования (установление тестовых случаев);
• тип и количество документов.
В ходе этой работы выявляются свойства, которыми должна обладать система в конечном виде (замысел), описываются функции системы, характеристики интерфейса.
Чтобы приступить к решению задачи, необходимо точно ее сформулировать. В первую очередь, это означает определение исходных и выходных данных, т. е. ответы на вопросы: а) что дано; б) что нужно найти. Дальнейшая детализация постановки задачи представляет собой ответы на серию вопросов такого рода:
как определить решение;
каких данных не хватает и все ли они нужны; какие сделаны допущения и т. п.
Проектирование программы. Сначала производится проектирование архитектуры программной системы. Это предполагает первичную (общую) стадию проектирования и заканчивается декомпозицией спецификаций в структуру системы. Обычно на модульном уровне по каждому модулю разрабатывается спецификация модуля:
имя/цель — дается имя модулю и предложение о функции модуля с формальными параметрами;
неформальное описание — обзор действий модуля;
ссылки — какие модули ссылаются на него и на какие модули ссылается данный модуль;
вход/выход — формальные и фактические параметры, глобальные, локальные и связанные (общие для ряда модулей) переменные;
примечания — полезные комментарии общего характера по модулю.
Следующим шагом является детальное проектирование. На этом этапе происходит процедурное описание программы, выбор и оценка алгоритма для реализации каждого модуля. Входной информацией для проектирования являются требования и спецификации системы.
Для проектирования программ существуют различные подходы и методы. Современный подход к проектированию основан на декомпозиции, которая, в свою очередь, основана на использовании абстракции. Целью при декомпозиции является создание модулей, которые взаимодействуют друг с другом по определенным и простым правилам. Декомпозиция используется для разбиения программы на компоненты, которые затем могут быть объединены.
Методы проектирования архитектуры делятся на две группы: ориентированные на обработку и ориентированные на данные.
Методы, ориентированные на обработку, включают следующие общие идеи:
Модульное программирование.
Основные концепции:
• каждый модуль реализует единственную независимую функцию;
• имеет единственную точку входа/выхода;
• размер модуля минимизируется;
• каждый модуль разрабатывается независимо от других модулей;
• система в целом построена из модулей.
Исходя из этих принципов, каждый модуль тестируется отдельно, затем после кодирования и тестирования происходит их интеграция и тестируется вся система.
Функциональная декомпозиция.
Подобна стратегии "разделяй и управляй". Практически является декомпозицией в форме пошаговой детализации и концепции скрытия информации. Каждый модуль характеризуется субъективным решением проектировщика, связь осуществляется с помощью хорошо организованных интерфейсов.
Проектирование с использованием потока данных.
Использует поток данных как генеральную линию проектирования программы. Содержит элементы структурного проектирования сверху-вниз с пошаговой детализацией:
• экспертиза потоков данных и отображение графа потока данных;
• анализ входных, центральных и выходных преобразующих поток данных элементов;
• формирование иерархической структуры программы;
• детализация и оптимизация структуры программы.
Технология структурного анализа проекта.
Основана на структурном анализе с использованием специальных графических средств построения иерархических функциональных связей между объектами системы. Эффективна на ранних стадиях создания системы, когда диаграммы просты и читаемы.
Методы проектирования, основанные на использовании структур данных, описаны далее.
Методология Джексона.
Здесь структура данных — ключевой элемент в построении проекта. Структура программы определяется структурой данных, подлежащих обработке. Программа представляется как механизм, с помощью которого входные данные преобразуются в выходные. В методе предусматривается:
• разработка и изображение структуры входных и выходных данных;
• изображение структуры программы путем соединения изображений этих структурных элементов;
• определение дискретных операций над структурами данных;
• построение алгоритмов обработки структур данных.
Методология Уорнера.
Подобна предыдущей, но процедура проектирования более детализирована. Используются следующие виды представления проекта:
• диаграммы организации данных (описывают входные и выходные данные);
• диаграммы логического следования (логический поток этих данных);
• список инструкций (команды, используемые в проекте);
• псевдокод (описание проекта);
• определение входных данных системы;
• организация входных данных в иерархическую структуру;
• детальное определение формата элементов входного файла;
• то же самое для выходных данных;
• спецификация программы: чтение, ветвление, вычисление, выходы, вызовы подпрограмм;
• составление диаграммы (по типу блок-схем), указывающей логическую последовательность инструкций.
Метод иерархических диаграмм.
В этом методе определяется связь между входными, выходными данными и процессом обработки с помощью иерархической декомпозиции системы (без детализации). По сути, используются три элемента: вход, обработка, выход.
Алгоритм проектирования по этому методу заключается в следующих шагах:
• начать с наивысшего уровня абстракции, определив вход, выход, обработку;
• соединить каждый элемент входа и выхода с соответствующей обработкой;
• документировать каждый элемент системы, используя диаграммы;
• детализировать диаграммы, используя предыдущие шаги.
Объектно-ориентированная методология проектирования.
Основана на концепции упрятывания информации и абстрактных типов данных. Рассматриваются данные, модули и системы в качестве объектов.
Каждый объект содержит некоторую структуру данных с набором процедур, знающих, как работать с этими данными. По этой методологии создаются абстракции по заданной проблемной области:
• определение проблемы;
• развитие неформальной стратегии, удовлетворяющей требованиям к системе;
• формализация стратегии;
• создание объектов и их атрибутов;
• определение операций над объектами;
• установка интерфейсов;
• реализация операций.
Построение модели в большинстве случаев является непростой задачей. Чтобы приобрести опыт в моделировании, необходимо изучить как можно больше известных и удачных моделей.
При построении моделей, как правило, используют два принципа: дедуктивный (от общего к частному) и индуктивный (от частного к общему).
При дедуктивном подходе (рис. 5.2) рассматривается частный случай общеизвестной модели. Здесь при заданных предположениях известная модель приспосабливается к условиям моделируемого объекта. Например, можно построить модель свободно падающего тела на основе известного закона Ньютона
ma mg= −Fсопр
и в качестве допустимого приближения принять модель равноускоренного движения для малого промежутка времени.
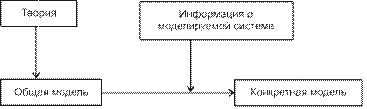
Рис. 5.2. Схема построения модели при дедуктивном способе
Индуктивный способ (рис. 5.3) предполагает выдвижение гипотез, декомпозицию сложного объекта, анализ, затем синтез. Здесь широко используется подобие, аналогичное моделирование, умозаключение с целью формирования каких-либо закономерностей в виде предположений о поведении системы.
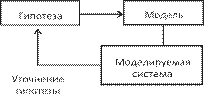
Рис. 5.3. Схема построения модели при индуктивном способе
Технология построения модели при индуктивном способе:
1. Эмпирический этап:
• умозаключение; • интуиция;
• предположение;
• гипотеза.
2. Постановка задачи для моделирования.
3. Оценки, количественное и качественное описание.
4. Построение модели.
Разработка алгоритма — самый сложный и трудоемкий процесс, но и самый интересный в творческом отношении. Выбор метода разработки зависит от постановки задачи, ее модели. На этом этапе необходимо провести анализ правильности алгоритма, что очень непросто и трудоемко. Наиболее распространенная процедура доказательства правильности алгоритма — это прогон его на множестве различных тестов. Однако это не гарантирует того, что не может существовать случая, в котором программа "не сработает". В общей методике доказательства правильности алгоритма предполагают, что алгоритм описан в виде последовательности шагов. Для каждого шага предлагается некое обоснование его правильности для всех подходящих входных (условиях до данного шага) и выходных данных (условиях после этого шага). Затем предлагается доказательство конечности алгоритма с окончательными исходными входными и выходными данными.
На этапе реализации алгоритма происходит конструирование и реализация алгоритма, включая:
кодирование;
интеграцию;
тестирование (сертификацию).
По сути, проводится перевод проекта в форму программы для конкретного компьютера, сборка системы и ее прогон при тестовых и нормальных условиях для подтверждения ее работы в соответствии со спецификациями системы. Этот этап зависит от того, какой язык программирования выбран, на каком компьютере алгоритм будет реализован. С этим связаны выбор типов данных, вводимых структур данных, связь с окружающей средой и т. п. Важно осознавать интерактивность, вид транслятора (компилятор или интерпретатор), наличие библиотек подпрограмм, модулей и объектов.
Анализ алгоритма и его сложностей необходим для оценки ресурсов компьютеров, на которых он будет работать, времени обработки конкретных данных, приспособления в работе в локальных сетях и телекоммуникациях. Хотелось бы также иметь для данной задачи количественный критерий для сравнения нескольких алгоритмов с целью выбора более простого и эффективного среди них.
Перед началом эксплуатации программы необходим этап ее отладки и тестирования.
Тестирование — это процесс исполнения программ с целью выявления (обнаружения) ошибок. Хорошим считается тест, который имеет большую вероятность обнаружения еще не выявленной ошибки. Удачным считается тест, который обнаруживает еще не выявленную ошибку. Существуют различные способы тестирования программ.
Тестирование программы как "черного ящика" (стратегия "черного ящика" определяет тестирование с анализом входных данных и результатов работы программы). Критерием исчерпывающего входного тестирования является использование всех возможных наборов входных данных.
Тестирование программы как "белого ящика" заключается в стратегии управления логикой программы, позволяет использовать ее внутреннюю структуру. Критерием выступает исчерпывающее тестирование всех маршрутов и управляющих структур программы.
Разумная и реальная стратегия тестирования — сочетание моделей "черного" и "белого" ящиков. Принципы тестирования:
описание предполагаемых значений выходных данных или результатов должно быть необходимой частью тестового набора;
тесты для неправильных и непредусмотренных входных данных следует разрабатывать так же тщательно, как для правильных и предусмотренных;
необходимо проверять не только делает ли программа то, для чего она предназначена, но и не делает ли она то, что не должна делать;
нельзя планировать тестирование в предположении, что ошибки не будут обнаружены;
вероятность наличия необнаруженных ошибок в части программы пропорциональна числу ошибок, уже обнаруженных в этой части; тестирование — процесс творческий.
При разработке программ очень полезным бывает метод "ручного тестирования" без компьютера на основе обнаружения ошибок при чтении текста.
Основные типы ошибок, встречающихся при программировании:
обращения к переменным, значения которым не присвоены или не инициализированы;
выход индексов за границы массивов;
несоответствие типов или атрибутов переменных величин;
явные или неявные проблемы адресации памяти;
ошибочные передачи управления; логические ошибки.
При проектировании процедуры тестирования предусматривают серии тестов, имеющих наивысшую вероятность обнаружения большинства ошибок. Для целей исчерпывающего тестирования создают эквивалентные разбиения входных параметров, причем предусматривают два класса: правильные входные данные и неправильные (ошибочные входные значения). Для каждого класса эквивалентности строят свой тест. Классом эквивалентности тестов можно назвать такое множество тестов, что выполнение алгоритма на одном из них гарантирует аналогичный результат прогона для других.
Особое внимание необходимо уделять тестам на граничных условиях. Граничные условия — это ситуации, возникающие непосредственно выше или ниже границ входных и выходных классов эквивалентности (т. е. вблизи границ эквивалентных разбиений). В частности, примерами классов эквивалентных тестов для алгоритма решения квадратного уравнения могут служить следующие классы: множество действительных, отличных от нуля, чисел a, b, c, таких, что b·b — 4·a·c < 0; множество чисел a = 0, b и c не равны нулю; b = 0, a и с не равны нулю и т. п.
Сам процесс тестирования может быть пошаговым и/или сплошным. В том и в другом случае используют стратегии нисходящего тестирования, — начиная с верхнего (головного) модуля и затем подключая последовательно другие модули (аппарат заглушек), и восходящего тестирования, начиная с тестирования отдельных модулей.
В процессе отладки программы используют метод трассировки — использование выводов промежуточных данных по всей программе или использование автоматических инструментов. Например, в Турбо Паскале имеется в наличии мощный аппарат автоматической отладки программ (режим DEBUG).
Есть золотое правило программистов — оформляй свои программы в том виде, в каком бы ты хотел видеть программы, написанные другими. К каждому конечному программному продукту необходимо документированное сопровождение в виде помощи (help), файлового текста (readme.txt).
При построении алгоритма для сложной задачи используют системный подход с применением декомпозиции (нисходящее проектирование сверху-вниз) и синтеза (программирование снизу-вверх). Как и при разработке структуры любой сложной системы, при формировании алгоритма используют дедуктивный и индуктивный методы.
При дедуктивном подходе рассматривается частный случай общеизвестных алгоритмических моделей. Здесь при заданных предположениях известный алгоритм приспосабливается к условиям решаемой задачи. Например, многие вычислительные задачи линейной алгебры, в частности нелинейные уравнения, системы алгебраических уравнений и т. п., могут быть решены с использованием известных методов и алгоритмов, для которых существует множество специальных библиотек подпрограмм, модулей. В настоящее время получили распространение специализированные пакеты, позволяющие решать многие задачи (Mathcad, Mathlab, Autocad и т. п.).
Индуктивный способ предполагает эвристический системный подход (декомпозиция — анализ — синтез). В этом случае не имеется универсальных методов разработки алгоритмов. Существуют подходы, позволяющие в каждом конкретном случае строить алгоритмы. Их можно разбить на методы частных целей, подъема, отрабатывания назад, ветвей и границ и т. п.
Одним из системных методов разработки алгоритмов является структурное программирование. Повторим их более формально с упором на реализацию в практическом программировании.
Структурное программирование основано на использовании блок-схем, формируемых с помощью управляющих структурных элементов. Выделяют три базовых структурных элемента (управляющие структуры): композицию, альтернативу, итерацию.
Композиция — это линейная конструкция алгоритма, составленная из последовательно следующих друг за другом функциональных вершин, рис. 5.4. begin S1; S2; end
Альтернатива — это конструкция ветвления. Конструкция ветвления в алгоритмах может быть представлена в виде развилки (рис. 5.5, а), неполной развилки (рис. 5.5, б) и выбора (рис. 5.5, в).
![]()
Рис. 5.4. Структура "композиция"
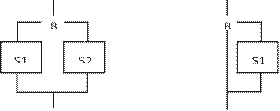
if B then S1 else S2 if B then S1 а б
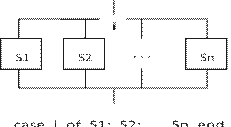
в
Рис. 5.5. Структура "альтернатива".
Здесь В — условие (логическое выражение)
Итерация — это циклическая конструкция алгоритма, которая, вообще говоря, является составной структурой, состоящей из композиции и альтернативы. Итерации могут быть представлены в двух формах: с предусловием
(рис. 5.6, а) и с постусловием (рис. 5.6, б).
Каждая из рассмотренных структур имеет один вход и один выход. Поэтому любая компьютерная программа может быть представлена блок-схемой, сформированной из представленных трех управляющих структур.

while B do S1; repeat S1 until B; а б
Рис. 5.6. Структура "итерация"
Процесс структурного программирования обычно начинается с разработки блок-схемы. Для представления алгоритма в полном и законченном виде, а также для обозначения связей с окружающей средой добавляют дополнительные структуры ввода-вывода и начала-конца программного блока, модуля, алгоритма:
![]()
![]()
Заметим, что для начального шага разработки программы чрезвычайно важным и необходимым является определение исходных (ввод) и выходных (вывод) данных задачи. С этого этапа начинается разработка практически любого алгоритма.
Метод разработки программы сверху-вниз предполагает процесс пошагового разбиения алгоритма (блок-схемы) на все более мелкие части до уровня элементарных конструкций, для которых можно составить конкретные команды. Идея структурного программирования сверху-вниз состоит в том, что если для некоторой функции f существует ее композиция через две другие функции g и h, т. е. f = h g x( ( )), то проблема разработки алгоритма для f сводится к проблемам разработки алгоритмов для h и g . В структурном программировании сверху-вниз на каждом шаге пытаются текущую функцию выразить как композицию двух (или более) других функций, которые представимы в виде рассмотренных ранее управляющих структур.
Для иллюстрации технологии структурного программирования сверху-вниз рассмотрим два примера — сначала простой, затем существенно более сложный.
Пример 1. Технология разработки программы решения квадратного уравнения.
На рис. 5.7 проиллюстрирована пошаговая детализация процесса построения алгоритма. Заметим, что для начального шага разработки программы имеем в качестве исходных данных коэффициенты a , b, c квадратного уравнения
2
ax + + =bx c 0, а на выходе — значения двух корней x1, x2.
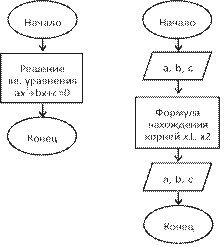
Рис. 5.7. Пошаговая детализация построения алгоритма
Пример 2. Рассмотрим более сложный и поучительный пример структурного программирования, известный в литературе как "обход конем шахматного поля". В задаче необходимо ответить на вопрос, существует ли при заданном положении шахматного коня последовательность его ходов однократного обхода всех клеток шахматного поля.
Попытка быстро ответить на этот вопрос приводит к перебору всех возможных маршрутов коня. Число вариантов перебора чрезвычайно велико, и поиск нужного маршрута лучше поручить компьютеру.
Одной из эвристических стратегий алгоритма может быть следующая. Начиная с произвольного поля i , j (на рис. 5.8 i =4, j =4), пытаемся пойти на поле *1, если невозможно, то на поле *2; при неудаче — на поле *3 и т. д. по часовой стрелке (варианты возможных ходов приведены на рис. 5.8). Сделав очередной ход на пустую клетку, запишем в нее номер очередного хода и снова осуществляем процедуру поиска нового хода. В случае, когда из очередной клетки невозможно сделать ход, прерываем маршрут и выводим результат в виде таблицы, соответствующей шахматному полю, в которой расставлены ходы коня. Очевидно, что такая стратегия лишь при удаче может дать полный обход шахматной доски конем.
Итак, исходные данные задачи — произвольные начальные координаты коня i , j от 1 до 8. Результат — возможный маршрут коня из заданного поля.
Удачным считается маршрут, содержащий все 64 хода, т. е. полный обход доски конем.
j

Рис. 5.8. Иллюстрация к задаче "обход конем шахматной доски"
Инициализация доски предполагает задание двумерного массива размером
8×8 с нулевыми элементами (рис. 5.9). В дальнейшем элемент a[i,j] принимает значения номера очередного хода. Распечатать результат — означает вывести таблицу a[1..8,1..8]. На рис. 5.10 показан один из результатов возможного маршрута коня из начального поля i=1, j=1.
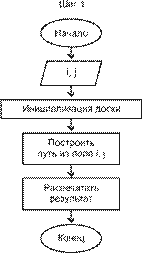
Рис. 5.9а. Пошаговая детализация построения алгоритма к примеру 2
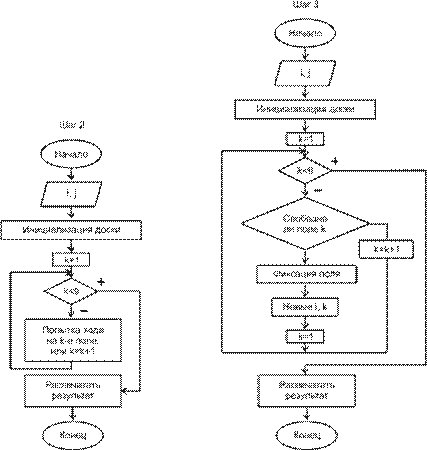
Рис. 5.9б. Пошаговая детализация построения алгоритма к примеру 2
![]()
Program Tur_Konja; var a: array[1..8,1..8] of integer; im, jm :array[1..8] of integer; i, j, k, n, inac, jnac: integer; inext, jnext: integer; begin {-----инициализация шахматной доски-----} for i:=1 to 8 do for j:=1 to 8 do a[i,j]:=0; im[1]:=–2; jm[1]:=1; im[2]:=–1; jm[2]:=2; im[3]:=1; jm[3]:=2; im[4]:=2; jm[4]:=1; im[5]:=2; jm[5]:=–1; im[6]:=1; jm[6]:=–2; im[7]:=–1; jm[7]:=–2; im[8]:=–2; jm[8]:=–1;
write('введи начальные координаты коня 0<i,j<9: '); readln(inac,jnac); a[inac,jnac]:=1; i:=inac; j:=jnac; n:=2; k:=1; while k<=8 do begin inext:=i+im[k]; jnext:=j+jm[k]; if (inext<1) or (inext>8) or (jnext<1) or
(jnext>8) or (a[inext,jnext]<>0) then k:=k+1 else begin a[inext,jnext]:=n; n:=n+1; i:=inext; j:=jnext; k:=1; end; end;
{--------вывод результата прохода--------} for i:=1 to 8 do begin writeln; writeln; for j:=1 to 8 do write(a[i,j]:2,' ') end; writeln; write('кол-во шагов = ',n–1); readln; end.
1 2 3 4 5 6 7 8
|
1 |
|
|
34 |
3 |
36 |
19 |
22 |
|
|
|
2 |
37 |
20 |
23 |
4 |
17 |
|
|
|
33 |
|
35 |
18 |
21 |
10 |
|
|
|
38 |
|
24 |
11 |
16 |
5 |
|
|
32 |
|
|
39 |
26 |
9 |
12 |
|
|
|
|
25 |
|
15 |
6 |
27 |
|
31 |
|
|
40 |
29 |
8 |
13 |
42 |
|
|
|
30 |
|
14 |
41 |
28 |
7 |
1
2
3
4
5
6
7
8
Рис. 5.10. Возможный результат маршрута коня с поля (1,1)
Зачастую используют альтернативный процедуре сверху-вниз метод структурного программирования снизу-вверх. По сути, мы приходим к конечному результату системным методом. Сначала разбиваем задачу на отдельные блоки (модули) с их связями между собой (декомпозиция), затем, после их разработки, проводим сборку блоков в единую программу (синтез). Принцип снизу-вверх широко распространен среди программистов, которые предпочитают модульный подход, предполагающий максимальное использование стандартных и специализированных библиотек процедур, функций, модулей и объектов.
Методы построения алгоритмов,
Мы уже отмечали, что правильный выбор структуры данных — залог эффективности, понятности программы, ее устойчивости по отношению к ошибкам. Структуры данных, используемых в программе, также влияют на технологию разработки алгоритма. Удачный выбор структур данных заметно облегчает построение эффективного алгоритма. Методы программирования, в которых такое влияние доминирует, называют методами, ориентированными на структуры данных.
Рассмотрим некоторые классы задач, где полезны такие структуры, как связные списки, очереди, стеки, деревья.
Сортировка массивов данных, т. е. расположение их элементов в определенном порядке, являясь одной из важнейших задач при создании информационных систем, требует больших временных затрат и ресурсов памяти компьютера. Легко представить возникающие трудности, когда в массиве данных происходят удаления и внесения новых записей. Быстродействие известных алгоритмов сортировки массивов пропорционально квадрату числа их элементов (n2). Обычные подходы заставят нас осуществлять заново сортировку измененного массива с физическими перестановками записей согласно известным процедурам упорядочивания.
Рассмотрим решение этой проблемы с помощью линейного связанного списка. Одномерный массив, требующий сортировки, преобразуют в двумерный, в котором по второму индексу (целые неотрицательные числа, называемые связями или указателями) располагают номера элементов массива.
Линейный связанный список — это конечный набор пар, состоящих из информационной части (Info) и указующей части (Link):
|
Info |
Link |
|
1 Петров |
3 |
|
2 Смирнов |
4 |
|
3 Алексеев |
1 |
|
........... |
|
|
nКузнецов |
2 |
Очевиден выигрыш такой структуры данных: теперь вместо сортировки, даже при добавлении новых элементов в середину массива, достаточно изменить лишь несколько указующих связей, оставляя сами элементы на своих местах.
Линейные связанные списки являются эффективной структурой данных для моделирования ситуаций, в которых подвергаются изменениям упорядоченные массивы элементов данных. Особенно важно их использование при процедурах внесения или удаления элементов из середины массива. Когда модификации касаются лишь начала или/и конца, то необходимость в связанных списках отпадает, и становится достаточным использование одномерного исходного массива. Здесь на помощь приходят стеки и очереди.
Пусть, например, задано арифметическое выражение. Требуется определить, правильно ли расставлены в выражении скобки.
Для решения подобных задач используют стек — уже упоминавшуюся динамическую структуру данных. В нашем случае в стек помещаются и удаляются скобки.
Первым необходимым условием правильности расстановок скобок является совпадение количества левых и правых скобок. Такой контроль легко осуществить, введя счетчик top, который при просмотре выражения и обнаружении левой скобки (допустим, что имеем только круглые скобки '(' ) увеличивается на +1. Если на очередном месте встретилась правая скобка, то значение счетчика уменьшается на 1. Тогда правильность расстановки определяется по итоговому значению top.
![]()
рrogram skobka1; (*проверка скобок по количеству*) var top, i, n: integer; slovo: string[100]; skob: string[100]; begin write('введи арифметическое выражение: '); readln(slovo); n:=length(slovo); top:=0; skob:=''; i:=1; while (i<=n) do begin if slovo[i]=')' then begin top:=top+1; skob:=skob+slovo[i] end; if slovo[i]=')' then begin top:=top–1; skob:=skob+slovo[i] end; i:=i+1 end;
writeln(skob);
if top=0 then write('выражение правильное') else write('выражение неправильное'); readln end.
Строковая переменная skob предназначена для визуализации всех имеющихся скобок в выражении.
В случае, когда в выражении используются фигурные, квадратные и круглые скобки, задача усложняется тем, что необходим еще контроль соответствия левых и правых скобок. В этой связи удобно использовать стек, в котором помещаются очередные левые скобки. При обнаружении правой скобки из вершины стека извлекается левая скобка, помещенная последней, и проводится их идентификация. Полный текст программы представлен далее.
![]()
program skobka2; (*проверка расстановок скобок*) var top, i, n: integer; slovo: string[100];
store: array[1..100] of char; x: char; skob: string[100]; p: boolean; begin
write('введи арифметическое выражение: '); readln(slovo); n:=length(slovo); top:=0; p:=true; skob:=''; i:=1; while (i<=n)and(p) do
begin if (slovo[i]='{') or (slovo[i]='[') or (slovo[i]='(') then begin top:=top+1; store[top]:=slovo[i]; skob:=skob+slovo[i] end;
if slovo[i]='}' then begin x:=store[top]; if x<>'{' then p:=false
else begin top:=top–1; skob:=skob+slovo[i] end; end;
if slovo[i]=']' then begin x:=store[top]; if x<>'[' then p:=false
else begin top:=top–1; skob:=skob+slovo[i] end; end;
if slovo[i]=')' then begin x:=store[top];
if x<>'(' then p:=false
else begin top:=top–1; skob:=skob+slovo[i] end; end; i:=i+1 end;
writeln(skob); if top=0 then write('выражение правильное') else write('выражение неправильное'); readln end.
Структура данных "очередь" используется для моделирования систем массового обслуживания: очереди людей в магазинах, транспортных потоков, производственных линий и т. п. Рассмотрим модельную ситуацию с формированием очереди в каком-нибудь учреждении сферы обслуживания, например в банке.
Пусть задана скорость поступления клиентов в банк и известна скорость обслуживания. Вместо скорости поступления клиентов будем задавать вероятность р их появления в единицу времени. За скорость обслуживания примем число v, соответствующее времени обслуживания одного клиента. Для простоты примем в качестве массива данных о клиентах банка числовой массив со случайными числами из интервала 1..100. Для формирования очереди достаточно ввести две переменные, которые указывают на начало и конец списка данных.
Следующая программа демонстрирует процесс обслуживания очереди.
![]()
program bank; uses crt; type item = integer;
var qq:array[1..100] of item; i, t, v, L, R: integer; p, x: real; st: string[10]; begin (*начальное состояние очереди*)
qq[1]:=random(100); qq[2]:=random(100); qq[3]:=random(100); L:=1; R:=3; p:=0.6; v:=2; randomize; t:=0; repeat
t:=t+1; x:=random; if x<p then begin R:=R+1; qq[R]:=random(100); end;
if (t mod v=0) then L:=L+1;
until keypressed or (R>100);
(*вывод состояния очереди на момент прерывания*) for i:=L to R do writeln(qq[i]); readln; end.
Изучая в предыдущей главе язык Паскаль, мы уже использовали понятие рекурсии. Однако оно столь важно и принципиально, что с ним следует познакомиться детальнее.
Рекурсией называют метод определения или вычисления функции, процедуры или решения задачи посредством той же функции, процедуры и т. д. Рекурсивные алгоритмы широко используют методы частных целей, подъема и отрабатывания назад. На эвристическом уровне рекурсия позволяет эффективно использовать метод проб и ошибок.
Продолжим рассмотрение примера задачи тура шахматного коня из предыдущего раздела. Приведенный там алгоритм строил возможный путь коня по простой стратегии очередного хода на свободное место по принципу часовой стрелки. Однако он не позволял гарантированно найти полный тур коня. Применим простую эвристическую модель решения задачи — в случае отсутствия возможности очередного хода осуществляется возврат коня на предыдущее поле и возобновление поиска дальнейшего маршрута по другому пути. Подобный процесс называют возвратом (или откатом). Его можно осуществлять по универсальной схеме:
procedure RETR; begin инициализация начального хода repeat выбор очередного хода if подходит then его запись; if решение не полное then RETR; if неудача then стирание хода и возврат на предыдущий until удача or нет хода end.
Подобная рекурсивная процедура и уже известный алгоритм, рассмотренный ранее, позволяют построить нужную программу. Далее представлена программа обхода шахматного поля конем для произвольного поля n×n, позволяющая отыскивать полный обход из любого начального положения. Для иллюстрации процесса поиска в глубину и в ширину с возвратами в программе в комментариях обозначены команды вывода промежуточных результатов.
![]()
program tur; var i, j, ii, jj, n, nn: integer; q: boolean; dx, dy:array[1..8] of integer; h: array[1..8,1..8] of integer;
(*рекурсивная процедура — попытка сделать ход*) procedure try(i,x,y:integer; var q:boolean); var k, u, v: integer; q1: boolean; begin k:=0; repeat k:=k+1; q1:=false; u:=x+dx[k]; v:=y+dy[k]; if ((1<=u)and(u<=n)and(1<=v)and(v<=n))and(h[u,v]=0) then begin h[u,v]:=i;
(*для отладки и наблюдения процесса поиска с возвратом*) for ii:=1 to n do begin for jj:= 1 to n do write(h[ii,jj]:5); writeln; end; readln; if i<nn then begin try(i+1,u,v,q1); if not(q1) then h[u,v]:=0 else q1:=true; end else q1:=true end; until (q1) or (k=8); q:=q1; end; (*конец процедуры*) begin dx[1]:=2; dx[2]:=1; dx[3]:=–1; dx[4]:=–2; dx[5]:=–2; dx[6]:=–1; dx[7]:=1; dx[8]:=2; dy[1]:=1; dy[2]:=2; dy[3]:=2; dy[4]:=1; dy[5]:=–1; dy[6]:=–2; dy[7]:=–2; dy[8]:=–1; write( 'введи n: '); readln(n); for i:=1 to n do for j:=1 to n do h[i,j]:=0; write( 'введи i,j : '); readln(i,j); nn:=n*n; h[i,j]:=1; try(2,i,j,q); if q then begin for i:=1 to n do begin for j:= 1 to n do write(h[i,j]:5); writeln; end; end
else writeln( 'нет маршрута'); readln end.
Для n=5 и n=6 алгоритм быстро находит искомые туры коня. Для n=8 время решения может возрасти в несколько десятков раз.
Одними из важнейших процедур обработки структурированной информации являются сортировка и поиск. Сортировкой называют процесс перегруппировки заданной последовательности (кортежа) объектов в некотором определенном порядке. Определенный порядок (например, упорядочение в алфавитном порядке, по возрастанию или убыванию количественных характеристик, по классам, типам и т. п.) в последовательности объектов необходим для удобства работы с этими объектами. В частности, одной из целей сортировки является облегчение последующего поиска элементов в отсортированном множестве. Под поиском подразумевается процесс нахождения в заданном множестве объекта, обладающего свойствами или качествами задаваемого априори эталона (или шаблона).
Очевидно, что с отсортированными (упорядоченными) данными работать намного легче, чем с произвольно расположенными. Упорядоченные данные позволяют эффективно их обновлять, исключать, искать нужный элемент и т. п. Достаточно представить, например, словари, справочники, списки кадров в неотсортированном виде, и сразу становится ясным, что поиск нужной информации является труднейшим делом, если не невозможным.
Существуют различные алгоритмы сортировки данных. И понятно, что не существует универсального, наилучшего во всех отношениях алгоритма сортировки. Эффективность алгоритма зависит от множества факторов, среди которых можно выделить основные:
числа сортируемых элементов;
степени начальной отсортированности (диапазона и распределения значений сортируемых элементов);
необходимости исключения или добавления элементов;
доступа к сортируемым элементам (прямого или последовательного).
Принципиальным для выбора метода сортировки является последний фактор. Если данные могут быть расположены в оперативной памяти, то к любому элементу возможен прямой доступ. Удобной структурой данных в этом случае выступает массив сортируемых элементов. Если данные размещены на внешнем носителе, то к ним можно обращаться лишь последовательно. В качестве структуры подобных данных можно взять файловый тип.
В этой связи выделяют сортировку двух классов объектов: массивов (внутренняя сортировка) и файлов (внешняя сортировка).
Процедура сортировки предполагает, что при наличии некоторой упорядочивающей функции F расположение элементов исходного множества меняется таким образом, что:
F
a a1 2, ,..., aN →a ak1, k2,..., akN F a( k1) ≤F a( k2) ≤ ≤... F a( kN ),
где знак неравенства понимается в смысле того порядка, который установлен в сортируемом множестве.
Поиск и сортировка являются классическими задачами теории обработки данных, решают эти задачи с помощью множества различных алгоритмов. Рассмотрим наиболее популярные из них.
Поиск. Для определенности примем, что множество, в котором осуществляется поиск, задано как массив: var a:array[0..N] of item;
где item — заданный структурированный тип данных, обладающий хотя бы одним полем (ключом), по которому необходимо проводить поиск.
Результатом поиска, как правило, служит элемент массива, равный эталону, или отсутствие такового.
Линейный поиск. Процедура заключается в простом последовательном просмотре всех элементов массива и сравнении их с эталоном Х.
i:=0; while (i<=N)and(a[i]<>X) do i:=i+1 end.
Часто бывает целесообразнее осуществлять поиск с барьером, вводя дополнительно граничный элемент массива a[N+1]:
a[N+1]:=X; i:=0; while a[i]<>X do i:=i+1 end.
Равенство i=N+1 означает, что совпадений не было, т. е. что эталонный элемент отсутствует.
Приведем пример программы поиска эталона х в массиве a[0..n].
![]()
program poisk1; (*линейный поиск*) const N=8; type item= integer; var a : array[0..n] of item; i :integer; x : item; begin
(*задание искомого массива*) for i:=0 to N do begin write('введи элемент a[ ',i, ']= '); readln(a[i]); end; writeln; write('введи эталон x= '); readln(x);
(* линейный поиск*) i:=0; while (i<=N)and(a[i]<>X) do begin i:=i+1 end;
(*вывод результата*) if i<=N then write( 'найден элемент на ',i, ' месте ') else write( 'такого элемента в массиве нет '); readln end.
Поиск делением пополам. В большинстве случаев процедура поиска применяется к упорядоченным данным (телефонный справочник, библиотечные каталоги и пр.). В подобных ситуациях эффективным алгоритмом является поиск делением пополам. В этом методе сравнение эталона Х осуществляется с элементом, расположенным в середине массива, и в зависимости от результата сравнения (больше или меньше) дальнейший поиск проводится в левой или в правой половине массива.
L:=0; R:=N; while L<R do begin m:=(L+R) div 2; if a[m]<X then L:=m+1 else R:=m; end;
Например, пусть эталонный ключ х=13, а в массиве имеются следующие элементы: a[0]=1; a[1]=3; a[2]=4; a[3]=7; a[4]=8; a[5]=9; a[6]=13; a[7]=20; a[8]=23.
Бинарный процесс поиска показан далее:
1 3 4 7 8 9 13 20 23 — элементы массива
0 1 2 3 4 5 6 7 8 — порядковые номера элементов
|
L |
|
|
m |
|
R |
|
|
L |
|
|
m |
|
R |
|
|
|
|
|
a[m]=x |
|
|
⇒ поиск закончен, и m=6 |
Программа поиска представлена далее.
![]()
program poisk2; (*поиск делением пополам*) const N=8; type item= integer; var a: array[0..n] of item; i, L, R, m:integer; x: item; f: boolean; begin
(*задание искомого массива*) for i:=0 to N do begin write( 'введи элемент a[',i, ']= '); readln(a[i]); end; writeln; write( 'введи эталон x= '); readln(x);
(*бинарный поиск*) L:=0; R:=N; f:=false; repeat m:=(L+R) div 2; if a[m]=X then f:=true; if a[m]<X then L:=m+1 else R:=m; writeln(m,L,R); until (L>=R)or(f); (*вывод результата*) if f then write('найден элемент на ',m, ' месте') else write('такого элемента в массиве нет '); readln end.
Сортировка массивов. Как и в случае поиска, определим массив данных: var a: array [0..N] of item
Важным условием сортировки массива большого объема является экономное использование доступной памяти. В прямых методах сортировки осуществляется принцип перестановки элементов "на том же месте". Далее рассмотрим три группы сортировок: с помощью включения, выбора и обмена.
Cортировка с помощью включения. Кто играл в карты, процедуру сортировки включениями осуществлял многократно. Как правило, после раздачи карт игрок, держа карты веером в руке, переставляет карты с места на место, стремясь их расположить по мастям и рангам, например сначала все тузы, затем короли, дамы и т. д. Элементы (карты) мысленно делятся на уже "готовую последовательность" и неправильно расположенную последовательность. Теперь на каждом шаге, начиная с i=2, из неправильно расположенной последовательности извлекается очередной элемент и перекладывается в готовую последовательность на нужное место.
for i:=2 to N do begin x:=a[i];
<включение x на соответствующее место готовой последовательности a[1],...,a[i]> end
Поиск подходящего места можно осуществить одним из методов поиска в массиве, описанном ранее. Затем х либо вставляется на свободное место, либо сдвигает вправо на один индекс всю левую сторону. Схематично представим алгоритм для конкретного примера:
|
Исходные элементы |
23 |
34 |
12 |
13 |
9 |
|
i=2 |
23 |
34 |
12 |
13 |
9 |
|
i=3 |
12 |
23 |
34 |
13 |
9 |
|
i=4 |
12 |
13 |
23 |
34 |
9 |
|
i=5 |
9 |
12 |
13 |
23 |
34 |
В алгоритме поиск подходящего места осуществляется как бы просеиванием х при движении по последовательности и сравнении с очередным a[j]. Затем х либо вставляется на свободное место, либо a[j] сдвигается вправо и процесс как бы "уходит" влево.
![]()
program sortirovka_1;
(*сортировка включением по линейному поиску*) const N=5; type item= integer;
var a: array[1..n] of item; i, j: integer; x: item; begin (*задание искомого массива*)
for i:=1 to N do begin write('введи элемент a[',i,']='); readln(a[i]) end;
for i:=1 to N do begin write(a[i], ' ' ); end; writeln;
(*алгоритм сортировки включением*) for i:=2 to n do begin
x:=a[i]; j:=i; a[0]:=x; (*барьер*) while x<a[j–1] do
begin a[j]:=a[j–1]; j:=j–1; end; a[j]:=x;
{for k:=1 to n do write(a[k], ' ') end; writeln;} end;
(*вывод отсортированного массива*) for i:=1 to N do begin write(a[i], ' '); end; readln; end.
В рассмотренном примере программы для анализа процедуры пошаговой сортировки можно рекомендовать использовать трассировку каждого прохода по массиву с целью визуализации его текущего состояния. В тексте программы в блоке непосредственного алгоритма сортировки в фигурных скобках находится строка, которая при удалении скобок выполнит требуемое (параметр k необходимо описать в разделе переменных — var k:integer;). Во всех последующих программах сортировки легко осуществить подобную процедуру.
Вернемся к анализу метода прямого включения. Поскольку готовая последовательность уже упорядочена, то алгоритм улучшается при использовании алгоритма поиска делением пополам. Такой способ сортировки называют методом двоичного включения.
![]()
program sortirovka_2;
(*сортировка двоичным включением*) const N=5; type item= integer; var a: array[1..n] of item; i, j, m, L, R: integer; x: item; begin
(*задание элементов массива*) for i:=1 to N do
begin write('введи элемент a[',i,']= '); readln(a[i]); end; for i:=1 to N do begin write(a[i], ' '); end;
writeln;
(*алгоритм сортировки двоичным включением*) for i:=2 to n do begin
x:=a[i]; L:=1; R:=i; while L<R do begin
m:=(L+R) div 2; if a[m]<=x then L:=m+1 else R:=m; end;
for j:=i downto R+1 do a[j]:=a[j–1]; a[R]:=x; end;
(* вывод отсортированного массива*) for i:=1 to N do begin write(a[i], ' '); end; readln; end.
Один из вариантов улучшенной сортировки включением был предложен Д. Шеллом. Его метод предполагает сначала отдельную группировку и сортировку элементов, отстоящих друг от друга на некотором расстоянии, например 4 (четвертная сортировка), после первого прохода — перегруппировку элементов таким образом, чтобы каждый элемент группы отстоял от другого на 2 номера, после двойной сортировки на третьем проходе — одинарную (обычную) сортировку.
|
Исходные элементы |
44 55 12 42 94 18 6 67 |
|
Четвертная сортировка |
44 18 6 42 94 55 12 67 |
|
Двойная сортировка |
6 18 12 42 44 55 94 67 |
|
Одинарная сортировка |
6 12 18 42 44 55 67 94 |
Каждая из сортировок основывается на алгоритме прямого включения и соответственно должна программироваться аналогично. Если для условия окончания поиска использовать барьер, а их необходимо ставить для каждой из сортировок, то необходимо расширить границы массива на несколько компонентов (барьеров) влево, т. е. использовать массив a[–r..n], где r — количество сортировок.
Сортировка с помощью прямого выбора. Алгоритм прямого выбора является одним из распространенных в силу своей простоты. Сначала определяют минимальный элемент среди всех элементов массива, затем его меняют местами с первым. Далее процесс повторяется с той лишь разницей, что минимальный ищется со второго и меняется со вторым и т. д.
1 2 3 4 5
12 15 17 11 13 i=2, min=11
11 15 17 12 13 i=3, min=12
11 12 17 15 13 i=4, min=13
11 12 13 15 17 i=5, min=15
![]()
program sortirovka_3;
(*улучшенная сортировка включением — сортировка Шелла*) const N=8; t=4; type item= integer; var a: array[–9..n] of item; i, j, k, s :integer; x: item; m: 1..t; h :array [1..t] of integer; begin
(*задание искомого массива*) for i:=1 to N do
begin write('введи элемент a[',i,']='); readln(a[i]) end;
for i:=1 to N do begin write(a[i], ' '); end; writeln;
(*алгоритм Шелла*)
h[1]:=9; h[2]:=5; h[3]:=3; h[4]:=1; for m:=1 to t do
begin k:=h[m]; s:=–k; (*барьеры для каждого шага*) for i:=k+1 to n do
begin x:=a[i]; j:=i–k; if s=0 then s:=–k; s:=s+1; a[s]:=x; while x<a[j] do begin a[j+k]:=a[j]; j:=j–k; end; a[j+k]:=x end; end;
(*вывод отсортированного массива*) for i:=1 to N do begin write(a[i], ' '); end; readln; end.
![]()
program sortirovka_4; (*сортировка прямым выбором*) const N=5; type item= integer;
var a: array[1..n] of item; i, j, k: integer; x: item; begin
(*задание искомого массива*) for i:=1 to N do
begin write('введи элемент a[', i, ']='); readln(a[i]); end;
for i:=1 to N do begin write(a[i],' '); end; writeln;
(*алгоритм прямого выбора*) for i:=1 to n–1 do
begin k:=i; x:=a[i]; (*поиск наименьшего элемента*) for j:=i+1 to n do (*и его индекса из a[i]...a[n]*) if a[j]<x then begin k:=j; x:=a[k] end;
a[k]:=a[i]; a[i]:=x; end;
(*вывод отсортированного массива*) for i:=1 to N do begin write(a[i], ' '); end; readln; end.
Сортировка с помощью обменов. Характерной чертой алгоритмов сортировки с помощью обмена является обмен местами двух элементов массива после их сравнения друг с другом. В так называемой "пузырьковой сортировке" проводят несколько проходов по массиву, в каждом из которых повторяется одна и та же процедура: сравнение двух последовательно стоящих элементов и их обмен местами в порядке меньшинства (старшинства). Подобная процедура сдвигает наименьшие элементы к левому концу массива. Название этого алгоритма связано с интерпретацией элементов как пузырей в сосуде с водой, обладающих весом соответствующего элемента (при этом массив надо представлять в вертикальном положении). При каждом проходе пузырьки всплывают до своего уровня.
![]()
program sortirovka_6;
(*сортировка прямым обменом — пузырьковая сортировка*) const N=5;
type item= integer; var a: array[1..n] of item; i, j: integer; x: item;
begin (*задание искомого массива*)
for i:=1 to N do begin write('введи элемент a[',i,']= '); readln(a[i]); end;
for i:=1 to N do begin write(a[i], ' '); end; writeln;
(*алгоритм пузырьковой сортировки*) for i:=2 to n do for j:=n downto i do begin
if a[j–1]>a[j] then begin x:=a[j–1];a[j–1]:=a[j]; a[j]:=x; end; end;
(*вывод отсортированного массива*) for i:=1 to N do begin write(a[i], ' '); end; readln; end.
Представленную программу можно легко улучшить, если учесть, что если после очередного прохода перестановок не было, то последовательность элементов уже упорядочена, т. е. продолжать проходы не имеет смысла. Читатель без труда сможет внести коррективы в программу, использовав логическую переменную, которая контролировала бы факт обмена.
Если чередовать направление последовательных просмотров, алгоритм улучшается. Такой алгоритм называют "шейкерной" сортировкой.
![]()
program sortirovka_7;
(*сортировка прямым обменом — шейкерная сортировка*) const N=5; type item= integer;
var a: array[1..n] of item; i, j, k, L, R: integer; x: item; begin (*задание искомого массива*)
for i:=1 to N do begin write('введи элемент a[',i,']='); readln(a[i]); end; for i:=1 to N do begin write(a[i],' '); end; writeln;
(*алгоритм шейкерной сортировки*) L:=2; R:=n; k:=n; repeat for j:=R downto L do begin if a[j–1]>a[j] then begin x:=a[j–1];a[j–1]:=a[j]; a[j]:=x; k:=j end; end; L:=k+1; for j:=L to R do begin if a[j–1]>a[j] then begin x:=a[j–1]; a[j–1]:=a[j]; a[j]:=x; k:=j end; end; R:=k–1; until L>R;
(*вывод отсортированного массива*) for i:=1 to N do begin write(a[i],' '); end; readln; end.
Пузырьковая сортировка является не самой эффективной, особенно для последовательностей, у которых "всплывающие" элементы находятся в крайней правой стороне. В улучшенной (быстрой) пузырьковой сортировке предлагается производить перестановки на большие расстояния, причем двигаться с двух сторон. Идея алгоритма заключается в сравнении элементов, из которых один берется слева (i=1), другой — справа (j=n). Если a[i]<=a[j], то устанавливают j=j–1 и проводят следующее сравнение. Далее уменьшают j до тех пор, пока a[i]>a[j]. В противном случае меняем их местами и устанавливаем i=i+1. Увеличение i продолжаем до тех пор, пока не получим a[i]>a[j]. После следующего обмена опять уменьшаем j. Чередуя уменьшение j и увеличение i, продолжаем этот процесс с обоих концов до тех пор, пока не станет i=j. После этого этапа возникает ситуация, когда первый элемент занимает ему предназначенное место, слева от него младшие элементы, а справа — старшие.
Далее подобную процедуру можно применить к левой и правой частям массива и т. д. Очевидно, что характер алгоритма рекурсивный. Для запоминания ведущих левого и правого элементов в программе необходимо использовать стек.
![]()
program sortirovka_8;
(*улучшенная сортировка разделением — быстрая сортировка с рекурсией*) const N=8; type item= integer; var a: array[1..n] of item; i: integer; procedure sort(L,R: integer); var i, j: integer; x, y: item; begin i:=L; j:=R; x:=a[(L+R) div 2]; repeat while a[i]<x do i:=i+1; while x<a[j] do j:=j–1; if i<=j then begin y:=a[i]; a[i]:=a[j]; a[j]:=y; i:=i+1; j:=j–1; end; until i>j; if L<j then SORT(L,j); if i<R then SORT(i,R); end; begin
(*задание искомого массива*) for i:=1 to N do begin write('введи элемент a[',i,']='); readln(a[i]); end; for i:=1 to N do begin write(a[i],' '); end; writeln;
(*алгоритм быстрой сортировки*)
SORT(1,n); (*рекурсивная процедура*) (*вывод отсортированного массива*) for i:=1 to N do begin write(a[i],' '); end; readln; end.
Сортировка файлов. Главная особенность методов сортировки последовательных файлов в том, что при их обработке в каждый момент непосредственно доступна одна компонента (на которую указывает указатель). Чаще процесс сортировки протекает не в оперативной памяти, как в случае с массивами, а с элементами на внешних носителях (винчестере, дискете и т. п).
Понять особенности сортировки последовательных файлов на внешних носителях позволит следующий пример.
Предположим, что нам необходимо упорядочить содержимое файла с последовательным доступом по какому-либо ключу. Для простоты изучения и анализа сортировки условимся, что файл формируем мы сами, используя, как и в предыдущем случае, некоторый массив данных. Его же будем применять и для просмотра содержимого файла после сортировки. В предлагаемом далее алгоритме необходимо сформировать вспомогательный файл, который позволит осуществить следующую процедуру сортировки. Сначала выбираем из исходного файла первый элемент в качестве ведущего, затем извлекаем второй и сравниваем с ведущим. Если он оказался меньше, чем ведущий, то помещаем его во вспомогательный файл, в противном случае во вспомогательный файл помещается ведущий элемент, а его замещает второй элемент исходного файла. Первый проход заканчивается, когда аналогичная процедура коснется всех последовательных элементов исходного файла. Ведущий элемент заносится во вспомогательный файл последним. Теперь необходимо поменять местами исходный и вспомогательный файлы. После n/2 проходов в исходном файле данные будут размещены в упорядоченном виде.
![]()
program sortirovka_faila_1;
{сортировка последовательного файла} const N=8; type item= integer; var a: array[1..n] of item; i,k: integer; x,y: item; f1,f2: text; {file of item}; begin
{задание искомого массива} for i:=1 to N do begin write('введи элемент a[ ',i,']='); readln(a[i]); end; writeln; assign(f1, 'dat1.dat'); rewrite(f1); assign(f2, 'dat2.dat'); rewrite(f2); {формирование последовательного файла} for i:=1 to N do begin writeln(f1,a[i]); end;
{алгоритм сортировки с использованием вспомогательного файла} for k:=1 to (n div 2) do begin {извлечение из исходного файла и запись во вспомогательный} reset(f1); readln(f1,x);
for i:=2 to n do begin readln(f1,y); if x>y then writeln(f2,y) else begin writeln(f2,x); x:=y; end; end; writeln(f2,x);
{извлечение из вспомогательного файла и запись в исходный}
rewrite(f1); reset(f2); readln(f2,x); for i:=2 to n do begin readln(f2,y); if x>y then writeln(f1,y) else begin writeln(f1,x); x:=y; end; end;
writeln(f1,x); rewrite(f2); end;
{вывод результата} reset(f1);
for i:=1 to N do readln(f1,a[i]); for i:=1 to N do begin write(a[i], ' '); end;
close(f1); close(f2); readln; end.
По сути, можно в программе обойтись без массива а[1..n]. В качестве упражнения попытайтесь создать программу, в которой не используются массивы.
Многие методы сортировки последовательных файлов основаны на процедуре слияния, означающей объединение двух (или более) последовательностей в одну, упорядоченную с помощью повторяющегося выбора элементов (доступных в данный момент). В дальнейшем (чтобы не осуществлять многократного обращения к внешней памяти) будем рассматривать вместо файла массив данных, обращение к которому можно осуществлять строго последовательно. В этом смысле массив представляется как последовательность элементов, имеющая два конца, с которых можно считывать данные. При слиянии можно брать элементы с двух концов массива, что эквивалентно считыванию элементов из двух входных файлов.
Идея слияния заключается в том, что исходная последовательность разбивается на две половины, которые сливаются вновь в одну упорядоченными парами, образованными двумя элементами последовательно извлекаемых из этих двух подпоследовательностей. Вновь повторяем деление и слияние, но упорядочивая пары, затем четверки и т. д. Для реализации подобного алгоритма необходимы два массива, которые поочередно (как и в предыдущем примере) меняются ролями в качестве исходного и вспомогательного.
Если объединить эти два массива в один, разумеется, двойного размера, то программа упрощается. Пусть индексы i и j фиксируют два входных элемента с концов исходного массива, k и L — два выходных, соответствующих концам вспомогательного массива. Направлением пересылки (сменой ролей массивов) удобно управлять с помощью булевой переменной, которая меняет свое значение после каждого прохода, когда элементы a1,..., an движутся на
место an+1,..., a2n и наоборот. Необходимо еще учесть изменяющийся на каждом проходе размер объединяемых упорядоченных групп элементов. Перед каждым последующим проходом размер удваивается. Если считать, что количество элементов в исходной последовательности не является степенью двойки (для процедуры разделения это существенно), то необходимо придумать стратегию разбиения на группы, размеры которых q и r могут не совпадать с ведущим размером очередного прохода. В окончательном виде алгоритм сортировки слиянием представлен далее.
![]()
program sortirovka_faila_2;
{сортировка последовательного файла слиянием} const N=8; type item= integer; var a: array[1..2*n] of item; i, j, k, L, t, h, m, p, q, r: integer; f: boolean; begin
{задание искомого массива} for i:=1 to N do begin write('введи элемент a[ ',i,']='); readln(a[i]); end; writeln;
{сортировка слиянием} f:=true; p:=1; repeat h:=1; m:=n; if f then begin i:=1; j:=n;k:=n+1; L:=2*n end
else begin k:=1; L:=n;i:=n+1; j:=2*n end; repeat
if m>=p then q:=p else q:=m; m:=m–q; if m>=p then r:=p else r:=m; m:=m–r; while (q<>0) and (r<>0) do begin if a[i]<a[j] then begin a[k]:=a[i]; k:=k+h; i:=i+1;q:=q–1 end else begin a[k]:=a[j]; k:=k+h; j:=j–1; r:=r–1 end; end; while r>0 do begin a[k]:=a[j]; k:=k+h; j:=j–1; r:=r–1; end; while q>0 do begin a[k]:=a[i]; k:=k+h; i:=i+1; q:=q–1; end; h:=–h; t:=k;k:=L; L:=t; until m=0; f:=not(f); p:=2*p; until p>=n; if not(f) then for i:=1 to n do a[i]:=a[i+n];
{вывод результата} for i:=1 to N do begin write(a[i], ' '); end; readln; end.
Рассмотренные два предыдущих примера иллюстрируют большие проблемы сортировки внешних файлов, если в них часты изменения элементов, например удаления, добавления, корректировки существующих.
В подобных ситуациях эффективными становятся алгоритмы, в которых обрабатываемые элементы представляются в виде структур данных, удобных для поиска и сортировки. В качестве структур данных можно отметить, в частности, линейные списки, очереди, стеки, деревья и т. п. О них было рассказано в предыдущем разделе.
1. Каковы основные этапы проектирования и разработки программы?
2. Что означает хорошо сформулированная постановка задачи?
3. Назовите методологии проектирования и разработки программ.
4. Как выбрать модель задачи?
5. Что такое тестирование программы?
6. Постройте группу тестов для алгоритма решения системы линейных уравнений.
7. Как в общем случае формулируется задача поиска, сортировки?
8. Почему внутренняя и внешняя сортировки реализуются разными мето- дами?
9. В чем состоят принципы линейного поиска, поиска делением пополам?
10. Какие вы знаете методы внутренней сортировки?
11. Как соотносятся эффективности различных методов сортировки мас- сивов?
12. В чем состоит принцип метода слияния упорядоченных файлов?
13. Разработайте программу упорядочивания списка группы студентов:
• методом прямого включения;
• методом выбора;
• методом обмена.
1. Алгоритмы поиска и сортировки.
2. Управление программными проектами.
3. Проектирование и разработка больших программных проектов.
4. Дисциплина программирования.
5. Искусство и дисциплина программирования.
6. Доказательство правильности программ.
1. Каковы наиболее сложные программы, созданные человеком?
2. От чего в большей степени зависит развитие программирования: от развития архитектуры компьютеров или от развития языков программирования и методов управления программными проектами?
1. Разработайте алгоритм и программу расстановки ферзей на шахматном поле таким образом, чтобы ни один из них не бил другого.
2. Разработайте программу игры "Ханойские башни".
3. Предложите другие модификации алгоритма полного обхода шахматной доски конем.
4. Какое наименьшее число ферзей можно расставить на доске так, чтобы они держали под боем все ее свободные поля? Модификация задачи. Найти расстановку ферзей, которая одновременно решает задачу для досок 9*9, 10*10 и 11*11.
5. Расставить на доске N * N ( N≤12 ) N ферзей так, чтобы наибольшее число ее полей оказалось вне боя ферзей.
6. Расставить на доске как можно больше ферзей так, чтобы при снятии любого из них появлялось ровно одно не атакованное поле.
7. За какое наименьшее число ходов ферзь может обойти все поля доски 8*8?
8. Расставить на доске 8*8 максимальное число ферзей так, чтобы каждый из них нападал ровно на p ( p≤2 ) ферзей. (Ответ. При p=1 десять, а при p=2 четырнадцать.)
9. Задача о коне Аттилы ("Трава не растет там, где ступил мой конь!"). На шахматной доске стоят белый конь и черный король. Некоторые поля доски считаются "горящими". Конь должен дойти до неприятельского короля, повергнуть его и вернуться на исходное место. При этом ему запрещено становиться как на горящие поля, так и на поля, которые уже пройдены.
10. Магараджа — это фигура, которая объединяет ходы коня и ферзя. Для доски 10*10 найти способ расстановки 10 мирных магараджей.
11. Пронумеровать позиции в матрице (таблице) размером 5*5 следующим образом. Номер i (1≤ ≤i 25 ) соответствует позиции с координатами (x,y), вычисляемыми по одному из следующих правил:
• (z,w)=(x±3,y); • (z,w)=(x,y±3);
• (z,w)=(x±2,y±2).
Требуется:
• написать программу, которая последовательно нумерует позиции матрицы 5*5 при заданных координатах позиции, в которой поставлен номер 1 (результаты должны быть представлены в виде заполненной матрицы);
• вычислить число всех возможных расстановок номеров для всех начальных позиций, расположенных в правом верхнем треугольнике матрицы, включая ее главную диагональ.
1. Используя принцип проектирования сверху-вниз, постройте блок-схему и программу для решения системы линейных алгебраических уравнений методом Гаусса.
2. Разработайте алгоритм и программу поиска тура коня по другой стратегии, например по случайному выбору очередного хода из числа возможных.
3. Постройте программу упорядочивания списка фамилий учащихся вашего класса с использованием линейного списка.
4. С помощью стека организуйте алгоритм, который определяет, является ли заданное слово палиндромом ("перевертышем").
5. Придумайте и решите задачу на использование очереди.
Язык программирования Си — это универсальный язык с богатым набором операторов и компактным способом записи выражений. Благодаря гибкости, выразительности и компактности своих конструкций Си завоевал наибольшую популярность в среде профессиональных программистов и широко используется при разработке системных и прикладных программ.
Язык Си представляет собой удачный компромисс между желанием располагать теми возможностями, которые обычно предоставляют программисту столь понятные и удобные языки высокого уровня, и стремлением эффективно использовать особенности компьютера. Кроме набора средств, присущих современным языкам программирования высокого уровня (структурность, модульность, определяемые типы данных), в него включены средства для программирования "почти" на уровне ассемблера (использование указателей, побитовые операции, операции сдвига). Большой набор операторов позволяет писать компактные и эффективные программы. Однако такие мощные средства требуют от программиста осторожности, аккуратности и хорошего знания языка со всеми его преимуществами и недостатками. В отличие от языков программирования типа Паскаль, требующих жесткой дисциплины программирования, ограничивающих свободу программиста, содействующих устранению многих ошибок в программах еще на стадии их трансляции, язык Си предоставляет программисту наибольшую свободу. Однако ответственность за корректность программ при этом полностью ложится на програм- миста.
Си был создан Деннисом Ритчи как инструмент для разработки операционной системы UNIX и реализован в рамках этой операционной системы. Название языка имеет случайное происхождение: "С" — третья буква английского алфавита. Это наименование говорит о чувстве юмора у создателей языка — его предшественником был язык B ("В" — вторая буква английского алфавита).
В настоящее время имеется большое количество систем программирования на Си для разных типов компьютеров. Разработано много библиотек модулей, инструментальных средств разработки и отладки, облегчающих создание новых программ. Программы на Си обладают высокой мобильностью, без каких-либо изменений они переносятся, транслируются и выполняются на машинах различных типов.
Язык Си — компилирующего типа. Текст программы на Си, подготовленный с помощью текстового редактора, для получения объектного модуля обрабатывается компилятором, причем компиляция выполняется в два прохода. При первом проходе (претрансляции) обрабатываются строки-директивы, начинающиеся со знака #, при втором — транслируется текст программы и создается объектный (машинный) код. Для получения загрузочного (исполняемого) модуля теперь необходимо отредактировать внешние связи объектного модуля — подсоединить к нему соответствующие библиотечные модули.
Рассмотрим простую программу на языке Си. Такой пример позволит нам выявить некоторые основные черты любой программы, написанной на языке Си.
![]()
#include <stdio.h>
main() /* Простая программа */
{ int num; num = 1;
printf ("Это моя %d-я программа на языке Си.\n",num);
}
Результат выполнения программы:
Это моя 1-я программа на языке Си.
Поясним строки этой программы:
#include <stdio.h>
Подключение файла stdio.h, который является частью пакета, имеющегося в любом компиляторе языка Си и описывающего функции ввода/вывода (например, средства взаимодействия программы с терминалом). В качестве имени файла используется аббревиатура английских слов: STandard Input/Output header — стандартный заголовок ввода/вывода. Данная строка не является оператором языка Си. Символ # указывает, что она должна быть обработана "препроцессором" компилятора. Препроцессор осуществляет некоторую предварительную обработку текста программы перед началом компиляции.
main()
Имя функции (в переводе с английского main — "главная"). Любая программа, написанная на языке Си, состоит из одной или более "функций", являющихся модулями, из которых она собирается. Данная программа состоит из одной функции main. Круглые скобки указывают именно на то, что main() — имя функции. Программа, написанная на языке Си, всегда начинает выполняться с функции, называемой main(). У программиста есть возможность выбирать имена для всех используемых им функций, кроме main. В круглых скобках в общем случае содержится информация (параметры), передаваемая этой функции. В нашем примере параметры не требуются и, следовательно, в скобках ничего не содержится.
/* Простая программа */
Комментарий. Использование комментариев облегчает процесс понимания программы любым программистом. Большим удобством при написании комментариев является возможность располагать их в той же строке, что и операции, которые они объясняют. Длинный комментарий может помещаться в отдельной строке или даже занимать несколько строк. Все, что находится между символом, указывающим начало комментария /*, и символом, указывающим его конец */, игнорируется компилятором, поскольку он не в состоянии интерпретировать язык, отличный от Си.
{ }
Фигурные скобки отмечают начало и конец тела функции. Фигурные скобки применяются также для того, чтобы объединить несколько операторов программы в сегмент или "блок".
int num;
Оператор описания. С помощью такого оператора мы объявляем, что будем использовать в программе переменную num, которая принимает целые (int) значения.
Точка с запятой в конце строки является частью оператора языка Си, а не разделителем операторов, как в Паскале.
Слово int служит "ключевым словом", определяющим один из основных типов данных языка Си. Ключевыми словами называются специальные зарезервированные слова, используемые для построения фраз языка.
В языке Си все переменные должны быть объявлены. Это означает, что, вопервых, в начале программы необходимо привести список всех используемых переменных, а во-вторых, необходимо указать тип каждой из них. Вообще объявление переменных считается "хорошим стилем" программирования.
num=1;
Оператор присваивания. Служит для присваивания переменной num значения 1.
printf("Это моя %d-я программа на языке Си.\n",num);
Вызов функции printf() форматного вывода на печать. Этот оператор выводит на печать значение переменной num в формате, содержащемся в строке в кавычках (в данном случае печатается приведенная в кавычках фраза). Символы %d указывают компилятору, где в выводимой строке и в какой форме необходимо вставить значение переменной num. Символ % сигнализирует программе, что, начиная с этой позиции, необходимо вывести значение переменной, а d указывает, что число надо печатать в десятичном формате.
Символы \n не появляются на экране. Эти символы служат директивой для начала новой строки на устройстве вывода. Комбинация символов \n на самом деле представляет собой один символ, называемый "новая строка". Для этого символа (\n) не существует соответствующей клавиши на клавиатуре. Символ "новая строка" служит примером управляющей последовательности, которую невозможно ввести с клавиатуры.
В общем случае обращение к этой функции имеет вид: printf(<формат>,<выражение1>,<выражение2>,...,<выражениеN>);
где <выражение1>, <выражение2>, ..., <выражениеN> — произвольные выражения, результаты которых надо вывести.
Управляющая строка "формат" содержит объекты двух типов: обычные символы, которые просто копируются в выходной поток (печатаются), и спецификации преобразования значений из внутреннего машинного представления в текстовое для вывода на печатающем устройстве.
Каждая спецификация преобразования начинается с символа % и заканчивается символом преобразования. Между % и символом преобразования могут (не обязательно) находиться:
знак минус, указывающий, что преобразуемый параметр должен быть выровнен влево в своем поле;
целое число, задающее минимальный размер поля; преобразованный параметр будет напечатан в поле указанного размера; а если в преобразованном параметре символов меньше, чем размещается в указанном поле, то слева будут добавлены пробелы (или справа, если указано выравнивание влево);
строка цифр с начальным нулем — лишние позиции поля заполняются нулями, а не пробелами;
точка, отделяющая размер поля от последующей строки цифр (только для преобразования строк %s) — строка цифр указывает максимальное число символов, выводимых в одной строке.
Символы преобразования:
d — десятичное число со знаком;
u — десятичное число без знака;
o — восьмеричное число без знака (и без ведущего 0);
x — шестнадцатеричное число без знака (и без ведущего 0);
s — символьная строка;
c — одиночный символ;
f — действительное число в представлении с фиксированной точкой;
e — действительное число в экспоненциальном представлении;
g — наиболее короткое представление действительного числа; и др.
Функцией ввода, аналогичной функции вывода printf(), является scanf() — стандартная функция форматного ввода. Обращение к этой функции имеет вид scanf(<формат>,<&имя1>,<&имя2>,...,<&имяN>);
где <имя1>, <имя2>, ..., <имяN> — имена переменных, значения которых надо ввести. Наличие символа & перед каждым именем обязательно (кроме переменных строкового типа), его смысл будет пояснен далее.
При обращении к функции scanf выполнение программы приостанавливается, ожидается ввод значений указанных переменных, после чего работа программы продолжается.
В качестве спецификаций в формате можно использовать те же символы, что и в функции printf(). Спецификации формата должны соответствовать количеству и типу вводимых переменных. В управляющей строке функции scanf нет промежуточных управляющих символов между % и символом преобразования, за исключением *. Если присутствует символ *, входное поле просто пропускается и никакого присваивания не производится. Обычные символы (кроме %) сопоставляются с очередными (отличными от символов промежутков) символами входного потока, и, в случае отличия, дальнейший ввод игнорируется.
![]()
#include <stdio.h> main() { int data,month,year; char name[15],town[15]; printf("Как вас зовут? "); scanf("%s",name); printf("Укажите дату, месяц и год вашего рождения.\nДата:"); scanf("%d",&data); printf("Месяц(числом):"); scanf("%d",&month); printf("Год:"); scanf("%d",&year); printf("А в каком городе? "); scanf("%s",town); printf("Вот мы и познакомились...\n"); printf("Вас зовут %s ",name); printf("Вы родились в городе %s (%d.%d.%d)",town,data, month,year); }
Результат работы программы:
Как вас зовут? Иван
Укажите дату, месяц и год вашего рождения.
Дата : 23
Месяц (номером) : 02
Год : 1054
А в каком городе? Новгород Вот мы и познакомились...
Вас зовут Иван
Вы родились в городе Новгород
(23.02.1054)
Перечислим основные символы языка Си, образующие его алфавит:
строчные латинские буквы:
a b c d e f g h i j k l m n o p q r s t u v w x y z прописные латинские буквы:
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
арабские цифры:
0 1 2 3 4 5 6 7 8 9 специальные символы:
* звездочка ( круглая скобка левая
+ плюс ) круглая скобка правая
– минус < меньше
/ дробная черта > больше
% процент \ обратная дробная черта
! восклицательный знак ^ стрелка вверх
= знак равенства [ квадратная скобка левая
? вопросительный знак ] квадратная скобка правая
: двоеточие # номер
; точка с запятой { фигурная скобка левая
& коммерческое "и" (амперсанд) } фигурная скобка правая
' апостроф | вертикальная черта
. точка ~ черта сверху (тильда)
, запятая " кавычки
_ подчеркивание пробел
управляющие символы:
\t горизонтальная табуляция
\n перевод строки и возврат каретки
\r возврат каретки
\f перевод страницы
\b возврат на шаг (на один символ)
Множество основных символов расширено буквами русского алфавита (строчными и прописными). Они могут быть использованы только в комментариях, символьных константах и строках.
Лексемами называют последовательности символов языка (идентификаторы, служебные слова, константы, строки, составные знаки операций, разделители). Лексемы разделяются пробелами и другими неграфическими символами языка.
Идентификатор — это последовательность латинских букв, цифр и символа "_", начинающаяся с буквы или символа "_".
Прописные и строчные латинские буквы считаются различными! Например, y и Y — это разные имена. Рекомендуется в именах переменных использовать только строчные буквы.
Примеры правильных идентификаторов: schetchik get_line a12 Param1 _ab Примеры неправильных идентификаторов:
%ab 12abc —x вася
Литералы — это неизменяемые объекты языка (константы). Литерал может быть числовым, символьным или строковым. Числовые литералы могут быть десятичными (целыми и вещественными, простыми и длинными), восьмеричными, шестнадцатеричными.
Примеры:
/* Целые десятичные литералы */
57 3200000l /* длинный */ 2e3 5E3
/* Вещественные десятичные литералы */
0.00 5.3 7.1e–3 6.34E–2 .21e+56
Лидирующий нуль (0) указывает на числовой восьмеричный литерал:
030 /* Десятичное 24 */
040 /* Десятичное 32 — символ пробел */
Лидирующий 0x указывает на числовой шестнадцатеричный литерал:
0x22 /* Десятичное 34 — символ "*/
0x6С /* Десятичное 108 — символ i */
Символьный литерал — это один символ, заключенный в одинарные кавычки: 'c', '*', 'q'.
"\007" /* Звонок, восьмеричный код после \ */
"\x0a" /* Перевод на новую строку, шестнадцатеричный код после \x */
Последовательность символов, заключенных в двойные кавычки, называется строковым литералом.
Примеры:
"STRING\n"
"" /* Строчный литерал состоит из одного символа "\0" */
"Очень,"\
"очень,"\
"очень длинный строковый литерал!"
Следующие зарезервированные служебные (ключевые) слова языка запрещено использовать в качестве идентификаторов:
|
auto — автоматический; |
default |
— по умолчанию; |
|
break — завершить; |
do |
— выполнить; |
|
case — вариант; |
double |
— двойной точности; |
|
char — символьный; |
else |
— иначе; |
|
continue — продолжить; |
entry |
— вход; |
|
extern — внешний; |
short |
— короткий; |
|
for — для; |
sizeof |
— размер; |
|
float — плавающее; |
static |
— статический; |
|
goto — перейти; |
struct |
— структура; |
|
if — если; |
switch |
— переключатель; |
|
int — целое; |
typedef |
— определение типа; |
|
long — длинное; |
union |
— объединение; |
|
register — регистровый; |
unsigned |
— без знака; |
|
return — возврат; |
while |
— пока. |
Типы данных. Программа на процедурных языках, к которым относится Си, представляет собой описание операций над величинами различных типов. Тип определяет множество значений, которые может принимать величина, и множество операций, в которых она может участвовать.
В языке Си типы связаны с именами (идентификаторами) величин, т. е. с переменными. С переменной в языке Си связывается ячейка памяти. Тип переменной задает размер ячейки, способ кодирования ее содержимого, допустимые преобразования над значением данной переменной. Все переменные должны быть описаны до их использования. Каждая переменная должна быть описана только один раз.
Описание состоит из спецификатора типа и следующего за ним списка переменных. Переменные в списке разделяются запятыми. В конце описания ставится точка с запятой.
Примеры описаний:
char a,b; /* Переменные a и b имеют тип char */ int x; /* Переменная x — типа int */
char sym; /* Описана переменная sym типа char; */ int count,num; /* num и count типа int */
Переменным могут быть присвоены начальные значения внутри их описаний. Если за именем переменной следует знак равенства и константа, то эта константа служит в качестве инициализатора.
Примеры:
char backch = '\0'; int i = 0;
Рассмотрим основные типы в языке Си.
int — целый ("integer"). Значения этого типа — целые числа из некоторого ограниченного диапазона (обычно от –32 768 до 32 767). Диапазон определяется размером ячейки для типа и зависит от конкретного компьютера. Кроме того, имеются служебные слова, которые можно использовать с типом int: short int (от short integer — короткое целое), unsigned int (от unsigned integer — целое без знака), long int (длинное целое), они сокращают или, наоборот, расширяют диапазон представления чисел.
char — символьный ("character"). Допустимое значение для этого типа — один символ (не путать с текстом!). Символ записывается в апострофах.
Примеры:
'x' '2' '?'
В памяти компьютера символ занимает один байт. Фактически хранится не символ, а число — код символа (от 0 до 255). В специальных таблицах кодировки указываются все допустимые символы и соответствующие им коды.
В языке Си разрешается использовать тип char как числовой, т. е. производить операции с кодом символа, применяя при этом спецификатор целого типа в скобках — (int).
float — вещественный (с плавающей точкой). Значения этого типа — числа, но, в отличие от char и int, не обязательно целые.
Примеры:
12.87 –316.12 –3.345e5 12.345e–15
double — вещественные числа двойной точности. Этот тип аналогичен типу float, но имеет значительно больший диапазон значений (например, для системы программирования Borland C от 1.7E–308 дo 1.7E+308 вместо диапазона от 3.4E–38 дo 3.4E+38 для типа float). Однако увеличение диапазона и точности представления чисел ведет к снижению скорости выполнения программ и неэкономному использованию оперативной памяти компьютера.
Обратите внимание на отсутствие в этом списке строкового типа. В языке Си нет специального типа, который можно было бы использовать для описания строк. Вместо этого строки представляются в виде массива элементов типа char. Это означает, что символы в строке будут располагаться в соседних ячейках памяти.
Необходимо отметить, что последним элементом массива является символ \0. Это "нуль-символ", и в языке Си он используется для того, чтобы отмечать конец строки. Нуль-символ не цифра 0; он не выводится на печать и в таблице кодов ASCII имеет номер 0. Наличие нуль-символа означает, что количество ячеек массива должно быть, по крайней мере, на одну больше, чем число символов, которые необходимо размещать в памяти.
Приведем пример использования строк.
![]()
#include <stdio.h> main() {
char string[31]; scanf("%s",string); printf("%s",string);
}
В этом примере описан массив из 31 ячейки памяти, в 30 из которых можно поместить один элемент типа char. Он вводится при вызове функции scanf("%s",string);. "&" отсутствует при указании массива символов.
Указатели. Указатель — некоторое символическое представление адреса ячейки памяти, отведенной для переменной.
Например, &name — указатель на переменную name.
Здесь & — операция получения адреса. Фактический адрес — это число, а символическое представление адреса &name является константой типа "указатель".
В языке Си имеются и переменные типа указатель. Точно так же, как значением переменной типа char является символ, а значением переменной типа int — целое число, значением переменной типа указатель служит адрес некоторой величины.
Если мы дадим указателю имя ptr, то сможем написать такой оператор: ptr = &name; /* присваивает адрес name переменной ptr */
Мы говорим в этом случае, что prt "указатель на" name. Различие между двумя формами записи: ptr и &name — в том, что prt — это переменная, в то время как &name — константа. В случае необходимости можно сделать так, чтобы переменная ptr указывала на какой-нибудь другой объект: ptr = &bah; /* ptr указывает на bah, а не на name */
Теперь значением переменной prt является адрес переменной bah.
Предположим, мы знаем, что в переменной ptr содержится ссылка на переменную bah. Тогда для доступа к значению этой переменной можно воспользоваться операцией "косвенной адресации" *: val = *ptr; /* определение значения, на которое указывает ptr */ Последние два оператора, взятые вместе, эквивалентны следующему: val = bah;
Итак, когда за знаком & следует имя переменной, результатом операции является адрес указанной переменной; &nurse дает адрес переменной nurse; когда за знаком * следует указатель на переменную, результатом операции является величина, помещенная в ячейку памяти с указанным адресом.
Пример:
nurse = 22; ptr = &nurse; /* указатель на nurse */ val = *ptr;
Результат — присваивание значения 22 переменной val.
Недостаточно сказать, что некоторая переменная является указателем. Кроме этого необходимо сообщить, на переменную какого типа ссылается данный указатель. Причина заключается в том, что переменные разных типов занимают различное число ячеек памяти, в то время как для некоторых операций, связанных с указателями, требуется знать объем отведенной памяти.
Примеры правильного описания указателей: int *pi; char *pc;
Спецификация типа задает тип переменной, на которую ссылается указатель, а символ * определяет саму переменную как указатель. Описание вида int *pi; говорит, что pi — это указатель, и что *pi — величина типа int.
В языке Си предусмотрена возможность определения имен типов данных. Любому типу данных с помощью определения typedef можно присвоить имя и использовать это имя в дальнейшем при описании объектов. Формат: typedef <cтарый тип> <новый тип> Пример: typedef long LARGE; /* определяется тип large, эквивалентный типу long */ Имена производного типа рекомендуется записывать прописными буквами, чтобы они выделялись в тексте программы.
Определение typedef не вводит каких-либо новых типов, а только добавляет новое имя для уже существующего типа. Описанные таким способом переменные обладают точно теми же свойствами, что и переменные, описанные явно. Переименование типов используется для введения осмысленных или сокращенных имен типов, что повышает понятность программ, и для улучшения переносимости программ (имена одного типа данных могут различаться на разных компьютерах).
Операции. Язык Си отличается большим разнообразием операций (более 40). Здесь мы рассмотрим лишь основные из них, табл. 5.4.
Арифметические операции. К ним относят:
сложение (+),
вычитание (бинарное) (–),
умножение (*),
деление (/),
остаток от деления нацело (%), вычитание (унарное) (–) .
В языке Си принято правило: если делимое и делитель имеют тип int, то деление производится нацело, т. е. дробная часть результата отбрасывается.
Как обычно, в выражениях операции умножения, деления и нахождения остатка выполняются раньше сложения и вычитания. Для изменения порядка действий используют скобки.
![]()
#include <stdio.h> main() { int s; s = –3 + 4 * 5 — 6; printf("%d\n",s); s = 3 + 4%5 — 6; printf("%d\n",s); s = –3 * 4% — 6/5; printf("%d\n",s); s= (7 + 6)%5/2; printf("%d\n",s);
}
Результат выполнения программы: 11 1 0 1
Таблица 5.4. Старшинство и порядок выполнения операций
|
Приоритет |
Операция |
Название |
Порядок выполнения |
|
Высший |
() |
Круглые скобки |
Слева направо |
|
|
[] |
Квадратные скобки |
Слева направо |
|
|
++ |
Увеличение |
Справа налево |
|
|
-- |
Уменьшение |
Справа налево |
|
|
(тип) |
Приведение |
Справа налево |
|
|
* |
Содержимое |
Справа налево |
|
1 |
& |
Адрес |
Справа налево |
|
|
– |
Унарный минус |
Справа налево |
|
|
! |
Логическое "НЕ" |
Справа налево |
|
|
\~ |
Инверсия битов |
Справа налево |
|
|
sizeof |
Размер объекта |
Справа налево |
|
|
* |
Умножение |
Слева направо |
|
2 |
\ |
Деление |
Слева направо |
|
|
% |
Остаток |
Слева направо |
|
3 |
+ |
Сложение |
Слева направо |
|
|
– |
Вычитание |
Слева направо |
|
4 |
>> |
Сдвиг вправо |
Слева направо |
|
|
<< |
Сдвиг влево |
Слева направо |
|
|
> |
Больше |
Слева направо |
|
5 |
>= |
Больше или равно |
Слева направо |
|
|
< |
Меньше |
Слева направо |
|
|
<= |
Меньше или равно |
Слева направо |
|
6 |
== |
Равно |
Слева направо |
|
|
!= |
Не равно |
Слева направо |
|
7 |
& |
Битовое "И" |
Слева направо |
|
8 |
~ |
Битовое исключающее "ИЛИ" |
Слева направо |
|
9 |
| |
Битовое "ИЛИ" |
Слева направо |
|
10 |
&& |
Логическое "И" |
Слева направо |
Таблица 5.4 (окончание)
|
Приоритет |
Операция |
Название |
Порядок выполнения |
|
11 |
|| |
Логическое "ИЛИ" |
Слева направо |
|
|
= |
Операция присваивания |
Справа налево |
|
|
+= |
Справа налево |
|
|
12 |
–= |
Специальная |
Справа налево |
|
|
*= |
форма |
Справа налево |
|
|
/= |
операции |
Справа налево |
|
|
%= |
присваивания |
Справа налево |
В программировании часто встречаются ситуации, когда надо увеличить или уменьшить значение некоторой переменной на 1. Для этого обычно выполняется оператор присваивания вида: s=s+1;.
В языке Си для таких действий существуют специальные операции:
увеличение (++);
уменьшение (––).
Следующие записи на языке Си являются эквивалентными: i=i+1; и i++; j=j–1; и j––;
Символы "++" или "––" записываются после имени переменной или перед ним.
Пример:
s++; /* s увеличить на единицу */ t––; /* t уменьшить на единицу */ ++a; /* a увеличить на единицу */
––b; /* b уменьшить на единицу */
Как и обычные присваивания, увеличение и уменьшение можно использовать в выражениях. При этом существенно, с какой стороны от имени стоит знак "++" или "––". Если знак стоит перед переменной (в этом случае говорят о префиксной форме операции), то сначала выполняется увеличение (уменьшение) значения переменной, а лишь затем полученный результат используется в выражении. Если же знак стоит после переменной (постфиксная форма операции), то в выражении используется старое значение переменной, которое затем изменяется.
Пример:
int i, j, s;
i=j=2; /* i и j получают значение 2 */ s=(i++)+(++j);
После выполнения этих действий переменные имеют такие значения: i=3; j=3; s=5;
Операции увеличения ++ и уменьшения –– можно применять только к переменным, выражения типа s=(i+j)++ являются незаконными! Кроме того, не рекомендуется:
применять операции увеличения или уменьшения к переменной, присутствующей в более чем одном аргументе функции;
применять операции увеличения или уменьшения к переменной, которая входит в выражение более одного раза.
Операции отношения и логические операции:
больше или равно (>=);
больше (>);
меньше или равно (<=);
меньше (<);
равно (==);
не равно (!=);
логическое "и"(&&);
логическое "или"(||); отрицание "не" (!).
Логическое значение "ложь" представляется целым нулевым значением, а значение "истина" представляется любым ненулевым значением.
Выражения, связанные логическими операциями && и ||, вычисляются слева направо, причем вычисление значения выражения прекращается сразу же, как только становится ясно, будет ли результат истинным или ложным.
Старшинство операции && выше, чем у операции ||.
![]()
#include <stdio.h> main()
{ int x, y, z; x=1; y=1; z=0; x=x&&y||z; printf("%d\n",x); x=x||!y&&z; printf("%d\n",x); x=y=1; z=x++–1; printf("%d\n",x);printf("%d\n",z); z+=–x++ + ++y; printf("%d\n",x); printf("%d\n",z); z=x/++x; printf("%d\n",x); printf("%d\n",z);
}
Результат выполнения программы: 1 1 2 0 3 0 4 1
Битовые операции:
битовое "и" (&);
битовое "или" (|);
битовое исключающее "или" (~);
сдвиг влево (<<);
сдвиг вправо (>>);
инверсия битов (унарная операция) (\~).
![]()
#include <stdio.h> main() { int y, x, z, k; x=03; y=02; z=01; k=x|y&z; printf("%d\n",k); k=x|y&~z; printf("%d\n",k); k=x^y&~z; printf("%d\n",k); k=x&y&&z; printf("%d\n",k); x=1; y=–1; k=!x|x; printf("%d\n",k); k=–x|x; printf("%d\n",k); k=x^x; printf("%d\n",k); x<<=3; printf("%d\n",x); y<<=3; printf("%d\n",y); y>>=3; printf("%d\n",y);
}
После выполнения программы получаем следующие результаты:
3 3 1 1 1 –1 0 8 –8 8 1 9 1
Выражения. Конструкции, включающие константы (литералы), переменные, знаки операций, скобки для управления порядком выполнения операций, обращения к функциям, называют выражениями.
Если в выражениях встречаются операнды различных типов, то они преобразуются к общему типу в соответствии с определенными правилами:
переменные типа char интерпретируются как целые без знака (unsigned);
переменные типа short автоматически преобразуются в int; если один из операндов имеет тип unsigned, то другой (другие) также преобразуется к типу unsigned и результат имеет тип unsigned;
если один из операндов имеет тип int, то другой (другие) также преобразуется к типу int и результат имеет тип int;
если один из операндов имеет тип char, то другой (другие) также преобразуется к типу char и результат имеет тип char;
во время операции присваивания значение правой части преобразуется к типу левой части, который и становится типом результата;
в процессе преобразования int в char лишние старшие 8 бит просто отбрасываются.
Кроме того, существует возможность точно указывать требуемый тип данных, к которому необходимо привести некоторую величину (в скобках перед этой величиной). Скобки и имя типа вместе образуют операцию, называемую приведением типов. Например: z=(int)x+(int)y;
Операторы служат основными строительными блоками программы. В языке Си указанием на наличие оператора служит символ "точка с запятой", стоящий в конце него.
Операторы состоят из выражений. Выражение представляет собой объединение операций и операндов. Операндом называется то, над чем выполняется операция.
Общий вид оператора присваивания:
<Имя> = <Выражение>;
Пример:
int x, y, a; x=5; y=x*2+7; a=y/4;
Переменные получают значения: x=5, y=17, a=4.
В языке Си разрешается включать присваивания в выражения, т. е. присваивание может рассматриваться как операция с учетом старшинства и влияния скобок. Пример: a=(y=(x=5)*2+7)/4;
В результате переменная x получает значение 5, причем это значение участвует в дальнейших вычислениях. Затем выполняется умножение (5*2), сложение (10+7) и еще одно присваивание (y=17). Переменная y получает значение 17, после чего производится деление (17/4), результат которого присваивается переменной a.
В языке Си для компактной записи операторов присваивания имеются специальные операции:
+= –= *= /= %=
Так, следующие две записи на языке Си эквивалентны: i=i+2 и i+=2.
Пример:
int x,y; x=y=5; x+=2; /* x увеличить на 2, результат x=7 */ y–=3; /* y уменьшить на 3, результат y=2 */ x*=y; /* x умножить на y, результат x=14 */
x/=++y; /* разделить x на увеличенный y; результат y=3, x=12/3 */
Операция присваивания сама по себе имеет значение (равное значению выражения, стоящего справа от знака "=") и может входить в выражения.
Общий вид оператора:
if (<выражение>) <оператор1> else <оператор2>;
Здесь часть else <оператор2> является необязательной, можно применять и одиночный оператор if(<выражение>) <оператор1>;
Вначале вычисляется значение выражения. Оператор1 выполняется, если значение выражения истинно. Если выражение ложно (его значение равно нулю), и если есть часть с else, то выполняется оператор2.
![]() Программа 50 (нахождение наибольшего
из двух целых чисел a и b)
Программа 50 (нахождение наибольшего
из двух целых чисел a и b)
#include <stdio.h> main( ) { int a,b; printf("Введите первое число — "); scanf("%d", &a); printf("Введите второе число — "); scanf("%d", &b); if (a==b) printf("Заданные числа равны.\n"); else if (a>b) printf("Первое число больше второго."); else printf("Второе число больше первого.");
}
При программировании требуется аккуратно различать знаки = и ==, потому что в ряде случаев компилятор не сможет обнаружить ошибки, связанной с неправильным использованием знаков этих операций, что приведет к неверным результатам.
В качестве оператора1 может стоять любой оператор, в частности, снова оператор if/else. При этом может возникнуть неоднозначность, если во вложенной последовательности операторов if/else часть else опускается. Else всегда соответствует ближайшему предыдущему if, не содержащему else.
Например, в конструкции:
if (n>0) if (a>b) z=a; else z=b;
else относится к внутреннему if. Если требуется отнести else к внешнему if, то необходимо использовать фигурные скобки:
if (n>0) { if (a>b) z=a; } else z=b;
Часто приходится осуществлять выбор более чем из двух вариантов. Чтобы учесть это, конструкция if/else расширяется конструкцией else/if. Распространенный способ выбора по значению из нескольких вариантов:
if (<выражение1>) <оператор1> else if (<выражение2>) <оператор2> else if (<выражение3>) <оператор3> else <операторN>;
Выражения просматриваются последовательно сверху вниз; как только какое-то выражение становится истинным, выполняется следующий за ним оператор, и на этом вся цепочка заканчивается. Последняя часть else, как и раньше, может быть опущена.
В языке Си имеется компактный способ записи одного из видов оператора if/else. Он называется "условным выражением" или "тернарной операцией". Такое выражение выглядит в общем виде так:
В1 ? В2 : В3
Сначала вычисляется значение выражения В1. Если оно отлично от нуля (истинно), то вычисляется значение выражения В2, которое и становится значением условного выражения. В противном случае вычисляется значение выражения В3, и оно становится значением условного выражения.
Условное выражение удобно использовать в тех случаях, когда имеется отдельная переменная, которой можно присвоить одно из двух возможных значений. Типичными примерами являются присваивание переменной значения большей из двух величин: max = (a>b)?a:b; и нахождение абсолютного значения числа: x = (y<0)?–y : y;
В тех случаях, когда в программе необходимо произвести выбор одного из нескольких вариантов, удобно применять оператор switch.
Его синтаксис:
switch (<выражение>)
{ сase <константа1>: <список операторов1>; case <константа2>: <список операторов2>; ...
case <константаN>: <список операторовN>; default: <список операторов>;
}
Оператор-переключатель выполняется следующим образом. Вычисляется значение выражения в скобках, приведенного после ключевого слова switch, затем программа просматривает список меток, указанных после слов case, до тех пор, пока не находит ту, которая соответствует данному значению. Далее программа переходит к выполнению оператора, расположенного в этой строке. Если подходящей метки не найдется и если существует строка с меткой default:, то будет выполняться оператор, помеченный этой меткой. В противном случае произойдет переход к оператору, расположенному за оператором switch.
Метки, имеющиеся в операторе switch, должны быть константами или константными выражениями (выражениями, операнды которых — константы) целого или символьного типа. Запрещается использовать в качестве метки переменную. Значением выражения в скобках должна быть величина целого или символьного типа. Список операторов варианта может быть либо пустым, либо заканчиваться одним из операторов завершения (break, continue, goto, return). Если у вариантов нет общих частей, то рекомендуется каждый вариант завершать оператором break.
![]()
#include <stdio.h> main () { int c; printf("Введите цифру от 1 до 7:"); c=getchar(); printf("\nСоответствующий день недели:"); switch (c)
{ case '1' : {printf("\nПонедельник!");break;} case '2' : {printf("\nВторник!");break;} case '3' : {printf("\nСреда!");break;} case '4' : {printf("\nЧетверг!");break;} case '5' : {printf("\nПятница!");break;} case '6' :{printf("\nСуббота!");break;} default: printf("\nВоскресенье! ");
}
}
Если не использовать оператор завершения, то по окончании выполнения списка операторов выбранного варианта произойдет переход на следующий вариант из списка.
Оператор for (<оператор1>;<выражение>;<оператор2>) <оператор3>;
позволяет организовать повторяющийся вычислительный процесс и называется оператором цикла. Как правило, оператор1 и оператор2 являются операторами присваивания или обращениями к функции, а выражение1 — условным выражением.
Цикл for удобно использовать в тех случаях, когда заранее известно количество повторений тела цикла или имеется явно выраженная переменная, управляющая циклом. В этом случае выражение1 вычисляется один раз и задает инициализацию управляющей переменной.
Выражение1 является условием завершения цикла, а оператор2 задает приращение управляющей переменной. Например, следующая конструкция: for (i=1; i<n; i++) <оператор>;
является широко распространенной и позволяет "перебрать" первые n натуральных чисел. Из первой строки цикла for можно сразу узнать всю информацию о параметрах цикла: начальное значение переменной i, ее конечное значение, а также насколько увеличивается значение переменной i при каждом выполнении тела цикла.
Любой из операторов и выражений в цикле for может быть опущен, хотя точка с запятой при этом должна оставаться. Если отсутствует оператор1 или оператор2, то он просто выпадает из вычислений. Если же отсутствует выражение1, то считается, что оно всегда истинно. Например, цикл
for (i=1;;i++)
{
... } является бесконечным.
Существуют разнообразные возможности применения цикла for:
можно применять операцию уменьшения для счета в порядке убывания вместо счета в порядке возрастания:
for (n=10;n>0;n– ) printf("%d \n",n);
при желании можно вести счет двойками, десятками и т. д.:
for (n=2;n<60;n+=2) printf("%d\n",n);
можно вести подсчет при помощи символов, а не только чисел: for(ch='a';ch<='z';ch++) printf("Величина кода ASCII для %c равна %d.\n",ch,ch);
можно проверить выполнение некоторого произвольного условия, отличного от условия, налагаемого на число итераций:
for (num=1;num*num*num<216;num++)
можно сделать так, чтобы значение некоторой величины возрастало не в арифметической, а в геометрической прогрессии:
for(n=1;n<1500;n*=3) printf("%d \n",n);
в качестве третьего выражения можно использовать любое правильно составленное выражение; какое бы выражение вы ни указали, его значение будет меняться при каждой итерации:
for(x=1;y<=75;y=5*(x++)+10) printf("%d, %d\n",x,y);
можно даже опустить одно или более выражений (но при этом нельзя опускать символы ";"); необходимо только включить в тело цикла несколько операторов, которые в конце концов приведут к завершению его работы:
ans=2; for(n=3;ans<=25;) ans=ans*n; Тело цикла for(;;) printf("* \n"); будет выполняться бесконечное число раз, поскольку пустое условие всегда считается истинным;
первое выражение не обязательно должно инициализировать переменную; вместо этого, например, там мог бы стоять оператор printf() некоторого специального вида; необходимо помнить, что первое выражение вычисляется только один раз перед тем, как остальные части цикла начнут выполняться:
for(printf("Запоминайте введенные числа!\n");num == 6;) scanf("%d",&num); printf("Это как раз то, что я хочу!\n");
В этом фрагменте первое сообщение оказывается выведенным на печать один раз, а затем осуществляется прием вводимых чисел до тех пор, пока не поступит число 6;
параметры, входящие в выражения, находящиеся в спецификации цикла, можно изменить при выполнении операций в теле цикла; предположим, например, что есть цикл со спецификацией следующего вида:
for(n=1;n<1000;n+=delta) и если после нескольких итераций программа решает, что величина параметра delta слишком мала или велика, оператор if внутри цикла может изменить значение этого параметра (в диалоговой программе пользователь может изменить этот параметр в процессе выполнения цикла).
В качестве оператора в теле цикла также может быть цикл. На количество вложений циклов друг в друга ограничений нет.
В спецификацию цикла for может быть включено несколько инициализирующих или корректирующих выражений. Например, два вложенных цикла можно записать двумя различными способами:
1. for(i=1; i<10; i++) for(j=1; j<10; j++)
<оператор>
2. for(i=1, j=1; i<10, j<10; i++, j++)
<оператор>
В следующей программе переменные x, y, z изменяются параллельно.
![]()
#include <stdio.h> main() { int x,y,z,v,u,zero(); for(x=1,y=1,z=1;x<10;x++,y++,z++) printf("x=%d y=%d z=%d\n", x, y, z);
}
Результат работы программы:
x=1 y=1 z=1 x=2 y=2 z=2 x=3 y=3 z=3 x=4 y=4 z=4 x=5 y=5 z=5 x=6 y=6 z=6 x=7 y=7 z=7 x=8 y=8 z=8 x=9 y=9 z=9
В общем виде цикл while записывается так: while (<выражение>) <оператор>;
Цикл while является "условным" циклом, использующим предусловие (т. е. условие на входе). Он называется условным, потому что выполнение оператора зависит от истинности условия, описываемого с помощью выражения.
Если выражение "истинно" (или в общем случае не равно нулю), то оператор, входящий в цикл while, выполняется один раз, а затем выражение проверяется снова. Эта последовательность действий, состоящая из проверки и выполнения оператора, периодически повторяется до тех пор, пока выражение не станет ложным (или в общем случае равным нулю). После этого управление передается оператору, следующему за оператором цикла while.
При построении цикла while необходимо включить в него какие-то конструкции, изменяющие величину проверяемого выражения так, чтобы в конце концов оно стало ложным. В противном случае выполнение цикла никогда не завершится.
Пример 1. Алгоритм Евклида.
![]()
#include <stdio.h> main() { int x,y; scanf("\n%d",&x); scanf("\n%d",&y); while (x!=y)
{ if (x>y) x=x–y; else y=y–x;
}
printf("\n%d",x);
}
Пример 2. Проверить, содержит ли квадрат натурального числа n цифру 3.
![]()
#include <stdio.h> main() { int i,n,a; scanf("%d",&n); n=n*n; i=10000; while(i>=1)
{ a=n/i; /* если результат целочисленного деления n/i меньше 1, то a=0 */ n=n–a*i; if(a==3) goto abc; else i=i/10;
} printf("цифры 3 в числе n^2 нет"); goto cd; abc: printf("цифра 3 в числе n^2 есть"); cd: ;
}
В языке Си имеется также конструкция цикла с постусловием (условие на выходе), где истинность условия проверяется после выполнения каждой итерации цикла. Этот подход реализуется с помощью цикла do/while.
Тело цикла do/while всегда выполняется по крайней мере один раз, поскольку проверка условия осуществляется только после его завершения.
Форма записи:
do <оператор> while (<выражение>);
Оператор break дает возможность выйти из операторов цикла for, while, do/while, а также из переключателя switch без проверки условия. Оператор break приводит к немедленному выходу из самого внутреннего охватывающего его цикла или из переключателя.
Оператор break может использоваться для выхода из цикла в тех случаях, когда заданы два разных условия прекращения его работы.
![]()
#include <stdio.h> main() { int x=1,y,z; рrintf("Мы будем вычислять значение функции y=2*x+z\n"); printf("Введите значение z:"); scanf("%d",&z); while(x<1000)
{ y=2*x+z;x++; if y=100 { printf(= 100\n"); break; }
} if y=100 printf("Цикл закончен!!!"); else printf("Цикл закончен!!! Но y<>100.");
}
Наличие оператора break позволяет использовать "бесконечные циклы". В ряде случаев весьма удобно записать заголовок цикла без всякого условия в виде: for(;;) , а выход из цикла оформить с помощью операторов break.
Оператор continue вызывает преждевременное завершение выполнения тела цикла и переход к следующему шагу цикла. Оператор continue действует только на самый внутренний цикл, частью которого он является.
![]()
#include <stdio.h> main() { int x,y,z; printf("Мы будем вычислять значение функции y=2*x+z\n"); printf("в промежутках [1;6] и [13;18]."); рrintf("Введите значение z= "); scanf("%d",&z); for(x=1;x<18;x++)
{
if ((x>6) and (x<13)) continue;
y=2*x+z; printf(= %d, y= %d",x,y);
}
}
Оператор перехода предназначен для безусловной передачи управления в заданную точку программы. Его выполнение заключается в передаче управления оператору, помеченному заданной меткой.
В качестве метки используется идентификатор. Метка отделяется от оператора, к которому она относится, двоеточием. Помеченный оператор должен находиться в пределах той же функции, что и оператор goto. Может быть помечен любой оператор, но никакие два разных оператора не должны иметь одинаковые метки (внутри одной и той же функции). Кроме того, один оператор может быть помечен несколькими метками.
Форма:
goto <метка>; ... <метка>: <оператор>
Символы "{" и "}" используются для объединения описаний и операторов в составной оператор или блок, так что все конструкции, заключенные в фигурные скобки, оказываются синтаксически эквивалентными одному оператору. Точка с запятой никогда не ставится после первой фигурной скобки, которая завершает блок.
Составной оператор — последовательность операторов, заключенная в фигурные скобки (при необходимости его используют в качестве "внутреннего" оператора в операторах ветвления и цикла). Он называется также блоком. Блоки не могут быть вложенными.
![]()
#include <stdio.h> main() { int sam,index=0;
/* В цикл включен только оператор присваивания. Печать данных */ /* будет произведена только один раз — после завершения цикла. */ while(index++<10) sam=10*index+2; printf("sum= %d\n",sam);
}
Результат работы программы:
sam = 102
![]()
#include <stdio.h> main() { int sam,index=0;
/* Наличие фигурных скобок гарантирует, что оба оператора */
/* являются частью цикла while, и печать результатов будет */
/* производиться на каждом шаге работы цикла. Весь составной */
/* оператор рассматривается как один оператор, являющийся */
/* составной частью оператора while. */ while(index++<10)
{ sam=10*index+2; printf("sum = %d\n",sam);
}
}
Результат работы программы:
sam = 12 sam = 22 sam = 32 sam = 42 sam = 52 sam = 62 sam = 72 sam = 82 sam = 92 sam = 102
Пустой оператор состоит только из точки с запятой (;) и используется для обозначения пустого тела управляющего оператора.
Программа на языке Си представляет собой набор последовательно описанных функций (процедуры и подпрограммы в языке Си считаются частным случаем функций). Каждая функция — самостоятельная единица программы, предназначенная для решения определенной задачи (или подзадачи).
При описании она имеет следующий вид:
Тип_функции Имя (<cписок аргументов>)
<описания аргументов>
{
<описания>
<операторы>
}
Отметим, что список аргументов может быть пустым (однако скобки после имени функции сохраняются). В этом случае, естественно, нет и их описаний.
Имеется одна главная функция (с именем main), с которой начинается выполнение программы. Функции могут обращаться к другим функциям посредством конструкций вызова. Вызов функции используется при вычислении значения выражения. В результате вызова функция возвращает вычисленное значение, которое и является значением вызова функции. Попутно функция может преобразовывать значения своих аргументов. Такой результат вызова функции называется побочным эффектом.
В модуле, вызывающем данную функцию, тип возвращаемого ею значения должен быть описан (даже если это неопределенное значение) вместе с описанием переменных.
Пример. Пусть необходимо вывести на экран словосочетание "Простая функция без аргументов" 15 раз, используя функции.
![]()
#include <stdio.h> main() { int i,print(); for (i=1;i<=15;i++) print();
{ print() /* вызываемая функция без аргументов */
} printf ("Простая функция без аргументов\n");
}
Аргументы передаются по значению путем копирования в соответствующие (по порядку) параметры, указанные в определении функции. Соответствие аргументов и параметров по количеству и типу не контролируется в языке Си. Такой контроль может быть выполнен с помощью дополнительных средств отладки.
Следует различать формальные аргументы, используемые при описании функций, и фактические, задаваемые при вызове функций. Формальный аргумент — переменная в вызываемой программе, а фактический аргумент — конкретное значение, присвоенное этой переменной вызывающей программой. Фактический аргумент может быть константой, переменной или даже более сложным выражением. Независимо от типа фактического аргумента он вначале вычисляется, а затем его величина (в данном случае некоторое целое число) передается функции (см. программу 59).
Можно задавать список аргументов, разделенных запятыми.
Пример: программа 60, которая находит числа x, y, z, принадлежащие отрезку [1;20] и удовлетворяющие условию x^2=y^2+z^2.
![]()
#include <stdio.h> main() {
int x, y, z, zero(); char p, q, ch(); x=2; y=45; z=0; q='o';
printf("x= "); zero(x);
printf("x+y+(x+y)^z= "); zero(x+y+(x+y)^z); printf("q= "); ch(q);
} int zero(u) int u; {
printf("%d\n",u);
} char ch(u) char u; {
printf("%c\n",u);
}
Результат работы программы:
x= 2 x+y+(x+y)^z= 94 q= о
![]()
#include <stdio.h> main() { int x,y,z; int zero(); printf("Следующие величины могут быть сторонами прямоугольного треугольника:\n"); for (x=1;x<=20;x++) for (y=1;y<=20;y++) for (z=1;z<=20;z++) if (y*y+z*z==x*x) zero(x,y,z);
} int zero(f,g,h) int f,g,h; { printf ("x= %d, y= %d, z=%d\n",f,g,h);
}
Результат работы программы:
Cледующие величины могут быть сторонами прямоугольного треугольника: x= 5, y= 3, z= 4 x= 5, y= 4, z= 3 x= 10, y= 6, z= 8 x= 10, y= 8, z= 6 x= 13, y= 5, z= 12 x= 13, y= 12, z= 5 x= 15, y= 9, z= 12 x= 15, y= 12, z= 9 x= 17, y= 8, z= 15 x= 17, y= 15, z= 8 x= 20, y= 12, z= 16 x= 20, y= 16, z= 12
Завершает выполнение данной функции и передает управление вызывающей функции оператор return; в главной функции main он же вызывает завершение выполнения всей программы. Оператор return может содержать любое выражение: return (<выражение>);
Если выражение не пусто, то вычисляется его значение, которое и становится значением данного вызова функции.
Достижение "конца" функции (правой закрывающей фигурной скобки) эквивалентно выполнению оператора return без возвращаемого значения (т. е. оператор return в конце функции может быть опущен).
Пример: данная программа вычисляет факториал, если число меньше 8; если вводимое число больше или равно 8, то выводится сообщение "Очень большое число".
![]()
#include <stdio.h> main() { int n, s(); printf("Введите число "); scanf("%d", &n); if (n<8) printf("p=%d", s(n)); else printf("Очень большое число");
} int s(x) /* определение функции с параметром */ int x; { int y,p=1; for (y=x; y>0; y– ) p*=y; return(p); /* Возвращает в основную программу значение p */ }
Результат работы программы:
1. Введите число 4 p=24
2. Введите число 9
Очень большое число
Пример: предположим, что нужно вычислить x2 (для некоторого неотрицательного целого y) (очевидный способ реализации возведения в целочисленную степень — многократное умножение, но существует более эффективный алгоритм, приведенный далее).
![]()
#include <stdio.h> main() {
int a, b, x, y, z; int odd(); printf("\nВведите x, y через пробел: "); scanf("%d %d", &x, &y); a=x; b=y; z=1; while (b!=0) if (odd(b)) { z=z*a; b– –;} else
{ a=a*a; b=b/2;} printf("\n%d", z);
} int odd(t) int t; { return((t%2==0)? 0:1);
}
Результат работы программы:
Введите x, y через пробел: 15 2
225
Если функции необходимо вернуть несколько значений, можно использовать два различных приема:
применить глобальные переменные (в этом случае кроме изученных ранее характеристик переменных (имени, типа, значения) используется еще одна — класс памяти, см. далее);
применить переменные типа "указатель" в качестве аргументов функции.
При вызове функции информация о переменной может передаваться функции в двух видах. Если мы используем форму обращения function1(x);
то происходит передача в функцию значения переменной x. Изменение этого значения в вызывающую функцию не возвращается. Если мы используем форму обращения function2(&x);
то происходит передача адреса переменной x. Теперь измененное значение переменной x может использоваться в вызывающей функции. Первая форма обращения требует, чтобы определение функции включало в себя формальный аргумент того же типа, что и x:
function1(num) int num;
Вторая форма обращения требует, чтобы определение функции включало в себя формальный аргумент, являющийся указателем на один из объектов соответствующего типа:
function2(x) int *x;
Обычно пользуются первой формой, если входное значение необходимо функции для некоторых вычислений или действий, и второй формой, если функция должна будет изменять значения переменных в вызывающей программе. Ранее вторая форма вызова уже применялась при обращении к функции scanf(). Когда мы хотим ввести некоторое значение в переменную num, мы пишем scanf("%d",&num). Данная функция читает значение, затем, используя адрес, который ей дается, помещает это значение в память.
Пример: пусть необходимо поменять местами заданные значения переменных x и y.
![]()
#include <stdio.h> main() { int x, y; int interchange(); /* описание функции типа int */ x=1; y=3;
printf("Имели... x=1 y=3\n");
interchange(&x, &y); /* обращение к функции (в данном случае передаются адреса переменных) */
printf("Получили... x=%d y=%d", x, y);
}
/* вызываемая функция */ int interchange(u, v) int *u, *v;
{ int p; p=*u; *u=*v; *v=p;
}
Результат работы программы:
Имели x=1 y=3
Получили x=3 y=1
В этой программе в вызове функции interchange(&x,&y) вместо передачи значений x и y мы передаем их адреса. Это означает, что формальные аргументы u и v, имеющиеся в спецификации interchange(u,v), при обращении будут заменены адресами и, следовательно, они должны быть описаны как указатели.
Поскольку x и y целого типа, u и v являются указателями на переменные целого типа, и мы вводим следующее описание: int *u,*v; int p;
Оператор описания используется с целью резервирования памяти. Мы хотим поместить значение переменной x в переменную p, поэтому пишем: p=*u;. Вспомните, что значение переменной u — это &x, поэтому переменная u ссылается на x. Это означает, что операция *u дает значение x, которое как раз нам и требуется. Мы не должны писать, например, так: p=u; /* неправильно */
поскольку при этом происходит запоминание адреса переменной x, а не ее значения. Аналогично, оператор *u=*v соответствует оператору x=y.
Тип функции определяется типом возвращаемого ею значения, а не типом ее аргументов. Если указание типа отсутствует, то по умолчанию считается, что функция имеет тип int. Если значения функции не принадлежат типу int, то необходимо указать ее тип в двух местах. Описать тип функции в ее определении:
char pun(ch,n) /* функция возвращает символ */ int n; char ch;
Описать тип функции также в вызывающей программе. Описание функции должно быть проведено наряду с описаниями переменных программы; необходимо только указать скобки (но не аргументы) для идентификации данного объекта как функции.
main() char rch,pun();
Помимо изученных ранее характеристик переменных (имени, типа, значе- ния) в ряде случаев оказывается важной еще одна — класс памяти. Класс памяти характеризует время существования и место хранения объекта в программе.
Для обозначения класса памяти в языке Си используются следующие служебные слова:
auto extern register static
Автоматические объекты (auto) являются локальными по отношению к блоку и хранятся внутри того блока, где они описаны. Автоматические переменные можно инициализировать произвольными выражениями, включающими константы и ранее описанные переменные и функции.
Автоматические объекты существуют только во время выполнения данного блока и теряют свои значения при выходе из него. При каждом вхождении в блок им присваиваются начальные значения, заданные в описании. Если начальные значения не заданы, то значения автоматических объектов при входе в блок не определены. До сих пор в этой главе рассматривались именно автоматические объекты.
Объекты, описанные внутри блока с классом памяти register, называются регистровыми переменными. Они подчиняются всем правилам, касающимся автоматических переменных. Описание register указывает компилятору, что данная переменная будет часто использоваться. Когда это возможно, переменные, описанные как register, располагаются в машинных регистрах. Это приводит к меньшим по размерам и более быстрым программам.
Объекты, описанные внутри функции с добавлением класса памяти extern или описанные вне функции без указания класса памяти, относятся к внешним. Внешние объекты хранятся вне любой функции, входящей в состав программы, и существуют в течение выполнения всей программы. Они могут быть использованы для передачи значений между различными, в том числе и отдельно компилируемыми, функциями. Сами функции также являются внешними объектами, поскольку правила языка Си не позволяют определять одни функции внутри других. Внешние переменные можно инициализировать только выражениями с константами и указателями на ранее описанные объекты. По умолчанию (если не задана инициализация) внешние объекты получают нулевые начальные значения.
Внешние объекты делятся на внешние глобальные и внешние статические.
Важно различать описание внешнего объекта и его определение. Описание указывает свойства объекта (тип, размеры и т. д.); определение же вызывает еще и отведение памяти установке начального значения, если используется инициализация.
Например, появившиеся вне определения какой-либо функции строчки
int max; char save[maxline];
определяют внешние переменные max и save, вызывают отведение для них места в памяти и служат в качестве описания для остальной части этого файла.
В то же время строчки
extern int max; extern char save[];
описывают в остальной части данного блока переменную max как int, a save как массив типа char (размеры которого указаны в другом месте), но не создают переменных и не отводят для них места в памяти.
Во всех блоках, составляющих исходную программу, должно содержаться только одно определение внешней переменной; другие блоки могут содержать описания extern для доступа к ней.
![]()
#include <stdio.h> int i=0;
/* Класс памяти переменной — внешний.
/* Область действия переменной — любая программа, */ /* загружающаяся с данным файлом.
/* Время существования i=0 — все время выполнения программы. */ main() /* Блок уровня 1. */
{ auto int i=1;
/* В блоке 1 область действия i=1 — функция main().*/
/* Время существования i=1 — все время выполнения /*
/* главной функции main(). /* printf("%d\n", i);
/* Если две переменные имеют одно и то же имя, то по этому */
/* имени обращаются к внутренней переменной, */
/* внешняя переменная непосредственно недоступна, поэтому */
/* после выполнения блока 1 программа напечатает i=1. */ { /* Блок уровня 2. */ int i=2;
/* Класс памяти переменной i=2 — auto. Область */
/* действия i=2 — блок 2, время существования — время */
/* существования блока 2. блок 2, время существования —*/
/* время существования блока 2. */ printf("%d\n", i);
/* Программа напечатает i=2. */
{ /* Блок уровня 3. */ i+=1; printf("%d\n", i);
/* Печатается самая внутренняя переменная с именем i,/*
/* которая после выполнения операции данного блока */
/* становится равной 3. */
}
/* Возвращение к блоку уровня 2. */ printf("%d\n", i);
/* Опять печатается i=3. */
}
/* Возвращение к блоку уровня 1. */ printf("%d", i);
/* Переменная i=3 исчезает. Теперь самой внутренней переменной */
/* с именем i будет i=1. */
}
![]()
#include <stdio.h> int a; main() {
extern int a; int P(); a=6; P();
} int P() {
extern int a; printf("a=%d",a);
}
Результат работы программы: a=6
Областью действия статического внешнего объекта является модуль, в котором описан данный объект. При этом где-либо во внешних описаниях (т. е. вне определения функций) должно быть расположено определение внешнего статического объекта в виде: static <Спецификация типа> <Спецификация данных>;
На основании определения под объект отводится память и может быть произведена инициализация. Статические переменные можно инициализировать только выражениями с константами и с указателями на ранее описанные объекты.
При первом входе в соответствующую локальную область (блок или модуль) статические переменные инициализируются один раз (по умолчанию — нулем). При последующих входах в данную область статические переменные получают те значения, которые они имели при последнем выходе из области.
По умолчанию все функции данного модуля, расположенные ниже определения статического объекта, включаются в его область действия — в них не обязательно дополнительно описывать объект для получения к нему доступа. Функции, определения которых расположены в модуле выше определения внешнего статического объекта, для получения доступа к нему должны содержать описание этого объекта с классом памяти extern. Константы являются объектами статического класса памяти.
Функция может быть определена как статический внешний объект. В этом случае она будет доступной в любой точке данного модуля и не доступной за пределами модуля.
![]()
#include <stdio.h> main() {
int count; int trystat();
for (count=1; count<=3; count++)
{
printf ("Итерация %d:\n", count); trystat();
} } trystat() {
int fade=1; static int stay=1;
printf("fade = %d и stay = %d\n", fade++, stay++);
}
Результат работы программы:
Итерация 1:
fade = 1 и stay = 1 Итерация 2:
fade = 1 и stay = 2 Итерация 3:
fade = 1 и stay = 3
Если мы лишь немного видоизменим в программе функцию trystat():
trystat() { int fade=1; int stay=1; printf("fade = %d и stay = %d\n", fade++, stay++);
} то получим следующий результат:
Итерация 1:
fade = 1 и stay = 1 Итерация 2:
fade = 1 и stay = 1 Итерация 3: fade = 1 и stay = 1
Средства ввода/вывода не являются составной частью языка Си. Имеется ряд библиотечных функций Си, обеспечивающих стандартную систему ввода/вывода для программ на Си. Макроопределения, описания переменных и определения этих функций содержатся в файле стандартных заголовков stdio.h. Поэтому, как указывалось ранее, каждая пользовательская программа должна содержать в начале ссылку:
#include <stdio.h>
В примерах программ мы неоднократно использовали форматные функции ввода (scanf()) и вывода (printf()). Набор стандартных функций ввода и вывода значительно шире и включает большое число функций для работы с данными различного типа, различными устройствами, буферизованного и небуферизованного, форматного и бесформатного ввода и вывода.
Система ввода/вывода Си обеспечивает некоторый уровень абстракции между программистом и используемым устройством. Эта абстракция называется потоком, а фактическое устройство ввода/вывода называется файлом. Буферизованная файловая система преобразует каждое физическое устройство в логическое устройство, называемое потоком. Существуют потоки двух типов: текстовые и двоичные.
Текстовый поток — это последовательность символов, которая организуется в строки, завершающиеся символами новой строки. Обработка текстового потока предполагает преобразование данных из текстового (внешнего) представления в машинное (внутреннее) или наоборот. При обработке двоичного потока последовательность его байтов взаимно однозначно соответствует байтам во внешнем устройстве.
В языке программирования Си файл — это логическое понятие, которое система может относить к чему угодно (от дисковых файлов до терминалов). Поток связывается с конкретным файлом выполнением операции "открыть". Как только файл открывается, можно обмениваться информацией между ним и программой. Закрытие выводимого потока заставляет компьютер записывать содержимое этого потока на внешнее устройство. Этот процесс обычно называется промыванием потока. В начале выполнения программы компьютер открывает три предопределенных текстовых потока stdin, stdout и stderr, связанных со стандартными устройствами ввода/вывода (консоль — клавиатура и дисплей). Допускается переадресация ввода/вывода к другим устройствам.
Простейшими функциями консольного ввода/вывода являются функция getche(), которая читает символ с клавиатуры, и функция putchar(), которая печатает символ на экране. Функция getche() ждет, пока не будет нажата клавиша, а затем возвращает ее значение, автоматически выдавая на экран
"эхо" нажимаемой клавиши. Функция putchar() записывает ее символьный аргумент на экран в текущую позицию курсора.
Далее приводится пример простой программы, которая принимает один символ с клавиатуры и выводит его на экран.
![]()
#include <stdio.h> main() { char ch; ch = getchar(); putchar(ch);
}
Есть две важные версии функции getche(). Первая — getchar() — буферирует ввод до тех пор, пока не введен возврат каретки. Второй версией является функция getch(), которая работает точно так же, как getchar(), за исключением того, что getch() не возвращает на экран эхо введенного символа.
Функции gets() и puts() позволяют читать и писать цепочки символов (строки) с консоли. Функция gets() читает цепочку символов, которая вводится с клавиатуры (ввод оканчивается возвратом каретки), помещает ее с адреса, который указывает ее аргумент — указатель символа. Функция puts() выводит на экран ее аргумент — цепочку символов, а затем символ новой строки.
Например, следующая программа читает цепочку в массив str и тут же печатает ее.
![]()
main() { char str[80]; gets(str); puts(str);
}
Функция puts() занимает меньше памяти и работает быстрее, чем printf() при выводе символьных цепочек, поэтому программисты часто используют функцию puts() в тех случаях, когда важно иметь высоко минимизированный код.
Таблица 5.5. Некоторые функции буферизованной системы ввода/вывода
|
Имя |
Функция |
|
fopen() |
Открывает поток |
|
fclose() |
Закрывает поток |
|
putc() |
Выводит символ в поток |
|
getc() |
Вводит символ из потока |
|
fseek() |
Ищет указанный байт в потоке |
|
fprintf() |
Форматный вывод в поток |
|
fscanf() |
Форматный ввод из потока |
|
feof() |
Возвращает истину, если достигается метка EOF (конец файла) |
|
ferror() |
Возвращает истину, если встретилась ошибка |
|
rewind() |
Устанавливает начальную позицию файла |
|
remove() |
Стирает файл |
Для работы с файлами в Си применяются функции буферизованной системы ввода/вывода, табл. 5.5. Обращение к ним использует указатель файла, который определяет различные характеристики файла, включая его имя, статус и текущую позицию; используется связанным с этим файлом потоком для привязки каждой функции буферированного ввода/вывода к месту, над которым она выполняет свои операции. Указатель файла является переменной типа FILE, которая определяется в файле заголовков stdio.h.
Функция fopen() вызывается так: fopen(<имя_файла>, <режим>);
Имя файла должно быть цепочкой символов, которая составляет правильное имя файла для операционной системы и может включать спецификацию пути. Режим задает желаемый статус открытия, табл. 5.6.
Таблица 5.6. Значения режимов в Турбо Си
|
Режим |
Смысл |
|
"r" |
Открыть файл для чтения |
|
"w" |
Создать файл для записи |
|
"a" |
Добавлять в файл |
|
"r+" |
Открыть файл для чтения/записи |
|
"w+" |
Создать файл для чтения/записи |
|
"a+" |
Открыть или создать файл для чтения/записи |
Например, для того чтобы открыть файл с именем test для записи, можно написать fp = fopen("test", "w"); где fp — переменная типа FILE*. Переменная fp является указателем файла.
Следующий оператор обнаруживает любую ошибку при открытии файла, такую как, например, попытку открыть защищенный от записи диск или заполненный диск, прежде чем состоится попытка записи на него:
if ((fp = fopen("test", "w"))==NULL)
{ puts("Нельзя открыть файл!\n"); exit(1); }
NULL — это макро, которое определяется в файле заголовка stdio.h. Функция putc() в виде putc(<символ>, fp);
используется для записи символа в поток, который предварительно открыт для записи с помощью функции fopen(); fp — возвращаемый функцией fopen() указатель файла.
Функция getc() в виде getc(fp)
используется для чтения символов, которые она возвращает из потока, открытого в режиме чтения функцией fopen(). fp является указателем файла типа FILE, который возвращается функцией fopen(). В тех случаях, когда достигается конец файла, функция getc() возвращает маркер его конца EOF. Например, для чтения текстового файла до маркера конца файла можно использовать следующие операторы:
ch = getc(fp); while(ch!=EOF)
{ ch = getc(fp); }
Функция feof() использует аргумент указателя-файла и возвращает 1, если достигнут конец файла, или 0, если не достигнут. Например, приведенная далее программа читает двоичный файл до тех пор, пока компьютер не встречает маркер конца файла: while(!feof(fp)) ch = getc(fp);
Функцию fclose() используют для закрытия потока, который был открыт с помощью функции fopen(). Все потоки необходимо закрыть перед завершением программы. Аргументом функции является указатель файла, который закрывается.
Функции fopen(), getc(), putc() и fclose() составляют минимальный набор функций ввода/вывода. Простым примером использования функций putc(), fopen() и fclose() является программа, которая приведена далее. Эта программа просто читает символы с клавиатуры и записывает их в дисковый файл до тех пор, пока не введен знак $. Имя выходного файла задается из командной строки. Например, если вы назовете программу ktod ("клавиша — на диск"), то набор на клавиатуре ktod test будет позволять вам вводить строки текста в файл с именем test.
![]()
#include .h" main(argc,argv) /* ktod — клавиша на диск */ int argc; char *argv[];
{
FILE *fp; char ch; if(argc!=2)
{ printf("Вы забыли ввести имя файла\n); exit(1);
} if((fp=fopen(argv[1], "w"))== NULL)
{ printf("не может открыть файл\n); exit(1);
} do { ch = getchar(); putc(ch, fp);
} while (ch!='s'); fclose(fp);
}
Еще одним примером является программа dtos, которая будет читать любой ASCII-файл и выводить его содержимое на экран.
![]()
#include "studio.h" main(argc, argv) /* dtos — диск на экран */ int argc; char *argv[];
{
FILE *fp; char ch; if(argc!=2) { printf("Вы забыли ввести имя файла\n"}; exit(1);
} if((fp=fopen(argv[1], "r"))==NULL){ printf("Не может открыть файл\n"}; exit(1);
}
ch=getc(fp); /* читать один символ */ while(ch!=EOF)
{ putchar(ch); /* печать на экран */ ch=getc(fp);
} fclose(fp);
}
Под управлением буферизованной системы ввода/вывода можно выполнять операции чтения и записи с произвольным доступом с помощью функции fseek(), которая устанавливает файловую позицию.
Например, для чтения 234-го байта в файле с именем test можно использовать следующую функцию:
func1()
{
FILE *fp; if((fp=fopen("test" ,"r"))==NULL)
{ printf("не могу открыть файл\n"); exit(1);
} fseek(fp,234L,0); return getc(fp); /*читать один символ в 234-й позиции*/ }
В дополнение к рассмотренным до сих пор основным функциям ввода/вывода буферизованная система ввода/вывода включает функции fprintf() и fscanf(). Эти функции ведут себя точно так же, как функции printf() и scanf(), за исключением того, что они работают с дисковыми файлами. Обращения к функциям fprintf() и fscanf() имеют следующий вид:
fprintf(fp,<формат>,<список аргументов>); fscanf(fp,<формат>,<список аргументов>);
где fp является файловым указателем, который возвращается вызовом функции fopen().
Препроцессор — это программа, которая производит некоторые, иногда весьма значительные, манипуляции с первоначальным текстом программы перед тем, как он подвергается трансляции.
Оператор препроцессора — это одна строка исходного текста, начинающаяся с символа #, за которым следуют название оператора и операнды.
Операторы препроцессора могут появляться в любом месте программы и их действие распространяется на весь исходный файл.
Весьма часто используют следующие операторы препроцессора:
#include
#define
Более специфичными являются директивы #pragma, #if, #error и др.
Важная возможность препроцессора — включение в исходный текст содержимого других файлов. Эта возможность в основном используется для того, чтобы снабжать программы какими-то общими для всех данными, определениями.
Например, чрезвычайно часто в начале программы на языке Си встречается препроцессорная конструкция:
#include <stdio.h>
Когда исходный текст программы обрабатывается препроцессором, на место этой инструкции ставится содержимое расположенного в некоем стандартном месте файла stdio.h, содержащего макроопределения и объявления данных, необходимых для работы функций из стандартной библиотеки ввода/вывода. Для использования различных математических функций необходимо подключать файл описаний math.h. Функции, оперирующие со строками, описаны в файле string.h, функции общего назначения — в stdlib.h, функции даты и времени — в time.h, диагностика — в assert.h и т. д.
Директива #define позволяет дать в программе макроопределения (или задать макросы). Оператор макроопределения имеет вид:
#define <макроимя> <строка лексем> или
#define <макроимя(<список параметров>)> <строка лексем>
Макроимя — это идентификатор. Строка лексем — это последовательность лексем от макроимени до конца строки. Точка с запятой в конце макроопределения не ставится.
Препроцессорная обработка макроопределения сводится к тому, что любое появление макроимени (макровызов) в качестве отдельной лексемы в тексте программы, расположенном после макроопределения, ведет к замене этого макроимени на указанную строку лексем. Например, прочитав определения
#define PI 3.14159 #define E 2.711828
препроцессор заменит в программе все имена PI и E на соответствующие числовые константы.
Препроцессор языка Си позволяет переопределять не только константы, но и целые программные конструкции. Например, можно написать определение
#define forever for(;;)
и затем всюду писать бесконечные циклы в виде forever
Определение макроимени с параметрами имеет некоторую специфику. Список параметров макроимени — это список идентификаторов, разделенных запятыми. Следующая после списка параметров строка лексем также может содержать эти параметры, которые при макровызове будут заменены на соответствующие аргументы.
Макровызов должен быть отдельной лексемой и состоять из макроимени и заключенного в круглые скобки списка аргументов. При обработке макровызова препроцессор заменяет каждый параметр в строке лексем на соответствующий аргумент макровызова.
В следующих программах иллюстрируются некоторые применения операторов препроцессора.
Пример 1: найти большее из двух чисел.
![]()
#include <stdio.h>
#define MAX(X,Y) ((X)>(Y) ? (X) : (Y)) main() { int x,y; scanf ("%d %d", &x, &y); printf ("%d", MAX(x, y));
}
Результат работы программы:
3 5
5
Пример 2: использование макроимен для задания выражений и вызова функций.
![]()
#include <stdio.h>
#define S(x) x*x
#define P(x) printf("х равен %d.\n",x) main() { int x=4; int z;
z = S(x); P(z); z = S(2);
P(z);
P(S(x));
P(S(x+2));
P(100/S(2));
P(S(++x));
}
Результат работы программы:
x равен 16. x равен 4. x равен 16. x равен 14. x равен 100. x равен 30.
Оператор препроцессора #pragma позволяет записывать самые различные указания компилятору (зависящие от конкретного компилятора). Например, следующие два предложения препроцессора:
#pragma recursive #pragma nonrec
устанавливают режим всех функций программы по умолчанию рекурсивным или нерекурсивным. Указание препроцессора
#pragma optimize time
воспринимается компилятором таким образом, что он старается сгенерировать объектный код, отличающийся более высокой скоростью выполнения, чем в случае, когда он должен быть более компактным.
При знакомстве с языком Си, особенно после изучения Паскаля, погружение в детали его изобразительных средств может затушевать важную мысль: хотя на Си можно написать практически любую прикладную программу, он изначально для этого не предназначен. Си является результатом эволюционного развития языков создания системных программных средств. Если в прикладном программировании эволюция шла от Фортрана к Алголу, Коболу, Паскалю и т. д., то в системном — от Ассемблеров, привязанных к архитектуре компьютера, к Си, для которого созданы трансляторы, делающие его хоть и независимым от архитектуры, но не меняющим основного предназначения.
С помощью Си можно сделать то, что на Паскале сделать невозможно (или почти невозможно), — например, написать фрагмент операционной системы (или новую операционную систему), утилиты и т. п. Так, ряд трансляторов с Паскаля написаны на Си; обратное невозможно представить. В то же время не раз отмечалось, что прикладные программы, написанные на Паскале, отличаются большей надежностью, чем написанные на Си; их легче читать, передавать от одного программиста другому для совершенствования и сопровождения. Это связано с тем, что Паскаль содержит существенно больше ограничений и является языком более высокого уровня с сильной типизацией данных. Для языка же, который предназначен для разработки системного программного обеспечения, чем меньше ограничений, тем лучше; так, в Си возможны неявные преобразования всех базовых типов данных и указателей друг в друга, что крайне желательно при создании системных средств, но при не- внимательности программиста приводит к ошибкам, не улавливаемым транслятором с Си (Паскаль же подобные недопустимые операции пресекает немедленно).
Разумеется, сказанное не следует абсолютизировать. Программисты, привыкшие к Си, успешно пишут на нем программы различных классов. Это касается не только Си. Даже на Бейсике можно писать экспертные системы. В то же время при массовом программировании придерживаться "разделения труда" между языками представляется более естественным.
1. Охарактеризуйте назначение и особенности языка Си.
2. Какие символы образуют алфавит языка Си?
3. Что называется лексемами, идентификаторами, литералами? Приведите примеры.
4. Какие типы данных используются в Си? Приведите примеры описания переменных.
5. Охарактеризуйте арифметические, логические и битовые операции Си.
6. Какие разновидности оператора присваивания имеются в Си?
7. Как на языке Си можно описать ветвление?
8. Охарактеризуйте возможности цикла for. Приведите примеры.
9. Какие логические циклы имеются в Си? Приведите примеры их использования.
10. Какие операторы управления имеются в Си?
11. Какова структура программы на Си? Что такое функция?
12. Приведите примеры использования функций (с аргументами и без, возвращающих и не возвращающих значения).
13. Для чего в качестве аргументов функций используются указатели? Приведите примеры.
14. Для чего в Си существуют классы памяти?
15. Что такое потоки и файлы в Си?
16. Охарактеризуйте стандартные функции ввода и вывода в Си.
17. Что такое препроцессор Си? Приведите примеры директив препроцес- сора.
 Темы для рефератов и докладов
Темы для рефератов и докладов 1. История возникновения и развития языка Си.
2. Системы программирования на Си.
3. С, С++ и ObjectC.
1. Какой язык вам больше понравился, Паскаль или Си? Почему?
2. Почему в программе на Си труднее найти ошибки, чем в программе на Паскале?
1. Вычислить дробную часть среднего геометрического трех заданных положительных чисел.
2. Определить, является ли треугольник, заданный длинами его сторон, остроугольным.
3. Вычислить периметр и площадь прямоугольного треугольника по длинам двух катетов.
4. По координатам трех вершин некоторого треугольника найти его площадь и периметр.
5. По длинам двух сторон некоторого треугольника и углу (в градусах) между ними найти длину третьей стороны и площадь этого треугольника.
6. Найти произведение цифр заданного четырехзначного числа.
7. Определить число, полученное выписыванием в обратном порядке цифр заданного трехзначного числа.
8. Определить, равна ли сумма двух первых цифр заданного четырехзначного числа сумме двух его последних цифр.
9. Даны три произвольных числа. Определить, можно ли построить треугольник с такими длинами сторон.
10. Даны координаты (как целые от 1 до 8) двух полей шахматной доски. Определить, может ли конь за 1 ход перейти с одного из полей на другое.
11. Не пользуясь вспомогательными переменными, перераспределить значения переменных x и y так, чтобы в x оказалось большее из этих значений, а в y — меньшее.
12. Переменной k присвоить номер четверти плоскости, в которой находится точка с координатами x, y , ( x y* <>0).
Вычислить:
max(x y z, , ) − 2x⋅min(x y z,
, ) y = ![]() sin2
+ max(x y z, , )/min(x y z, , )
sin2
+ max(x y z, , )/min(x y z, , )
13. Даны числа a b c a b c1 1 1 2 2 2, , , , , . Напечатать координаты точки пересечения прямых, описываемых уравнениями a x b y c1 + 1 = 1 , a x b y c2 + 2 = 2, либо сообщить, что прямые совпадают, не пересекаются или вообще не существуют.
14. Дано целое k от 1 до 180. Определить, какая цифра находится в k -й позиции последовательности 10111213...9899, в которой выписаны подряд все двузначные числа.
15. Даны действительные числа x x x y y y1 2 3 1, , , , 2, 3. Определить, принадлежит ли начало координат треугольнику с вершинами (x y1 1, ), (x y2 2, ) ,
(x y2 2, ) .
16. Дано натуральное число n< 9999. Является ли это число "перевертышем" (палиндромом)?
17. На поле (k,1) шахматной доски расположен ферзь. Угрожает ли он полю (m n, ) ?
18. Выяснить, являются ли поля (k,1) и (m n, ) шахматной доски полями одного цвета.
19. Проверить, является натуральное число k степенью 3 или нет.
20. Дано 10 вещественных чисел. Вычислить разность между максимальным и минимальным из них.
21. Даны целое n>0 и последовательность из n вещественных чисел, среди которых есть хотя бы одно отрицательное число. Найти величину наибольшего среди отрицательных чисел этой последовательности.
22. Вычислить по алгоритму Горнера y x= 10 + 2x9 + 3x8 + +... 10x+11;
10 9 8
y=11x +10x +9x + + +... 2x 1.
23. Дана непустая последовательность различных натуральных чисел, за которой следует 0. Определить порядковый номер наименьшего из них.
24. Даны натуральное число n и вещественные числа t a, 0 1, a ,..., an. Вычис-
лить значение многочлена a x0 n +a x1 n−1+ +... a x an−1 + n и его производ-
2 ной в точке t + 0,5 .
25. Пусть задано значение x. Найти первое из чисел sin x , sinsin x , sinsinsin x ,..., меньшее по модулю 10–4.
26. Вычислить s — сумму всех чисел Фибоначчи, которые не превосходят 1000.
27. Вычислить для заданного n
n
∑sin(kn)
k=1
28. Выяснить, можно или нет натуральное число n представить в виде суммы трех полных квадратов.
29. Даны n — натуральное и вещественные пары x y1 1, ,..., x yn, n. Определить радиус наименьшего круга с центром в начале координат, внутрь которого попадают эти точки.
30. Дано 10 вещественных чисел. Найти порядковый номер того из них, которое наиболее близко к целому числу.
31. Дано 10 целых чисел. Определить, сколько из них принимает наибольшее значение.
32. Вычислить k — число точек с целочисленными координатами, попадающих в круг радиуса R .
33. Дано 10 вещественных чисел. Определить, образуют ли они возрастающую последовательность.
34. Дана последовательность положительных целых чисел, за которой следует 0 (признак конца последовательности). Вычислить среднее геометрическое этих чисел.
35. Подобрать всевозможные варианты размена произвольной > 6 руб. суммы с помощью двух- и пятирублевых монет.
36. Получить сумму нечетных отрицательных элементов последовательности целых чисел a a1 2, ,..., an.
37. Дано натуральное число n. Вычислить 1 2⋅ + 2 3 4⋅ ⋅ +...+ n n⋅( +1) ... 2 .⋅ ⋅ n
38. Преобразовать массив X , расположив его элементы в обратном порядке.
39. Преобразовать массив по следующему правилу (воспользовавшись массивом y как вспомогательным): все отрицательные элементы массива x перенести в его начало, а все остальные — в конец, сохраняя исходное взаимное расположение всех элементов (отрицательных в том числе).
40. Дано натуральное n. Сколько различных цифр встречается в его записи?
41. Переменной k присвоить либо номер первого вхождения y в массив x, либо число n+1, если y не входит в x.
42. Вычислить для массива из n элементов:
y x= 1 + x x1 2⋅ + x x x1 2⋅ ⋅ 3 +...+ x x x x1 2 3⋅ ⋅ ... m,
где m — либо номер первого отрицательного элемента массива x, либо число n, если в массиве x нет отрицательных элементов.
43. Элементы целочисленного массива x упорядочены по возрастанию. Требуется присвоить переменной k номер элемента массива x, равного числу y , или 0, если такого элемента нет.
44. Даны действительные числа a a1 2, ,..., an, b b1 2, ,..., bn. Вычислить
(a b1 + n) (⋅ a2 +bn−1) ... (⋅ ⋅ an +b1).
45. Проверить, имеется ли среди элементов массива x хотя бы одно число Фибоначчи.
46. Рассматривая массивы x, y и z как представление некоторых множеств из объектов типа индекс ( x k[ ] 1= , если элемент k принадлежит множеству x, и x k[ ] 0= иначе), реализовать следующие операции над этими массивами-множествами:
• z — объединение множеств x и y ;
• z — пересечение множеств x и y ;
• z — разность множеств x и y .
47. Дана последовательность из 10 целых чисел. Определить число инверсий в этой последовательности.
48. Дана последовательность из 10 целых чисел. Найти сумму чисел этой последовательности, расположенных между максимальным и минимальным числами (в сумму включить и оба этих числа).
49. Рассматривая массивы x и y как представление некоторых множеств из объектов типа индекс ( x k[ ] 1= , если элемент k принадлежит множеству x, и x k[ ] 0= иначе), проверить, что множество x является подмножест-
вом множества y .
50. Даны координаты n точек на плоскости: x y1 1, ,..., x yn, n (n=20). Найти номера двух точек, расстояние между которыми наибольшее (считать, что такая пара точек единственная).
51. Даны вещественные числа a a0 1, ,..., a15. Найти коэффициенты многочле-
на (x a x a− 0)( − 1)...(x a− 15).
52. Даны целые числа a a0 1, ,..., an. Получить новую последовательность, выбросив из исходной все члены, равные max(a a0 1, ,..., an).
53. В последовательности a a0 1, ,..., an поменять местами наибольший и наименьший члены.
54. Даны целые числа a a0 1, ,..., an. Получить новую последовательность, заменяя ai нулями, если ai не равно max(a a0 1, ,..., an), и единицами в противном случае.
55. Даны целые числа a a0 1, ,..., a2n. Получить
max(a a a a1+ 2n, 2 + 2 1n− ,..., a an + n+1).
56. Определить число различных элементов массива X.
57. Заполнить массив A следующим образом:
1 2 . . .10
11 12 . . .20
21 22 . . .30
. . . . . . . . . .
91 92 . . .100
58. Дана вещественная матрица порядка n m× . Упорядочить ее строки по неубыванию их наибольших элементов.
59. Определить, симметрична ли заданная целая квадратная матрица n-го порядка (относительно главной диагонали)
60. Дана вещественная матрица n m× , все ее элементы различны. Найти скалярное произведение строки с наибольшим элементом матрицы на столбец с наименьшим элементом.
61. Определить, является ли магическим квадратом заданная целая квадратная матрица n-го порядка (т. е. таким, где суммы элементов во всех строках и столбцах одинаковы).
62. Дана матрица n m× . Переставляя ее строки и столбцы, переместить наибольший элемент в верхний левый угол.
63. Заполнить массив A следующим образом:
1 2 3 . . .10
0 1 2 . . . 9
0 0 1 . . . 8
. . . . . . . . .
0 0 0 . . . 1
64. Получить массив B из массива A удалением n-й строки и k -го столбца.
65. В заданной квадратной целочисленной матрице указать индексы всех элементов с наибольшим значением.
66. Дана вещественная матрица n m× . Упорядочить ее строки по неубыванию суммы их элементов.
67. Преобразовать массив S , поворачивая его вокруг центра на 90 градусов против часовой стрелки.
68. Cедловая точка — элемент матрицы, наименьший в своей строке и одновременно наибольший в своем столбце или наоборот. Для заданной матрицы n m× найти индексы всех ее седловых точек.
69. Определить, является ли заданная целая квадратная матрица 10-го порядка ортонормированной, т. е. такой, что скалярное произведение каждой пары различных строк равно нулю, а каждой строки на себя равно еди- нице.
70. Все элементы с наибольшим значением в данной целочисленной матрице заменить нулями.
71. Найти номера строк квадратной целочисленной матрицы, элементы в каждой из которых одинаковы.
72. Найти номера строк квадратной целочисленной матрицы, элементы каждой из которых образуют монотонную последовательность.
73. Напечатать в одну строку все буквы между 'A' и 'Z', включая и эти буквы.
74. Проверить, правильно ли в текст входят круглые скобки. Ответ ДА или
НЕТ.
75. Удалить из текста все буквы 'b'.
76. Удалить из текста все буквы 'k', идущие сразу за буквой 'n'.
77. Напечатать текст, удалив из него лишние пробелы, т. е. чтобы пробелы встречались по одному.
78. Подсчитать число слов в тексте, содержащих букву 'd'.
79. Подсчитать число слов в тексте, содержащих 1 букву 'a' и 2 буквы 'b'.
80. Напечатать текст, подчеркивая в нем заглавные буквы (строкой ниже).
81. Если в заданный текст входит каждая из букв слова 'key', напечатать yes, иначе no.
82. Напечатать букву, которая идет в тексте непосредственно за буквой 'a'.
83. Удалить из текста все пары букв 'oo'.
84. Напечатать все слова в тексте задом наперед.
85. Подсчитать число слов в тексте, оканчивающихся буквой 'w'.
86. Проверить, является ли данное слово перевертышем.
87. Подсчитать число слов в тексте, содержащих ровно 3 буквы 'е'.
88. Значениями литерных переменных являются цифры. Присвоить составленное из них число целой переменной.
89. Удалить из слов в тексте все гласные буквы.
90. Если слово нечетной длины, удалить из него среднюю букву.
91. Рассортировать английские слова в алфавитном порядке.
92. Подсчитать частоты вхождения букв в текст.
93. Заменить в тексте строчные буквы прописными, а прописные строчными.
94. Найти в тексте самое большое целое число.
95. Определить наибольший общий делитель трех натуральных чисел.
96. Получить число 2500, выводя его по одной цифре.
97. Вывести таблицу зависимости от n количества целых чисел взаимно простых с n.
98. Даны коэффициенты многочленов P x( ), Q x( ) и число a . Вычислить P a Q a P a( + ( ) ( +1)).
99. Три прямые заданы уравнениями. Если они попарно пересекаются и образуют треугольник, то найти его площадь.
100. Даны координаты вершин двух треугольников. Определить, какой из них имеет наибольшую площадь.
101. Получить число 1!+2!+...+100!, выводя его по одной цифре.
102. Получить число 1!+2!+...100!, выводя по n цифр.
103. Вывести таблицу зависимости от n количества положительных делителей числа n.
104. Напечатать пары дружественных чисел, не превосходящих n.
105. Найти наименьшее общее кратное четырех заданных натуральных чисел.
106. Даны координаты вершин треугольника и точки внутри него. Найти расстояние от этой точки до ближайшей стороны.
107. Дано m n-мерных матриц. Выбрать из них матрицу с наименьшим следом.
108. Заменить члены последовательности ai величинами aii.
109. Даны координаты вершин треугольника и точка. Определить, принадлежит ли эта точка треугольнику.
110. Заменить полные квадраты в матрице их квадратными корнями, остальные элементы — нулями.
111. Найти периметр десятиугольника, заданного координатами вершин.
112. Для четного числа n>2 проверить гипотезу Гольдбаха.
113. Составить функцию, заменяющую в тексте буквы их номерами по порядку в алфавите.
Лабораторная работа 1. Выражения, ветвление.
1. Определить, есть ли среди первых трех цифр из дробной части заданного положительного вещественного числа цифра 0.
2. Определить, есть ли среди цифр заданного трехзначного числа одинаковые.
3. Определить, равен ли квадрат заданного трехзначного числа кубу суммы цифр этого числа.
Лабораторная работа 2. Циклы и ветвления.
1. Подсчитать k — число цифр в десятичной записи целого неотрицательного числа n.
2. Дано не менее трех различных натуральных чисел, за которыми следует нуль. Определить три наибольших числа среди них.
3. Напечатать в возрастающем порядке все трехзначные числа, в десятичной записи которых нет одинаковых цифр (деления не использовать!).
Лабораторная работа 3. Одномерные массивы.
1. В целочисленном массиве A содержится 10 чисел от 0 до 9 включительно, а в целочисленном массиве B — 2 целых числа от 0 до 9. Переменной x
bb1 2 присвоить вещественное число 0.a a a0 1... 9 ⋅10 .
2. По массиву t , где указана температура каждого дня некоторого невисокосного года, определить m — название месяца с наибольшей среднемесячной температурой.
'
3. Преобразовать массив X по следующему правилу ( xk — значение k -го
' элемента массива после преобразования): xk = max( )xi при 1< <i k.
Лабораторная работа 4. Двумерные массивы.
1. Заполнить массив A по правилу: A Xij = ij, где массив X задан.
2. Определить k — число "особых" элементов массива C, считая элемент "особым", если он больше суммы остальных элементов своего столбца.
3. Определить k — число различных элементов матрицы C (т. е. повторяющиеся элементы считать один раз)
Лабораторная работа 5. Литеры и строки.
1. Подсчитать число слов в тексте, начинающихся и заканчивающихся одной и той же буквой.
2. Удалить из слова повторяющиеся буквы.
3. Подсчитать частоты длин слов в тексте.
Лабораторная работа 6. Функции.
1. Получить число 2500, выводя по n цифр.
2. Написать функцию, приводящую дробь к несократимому виду.
3. Составить функцию сжатия исходной последовательности символов (для повторяющихся символов ввести число повторений: aaaaaa a→ (6) ).
5.6. Элементы объектного программирования
![]() Учебный материал
Учебный материал
Современный подход к проектированию программ основан на декомпозиции задач. Целью при декомпозиции является создание модулей, которые представляют собой небольшие, относительно самостоятельные программы, взаимодействующие друг с другом по хорошо определенным и простым правилам. Если эта цель достигнута, то разработка отдельных модулей может осуществляться различными людьми независимо друг от друга, при этом объединенная программа будет функционировать правильно.
Основой декомпозиции является использование абстракций.
Различают абстракцию через параметризацию и через спецификацию. Суть абстракции через параметризацию состоит в том, что один алгоритм можно применять для решения задач, отличающихся различными исходными данными, задаваемыми как параметры. Суть абстракции через спецификацию состоит в том, что одну и ту же задачу можно решить по разным алгоритмам и получить один и тот же искомый результат. При абстракции через спецификацию описываются результаты работы программы.
На стадии проектирования программы спецификации трансформируются в структуру системы. Методологии, используемые на этой стадии, делятся на две группы:
ориентированные на обработку; ориентированные на данные.
Наиболее известны следующие методологии, ориентированные на обработку:
модульное программирование;
метод функциональной декомпозиции;
метод проектирования потока данных;
метод проектирования структур данных;
метод HIРO (иерархия, ввод, обработка и вывод) фирмы IBM. Познакомиться с этими методиками можно по специальной литературе.
Среди методов, ориентированных на данные, следует упомянуть методологии Джексона и Уорнера. Структура данных в них используется как ключевой элемент в построении хорошего программного проекта. Используя входные и выходные структуры как основу, пытаются получить хорошо структурированные программы. Программа рассматривается как механизм, с помощью которого входные данные преобразуются в выходные.
В методологии Джексона основные действия сводятся к следующему:
1. Идентифицировать и изобразить структуру входных данных и структуру выходных данных.
2. Изобразить структуру программы, соединяя изображения этих структурных элементов.
3. Определить дискретные операции, составляющие программу.
4. Превратить операции в текст программы.
Методология Уорнера подобна методологии Джексона в том, что ключом к проекту программы являются структуры данных. Однако процедура проектирования более детализирована. Используются четыре вида представления проекта: диаграммы организации данных, диаграммы логического следования, список инструкций, псевдокод. Диаграмма организации данных описывает входные и выходные данные. Диаграммы логического следования представляют поток этих данных. Список инструкций содержит команды, используемые в проекте. Псевдокод используется при описании конечных результатов проектирования. Методология Уорнера может быть обобщена следующим образом:
1. Идентифицировать все входные данные системы.
2. Организовать входные данные в иерархическую форму.
3. Определить детальный формат каждого элемента входного файла и зафиксировать число их появлений.
4. Повторить шаги 1—3 для выходных данных.
5. Специфицировать детали программы, идентифицируя типы команд, содержащихся в проекте, в следующем порядке: чтение, ветвление, вычисление, выходы, вызовы подпрограмм.
6. Использовать диаграммы типа блок-схем для показа логической последовательности инструкций, применяя специальные символы для представления начала процесса, конца процесса, ветвления и вложения.
7. Пронумеровать элементы логической последовательности и раскрыть их с помощью инструкций, записанных на шаге 5.
В настоящее время популярность методологий, ориентированных на данные, растет. В первую очередь, это объектно-ориентированное программирование. Использование объектно-ориентированной технологии разработки программ позволяет повысить качество разработок и сократить время на них более чем в 10 раз.
Объектно-ориентированная методология проектирования программ основана на концепции совместного хранения данных и обрабатывающих их алгоритмов. В объектном подходе используются три базовых элемента: объекты, сообщения и классы.
Каждый объект содержит некоторую структуру данных (или тип данных) и набор процедур (методов), предназначенных для манипулирования этими данными. Объекты являются автономными модулями, содержащими всю необходимую для их выполнения информацию, что делает их идеальными строительными блоками для создания сложных программных систем различного назначения.
Сообщения используются для связи между объектами. В общем случае сообщение состоит из трех частей: идентификатора объекта-адресата, имени метода (процедуры), который должен выполняться в объекте-адресате, а также необходимой для определения режима выполнения метода дополнительной информации.
Классы объектов вводятся в случаях, когда требуется большое количество однотипных объектов, в этом случае неэффективно для каждого объекта хранить всю информацию о его методах и переменных. Классы являются своего рода шаблонами для объектов-экземпляров, содержащих информацию, необходимую для генерации объектов, включая определения методов и переменных. Экземпляры объектов при этом отличаются лишь значениями объектных переменных. Внутри классов часто имеется сложная иерархия подклассов. Подклассы высших в иерархии классов наследуют свойства низших подклассов и, таким образом, оказываются гибким и мощным средством проектирования модульных программных систем на основе готовых методов.
Основные шаги разработки программы, предусмотренные данной методологией:
1. Определить проблему.
2. Разработать неформальную стратегию, представляющую общую последовательность шагов, удовлетворяющую требованиям к будущей программе.
3. Формализовать стратегию, для чего:
• идентифицировать объекты и их атрибуты;
• идентифицировать операции;
• установить интерфейсы;
• реализовать операции.
Большинство современных языков и систем программирования развивается в направлении все большего использования объектной методологии в создании программ. Характерными примерами являются универсальные языки Паскаль, Си и даже Бейсик, в современных версиях которых появились средства объектно-ориентированного программирования. Так, начиная с версии 5.5, наиболее широко распространенные системы программирования на Паскале компании Borland предусматривают метод проектирования программ на основе объектно-ориентированного программирования. Ярким примером объектно-ориентированного программирования является операционная среда Windows. Существуют и языки программирования, полностью ориентированные на объектный подход к программированию. Таким языком является SmallTalk, считающийся языком разработки систем искусственного интел-
лекта.
Рассмотрим основы объектного программирования в системе Паскаль компании Borland.
Объект в Турбо-Паскале — это структура данных, содержащая поля данных (аналогично типу record — запись) различных типов и заголовки методов. Методы — это процедуры и/или функции, объявленные и действующие внутри объекта. Основными отличительными свойствами объектов являются:
инкапсуляция — объединение записей с процедурами и функциями, работающими с этими записями, что превращает их в новый тип данных — объекты;
наследование — задание объекта с последующим использованием его для построения иерархии порожденных объектов с наследованием доступа каждого из порожденных объектов к процедурам и данным предка;
полиморфизм — присвоение одного имени процедуре, которая передается вверх и вниз по иерархии объектов, с выполнением этой процедуры способом, соответствующим каждому объекту в иерархии.
Синтаксис описания объекта:
<ИмяПотомка>= object<ИмяПредка> поле; ...
поле; метод; ... метод; end;
В отличие от записи, полями объекта могут быть, кроме данных, еще и методы, обрабатывающие эти данные.
Метод — это процедура или функция, объявленные внутри описания объекта.
Синтаксис описания метода: procedure <Заголовок> (<Параметр1>, <Параметр2>: integer);
Метод имеет доступ к полям данных объекта, не требуя передачи их ему в виде параметров. Так же, как модуль скрывает детали реализации процедур от пользователя, объект может скрывать свои поля и методы. Для этого используется ключевое слово private (личный). Личные поля и методы доступны только внутри метода.
Объявление метода внутри объявления объектного типа содержит только заголовок. Тело метода определяется вне объявления объекта. Его заголовок должен содержать имя объекта, которому принадлежит метод.
procedure <ТипОбъекта.Метод> (<Параметр1>, <Параметр2> : integer); begin ... ... end;{Метод} Пример:
type
Point = object
X,Y : integer; Visible : boolean; procedure Create (a,b: integer); procedure SwitchOn; procedure SwitchOff; procedure Move (dx,dy : integer); function GetX : integer; function GetY : integer; end;
Методы подразделяют на статические и виртуальные. Виртуальный метод отличается от статического тем, что реализующий его код подсоединяется к исполняемой программе не в процессе компиляции, а в процессе выполнения, что достигается так называемым поздним связыванием. Это дает возможность строить иерархию объектов с одинаковыми названиями методов, реализуемыми, однако, различными кодами.
Связь между методами и вызывающими их процедурами может устанавливаться во время трансляции (раннее связывание) или во время выполнения программы (позднее связывание). Такие методы должны быть виртуальными (ключевое слово — virtual). Синтаксис виртуального метода: procedure <Метод> (<Параметр1>, <Параметр2> : integer) : virtual;
При указании в описании объекта родительского типа методы объекта предка наследуются потомком, но при необходимости они могут быть переопределены. Для этого достаточно задать новый метод с тем же именем, что и родительский, но с другим телом (и набором формальных параметров, если необходимо).
Методы подразделяются на статические и виртуальные. Статические методы размещаются в памяти, и на них разрешаются ссылки во время компиляции программы. Размещение виртуальных методов и разрешение на них ссылок происходит динамически во время выполнения программы. Виртуальные методы позволяют реализовать чрезвычайно мощное свойство объектов — полиморфизм. Преимуществом полиморфных объектов является то, что они допускают обработку объектов, тип которых неизвестен во время компиляции программы.
Существуют специальные виды методов, имеющие возможность динамически распределять и освобождать объекты в памяти компьютера. Такие методы называются конструкторами (constructor) и деструкторами (destructor):
constuctor [ИмяОбъекта.]<ИмяМетода>[(Параметры)]; destuctor [ИмяОбъекта.]<ИмяМетода>[(Параметры)];
Конструктор — это специальный метод, инициализирующий объект, содержащий виртуальные методы. Конструктор инициализирует объект путем установления связи между объектом и специальной таблицей виртуальных методов, содержащей адреса кодов, реализующих виртуальные методы. Конструктор может также использоваться для инициализации полей данных объекта. Конструкторы используются для инициализации вновь образованных объектов, состоящей в передаче значений в параметры конструктора.
Применение виртуальных методов налагает ограничения на процедуры инициализации, которые должны записываться с зарезервированным словом constructor и иметь общее имя Init.
Каждый отдельный экземпляр объекта должен инициализироваться с помощью отдельного вызова конструктора.
Заголовок конструктора начинается словом constructor вместо procedure. Действия, обратные действиям конструктора, выполняет специальный метод деструктор (заголовок — destructor).
Деструктор — это специальный метод, освобождающий память "кучи" (heap) от динамических объектов.
Слово privat позволяет ограничить доступ к полям объекта, оставляя возможность их использовать лишь через методы этого объекта.
Переменные объектного типа могут быть динамическими, то есть размещаться в памяти только на время их использования. Для работы с динамическими объектами используется расширенный синтаксис процедур New и Dispose, содержащих в качестве второго параметра вызов конструктора или деструк-
тора:
New (P, Conctructor);
Dispose(P, Destructor);
Эквивалентные операторы:
New (P);
P^.Constructor;
P^.Dispose;
Dispose(P);
Основными отличительными свойствами объекта являются:
инкапсуляция — объединение записей с процедурами и функциями, работающими с этими записями;
наследование — задание объекта, затем использование его для построения иерархии порожденных объектов с наследованием доступа каждого из порожденных объектов к коду и данным предка;
полиморфизм — задание одного имени действию, которое передается вверх и вниз по иерархии объектов, с реализацией этого действия способом, соответствующим каждому объекту в иерархии.
Рассмотрим смысл каждого из перечисленных свойств на примере построения на экране дисплея точек разных цветов (звездного неба).
Инкапсуляция — это объединение в одном понятии информации о свойствах некоторого объекта и операций над ним. Основой решения задачи является задание положения (позиции) отдельной точки на экране, описываемого координатами X и Y. Для задания координат подходит тип "запись":
Pozition = record X, Y : integer; end;
Далее может быть необходимо задать значения координат (такая процедура носит название инициализации). Создадим соответствующую процедуру:
procedure Init(CoordX, CoordY : integer); begin
X: = CoordX; Y: = CoordY; end;
Затем потребуется знание фактических значений координат. Для этого вводим две функции:
function GetX: integer; begin GetX: = X; end; function GetY: integer; begin GetY: = Y; end;
По нашему замыслу процедура Init и функции GetХ и GetY должны работать только с полями записи Pozition.
Введение объектов позволяет зафиксировать это положение, объявив и поля, и действия над ними в единой конструкции:
Pozition = object X,Y: integer; procedure Init(CoordX, CoordY : integer); function GetX: integer; function GetY: integer; end;
Процедура Init и функции GetX и GetY являются методами объекта Pozition.
Для инициализации экземпляра типа Pozition достаточно вызвать его метод, как если бы он был полем записи:
var
FirstPozition: Pozition; ...
FirstPozition.Init(10,15);
Метод задается так же, как и процедура в модуле: внутри объекта записывается заголовок (как в секции Interface модуля); при этом все поля, используемые методом, должны предшествовать его объявлению. Определение метода (расшифровка действий) происходит вне объявления объекта. Имя метода должно предваряться названием типа объекта, которому метод принадлежит, сопровождаемым точкой.
Например:
procedure Pozition.Init (CoordX, CoordY: integer); begin
X: = CoordX; Y: = CoordY; end;
Заметим, что имена формальных параметров метода не могут совпадать с именами полей данных объекта.
Так же как модуль скрывает детали реализации процедур от пользователя, объект может скрывать свои поля и методы. Для этого используется ключевое слово private (личный). Личные поля и методы доступны только внутри метода. Объявление выглядит следующим образом:
type
ObjectName=object поле; . . . поле; метод; . . . метод; private поле; . . . поле; метод; . . . метод; end;
Наследование — определение нового объекта с использованием свойств ранее объявленных объектов, дополняя или изменяя их.
type
Star = object(Point) procedure Create (a,b: integer); procedure Move (dx,dy : integer); end;
Рассмотрим точку с координатами X и Y. Ее можно сделать видимой или невидимой, ей можно задать цвет, ее можно переместить.
Создадим объект с такими возможностями:
Point=object X,Y : integer; procedure Init(CoordX, CoordY : integer); function GetX : integer; function GetY : integer;
Visible: Boolean; Color: Word; procedure Init(CoordX, CoordY: integer; InitColor: Word); function Is Visible : Boolean; procedure Show;{показывает точку} procedure Blind;{стирает точку} procedure Jump(NextX, NextY : integer);{перемещает точку} end;
Заметим, однако, что поля X, Y и методы GetX, GetY практически совпадают с соответствующими полями и методами объекта Pozition.
Турбо-Паскаль предоставляет возможность учесть эту ситуацию. Следует считать тип объекта Point порожденным типом Pozition, записав это следующим образом:
Point=object(Pozition)
Visible: Boolean; Color: Word; procedure Init(CoordX, CoordY: integer; InitColor: Word); function Is Visible: Boolean; procedure Show; procedure Blind; procedure Jump(NextX, NextY : integer); end;
Объект Point теперь наследует свойства объекта Pozition. Поля X, Y явно не заданы в Point, но Point ими обладает благодаря наследованию, т. е. можно написать:
Point.Х:=17;
Смысл объектно-ориентированного программирования заключается в работе с полями объекта через его методы.
Полиморфизм — следствие наследования, возможность использования одного имени для различных действий, в зависимости от типа объекта. Предположим, надо создать объект "кружок". Очевидно, что новый объект должен иметь предком объект Point, обладая всеми его свойствами, кроме того, быть больше по размеру. Однако ясно, что "высветить" точку и закрашенную окружность не удастся одними и теми же командами. Турбо-Паскаль разрешает сохранить потомку имя родительского метода, "перекрывая" его. Чтобы перекрыть родительский метод, надо просто задать его с тем же именем, но с другим телом (кодом) и, если необходимо, с другим набором параметров. Такой метод делается виртуальным, и к его объявлению добавляется слово virtual. Применение виртуальных методов налагает ограничения на процедуры инициализации, которые должны записываться с зарезервированным словом constructor и иметь общее имя Init.
Каждый отдельный экземпляр объекта должен инициализироваться с помощью отдельного вызова конструктора.
Для очистки и удаления динамически распределенных объектов существует специальная процедура destructorDone.
Деструктор комбинирует шаг освобождения памяти в "куче" с некоторыми другими задачами. Метод деструктора может быть пустым, поскольку работу выполняет не только код тела, но и код, генерируемый Турбо-Паскалем в ответ на зарезервированное слово destructor.
Тип "объект" в Паскале тесно связан с модульным программированием. В этой связи вспомним основные понятия модуля. Модуль в Паскале — это самостоятельная программная единица, объединяющая совокупность программных ресурсов, предназначенных для использования другими модулями и программами. Структура модуля представлена далее:
Unit <UnitName>;
Interface
<описания видимых объектов>
Implementation
<описания скрытых объектов> begin
<операторы инициализации объектов модуля> end.
Каждый модуль компилируется отдельно с созданием файла с расширением tpu. Доступ к интерфейсным объектам модуля осуществляется специфика- цией uses UnitName;
Как правило, в интерфейсной части модуля определяют объектные типы.
В разделе implementation осуществляется реализация методов объектов.
Пример:
unit matrices; interface uses crt; const max = 3; type str10 = string[10]; matrix = array[1..max,1..max] of pointer; complex = record re, im : real; end; complex_ptr = ^complex; complex_matrix = array[1..max, 1..max] of complex;
matrix_obj = object M : matrix; constructor init; procedure set_to_zero(var p:pointer); virtual; procedure scalar_sum(const p,q: pointer; var r: pointer);virtual; procedure scalar_product(const p,q: pointer; var r: pointer); virtual; procedure matrix_sum(const A,B: matrix); procedure print(name : str10); destructor done; end; implementation constructor matrix_obj.init; begin end; procedure matrix_obJ.matrix_product(const A,B: matrix); var i,j,k: word; prod, sum: pointer; begin getmem(prod, SizeOf(M[1,1])); for i:=1 to max do for k:=1 to max do begin sum:= M[i,k]; set_to_zero(sum); for J:=1 to max do begin scalar_product(A[i,J], B[J,k], prod);
scalar_sum(sum, prod, sum); end end; freemem(prod,SizeOf(M[1,1])); end; . . . destructor matrix_obJ.done; begin end; end.
Объектно-ориентированный подход позволяет создавать объектные среды, библиотеки объектов для последующего использования при разработке программ. Особенно широкую известность получили объектные оболочки для разработки интерфейсов программ в некотором едином, ставшем стандартным, стиле, включающем:
многократные перекрывающиеся окна с изменяемыми размерами;
выпадающие меню;
поддержку мыши;
встроенную установку цвета;
кнопки, полосы прокрутки, окна ввода, зависимые и независимые кнопки;
стандартную обработку клавиш и нажатий мыши; и многое другое.
Программа обычно взаимодействует с пользователем через одно или более окон или диалоговых окон, которые появляются и исчезают на рабочем столе в соответствии с командами от мыши или клавиатуры.
Современные объектно-ориентированные системы типа Visual Basic, Delphi совершенно скрывают механизмы программирования и позволяют разрабатывать интерфейсы программ-приложений вообще без кодирования команд, пользуясь лишь средствами наглядного проектирования на экране дисплея.
С появлением графической среды Windows стандартных возможностей языка Паскаль стало недостаточно для эффективной разработки программных комплексов, имеющих развитый пользовательский интерфейс. Конечно, реализовать программу с современным оконным интерфейсом на Паскале было возможно, но для этого требовалось немалое мастерство и достаточно большое количество времени.
Чтобы исправить это положение, в 1996 году фирма Borland, известная во всем мире своими разработками в области реализации языков программирования, выпустила компилятор нового поколения Delphi (Дельфи). По единодушному мнению специалистов, Delphi для Windows стал "одним из самых замечательных продуктов современной компьютерной индустрии". Программисты всего мира утверждают, что Delphi снова сделала программирование удовольствием.
Delphi — это развитая система программирования, включающая мощный компилятор языка Паскаль, дополненный рядом существенно новых возможностей для программирования в среде Windows; имеющая интерфейс качественно нового типа, позволяющий при составлении текста программы видеть те графические объекты, для которых она пишется, — так называемая система визуального программирования.
Delphi является системой программирования очень высокого уровня. Она берет на себя значительную часть работы по управлению компьютером, что делает возможным в простых случаях обходиться без особых знаний о деталях его работы. В отличие от традиционных систем программирования, Delphi даже пишет "за нас" значительную часть текста программы: описания объектов, заголовки процедур и многое другое. Нам остается только вписать необходимые строчки, определяющие индивидуальное поведение программы, которые система "не в состоянии предугадать". Но даже здесь Delphi во многих случаях сама указывает место, где нужно разместить эти строки.
Вершиной автоматизации процесса программирования являются так называемые эксперты. Эксперт — это диалоговое окно, которое помогает пользователю описать, что он хочет видеть в своей программе. Например, эксперт проекта спрашивает, нужно ли вам системное меню (а если да, то достаточно пометить требуемые его стандартные пункты), и какого из предложенных типов ваш проект.
Проанализировав введенные ответы, Delphi пишет код программы на Паскале. Отметим, что эксперты могут быть созданы самим пользователем.
Чтобы составить себе некоторое представление о работе в Delphi, давайте проследим за реализацией в системе конкретной пробной программы, рекомендованной в качестве первого шага освоения Delphi. Прежде всего, договоримся опустить для простоты описание несущественных сейчас деталей, касающихся вида экрана и объектов управления на нем (тем более, что эта часть как раз подробно описывается в литературе). Сосредоточим все свое внимание на сути процесса создания программы в среде Delphi.
Итак, приступим к работе над нашей первой задачей. Хотя до сих пор мы еще ничего не успели сделать, система при запуске уже выполнила значительную работу. Во-первых, она создала для нашей программы стандартное окно (в Delphi его принято называть формой), и мы видим его на экране. Во-вторых, уже сгенерирован текст программы довольно приличной длины, который необходим для порождения этой формы на экране.
Теперь попробуем что-нибудь сделать сами. Выберем из предлагаемого нам широкого ассортимента стандартных объектов наиболее простой — кнопку. Найдем ее изображение в верхней части экрана (в Delphi ее называют Палитрой компонентов) и щелкнем на нем мышью. Тем самым мы дали системе знать, что нам нужна именно кнопка. Остается указать, в какое место формы поместить компонент. Подведем курсор мыши к требуемому месту и снова щелкнем — появится изображение кнопки. При необходимости с помощью мыши кнопку можно легко передвинуть или изменить ее размеры.
Заметим, что текст программы после появления кнопки увеличился — Delphi автоматически добавила необходимое описание.
Уже сейчас можно посмотреть на то, что получилось, в действии. Запустим программу и увидим на экране симпатичное стандартное окно Windows, содержащее кнопку. В отличие от этапа проектирования, компоненты при выполнении программы "оживают" — если щелкнуть по нашей кнопке мышкой, то будет видно, как она нажимается. Правда, никакого эффекта пока нет, т. к. мы этим еще не занимались.
Итак, мы уже запустили собственное Windows-приложение, хотя не набрали еще ни одной строчки текста с клавиатуры!
Теперь заставим нашу кнопку что-нибудь сделать. Для этого придется, наконец, начать писать программу. К счастью, и это совсем несложно. Вернемся в режим проектирования и дважды щелкнем мышью по нашей кнопке. При этом мы увидим, что Delphi вынесла на первый план текст программы и установила маркер в то место, где мы должны набирать текст, тем самым как бы призывая описать действия по нажатию на кнопку. Давайте введем строку
Form1.Color:=clAqua;
Несколько слов о смысле этой строки. Свойство Color (цвет) объекта Form1 (нашей формы) получает значение clAqua (буквы cl указывают на цвет, а Aqua — это название одного из 16 стандартных цветов. Снова запустим программу и нажмем нашу кнопку — форма поменяет свой цвет!
Описанный ранее пример очень хорошо показывает стиль работы с Delphi. Конечно, реальные задачи посложнее, но работа протекает примерно так же. Очевидно, что Delphi вполне доступна для освоения школьнику.
На примере нашей первой программы мы видели, что многие компоненты Delphi имеют свое визуальное изображение.
Замечательным достоинством системы является то, что размещение компонентов на экране, а также задание начальных значений их свойств (размеры, цвет, вид бордюра и др.) Delphi позволяет осуществлять на этапе конструирования формы без написания какой-либо программы. Для этой цели предусмотрено специальное окно, называемое Инспектором объектов, в котором перечислены все доступные в режиме проектирования свойства выделенного компонента и их текущие значения. Разумеется, любое из них при необходимости легко изменить, что немедленно скажется на внешнем виде объекта.
Например, если в окне Инспектора объектов изменить цвет, то система тут же перекрасит компонент. Иными словами, можно до запуска программы видеть, как будет выглядеть на экране проектируемая форма.
Такой способ работы с объектами, имеющими графическое представление, принято называть визуальным программированием.
Delphi — не единственная система визуального программирования, но на сегодняшний день она, несомненно, самая передовая — это попытка фирмы Borland обобщить лучшее, что было создано на тему визуального программирования, в единый продукт.
Визуализация процесса позволяет значительно быстрее увидеть результат своих усилий, делает его очень наглядным и опирающимся на достаточно глубокие понятия и навыки человека. Не последнюю роль при этом, повидимому, играют эмоции и эстетические чувства, стремление красиво разместить объекты, подобрать их цвет и т. п.
Замечено, что даже люди, которые не умеют рисовать, часто с интересом и удовольствием занимаются построением изображений из готовых элементов.
Какие еще перспективные черты заложены в систему Delphi?
Напомним, что Delphi работает в самой современной на сегодня среде Windows и позволяет создавать для нее программные продукты.
Delphi является системой объектного программирования, которое сейчас также переживает период бурного роста. Delphi позволяет не только использовать уже ставшие классическими объекты типа Object, но и позволяет создавать новые, которые могут иметь графическое изображение и обладать свойствами стандартных элементов среды Windows. Такие объекты получили название визуальных компонентов; для их описания используется специальное зарезервированное слово Class. Помимо уже встречавшихся ранее формы и кнопки, примерами визуальных компонентов могут служить меню, списки, поля редактирования, полосы прокрутки, таблицы и многое, многое другое. К Delphi прилагается целая библиотека стандартных визуальных компонентов — Visual Component Library. Очень важно, что библиотека эта не является чем-то законченным, и каждый пользователь может научиться добавлять в нее собственные компоненты.
Еще одной существенной чертой системы программирования Delphi является ее открытость: почти все имеющиеся в системе объекты реализованы на языке Паскаль и могут быть легко дополнены новыми. Например, если вас по какой-то причине не устраивает стандартный редактор чисел, вы можете написать собственный и подключить его к системе. Таким образом, среда Delphi содержит все наиболее передовые черты системы программирования. Она является мощным и в то же время несложным в использовании инструментальным средством для создания приложений с современным интерфейсом, в том числе и обучающих программ.
Delphi сделала разработку мощных приложений Windows быстрым процессом. Приложения Windows, для создания которых требовалось большое количество умелых программистов на C++, теперь могут быть написаны одним человеком, использующим Delphi. Из-за своего высокого уровня системы программирования типа Delphi даже получили специальное название — среда быстрой разработки приложений (Rapid Application Development, RAD).
Если посмотреть на компоненты, входящие в стандартную библиотеку, то многие из них словно специально созданы для обучающих программ. Рассмотрим несколько примеров.
Возьмем переключатель, иначе радиокнопку — группу кнопок, названную так благодаря функциональному сходству с переключателями в радиоаппаратуре. Основной особенностью переключателей является то, что из всей группы в нажатом состоянии всегда находится только одна кнопка. В педагогической интерпретации это выглядит как наиболее примитивный метод опроса — выбор единственного правильного ответа из списка предложенных. Если же вам захочется иметь несколько правильных ответов на вопрос, возьмите другую разновидность кнопок — Check Box (обычно этот термин переводят как "кнопки с независимой фиксацией"). У таких кнопок состояние никак не зависит от окружающих кнопок.
Для тех, кому традиционное тестирование кажется устаревшим, найдутся другие компоненты, например Image — образ, изображение. Помимо возможности разместить картинку на экране, этот полезный компонент обладает способностью "чувствовать на себе" щелчок мыши, что позволяет элементарно реализовать контроль вопросов типа "Найдите и укажите на карте остров Мадагаскар". Кроме того, во все компоненты библиотеки Delphi заложена технология Drag and Drop (перетащи и оставь). Благодаря ей можно при выполнении задания располагать объекты на экране определенным образом — "Составьте схему из батареи, амперметра, выключателя и резистора".
Наконец, если у вас в компьютере есть устройство считывания с компактдисков или хотя бы набор звуковых файлов, в Delphi предусмотрен специальный компонент — проигрыватель, позволяющий включить в ваш урок музыку или звуки.
Важным достоинством Delphi как инструментальной среды является то, что ее компилятор делает автономные (!) EXE-файлы.
Они будут работать в среде Windows НА ЛЮБОЙ машине, даже если там нет и никогда не было самой системы Delphi. Это свойство выгодно отличает Delphi от других аналогичных сред, например от Microsoft Visual Basic.
Завершая наше краткое знакомство с системой Delphi, рассмотрим некоторые наиболее важные базовые понятия, лежащие в ее основе.
Все объекты в Delphi характеризуются свойствами. Свойство — это атрибут объекта, определяющий то, как объект выглядит или как он может себя вести. Например, свойства, определяющие внешний вид кнопки: color — ее цвет, left и top — координаты левого верхнего угла, heigt и width — высота и ширина. В качестве примера свойств, определяющих, как кнопка может себя вести, опишем свойство enabled (от английского "давать возможность", "разрешать", "разблокировать", "включать"). Оно может принимать значения true или false — в зависимости от этого кнопка либо будет фиксировать на себе щелчок мыши, либо нет.
Отметим, что свойство является своеобразным обобщением понятия поля объекта Object, т. к. помимо имени и типа дополнительно содержит способы записи и чтения значения поля.
Например, при выполнении строки
Form1.Color := clAqua;
происходит не просто запись значения, характеризующего цвет, в определенное место памяти, а вызывается метод Form1.SetColor(clAqua). Этот метод не только производит присвоение, но и перекрашивает форму.
Еще одно важное понятие Delphi — это событие. Термин "событие" заимствован из Windows, его значение проще всего определить на примерах. В частности, событиями являются воздействия пользователя на клавиатуру или мышь (нажатие клавиши или ее отпускание, движение мыши и т. п.). Кроме того, событиями являются любые изменения состояния экрана: создание окна, изменение его размеров и многие другие. Таблица с описанием полного списка событий обычно занимает несколько страниц.
В ответ на любое событие в системе Windows передает управление обработчику события (event handler). Обработчик события — это программа, которая определяет реакцию объекта на это событие. Если пользователь не предусмотрел действия по данному событию, Windows обработает его сама; в частности, она может просто проигнорировать событие.
Благодаря такой идеологии, программа на Delphi фактически представляет собой совокупность относительно самостоятельных обработчиков всевозможных событий.
Остается рассмотреть последнее понятие — метод — это процедура или функция класса, определяющая поведение объекта.
Метод приводит к выполнению определенной последовательности действий, часть из которых может быть связана с изменением внешнего вида объекта. Скажем, применение к форме Form1 процедуры Close не просто удаляет ее из списка окон Windows, но и обеспечивает ее исчезновение с экрана. Другой пример — метод SetFocus для формы переносит на нее фокус ввода, т. е. она становится активной и принимает набор с клавиатуры. Кроме того, метод выносит изображение активного окна на первый план и выделяет цветом его заголовок.
Отметим, что понятие метода в Delphi не отличается от введенного ранее в Object Pascal.
![]() Контрольные вопросы
Контрольные вопросы
1. Какие методологии могут использоваться при проектировании программных систем?
2. В чем состоит смысл объектно-ориентированной методологии проектирования программ?
3. Каковы основные шаги разработки программы в объектно-ориентированной методологии?
4. Как описываются объекты в Паскале?
5. Какое отношение объекты в Паскале имеют к типу "запись"?
6. В чем отличие методов объектов от обычных процедур? Как методы задаются?
7. Что такое инкапсуляция, наследование и полиморфизм? Приведите примеры.
8. Чем отличаются статический и динамический методы?
9. Что такое конструктор и деструктор?
10. Охарактеризуйте библиотеки и средства объектно-ориентированного программирования.
 Темы для рефератов и докладов
Темы для рефератов и докладов
1. Развитие объектно-ориентированного программирования.
2. Smalltalk — язык объектного программирования.
3. Объектные возможности современных версий языка Basic.
4. Основы объектно-ориентированного языка программирования интернетприложений Java.
5. Средства визуального создания программ и объектно-ориентированное программирование.
6. Объектный подход за пределами программирования и информатики.
![]() Вопросы для обсуждения
Вопросы для обсуждения
1. Имеет ли пределы совершенствование методов и технологий программирования?
2. Как применить идеи объектно-ориентированного программирования в повседневной жизни?
![]() Задачи и упражнения
Задачи и упражнения
1. Определите объект "рациональные числа" (являющийся отношением целых чисел). Напишите методы для сложения, вычитания, умножения и деления дробей, приведения их к наименьшему общему знаменателю.
2. Определите объект "комплексные числа". Напишите методы для вычитания, сложения и умножения комплексных чисел.
![]() Лабораторные работы
Лабораторные работы
1. Изучите текст демонстрационных программ из коллекции фирмы Borland, поставляемых со средой программирования Turbo Pascal for Windows. Откомпилируйте и проверьте их выполнение. Как в этих примерах используется объектная библиотека Object Vision?
2. Создайте с помощью среды программирования Delphi оконный интерфейс к программам, написанным по задачам к этой главе.
5.7. Основы логического программирования на языке Пролог
![]() Учебный материал
Учебный материал
Общие сведения
Язык Пролог является представителем семейства языков логического программирования и в сравнении с традиционными языками программирования, предназначенными для записи алгоритмов, такими как Бейсик, Фортран, Паскаль, Си, обладает существенными особенностями:
программа на Прологе не является алгоритмом, а представляет собой запись условия задачи на языке формальной логики (т. е. это дескриптивный, описательный язык программирования);
язык Пролог предназначен не для решения вычислительных или графических задач, а для решения логических задач, для моделирования процесса логического умозаключения человека; вычисления же и графические построения выполняются в Прологе как побочный продукт логического вывода;
Пролог требует особого стиля мышления программиста, что затрудняет изучение его теми, кто уже привык к процедурному программированию, поэтому так называемые практические программисты не стремятся переходить на этот язык, что мешает росту популярности Пролога; однако во многих странах (Японии, Англии, Франции, Германии, Израиле и т. д.) расширяется практика применения Пролога в образовании как первого изучаемого языка программирования; переход к процедурным языкам типа Паскаля в этом случае трудностей не вызывает.
Все это позволяет отнести Пролог в существующем делении языков программирования на языки низкого и высокого уровня к языкам сверхвысокого уровня. В 90-х годах XX века в японском проекте создания компьютеров 5-го поколения (обладающих искусственным интеллектом) Пролог положен в основу аппаратной организации и разработки программного обеспечения. Нынешний Пролог, безусловно, не является окончательным вариантом языка программирования ЭВМ 5-го поколения и в ближайшие годы получит существенное развитие. По-видимому, он сыграет роль Бейсика дескриптивного программирования: его значение и возможности в популяризации и распространении идей логического программирования чрезвычайно велики.
Изучению языка Пролог очень способствует предшествующее изучение математической логики, понятийной системой которой он пользуется.
Программирование на Прологе включает следующие этапы:
1. Объявление фактов об объектах и отношениях между ними.
2. Определение правил взаимосвязи объектов и отношений между ними.
3. Формулировка вопроса об объектах и отношениях между ними.
Имена — это последовательности букв и цифр, начинающиеся с буквы (строчной!). Системы программирования на Прологе для компьютеров допускают использование лишь латинских строчных и прописных букв: a .. z, A .. Z. Не допускается применение русских строчных и прописных букв: а .. я, А .. Я. При практической работе с интерпретатором рекомендуется использовать в качестве имен запись русских слов латинскими буквами, чтобы смысл имен оставался понятным. В данном параграфе мы будем записывать все имена русскими буквами, чтобы сделать смысл программ наиболее понятным. При запуске этих программ в "англоязычных" системах программирования нужно заменять русские буквы в именах на латинские.
Типы данных включают переменные, атомарные значения и структуры
(рис. 5.11).
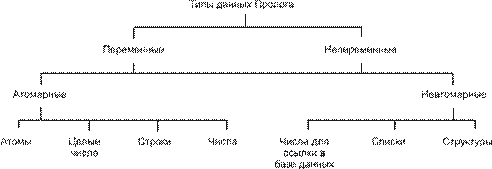
Рис. 5.11. Классификация типов данных Пролога
Примеры специальных атомов:
:– (обозначает импликацию);
? (вопрос, обозначающий отрицание);
! (предикат отсечения, рассматривается далее).
Переменные обозначаются последовательностью букв и цифр, начинающейся с заглавной буквы. Особый вид переменной — анонимная переменная _, используемая в качестве аргумента предиката, когда конкретное значение переменной несущественно.
Структура — это конструкция, состоящая из имени структуры и заключенного в скобки списка ее аргументов, разделенных запятыми. Элементами структур могут быть числа, атомы, переменные, другие структуры и списки. Примеры структур: str(А,B,C), носит(юрий,пиджак).
Списки представляют собой объединение элементов произвольных видов, разделенных запятыми и заключенных в квадратные скобки. Списки отличаются от структур тем, что количество элементов может меняться при выполнении программы. Примеры списков: [1,3,5,7], [красный,желтый,зеленый].
Основная операция, выполняемая в языке Пролог, — это операция сопоставления (называемая также унификацией или согласованием). Операция сопоставления может быть успешной, а может закончиться неудачно. Определяется операция сопоставления так:
константа сопоставляется только с равной ей константой;
идентичные структуры сопоставляются друг с другом;
переменная сопоставляется с константой или с ранее связанной переменной (и становится связанной с соответствующим значением);
две свободные переменные могут сопоставляться (и связываться) друг с другом. С момента связывания они трактуются как одна переменная: если одна из них принимает какое-либо значение, то вторая немедленно принимает то же значение.
Примеры: 5 сопоставляется с 5, имеет сопоставляется с имеет, сергей не сопоставляется с юрий, имеет(сергей,машина) не сопоставляется с имеет(сергей,телевизор), имеет(сергей,машина) сопоставляется с имеет(Х,машина), в этом случае переменная Х получает в качестве значения атом сергей.
Факты — это предикаты с аргументами-константами, обозначающие отношения между объектами или свойства объектов, именованные этими константами. Факты в программе считаются всегда и безусловно истинными и таким образом служат основой доказательства, происходящего при выполнении программы.
Пример 1. Факты, описывающие телефонные номера:
телефон(иванов,т561532). телефон(петров,т642645). телефон(сидоров,т139833).
Это означает: телефон Иванова — 561532 и т. п. Заметим, что перед цифрами номера идет буква "т". Она делает номер телефона литерной константой, так как числа 561532, 642645, 139833 слишком велики, чтобы быть числовыми константами.
Пример 2. Факты, описывающие студентов:
нравится(сергей,рэп). нравится(юрий,джаз). носит(сергей,блейзер). носит(юрий,пиджак).
Это означает: "Сергею нравится рэп", "Юрию нравится джаз" и т. п.
Правила — это хорновские фразы с заголовком и одной или несколькими подцелями-предикатами. Правила имеют форму:
<голова правила> : — <список подцелей>.
где знак : — читается "если", а список подцелей состоит из отдельных подцелей, разделенных знаком "запятая" (читаемым как "и"). Правила позволяют определить новые отношения между объектами на основе уже объявленных с помощью фактов. В качестве аргументов в предикатах правила могут использоваться не только константы, но и переменные. На переменные в правилах действуют кванторы общности, поэтому правила очень концентрированно и лаконично выражают конструкции логического вывода. Так, к фактам примера 2 можно добавить следующее утверждение: крутойпарень(X) :- нравится(X,рэп),носит(X,блейзер).
Это означает "любой X — крутой парень, если Х нравится рэп и Х носит блейзер".
Еще примеры правил: ест(X,Y) : — пища(Y), любит(X,Y).
"Каждый X ест любой Y, если Y — пища, и X любит Y". владелец(А,В) : — купил(А,В).
"Любой А есть владелец каждого В, если А купил В".
В Прологе все предложения программы — факты, правила, вопрос — заканчиваются точкой.
Отметим, что в Прологе вместо оператора присваивания имеется более общий и мощный механизм задания значений переменных. Переменные в Прологе получают свои значения в результате сопоставления с константами в фактах и правилах. До тех пор, пока переменная не получила какого-либо значения, она называется "свободной". Когда переменная примет значение, она становится "связанной". Однако она остается связанной только в течение времени, необходимого для получения одного ответа на запрос, после этого Пролог "развязывает" ее, возвращается и ищет альтернативные решения. Это очень важный момент: нельзя хранить информацию, задавая значения переменных. Переменные служат частью процесса сопоставления, а не "хранилищем" информации. Область действия переменной — ровно одно предложение (правило или запрос программы).
Вопрос — отправная точка логического вывода, происходящего при выполнении программы. На любой вопрос компьютер будет пытаться дать ответ "Да" или "Нет" в зависимости от того, согласуется или нет утверждение, стоящее в вопросе, с фактами и правилами базы знаний. Вопрос, не содержащий переменных, является общим: "Имеет ли место факт... ?". Так, например, к базе знаний примера 1 можно поставить вопрос:
?–телефон(иванов,т123456).
и ответ будет "Нет", так как константа т123456 не согласуется ни с одним фактом.
Если к базе знаний (пример 3)
нравится(сергей,рэп). нравится(юрий,джаз). носит(сергей,блейзер). носит(юрий,пиджак). крутойпарень(X) : — нравится(X,рэп),носит(X,блейзер). задать вопрос
?–крутойпарень(юрий).
то будет получен ответ "Нет". В самом деле, в результате резолюции утверждение в этом вопросе согласно правилу заменится конъюнкцией утверж- дений: нравится(юрий,рэп), носит(юрий,блейзер).
(переменная Х в правиле получила значение юрий). Эти утверждения не согласуются с остальными фактами базы знаний.
Для вопроса
? — крутойпарень(сергей).
будет получен ответ "Да", так как в этом случае противоречий при согласовании вопроса и базы знаний не возникает.
Вопрос, в котором имеются переменные, является частным: "Для каких значений переменных факт ... имеет место?". В процессе сопоставлений при выполнении программы переменные получат значения тех констант (конкретизируются), для которых сопоставление запроса, в целом, успешно, и будут выведены на экран. Так, в ответ на вопрос
? — телефон(иванов,Х).
к базе знаний примера 1 на экране появится сообщение Х=т561532 и будет дан ответ "Да".
Если к базе знаний примера 3 задать вопрос в форме:
?– крутойпарень(А).
то свободная переменная А в вопросе сопоставляется со свободной переменной Х в правиле и совмещается с ней, т. е. становится одним и тем же. В результате резолюции согласно правилу произойдет замена крутойпарень(А) на нравится(А,рэп), носит(А,блейзер),
а затем предикат нравится(А,рэп) успешно согласуется с фактом нравится(сергей,рэп), и при этом переменная А конкретизируется значением сергей; от вопроса теперь остается носит(сергей,блейзер), а в базе знаний имеется соответствующий факт. Ответ: "Да", и на экране появится значение присутствовавшей в вопросе переменной А:
А=сергей.
Отметим, что машина "не понимает" используемых в программе имен: нравится, носит, сергей и т. д. Мы могли бы вместо них использовать любые другие обозначения. Для интерпретатора Пролога существенны только совпадения и различия имен, а также связи между предикатами, устанавливаемые с помощью конъюнкций и импликаций. Осмысленные имена мы будем использовать только для того, чтобы облегчить чтение и понимание программ самим себе. Однако в Прологе существуют предопределенные имена (встроенные предикаты), которые позволяют выполнить арифметические операции, сравнения, графические построения, ввод/вывод и другие полезные операции как побочный продукт выполнения программы. Встроенные предикаты ArityProlog описаны в справке по системе программирования, вызываемой нажатием клавиши <F1>.
Аналогичный набор встроенных предикатов имеется в других версиях языка Пролог.
Алгоритм выполнения программ на Прологе
Факты и правила программы на Прологе являются описанием отношений и связей между объектами некоторой предметной области, т. е. записью условия некой логической задачи, которую предстоит решить. Описанные отношения и связи рассматриваются статически. Такой подход к программе называется декларативным. Порядок следования фактов, правил и подцелей в правилах не влияет на декларативный смысл программы.
Вместе с тем программу можно рассматривать с точки зрения последовательности сопоставлений, конкретизаций переменных и резолютивных выводов, происходящих при ее выполнении. Такой подход называется процедурным. Процедурный смысл программы обязательно должен учитываться при программировании на Прологе. Так, факт можно рассматривать как полностью определенную процедуру, для выполнения которой больше ничего не нужно.
Правило
А : — B1, B2, ..., Bn. можно рассматривать как определение процедуры А, утверждающее, что для ее выполнения надо определить В1, В2, ..., Вn. Процедуры В1, В2, ..., Вn должны выполняться в определенном порядке — слева направо. Если выполнение очередной процедуры завершается успешно, то происходит переход к следующей процедуре. Если же по какой-либо причине очередная процедура выполняется неуспешно, то происходит переход к следующему варианту описания этой процедуры, и порядок поиска такого варианта в Прологе задан — сверху вниз. Поиск подходящих для согласования фактов и правил в базе знаний происходит последовательно сверху вниз, и если подходящих фактов не найдено — ответ отрицательный. Эта стратегия согласования называется "сверху вниз", или "замкнутый мир".
Рассмотрим процесс выполнения программы более подробно на примере.
![]()
a : – b, c, d. b : – e, f. c.
d.
e.
f.
? – a.
Выполнение программы начинается с применения метода резолюций к целевому и одному из предложений программы для получения их резольвенты. Подходящее предложение программы подбирается перебором сверху вниз так, чтобы сопоставление его заголовка с целевым предложением было успешным. В результате резолюции получается новое целевое предложение, и метод резолюции применяется к нему и к другому предложению программы. Процесс продолжается до тех пор, пока не будут согласованы с фактами все возникшие при резолюции подцели, табл. 5.7.
Таблица 5.7. К процессу выполнения программы на Прологе
|
Номер шага резолюции |
Целевое предложение |
Исходное предложение |
Резольвента |
|
1 |
?–a. |
a:–b,c,d. |
?–b,c,d. |
|
2 |
?–b,c,d. |
b:–e,f. |
?–e,f,c,d. |
|
3 |
|
?–e,f,c,d. |
e.?–f,c,d. |
|
4 |
|
?–f,c,d. |
f. ?–c,d. |
|
5 |
|
?–c,d. |
c.?–d. |
|
6 |
|
?–d. |
d.Пустая |
При выполнении логического вывода, если необходимо, происходит конкретизация переменных. Рассмотрим пример.
![]()
любит(юрий,музыку). любит(сергей,спорт).
любит(А,книги):–читатель(А),любопытный(А). любит(сергей,книги). любит(сергей,кино).
читатель(юрий). любопытный(юрий).
?– любит(Х,музыку), любит(Х,книги).
Двойной запрос в этой программе может быть представлен целевым деревом:

любит( музыку)X, любит(X,книги)
Вначале, просматривая программу сверху вниз, Пролог находит первое предложение, соответствующее первой подцели запроса:
 любит(X,книги)
любит(X,книги)
любит(юрий,музыку)
Переменная Х конкретизируется значением юрий. Начинается согласование 2-й подцели запроса с условием Х=юрий. 1-е и 2-е предложения программы не соответствуют подцели. В 3-м предложении: любит(А,книги):–читатель(А), любопытный(А).
аргумент А заголовка есть переменная, поэтому она может соответствовать Х, т. е. получает значение А=юрий; вторые аргументы совпадают. Теперь тело правила образует новое множество целей для согласования. Получаем целевое дерево:

Затем Пролог будет искать факты, соответствующие новым подцелям. Последнее результирующее дерево:
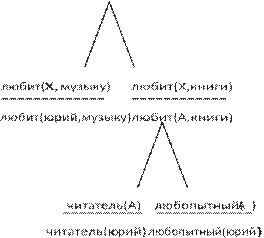
Рассмотрим еще один пример.
![]()
любит(оля,чтение).
любит(света,бадминтон). любит(юля,бадминтон). любит(лена,плавание). любит(лена,чтение).
?– любит(Х,чтение), любит(Х,плавание).
Запрос означает: есть ли люди, которым нравится и чтение, и плавание?
Сначала Пролог ищет факт, сопоставимый с первой частью вопроса: любит(Х, чтение). Подходит первый же факт программы: любит(оля,чтение).
и переменная Х связывается значением оля. В то же время Пролог фиксирует в списке фактов указатель, показывающий состояние процедуры поиска. Далее Пролог пытается согласовать вторую часть запроса при условии Х=оля, т. е. ищет с самого начала программы факт любит(оля,плавание). Такого факта в программе нет, и поиск заканчивается неуспешно. Тогда Пролог возвращается к первой части запроса: любит(Х,чтение), "развязывает" переменную Х и продолжает поиск подходящих фактов, начиная с ранее установленного в списке фактов указателя. Подходит факт любит(лена,чтение), переменная Х конкретизируется значением лена, и далее вторая часть вопроса успешно согласуется с фактом любит(лена,плавание). Пролог выполнил в данном примере поиск с возвратом.
Графически процесс выполнения программы представляется в виде обхода бинарного дерева — дерева вывода, типа изображенного на рис. 5.12. Вершины дерева обозначают вопросы, а ребра показывают возможные пути вывода, причем для каждого ребра характерны свои правила и унифицирующая подстановка значений переменных.
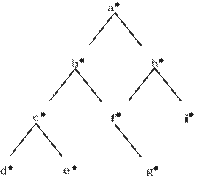
Рис. 5.12. Дерево вывода программы на Прологе
Обход дерева начинается с движения от вершины (запроса) по самой левой ветви вниз до конца (abcd), при этом запоминаются все точки ветвления (точки возврата). При достижении конца ветви решение будет либо найдено, либо нет. В обоих случаях Пролог продолжает дальнейший поиск решений. Выполняется возврат в последнюю точку ветвления с. При этом конкретные значения, присвоенные переменным при движении вниз на сегменте с—d, отменяются, и движение вниз продолжается по расположенной справа ветви c— e до конца дерева вниз. Затем произойдет возврат в предыдущую точку ветвления b, и движение продолжится по ветви bfg, и так до тех пор, пока все дерево вывода не будет пройдено.
Рекурсия
Существует целый класс задач, в которых отношения между объектами можно определить, только пользуясь самими определяемыми соотношениями. Получающиеся при этом правила называются рекурсивными.
Пример: рекурсивное определение натурального числа:
1) 1 — натуральное число;
2) число, на 1 большее натурального числа, также натуральное.
В системах логического программирования рекурсия служит также для описания циклов, повторений и является важнейшим методом программиро- вания.
Рассмотрим простой пример: вычисление факториала натурального чис- ла n (n!) .
Определение n! рекурсивно:
1) 1! = 1,
2) n! = (n-1)! * n
Для описания отношения "факториал" между n и n! будем использовать двухарный предикат: факт(N,M).
Тогда база знаний, соединенная с запросом, приобретает вид (программа 77).
![]()
факт(1,1). факт(N,X): — факт( №-1 ,Y), X is Y*N.
?– факт(3,A);
В данной программе правило факт вызывает само себя — это и есть рекурсия. Запись is Y*N представляет собой обращение к встроенному предикату is (есть) для описания арифметического действия.
Процесс работы программы можно изобразить следующим образом:
?факт(3,A0).
ОТВЕТ : А=6
?факт(2,A1). X1= 2*3 = 6
?факт(1,A2).
X2= 1*2 = 2 факт(1,1).
Здесь стрелочка вниз означает сопоставление и резолюцию, а стрелочка вверх — возврат и завершение отложенного вычисления.
Правило факт вызывает само себя — происходит углубление рекурсии (прямой ход). При этом в памяти ЭВМ выделяется место для переменных А, А0, А1, А2 и N, N0, N1, N2, образующих стеки. При согласовании вопроса с предикатом факт(1,1) рекурсия прекращается и начинается возврат из рекурсии (обратный ход) — выполнение отложенных на прямом ходе согласований. Предикат факт(1,1) играет очень важную роль — это ограничитель рекурсии, условие ее завершения.
Отметим, что Пролог стремится найти все решения поставленной задачи, а значит, после появления ответа А=6 происходит возврат к вопросу ?факт(1,A2) и попытке согласовать его с правилом факт. Это приводит к бесконечному процессу рекурсии с отрицательными аргументами в факт, которая завершается при исчерпании глубины зарезервированных интерпретатором Пролога стеков. Ускорить выход из рекурсии можно, добавив к предикату факт(1,1) отсечение !: факт(1,1) : — !.
Однако использование отсечения требует более подробного рассмотрения.
В общем случае последовательность предложений в базе знаний не имеет значения. Однако это не так для рекурсивно-определенных отношений. Например:
родитель(X):– родитель(Y),отец(Y,Z). родитель(коля). отец(коля,петя). родитель(петя).
В этом случае в первом предложении голова имеет ту же функцию, что и одна из целей — родитель. В процессе поиска ответа в этой базе знаний будет применено правило: предложение, стоящее первым, будет применено первым, — известное как принцип поиска в глубину.
Это приведет к тому, что система будет обращаться только к первому предложению базы знаний и ответ на вопрос не будет найден никогда (образуется бесконечная петля вывода). Однако небольшое изменение базы знаний — перестановка двух предложений местами — приведет к удачному поиску решения.
![]()
родитель(коля).
родитель(X):– родитель(Y), отец(Y,X). отец(коля,петя). ? — родитель(петя).
Неограничено-повторное обращение к предложению может быть и более замаскированным, так, как это получается в программе 79.
![]()
выше(А,В): — ниже(В,А). ниже(В,А): — выше(А,В).
выше(коля,петя).
?– ниже(петя,коля).
Однако если третье предложение стоит на первом месте, то повторного обращения не произойдет и ответ будет найден.
В общем виде рекурсия на Прологе выглядит так:
P(1,...).
P(n,...) :– Q1, ..., Qn, P(n–1,...), R1, ... Rm.
Правило Р обращается само к себе, при этом происходит углубление рекурсии. Предикаты Q1, ..., Qn выполняются на прямом ходе рекурсии, а R1, ..., Rm — на обратном; n — это некоторый условный параметр, входящий в условие продолжения рекурсии, а Р(1,...) — факт, завершающий процесс рекурсии.
Особенно простым случаем рекурсии является простое циклическое повторение. Один из способов организации повторения связан с наличием в базе знаний процедуры вида repeat. repeat : – repeat.
Использование repeat в качестве подцели некоторого правила приводит к многократному повторению остальных подцелей этого правила.
Предикат отсечения и управление логическим выводом в программах
Управление процессом просмотра предложений является важным аспектом программирования на Прологе. Это осуществляется с помощью специальной встроенной функции "резать", обозначаемой символом "!".
Данная встроенная функция может быть использована для достижения следующих трех целей:
исключения бесконечной петли при выполнении программы;
программирования взаимоисключающих утверждений; блокирования просмотра целей.
Продемонстрируем все три случая на примерах.
Пример 1. Устранение бесконечных циклов. Обратимся к утверждениям, определяющим последовательность Фибоначчи (числовая последовательность 1, 1, 2, 3, 5, 8, ..., в которой каждое число, начиная с третьего, есть сумма двух предыдущих).
![]()
fib (0,_,1). fib (1,1,1). fib (N,G,H) : – fib ( N–1 ,F,G), H is F+G.
На запрос
?– fib (0,_ ,F).
получим F=1, и Пролог сделает попытку сопоставить с запросом второй факт и потерпит неудачу. Однако сопоставление головы третьего утверждения с запросом происходит успешно и осуществляется попытка доказать цель fib(–
1,F0,F1), что, в свою очередь, приводит к цели fib(–2, .., ..) и так далее, т. е. образуется бесконечный цикл.
Однако мы можем устранить такие ситуации, используя отсечение и тем самым указывая Прологу, что не существует других решений в случае успешного согласования граничного условия.
![]()
fib (0,_,1) : – !. fib (1,1,1) : – !. fib (N,G,H) : – fib ( N–1 ,F,G), H is F+G.
Учитывая данное определение fib и задавая вопрос
?– fib(0,_ ,F).
получаем F=1. Других решений нет.
Пример 2. Программирование взаимоисключающих утверждений. Процедуру нахождения наибольшего из двух чисел можно записать в виде отношения
max(X, Y, M).
Здесь М=Х, если X>=Y, и M=Y, если X<Y. Соответствующие правила таковы:
max(X, Y, X) : – X>=Y. max(X, Y, Y) : – X<Y.
Эти правила являются взаимоисключающими. Возможна более экономная формулировка, использующая понятие иначе: если X>=Y то M=Х иначе M=Y.
На Прологе это записывается при помощи отсечения:
max(X, Y, X) : – X>=Y,!. max(X, Y, Y).
Пример 3. Блокирование просмотра целей.
![]()
B.
D.
A:– B, C. (1)
C: –D, !, E. (2) E: –F, G, H. (3) ?A.
Говорят, что дизъюнкт (1) "порождает" дизъюнкт (2), так как в правой части
(1) есть литера C и эта же литера — в левой части (2). Аналогично дизъюнкт (2) "порождает" дизъюнкт (3). Если (3) неудачен, то в (2) выполнится отсечение: дизъюнкт (2) также считается неудачным, восстанавливается "родительская среда" (1), делается попытка найти альтернативное решение для B. Если бы (2) имело вид C: –D, E., то при неудаче в (3) была бы сделана попытка найти альтернативное решение для D.
В других случаях может быть необходимым продолжение поиска дополнительных решений, даже если целевое утверждение уже согласовано. В этих случаях можно использовать встроенный предикат fail.
Встроенный предикат fail не имеет аргументов. Он считается всегда ложным.
Например, перебор всевозможных решений:
![]()
ос(cpm). ос(msdos). ос(unix). печать–всех:–ос(X), write(X), fail.
?–печать–всех.
Обработка списков
На практике часто встречаются задачи, связанные с перечислением объектов. В некоторых случаях при решении задач важно сохранять информацию об уже сделанных шагах решения, чтобы их не повторять. Для решения таких задач в языке Пролог предусмотрены списки.
Список можно задать перечислением элементов. Например, имена учеников класса:
[саша,петя,дима,ксюша,лена].
Элементами списка могут быть не только атомы, но и функции, и вообще любые элементы, даже списки. Заранее длина списка не задается, и в ходе выполнения программы она может меняться.
Альтернативный способ задания списка использует понятия головы и хвоста списка.
Например, в списке [X | Y] X — это голова списка, Y — его хвост.
Хвост списка по определению также является списком.
Теперь список может быть определен рекурсивно:
1) пустой список [ ] — список;
2) [X | Y] — список, если Y — список.
Определение списка через его голову и хвост в сочетании с рекурсией лежит в основе большого числа программ, оперирующих списками. Эти программы состоят:
из факта, ограничивающего рекурсию и описывающего операцию для пустого списка;
из рекурсивного правила, определяющего операцию над списком, состоящим из головы и хвоста ( в голове правила), через операцию над хвостом (в подцели).
Пример 1: определение числа элементов в списке.
![]()
сколько ([], 0). сколько ([А|В], N) :- сколько (В, М), N is М+1.
?– сколько ([саша, игорь, лена]), X).
Ответ: X=3.
Пример 2: принадлежность элемента списку.
![]()
принадлежит (X, [X | Y]).
принадлежит (X, [A |Y ]) : – принадлежит (X,Y).
?–принадлежит (4,[1,3,4,9]).
Ответ: "Да".
Данная программа имеет очень простой декларативный смысл: элемент принадлежит списку, если он является его головой или принадлежит хвосту списка.
Пример 3: соединение двух списков.
Эту задачу можно описать с помощью следующих предикатов:
ограничение рекурсии состоит в том, что если к пустому списку [] добавить список Р, то в результате получится Р;
рекурсия состоит в том, что можно список Р добавить к концу списка [X|Y], если Р будет добавлен к хвосту Y и затем присоединен к голове X (при этом получается список [X|T]).
![]()
присоединить([ ], P, P). присоединить([X|Y], P, [X | T]):–присоединить(Y, P, T).
? присоединить(L,[джим..R],[джек,бил,джим,тим,джим,боб]).
Ответ:
L=[джек,бил].
R=[тим,джим,боб].
L=[джек,бил,джим,тим].
R=[боб].
Существует традиция использовать для обозначения предиката слияния двух списков предикативный символ append (по-английски — добавить).
В некоторых случаях постановки вопросов к такого рода программам приходится использовать отсечение (!).
![]()
append([ ], L, L).
append([A | B], C, [A | D]):– append(B, C, D).
?–append(X,Y,[1,2]).
Ответ:
X=[ ]
Y=[1,2]
Х=[1]
Y=[2]
X=[1,2] Y=[ ].
Если же заменить первое предложение на append([ ], l, l):– !. и задать тот же вопрос, то получится правильный ответ:
X=[ ]
Y=[1,2].
Пример 4: удаление элементов из списка.
Программа 88 аналогична проверке принадлежности элемента списку, но требует уже трехарного предиката, один аргумент которого указывает удаляемый элемент, второй аргумент — исходный список и третий — списокрезультат.
![]()
удал (X, [X | Y], Y) : – !. удал (X, [Z | Y], [Z | W]) : – удал (X, Y, W).
Декларативный смысл: если удаляемый элемент совпадает с головой списка, то результатом программы является хвост списка, иначе удаления производятся из хвоста списка.
Данная программа удаляет первое вхождение в список элемента, связанного с переменной X. Знак отсечения "!" в конце правила предотвращает последующий поиск и вывод лишних вариантов ответов после выполнения ограничительного факта.
Для удаления всех вхождений элемента X программу надо дополнить:
удал (X,[ ], [ ]). удал (X, [X | Y], W) :– удал (X, Y, W). удал (X, [Z | Y], W) :– удал (X, Y, W).
Декларативный смысл программы таков: пока список не пуст, удалить элемент, если он совпадает с головой списка, значит, отбросить голову списка, а затем удалять его из оставшегося хвоста, иначе надо сразу удалять элемент из хвоста.
Пример 5: индексация элементов списка.
Смысл программы 89 состоит в том, чтобы получить элемент под номером N или узнать номер элемента X.
![]()
получить ([X | Y], 1, X). получить ([W | Y], N, X) :– N is M+1, получить (Y, M, X).
Пример 6: поиск максимального элемента.
![]()
max ([X], X). max ([X | Y], X) :- max (Y, W), X>W, !. max ([X | Y], W) :– max (Y, W).
Декларативный смысл программы: если в списке один элемент — он и является максимальным, если более одного, то это голова списка, если она больше максимального элемента хвоста, или максимальный элемент хвоста.
Пример 7: обращение списка.
Данная задача — самая сложная из рассмотренных. Для ее решения важно сообразить, что обратить список из одного элемента — означает оставить список без изменения. Обратить более длинный список — обратить его хвост, а потом сзади приставить к нему голову исходного списка.
![]()
обр ([X], [X]). обр ([X | Y], Z) :– обр (Y, W), присоединить (W, [X], Z).
В этой программе используется процедура слияния списков, описанная ранее.
Arity-Prolog располагает значительным числом встроенных предикатов для обработки списков, так что приведенные программы имеют в основном учебный характер.
Решение логических задач на Прологе
Целью всего предшествующего изложения была подготовка к данному разделу — решению содержательных логических задач на Прологе, т. е. задач невычислительного характера, в которых особенности Пролога и дескриптивной парадигмы программирования проявляются наиболее ярко.
Рассмотрим пример: нарисовать конверт, не отрывая карандаша от бумаги и не проводя два раза по одной и той же линии.
Введем обозначения, как показано на рис. 5.13. Ребра графа обозначены буквами а, б, в... (литерные константы), вершины — цифрами 1, 2, 3... Опишем структуру графа предикатом вида ребро(S,A,B), что означает, что от вершины А к вершине В идет ребро S. Так как граф неориентированный, помимо предикатов вида ребро (S,A,B) нужны и предикаты ребро (S,B,А). Знания о структуре графа можно представить так, как это записано рядом с рис. 5.13.
![]() ребро(а,1,2) ребро(а,2,1)
ребро(б,2,3) ребро(б,3,2) ребро(в,1,3) ребро(в,3,1) ребро(г,2,4) ребро(г,4,2)
ребро(д,2,5) ребро(д,5,2) ребро(е,3,4) ребро(е,4,3) ребро(ж,3,5) ребро(ж,5,3)
ребро(з,4,5) ребро(з,5,4)
ребро(а,1,2) ребро(а,2,1)
ребро(б,2,3) ребро(б,3,2) ребро(в,1,3) ребро(в,3,1) ребро(г,2,4) ребро(г,4,2)
ребро(д,2,5) ребро(д,5,2) ребро(е,3,4) ребро(е,4,3) ребро(ж,3,5) ребро(ж,5,3)
ребро(з,4,5) ребро(з,5,4)
Рис. 5.13. Задача "конверт"
Решением задачи должен явиться список пройденных ребер графа, причем длина его должна быть равна 8 и в нем не должно быть повторяющихся ребер, что можно описать так:
путь(Т,П) : — длина(П,8), write_list(П), !. (1) путь(Т,П) : — ребро(Р,Т,Н),не_принад(Р,П),путь(Н,[Р|П]). (2)
Переменная Т обозначает текущую вершину графа, а П — список пройденных ребер. Правило 1 означает, что если длина списка П пройденных вершин становится равной 8, список П выводится на печать. Это правило ограничивает рекурсивный перебор вершин и ребер, проводимый правилом 2. Правило 2 является генератором перебора, оно перебирает предикаты ребро()и находит такое ребро Р из текущей вершины Т в новую Н, чтобы оно не принадлежало списку П, затем это ребро добавляется в качестве головы к списку П, и поиск дальнейшего пути производится уже из новой вершины Н. Нам потребуется программа, определяющая длину списка:
длина ([ ], 0). длина ([А | В], N) :– длина (В, М), N is М+1.
а также программа вывода элементов списка на экран:
write_list([ ]). write_list([H | T]):–write(H),write_list(T).
Задание
?–путь(4,[ ]).
обозначает: искать путь, начиная с вершины 4 и пустого списка пройденных ребер.
Ответ: з, ж, в, а, б, д, г, е.
На вопрос ?–путь(1,[ ]) ответ — "Нет".
Аналогично решаются другие задачи, связанные с поиском пути в графе, удовлетворяющие каким-то дополнительным условиям, например задача о коммивояжере.
Программа будет состоять из:
базы знаний о структуре графа — вершинах и связывающих их ребрах (каждому ребру может сопоставляться набор весов);
правил, выражающих дополнительные условия и ограничения на решения задачи и часто связанных с обработкой списков;
рекурсивного правила — генератора перебора ребер и вершин с некоторым ограничивающим предложением, целевым условием;
дополнительных процедур и промежуточных определений.
Интересно, что большинство задач, которые считаются логическими, сводятся к задаче поиска пути в некотором графе — графе состояний задачи. К этому типу задач можно отнести и разнообразные игры. Характерными особенностями многих задач являются следующие:
наличие неких дискретных состояний, число которых конечно, и одно из них принимается за начальное, а другое (или несколько других) за конечное (искомое);
определены правила перехода между состояниями;
для каждого состояния заданы определенные условия допустимости (оценки) этого состояния.
При анализе предметной области задачи эти состояния, правила перехода и условия допустимости должны быть выявлены, получены соответствующие обозначения и затем записаны с помощью фраз Хорна.
Рассмотрим задачу: имеются два сосуда — на 3 и на 5 литров. Как отмерить с их помощью 4 литра воды?
В этой задаче состояния связаны с определенным количеством воды V в первом сосуде и W во втором. Начальным состоянием является V=0, W=0, а конечным V=0, W=4. Переходы между состояниями можно записать в виде правил: сосуды(V1, W1) :– сосуды(V2, W2). Например, правило сосуды(0, W) :– сосуды(V, W).
означает, что вся вода из первого сосуда вылита. Обратим внимание на слово "вода" в условии задачи. Для предметной области, связанной с водой, характерно то, что воду можно просто выливать, и данное правило перехода между состояниями допустимо. Если бы задача решалась для молока, то его выливать было бы нельзя, и такое правило было бы недопустимым! Правило сосуды(3, W) :– сосуды(V, W). означает, что первый сосуд заполнен полностью.
Не разливая, жидкость можно перелить из одного сосуда в другой только так, что один станет пустым, а другой наполнится. Это можно записать в виде правил
сосуды(3,W) :– сосуды(V,W–V+3). сосуды(V,0) :– сосуды(V–W,W). сосуды(V,5) :– сосуды(V–W+5,W). сосуды(0,W) :– сосуды(V,W–V).
При решении данной задачи необходимо также избежать повторения одних и тех же состояний — "переливания из пустого в порожнее". Для этого в предикат сосуды() следует добавить 3-й аргумент — список пройденных состояний П. Элементы в него будут добавляться парами: сосуды(V1,W1,[V1,W1|П]) :– не_принад(V1,W1,П), сосуды(V2,W2,П).
Условие, ограничивающее рекурсию, должно иметь вид: сосуды(_,4,П) :– write_list(П).
![]() Контрольные вопросы
Контрольные вопросы
1. В чем состоит принципиальное различие процедурных и декларативных языков программирования?
2. Каковы этапы программирования на Прологе?
3. Какие типы данных допускает Пролог?
4. В чем существо операции сопоставления?
5. Как реализуются вопросы к программе на Прологе?
6. Приведите примеры рекурсий, отличные от данных в тексте.
7. Для чего служит предикат отсечения?
8. Для чего служат списки и как они задаются?
 Темы для рефератов и докладов
Темы для рефератов и докладов
1. Технологии создания систем искусственного интеллекта.
2. Логика предикатов 1-го порядка.
3. Системы программирования на Прологе.
![]() Вопросы для обсуждения
Вопросы для обсуждения
1. На каком языке программировать легче: операционном или декларативном?
2. Что было бы, если бы существовали только декларативные языки программирования?
![]() Задачи и упражнения
Задачи и упражнения
1. Опишите на Прологе:
• свою родословную, определите бабушек, дедушек, прабабушек, прадедушек и т. д.;
• телефонную книгу;
• районы вашего города, республики, области, укажите численность их населения, местные достопримечательности;
• европейские государства (население, площадь и т. д.);
• таблицу дат и событий русской истории;
• небольшой словарь для перевода с русского языка на иностранный язык, который вы изучаете;
• ведомость зачета вашей группы;
• успеваемость вашей группы (дайте определение "отличника");
• каталог книг в библиотеке.
2. Запишите на Прологе правила, являющиеся решением следующих заданий:
• даны два числа a и b, получите их сумму, разность, произведение;
• дана длина ребра куба, найдите объем куба и площадь его боковой поверхности;
• дан радиус основания r и высота цилиндра h, найдите его объем и площадь боковой поверхности;
• даны стороны a и b параллелограмма, а также угол между ними, найдите диагонали параллелограмма и его площадь.
3. Вычислите значения выражений:
• 2x+3y+4
• (2x+8y+4)/2
• y–x^2
• x^2+xy+y^2
• x/2+5y
• x^2+3y^2
• 5(34x–y)
4. Напишите программы, выполняющие операции над списками:
• объедините два списка, найдите MAX и удалите его;
• удалите из списка элемент, найдите длину оставшегося списка;
• добавьте к списку элемент, вычислите среднее арифметическое его элементов;
• обратите список, найдите последний и предпоследний элементы;
• исключите из списка заданный элемент во всех вхождениях, кроме первого, найдите длину оставшегося списка;
• проверьте, имеются ли в списке повторяющиеся элементы, и все их удалите;
• удалите из списка все элементы, равные последнему, найдите длину оставшегося списка;
• объедините два списка, найдите MIN и удалите его;
• обратите список, найдите MAX и удалите его;
• к списку добавьте обращенный второй список, найдите длину результата;
• отсортируйте список, используя метод пузырька.
![]() Лабораторные работы
Лабораторные работы
1. Напишите программу, решающую задачу о волке, козе и капусте.
2. Напишите программу, решающую задачу о туземцаx и миссионерах (как переправиться через реку трем туземцам и трем миссионерам на двух- местной лодке, чтобы никогда на берегу не оставалось туземцев больше, чем миссионеров), аналогично задаче о конверте.
3. Напишите программу, решающую задачу об обходе препятствия.
4. Напишите программу, определяющую положение "шах королю".
5. Напишите программу, определяющую, как шахматному коню попасть с поля А на поле В.
6. Напишите программу, определяющую, как разлить 10 л молока по 5 л, пользуясь бидонами на 3, 7 и 10 л.
7. Напишите программу, аналитически дифференцирующую элементарную функцию.
8. Напишите программу, играющую в "крестики и нулики" на бесконечной плоскости.
9. Напишите программу, вычисляющую интервал между двумя датами одного года, например 7 марта и 9 сентября.
10. Напишите программу, решающую задачу о четырех ферзях на поле размером 4×4.
МОДУЛЬ 6
Компьютерные вычисления
6.1. Вычислительные методы
6.2. Понятие о компьютерном моделировании
14 Модуль 1. Информация и информационные процессы
6.1. Вычислительные методы
![]() Учебный
материал
Учебный
материал
Вычисление значений функций. Интерполяция
Одной из наиболее часто встречающихся задач компьютерных вычислений является задача вычисления значений функции. Эта задача имеет несколько разновидностей:
табулирование;
аппроксимирование;
интерполирование;
экстраполирование и др.
Табулирование функции — это вычисление значений функции при изменении аргумента от некоторого начального значения до некоторого конечного значения с определенным шагом.
Именно так составляются таблицы значений функций, отсюда и название — табулирование. Необходимость в табулировании возникает при решении достаточно широкого круга задач, например при численном решении нелинейных уравнений f x( ) = 0.
Путем табулирования можно отделить (локализовать) корни уравнения, т. е. найти такие отрезки, на концах которых функция имеет разные знаки. С помощью табулирования можно, хотя и очень грубо, найти минимум или максимум функции. Необходимость в табулировании возникает также при построении графиков функции на экране компьютера.
Иногда случается так, что функция не имеет аналитического представления, а ее значения получаются в результате вычислений, что часто бывает при ком-
пьютерном моделировании различных процессов. Если такая функция будет использоваться в последующих расчетах (например, она должна быть проинтегрирована или продифференцирована и т. п.), то часто поступают следующим образом: вычисляют значения функции в нужном интервале изменения ее аргумента, т. е. составляют таблицу значений (табулируют), а затем по этой таблице каким-либо образом строят другую функцию, заданную аналитическим выражением (формулой).
Итак, пусть необходимо протабулировать функцию y x( )=exp x(− 2) на интервале [–2;2] с шагом 0.1. Поскольку программа должна многократно вычислять значения функции (одной и той же), то разумно составить циклический алгоритм. Для организации цикла можно использовать любой из операторов цикла (WHILE, REPEAT...UNTIL или FOR). В данной постановке задачи наиболее удобны два первых оператора, поскольку для оператора FOR необходимо еще предварительно вычислить количество шагов.
Далее приведены две программы решения поставленной задачи, которые для организации цикла используют операторы WHILE и REPEAT...UNTIL.
В программах используются следующие переменные: xmin и xmax — для указания диапазона (интервала) табулирования; dx — для указания шага табулирования; x и y — для аргумента и значения функции соответственно.
![]()
program TablFunc_1; var x, y, xmin, xmax, dx: Real; begin writeln('Таблица значений функции y(x)=exp(-sqr(x))'); writeln; xmin:= -2; xmax:= 2; dx:= 0.1; x:= xmin; while x<=xmax do begin y:= exp(-sqr(x)); writeln(x:6:3,' ', y:6:3); x:= x+dx; end; {while} Readln; end.
![]()
program TablFunc_2; var x, y, xmin, xmax, dx : Real; begin writeln('Таблица значений функции y(x)=exp(-sqr(x))'); writeln; xmin:=-2; xmax:=2; dx:= 0.1; x:=xmin; repeat y:= exp(-sqr(x)); writeln(x:6:3, ' ', y:6:3); x:= x+dx; until(x>xmax); readln; end.
Любую из этих программ можно легко модифицировать таким образом, чтобы значения переменных xmin, xmax и dx, определяющих соответственно интервал и шаг изменения аргумента, задавались с клавиатуры.
Изменим немного постановку задачи: необходимо вычислить значения функции y x( )=exp(−x2) на интервале [–2;2] в 20 равноотстоящих точках (узлах).
Здесь шаг табулирования явно не задан, а указано количество значений аргумента N= 20 и, соответственно, количество значений функции. Шаг табулирования определяется простым соотношением:
dx = (xmax− xmin) / (N −1).
Значение аргумента на любом i− том шаге можно определить как: xi = xmin + dx⋅(i −1).
При решении этой задачи оператор FOR оказывается наиболее подходящим.
![]()
program TablFunc_3; var x, y, xmin, xmax, dx: Real; i, N: Integer;
begin
writeln('Таблица значений функции y(x)=exp(-sqr(x))'); writeln; xmin:=-2; xmax:=2; N:= 20;
dx:=(xmax-xmin)/(N-1); for i:=1 to N do begin
x:= xmin+dx*(i-1); y:=exp(-sqr(x)); writeln(x:6:3,' ', y:6:3); end; {for}; readln; end.
Во всех рассмотренных примерах результаты табулирования просто выводятся на экран и не доступны в дальнейшем. Для хранения результатов табулирования можно использовать два одномерных массива длиной N (для аргументов и значений функции соответственно). Если результаты необходимо сохранить и по окончании работы программы, то их можно записать в текстовый файл.
Далее приведен пример, в котором результаты табулирования записываются в массивы и одновременно сохраняются в текстовом файле с именем tabl.dat, хранящемся в текущем каталоге.
![]()
program TablFunc_4;
const N = 20; {табулируем функцию в 20 точках} var
X, Y: array[1..N] of Real; xmin, xmax, dx: Real; i: Integer;
f: Text; {файловая переменная} begin
writeln('Таблица значений функции y(x)=exp(-sqr(x))'); writeln;
assign(f,'tabl.dat'); {связываем переменную f с физическим файлом} rewrite(f); {открываем новый файл для записи} writeln(f,'Таблица значений функции y(x)=exp(-sqr(x))'); writeln(f);
xmin:=-2; xmax:=2; dx:=(xmax-xmin)/(N-1); for i:=1 to N do begin
X[i]:=xmin+dx*(i-1); Y[i]:=exp(-sqr(X[i])); writeln(X[i]:6:3,' ', Y[i]:6:3); {выводим данные на экран} writeln(f,X[i]:6:3,Y[i]:6:3); {выводим данные в файл} end; {for} close(f); {закрываем файл} {Здесь можно использовать массивы X и Y для дальнейших вычислений} readln; end.
Во время выполнения процедуры табуляции функции на конкретном промежутке с заданным шагом следует обращать внимание на ее область определения. Так, например, при табулировании функции y= −(1 x) / sin x на промежутке [ 2− π π;2 ] с шагом π / 2 из рассмотрения следует исключить точки, в которых sin x обращается в нуль.
Аппроксимирование, или аппроксимация — (от лат. approximo — приближаюсь) — замена одних математических объектов другими, в том или ином смысле близкими к исходным.
Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются или свойства которых уже известны). В теории чисел изучаются, например, приближения иррациональных чисел рациональными. В геометрии рассматриваются аппроксимации кривых, поверхностей и др. Некоторые разделы математики целиком посвящены аппроксимации, например приближение функций.
Постановка задачи приближения функции. Пусть величина у является функцией аргумента х. Это означает, что любому значению х из области определения поставлено в соответствие значение у. Вместе с тем на практике часто неизвестна явная связь между у и х, т. е. невозможно записать эту связь в виде зависимости y = f x( ). В некоторых случаях даже при известной зависимости y = f x( ) она настолько громоздка (например, содержит трудно вычисляемые выражения, сложные интегралы и т. п.), что ее использование в практических расчетах затруднительно.
Наиболее распространенным и практически важным случаем, когда вид связи между параметрами х и у неизвестен, является задание этой связи в виде некоторой таблицы {x yi; i}. Это означает, что дискретному множеству значений аргумента {xi} поставлено в соответствие множество значений функции
{yi} (i = 0, 1, …,n). Эти значения — либо результаты расчетов, либо экспериментальные данные. На практике могут понадобиться значения величины у и в других точках, отличных от узлов xi. Однако получить эти значения можно лишь путем очень сложных расчетов или проведением дорогостоящих экспериментов.
Таким образом, с точки зрения экономии времени и средств мы приходим к необходимости использования имеющихся табличных данных для приближенного вычисления искомого параметра у при любом значении (из некоторой области) определяющего параметра х, поскольку точная связь y = f x( ) неизвестна.
Этой цели и служит задача о приближении (аппроксимации) функции: заданную функцию f x( ) требуется приближенно заменить (аппроксимировать) некоторой функцией F(x) так, чтобы отклонение (в некотором смысле)
F(x) от f x( ) в заданной области было наименьшим. Функция F(x) при этом называется аппроксимирующей.
Если приближение строится на заданном дискретном множестве точек {xi}, то аппроксимация называется точечной. К ней относятся интерполирование, среднеквадратичное приближение и др. При построении приближения на непрерывном множестве точек (например, на отрезке [ab; ]) аппроксимация называется непрерывной (или интегральной).
Одним из основных типов точечной аппроксимации является интерполирование. В этом случае аппроксимирующая функция проходит через заданные узловые точки. Иногда приближение табличных данных методом интерполирования неудобно. Так, например, если данные в таблице не точны, то совпадение значений интерполяционной функции в узлах с табличными данными означает, что она точно повторяет ошибки таблицы. В таких случаях используют другие виды аппроксимации, например метод наименьших квадратов. По этому методу аппроксимирующая функция строится так, чтобы сумма квадратов расстояний от ординат точек до линии графика аппроксимирующей функции для одинаковых абсцисс была наименьшей.
Интерполирование (интерполяция) — приближенное или точное нахождение какой-либо величины по известным отдельным ее значениям или значениям других величин, связанных с ней. Интерполирование является разновидностью аппроксимирования.
В первоначальном понимании интерполирование — восстановление функции (точное или приближенное) по известным ее значениям или значениям ее производных на заданных отрезках.
Основное применение интерполяции — это вычисление значений табулированной функции для неузловых (промежуточных) значений аргумента, поэтому интерполяцию часто называют "искусством чтения таблиц между строками" (П. Ф. Фильчаков).
Теория интерполирования используется также при построении и исследовании формул для численного интегрирования, для получения методов решения дифференциальных и интегральных уравнений.
К интерполированию приходится иногда прибегать и в том случае, когда для функции f x( ) известно и аналитическое представление, с помощью которого можно вычислять ее значения для любого значения х из отрезка [ab; ], в котором она определена, но вычисление каждого значения сопряжено с большим объемом вычислений.
Если в процессе решения задачи необходимо находить значения функции f x( ) для очень большого количества значений аргумента, то прямой способ потребовал бы громадной вычислительной работы. В этом случае для уменьшения объема вычислений также прибегают к интерполированию, т. е. вычисляют несколько значений f x( i ) (i = 0, 1, ..., n) и по ним строят простую интерполирующую функцию F(x), с помощью которой и вычисляют приближенные значения f x( ) в остальных точках.
Интерполяцией функции f x( ) называется замена ее функцией F(x) определенного класса, совпадающей с f x( ) в точках xk. При этом точки xk называются узлами интерполяции, а функция F(x) — интерполяционной функцией (рис. 6.1).
Если интерполяционная функция F(x) строится на всем рассматриваемом интервале изменения аргумента х, то такая интерполяция называется глобальной (когда F(x) проходит через все узлы). В противном случае интерполяцию называют кусочной, или локальной (когда находим F(x) по некоторым узлам).
Пример интерполяции функции f (x) по четырем узлам приведен на рис. 6.1, из которого видно, что узлы интерполяции не обязательно должны располагаться равномерно на отрезке [ab; ].
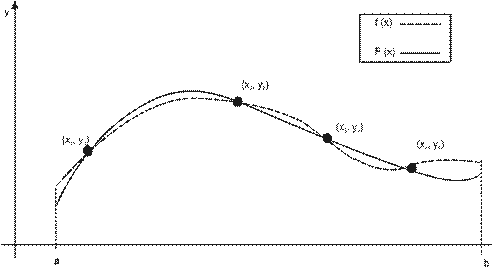
Рис. 6.1. Графический пример интерполяции F(x) функции по четырем узлам
Если f x( ) — табличная функция, скажем, полученная из эксперимента, т. е. известны только ее значения yk в точках xk, то, вообще говоря, о качестве полученного приближения судить трудно. Однако, если значения f x( ) могут быть вычислены в любой точке отрезка [ab; ], то в этом случае можно исследовать качество получающегося приближения, например найдя максимальное отклонение функции F(x) от функции f(x). На качество приближения сильное влияние оказывают количество и расположение узлов, а также гладкость функции f(x).
Погрешностью интерполяции функции f x( ) на некотором отрезке
называется максимум величины ![]() f (x)−
F x()
f (x)−
F x()![]() на
этом отрезке.
на
этом отрезке.
В качестве классов интерполирующих функций могут выступать полиномиальные, тригонометрические, экспоненциальные и другие функции. На практике чаще всего используется полиномиальная интерполяция. Это обусловлено как большей простотой вычисления полиномов по сравнению с другими классами интерполирующих функций, так и более развитым математическим аппаратом.
Для практики весьма важен случай аппроксимации функции f x( ) многочленом F( )x = +a0 a x a x1 + 2 2+…+a xn n. Такой способ приближения имеет в своей основе гипотезу, согласно которой на небольших отрезках изменения аргумента х функция f x( ) может быть достаточно хорошо приближена с помощью параболы некоторого порядка, аналитическим выражением которой и будет алгебраический многочлен.
Простейшим видом полиномиальной интерполяции является линейная интерполяция. Она заключается в замене f x( ) линейной функцией на основе значений f x( ) в двух точках.
Пусть y0= f x( 0), y1 = f x( 1), тогда линейная интерполяция задается уравнением: y= + −y0 [(x x y0)( 1−y0)]/ (x x1− 0).
Линейная интерполяция носит локальный характер и используется для нахождения значений f x( ) на отрезке [xi−1; xi ], [xi−1; xi ], где i = 1, 2, ..., n (рис. 6.2).
|
|
|
Рис. 6.2. Линейная интерполяция таблично заданной функции
В результате применения метода линейной интерполяции к узлам таблично заданной функции получаем систему линейных уравнений.
Говорят, что таблица допускает линейную интерполяцию, если на каждом отрезке [xk; xk+1] погрешность вычислений с ее помощью не превосходит погрешности значений таблицы.
Интерполяционная функция F(x) используется для нахождения значений f x( ) в промежуточных точках между крайними узлами интерполяции. Ино-
гда она используется и для приближенного вычисления f x( ) за пределами отрезка, содержащего узлы интерполяции.
Приближенное вычисление функции f x( ) с помощью функции F(x) за пределами отрезка, содержащего узлы интерполяции, называется экстраполяцией. Это также разновидность аппроксимирования.
Пусть нам даны значения функции f x( ) в n +1 точке:
yk = f x( k) при k = 0, 1, … n.
Тогда существует интерполяционный полином Ln(x) степени не больше n, значения которого совпадают со значениями f х( ) во всех точках хk и для которого выполняются условия Ln (xi )=yi. Этот полином называется полиномом Лагранжа и служит примером глобальной интерполяции (рис. 6.3).
Запишем полином Лагранжа в виде суммы:
Ln( )x = l0( )x +l x1( ) +l2( )x + +... ln( )x , (1)
где lk (xi )= ,yi если i = k, и lk (xi )= 0, если i ≠ k;
Полиномы n-й степени lk (x), называются лагранжевыми коэффициентами и имеют следующий вид:
(x − x0)(x − x1)...(x − xk−1)(x − xk+1)...(x − xn)
lk = ![]() (2)
(2)
(xk − x0)(xk − x1)...(xk − xk−1)(xk − xk+1)...(xk − xn)
Подставим (2) в (1) и перепишем Ln(x) в виде:
![]() L xn( ) = ∑j=n yj ⎛⎜⎜∏=n xx xj−−xii ⎞⎟⎟⎠, i
≠ j — интерполяционная формула Ла-
L xn( ) = ∑j=n yj ⎛⎜⎜∏=n xx xj−−xii ⎞⎟⎟⎠, i
≠ j — интерполяционная формула Ла-
0 ⎝ i 0
гранжа.
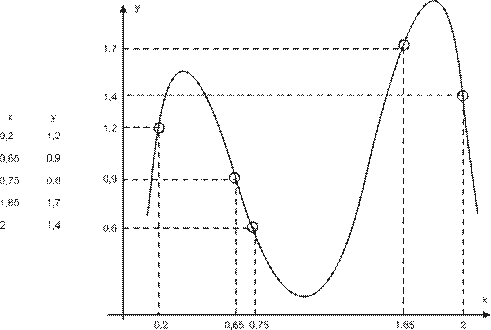
Рис. 6.3. Интерполяция таблично заданной функции полиномом Лагранжа
Погрешность интерполяции функции полиномом Лагранжа на отрезке [a b; ]=[x x0, n] оценивается формулой:
![]()
![]()
![]() Mn+1 f
( )x − L x( ) ≤ ⋅ (x − x0) (⋅ x
− x1) ... (⋅ ⋅ x − xn), (n +1)!
Mn+1 f
( )x − L x( ) ≤ ⋅ (x − x0) (⋅ x
− x1) ... (⋅ ⋅ x − xn), (n +1)!
где Mn+1 = max f (n+1)( ) .x
x ab∈[ ; ]
Формула Лагранжа является наиболее общей и может применяться даже в ситуациях, когда расстояния между соседними узлами интерполяции различны.
Решение нелинейных уравнений
с одной переменной
Множество задач, решаемых с помощью компьютера, сводятся к решению уравнений. Рассмотрим некоторые понятия, связанные с уравнениями и их численным решением.
Уравнение типа f x( )= 0 называется нелинейным, если график функции у = f x( ) отличен от прямой.
Нелинейные уравнения можно разделить на два класса: алгебраические и трансцендентные.
Алгебраическими уравнениями называют уравнения, содержащие только алгебраические функции (целые, рациональные, иррациональные). В частности, многочлен является целой алгебраической функцией.
Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и другие), называются трансцендентными.
Решить уравнение — значит найти такое значение x, при котором уравнение превращается в тождество. Если рассматривать f x( ) как функцию, то решение уравнения сводится к нахождению "нулей" функции, т. е. таких значений аргумента х, при которых функция пересекает ось абсцисс.
Число, обращающее f x( ) в нуль, т. е. такое, что f x( )= 0, называется корнем уравнения f x( )= 0 или нулем функции f x( ).
Методы решения нелинейных уравнений делятся на две группы:
точные методы;
итерационные методы.
Точные методы позволяют записать корни в виде некоторого выражения (формулы). Из школьного курса алгебры известны такие методы для решения тригонометрических, логарифмических, показательных, а также простейших алгебраических уравнений.
Как известно, многие уравнения и системы уравнений не имеют аналитических решений. В первую очередь это относится к большинству трансцендентных уравнений. Доказано также, что нельзя построить формулу, по которой можно было бы решить произвольное алгебраическое уравнение степени выше четвертой.
Кроме того, в большинстве случаев такие уравнения могут содержать коэффициенты, полученные экспериментальным путем. Следовательно, задача о "точном" определении корней уравнения теряет смысл, т. к. даже при использовании "точных" методов приходится проводить вычисления, которые приводят к приближенным результатам. В этих ситуациях важное значение приобретают методы приближенного вычисления корней уравнения и оценки степени их точности.
Суть приближенных методов вычисления корней нелинейного уравнения ви-
![]() да f x( )= 0 заключается
в том, чтобы найти такое х*, что х х− <* ε, где ε —
бесконечно малая наперед заданная положительная величина. В случае
да f x( )= 0 заключается
в том, чтобы найти такое х*, что х х− <* ε, где ε —
бесконечно малая наперед заданная положительная величина. В случае
нахождения "нулей" функции приближенные методы предполагают определение х*, удовлетворяющего условию | f х( *) |<=ε.
Корни уравнения могут быть как действительными, так и комплексными. Остановимся на определении только действительных корней.
В общем случае уравнение может иметь 0; 1; 2;...∞ корней, поэтому решение задачи разбивается на два этапа: на первом этапе осуществляется отделение (локализация) корней, на втором этапе проводится итерационное (пошаговое) их уточнение.
Процедура локализации корней состоит в установлении малых числовых промежутков (или промежутка, если корень единственный), которые содержат один и только один корень уравнения f x( )= 0.
Иногда вместо отрезка локализации достаточно указать начальное приближение к корню.
Чаще всего процедуру локализации корней реализуют графическим методом. Его суть заключается в построении графика функции у = f x( ) и определении достаточно узких отрезков, на каждом из которых функция непрерывна, монотонна и имеет значения разных знаков на его концах, т. е. выполняются необходимые и достаточные условия существования единственного корня на уравнения f x( ) = 0.
Пример. Рассмотрим уравнение х3 −соs x( ) + =1 0.
Построим график функции f x( ) = − х3 соs x( ) +1 (рис. 6.4).
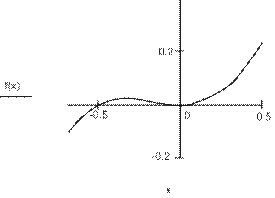
Рис. 6.4. Локализация (отделение) корней уравнения х3−соs x( ) + =1 0.
Получим два отрезка локализации: [–0.6;–0.4] и [–0.2;0.2].
На втором этапе вычисляют приближенное значение корня с заданной точностью. Рассмотренные далее приближенные (численные) методы решения нелинейных уравнений позволяют на заданном интервале [ab; ] находить корень с заданной точностью. При этом на интервале должен существовать только один корень.
Простейшими приближенными методами решения уравнений являются методы перебора, бисекции, хорд, касательных, итераций.
Метод перебора. При решении нелинейного уравнения методом перебора задаются начальное значение аргумента x a= и шаг h, который определяет и точность нахождения корня уравнения.
Пока выполняется условие f x( )⋅ f x( + h) > 0, аргумент x увеличивают на шаг h (x x h= + ). Как только произведение f x( )⋅ f x( + h) становится отрицательным, алгоритм перебора завершают. Решение уравнения находится на интервале [x x; + h]. Блок-схема метода приведена на рис. 6.5.
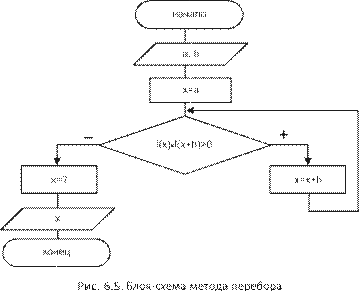
Метод бисекции. При решении нелинейного уравнения методом бисекции (половинного деления) задаются интервал [ab; ], на котором существует только один корень, и желаемая точность ε. Затем определяется середина интервала с= +(а b) / 2. Если f c( ) = 0, то c — корень уравнения, и задача решена. Если это условие не выполняется, то из двух половин отрезка выбираем ту, на концах которой функция имеет значения противоположных знаков.
Если выполняется условие f a( )⋅ f c( ) < 0, то правую границу интервала b переносим в среднюю точку с (b = c). Если это условие не выполняется, то в среднюю точку переносим левую границу (a c= ).
![]() Критерием окончания
итерационного процесса метода бисекции является выполнение условия: b a−
<= 2 .ε
В качестве значения корня с заданной точностью ε принимают середину
отрезка [ab; ], на котором выполнилось
условие. Блок-схема решения нелинейных уравнений методом бисекции приведена на
рис. 6.6.
Критерием окончания
итерационного процесса метода бисекции является выполнение условия: b a−
<= 2 .ε
В качестве значения корня с заданной точностью ε принимают середину
отрезка [ab; ], на котором выполнилось
условие. Блок-схема решения нелинейных уравнений методом бисекции приведена на
рис. 6.6.
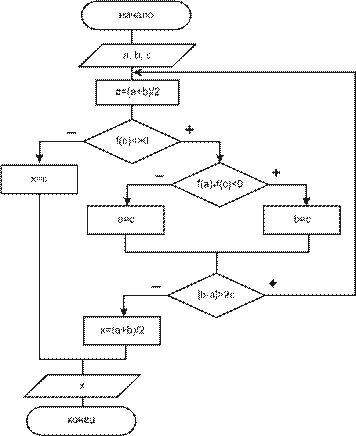
Рис. 6.6. Блок-схема метода бисекции
Метод бисекции не обеспечивает высокой скорости сходимости, однако он не требует никаких подготовительных операций (нахождения первой и второй производных, проверки условия сходимости). Использование метода рекомендуется для уточнения корней сложных и громоздких нелинейных уравнений.
Метод хорд. При решении нелинейного уравнения методом хорд задаются интервал [ab; ], на котором существует только одно решение, и точность ε.
Затем через две точки с координатами (a f a; ( )) и (b f b; ( )) проводим отрезок прямой линии (хорду) и определяем точку пересечения этой линии с осью абсцисс (точку c ).
Если f c( ) = 0, то точка c является корнем уравнения, и задача решена, в противном случае сужаем границу поиска корня по следующему правилу: если f a( )⋅ f c( ) < 0, то правую границу интервала переносим в точку с (b c= ); если указанное условие не выполняется, то в точку c переносится левая граница интервала (а с= ). Поиск решения прекращается при достижении заданной точности | f c( ) |<=ε.
Для определения точки пересечения хорды с осью абсцисс
воспользуемся следующей формулой: c = +a ![]() f a( )/ ( f a( )− f b()
f a( )/ ( f a( )− f b()![]() (b−a) (попытайтесь получить формулу самостоятельно,
воспользовавшись уравнением прямой, проходящей через точки M a f a( , ( )) и M '(b f
b, ( )), и положив в нем у=0).
(b−a) (попытайтесь получить формулу самостоятельно,
воспользовавшись уравнением прямой, проходящей через точки M a f a( , ( )) и M '(b f
b, ( )), и положив в нем у=0).
Блок-схема метода хорд показана на рис. 6.7.
Метод касательных. При решении нелинейного уравнения методом касательных (иначе его называют методом Ньютона — Рафсона) задаются начальное значение аргумента x0 и точность ε.
Условием сходимости метода касательных является выполнение неравенства f x( 0)⋅ f ''(x0) > 0, поэтому в зависимости от него в качестве x0 может быть
выбрана как точка а (начало отрезка локализации корня), так и точка b (конец этого отрезка). На рис. 6.8 приведены варианты выбора x0.
Выберем, например, x0 =b (рис. 6.8, а). В точке B0(x f x0; ( 0 )) проведем касательную к кривой у = f x( ) и, определив точку пересечения касательной с осью абсцисс ( x1), возьмем ее в качестве первого приближения к искомому корню. В точке B1(x f x1; ( 1)) снова строим касательную, находим следующее приближение искомого решения x2 и т. д. Указанную процедуру повторяем до тех пор, пока | f x( i ) |>ε.
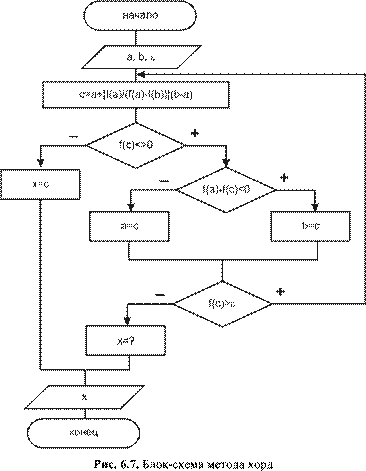
Для определения точки пересечения (i +1) касательной с осью абсцисс воспользуемся формулой: xi+1 = −xi f x( i ) / f '(xi ). Действительно, уравнение касательной к кривой у = f x( ) в точке Bi(x f x1; ( i )) имеет вид:
* у − f x( i )= f '(xi )(x− xi ). Полагая у=0 при x x» i+1, получим тождество:
0 − f x( i )= f '(xi )(xi+1− xi ).
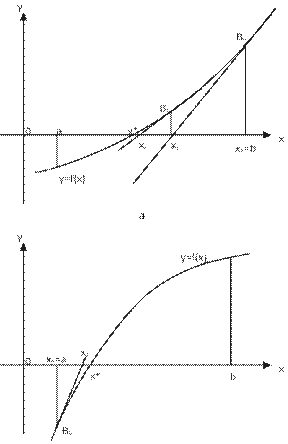
б
Рис. 6.8. Варианты выбора x0 при использовании метода касательных
Дальнейшее его преобразование xi+1− =−xi f x( i ) / f '(xi ) позволяет получить формулу xi+1 = −xi f x( i ) / f '(xi ), выражающую зависимость текущего приближения к корню (xi+1) от предыдущего (xi).
Блок-схема решения нелинейных уравнений методом касательных показана на рис. 6.9.
Метод касательных обеспечивает высокую скорость сходимости, которая тем больше, чем меньше величина первой производной функции f x( ). Теоретически скорость сходимости метода касательных на порядок выше скорости сходимости метода бисекции. Основной недостаток метода касательных заключается в необходимости вычисления производных функции.
Если производная f '(x) мало изменяется на отрезке [a b; ], то можно положить f '(xi )» f '(x0). Тогда рекуррентная формула для вычисления очередного приближения к корню через предыдущее значение примет вид: xi+1 = −xi f (xi ) / f '(x0 ).
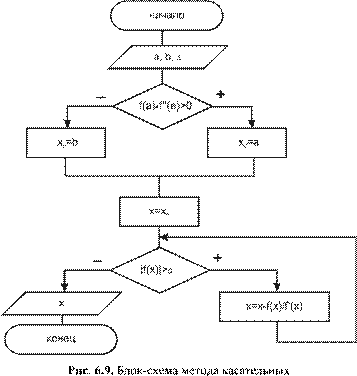
Такой подход к уточнению корней нелинейного уравнения получил название модифицированного метода Ньютона-Рафсона (касательных).
Метод хорд-касательных. Если в методе касательных производную функции f '(xi ) заменить отношением конечных приращений, то получаем расчетную формулу для метода хорд-касательных: xi 1+ = −xi ( f x( i )(xi − xi 1− )) / ( f x( i )− f x( i 1− )).
Порядок выполнения вычислений в данном методе аналогичен рассмотренному ранее.
Метод итераций. Для решения нелинейного уравнения методом итераций
(последовательных приближений) воспользуемся записью уравнения F x( )=0 в виде x = f x( ).
Функция x = f x( ) называется итерационной функцией.
![]() При
использовании метода задаются начальное значение аргумента x0 и
точность ε.
Первое приближение корня находим из выражения x1 = f x( 0),
второе — x2 = f
x( 1) и т. д. В общем случае i +1 приближение найдем по
формуле xi+1 = f
x( i ). Указанную процедуру повторяем до тех пор, пока f x( i ) >ε. Условием
сходимости метода итераций является выполнение неравенства f '(x) <1.
При
использовании метода задаются начальное значение аргумента x0 и
точность ε.
Первое приближение корня находим из выражения x1 = f x( 0),
второе — x2 = f
x( 1) и т. д. В общем случае i +1 приближение найдем по
формуле xi+1 = f
x( i ). Указанную процедуру повторяем до тех пор, пока f x( i ) >ε. Условием
сходимости метода итераций является выполнение неравенства f '(x) <1.
Геометрический смысл метода итераций поясним следующим образом. Построим на плоскости в прямоугольной системе координат ХОУ графики функций у = х и у = f x( ). Каждый действительный корень уравнения f x( )=0 является абсциссой точки пересечения кривой и у = f x( ) и прямой у х= . Начиная с некоторой точки А0 0(x ; f x( 0)), строим ломаную линию
АВ АВА0 0 1 1 2… ("лестница"), звенья которой попарно параллельны оси ОХ и оси ОУ. Вершины А А А0 1 2, , ,… лежат на кривой у = f x( ), а вершины В В В0 1 2, , ,… — на прямой у х= . Общие абсциссы точек А1 и В0, А2 и В1,... очевидно представляют собой последовательные приближения x x1 2, , … …, xn, искомого корня.
Решение в виде "лестницы" получается, если тангенс угла наклона касательной, проведенной к кривой у = f x( ) в точках А А А0 1 2, , ,…, — положительный, и при этом f '(x)<1 (рис. 6.10).
Возможен и другой вид ломаной АВ АВА0 0 1 1 2… — "спираль" (рис. 6.11).
Следует отметить, что если выполнено условие сходимости метода итераций
![]() ( f '( )x <1), то в качестве x0 может выступать любое число из
промежутка
( f '( )x <1), то в качестве x0 может выступать любое число из
промежутка
[ab; ]. Благодаря этому метод итераций является самоисправляющимся, т. е.
отдельная ошибка в вычислениях не повлияет на окончательный результат, т. к. ошибочное значение можно рассматривать как новое начальное приближение к корню x0. В этом случае лишь возрастает объем вычислений. Свойство самоисправления делает метод итераций одним из надежных методов решения нелинейных уравнений с одной переменной.
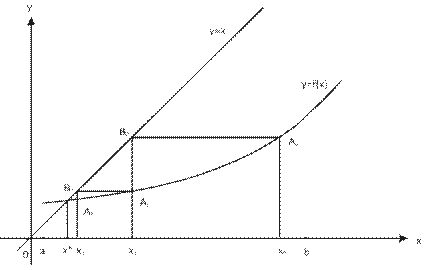
Рис. 6.10. Геометрическая интерпретация итерационного процесса в виде "лестницы"
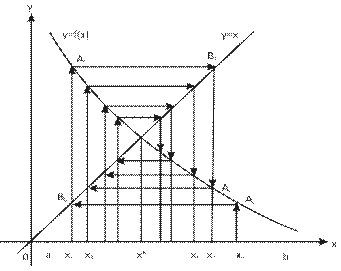
Рис. 6.11. Геометрическая интерпретация итерационного процесса в виде "спирали"
В случае, когда абсолютная величина тангенса угла наклона касательной, проведенной к кривой у = f x( ) в точках А А А0 1 2, , ,…, больше единицы, итерационный процесс расходится (рис. 6.12).
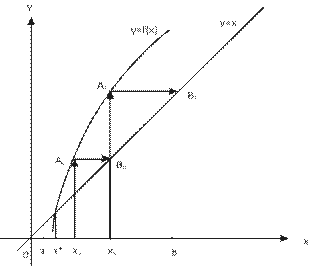
Рис. 6.12. Случай расходящегося итерационного процесса
Одной из серьезных проблем при использовании метода итераций является проблема подбора итерационной функции, т. е. преобразования исходного уравнения F x( )=0 к виду х = f x( ).
Пример. Рассмотрим уравнение 5х3 −20 3 0x+ = на отрезке [0;1].
Это уравнение можно привести к виду х = f x( ) следующими способами:
х х= +5х3 − 20x+ 3, тогда f1( )x =5х3 −19x+3;
х=(5х3 + 3) / 20, тогда f2( )x =(5х3 +3 / 20.)
Определим, какую из двух полученных функций f x( ) следует использовать в методе итераций. Вычислим и оценим значения производных обеих функций на заданном отрезке.
![]()
![]()
![]() f '1( )x = 15х2 −
>191 на [0;1];
f '1( )x = 15х2 −
>191 на [0;1];
f '2( )x = 15х2 / 20< 3х2 / 4 <1 на [0;1].
Следовательно, можно воспользоваться функцией f2(x) и уточнить корень
по формуле хi = (5х3i−1+ 3) / 20. За начальное приближение к корню x0 можно взять любую точку из отрезка [0;1].
Рассмотрим некоторые приемы преобразования уравнения f x( )=0 к виду х = f x( ).
![]() Пусть f x( )=0 преобразовано
к виду х = f
x( ). Если окажется, что
f '(x) >1, тогда вместо f x( ) рассмотрим обратную
функцию х =ϕ(у).
Пусть f x( )=0 преобразовано
к виду х = f
x( ). Если окажется, что
f '(x) >1, тогда вместо f x( ) рассмотрим обратную
функцию х =ϕ(у).
Перепишем х = f x( ) в виде у=ϕ(у) в старых обозначениях: х =ϕ(х).
![]() Согласно
свойству производных обратных функций, на отрезке [ab; ]
будет иметь место неравенство ϕ '(у) =1 / f '(x) <1, т. е. в качестве
итерационной функции можно воспользоваться функцией ϕ(у).
Согласно
свойству производных обратных функций, на отрезке [ab; ]
будет иметь место неравенство ϕ '(у) =1 / f '(x) <1, т. е. в качестве
итерационной функции можно воспользоваться функцией ϕ(у).
Уравнение f x( )=0 преобразуем к виду х = −x mf x( ), где m — константа (m> 0). Подбираем m таким образом, чтобы для всех х из отрезка [ab; ] выполнялось условие |1−mf '(x) |<1.
Решение систем линейных уравнений
Вслед за решением уравнений необходимо рассмотреть методы решения систем уравнений. Простейшей задачей в этом классе является задача решения систем линейных уравнений.
В общем виде система n линейных уравнений с n неизвестными может быть записана в виде:
⎧a x a x11 1+ 12 2 + +... a x1n n =b1 ⎪⎪a x a x21 1+ 22 2 + +... a x2n n =b2
⎨ (1)
⎪..............................................
⎩⎪a x a xn1 1+ n2 2 + +... a xnn n =bn
Решением системы n линейных уравнений с n неизвестными называют такую упорядоченную последовательность чисел (x x1 2; ;…; xn), при подстановке которой в каждое из уравнений системы все уравнения обращаются в истинные тождества.
Решить систему уравнений — значит найти множество всех ее решений.
Заметим, что множество решений системы уравнений может быть пустым. В этом случае говорят, что система не имеет решений или что система несовместна.
Рассмотрим метод Гаусса (или метод последовательного исключения неизвестных) решения системы уравнений. Этот метод предусматривает два этапа решения системы — так называемые прямой и обратный ходы.
Прямой ход метода состоит из n−1 шага исключения переменных, обеспечивающих приведение системы к "треугольному" виду.
Шаг 1. Исключим неизвестное x1 из уравнений с номерами i = 2,3,..., n .
Предположим, что a11 ≠ 0. Будем называть его ведущим элементом 1-го шага.
ai1
Найдем величины µi1
= ![]() , i = 2,3,..., ,n называемые
множителями 1-го ша-
, i = 2,3,..., ,n называемые
множителями 1-го ша-
a11
га. Вычтем последовательно из второго, третьего, ..., n− го уравнений системы первое уравнение, умноженное соответственно на µ µ21 31, ,...,µn1.
В результате 1-го шага получим систему уравнений (2), равносильную системе (1):
⎧a x11 1 +a x12 2 +a x13 3 + +... a x1n n =b1
⎪
⎪0x1 +a22(1)x2 +a23(1)x3 + +... a2(1)nxn =b2(1)
⎨ (2)
⎪.........................................................
⎪⎩0x +an(1)x2 +an(1)3 x3 + +... ann n(1)x =bn(1)
1 2
Аналогично проводятся остальные шаги прямого хода метода Гаусса. Опишем очередной k− й шаг. Предположим, что ведущий элемент akk ≠ 0. Вы-
(k−1) a
числим множители k−
го шага:µik = ![]() ik(k−1) , i = +k 1,...,
n и вычтем последо-
ik(k−1) , i = +k 1,...,
n и вычтем последо-
a
kk
вательно из (k + −1) го, (k+ −2) го, ..., n− го уравнений системы k− е урав-
нение, умноженное соответственно на µk k+1 ,µk k+2 ,..., µnk.
После (n− −1) го шага исключения получим систему уравнений (3), матрица которой является верхнетреугольной:
⎧a x a x11 1 + 12 2 +a x13 3 + +... a x1n n =b1
⎪
⎪0x1 +a x22(1) 2 +a x23(1) 3 + +... a x2(1)n n =b2(1)
⎨ (3)
⎪.........................................................
⎪⎩0x + 0x2 + 0x3 + +... ann(n−1)xn =bn(n−1)
1
На этом вычисления прямого хода заканчиваются.
Обратный ход представляет собой решение треугольной системы: вычисление значений переменных, начиная с последнего уравнения, и подстановку этого значения в предыдущее уравнение.
Из последнего уравнения системы находим xn (xn =bn(n−1)
![]() ann(n−1)).
Подстав-
ann(n−1)).
Подстав-
ляя найденное значение xn в предпоследнее уравнение, получим xn−1
(xn−1
= (bn(n−1−2) −an n(n−−12)xn)![]() an n(n− −−1 12) ). Далее
последовательно находим неизвест-
an n(n− −−1 12) ). Далее
последовательно находим неизвест-
ные xn−2, …, x x2 1, .
Преобразования Гаусса удобно проводить не с самой системой уравнений, а с матрицей ее коэффициентов. Введем матрицу
|
⎛a11 ⎜ A=⎜a21 ⎜ ⎜⎜an1 ⎝ |
a12 a22
an2 |
|
a b2n2⎟ ⎟, ⎟ a bnn n⎠ |
называемую расширенной матрицей системы (1) размера n⋅(n +1), т. к. матрица А дополнена столбцом свободных членов. Система (1) с использованием расширенной матрицы может быть переписана в виде: Ax b= .
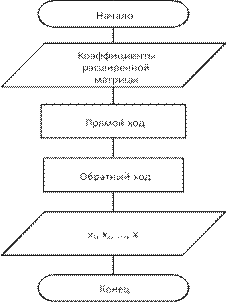
Рис. 6.13. Блок-схема алгоритма метода Гаусса
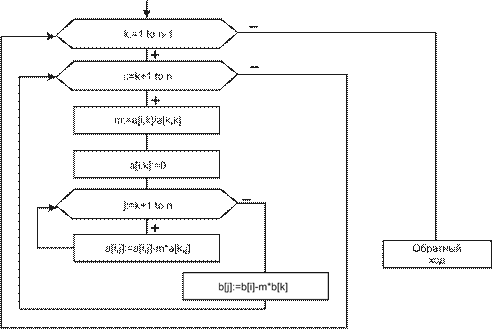
Рис. 6.14. Блок-схема прямого хода алгоритма Гаусса
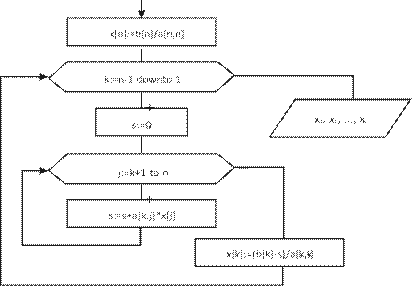
Рис. 6.15. Блок-схема обратного хода алгоритма Гаусса
Вследствие громоздкости задачи ее алгоритм требует пошаговой детализации. На первом этапе представим его в виде блок-схемы, приведенной на рис. 6.13.
Поскольку блоки ввода коэффициентов расширенной матрицы и вывода решения системы не представляют трудностей, рассмотрим детализацию прямого и обратного ходов алгоритма Гаусса (рис. 6.14, 6.15).
В рассмотренных блоках k — номер того уравнения, которое вычитается из остальных, а также номер того неизвестного, которое исключается из (n − k) оставшихся уравнений; i — номер того уравнения, из которого в данный момент исключается неизвестное; j — номер столбца расширенной мат- рицы.
Численное интегрирование
Интеграл, у которого известна его первообразная F( )x (то есть ее можно выразить через элементарные функции), вычисляется по формуле НьютонаЛейбница I = F a( ) − F b( ). Для этого достаточно вычислить значения функции F( )x в точках a и b, а саму функцию найти по таблице интегралов.
В тех случаях, когда нахождение первообразной ( F( )x ), непрерывной на отрезке [a b; ], функции f x( ) сложно или невозможно, применяется численное интегрирование. В этом случае полезно определение интеграла как предела суммы.
Определенным интегралом функции f x( ), взятом в интервале от a до b,
n
называется предел, к которому стремится интегральная сумма ∑ f x( )i Δxi
i=1 при стремлении всех промежутков Δxi к нулю:
b n
∫ f x dx( ) = ![]() lim f x( )i Δxi
lim f x( )i Δxi
a
Численное интегрирование функции f x( ) состоит в нахождении определенного интеграла от этой функции в некоторых пределах от x a= до x b= .
Геометрический смысл определенного интеграла непрерывной на промежутке [ab; ] функции f x( ) заключается в нахождении площади фигуры (криволинейной трапеции), образованной этой функцией, прямыми x=a, x b= и осью OX (рис. 6.16).
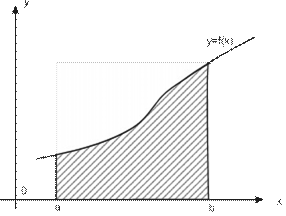
Рис. 6.16. Геометрический смысл определенного интеграла с конечными пределами
Суть приближенных методов вычисления определенного интеграла с конечными пределами заключается в том, что отрезок интегрирования [a b; ] точками a х= < < <… =0 х1 х2 хn b разбивается на n равных частей (шагов интегрирования) длины h =Δ = −x (b a) / .n
Затем на каждом шаге интегрирования подынтегральная функция f x( ) заменяется отрезками линий нулевого, первого или второго порядков. В результате получаются приближенные формулы для вычисления интеграла методами прямоугольников, трапеций и парабол (Симпсона) соответственно.
b n ![]() f x dx(
) = lim ∑ f x( i)Δ ≈xi ∑Ii, где Ii — элемент
интегральной суммы.
f x dx(
) = lim ∑ f x( i)Δ ≈xi ∑Ii, где Ii — элемент
интегральной суммы.
Δ →x 0
a i i=1
Метод прямоугольников. На каждом шаге интегрирования график функции f x( ) заменим горизонтальной линией (линией нулевого порядка) и вычис-
лим значение элемента интегральной суммы как площадь прямоугольника (рис. 6.17), где h — шаг интегрирования, у0 — значение функции в точке
х х= , у0 = f х( 0).
0
x +h
0
I1 = ∫ f x dx( ) ≈ y0 ⋅h
x0
Просуммировав площади всех прямоугольников, построенных на промежутке [ab; ], найдем приближенное значение площади рассматриваемой криволинейной трапеции, т. е. приближенное значение определенного интеграла
n b
∑I ≈∫ f x dx( ) .
i
i=1 a
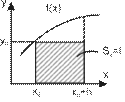
Рис. 6.17. Схема, поясняющая метод прямоугольника
Суть метода прямоугольников для отрезка [ab; ] проиллюстрирована на рис. 6.18, где площадь под кривой f x( ) (вспомните геометрический смысл определенного интеграла с конечными пределами) заменена суммой площадей заштрихованных прямоугольников. При этом в качестве одной стороны прямоугольника берется шаг интегрирования h, а в качестве другой стороны может быть выбрано значение функции f x( ) либо в начале (рис. 6.18, а), либо в конце (рис. 6.18, б), либо в середине (рис. 6.18, в) каждого элементарного отрезка.
Формулы прямоугольников для этих трех случаев запишутся в виде:
![]() S ≈ h⋅ f x —
формула левых прямоугольников;
S ≈ h⋅ f x —
формула левых прямоугольников;
лев
x a=
b
Sпр ≈ h⋅ ∑ f x( ) — формула правых прямоугольников;
x a h= +
S ![]() h f x
h f x ![]() — формула средних
прямоугольников. ср x a= 2
— формула средних
прямоугольников. ср x a= 2
Метод трапеций. Заменим на отрезке [x x0 0; +h] график подынтегральной функции f x( ) прямой, проходящей через две точки с координатами (х у0 0; ) и (х0 +h у; 1), и вычислим значение элемента интегральной суммы как площадь трапеции (рис. 6.19)
x h+
0 y0 + y1
I1 = ∫ f x dx( ) ≈ ⋅h .
x0 2
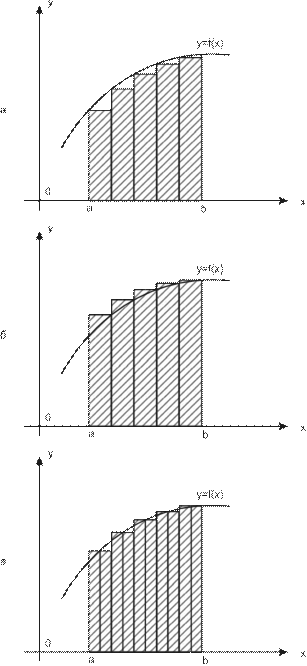
Рис. 6.18. Численное интегрирование методом прямоугольников
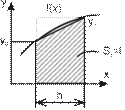
Рис. 6.19. Схема, поясняющая метод трапеций
Проведем аналогичную замену подынтегральной функции f x( ) на каждом шаге интегрирования (рис. 6.20).
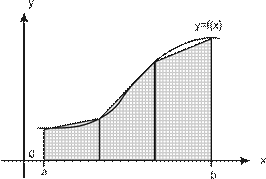
Рис. 6.20. Численное интегрирование методом трапеций
Вычислив общую сумму площади всех элементарных трапеций, построенных на промежутке [ab; ], найдем приближенное значение площади рассматриваемой криволинейной трапеции, т. е. приближенное значение определенного
b n b h−
f a( ) f b( )
интеграла ∫ f
x dx( ) ≈∑Ii
= ![]() + ∑ f x( ) +
+ ∑ f x( ) + ![]() .
.
a i=1 2 x a h= + 2
Метод Симпсона. Основная идея более точных методов интегрирования состоит в интерполяции подынтегральной функции f x( ) некоторой функцией
y x( ) и расчете интеграла уже от этой функции. Важно, чтобы при этом:
интеграл от y x( ) мог быть точно рассчитан аналитическими методами;
для уменьшения погрешности вычислений функция y x( ) была бы по возможности ближе к f x( ).
Очевидно, что наиболее простой подход заключается в интерполяции подынтегральной функции f x( ) на каждом из n шагов интегрирования какимлибо полиномом y x( ).
Известно, что могут быть предложены различные пути построения интерполирующих полиномов, отличающихся, например, порядком m. В частности, полиномы Лагранжа строятся при интерполяции f x( ) в N точках на каждом из n элементарных интервалов, на которые разбивается отрезок интегрирования [ab, ]. Семейство алгоритмов интегрирования в этом случае называется методами Ньютона-Котеса.
Если N=1, то полиномом является прямая линия, т. е. фактически мы возвращаемся к методу трапеций. Если же взять N= 2, то интерполирующим полиномом y x( ) на каждом шаге интегрирования будет квадратичная парабола, а сам алгоритм называется методом парабол, или методом Симпсона.
Заменим на отрезке [x x0 0; + 2 ]h график подынтегральной функции f x( ) квадратичной параболой, проходящей через три точки с координатами (х у0 0; ), (х0 +h у; 1), (х0 +2h у; 2) (рис. 6.21).
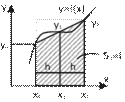
Рис. 6.21. Схема, поясняющая метод Симпсона
Расчетную формулу для вычисления элемента интегральной суммы получим, используя интерполяционный многочлен Лагранжа, в виде:
y x( )=y A x0 0( )+y A x1 1( )+y A x2 2( ),
где:
(x x x x− 1)( − 2) (x x x x− 0)( − 2) (x x x x− 0)( − 1)
A x0(
) = ![]() , A x1(
) =
, A x1(
) = ![]() , A x2(
) =
, A x2(
) = ![]() .
.
(x0 −x x x1)( 1− 2) (x x x x1− 0)( 1− 2) (x2 − x x0)( 2 − x1)
При x0 = 0; x1 = h; x2 = 2h, получим:
2 2
(x h x− )( − 2 )h x − x h⋅3 + 2h
![]() A x0( ) = 2 = 2 , 2h 2h
A x0( ) = 2 = 2 , 2h 2h
x x( − 2 )h x2 − 2hx
![]() A x1( ) = h h(− ) = −h2 ,
A x1( ) = h h(− ) = −h2 ,
2
x x h( − ) x −hx
![]() A x2( ) = 2 = 2 . 2h 2h
A x2( ) = 2 = 2 . 2h 2h
x0+2h 2h 2h 2h
I = ∫ y x dx( ) =∫ y A x dx0 0( ) + ∫ y A x dx1 1( ) + ∫ y A x dx2 2( )
x0=0 0 0 0
![]()
![]() 2∫0h y A x dx0 0( ) 2yh2 ⎡⎣⎢⎛⎝
x3 −3h x2 + 2h x2 ⎟⎞⎟ 02h⎤⎥ = y02 ⎡⎢⎢⎣8h33 − 3h⋅24h2 + 2h2 ⋅2h⎤⎥⎥⎦ =
2∫0h y A x dx0 0( ) 2yh2 ⎡⎣⎢⎛⎝
x3 −3h x2 + 2h x2 ⎟⎞⎟ 02h⎤⎥ = y02 ⎡⎢⎢⎣8h33 − 3h⋅24h2 + 2h2 ⋅2h⎤⎥⎥⎦ =
= 0 ⎢⎜⎜ 3 2 ⎠ ⎥⎦ 2h
![]() = y h0 3 ⋅16−36+
24 = y h0 .
= y h0 3 ⋅16−36+
24 = y h0 .
2
2h 6 3
2h 2h
Аналогично преобразуя ∫ y A x dx1 1( ) и ∫ y A x dx2 2( ) , получим формулу для
0 0
вычисления элементарной интегральной суммы по формуле Симпсона (пара-
y h0 4y h1 y h2 h
бол): I1 = + ![]() + =
+ =
![]() (y0 + 4y1+
y2).
(y0 + 4y1+
y2).
3 3 3 3
Сложив все элементарные интегральные суммы, получим формулу Симпсона для приближенного вычисления определенного интеграла на отрезке
b
![]() [a b, ]: ∫ f x dx( ) = (h3)( fa + 4 f1+ 2 f2 + 4 f3
+ +... 4 fb h− + fb), где h — шаг ин-
[a b, ]: ∫ f x dx( ) = (h3)( fa + 4 f1+ 2 f2 + 4 f3
+ +... 4 fb h− + fb), где h — шаг ин-
a
тегрирования, fa, fi, fb — значения функции при x, равном a, i и b соответственно.
![]() Контрольные вопросы
Контрольные вопросы
1. Приведите примеры практического использования результатов табулирования функций.
2. В чем заключается отличие точечной аппроксимации от непрерывной?
3. Дайте определение аппроксимирующей функции.
4. Поясните суть различных способов интерполяции.
5. Приведите примеры практического применения методов интерполяции.
6. Сформулируйте постановку задачи приближенного решения нелинейного уравнения с одной переменной и основные этапы ее решения.
7. Какое значение аргумента х будет являться приближенным корнем уравнения по окончании метода перебора? На сколько оно будет отличаться от точного значения корня? Ответ обоснуйте.
8. Поясните критерий завершения итерационного процесса метода бисекции.
9. Поясните критерий завершения итерационного процесса метода хорд. Какое значение аргумента х будет являться приближенным значением корня уравнения по окончании метода хорд? Ответ обоснуйте.
10. Что такое итерационная функция? Каковы правила ее получения?
11. Что называют решением системы n линейных уравнений с n неизвестными?
12. Какие системы уравнений называют равносильными?
13. Какие преобразования уравнений системы приводят к системе, равносильной исходной? Приведите примеры.
14. Обоснуйте необходимость использования методов численного интегрирования.
15. Поясните суть приближенных методов вычисления определенного интеграла с конечными пределами.
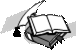 Темы для рефератов и докладов
Темы для рефератов и докладов
1. Интерполяционная формула Ньютона.
2. Сплайн-интерполяция.
3. Интерполяционные формулы с центральными разностями (Гаусса, Стирлинга, Бесселя, Эверетта и др.).
4. Рациональная интерполяция.
5. Интерполяция средствами Mathcad.
6. Экстраполяция.
7. Применение приближенных методов решения нелинейных уравнений с одной переменной в различных областях.
8. Исследование сходимости приближенных методов вычисления действительных корней уравнений с одной переменной.
9. Математические пакеты для решения систем линейных уравнений.
10. Экономичные методы решения линейных систем.
11. Применение интегрального исчисления в различных областях.
12. Применение определенных интегралов в геометрии.
13. Использование определенных интегралов для решения физических задач.
14. Пакеты прикладных программ для реализации численного интегрирования.
15. Методы Ньютона-Котеса для приближенного вычисления определенного интеграла с конечными пределами.
16. Численное интегрирование с заданной точностью.
17. Алгоритм Ромберга приближенного вычисления определенного интеграла с конечными пределами.
![]() Вопросы для обсуждения
Вопросы для обсуждения
1. От чего, по-вашему, зависит точность аппроксимации?
2. Сформулируйте этапы процесса интерполяции. Поясните суть каждого из них.
3. Всегда ли точность интерполяции зависит от количества узлов интерполяции? Ответ поясните.
4. В чем, по-вашему, преимущества и недостатки использования равноудаленных интерполяционных узлов? Ответ аргументируйте примерами.
5. Предложите другой (отличный от графического) метод локализации корней.
6. Предложите алгоритм для определения существования единственного корня на отрезке [ab; ].
7. От чего, по-вашему, зависит скорость сходимости приближенных методов вычисления корней нелинейных уравнений? Пояснения дайте для каждого метода.
8. Каким условиям должен удовлетворять график функции у = f x( ), чтобы итерационный процесс уточнения корня уравнения f x( )=0 проходил "по спирали"?
9. Для каких функций, на ваш взгляд, целесообразнее использовать тот или иной приближенный метод? Ответ поясните примерами.
10. Может ли система n линейных уравнений с n неизвестными иметь несколько решений? Ответ аргументируйте.
11. От чего, по вашему мнению, зависит точность методов численного интегрирования?
12. Есть ли отличие в использовании приближенных методов вычисления определенного интеграла от неотрицательных и от неположительных функций? Ответ поясните.
13. Какая из трех формул метода прямоугольников, на ваш взгляд, будет наиболее точной? Во всех ли случаях? Ответ аргументируйте.
14. Существуют ли функции, для которых невозможно применение численного интегрирования? Ответ обоснуйте.
![]() Задачи и упражнения
Задачи и упражнения
1. Протабулируйте функцию z=sin x+cos2x3 для x∈ −[ 2π π;6 ] с шагом π. Найдите максимальное значение функции и аргументы, при которых оно достигается.
x z+
2.
Найдите среднее арифметическое всех значений функции y= ![]() 2
для
2
для
(z−5) x∈[0,1] с шагом 0,2; для z∈ −[ 2;7] с шагом 0,5.
3.
![]() Для
функции y = − +x 27 tgx, −2≤x<3b шаг 0,2; a z< ≤ 6, шаг 0,5
напечатайте аргументы, при которых значения функции не превосходят некоторого
числа k.
Для
функции y = − +x 27 tgx, −2≤x<3b шаг 0,2; a z< ≤ 6, шаг 0,5
напечатайте аргументы, при которых значения функции не превосходят некоторого
числа k.
4.
![]() Для
функции y = +tgx xz, −2a x≤ < 4, шаг 0.5; − <3
z≤6b шаг 0,02 напечатайте аргументы, при которых значения функции не
превосходят ее первого значения.
Для
функции y = +tgx xz, −2a x≤ < 4, шаг 0.5; − <3
z≤6b шаг 0,02 напечатайте аргументы, при которых значения функции не
превосходят ее первого значения.
6
5.
Найдите среднее арифметическое всех значений функции y =tg ![]() для x
для x
⎡ π π ⎤
![]() x∈
−⎢⎣ 2 2;
⎥⎦ с шагом 0,5.
x∈
−⎢⎣ 2 2;
⎥⎦ с шагом 0,5.
6.
Найдите среднее арифметическое всех положительных значений функции 1 y =2cos![]() для x∈ −[ 2π π;2 ] с шагом 0,2. x
для x∈ −[ 2π π;2 ] с шагом 0,2. x
2
2sin x
7.
![]() Из
дробных значений функции y=16
xz + (a x
b< ≤
с шагом h; x−1.2
Из
дробных значений функции y=16
xz + (a x
b< ≤
с шагом h; x−1.2
c z≤ ≤16 с шагом 0,1), не превышающих некоторой величины k, сформируйте последовательность А.
![]()
![]() 7,3− 4z
7,3− 4z
8. Для функции y=, x a∈( ;8) с шагом с шагом 0,75
sin xz
найдите среднее арифметическое положительных значений. 1
2
9.
Протабулируйте функцию y x=
−![]() для x∈ −[ 3;3] с шагом 0,5; для
для x∈ −[ 3;3] с шагом 0,5; для
z
z∈ −[ 0,5;0,8] с шагом 0,01. Определите аргументы, в которых значение
функции минимально.
10. Найдите среднее арифметическое min и max значений функции
5 2
y= −x для x∈ −[ 2;3] с шагом 0,5; m∈ −[ 4;4]с шагом 0,2. m
11. Для функции у= − +х2 2z xz, −4 ≤x< 3; − <6 z≤4 с шагом 0,2 напечатайте аргументы, при которых функция не превосходит среднего арифметического первого и последнего своих значений.
⎡ π π ⎤
12.
![]() Протабулируйте
функцию y = +tgx z для x∈ −⎢⎣ 2 2; ⎥⎦ с шагом 0,5,
Протабулируйте
функцию y = +tgx z для x∈ −⎢⎣ 2 2; ⎥⎦ с шагом 0,5,
z∈ −[ 0,1;3] c шагом 0,48. Подсчитайте количество положительных значений, принимаемых функцией на заданиях интервалах изменения аргументов.
13. Найдите количество операций, необходимых для вычисления значения интерполяционного полинома Лагранжа в какой-либо точке по интерполяционной формуле Лагранжа.
14. Разработайте наиболее эффективный способ вычисления значения интерполяционного полинома Лагранжа в достаточно большом числе точек.
15. Дайте геометрическую интерпретацию метода перебора.
16. Запрограммируйте алгоритм метода перебора и проведите его тестирование на известных вам уравнениях.
17. Дайте геометрическую интерпретацию метода бисекции.
18. Запрограммируйте алгоритм метода бисекции и проведите его тестирование на известных вам уравнениях.
19. Дайте геометрическую интерпретацию метода хорд.
20. Запрограммируйте алгоритм метода хорд и проведите его тестирование на известных вам уравнениях.
21. Запрограммируйте алгоритм метода касательных (Ньютона-Рафсона) и проведите его тестирование на известных вам уравнениях.
22. Дайте геометрическую интерпретацию модифицированного метода Ньютона-Рафсона.
23. Дополните программу алгоритма метода Ньютона-Рафсона таким образом, чтобы она позволяла сравнивать этот метод с его модифицированным вариантом по количеству итераций (шагов) при одинаковом значении точности ε.
24. Изобразите блок-схему алгоритма метода хорд-касательных.
25. Запрограммируйте алгоритм метода хорд-касательных и проведите его тестирование на известных вам уравнениях.
26. Изобразите блок-схему алгоритма метода итераций.
27. Запрограммируйте алгоритм метода итераций и проведите его тестирование на известных вам уравнениях.
28. Можно ли гарантировать сходимость к корню, лежащему на отрез- ке [–2;–1] итерационного процесса, реализуемого по формуле
2
xn+ =3sin x( n)+ x n? 1
29. Методом итерации найдите корень уравнения x−sin x( ) = 0,25 на отрезке [0,5;1,5] с точностью ε = 0,1. Рассмотрите два варианта итерационных функций: x = sin x( ) + 0,25 и x = −х m x( −sin x( ) −0,25), где m — параметр итерационного метода. Сравните скорости сходимости полученных итерационных процессов.
30. Подсчитайте количество арифметических действий в методе Гаусса.
31. Запрограммируйте метод Гаусса решения систем линейных уравнений. Проведите тестирование программы на известных примерах.
32. Модифицируйте программу метода Гаусса таким образом, чтобы она позволяла осуществлять проверку правильности решения систем урав- нений.
33.
Вычислите определенный интеграл ![]() dx пятью рассмотренными
приближенными методами. Результаты численного интегрирования сравните
dx пятью рассмотренными
приближенными методами. Результаты численного интегрирования сравните
с точным значением интеграла. Этапы решения задачи приведены в табл. 6.1.
Таблица 6.1
|
№ п/п |
Этап |
Выполнение |
|
1. |
Постановка задачи |
1 Вычислить определенный интеграл пятью приближенными методами и сравнить полученные результаты с точным значением |
|
2. |
Математическое описание |
Аналитическое решение: 1
0 |
|
Численное решение: выполнить самостоятельно для каждого метода |
||
|
3. |
Разработка блок-схемы (желательно) |
Выполнить самостоятельно |
|
4. |
Написание программы |
Выполнить самостоятельно |
|
5. |
Отладка программы и получение результатов |
Выполнить самостоятельно |
34. Функция y y x= ( ) задана таблицей своих значений (табл. 6.2).
Таблица 6.2
|
x |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
|
y |
1 |
1.2 |
1.24 |
0.76 |
0.6 |
0,4
Вычислите приближенное значение интеграла ∫ y x dx( ) по формулам
0
трапеций и Симпсона.
![]() Лабораторные работы
Лабораторные работы
1. Разработайте программу вычисления значений функции с использованием интерполяционной формулы Лагранжа. Оттестируйте разработанную программу на примере известных функций. Определите погрешность формулы Лагранжа для различных функций. Сделайте выводы.
2. Для заданной таблично функции (табл. 6.3) постройте интерполяционный многочлен Лагранжа и с его помощью найдите значения функции в узлах, соответствующих полушагу таблицы.
Таблица 6.3. Варианты заданий
|
Вариант 1 |
Вариант 2 |
Вариант 3 |
Вариант 4 |
||||
|
x |
y x( ) |
x |
y x( ) |
x |
y x( ) |
x |
y x( ) |
|
1,0 |
0 |
4,0 |
0,000196 |
7,0 |
0,00018 |
10,0 |
0,000108 |
|
1,1 |
0,324097 |
4,1 |
–5,19505 |
7,1 |
0,856485 |
10,1 |
–1,02845 |
|
1,2 |
0,643881 |
4,2 |
–10,3689 |
7,2 |
1,640842 |
10,2 |
–1,96638 |
|
1,3 |
0,922415 |
4,3 |
–14,959 |
7,3 |
2,27459 |
10,3 |
–2,72032 |
|
1,4 |
1,1253 |
4,4 |
–18,4126 |
7,4 |
2,692863 |
10,4 |
–3,21408 |
|
1,5 |
1,224745 |
4,5 |
–20,25 |
7,5 |
2,851227 |
10,5 |
–3,3964 |
|
1,6 |
1,20301 |
4,6 |
–20,1243 |
7,6 |
2,730379 |
10,6 |
–3,24618 |
|
1,7 |
1,054847 |
4,7 |
–17,8711 |
7,7 |
2,338403 |
10,7 |
–2,77495 |
|
1,8 |
0,788625 |
4,8 |
–13,5425 |
7,8 |
1,710348 |
10,8 |
–2,02598 |
|
1,9 |
0,425989 |
4,9 |
–7,41942 |
7,9 |
0,905108 |
10,9 |
–1,07035 |
|
2,0 |
4,62*10–5 |
5,0 |
0 |
8,0 |
–9,6*10–5 |
11,0 |
–0,00023 |
|
2,1 |
–0,44776 |
5,1 |
8,037451 |
8,1 |
–0,91714 |
11,1 |
1,080087 |
|
2,2 |
–0,87178 |
5,2 |
15,89357 |
8,2 |
–1,75557 |
11,2 |
2,064282 |
|
2,3 |
–1,2269 |
5,3 |
22,72513 |
8,3 |
–2,43156 |
11,3 |
2,854531 |
|
2,4 |
–1,47335 |
5,4 |
27,73269 |
8,4 |
–2,8763 |
11,4 |
3,37121 |
|
2,5 |
–1,58114 |
5,5 |
30,25 |
8,5 |
–3,04297 |
11,5 |
3,560925 |
|
2,6 |
–1,53356 |
5,6 |
29,82532 |
8,6 |
–2,91168 |
11,6 |
3,402017 |
|
2,7 |
–1,3294 |
5,7 |
26,2854 |
8,7 |
–2,49175 |
11,7 |
2,90698 |
Таблица 6.3 (окончание)
|
Вариант 1 |
Вариант 2 |
Вариант 3 |
Вариант 4 |
||||
|
x |
y x( ) |
x |
y x( ) |
x |
y x( ) |
x |
y x( ) |
|
2,8 |
–0,98363 |
5,8 |
19,77381 |
8,8 |
–1,82115 |
11,8 |
2,121544 |
|
2,9 |
–0,52634 |
5,9 |
10,75785 |
8,9 |
–0,96308 |
11,9 |
1,120452 |
|
3,0 |
–0,00011 |
6,0 |
0,001176 |
9,0 |
–10–13 |
12,0 |
0,000357 |
|
3,1 |
0,543966 |
6,1 |
–11,4973 |
9,1 |
0,97427 |
12,1 |
–1,12952 |
|
3,2 |
1,051358 |
6,2 |
–22,5932 |
9,2 |
1,863736 |
12,2 |
–2,15806 |
|
3,3 |
1,469572 |
6,3 |
–32,1089 |
9,3 |
2,579679 |
12,3 |
–2,98314 |
|
3,4 |
1,753617 |
6,4 |
–38,9547 |
9,4 |
3,049516 |
12,4 |
–3,52184 |
|
3,5 |
1,870829 |
6,5 |
–42,25 |
9,5 |
3,224158 |
12,5 |
–3,71872 |
|
3,6 |
1,804553 |
6,6 |
–41,4287 |
9,6 |
3,083118 |
12,6 |
–3,55153 |
|
3,7 |
1,556275 |
6,7 |
–36,3182 |
9,7 |
2,636854 |
12,7 |
–3,03371 |
|
3,8 |
1,145949 |
6,8 |
–27,1814 |
9,8 |
1,926069 |
12,8 |
–2,21331 |
|
3,9 |
0,610438 |
6,9 |
–14,7151 |
9,9 |
1,01801 |
12,9 |
–1,16858 |
3. Постройте интерполяционный многочлен Лагранжа для функции, заданной таблично (табл. 6.4). Используя программу MS Excel, постройте график полученного полинома и отметьте на нем узлы интерполяции. Вычислите значение функции в точке х=1,2.
Таблица 6.4
|
x i |
0 |
0,25 |
1,25 |
2,125 |
3,25 |
|
yi |
5,0 |
4,6 |
5,7 |
5,017 |
4,333 |
4. Используя табличный процессор Ехсеl, графическим методом определите
количество корней уравнения х4 − −1 cos x( ) 0= и для каждого корня найдите отрезки локализации.
5. Определите отрезок существования корня уравнения (10)х + − =х2 2 0.
Запишите расчетную формулу метода Ньютона-Рафсона и укажите критерий окончания итерационного процесса этого метода для решения заданного уравнения. Вычислите два первых приближения к корню.
6. Установите отрезок локализации корня уравнения х3 + − =2x 6 0. Методом деления отрезка пополам найдите его корень с точностьюε = 0,3. Подсчитайте количество итераций, необходимых для получения корня с точностью ε = 0,01.
7. Решите нелинейное уравнение указанными в табл. 6.5 методами, предварительно определив интервал [ab; ], на котором существует корень уравнения. Сравните скорости сходимости используемых методов. Сделайте проверку решения.
Таблица 6.5. Варианты уравнений и методов их решения
|
№ |
Уравнение |
Методы решения |
|
1 |
x=exp x(− ) |
Перебора и бисекции |
|
2 |
x=cos x( ) |
Перебора и хорд |
|
3 |
2 х x= −1 |
Перебора и модифицированного метода касательных |
|
4 |
x=2exp x(− ) |
Перебора и хорд-касательных |
|
5 |
x=exp(−3x) |
Перебора и бисекции |
|
6 |
x=3cos x( ) |
Перебора и хорд |
|
7 |
2 x=exp(−3x ) |
Перебора и касательных |
|
8 |
x = tg x( ) |
Перебора и хорд-касательных |
|
9 |
x=cos x(2 ) |
Перебора и бисекции |
|
10 |
x = tg(2x)−1 |
Перебора и хорд |
|
11 |
x exp= (− +3x) 1 |
Перебора и касательных |
|
12 |
2 x=exp x(− ) |
Перебора и хорд-касательных |
|
13 |
x = ln x( )+2 |
Перебора и бисекции |
|
14 |
x=exp(−3x) |
Перебора и хорд |
|
15 |
2 2 x =exp x(− ) |
Перебора и касательных |
|
16 |
x=2exp(− +3x) 1 |
Перебора и хорд-касательных |
Таблица 6.5 (окончание)
|
№ |
Уравнение |
Методы решения |
|
17 |
x exp x= (− +2) 2 |
Перебора и бисекции |
|
18 |
x = ln x( )+3 |
Перебора и хорд |
|
19 |
x=3exp(−3x) |
Перебора и касательных |
|
20 |
2 2 x =exp x(− −) 1 |
Перебора и хорд-касательных |
|
21 |
2 x=exp(−3x ) |
Перебора и бисекции |
|
22 |
x = tg x( ) |
Перебора и хорд |
|
23 |
x=cos x(2 ) |
Перебора и модифицированного метода касательных |
|
24 |
x = tg(2x)−1 |
Перебора и хорд-касательных |
|
25 |
x exp= (− +3x) 1 |
Перебора и бисекции |
8. Методом бисекции найдите решение нелинейного уравнения на отрезке [ab; ] с точностью ε =10−2. Выбрав полученное решение в качестве начального приближения, найдите решение уравнения методом итерации с точностью ε =10−4. Для метода итерации обоснуйте сходимость и оцените достаточное для достижения заданной точности число итераций
(табл. 6.6).
Таблица 6.6. Варианты
|
№ |
Уравнение |
[ab; ] |
№ |
Уравнение |
[ab; ] |
|
1 |
lnx = tgx |
[3,5;4,5] |
2 |
ln(x+ 2,5) = −x2 1 |
[–1,3;–0,7] |
|
3 |
xcosx+sinx= 0 |
[1,8:2,2] |
4 |
xsinx+ cosx= 0 |
[2,7;2,9] |
|
5 |
−x e = sinx |
[0;0,6] |
6 |
lnx= −4 x2 |
[1,5;2] |
|
7 |
2
|
[2,6;3] |
8 |
5 x + − =2 8 0x |
[1;1,5] |
|
9 |
|
[0,5;0,7] |
10 |
2 −x 2 e = −x 2x |
[–1;–0,5] |
|
11 |
|
[0,3;0,8] |
12 |
|
[0,5;1] |
Таблица 6.6 (окончание)
|
№ |
Уравнение |
[ab; ] |
№ |
Уравнение |
[ab; ] |
|
13 |
|
[1,4;2] |
14 |
|
[1;2] |
|
15 |
|
[0,2;1] |
16 |
2x = −2 x2 |
[0,5;0.8] |
|
17 |
sinx=1/(1+x2) |
[0,5;1] |
18 |
|
[0,3;1,3] |
|
19 |
2 x = ctgx |
[0,5;1] |
20 |
x+1/x= +2 cos(x−1) |
[1,8;2,3] |
|
21 |
x −x
|
[1;1,5] |
22 |
sinx= cos(x2) |
[0,7;1] |
|
23 |
cosx= sin(x2) |
[1,5;2] |
24 |
−x tgx = e |
[3;3,3] |
|
25 |
x xe =3 |
[1;1,5] |
26 |
2sin x e =x |
[2,5;3] |
|
27 |
3
|
[1;1,5] |
28 |
4 3 x − − =x 1 0 |
[–1;–0,5] |
|
29 |
2 −x /4 2 e = −2x x |
[1,5;2] |
30 |
lnx= cosx |
[1;1,5] |
9. Решите систему уравнений методом Гаусса:
⎧x x1+ −2 3x3 +2x4 =6
⎪
⎪x1−2x2 − =−x4 6
⎨
⎪x2 + +x3 3x4 =16
⎪⎩2x1−3x2 +2x3 =6
Проверьте правильность решения.
10. Методом Гаусса найдите решение системы уравнений:
|
а) |
⎧x1+x2 −x3 +x4 = 4 ⎪ ⎪2x1−x2 +3x3 − 2x4 =1 ⎨ ⎪x1−x3 + 2x4 = 6 ⎪3x1−x2 +x3 = 0 ⎩
|
⎧x1−4x2 +3x3 =−22 ⎪ в) ⎨2x1+3x2 +5x3 =12 ⎪3x x− −2 2x3 =0 ⎩ 1 |
|
б) |
⎧5x y z− − = 0 ⎪ ⎨x+ 2y+3z=14 ⎪ +3y+ 2z=16 ⎩4x |
⎧2x x1+ − =2 x3 5 ⎪ г) ⎨x1−2x2 +3x3 =−3 ⎪7x x+ − =2 x3 10 ⎩ 1 |
11. Решите систему Ax b= методом Гаусса:
⎛5 1 2 ⎞ ⎛ 8 ⎞ ⎛ 0 1 3⎞ ⎛ 2 ⎞
⎜ ⎟ ⎜ ⎟ =⎜⎜ 1 3 0⎟⎟; b = −⎜⎜ 1,5⎟⎟
а) A=⎜1 3 −1⎟; b=⎜6,5⎟ б) A
⎜⎝2 −1 6 ⎟⎠ ⎜⎝ 3 ⎟⎠ ⎜⎝−4 2 1⎠⎟ ⎜⎝ −7 ⎟⎠
b
12. Вычислите значение определенного интеграла I =∫ f x dx( ) аналитически
a
и численно методами левых, правых и средних прямоугольников, а также методами трапеций и парабол для пяти значений N, где N — число разбиений интервала интегрирования N=10; 20; 50; 100; 1000. Результаты расчета выведите на экран и распечатайте в виде табл. 6.7. Проанализируйте зависимость точности численного интегрирования от шага интегрирования.
Таблица 6.7. Результаты вычисления определенного интеграла
|
N |
Аналитич. метод |
Метод левых прямоуг. |
Метод правых прямоуг. |
Метод средних прямоуг. |
Метод трапеций |
Метод Симпсона |
|
10 |
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
1000 |
|
|
|
|
|
|
13. Определите, с каким шагом нужно вычислять приближенное значение
2
интеграла ∫ ln( )x dx по формуле трапеций для того, чтобы обеспечить
1,5
точность 0,00001.
![]() Задания для самостоятельных и
контрольных работ
Задания для самостоятельных и
контрольных работ
2,6
1. Вычислите интеграл ∫ f x dx( ) , используя формулы:
1,0
• средних прямоугольников с шагом h= 0,4; • трапеций с шагами h= 0,4 и h= 0,2;
• Симпсона с шагом h= 0,4.
УКАЗАНИЕ
Результаты вычислять с шестью значащими цифрами. Аргументы тригонометрических функций вычислять в радианах.
Таблица 6.8. Варианты к задаче
|
№ п/п |
f x( ) |
№ п/п |
f x( ) |
№ п/п |
f x( ) |
|
1 |
2 −0,5x e |
2 |
sin(0,5x2) |
3 |
cos( ) e x |
|
4 |
|
5 |
sin( ) e x |
6 |
3sin(0,06x3) |
|
7 |
e |
8 |
2cos(0,2x2) |
9 |
−cos( )x e |
|
10 |
4cos(0,02x3) |
11 |
e |
12 |
|
|
13 |
sin ( )2 x e |
14 |
−0,2sin x e |
15 |
2
e |
|
16 |
|
17 |
|
18 |
2
e |
|
19 |
|
20 |
|
21 |
2 cos x e |
|
22 |
|
23 |
ex |
24 |
|
|
25 |
e x x |
26 |
|
27 |
|
|
28 |
ex |
29 |
0,5
|
30 |
2 0,3x e |
6.2. Понятие о компьютерном моделировании
![]() Учебный
материал
Учебный
материал
Моделирование как метод познания
Моделирование является мощным методом познания окружающего мира — природы и общества. Человек издавна использует моделирование для исследования объектов, процессов, явлений в различных областях. Результаты этих исследований служат для определения и улучшения характеристик реальных объектов и процессов; для понимания сути явлений и выработки умения приспосабливаться или управлять ими; для конструирования новых объектов или модернизации старых. Моделирование помогает человеку принимать обоснованные и продуманные решения, предвидеть последствия своей деятельности.
Так, например, понятийная модель помогает понять, как устроен объект (или как протекает процесс, происходит явление), каковы его структура, свойства, законы развития и функционирования, каково его взаимодействие с окружающим миром. Управленческая модель нужна для того, чтобы определить наилучшие способы управления объектом или процессом. Целью прогностической модели является прогноз прямых и косвенных последствий функционирования или развития объекта, явления или процесса. Учебные модели способствуют оптимизации процессов обучения или самообучения.
Модель важна не сама по себе, а как инструмент, облегчающий познание или наглядное представление.
Например:
модель самолета предназначается для исследования его полетных свойств;
макет будущей застройки района создается с целью оценки предлагаемого архитектурного решения;
схема, чертеж или рисунок изделия используется для его изготовления;
макет строения кристаллической решетки молекул какого-либо вещества нужен для наглядного представления расположения атомов в пространстве;
с помощью текста, описывающего явление или процесс (процесс — это последовательная смена состояний объекта), передаются сведения об этом явлении или процессе другим людям.
К созданию моделей прибегают в тех случаях, когда исследуемый объект либо очень велик (модель Солнечной системы), либо очень мал (модель атома), когда процесс протекает очень быстро (модель двигателя внутреннего сгорания) или очень медленно (геологические модели), когда исследование объекта может привести к его разрушению (модель самолета) или создание модели очень дорого (архитектурный макет города) и т. п.
Само слово "модель" вам знакомо из других школьных предметов. Ведь практически любое наглядное пособие является моделью какого-либо фрагмента окружающей действительности или нашего представления о ней: карта и глобус, муляжи и рисунки, схемы и таблицы и пр. В школе вы часто используете такие модели: рисунок цветка (ботаника), карта (география), формула (физика), блок-схема алгоритма (информатика), периодическая система элементов Д. И. Менделеева (химия), уравнение (математика) и т. д. Каждый объект имеет большое количество различных свойств. В процессе построения модели выделяются главные, наиболее существенные для исследования интересующих параметров объекта свойства. В этом главная особенность и главное назначение моделей.
Модель — это соответствующее целям моделирования и сохраняющее существенные свойства представление некоторого объекта (процесса или явления) другим объектом (процессом или явлением), которое может быть изучено уже имеющимся инструментарием той или иной науки.
Модель — это, как правило, искусственно созданный объект, воспроизводящий строение и свойства исследуемого объекта (оригинала) (рис. 6.22).
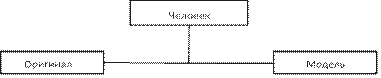
Рис. 6.22. Схема, иллюстрирующая взаимоотношения объекта, модели, человека
Моделирование — это процесс изучения строения и свойств оригинала с помощью модели.
Приступая к построению модели, прежде всего надо знать ответ на вопросы: для чего нужна модель? как ею пользоваться? В зависимости от ответов могут получиться совершенно разные модели одного и того же объекта.
Разные науки исследуют объекты и процессы под разными углами зрения и строят различные типы моделей. В физике изучаются процессы взаимодействия и движения объектов, в химии — их внутреннее строение, в биологии — поведение живых организмов и т. д. Так, человека в разных науках можно исследовать в рамках различных моделей. В рамках механики его можно рассматривать как материальную точку, в химии — как объект, состоящий из различных химических веществ, в биологии — как систему, стремящуюся к самосохранению, и т. д. С другой стороны, разные объекты могут описываться одной моделью. Так, в механике различные материальные тела (от планеты до песчинки) могут рассматриваться как материальные точки.
Один и тот же объект может иметь множество моделей, а разные объекты могут описываться одной моделью.
Все модели можно разбить на два больших класса: натурные (материальные или физические) и абстрактные (знаковые) (рис. 6.23).
Натурные модели воспроизводят геометрические, физические и другие свойства объектов в материальной форме. В процессе обучения вы часто использовали такие модели: глобус (география), муляжи (биология), модели кристаллических решеток (химия) и др. Самым существенным моментом абстрактных моделей является замена реального предмета знаком или совокупностью знаков. Цель этих знаков — что-то сообщить об объекте, выделить его из множества других объектов. Говоря современным языком, знак должен нести информацию об объекте. Так, например, в школьном курсе физики рассматривается много разнообразных уравнений, которые, по сути, представляют собой модели изучаемых явлений или процессов. Если вас просят решить физическую задачу, то вы начинаете, как правило, с поиска подходящего уравнения, т. е. с подбора модели, которая отвечает требованиям вашей задачи. Вы уже заранее предполагаете, что нужно искать модель в виде уравнения. При изучении географии используются карты (модели земной поверхности), в химии мы составляем уравнения химических реакций — модели их протекания и т. д.
Среди абстрактных моделей предлагается различать в прикладных областях:
традиционное (прежде всего, для теоретической физики, а также механики, химии, биологии, ряда других наук) математическое моделирование без какой-либо привязки к техническим средствам информатики;
информационные модели и моделирование, имеющие приложения в информационных системах;
вербальные (т. е. словесные, текстовые) языковые модели;
информационные (компьютерные) технологии, которые нужно делить на:
• инструментальное использование базовых универсальных программных средств (текстовых редакторов, СУБД, табличных процессоров, телекоммуникационных пакетов);
• компьютерное моделирование, представляющее собой:
вычислительное (имитационное) моделирование;
"визуализацию явлений и процессов" (графическое моделирование);
"высокие" технологии, понимаемые как специализированные прикладные технологии, использующие компьютер (как правило, в режиме реального времени) в сочетании с измерительной аппаратурой, датчиками, сенсорами и т. д.
Этапы и цели компьютерного моделирования
Основной задачей процесса моделирования является выбор наиболее адекватной оригиналу модели и перенос результатов исследования на оригинал. На начальном этапе моделирования проводится системный анализ изучаемого объекта: выделяются его существенные признаки и дается развернутое содержательное описание связей между ними ("один-к-одному", "один-комногим", "многие-ко-многим"), т. е. осуществляется неформальная постановка задачи. Следующим важным этапом моделирования является формализация содержательного описания связей между выделенными признаками с помощью некоторого языка кодирования: языка схем, языка математики и т. д. ("перевод" полученной структуры в какую-либо заранее определенную форму).
Формализация — этап перехода от содержательного (словесного) описания связей между выделенными признаками объекта к описанию, использующему некоторый язык кодирования (язык схем, язык математики и т. п.).
Формализация — процесс построения информационных моделей с помощью формальных языков. Одним из наиболее распространенных формальных языков является алгебраический язык формул в математике, который позволяет описывать функциональные зависимости между величинами. Модели, построенные с использованием математических понятий и формул, называются математическими моделями. Так, чтобы формализовать гелиоцентрическую модель, необходимо воспользоваться законами Ньютона и законом всемирного тяготения.
Моделирование любой системы невозможно без предварительной формализации. По сути, формализация — это первый и очень важный этап процесса моделирования. Примерами неформального описания моделей являются кулинарные рецепты, словесное описание модели парусника, словесная формулировка второго закона Ньютона и т. п.
В тех случаях, когда моделирование ориентировано на исследование моделей с помощью компьютера, результатом формализации модели должно быть программное средство. Поэтому принципы формализации можно сформулировать в следующем виде:
разработка неформального описания модели (словесное описание существенных для рассматриваемой задачи характеристик изучаемого объекта и связей между ними);
составление формализованного описания на некотором языке кодирования (с использованием математических соотношений и текстов);
реализация формализованного описания в виде программы на некотором языке программирования.
Например, формула F = m a ⋅ является формализованным описанием второго закона Ньютона.
Существуют достаточно общие методы и способы (технологии) моделирования. В настоящее время весьма эффективным и значимым является метод компьютерного моделирования. Благодаря компьютерам не только существенно расширяются области применения моделирования, но и обеспечивается всесторонний анализ получаемых результатов.
Компьютерное моделирование начинается, как обычно, с объекта изучения, в качестве которого могут выступать: явления, процессы, некоторая предметная область, жизненные ситуации и т. п. После определения объекта изучения строится модель. При построении модели выделяют основные, доминирующие для проводимого исследования свойства оригинала, отбрасывая второстепенные, несущественные. Выделенные свойства перекладывают на понятный машине язык. Строят алгоритм, программу.
Когда программа готова, проводят компьютерный эксперимент и анализ полученных результатов моделирования при вариации модельных параметров.
И уже в зависимости от этих выводов делают нужную коррекцию на одном из этапов моделирования: уточняют модель, алгоритм, либо точнее, корректнее определяют объект изучения.
Компьютерные модели претерпевают очень много изменений и доработок прежде, чем принимают свой окончательный вид. Этапы компьютерного моделирования можно представить в виде схемы, изображенной на рис. 6.24.
Моделирование Программирование Компьютерный Знание эксперимент
![]()
Рис. 6.24. Этапы компьютерного моделирования
Однако важно не путать компьютерную модель (моделирующую программу) с самим явлением. Модель полезна, когда она хорошо согласуется с реальностью. Но модели могут предсказывать и те вещи, которые не произойдут, а некоторые свойства действительности модель может и не прогнозировать. Тем не менее полезность модели очевидна, в частности, она помогает понять, почему происходят те или иные явления.
Современное компьютерное моделирование выступает как средство общения людей (обмен информационными, компьютерными моделями и программами), осмысления и познания явлений окружающего мира (компьютерные модели солнечной системы, атома и т. п.), обучения и тренировки (тренажеры), оптимизации (подбор параметров).
Компьютерная модель — это модель реального процесса или явления, реализованная компьютерными средствами.
Главной задачей компьютерного моделирования выступает построение информационной модели объекта, явления.
Информационная модель — знаковая модель, описывающая информационные процессы (возникновение, передачу, преобразование и использование информации) в системах самой разнообразной природы.
Как и любая модель, информационная модель содержит не всю информацию о моделируемом объекте, а только ту ее часть, которая существенна для рассматриваемой информационной задачи.
Для примера рассмотрим информационную модель оценивания знаний обучаемых. Для любой оценки ее существенными характеристиками являются: фамилия ученика, получившего оценку, предмет, по которому оценка получена, и балл. Связи между объектом и его характеристиками представлены на рис. 6.25, который дает схемное описание рассматриваемой модели. В этом описании используемые характеристики принимают следующие значения: фамилия — текстовые значения (фамилия одного из учеников класса), предмет — также текстовые значения, сама оценка — числовые значения (5, 4,
3, 2).
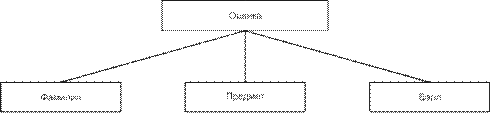
Рис. 6.25. Связи между объектом и его характеристиками
От схематичного описания информационной модели перейдем теперь к формализованному описанию. Такое описание можно дать в виде трехместного предиката с именем оценка (язык программирования Пролог):
оценка (фамилия, предмет, балл).
Для конкретных значений аргументов этот предикат превращается в факт. Например, если ученик Иванов по математике получил оценку 5, то имеет место факт:
оценка (Иванов, математика, 5).
С помощью таких фактов можно рассматривать различные характеристики оценки, например, можно выделить учеников, получивших по математике балл 5.
Иногда информационной моделью называют просто набор неких величин, которые содержат необходимую нам информацию об объекте, системе объектов, процессе или явлении. Под это определение попадает очень широкий класс информационных моделей (например, модели города, исторической эпохи, транспортной сети и т. д.).
Фундаментальными понятиями информационной модели являются: объект (нечто существующее и различимое, например видеокассета), атрибут (свойство, характеристика объекта, например название фильма), значение атрибута (например, "Дневной дозор").
Экземпляром объекта называется представление объекта с помощью некоторого набора его характеристик, существенных для решения данной информационной задачи.
Множество экземпляров, имеющих одни и те же характеристики и подчиняющихся одним и тем же правилам, называется объектом.
Таким образом, объект является абстракцией предметов реального мира, объединяемых общими характеристиками и поведением. Объект можно рассматривать как типичный, но неопределенный экземпляр чего-либо в реальном мире.
Так как передача информации невозможна без того, чтобы как-то именовать предметы и их свойства, то каждый объект идентифицируется некоторым именем.
Предметы реального мира имеют характеристики (такие, например, как имя, регистрационный номер и т. д.). Каждая отдельная характеристика, общая для всех возможных экземпляров объекта, называется атрибутом. Для каждого экземпляра атрибут принимает определенное значение.
Информационная модель объекта или набора объектов — совокупность атрибутов (характеристик) данного объекта вместе с числовыми или иными значениями этих атрибутов.
Это определение поясним примером. Допустим, вы хотите создать информационную модель своей видеотеки. Видеотека — это некоторое количество однородных объектов (видеокассет), причем на каждой кассете записан некий видеоматериал (фильм, клип, личные съемки и т. п.).
Простейшая модель видеотеки — это просто список всех кассет, составленный в произвольной форме, с указанием, скажем, номера кассеты, названия видеоматериала, длительности воспроизведения и т. п. Если вы желаете составить более точную информационную модель, можно написать на карточках связный рассказ о видеотеке, что-то вроде: "У меня двести десять пронумерованных кассет. На кассете номер девять хранится мой любимый фильм "Дневной дозор" c ... в главной роли ...".
Однако ни ту, ни другую модель компьютер обрабатывать не сможет, да и не всякий человек сумеет так составить рассказ, чтобы из него можно было извлечь всю информацию обо всех материалах вашей видеотеки. Поэтому придумаем для видеотеки набор атрибутов. Для каждой кассеты укажем:
номер кассеты;
название видеоматериала;
фамилию режиссера;
год создания;
рубрику;
краткое содержание; длительность и т. д.
У конкретной кассеты каждый из этих атрибутов примет то или иное значение. Например, на кассете номер пятнадцать: фильм "Тайна Голубой долины" (текст), год создания 1992 (дата), длительность 110 минут (число) и т. д.
У вас получится более или менее полноценная информационная модель, которую уже можно использовать в компьютерной технологии. Безусловно, вы вправе сказать, что в своей видеотеке разберетесь сами, — и без моделей, и без компьютера. Однако вспомните о грандиозных видеоархивах телекомпаний и других мощных структур, в которых надо вести поиск, исследовать коллекции по различным признакам и т. д.
Одновременно из этого примера видно, что наша модель содержит не всю, а только существенную для нас информацию о системе объектов. Вы можете уточнять модель, дополняя ее новыми атрибутами, например:
тип видеоматериала (художественный фильм, документальный фильм, клип и т. п.);
персонажи и исполнители; сценарист и т. д. и т. п.
В конце концов, вы можете указать даже название фирмы-изготовителя, качество изображения и пр.
Точность модели можно повышать, но собрать всю информацию о кассетах вам не удастся в принципе. Например, вряд ли у вас будет возможность учесть количество, форму и расположение царапин на корпусе кассеты, измерить толщину ленты и т. п.
Классификация информационных моделей
Информация поступает к человеку через его органы чувств и, следовательно, имеет пространственно-временные характеристики. Это значит, что информация воспринимается нами либо как информационная система, либо как информационный процесс, либо как то и другое вместе.
Под информационной системой понимается представление информации в виде системы, состоящей из элементов, несущих информацию, и связей между ними.
Информационный процесс дает представление о том, как возникает и преобразуется информация.
Например, книгу можно считать информационной системой, а человек, который ее пишет, осуществляет информационный процесс. Своеобразной информационной моделью является текст, способный содержать, хранить и передавать смысл, информацию.
Информационные модели подразделяются на структурные (статические), дающие описание объекта (системы), и динамические, описывающие информационные процессы (рис. 6.26).
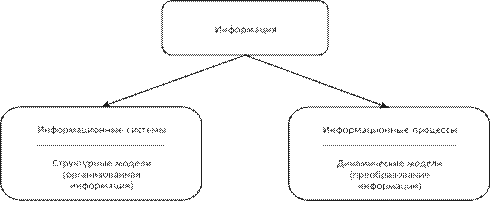
Рис. 6.26. Виды информационных моделей
Статическая модель представляет собой единовременный срез информации о данном объекте. Например, обследование учащихся в стоматологической поликлинике дает информацию о состоянии их зубов на данный момент времени: соотношение молочных и постоянных, наличие пломб, дефектов и т. п.
Модели, описывающие систему в определенный момент времени, называются статическими информационными моделями.
В физике, например, статические информационные модели описывают простые механизмы, в биологии — классификацию животного мира, в химии — строение молекул и т. д.
Динамические модели показывают изменение объекта во времени. Например, динамической моделью успеваемости учащегося за данный учебный год является его дневник, в котором отражены оценки по всем предметам, полученные им в течение года. В примере с поликлиникой медицинскую карту ученика, отражающую изменение состояния его зубов в течение многих лет, также можно считать динамической моделью.
Модели, описывающие процессы изменения и развития систем, называются динамическими информационными моделями.
В физике динамические информационные модели описывают движение тел, в биологии — развитие организмов или популяций животных, в химии — процессы протекания химических реакций и т. п.
При строительстве дома рассчитывают прочность его фундамента, стен, балок и устойчивость их к постоянной нагрузке. Это статическая модель здания. Но надо также обеспечить противодействие ветрам, движению грунтовых вод, сейсмическим колебаниям и другим изменяющимся во времени факторам. Эти вопросы можно решить с помощью динамических моделей.
При составлении информационной модели нужно не только выбрать признаки объекта, которые в нее будут включены, но и решить, как будет организована информация в памяти компьютера. Ведь чтобы данными можно было воспользоваться, они не должны быть "свалены в кучу", их необходимо структурировать, т. е. выделить элементарные составляющие и определить их взаимосвязи.
Структурная информационная модель объекта — представление информационной знаковой модели в виде структуры.
Основными структурными моделями являются: табличная, сетевая и иерархическая.
Табличные информационные модели. Одной из наиболее часто встречающихся структур информационных моделей является таблица, которая состоит из строк и столбцов. В табличной информационной модели элементы информации размещаются в отдельных ячейках. С помощью таблиц могут быть выражены как статические, так и динамические информационные модели.
С помощью таблиц строятся информационные модели в различных предметных областях. Широко известно табличное представление математических функций, статистических данных, расписаний движения поездов и самолетов, уроков, спортивных соревнований и т. д.
В табличной информационной модели объекты или их свойства представлены в виде списка, а их значения размещаются в ячейках прямоугольной таблицы. Например, информационную модель Солнечной системы можно представить в виде табл. 6.9.
Таблица 6.9
|
Планета |
Среднее расстояние от Солнца (астр. ед.) |
Период обращения вокруг Солнца (лет) |
|
Меркурий |
0,387 |
0,24 |
|
Венера |
0,723 |
0,62 |
|
Земля |
1,000 |
1,00 |
|
Марс |
1,524 |
1,88 |
|
Юпитер |
5,203 |
11,86 |
|
Сатурн |
9,539 |
29,46 |
|
Уран |
19,180 |
84,02 |
Таблица 6.9 (окончание)
|
Планета |
Среднее расстояние от Солнца (астр. ед.) |
Период обращения вокруг Солнца (лет) |
|
Нептун |
31,070 |
164,79 |
|
Плутон |
39,440 |
247,70 |
В общем случае таблица не дает представления о каких-либо закономерностях, однако бывают и исключения. Великий русский химик Д. И. Менделеев, расположив для удобства химические элементы в таблицу по возрастанию атомных весов, открыл периодический закон, который оказал решающее влияние на развитие химии и физики.
Табличные информационные модели проще всего строить и исследовать на компьютере с помощью электронных таблиц и систем управления базами данных.
Сетевые информационные модели. Сетевые информационные модели применяются для отражения таких систем, в которых связь между элементами имеет сложную структуру. Например, различные части глобальной компьютерной сети Интернет (американская, европейская, российская и т. д.) связаны между собой высокоскоростными линиями связи. При этом одни части (американская) имеют прямые связи со всеми региональными частями, в то время как другие могут обмениваться информацией между собой только через американскую часть (например, российская и японская).
Сетевые информационные модели удобно изображать с помощью графов
(рис. 6.27).
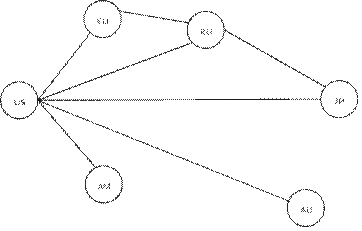
Рис. 6.27. Сетевая модель компьютерной сети Интернет
Другим примером сети может служить модель организации данных об учителях и классах, в которых они преподают (каждый учитель работает с несколькими классами, но и в каждом классе — несколько учителей).
Иерархические информационные модели. Одной из наиболее удобных при описании систем объектов, в которых можно выделить "главные" и "подчиненные", является иерархическая информационная модель, называемая деревом. На верхнем уровне такой структуры находится один объект (его называют корнем). На следующем (втором) уровне — несколько объектов, входящих в объект первого уровня или подчиняющихся ему. Каждому из объектов второго уровня подчиняется несколько объектов третьего уровня и т. д. Объекты самого нижнего уровня называют листьями. (Получается, дерево растет... вниз!) Отсюда другое название иерархической информационной модели — древовидная.
С помощью такой структуры можно, например, описать армейское подразделение: корень — рота; на втором уровне — взводы этой роты; третий уровень — отделения, входящие в соответствующий взвод, наконец, "листьями" будут отдельные бойцы. Имея организованную таким образом информацию, можно легко узнать не только сведения о конкретном военнослужащем, но и о взводе и роте, в которой он служит; и наоборот, можно получить информацию не только о взводе, но и о каждом из бойцов этого взвода (рис. 6.28).
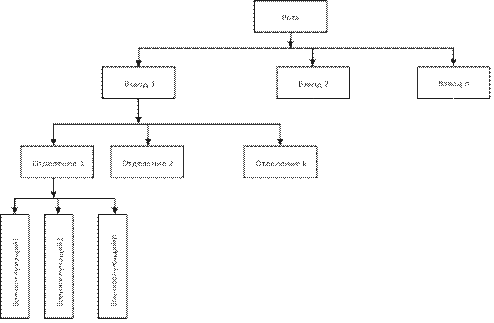
Рис. 6.28. Пример представления структуры с помощью иерархической информационной модели — дерева
Для описания исторического процесса смены поколений семьи используются динамические информационные модели в форме генеалогического дерева.
Компьютерной информационной моделью объекта называется его представление в виде текста на некотором искусственном языке, доступное компьютерной обработке.
Для преобразования информационной модели в компьютерную модель обычно используются средства языков программирования, например, таких как Паскаль или Пролог.
В качестве примера рассмотрим древовидную модель родственных отношений по женской линии, включающую в себя связи типа бабушка — дочки — внучки.
В построенном нами дереве родственных отношений (рис. 6.29) Ольга является бабушкой для Светы, Нины, Кати и Лизы.
Для примера осуществим формализацию рассматриваемой модели родственных отношений средствами языка Пролог. С этой целью воспользуемся двухместными предикатами мама(х,у) и бабушка(х,у). С их помощью связи между объектами могут быть записаны следующими предложениями: мама(Ольга,Елена); мама(Ольга,Марина); мама(Елена,Света); мама(Елена,Нина); мама(Марина,Катя); мама(Марина,Лиза);
бабушка(X,Y):- мама(X,Z),мама(Z,Y);
Составленная совокупность предложений образует программу на Прологе-Д
(школьная версия Пролога). Первые шесть предложений этой программы являются фактами. Так, например, первое из этих предложений выражает тот факт, что Ольга — мама Елены. Седьмое предложение является правилом. Правила позволяют определять новые отношения в терминах существующих отношений. В рассматриваемом случае правило бабушка(X,Y) утверждает, что X будет бабушкой для Y, если найдется такое Z, что X будет мамой для Z, а Z — мамой для Y. Левая часть правила отделяется от правой с помощью операции следования (:-).
Модели, которые мы рассматривали в этом разделе, относятся к описательным. Такие модели описывают (воспроизводят в соответствии с известными математическими зависимостями) действие реальных систем. Но не менее широко используются математические модели и других классов.
Оптимизационные модели описывают некоторую систему совокупностью соотношений, причем ряд параметров в этих соотношениях находятся во власти человека. Назначение данных моделей — найти такое сочетание значений этих параметров, при котором будет получен наилучший результат из возможных. Наиболее широко оптимизационные модели используются в экономических расчетах.
Описательные и оптимизационные модели применимы в тех случаях, когда нет сил, противодействующих выбранной цели. Реально же нередки ситуации, в которых различные участники имеют несовпадающие интересы. Яркими примерами являются игры "верю — не верю", "крестики-нолики", "шахматы" и др. Раздел математики, занимающийся моделированием таких ситуаций, называется теорией игр, а соответствующие модели — игровыми. Однако это не значит, что это нечто несерьезное. Использовать такие модели приходится и в весьма серьезных ситуациях.
Наиболее сложным является имитационное моделирование, позволяющее исследовать сложные системы, прогнозировать будущее их состояние в зависимости от различных стратегий управления.
Для практических приложений наиболее важным является создание информационных моделей в базах данных и в электронных таблицах.
Построение компьютерной модели. Моделирование
При построении моделей используют два принципа: дедуктивный (от общего к частному) и индуктивный (от частного к общему).
При первом подходе рассматривается частный случай общеизвестной фундаментальной модели. Здесь при заданных предположениях известная модель приспосабливается к условиям моделируемого объекта. Например, можно построить модель свободно падающего тела на основе известного закона Ньютона ma mg F= − сопр и в качестве допустимого приближения принять модель равноускоренного движения для малого промежутка времени.
Второй способ предполагает выдвижение гипотез, декомпозицию сложного объекта, анализ, затем синтез. Здесь широко используется подобие, аналогичное моделирование, умозаключение с целью формирования каких-либо закономерностей в виде предположений о поведении системы. Например, подобным способом происходит моделирование строения атома. Вспомним модели Томсона, Резерфорда, Бора.
Технология построения модели при дедуктивном способе (рис. 6.30):
1. Теоретический этап, на котором выясняются:
• оценки;
• аналогии;
• подобия.
2. Выявление знаний, информации об объекте (исходные данные об объекте).
3. Постановка задачи для целей моделирования.
4. Выбор модели (математические формулировки, компьютерный дизайн).
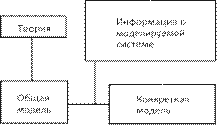
Рис. 6.30. Схема дедуктивного построения модели
Технология построения модели при индуктивном способе (рис. 6.31):
1. Эмпирический этап, на котором формируются:
• умозаключения;
• интуитивные предположения;
• гипотезы.
2. Постановка задачи для моделирования.
3. Оценки. Количественное и качественное описание.
4. Построение модели.
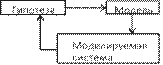
Уточнение
гипотезы
Рис. 6.31. Схема индуктивного построения модели
Информационные модели баз данных
I ЭТАП. Постановка задачи
Наши знания о реальном мире складываются из множества информационных моделей. Это сведения о свойствах разнообразных объектов и их взаимодействии между собой. С развитием производства и общества поток информации непрерывно растет. Все труднее становится найти в этом мощном потоке те сведения, которые интересуют нас в данный момент. Чтобы ориентироваться в таком обилии и разнообразии данных, мы стремимся их систематизировать. Это особенно актуально в тех случаях, когда нужно описать совокупность объектов, у которых можно выделить общие свойства, например книжный фонд библиотеки или пациентов поликлиники.
Современное развитие компьютерной техники помогает справляться с колоссальными объемами информации. Компьютер позволяет технически развитым странам перейти на безбумажную технологию хранения, обмена и обработки информации — электронные картотеки. Специальные программы — Системы Управления Базами Данных (СУБД) — позволяют упорядочить многообразие накопленной человечеством информации об окружающем мире в виде компьютерных информационных моделей.
Как и любая картотека, компьютерная информационная модель должна отвечать интересам определенного пользователя. Поэтому постановка задачи создания информационной модели тесно связана с целями моделирования. В самом общем приближении можно выделить следующие цели:
хранение информации;
возможность упорядочения данных по некоторым признакам;
возможность создания различных критериев выбора данных;
представление информации в удобном для пользователя виде.
II ЭТАП. Разработка модели
Обсудим особенности этапа разработки компьютерной информационной модели в среде баз данных.
Основные стадии построения модели:
сбор данных об объекте;
выделение группы исходных данных;
формирование структуры базы;
наполнение структуры данными.
Вначале необходимо выделить из разнообразной информации, характеризующей объект, только ту, которая обусловлена целями моделирования. Затем на основе исходных данных формируется структура будущей базы данных с указанием типов и ширины полей.
Наиболее простой способ организации данных в компьютере — реляционный, когда информационная модель объекта представлена в виде знакомой нам таблицы, состоящей из столбцов и строк. Число столбцов определяется количеством параметров (признаков) объекта, по которым строится его информационная модель. Каждый столбец имеет имя, непосредственно указывающее на его содержимое. Число строк соответствует количеству описываемых объектов. Каждая строка содержит информацию об одном объекте по множеству параметров. По терминологии баз данных столбцы называются полями, строки — записями.
Формирование структуры информационной модели и, соответственно, структуры базы данных означает определение полей или, иначе говоря, параметров, по которым будет систематизироваться информация о различных объектах.
Структура информационной модели в базах данных — описание полей, соответствующих параметрам объекта или процесса.
После определения и задания структуры базы данных компьютерная среда предлагает перейти в режим заполнения. Реальная информационная модель может содержать от нескольких штук до десятков тысяч записей. Наполнение базы — это ввод записей в созданную структуру. СУБД позволяет осуществлять ввод новых записей, редактировать имеющиеся, удалять устаревшие. И в этом смысле база данных напоминает живой организм.
Список — наиболее наглядная форма отображения информации. В ней поля и записи представлены в классическом для реляционных баз данных табличном виде. Такой вид представления данных удобен на этапе разработки и тестирования модели.
III ЭТАП. Компьютерный эксперимент
Применительно к базе данных компьютерный эксперимент означает манипулирование данными в соответствии с поставленной целью с помощью инструментов СУБД. Цель эксперимента может быть сформулирована на основании общей цели моделирования и с учетом требований конкретного пользователя. Например, имеется школьная база данных. Общая цель создания этой модели — управление школой. В школу обратился представитель военкомата с просьбой выдать список юношей, достигших 16-летнего возраста. Он не имеет никакого отношения к школе, но на основании его запроса можно осуществить эксперимент для выборки нужной информации.
Инструментарий среды позволяет выполнять следующие операции над данными:
сортировку — упорядочение данных по какому-либо признаку;
поиск (фильтрацию) — выбор данных, удовлетворяющих некоторому условию;
создание расчетных полей — преобразование данных в другой вид на основании формул.
Управление информационной моделью неразрывно связано с разработкой различных критериев поиска и сортировки данных. В отличие от бумажных картотек, где сортировка возможна по одному-двум критериям, а поиск вообще проводится вручную — перебором карточек, компьютерные базы данных позволяют задавать любые формы сортировки по различным полям и разнообразные критерии поиска.
Для успешной работы с информационной моделью программные среды баз данных позволяют создавать расчетные поля, в которых исходная информация преобразуется в другой вид. Например, по дате рождения с помощью специальной встроенной функции можно рассчитать возраст (количество полных лет), или по росту человека определить, на сколько он выше среднего роста людей всего списка. Такие расчетные поля используются либо как дополнительная информация, либо как критерий для поиска и сортировки.
Компьютерный эксперимент включает две стадии: тестирование (проверка правильности выполнения операций) и проведение эксперимента с реальными данными.
После составления формул для расчетных полей и фильтров необходимо убедиться в правильности их работы. Для этого можно ввести тестовые записи, для которых заранее известен результат операции. Подбор исходных данных для тестирования — это очень важное умение, которое приходит с опытом.
Компьютерный эксперимент завершается выдачей результатов в удобном для анализа и принятия решения виде. Одно из преимуществ компьютерных информационных моделей — возможность создания различных форм представления выходной информации, называемых отчетами. Каждый отчет содержит информацию, отвечающую цели конкретного эксперимента. Удобство компьютерных отчетов заключается в том, что они позволяют сгруппировать информацию по заданным признакам, ввести итоговые поля подсчета записей по группам и в целом по всей базе, а в дальнейшем использовать эту информацию для принятия решения.
Среда позволяет создавать и хранить несколько типовых, часто используемых форм отчетов. По результатам некоторых экспериментов можно создать временный отчет, который удаляется после копирования его в текстовый документ или распечатки. Некоторые эксперименты вообще не требуют составления отчета.
IV ЭТАП. Анализ результатов моделирования
Конечный пункт всякого моделирования — принятие решения. Полученные в результате компьютерных экспериментов различные формы представления данных позволяют сделать выводы на основе анализа информации, представленной в отчетах.
Иногда в процессе работы появляется необходимость дополнить базу новыми полями исходных данных для более полной характеристики объектов, т. е. принимается решение о корректировке информационной модели. Среда СУБД позволяет сделать это. В результате получается новая информационная модель.
Информационное моделирование в электронных таблицах
Громадные возможности для моделирования несет в себе среда электронной таблицы (табличного процессора). Тому есть несколько причин. Во-первых, электронная таблица (ЭТ) — это одна из самых распространенных программных сред общего назначения, и владение технологией работы в ней является одним из показателей информационной культуры человека. Во-вторых, существует большое разнообразие задач, которые достаточно просто решать в этой среде. В-третьих, технология работы в ЭТ проста, и результаты моделирования появляются практически мгновенно.
Моделирование в ЭТ проводится по общей схеме, включающей этапы: постановка задачи, разработка модели, компьютерный эксперимент, анализ результатов моделирования.
Рассмотрим особенности проведения моделирования в ЭТ по каждому этапу.
I ЭТАП. Постановка задачи
Описание задачи. По характеру постановки задачи все многообразие математических моделей можно разделить на две основные группы "что будет, если..." и "как сделать, чтобы...". Например, задача с формулировкой "что будет, если...": рассчитать характеристики модели при изменении исходных данных в заданном диапазоне с некоторым шагом. Такие расчеты позволяют проследить зависимость расчетных параметров модели от исходных данных. Подобную зависимость часто оформляют в виде графиков и диаграмм.
Другая группа задач часто называется "как сделать, чтобы...". Какое количество реактивного топлива надо загрузить в космическую ракету, чтобы вывести ее на орбиту с первой космической скоростью? Для расчета этой задачи используются сложные математические формулы реактивного движения.
Большинство задач моделирования, как правило, комплексные. В них на основе математических формул сначала строится модель расчета для одного набора исходных данных. Затем строятся расчетные таблицы по аналогичным формулам с изменением исходных данных в некотором диапазоне. По таблицам проводится анализ зависимости параметров модели от исходных данных, и в результате анализа производится подбор таких исходных данных, при которых модель будет удовлетворять некоторым проектируемым свойствам.
Цель моделирования. Цели моделирования определяются расчетными параметрами модели. Чаще всего это поиск ответа на вопрос, поставленный в формулировке задачи.
Далее переходят к описанию объекта или процесса. На этой стадии выявляются факторы, от которых зависит поведение модели. По сути, это входные параметры. Их может быть довольно много, причем некоторые невозможно описать количественными соотношениями. При моделировании в электронных таблицах учитывать можно только те параметры, которые имеют количественные характеристики. Иногда задача может быть уже сформулирована в упрощенном виде, и в ней четко поставлены цели и определены параметры модели, которые надо учесть.
Анализ объекта. После описания задачи и определения цели исследования вы оказываетесь в положении человека, который хорошо понимает, что он хочет получить. Далее необходимо приступить к анализу объекта. Здесь следует задать себе несколько вопросов и попытаться ответить на них.
Исследуемый объект или процесс надо рассматривать как единое целое или как систему из более простых объектов?
Если это единое целое, то можно перейти к построению информационной модели. Если система — надо перейти к анализу объектов, ее составляющих.
Из каких простых объектов состоит исследуемый объект, если он рассматривается как система, и какие между его составляющими существуют связи?
Как только представите себе систему, состоящую из простых объектов, и определите их связи, можно приступить к разработке информационной модели.
II ЭТАП. Разработка модели
Информационная модель. По результатам анализа объекта составляется информационная модель. В ней детально описываются все свойства объекта, их параметры, действия и взаимосвязи. Все входные параметры располагаются в порядке убывания их значимости, после чего проводится упрощение информационной модели ("отбрасывание" незначимых параметров). Во многих исследованиях используется прием, когда сначала строится модель для упрощенного объекта с минимальным набором входных параметров, а затем она постепенно уточняется путем введения некоторых из отброшенных ранее характеристик.
Математическая модель. Далее информационная модель должна быть выражена в одной из знаковых форм. Учитывая, что мы ограничили себя средой ЭТ, предназначенной для автоматизации вычислений, то информационную модель необходимо преобразовать в математическую. Составление такой модели заключается в выводе математических формул, связывающих ее параметры, по которым в дальнейшем будет производиться расчет.
Компьютерная модель. На основе информационной и математической моделей составляется компьютерная модель. Она непосредственно связана с прикладной программой, с помощью которой проводится моделирование. При разработке компьютерной модели в форме таблиц надо четко выделить три основные области данных: исходные данные, промежуточные расчеты, результаты. Исходные данные вводятся вручную. Расчеты, как промежуточные, так и окончательные, проводятся по формулам, составленным на основе математической модели и записанным по правилам ЭТ. В формулах используются абсолютные и относительные ссылки на исходные и промежуточные данные.
III ЭТАП. Компьютерный эксперимент
После составления компьютерной модели проводится тестирование по заранее составленной задаче. В ней всегда известны значения выходных параметров, которые определяются вручную. Очень важно предусмотреть в тесте все возможные варианты получения результатов.
Затем надо продумать план проведения экспериментов при моделировании, в котором должны найти отражение все интересующие вас вопросы.
IV ЭТАП. Анализ результатов моделирования
Заключительный этап моделирования — анализ модели. По полученным расчетным данным проверяется, насколько расчеты отвечают нашему представлению и целям моделирования. И тут очень важно, чтобы исследователь умел увидеть реальный объект или процесс в числах. На этом этапе определяются рекомендации по совершенствованию принятой модели и, если возможно, объекта или процесса.
![]() Контрольные вопросы
Контрольные вопросы
1. Что такое модель? Для чего человеку нужны модели?
2. Когда прибегают к созданию моделей?
3. В чем главное назначение моделей?
4. В чем заключается суть моделирования?
5. Что вы понимаете под материальной моделью объекта?
6. Может ли один и тот же объект иметь разные информационные модели?
7. Какие свойства реальных объектов воспроизводят муляжи продуктов в витрине магазина?
8. Какие свойства реальных объектов воспроизводят заводные игрушечные автомобили?
9. Что такое формализация?
10. Прокомментируйте основные принципы формализации.
11. Какие формальные языки вы знаете, в чем их специфика?
12. Дайте два различных определения информационной модели. Чем они похожи?
13. Как соотносятся компьютерная и информационная модели объекта?
14. Каково назначение каждого из основных этапов компьютерного моделирования?
15. Какие средства используются для построения компьютерных моделей?
16. С какой целью разрабатывается структурная информационная модель объекта?
17. В каких случаях применяются сетевые информационные модели? Каковы их основные черты?
18. Каковы характерные особенности табличных информационных моделей?
19. Каковы основные особенности иерархических информационных мо- делей?
20. Какие модели называются статическими? Приведите примеры.
21. Какие модели называются динамическими? Приведите примеры.
22. Что называется компьютерной информационной моделью объекта?
23. Каково назначение оптимизационных моделей?
24. В каких случаях используют имитационное моделирование?
25. Приведите пример индуктивного метода построения модели.
26. Приведите пример дедуктивного метода построения модели.
27. Приведите пример технологии разработки модели с использованием СУБД.
28. Приведите пример технологии разработки модели в среде табличного процессора.
 Темы для рефератов и докладов
Темы для рефератов и докладов
1. Моделирование как метод познания.
2. Художественный образ как модель.
3. Роль "высоких" технологий в современном мире.
4. Моделирование в истории великих открытий.
5. Проблематика искусственного интеллекта.
6. Язык программирования как логико-лингвистическая модель.
7. Математическое моделирование в гуманитарных дисциплинах.
8. Оптимизационное моделирование.
9. Имитационное моделирование.
10. Игровые модели.
11. Прогнозные модели.
12. Методы моделирования.
13. Использование аналогий в моделировании.
![]() Вопросы для обсуждения
Вопросы для обсуждения
1. В каких случаях и с какой целью мы пользуемся моделями в повседневной жизни?
2. Какое место среди моделей занимают натурные модели и почему?
3. Хорошо или плохо быть "моделью" в сфере моды и рекламы? Почему?
4. В чем разница между формальными и естественными языками?
5. Что с точки зрения моделирования представляет собой алгоритм?
6. Каковы, по-вашему, последствия чрезмерной (недостаточной) детализации разрабатываемой компьютерной модели? Ответ поясните примерами.
7. Все ли процессы окружающей действительности могут быть описаны моделями?
8. Каким видом модели является блок-схема алгоритма?
9. Какой вид модели, на ваш взгляд, будет наиболее полно отражать политические процессы общества? Почему?
10. В каких случаях целесообразнее применять индуктивный, а в каких — дедуктивный методы построения моделей?
11. Можно ли с помощью баз данных построить модели всех объектов?
![]() Задачи и упражнения
Задачи и упражнения
1. Приведите пример материальной и информационной модели земного шара.
2. Приведите пример материальной и информационной модели автомобиля.
3. Приведите свои примеры моделей и объясните, для чего они предназначены.
4. Разработайте информационные модели объектов, часто встречающихся в вашей повседневной деятельности. Представьте в таблице их идентификаторы, атрибуты. Каковы типы этих атрибутов?
5. Приведите примеры связей в информационных моделях. Расклассифицируйте их по признаку множественности.
6. Придумайте как можно больше конкретных примеров статических информационных моделей из различных школьных дисциплин.
7. Придумайте как можно больше конкретных примеров динамических информационных моделей из различных школьных дисциплин.
8. Разработайте информационную модель генеалогического дерева вашей семьи по материнской (отцовской) линии.
9. Разработайте иерархическую модель "Персональный компьютер".
10. Разработайте иерархическую модель "Программное обеспечение персонального компьютера".
11. Разработайте и представьте в виде таблицы информационную модель развития вычислительной техники.
12. Спроектируйте базу данных "Библиотека" с полями:
• инвентарный номер;
• автор;
• название;
• издательство;
• год издания;
• цена;
• количество экземпляров книги.
Введите несколько записей в БД. Определите:
• инвентарные номера книг, выпущенных раньше 1980 года;
• книги Пушкина или Лермонтова издательства "Художественная литература";
• книги авторов, фамилии которых начинаются на буквы от "А" до "К";
• книги, цена которых от 20 до 100 рублей.
Результаты оформите в виде отчета. Какие еще задачи можно решить с помощью созданной информационной модели? Решение представьте в форме отчета.
13. Разработайте базу данных "Видеотека" с полями:
• название;
• режиссер;
• страна-изготовитель;
• год выпуска;
• жанр;
• цена;
• "пиратская" копия (логическое поле).
Введите несколько записей в БД. Исследуя получившуюся модель, составьте отчет, содержащий информацию:
• обо всех американских фильмах 1998 года выпуска;
• о фирменных кассетах с английскими и французскими фильмами;
• обо всех фильмах, выпущенных раньше 1990 года;
• о мелодрамах, цена которых меньше 50 рублей.
Какие еще задачи можно решить на основе построенной информационной модели? Ответ оформите в форме отчета.
14. В табличном процессоре решите задачу:
Дан список исполнителей, содержащий N строк. Известны фамилия, должность, даты начала D1, планового окончания D2 и фактического окончания D3 порученной работы для каждого исполнителя. Если работа выполнена раньше на М дней, исполнитель поощряется денежной премией в размере S руб. Если работа выполнена с опозданием, то исполнителю начисляется штраф размером в Н руб. Если опоздание превысило К дней, размер штрафа увеличивается в Т раз.
Требования к выполняемой работе:
• Провести анализ полученной задачи, формализовать ее (сконструировать рациональную табличную форму и определить расчетные соотношения).
• В таблице предусмотреть не менее 10 записей.
• Провести несколько вариантов вычислений, результаты которых станут своеобразным тестом выполненного задания.
• Выполнить графическую интерпретацию результатов моделирования.
15. В табличном процессоре решите задачу:
Определить размер фонда оплаты труда педагогического коллектива школы, исходя из единой тарифной сетки (ETC). ETC включает в себя для учителей и воспитателей разряды с 7 по 16. Тарифный коэффициент для 7 разряда равен К, другие коэффициенты вычисляются по закону геометрической прогрессии с множителем М. Расчеты выполнить для трех вариантов значений К и M.
Требования к работе взять из задания 3.
16. В табличном процессоре решить задачу:
Известна стоимость Si 1 кг каждого из N продуктов. Составить таблицу размером N×N для определения стоимости различной массы продукта, когда эти массы меняются по закону арифметической прогрессии. Расчет произвести для трех множеств переменных Si.
Требования к работе взять из задания 3.
![]() Лабораторные работы
Лабораторные работы
1. Составьте список всех школьных дисциплин. Приведите примеры моделей, используемых в процессе изучения каждой из них. Определите тип этих моделей. Результаты оформите в виде таблицы (структуру таблицы разработайте самостоятельно).
2. Познакомьтесь с компьютерными моделями физических, биологических, технических, социальных процессов, предложенных вам преподавателем. Опишите, какие параметры (данные) являются для этих моделей входными, а какие параметры являются выходными. Изменяя входные параметры, наблюдайте за ходом моделируемых процессов и фиксируйте выходные параметры. Какие гипотезы могут быть выдвинуты относительно рассматриваемых процессов? Какие гипотезы подтверждаются при моделировании?
3. Используя карту вашего города, спроектируйте наиболее оптимальную, на ваш взгляд, модель маршрутов городского транспорта. Изобразите ее в виде графа.
4. Создайте среду для расчета календаря биоритмов, вычисления дат критических дней и построения графиков биоритмов.
Математическая постановка задачи 4
Существует легенда о том, что в древнем Китае монахи день за днем вели наблюдения за человеком, записывая параметры его физической активности, умственных способностей и эмоционального состояния. В результате многолетних исследований они пришли к выводу, что эти функции являются периодическими с периодами для физической активности — 23 дня, эмоциональной — 28 дней и интеллектуальной — 33 дня. Характерная особенность этой гипотезы заключается в том, что функции состояния человека в момент его рождения равны нулю, затем начинают возрастать, каждая за свой период принимает одно положительное максимальное и одно отрицательное минимальное значение (рис. 1).
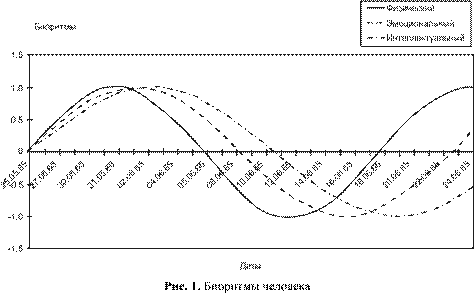
Проанализировав эту информацию, можно сделать вывод, что биологические ритмы могут быть описаны функциями вида: sin(2p t( −t0) /Tk), гдеt — время, Tk — периоды, а k — номер периода.
Началом всех трех кривых является день рождения t = t0, sin(0) = 0.
Исходные данные: дата рождения и дата начала исследования.
I. Разработка общего вида Исходных данных таблицы.
1. Измените название Листа 1 на новое — Исходные данные. Создайте на первом листе таблицу вида — рис. 2.
2. Присвойте ячейкам, где находится вводимая информация о дне, месяце и годе рождения, соответственно имена: день, месяц, год.
3. Заполните раздел Справочная информация:
• запишите формулу, определяющую текущую дату СЕГОДНЯ();
• запишите формулу, определяющую по году, месяцу и дню дату (ДАТА(год;месяц;день)) в графу Дата рождения. Присвойте этой ячейке имя день_рожден;
• измените формат представления данных типа ДАТА, например
27 Декабрь, 2006;
• самостоятельно определите формулы для подсчета Количества дней, которые вы прожили, а также количества дней, которые вы проживете до 18 лет, до 25 лет, до 50 лет.
Введите
|
|
|
|
|
|
|
Фамилию и имя |
|
|
|
|
|
|
День |
Месяц |
Год |
|
|
дату рождения |
|
|
|
|
|
|
|
|
|
|
|
дату для биоритмов |
|
|
|
|
|
|
|
|
|
|
Справочная информация
|
Сегодня |
|
Дата рождения |
|
День недели рождения |
|
Вы родились в год |
|
Ваш знак Зодиака |
|
Количество дней |
|
|
|
вы уже прожили |
|
|
до 18 лет |
|
|
до 25 лет |
|
|
до 50 лет |
Рис. 2
4. Для определения данных других строк из раздела Справочная информация создадим на новом листе (назовем его Справочная информация) три дополнительные таблицы.
Таблица 1. Недели
|
1 |
Воскресенье |
|
2 |
Понедельник |
|
3 |
Вторник |
|
4 |
Среда |
|
5 |
Четверг |
|
6 |
Пятница |
|
7 |
Суббота |
Дадим диапазону этой таблицы имя Недели. Тогда формула для определения Дня недели рождения на листе Исходные данные будет следующая: ВПР(ДЕНЬНЕД(день_рожден);недели;2).
По восточному календарю каждому году соответствует название определенного животного. Полный цикл восточного календаря — 12 лет. Информация о 12-летнем цикле и соответствующих каждому году животных приведена в табл. 2.
Таблица 2. Годы
|
0 |
Обезьяны |
|
1 |
Петуха |
|
2 |
Собаки |
|
3 |
Свиньи |
|
4 |
Крысы |
|
5 |
Быка |
|
6 |
Тигра |
|
7 |
Кролика |
|
8 |
Дракона |
|
9 |
Змеи |
|
10 |
Лошади |
|
11 |
Козы |
Дадим диапазону этой таблицы имя Годы.
Для определения животного, соответствующего году рождения, необходимо найти остаток от деления Год (название ячейки) на 12 и по таблице определить название животного. Формулу составьте сами.
Для определения знака Зодиака, соответствующего вашему году рождения, необходимо воспользоваться табл. 3.
Таблица 3. Зодиак
|
=ДАТА(ГОД(день_рожден);1;1) |
Козерог |
|
=ДАТА(ГОД(день_рожден);1;21) |
Водолей |
|
=ДАТА(ГОД(день_рожден);2;20) |
Рыбы |
|
=ДАТА(ГОД(день_рожден);3;21) |
Овен |
Таблица 3 (окончание)
|
=ДАТА(ГОД(день_рожден);4;21) |
Телец |
|
=ДАТА(ГОД(день_рожден);5;22) |
Близнецы |
|
=ДАТА(ГОД(день_рожден);6;22) |
Рак |
|
=ДАТА(ГОД(день_рожден);7;23) |
Лев |
|
=ДАТА(ГОД(день_рожден);8;24) |
Дева |
|
=ДАТА(ГОД(день_рожден);9;24) |
Весы |
|
=ДАТА(ГОД(день_рожден);10;24) |
Скорпион |
|
=ДАТА(ГОД(день_рожден);11;23) |
Стрелец |
|
=ДАТА(ГОД(день_рожден);12;22) |
Козерог |
Дадим диапазону этой таблицы имя Зодиак.
Тогда формула для определения Ваш знак Зодиака на листе Исходные данные будет следующая: ВПР(день_рожден;Зодиак;2).
II. Разработка Справочной таблицы для построения таблицы и графика биоритмов.
1. Для того чтобы построить график биоритмов, необходимо подготовить таблицу значений, которая ляжет в основу этого графика. Создайте на новом листе (назовите его Справочная таблица) таблицу вида — рис. 3.
2. Определите дату начала для построения графика. Для этого запишите формулу, определяющую по введенной Дате для биоритмов на листе Исходные данные дату в ячейке Дата начала графика. Присвойте этой ячейке имя биоритм.
3. Далее необходимо построить графики тригонометрических функций вида sin(2π (t −t0) /Tk), где t — время начала для построения графика, t0 —
день рождения, sin t( 0)= 0, Tk — периоды (физический = 23,6884; эмоциональный = 28,4261; интеллектуальный = 33,1638). Постройте справочную таблицу (рис. 4), которая будет содержать информацию о периодах биоритмов и перевод этих значений в радианы (в электронных таблицах аргумент тригонометрической функции необходимо выражать в радианах)
по формуле 2π /Tk.
4. Заполните основную часть таблицы.
В первую строку графы "Прожитые дни" (t −t0) запишите формулу
= биоритм — день_рожден., а в последующие строки — формулу, увеличивающую значение предыдущей строки на 1. С помощью маркера заполнения скопируйте формулы вниз до 42-й строки (составляем график биоритмов на 30 дней).
|
1 |
А |
B C D E F G H |
I |
||||||
|
|
Справочная таблица для построения графика биоритмов |
|
|||||||
|
2 3 |
|
Дата начала графика |
|
||||||
|
4 5 6 7 8 9 10 |
|
|
|
||||||
|
11 12 13 14 15 16
40 42 |
Прожитые дни (Х)
|
Дата
|
Физический
|
Эмоцио- нальный
|
Интеллектуальный
|
Подъемы и упадки |
Коли- чество совпа- дений
|
||
|
Ф |
Э |
И |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3
Периоды биоритмов
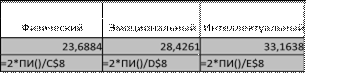
Рис. 4
В первую строку графы Дата запишите формулу = биоритм, а в последующие строки — формулу, увеличивающую значение предыдущей строки на 1. С помощью маркера заполнения скопируйте формулы вниз до 42-й строки. Эта графа будет использоваться для задания на графике значений на оси OX , поэтому установим формат для этой графы ДАТА.
В первую строку графы Физический (sin(2π (t −t0)/Tk) ) запишите формулу =SIN(C$9*$A13) и скопируйте ее в графы Эмоциональный и Интеллектуальный. В результате должны получиться соответственно формулы =SIN(D$9*$A13) и =SIN(E$9*$A13). Распространите эти формулы вниз, на всю таблицу.
При заполнении граф Подъемы и упадки необходимо проанализировать числовые значения в графах Физический, Эмоциональный и Интеллектуальный. Если значение положительное, то в соответствующую графу нужно записать 1, в противном случае — 0. Для графы Подъемы и упадки (Ф) запишите формулу =ЕСЛИ(C13<=0;0;1). Распространите эту формулу вправо на две следующие графы, затем вниз.
Осталось заполнить графу Количество совпадений. Запишите в нее формулу, которая подсчитывает сумму значений трех предыдущих граф — =СУММ(F13:H13).
III. Разработка Графика биоритмов.
Постройте график биоритмов (см. рис. 6.32) на отдельном листе. Для этого воспользуйтесь информацией на листе Справочная таблица.
Выполните построение Графика биоритмов самостоятельно.
IV. Разработка Таблицы биоритмов.
Таблица биоритмов представляет собой обобщенную информацию из листа Справочная таблица. Вид таблицы может быть следующим — рис. 5.
Таблица состоит из шести граф. Заполнение первых двух аналогично заполнению графы Дата листа Справочная таблица и ячейки День недели рождения на листе Исходные данные.
Биоритмы
за период с 11 Март, 2007 по 9 Апрель, 2007
|
Дата |
День недели |
Физическое |
Эмоциональное |
Интеллектуальное |
Прогноз |
|
11.03.07 |
Воскресенье |
- |
- |
- |
Плохо |
|
12.03.07 |
Понедельник |
- |
- |
- |
Плохо |
|
… |
|
|
|
|
|
|
03.04.07 |
Вторник |
+ |
- |
- |
Удовл. |
|
04.04.07 |
Среда |
+ |
+ |
+ |
Отлично |
|
05.04.07 |
Четверг |
+ |
+ |
+ |
Отлично |
|
… |
|
|
|
|
|
|
09.04.07 |
Понедельник |
- |
- |
- |
Плохо |
Рис. 5
Заполнение граф Физическое, Эмоциональное и Интеллектуальное производится на основе граф Подъемы и упадки: Ф, Э, И листа Справочная таблица. Если значение графы равно нулю, то в соответствующую графу листа Таблица биоритмов записывается "минус", а если единица, то "плюс".
Для заполнения графы Прогноз необходимо создать дополнительную таблицу на листе Справочная информация, дав ей название Состояния (табл. 4).
Таблица 4. Состояния
|
0 |
Плохо |
|
1 |
Удовл. |
|
2 |
Хорошо |
|
3 |
Отлично |
Значение графы Прогноз определяется по созданной таблице в зависимости от значений графы Количество совпадений листа Справочная таблица.
Для большей наглядности при оформлении таблицы воспользуйтесь командой Условное форматирование.
После заполнения всех листов протестируйте электронную таблицу, проверьте, правильно ли осуществляются расчеты.
В заключение скройте листы Справочная информация и Справочная таблица.
Справочная информация (формулы для подсчета)
Лист Исходные данные
|
Количество дней: |
|
|
вы прожили |
=СЕГОДНЯ()-день_рожден |
|
до 18 лет |
=ДАТА(год+18;месяц;день)-СЕГОДНЯ() |
|
до 25 лет |
=ДАТА(год+25;месяц;день)-СЕГОДНЯ() |
|
до 50 лет |
=ДАТА(год+50;месяц;день)-СЕГОДНЯ() |
|
Вы родились в год |
=ВПР(ОСТАТ(ГОД(день_рожден);12);Года;2) |
|
Дата начала графика |
=ДАТА('Исходные данные'!E8;'Исходные данные'!D8; 'Исходные данные'!C8) |
Лист Таблица биоритмов
|
День недели |
=ВПР(ДЕНЬНЕД(A5);недели;2) |
|
Физическое |
=ЕСЛИ('Справочная таблица'!F13=0;"-";"+") |
|
Эмоциональное |
=ЕСЛИ('Справочная таблица'!G13=0;"-";"+") |
|
Интеллектуальное |
=ЕСЛИ('Справочная таблица'!H13=0;"-";"+") |
|
Прогноз |
=ВПР('Справочная таблица'!I13;Состояния;2) |
 Литература
Литература
1. Архангельский Н. А. Вычислительные методы алгебры в приемах и задачах. — М.: МАИ, 1976.
2. Виленкин Н. Я. "Итерационные методы". — М.: Наука, 1984.
3. Демидович Б. П., Марон И. А. Основы вычислительной математики. — М.: Наука, 1970.
4. Дж. Форсайт, М. Мальком, К. Моулер. Машинные методы математических вычислений. — М.: Мир, 1980.
5. Иванов В. В. Методы вычислений на ЭВМ. Справочное пособие. — Киев: Наукова думка, 1986.
6. Калиткин Н. Н. Численные методы. — М.: Наука, 1987.
7. Кудрявцев Л. Д. Математический анализ, т. 2. — М.: Наука, 1984.
8. Неймарк Ю. И. Математические модели естествознания и техники. — Нижний Новгород: ННГУ, 1994. Вып. 1. 83 с.; 1996. Вып. 2. 154 с.
9. Тихонов А. Н. Вводные лекции по прикладной математике. — М.: Наука, 1984.
10. Тихонов А. Н., Костомаров Д. П. Вводные лекции по прикладной математике. — М.: Наука, 1984.
11. Фильчаков П. Ф. Численные методы. — Киев: Наукова думка, 1976.
12. Фильчаков П. Ф. Справочник по высшей математике. — Киев: Наукова думка, 1973.
Предметный указатель
D
Delphi
◊ визуальные компоненты 201
◊ инспектор объектов 200
◊ эксперт 199
Delphi 16, 198
◊ метод 204
◊ обработчик события 203
◊ свойство объекта 203
◊ событие 203
◊ форма 199
P
PL/1 14
S
SmallTalk 189
V
Visual Basic 16, 198
![]()
А
АДА 15
Алгебраическое уравнение 246
Алгол 13, 14
Алгоритмы поиска и сортировки 105
Алфавит 20, 23
Аппроксимирование функции, аппроксимация 239, 240
Б
Бейсик 13, 189
Блок-схема программы 93
В
Величины 24
Визуальное программирование 201 Выражения 26
Д
Декомпозиция задачи 83, 186
Дерево 293
Диаграммы Вирта 20
З
|
Предметный указатель |
Задача приближения функции 239
Задачи компьютерных вычислений
◊ аппроксимирование функции 239
◊ вычисление значений функции 235
◊ интерполирование функции 240
◊ решение нелинейных уравнений 245
◊ решение систем линейных уравнений
257
◊ табулирование функции 235
◊ численное интегрирование 261
И
Инкапсуляция 192
Интеграл 261
Интерполирование функции, интерполяция 240
Интерполяционная формула Лагранжа 244
Информационная система 289
Информационный процесс 289
Итерационная функция 254
К
Классы 188
Компилятор 12
Конструкция алгоритма
◊ альтернатива 92
◊ итерация 93
◊ композиция 92
Л
Линейная интерполяция 243
Лисп 14, 17
ЛОГО 14
Локализация корней уравнения 247
М
Машинные коды 12
Металингвистические формулы Бэкуса — Наура 20
Метаформула 21
Метод бисекции 248 Гаусса 258
итераций 254 касательных 250 Ньютона — Рафсона 250
перебора 248
прямоугольников 262
◊ Симпсона 265
◊ трапеций 263
◊ хорд 250 ◊ хорд-касательных 253
Методология Джексона 187
Методология Уорнера 187
Модели баз данных ◊ информационные 297
Моделирование 281, 282, 295
◊ в электронных таблицах 300
◊ имитационное 295
◊ этапы 284, 286
Модель 282
◊ динамическая информационная 290
◊ иерархическая информационная 293
◊ информационная 286, 289
◊ классификация 283
◊ компьютерная 286
◊ компьютерная информационная 294
◊ математическая 285
◊ описание 286
◊ оптимизационная 295
◊ понятийная 281
◊ построение 295, 296
◊ прогностическая 281
◊ сетевая информационная 292
◊ статическая информационная 290
◊ табличная информационная 291
◊ управленческая 281
◊ учебная 281 ◊ формализация 284
Модуль 27
Модульное программирование 196
Н
Наследование 194
О
Объект 188
Объектно-ориентированное программирование 195
|
Предметный указатель 319 |
Оператор 23
Описания объектов данных 25 Определенный интеграл 261
П
Парадигма 15
Паскаль 13, 30, 189, 198, 201
◊ вещественные величины 35
◊ выражения 35
◊ графика 69
◊ графики функций 74
◊ движущиеся изображения 75
◊ динамические переменные 65
◊ зарезервированные слова 32
◊ интервальный тип 43
◊ комбинированный тип (записи) 51
◊ линейный связанный список 99
◊ логические величины 35
◊ множество 49
◊ модули 57
◊ оператор выбора 38
◊ оператор присваивания 35
◊ оператор условия 37
◊ операции 34
◊ очередь 102
◊ переменные 34
◊ перечисляемый тип 42
◊ поиск 106
◊ программа 31, 33
◊ процедуры 35, 54
◊ рекурсия 56, 103
◊ символьные величины 35
◊ сортировка массива 108
◊ сортировка методом двоичного включения 110
◊ сортировка с помощью обменов
(пузырьковая, шейкерная) 113
◊ сортировка с помощью прямого выбора
111
◊ сортировка файлов 116
◊ сортировка файлов слиянием 118
◊ составной оператор 37 составной тип (массив) 44 списки 67
статические переменные 64
стек 100
строка 46 типы данных 34, 42 Турбо- 77, 189
◊ указатели 65
◊ файлы 58
◊ файлы, текстовые 61
◊ формат данных 36
◊ функции 55
◊ целые величины 34
◊ циклы 39
Переменные 26
Погрешность интерполяции функции 242
Полиморфизм 196
Полином Лагранжа 244
Понятие 20
Построение алгоритмов, ориентированное на структуры данных 99
Препроцессор 171
Принцип поиска в глубину 219
Принципы разработки и анализа алгоритмов 92
Программирование 11
◊ декларативное 16
◊ модульное 186
◊ объектно-ориентированное 16, 188
◊ процедурное 16
◊ решение логических задач 226
◊ структурное 16
◊ структурное 94
Проектирование и разработка программ
◊ методологии, ориентированные на данные 187
◊ методологии, ориентированные на обработку 186
Проектирование и разработка программ
83, 84, 186
◊ анализ алгоритма 90
◊ документирование 92
◊ методы проектирования архитектуры 85 ◊ непосредственное проектирование 85
◊ объектно-ориентированная методология
188, 198
◊ постановка задачи 84
◊ построение модели 88
◊ разработка алгоритма 89
◊ реализация алгоритма 89
◊ тестирование 90
|
Предметный указатель |
Пролог 14, 17, 207
◊ вопрос 211
◊ имя 208
◊ операции 209
◊ переменная 209
◊ правило 210
◊ программа 213
◊ просмотр предложений 220
◊ рекурсия 217
◊ решение логических задач 226
◊ список 209, 222
◊ структура 209
◊ факт 209 Процедура 26
Р
Рекурсивные алгоритмы 103
Рекурсия 217
Решение нелинейных уравнений 246
◊ приближенные методы 248, 250, 253,
254
◊ точные методы 246
Решение уравнения 246
С
Связывание, раннее, позднее 191
Семантика 20
Си 14, 124, 174, 189
◊ алфавит 129
◊ выражения 141
◊ зарезервированные слова 132
◊ классы памяти 160 ◊ оператор break 150
◊ оператор continue 151
◊ оператор goto 152
◊ оператор препроцессора 171
◊ оператор присваивания 141
◊ оператор условия 142
◊ операторы 141
◊ операции 136
◊ переменные 161
программа 125, 153 составные операторы 152 типы данных 132 указатели 134
файлы 166 функции 153, 158, 164, 165 циклы 146
Си++ 16
Синтаксис 20
Синтаксические диаграммы 22
Система визуального программирования 199
Сообщения 188
Среда быстрой разработки приложений
202
Структурное программирование 92 Т
Табулирование функции 235
Транслятор 20
Турбо-Паскаль
◊ деструктор 192
◊ конструктор 191
◊ метод 190
◊ объект 189
◊ свойства объекта 192
Ф
Фортран 13 Функция 26
Ц
Цикл 11
Э
Экстраполяция 244
Я
Язык БНФ 21
Язык нормальных форм 21
Язык программирования 11, 19
◊ высокого уровня 19, 20
◊ классификация 17
◊ машинно-ориентированный 19
◊ метаязык 20
◊ низкого уровня 19
◊ описание 20
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.