Проверочная работа. Линейные неравенства. 7класс

Подготовка к ОГЭ 9 класс. Тема: «Линейные неравенства».

Назначение проверочной работы – оценить уровень общеобразовательной подготовки обучающихся 7 класса по теме «Линейные неравенства» в соответствии с «Кодификатором проверяемых требований к результатам освоения основной образовательной программы основного общего образования и элементов содержания для проведения основного государственного экзамена по математике». Материал может быть использован и  в 9 классе при подготовке к ОГЭ.

Проверочная работа содержит задания направленные на проверку теоретических знаний по указанной теме, умения оценивать логическую правильность рассуждений, распознавать ошибочные заключения, а так же задачи с сайта ФИПИ и из других источников направленные на проверку умений применять полученные теоретические знания при решении неравенств и позволяет выявить «пробелы» в знаниях по теме.

На выполнение работы даётся 25-30 минут. 

За верное выполнение каждого задания учащийся получает 1 балл. 

Ответы для проверки и рекомендации по переводу первичных баллов в отметки по пятибалльной шкале прилагаются.

Рекомендации по переводу первичных баллов в отметки по пятибалльной шкале

Ответы для проверки учителя:

Выбери ОДИН правильный вариант ответа и запиши в таблицу. 

1.    Какое выражение не является неравенством:

А) 2х(х +3) -10 < 6х

Б) 2х+у≥ 0

В) 2x+4)+x-4∙(x-5)=18x-28

Г) 5(12+4x)+x²-4>x+x²+14

2.    Какого вида неравенства не существует:

А) линейное неравенство;

Б) квадратное неравенство;

В)дробно рациональное неравенство;

Г) кубическое  неравенство.

3.    Соотнести графическое решение линейного неравенства с формой записи ответа:

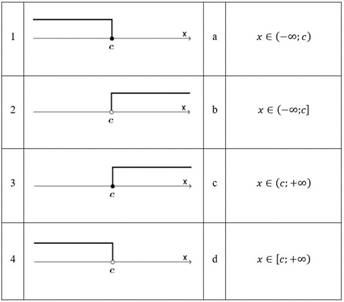
А) 1-b, 2-c, 3-d, 4-a;                     Б) 1-a, 2-a, 3-d, 4-b;

В) 1-b, 2-d, 3-c, 4-a;                      Г) 1-a, 2-d, 3-c, 4-b.

4.    Решить линейное неравенство 3∙(2x+4)+x-4∙(x-5)≥18x-28

А) x(-∞;4);              Б) x(-∞;4];            В)  x[4;+∞);                       Г) x(4;+∞).

5.    Решить линейное неравенство: 9x-x²+2∙(0,5x-2)-x∙(4-x)≤6x+4

А)  x∈(-∞;+∞);                Б) x∈(-∞;0];             В) x∈[0;+∞);                  Г) x∈0.

6.    Решить линейное неравенство: 7x+3∙(2x-5)-x-2∙(4x+5)<6x+4∙(x-7)+9

А) x∈(-∞;1);                   Б) x∈(-∞;1];             В) x∈[1;+∞);                    Г) x∈(1;+∞).

7.    Решить линейное неравенство: 7-4x+2∙(x+7)-2x∙(2+2x)+3x²>6x-x²+9

А) x∈(-∞;1);                   Б) x∈(-∞;1];              В) x∈[1;+∞);                   Г) x∈(1;+∞).

8.    Решить линейное неравенство: 3x-2x²+4∙(0,25x-2)>2x²+4x+12

А) x∈(-∞;+∞);                Б) x∈(-∞;20];            В) x∈[20;+∞);                  Г) x∈∅.