Методы разработки и объекты прогнозов на уровне предприятия (фирмы)

Методы разработки и объекты прогнозов на уровне предприятия (фирмы)

Мы видим, что прогнозы занимают ведущее (исходное) положение во всей системе прогнозов и планов фирмы. По существу между прогнозом (предвидением будущего) и планом нет резкой границы. Можно сказать, что прогноз - недостаточно определенный план, а план - это уточненный прогноз. Наиболее существенным отличием плана от прогноза является наличие в плане элементов выбора, принятия решений и мероприятий по осуществлению этих решений.

Как указывалось в рис. 32, основными объектами прогнозирования на уровне предприятия (фирмы) являются:

- потребность в продукции предприятия,

- потребности предприятия в производственных ресурсах (материальных, финансовых, трудовых, информационных).

Разработкой методов прогнозирования занимается прогностика.

Все методы прогнозирования (их более 100) можно разделить на две группы:

- неформализованные (эвристические),

- формализованные.

К числу неформализованных относят:

- индивидуальные экспертные оценки,

- коллективные экспертные оценки,

- написание сценариев и т.д.

К фрмализованным методам относят:

- методы экстраполяции,

- моделирование.

Неформализованные (эвристические) методы применяются в тех случаях, когда невозможно использовать знания экспертов в формализованном виде.

Наиболее широко используются методы интервью, "мозговой атаки", коллективных экспертных опросов.

8.5. Экстраполяционное прогнозирование

Из формализованных методов наиболее широко применяются экстраполяционные, т.е. те, когда прогноз производится по такому алгоритму:

1. Упорядочение прошлых данных;

2. Сглаживание временного ряда;

3. Выделение тренда;

4. Определение уравнения тренда;

5. Расчет прогнозного значения;

6. Оценка доверительного интервала с заданной вероятностью.

Наиболее простым является экстраполяция с линейным сглаживанием.

Прогнозное значение определяется подстановкой нужного значения времени в уравнение тренда y = f(t), а доверительный интервал по формуле

,

где ta - табличное значение t-критерия Стьюдента при вероятности p и n-1 степени свободы (табл.15.1); n - число прошлых значений объекта прогноза, 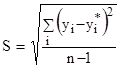; y - текущее значение объекта прогнозирования в прошлом, y* - текущее теоретическое значение объекта прогнозирования (исходя из уравнения тренда).

Таблица 7.1

Таблица значений t-критерия Стьюдента

Этот метод прогнозирования имеет смысл при сравнительно краткосрочном прогнозировании (5-7 лет) и уверенности в том, что основная модель процесса (а, следовательно, и тренд) за это время не изменяются.

Ясно, что с целью несмещенности оценки уравнение тренда следует выбирать таким образом, чтобы S было минимальным (т.е. по методу наименьших квадратов). Практически допустимо использовать критерий

.

В том случае, если тренд целесообразно аппроксимировать монотонной произвольной кривой, то можно использовать преобразование масштабов осей ординат с целью "выпрямления" кривой (практически удобно преобразовывать только ось y - ов).

Такое преобразование выполняют последовательно согласно следующей "лестнице преобразований":

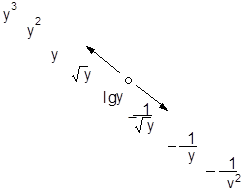
Движение в ту или иную сторону по "лестнице преобразований" определяется направлением выпуклости непреобразованной кривой тренда (куда направлена, туда и надо двигаться по "лестнице"). Критерием достижения цели является равенство тангенсов углов наклона, построенных на трех характерных точках кривой (обычно начало, конец и зона изменения угла наклона). В результате получаем уравнение прямой линии преобразованной величины (например, ). Обратное преобразование дает уравнение тренда (соответственно ). Далее нахождение доверительного интервала и прогнозного значения исследуемой величины осуществляется по вышеприведенным формулам.

В некоторых случаях первоначальному выделению тренда мешает неопределенность исходных данных (их "кучность" или "разреженность"). В этом случае возникает необходимость предварительного сглаживания. Наиболее прост метод сглаживания "по медианам троек". Его просто показать на примере. Предположим есть числовой ряд:

10 1 3 5 20 7 4 10 24 25 30.

Выписываем медианы троек, последовательно передвигаясь на одно число:

3 3 5 7 7 25 25 25 30 30.

Эффект сглаживания очевиден. В целях сохранения числа данных добавляем по одному числу в начале и в конце ряда. Если полное сглаживание не достигнуто, процедура повторяется.

Скачано с www.znanio.ru