Методы решения логических задач

Методы решения логических задач

Введение

Вся наша жизнь - это непрерывное решение больших и маленьких логических проблем. Без умения правильно, логически рассуждать, поступать разумно, жить трудновато. 

Каждый день мы, сами того не замечая, решаем логические задачи. Логические задачи также развивают умение анализировать и обобщать данные, искать возможные пути решения, формировать стратегию, проверять данные на достоверность. 

Логические навыки применяются во многих профессиях: например, водителю транспорта нужно уметь логически мыслить, чтобы выбрать верный путь. Рабочим в цехах нужно знать логику, чтобы сократить время производства одной единицы вырабатываемого объекта и, следовательно, увеличить дневную выработку. Космонавтам при проблемах с космическим кораблём необходима логика для продумывания дальнейшей стратегии. Планировщикам также нужна логика, чтобы подобрать правильное место для строительства здания и т.д. Также логика используется и в обычной жизни, например, поход за продуктами, выбор одежды, сбор вещей и т. д. 

К «классическим» логическим задачам относятся текстовые задачи, цель решения которых состоит в распознавании объектов или расположении их в определенном порядке в соответствии с заданными условиями. Задачи на перемещение, перекладывание, взвешивание, переливание — самые яркие примеры нестандартных задач на логику. Знание и понимание различных методов решения поможет определить, какой способ подойдет лучше в каждом конкретном случае, чтобы выбрать наиболее быстрый и простой путь получения ответа.

 Работа посвящена изучению способов решения логических задач. 

Актуальность работы в том, что знание различных методов решения логических задач увеличивает успешность их решения, позволяет учиться мыслить логически, творчески.

            Методы, используемые при работе над темой: теоретический анализ специальной литературы, экспериментальная работа, анализ собственного опыта.

Объект исследования – логические задачи.

Предметом исследования являются методы решения логических задач.

Гипотеза исследования: знание различных методов решения логических задач поможет развить логическое мышление.

 Цель исследовательской работы: рассмотреть методы решения логических задач.

Задачи: 

• изучить литературу по данной теме.

·         ознакомиться с понятием «логические задачи», исследовать методы их решения; 

·         показать преимущества решения математических задач на уроке информатики;

·         научиться решать логические задачи; 

·         расширить свой кругозор и развивать логическое мышление.

       Теоретическая и практическая значимость данной работы определяется тем, что результаты могут быть использованы на информатике, математике и других школьных предметах и сферах жизни. Данный материал можно использовать на внеурочных занятиях по математике.

Что такое логическая задача

            Логика – древняя наука. Ее название происходит от древнегреческого многозначного слова «логос» - мысль, речь, слово, понятие, разум. Древние философы пытались найти ответ на вопрос, как и по каким законам мыслит человек, какими путями мышления можно прийти к истине в рассуждениях о событиях и явлениях окружающего мира. По дошедшим до нас рукописям Аристотеля считают, что именно он явился основоположником логики как науки. Логика Аристотеля – это так называемая классическая, формальная логика. 

Формальная логика не утратила своего значения со временем и используется в гуманитарных науках, таких как криминалистика, философия, юриспруденция, психология. 

Алгебра логики – это раздел математики, нашедший большое практическое применение в технической области знаний. Она используется для решения сложных математических задач, при написании программ и алгоритмов, разработке компьютеров, электронных устройств, автоматических систем, в робототехнике и т. д. 

             Что же представляют собой логические задачи? Логические задачи или, как их еще иногда называют, нечисловые, представляют собой текстовые задачи, в которых требуется распознать объекты или расположить их в определенном порядке по имеющимся свойствам. При этом часть утверждений  задачи может выступать с различной истинностной оценкой (быть истинной или ложной). А любые вычисления и построения играют вспомогательную роль или вообще отсутствуют. То есть – логические задачи отличаются от обычных тем, что в них чаще не требуется умение вычислять, а требуется умение рассуждать.

Чтобы научиться решать типовые логические задачи, простые и нестандартные математические задачи, важно знать основные приемы и методы их решения. Ведь решить одну и ту же задачу и прийти к правильному ответу во многих случаях можно разными способами.

Существуют разные типы логических задач и разные способы их решения: Каждый из этих способов обладает своими достоинствами.

Виды логических задач: задачи на соответствие и исключение неверных вариантов, задачи на упорядочивание множеств, задачи о лгунах, числовые ребусы, игровые задачи, задачи на переливания, взвешивания.

Основные методы решения логических задач:

v  Метод  рассуждений

v  Метод таблиц

v  Метод графов

v  Метод кругов Эйлера

v  С помощью таблиц истинности

v  Средствами алгебры логики

v  С помощью языка программирования.

Рассмотрим некоторые методы решения логических задач.

Метод рассуждений.

Метод рассуждений является самым примитивным способом и его обычно применяют для решения самых простых логических задач. Идея метода заключается в проведении рассуждений при последовательном использовании всех условий задачи, вследствие чего приходят к выводу, который является ответом задачи.

Пример. Владимир, Семен и Олег изучают разные иностранные языки: английский, французский и немецкий. На вопрос, какой язык изучает каждый из них, один ответил: "Владимир изучает английский, Семен не изучает английский, а Олег не изучает немецкий". Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из студентов?

Решение: Имеем три утверждения. Если принять за истину первое утверждение, то правдиво и второе, т.к. студенты изучают разные языки, что противоречит условию задачи. Таким образом первое утверждение ложно. Если правдивым является второе утверждение, то первое и третье должны быть ложными. В таком случае получаем, что никто не изучает английский. Это противоречит условию, таким образом, второе утверждение также является ложным. Остается третье утверждение, которое можем считать верным, а первое и второе -- ложными. Таким образом, Владимир не изучает английский, его изучает Семен.

 Ответ: Семен изучает английский язык, Олег -- французский, Владимир -- немецкий.

Метод таблиц

Основным приемом для решения текстовых логических задач является метод таблиц. С помощью таблиц можно наглядно представить условие задачи или ее ответ, кроме того их использование значительно помогают в принятии правильных логических решений.

Пример У трех кукол Маши, Даши и Алены были платья трех разных цветов: красного, зеленого и синего. Туфли у них были таких же цветов. У Маши цвет платья и туфель совпадали. У Алены ни туфли, ни платье не были красными. Даша была в зеленых туфлях и в платье другого цвета. Как были одеты куклы?

Решение: Составим таблицу, в которой отметим возможные цвета платьев и туфель кукол.

            По условию задачи заполним таблицу: туфли Даши зеленые, а платье не зеленое. Следовательно, у Маши и Алены туфли уже не могут быть зелеными, так же как не могут быть туфли Даши синими или красными. Отмечаем все в таблице: туфли и платье Алены не являются красными. Из таблицы видим, что красные туфли могут быть только у Маши, а, следовательно, туфли Алены -- синие. Правая часть таблицы заполнена.

 Рисунок 1.

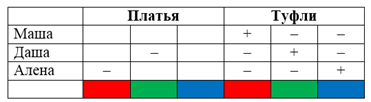Цвет платья Маши совпадает с цветом ее туфель, значит оно красное. Теперь легко увидеть, что у Алены -- зеленое платье, а у Даши -- синее.

Рисунок 2.

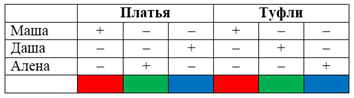Таблица полностью заполнена и в ней однозначно установлены цвета туфель и платьев кукол. Ответ: Маша одета в красное платье и красные туфли, Даша в синем платье и зеленых туфлях, Алена в зеленом платье и синих туфлях.

Метод графов

Граф – это несколько точек, часть которых соединены друг с другом отрезками или стрелками (в этом случае граф называется ориентированным). Рассмотрим метод графов на примере решения задачи. 

Задача . В начале лета школьники организовали сельскохозяйственную бригаду и избрали бригадира, заместителя бригадира и звеньевых первого, второго и третьего звеньев. Их имена: Аня, Боря, Вася, Гриша и Дина. Звеньевая первого звена решила подружиться со звеньевой второго звена. Дина удивилась, узнав, что бригадир и звеньевая второго звена — брат и сестра. Гриша дружит с бригадиром и его заместителем. У Васи нет сестер. Назовите должности каждого из ребят.

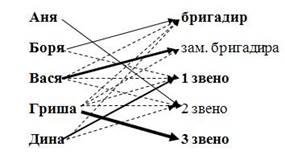Ответ: Гриша — 3 звено,  затем Вася — зам. бригадира, Дина — 1 звено, Аня — 2 звено, Боря — бригадир.

Метод графов помогает видеть ход доказательства и решения задач более наглядным и позволяет кратко и точно изложить доказательства теорем и решения задач. Этот метод применим к задачам типа «Кто есть кто?».

Метод кругов Эйлера.

Круги Эйлера – это схематическое изображение в виде круга, которое позволяет более наглядно изобразить множества и отношения между ними.

 Эйлер впервые использовал круги в известных «Письма о разных физических и философических материях, написанные к некоторой немецкой принцессе...». Здесь он указывает, что «круги очень подходят для того, чтобы облегчить наши размышления». Для решения целого ряда задач Леонард Эйлер использовал идею геометрического изображения с помощью кругов, и этот ряд включал не только задачи из теории множеств. Такое изображение получило название «круги Эйлера».

Таким образом, некоторое множество можно изобразить в виде круга, а элементы множества при этом представляют собой множество точек, принадлежащих этому кругу.

Алгоритм решения логических задач с помощью кругов Эйлера:

  1. Внимательно изучаем и кратко записываем условие задачи.

2. Определяем количество множеств и обозначаем их.

3. Выполняем рисунок. Строим пересечение множеств.

4. Записываем исходные данные в круги.

5. Выбираем условие, в котором содержится больше свойств.

6. Записываем недостающие данные в круги Эйлера (рассуждая и анализируя)

7. Проверяем решение задачи и записываем ответ.

Рассмотрим следующую задачу.

Из 100 туристов  немецким языком владеют 30 человек, английским – 28, французским – 42, английским и немецким владеют 8 человек, английским и французским -10 , немецким и французским – 5, всеми тремя языками – 3.

Сколько туристов не владеют ни одним языком?

 При решении задач круги Эйлера помогают более наглядно представить схему решения.

Решение логических задач с помощью таблиц истинности

Для этого необходимо:

1. Внимательно изучить условие задачи;
2. Выделить простые высказывания и обозначить их буквами;
3. Записать условие задачи на языке алгебры логики;
4. Составить единое логическое выражение для всех требований задачи;
5. Построить таблицу истинности для рассматриваемого выражения;
6. Найти набор значений переменных, при которых выражение является истинным;
7. Проанализировать полученный результат.

 Определить участника преступления, исходя из двух посылок:

     1) «Если Иванов не участвовал или Петров участвовал, то Сидоров участвовал»;

     2) «Если Иванов не участвовал, то Сидоров не участвовал».

     Составим выражения:

     I - "Иванов участвовал в преступлении";

     P - "Петров участвовал в преступлении";

     S - "Сидоров участвовал в преступлении"

    Запишем посылки в виде формул:

¬I˅P→S и ¬I→¬S.

Рисунок 4.

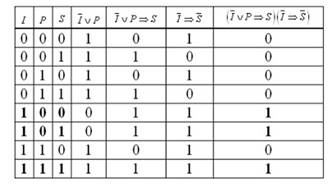
Из таблицы видно, что совершил преступление Иванов.

Решение логических задач средствами алгебры логики

            Обычно используется следующая схема решения:

1.  изучается условие задачи;

2.   вводится система обозначений для логических высказываний;

3.  конструируется логическая формула, описывающая логические связи между всеми высказываниями условия задачи;

4.  определяются значения истинности этой логической формулы;

5.  из полученных значений истинности формулы определяются значения истинности введённых логических высказываний, на основании которых делается заключение о решении.

Задача «Прогноз погоды»

     На вопрос, какая завтра будет погода, синоптик ответил:

1.  Если не будет ветра, то будет пасмурная погода без дождя.

2.  Если будет дождь, то будет пасмурно и без ветра.

3.  Если будет пасмурная погода, то будет дождь и не будет ветра.

Так какая же погода будет завтра? 

Решим эту задачу средствами алгебры логики.

Решение:

1.           Выделим простые высказывания и запишем их через переменные:

A – «Ветра нет»

B – «Пасмурно»

С – «Дождь»

2.Запишем логические функции (сложные высказывания) через введенные переменные:

Если не будет ветра, то будет пасмурная погода без дождя: A → B & ØC 

Если будет дождь, то будет пасмурно и без ветра: С → B & A 

Если будет пасмурная погода, то будет дождь и не будет ветра B → C &А 

3. Запишем произведение указанных функций:

 F=(A→ B & ØC) & (C→B & A) & (B→ C & A) 

 Упростим формулу (используются законы де Моргана, переместительный закон, закон противоречия):

F=(A→ B & ¬C) & (C→B & A) & (B→ C & A)

 = (¬A v B & ¬C) & (¬C v B&A) & (¬B v C&A) =

= (¬A v B & ¬C) & (¬B v C&A) & (¬C v B&A) =

= (¬A &¬ B v B&¬C&¬B v ¬A&C&A v B&¬C&C&A) & (C v B&A)=

= ¬A & ¬B &(C v B&¬A) =A&¬B&C v¬ A&¬B&B&¬A =

= ¬A&¬B&¬C

4. Приравняем результат  единице, т.е. наше выражение должно быть истинным:

F = ¬A &¬ B & ¬C = 1 и проанализируем результат:

Логическое произведение равно 1, если каждый множитель равен 1.

¬A = 1; ¬B = 1; ¬C = 1.значит: A = 0; B = 0; C = 0;

Ответ: погода будет ясная, без дождя, но ветреная.

Решение логических задач с помощью  языка программирования

В соревнованиях по гимнастике участвуют Алла, Валя, Сима и Даша. Болельщики высказали предположения о возможных победителях:

1)     Сима первой, Валя — второй.

2)     Сима будет второй, Даша — третьей.

3)     Алла будет второй, Даша — четвертой.

По окончании соревнований оказалось, что в каждом из предположений только одно из высказываний истинно, другое — ложно.

Какое место на соревнованиях заняла каждая из девушек, если все они оказались на разных местах?

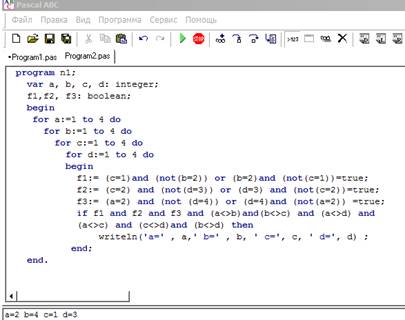А = Сима первая. В = Алла вторая. С = Даша третья. D = Валя вторая.

Как видно, программа для ПК занимает несколько строк, а результат можно увидеть за секунды. Эффективность использования компьютера налицо. Остаётся только продолжить работу над изучением видов логических задач и методов их решения с использованием программирования.

ЗАКЛЮЧЕНИЕ

           Целью данной работы было рассмотреть методы решения логических задач.           Чтобы успешно их решать, нужно знать способы решения, иметь развитое логическое мышление, обладать графической культурой. Задачи на логическое мышление, как правило, требуют не столько большого объема знаний, сколько умения эти знания применить, находить нестандартные подходы, проявлять сообразительность, умение рассуждать и анализировать.

           Были изучены материалы учебно-методической литературы, материалы из интернета. Решено множество задач. Подтвердилась гипотеза исследования: решение логических задач развивает мышление, расширяет кругозор.

По результатам исследования можно сделать следующие выводы:

1)      Существуют разные типы логических задач и разные методы их решения.

2)   Более подробно были изучены семь методов решения. Каждый из этих методов обладает своими достоинствами при решении задач определенного типа.

3)      Преимущества:

Метод рассуждений – простой, доступный, надо только думать, развивает мышление, память, применим  ко всем задачам.

Метод графов, метод таблиц, метод блок-схем, метод кругов Эйлера, метод математического бильярда – быстрота, наглядность, привлекательность, контроль над процессом рассуждений, избавляют от лишних рассуждений, сокращают нагрузку на память.

4)   Логика помогает нам не только при решении задач, но и в повседневной жизни: правильно строить свои мысли, и верно их выражать, убеждать других людей, отстаивать свою точку зрения.

5)   Решение логических задач – это не только увлекательный, но и полезный способ времяпровождения. Логические задачи - это зарядка для ума!

Литература

1.      Босова Л.Л. Информатика: учебник для

2.       8 класса. – М.: БИНОМ. Лаборатория знаний, 2018.

3.      Андреева Е. В., Босова Л. Л., Фалина И. Н. Математические основы информатики. Учебное пособие. - М.: БИНОМ,

4.      Лыскова В., Ракитина Е. Логика в информатике. - М.: БИНОМ, Шауцукова Л. З. Информатика : Учебное пособие для 10 кл. – М. Просвещение, 2005

5.      Скачано с www.znanio.ru