Поделиться
Моделирование работы системы скремблер дескремблер.docx
Рассмотрим особенности системы скремблер/дескремблер на примере её моделирования с
3-х разрядным регистром сдвига.
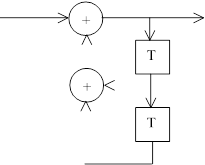
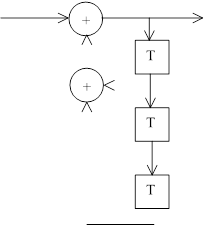
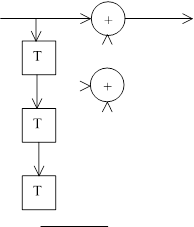
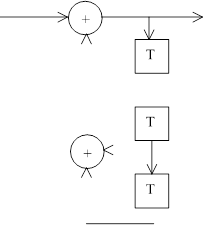
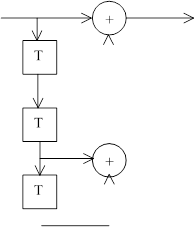
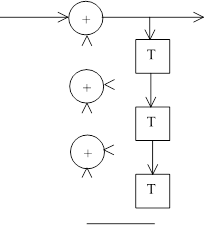
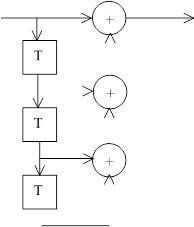
На рисунках 1-5 представлены все возможные конфигурации схем, определяемые числом и расположением сумматоров по модулю 2 относительно ячеек регистра.
На этих схемах приведены логические формулы работы и порождающий многочлен g(x), на который делится входное слово скремблера и умножается выходное слово дескремблера.
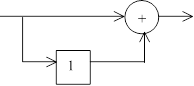Интересно отметить, что структура
на рис.1 известна программистам как операция ксорки/расксорки, часто
применяемая для затруднения несанкционированного чтения (вскрытия) своих
программ.
 |
 |
 |
||
 |
 |
 |
||
 |
 |
||
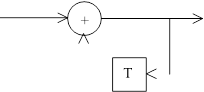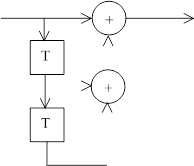
Найдём слово скремблера, то есть псевдослучайную последовательность (ПСП) бит на выходе Sn при Kn = const на входе, расписав для этого потактно состояния регистра сдвига RG, например для схемы на рис.4.
При Kn = 0 и исходном состоянии RG = 111 имеем:
|
n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Sn |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
|
|
Sn-1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
|
Sn-2 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
|
Sn-3 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
Получим максимальную длину слова (23 - 1) = 7 бит. S(n) = 0010111. Если взять Kn = 1, RG
= 000, то получим инверсно S(n) = 1101000. Для других начальных условий длина слова скремблера будет меньше максимальной.
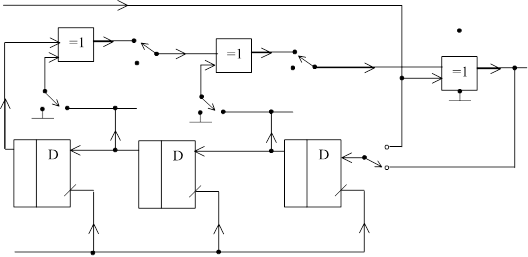Принципиальная
схема опытного макета скремблера/дескремблера.
 |
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
