начало анализа

Обобщающий урок по теме  «ФУНКЦИЯ».

(Учебник: Алгебра 7 класс, автор Макарычев )

Цель:

Ø Обобщение и систематизация знаний по данной теме;

Ø Закрепление умений определять вид функции по формуле и по графику, умение дать ее краткую характеристику;

Ø Закрепление умений определять принадлежность точки графику функций аналитическим и графическим способом;

Ø Отработка навыков составления формулы, задающей функцию, по графику функции.   (2 слайд)

План урока.

I.      Организационный момент.

II.   Повторение теоретического материала по данной теме. (3слайд)

    Форма повторения - игра «Лото». материал: 1) кубики с номерами пунктов данной темы; 2) вопросы по теории, заготовленные учащимися при подготовке к уроку; 3) жетоны разного цвета, соответствующие полученным оценкам (например: 5-красные,4-синие, 3-зеленые,2-черные).

    Один из учащихся вынимает кубик с номером пункта. Остальные задают ему вопросы в соответствии с выбранным номером. Если отвечающий затрудняется  с ответом, то его дает тот, кто задал вопрос. Когда вопросы по данному пункту закончились, в игру вступает второй ученик, затем третий и т.д.

    Каждый игрок получает жетоны (на всех этапах урока), которые суммируются в конце урока и дают итоговую оценку. Жетоны получают и те учащиеся, которые задали наибольшее число вопросов и дали  большее число ответов или дополнений.

    Примерные вопросы:

     -Что такое  функция?

     -Что такое независимая и зависимая переменные? Как их называют иначе?

     -Что называется областью определения функции? Областью значения?

     -Дайте  определение линейной функции.

     -Что является графиком линейной функции?

     -Сколько точек достаточно взять для построения графика и почему?

     -За что отвечают коэффициенты  к и в? Поясните.

      -При каком условии графики линейных функций параллельны, пересекаются?

     -Как найти координаты точки пересечения графиков?

Таким образом составляются вопросы по пунктам 10-15. 

III.           Применение теоретического материала при выполнении упражнений. 

v Игра «Отгадай функцию».  (4слайд)

     Учащийся у доски заполняет таблицу соответствующих значений  х  и  у,         например, для функции у = х - 2

     Значение аргумента задает класс, а значение функции находит водящий у доски. Кто первым отгадает функцию, должен дать ее краткую характеристику.                 ( линейная функция; график прямая, образующая с осью ОХ острый угол, т.к. угловой коэффициент к=1>0; ось ОУ пересекает в точке, лежащей ниже оси ОХ, т.к. в=-2<0, точка имеет координаты (0;-2)).

v Построение и работа с графиком функции. (5 слайд)

     Построить график отгаданной функции, для построения используем таблицу предыдущего задания (координатная плоскость строится заранее и в тетради, и на доске). У доски график строит ученик, заполнявший таблицу. Он  же объясняет правила работы с графиком по определению значения аргумента (функции) по заданному значению функции (аргумента).

     Используя график найти:   а) точку на графике, абсцисса которой равна 3. определить ее  ординату.  (А(3;1)); б) у точки, лежащей на графике, соответствующее ей значение функции равно 4, а чему равно значение аргумента? (В(6;4)).

Данное задание проверяет знание и связь терминов: абсцисса - аргумент и ордината - функция.

v Аналитическое определение принадлежности точки графику функции. 

    В предыдущем задании определяли координаты точек с помощью графика, а как  определить принадлежит ли точка графику функции, если этот график не построен?  (Подставить координаты точки в формулу функции, проверить полученное равенство. Если оно верно - точка принадлежит графику, если нет – не принадлежит).

     Используя данное свойство решить кроссворд. (6 слайд)

     Формула  у =4 – 2х задает функцию, найдите точки, принадлежащие ее графику. Для каждой точки выпишите соответствующую ей букву, решите анаграмму. Дайте определение зашифрованного понятия.

(-1;-6) –А, (0;4)- Г, (3;0) – У, (-1;6) – Р, (2;0) – А, (5;14) – Я, (0;2) – Ц, (1/2;3) –Ф, (0;0) – О. (4;5) – Н, (-10;24) –И, (10;-16) –К.

При решении анаграммы получается слово «функция». (Понятие забывается часто.)

v Определение вида функции по формуле. (7 слайд)

     По виду формулы функции мы можем сказать, что это за функция, каков ее график и как он располагается в координатной плоскости. Поэтому определение вида функции по формуле очень важно.  

     Умение распознать функцию по формуле проверяем при решении теста.

v Правильность решения проверяют соседи (взаимопроверка) по готовым ответам, вынесенным на доску.

1-А    2- Б    3- Б     4 - А    5- В    6 - В    7 - А     8 – А

Выясняем какие допущены ошибки и почему, объясняем правильный ход решения. Жетоны по количеству верных ответов.

v Определение вида функции по графику. (8 слайд)

     Не менее важное умение соотнести график и вид функции проверяем с помощью еще одного теста.

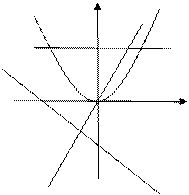                                                  У       2   4  

                                     1        

                              3

                                                                                                           Х      

Код правильных ответов:  1 – Б,  2 – А,  3 – Б,  4 – В.

Разбор ошибок.

v Определить координаты точки пересечения графиков функций, не выполняя их построения ( дифференцированное задание). Изобразить  схематично графики функций с учетом их взаимного расположения. (9 слайд)

     Повторяя теоретический материал во время игры в «лото», вспомнили как найти координаты точек пересечения графиков без их построения. (Найдется значение «х», при котором равны значения «у». Поэтому приравниваем значения «у» и решаем уравнение. Находим значение «х», а затем «у»). При схематичном построении графиков учитываем их расположение в зависимости от коэффициентов к и в.

Насколько хорошо усвоили  эту часть материала, проверяем в виде самостоятельной работы.

2.     Изобразить  схематично графики функций с учетом их взаимного расположения: 

а)  у₁ = - 2х   и   у₂ = -2х + 9;

б)  у₁ = 3х – 4   и  у₂ = -5х – 4

Графики строятся на двух координатных плоскостях, заготовленных заранее.

Проверка  - 10 слайд. Разбор допущенных ошибок.

Скорость выполнения заданий у детей различна, поэтому для тех, кто справится быстрее  с данными упражнениями, предлагается следующее.

Составить формулу функции по его графику. (11 слайд)

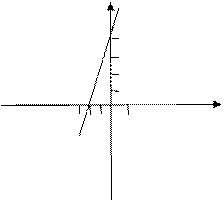                                   у

                                        1

                                                    1               х

Угол наклона острый, значит  к >0,  к = у : х = 4:2 = 2.

Значение   в  равно значению ординаты точки пересечения графика с осью ОУ, т.е. в = 4.

Таким образом   у = 2х + 4  (12 слайд).

v Немного из истории функции. (13 слайд)

v Домашнее задание п 10-15, построить график функции; найти точку пересечения графиков двух без построения; определить принадлежность точки графику. Задания учащиеся либо составляют сами, либо берут из дополнительных задач к главе. Задание получают в печатном виде.

v Подводим итоги в соответствии с целями урока. Оцениваем детей по «количеству» и «качеству» набранных жетонов на всех этапах урока. Если отметка ребенка не удовлетворяет, можно не выставлять.

v Задания темы «функция» на соотношения «формула-вид-график-принадлежность-пересечение» часто используются при Государственной Итоговой Аттестации, поэтому уже в 7 классе обращаю особое внимание на отработку данных навыков.