«Нахождение площади фигур произвольной формы различными способами».

Сценарий бинарного образовательного события по физике и математике

«Нахождение площади фигур произвольной формы различными способами».

Цель: познакомить учащихся с различными способами нахождения площади фигуры произвольной формы.

Задачи: Рассчитать площадь фигуры различными способами; сравнить полученные результаты.

Формируемые УУД:

1. Мобилизующий момент.

                    Сл.1                                    Физика! Какая емкость слова!

Физика для нас не просто звук!

А математика – опора и основа

Всех без исключения наук!

       Наше сегодняшнее мероприятие мы посвящаем именно этим наукам, – одним из древнейших наук, наук, без которых немыслимо дальнейшее развитие человечества.

   2. Мотивация.

         Сл.2

  Начать я хочу с одной истории, которая служит примером того, что не всегда просто дать единственно правильный ответ на вопрос.

Один студент сдавал экзамен по физике, и преподаватель хотел поставить ему низкую отметку за ответ, студент же утверждал, что заслуживает высшего балла.

Экзаменационный вопрос гласил: «Объясните, каким образом можно измерить высоту здания с помощью барометра». Ответ студента был таким: «Нужно подняться с барометром на крышу здания, спустить барометр вниз на длинной веревке, а затем втянуть его обратно и измерить длину веревки, которая и покажет точную высоту здания».

Случай был сложный, так как ответ был абсолютно полным и верным! С другой стороны, экзамен был по физике, а ответ имел мало общего с применением знаний в этой области.

Студенту было предложено попытаться ответить еще раз. Ему дали шесть минут на подготовку и предупредили, что ответ должен демонстрировать знание физических законов. По истечении пяти минут он так и не написал ничего в экзаменационном листе. Преподаватель спросил его, сдается ли он, но он заявил, что у него есть несколько решений проблемы, и он просто выбирает лучшее.

Студента попросили озвучить решение проблемы, и он привел более 10 решений. Среди них были не только физические решения, но и другие.  Не было только общепринятого решения.

Преподаватель спросил студента — неужели он действительно не знал общепринятого решения этой задачи. Студент признался, что знал, но сказал при этом, что не хотел давать общепринятый ответ, а решил показать, что существует множество решений у задачи, стоит только творчески подойти к проблеме.

Этим студентом был великий физик – Нильс Бор.

         Согласны ли вы с высказыванием на слайде? Сегодня мы будем работать под этим девизом! («Мало иметь хороший ум, главное – это хорошо применять его» Р. Декарт)

А какие величины вы можете измерить различными способами?

- …(перечисляют)

Величин много, но сегодня на уроке мы остановимся на измерении одной из них. Какой? Вы узнаете когда разгадаете кроссенс.

Сл.3 (разгадывают)

Все эти картинки объединены одним понятием – площадь.

3. Проблемная ситуация. Формулирование темы, цели и задач мероприятия.

Сл.4

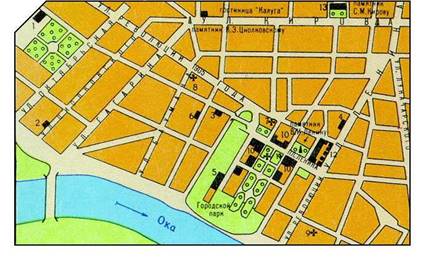
Давайте посмотрим на план центральной части города Калуги. Мы видим, что она разбита на отдельные участки.

Что представляет собой каждый из этих участков?

- геометрические фигуры: прямоугольник, трапецию, треугольник….

 

Сл.5.

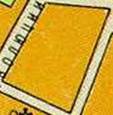               Можете ли вы найти площадь участков, представленных на слайде?

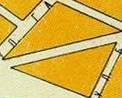- да, это трапеция и треугольник. Их площадь мы можем найти по формулам.

На третьем слайде мы можем разбить фигуру на прямоугольник и 2 треугольника и тоже найти площадь по формулам.

 

Но в жизни нам не всегда встречаются фигуры, площадь которых мы можем найти по формулам. Поэтому необходимо знать способы нахождения площади фигуры произвольной формы.            

 

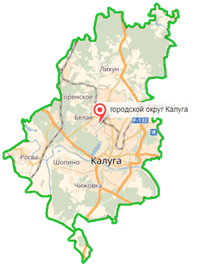Перед вами карта города Калуги. Как найти такую площадь?

 

- ….(выдвигают предположения).

 С какой проблемой мы столкнулись?

-  ……

Какова будет тема нашего занятия?

- нахождение площади фигуры произвольной формы.

Какую цель мы поставим?

- …

Цель нашего мероприятия: рассмотрение различных способов вычисления площади фигуры произвольной формы.

Для достижения цели определим задачи, которые нам нужно выполнить …

Задачи: 1. рассчитать площади произвольной фигуры различными способами; 2. сравнить полученные результаты.

4. Работа в творческих группах.

Для нахождения площади данной фигуры предлагаю поработать в творческих группах. Каждой группе достанется свой способ нахождения площади. (Приложение 1)

Каждая группа выбирает карточку определенного цвета, и берет оборудование согласно цвету карточки.

После выполнения работы подводятся итоги. Каждая группа отчитывается по плану:

- каким способом находили площадь

- какой результат получили

- с какими трудностями столкнулись

Во время выступления учащихся, остальные учащиеся внимательно слушают и заполняют таблицу

Название метода	Плюсы метода	Минусы метода

От каждой группы представители или желающие высказываются по данной таблице.

5. Рефлексия.

Заполнение таблицы. Учащиеся выбирают тот метод, который им понравился больше всего и наклеивают стикеры напротив названия данного метода. (Приложение 2)

 

Подводим итоги: все ли поставленные задачи были нами выполнены? достигли ли мы цели? Давайте проанализируем таблицу, в которую вы наклеивали стикеры. Как мы видим, стикеры наклеены напротив каждого метода. Это говорит о том, что нет какого – то одного метода решения задачи. Для каждого он будет свой.

Закончить наше занятие хочется словами известного математика, механика Пафнутия Львовича  Чебышева

 «Сближение теории с практикой дает самые благотворные результаты, и не одна только практика от этого выигрывает, сами науки развиваются под влиянием ее»

Приложение 1

 

разбиение.

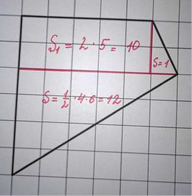Смысл данного способа состоит в том, что фигура разрезается на прямоугольники и (или) прямоугольные треугольники с вершинами в узлах сетки. Тогда площадь фигуры можно сосчитать по формуле:

Sф = S1 + S2 + S3 = 10 + 1 + 12 = 23.    

 

 

 

 

Задание:

1. Перенесите фигуру на миллиметровую бумаги.

2. Используя данный способ найдите площадь фигуры в см²

3. Запишите результат.

4. Подготовить отчет по следующему плану:

- описать способ нахождения площади

- какой результат получили

- с какими трудностями столкнулись

 

 

 дополнение до прямоугольника.

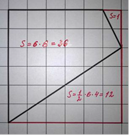Смысл данного способа – это дополнение многоугольника до прямоугольника так, чтобы его стороны проходили через вершины четырехугольника, а затем вычитание лишних частей. Получим, что площадь фигуры равна:

Sф = Sпр - (S1 + S2) = 36 - (1 + 12) = 23.

 

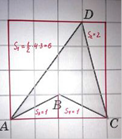
 Sф = S - (S1 + S2 + S3 + S4) = 42 - (6 + 2 + 1 + 1) = 16 - 10 = 6.

 

 

 

 

 

Задание:

1. Перенесите фигуру на миллиметровую бумаги.

2. Используя данный способ  найдите площадь фигуры в см²

3. Запишите результат.

4. Подготовить отчет по следующему плану:

- описать способ нахождения площади

- какой результат получили

- с какими трудностями столкнулись

 

 формула Пика.

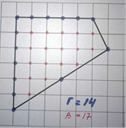Любая фигура изображенная на листе бумаги делит его на внутреннюю область и внешнюю, а еще есть граничные точки многоугольника. Нас интересуют внутренние узлы и узлы, которые лежат на границе многоугольника. Тогда формула выглядит так

S = В + Г/2 - 1, где В - количество внутренних узлов, а Г - количество узлов на границе многоугольника.

Эта формула получила название формула Пика в честь австрийского математика Георга Пика которая появилась в его восьмистраничной работе 1899 года, опубликованной в Праге.

Используя рисунок В= 17, Г = 14, получаем S = 17 + 14/2 - 1 = 23.

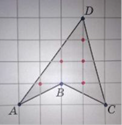 В = 5; Г = 4; S = 5 + 4/2 - 1 = 6.

Задание:

1. Перенесите фигуру на миллиметровую бумаги.

2. Используя данный способ найдите площадь фигуры в см²

3. Запишите результат.

4. Подготовить отчет по следующему плану:

- описать способ нахождения площади

- какой результат получили

- с какими трудностями столкнулись

 

метод взвешивания.

Цель: измерение площади фигуры неправильной формы

Оборудование: электронные весы, ножницы, тело неизвестной площади

 

Метод измерения вспомогательной величины придуман еще в древности и заключается в измерении массы плоской копии измеряемой фигуры. Если толщина листа, из которого изготовлены взвешиваемая фигура, постоянна, то масса фигуры прямо пропорциональна ее площади.

 

Нужно вырезать квадрат, площадь которого S₀ точно известна и определить на весах его массу m₀.

Определите массу m фигуры с искомой площадью S.  

Затем, пользуясь правилом пропорции – S/S₀ =m/m₀, вычислить искомую площадь.                                 

                                             

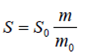
So, см2	m0,г	m,г	S, см2

 

МЕТОД РЫЧАГА

Цель: вычисление площади тела неправильной формы

Оборудование: электронные весы, тело, линейка

                                              m=Vρ=Shρ

Выразите искомую величину S

Для вычисления толщины листа h используйте метод рядов

 

m г	ρ  г/см3	H            см	N	h  см	S  см2

 

 

МЕТОД МОМЕНТ СИЛ

Цель: измерение площади тела неправильной формы

Оборудование: рычаг, груз известной массы, тело неправильной формы, штангенциркуль

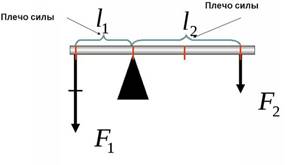
Уравновесьте на рычаге тело неизвестной площади и груз известной массы

Если  F₁*L₁=F₂*L₂,

m₁gL₁= m₂gL₂

m₁L₁= m₂L₂

ρV L₁= m₂L₂

V=Sh,

ρSh L₁= m₂L₂

                                 Получите формулу для расчета S

ρ, г/см3	L1 ,см	L2 ,см	m2 ,г	h, мм	S, см2

 

Считая, что ρ=        г/см³

Для измерения h используйте штангенциркуль

 

 

Приложение 2

 

разбиение
дополнение до прямоугольника
формула Пика
взвешиваниЕ
РЫЧАГ
МОМЕНТ СИЛ