НАХОЖДЕНИЕ СРЕДНИХ СТАТИСТИЧЕСКИХ

Нахождение средних статистических
характеристик

Цели: ввести понятия частоты появления числа в ряду, таблицы частот и таблицы относительных частот; формировать умения составлять таблицы частот, а также находить средние статистические характеристики.

Ход урока

I. Организационный момент.

II. Устная работа.

Даны ряды:

1) 4; 1; 8; 5; 7.

2) ; 9; 3; 0,5; .

3) 6; 0,2; ; 4; 7,3.

Найдите:

а) наибольшее и наименьшее значения каждого ряда;

б) размах каждого ряда.

III. Объяснение нового материала.

1. Объяснение проводить согласно пункту учебника.

Учащихся знакомим с элементами статистики как научного направления. Прежде всего речь идёт об элементах так называемой «описательной» статистики, которая занимается вопросами сбора и представления первичной статистической информации в табличной и графической формах, вычисления числовых характеристик для совокупности статистических данных.

На примере таблицы частот со с. 215 учебника показываем, как анализируются данные статистического исследования, какие обобщающие показатели используются.

Необходимо затем подытожить, какие статистические характеристики теперь могут находить учащиеся. Для этого на доску можно вынести пример:

2. Вводится понятие таблицы относительных частот – таблица, в которой для каждого данного указывается не частота, а отношение частоты к общему числу данных в ряду, выраженное в процентах.

IV. Формирование умений и навыков.

На этом уроке учащиеся отрабатывают умения составления таблиц частот и таблиц относительных частот, а также статистических характеристик. Необходимо следить, чтобы учащиеся чётко мотивировали свои ответы, избегали формализации.

1. № 1028.

Р е ш е н и е

Проверяем, что 13 + 23 + 14 = 50.

Данных недостаточно, чтобы сделать вывод о предстоящих результатах голосования.

2. Подсчитывая число семян сорных растений в 15 одинаковых пакетах, получили такие данные:

3, 1, 0, 3, 2, 2, 1, 0, 1, 3, 2, 1, 0, 0, 2.

Представьте эти данные в виде таблицы частот.

Р е ш е н и е

Проверяем, что 4 + 4 + 4 + 3 = 15.

3. № 1030.

Р е ш е н и е

Находим  общее  число  учащихся  (сумма  чисел  в  правом  столбце);
п = 625.

Относительные частоты вычисляем делением каждого числа в правом столбце на 625 и умножаем на 100 % (с округлением до 1 %):

Проверяем: 0 + 4 + 8 + 14 + 36 + 23 + 14 = 99 %. А должно быть 100 %. Это результат округления. В таких случаях увеличивают на 1 число, которое имеет самую большую отброшенную дробную часть; в данном случае это 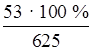 = 8,48; в таблице процент выполнивших 2 задания следует записать 9 вместо 8.

4. № 1031.

Р е ш е н и е

Наибольшее различие в числе допущенных ошибок: 6 – 0 = 6.

Типичное число ошибок: 3 (встречается 26 раз из 70).

Использованы: размах и мода.

5. № 1032.

Р е ш е н и е

1) Данные представлены в виде таблицы частот, поэтому среднее арифметическое находим по формуле.

.

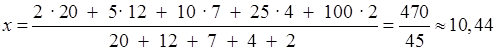Эта величина характеризует среднее количество акций на руках одного сотрудника.

2) Размах А = х_max – x_min = 100 – 2 = 98.

Размах показывает, что разброс наблюдаемых значений очень велик.

3) Мода М = 2 показывает, что наибольшее число сотрудников приобрело по 2 акции.

О т в е т: ≈10,44; ≈98; 2.

V. Итоги урока.

В о п р о с ы   у ч а щ и м с я:

– Что называется таблицей частот?

– Какие данные заносятся в таблицу относительных частот?

– Какие существуют средние статистические характеристики?

– Объясните на примере, как по таблице частот находят среднее арифметическое, размах и моду.

Домашнее задание: № 1029, № 1033, № 1034, № 1093.