Исследовательская работа по дисциплине «Математика»

ТЕМА: «МАТЕМАТИКА В СКУЛЬПТУРЕ: 

СИММЕТРИЯ И АСИММЕТРИЯ, ПРОПОРЦИИ»

Выполнил:

Котов Александр, гр. 1 Ск Руководитель проекта: Константинова М.В., преподаватель математики

МАХУ

                                                                                          Москва, 2024                                                 

Введение

Математика и искусство связаны между собой разнообразными отношениями. Математика сама по себе может считаться видом искусства, поскольку в ней обнаруживается своеобразная красота. Следы математического мышления проявляются в музыке, танце, живописи, архитектуре и искусстве ткачества.

Скульптура — уникальное искусство создания объемных художественных произведений. Скульптура (от латинского sculpo — «вырезаю», «высекаю») — это вид изобразительного пластического искусства, в котором художник создает объемное произведение из твердых материалов. В процессе работы мастер либо высекает (удаляет) лишние слои из исходного цельного блока, либо наращивает на каркас пластический материал (лепит скульптуру).

Скульптура тесно связана с математикой. Эта связь становится более очевидной в скульптуре, разработанной в 20-м веке и в настоящее время. Математическая скульптура использует большое разнообразие математических элементов из: геометрии, алгебры, логики. Причем для некоторых направлений скульптуры, использование математики становится существенным в их концепции, дизайне, разработке и исполнении

1. Золотое сечение

Скульптурные сооружения, памятники воздвигаются, чтобы увековечить знаменательные события, сохранить в памяти потомков имена прославленных людей, их деяния и подвиги. Известно, что еще в древности основу скульптуры составляла теория пропорций. Отношения частей человеческого тела связывались с формулой золотого сечения. Пропорции “золотого сечения” создают впечатление гармонии красоты, поэтому скульпторы использовали их в своих произведениях. 

Золотое сечение — это соотношение двух неравных чисел, при котором большее так же относится к меньшему, как сумма этих чисел к большему. Золотое сечение равно примерно 1,618, или 1,62, если округлить, и обозначается греческой буквой φ, «фи» — от имени древнегреческого скульптора Фидия. Считается, что он использовал такие пропорции при оформлении Парфенона.

На изображении ниже представлена концепция золотого сечения:

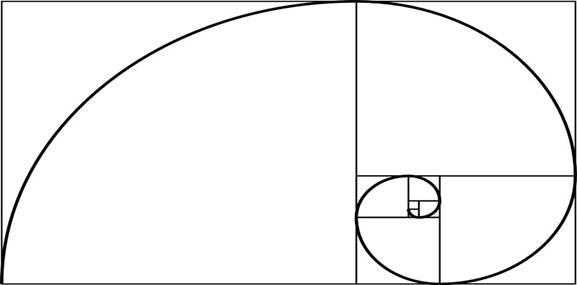
Тема золотого сечения была и будет актуальной, ведь мы всегда и во всем ищем красоту. Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление совершенства целого и его частей в искусстве, науке, технике и природе.

Скульпторы утверждают, что талия делит совершенное человеческое тело в отношении “золотого сечения”. Так, например, знаменитая статуя Аполлона Бельведерского, считающаяся эталон мужской красоты, состоит из частей, делящихся по золотым отношениям: a  кратно 0,618,   b кратно 0,382. Великий древнегреческий скульптор Фидий часто использовал “золотое сечение” в своих произведениях. Самыми знаменитыми из них были статуя Зевса Олимпийского (которая считалась одним из чудес света) и Афины Парфенос. 

Рис.1 Аполлон Бельведерский

Одним из достижений классического греческого искусства может являться статуя Дорифора (что означает копьеносец), изваянная  Поликтетом в V веке до

н.э. Эта статуя считается наилучшим примером для анализа пропорций идеального человеческого тела, установленных античными греческими скульпторами, и напрямую связана с золотым сечением и числом φ = 0,618.

Рассмотрим, как оно представлено в статуе Дорифора. Это отношение расстояний:

•      от талии до стопы к расстоянию от макушки до талии;

•      от талии до шеи к длине головы;

•      от подбородка до линии бровей к расстоянию от линии бровей до макушки.

                            Рис.2 статуя Дорифора        Рис.3 статуя Афины

2. Симметрия и асимметрия

Не будем акцентировать внимание на золотом сечении, чтобы разобрать менее очевидные моменты, где математика и скульптура сталкиваются.

Понятие гармонии, симметрии (в основе чего лежат математические принципы) являются основными критериями, лежащими в основе любого скульптурного произведения.

Изначально под словом симметрия подразумевали соразмерность, но по мере развития геометрии и теории искусства значение этого слова было расширенно. Сегодня под ним понимают соответствие частей одной композиции, которое включает массу предметов, их расположение, соотношение объемов.

Существуют следующие виды симметрии:

             зеркальная

В основе этого типа симметрии лежит принцип разделения массы композиции на две равные части по обе стороны вертикально или горизонтально ориентированной оси. Две половины изображения полностью соответствуют друг другу. Каждая точка в такой композиции имеет в соседней плоскости свое зеркальное отражение, расположенное в том же месте пересечения осей координат. 

В качестве примера представлен конкистадор, стоящий в портале над парадным входом ряда дворцов (выставочных зданий) в Сан Франциско.

             осевая

Один из самых популярных видов симметрии. Образуется путем вращения плоской фигуры вокруг центральной оси, при котором она несколько раз совмещается сама с собой. Осевую симметрию можно наблюдать в рисунках тарелок, дисков и куполах храмов. Она может иметь порядки (количество совпадений фигуры с самой собой) и несколько горизонтально или вертикально ориентированных поперечных осей.

Осевую симметрию мы можем видеть в оформлении собора Санта-Мариядель-Фьоре, Флоренция:

             винтовая

Ее также называют симметрией вращения. Избегая сложных математических определений, мы можем описать ее как симметрию, возникающую в результате винтообразного движения точки или линии вокруг неподвижной оси.

               симметрия переноса

Этот вид симметрии мы можем наблюдать при создании однотипных, повторяющихся изображений. В архитектуре симметрия переноса может быть создана на базе нескольких непараллельных осей, лежащих в одной или нескольких плоскостях.

Примером использования симметрии переноса мы можем видеть на соборе Санто-Доминго-де-ла-Кальсада:

Наиболее используемыми видами симметрии в скульптуре являются: зеркальная; осевая; переноса.

3. Асимметрия

Это, соответственно, нарушение законов симметрии. 

Отсутствие симметрии в определенных случаях может придать композиции динамики и разнообразия. При соблюдении определенных условий непринужденность и необычность образов оживляет статическую картину и позитивно сказывается на ее эмоциональном восприятии. Кроме того, в классическом искусстве асимметрия используется для создания контраста с симметрией. Этот художественный прием дает возможность усилить восприятие красоты объектов с правильными пропорциями соразмерными элементами.

4. Пропорции

Пропорции являются основой изобразительного искусства. В основе определения пропорций лежит метод сравнения. В художественной практике существует известный метод         определения        пропорций,          называемый визированием.

Как им пользоваться?  Берется карандаш и на вытянутой руке замеряется длина или ширина предмета и затем, все еще на вытянутой руке, это расстояние, которое замеряли, прикладывают к расстоянию, с которым сравнивают, и смотрят, сколько раз меньшее откладывается в большем. Полученное соотношение и переносится на рисунок.

В скульптуре для измерения и переноса размеров, форм и объёмов используются скульптурные циркули. В пример можно привести пропорции человека. Для избегания ошибок стоит соблюдать основные пропорции в строении человека, отношение головы к телу, ног, рук, ширины плеч и т. д., а это всё опять же математика.

На статуе Давида (работе Микеланджело) мы можем наблюдать соблюдение пропорций человека, однако в некоторых местах есть намеренное их нарушение, свойственное для монументальных скульптур.

5. Математическая скульптура

Рассмотрим отдельный вид скульптуры, в основе которого преобладают принципы математики. 

 Математическая скульптура использует различные направления математики: геометрию, алгебру, векторное исчисление, логику.  Д. Скульптуры, для которых использование математики становится существенным в их концепции, дизайне, разработке или исполнении. Скульптура в парке-музее Ёстеррайхишер Скульптурен:

Эта связь может быть даже распространена на большинство художественных проявлений, взятых в ее более широком смысле. Великие успехи в математике в современную эпоху и современный век сделали возможным развитие концептуально-математического искусства.

Ярким примером являются работы Генри Сегерман. Художник, который превращает абстрактные математические концепции в реальные и завораживающие физические объекты.

Сегерман пришел в скульптуру, вооружившись формулами и числами, и обустроил свой виртуальный мир на математический лад, наполнив его невиданными фрактальными фигурами, спиралями, четырехмерными гиперкубами. «Получилась такая проекция четырехмерного гиперкуба в трехмерной вселенной Second Life — которая сама по себе является проекцией трехмерного виртуального мира на двумерный, плоский экран», — замечает художник.

 Начиная с 2009 года Сегерман создал чуть больше сотни скульптур, и каждая из них — наглядное и, насколько возможно, точное физическое воплощение абстрактных математических концепций и законов.   

 В конечном итоге эволюция математических скульптур заводит нас в сложную и завораживающую область топологии. Этот раздел математики изучает свойства и деформации плоских поверхностей и пространств разной размерности, где более важны их характеристики, чем для классической геометрии. Куб здесь можно легко, как пластилин, превратить в шар, а чашку с ручкой скатать в бублик, не нарушив в них ничего важного — известный пример, который нашел воплощение в изящной «Топологической шутке» Сегермана.

Заключение

Подводя итог, можно сказать, что математика и скульптура неотъемлемо связаны. На первый взгляд может показаться, что математика и скульптура не сильно связаны, но это не так.   В принципе, создание любой скульптуры не обходится без математики, необходимо соблюдать пропорции, отношения одних частей и фрагментов к другим. Математика облегчает создание скульптур, придерживаясь всем критериям пропорций, перспективы и композиции.

Глубокая красота математики может пугать. Однако вся эта холодная гармония неизменно отражает внутреннюю упорядоченность и закономерность Вселенной, в которой мы живем. Математика — лишь язык, который безошибочно соответствует этому изящному и сложному миру. Парадоксально, но в нем находятся физические соответствия и приложения для почти любого высказывания на языке математических формул и отношений. Даже самым абстрактным и «искусственным» построениям рано или поздно находится приложение в реальном мире.

Список литературы

1.            Волошинов А. В. «Математика и искусство» М.: Просвещение, 2000

2.            Давыдов М. «Красота математики». Н. Новгород, 2007.

3.            И. Ф. Шарыгин Л.Н. Ерганжиева. «Наглядная геометрия»  М.: Чистые пруды, 1995.

4.            Нафиков Н.Н. « Гипотеза об истоках золотого сечения», Ж. “Математика в школе”№ 3, 1994.

5.            https://veryimportantlot.com/ru/news/blog/chto-takoe-skulptura

6.            https://elementy.ru/nauchnopopulyarnaya_biblioteka/433232/Genri_Segerman_ i_ego_matematicheskie_etyudy

7.            www.bymath.net

8.            www.exponenta.ru