Научно-исследовательская работа по теме "Золотое сечение-красота и гармония в математических расчетах"

 

Муниципальное казённое общеобразовательное  учреждение «Средняя общеобразовательная школа   им. З.Б. Максидова сельского поселения  Хамидие»

Терского муниципального района КБР

 

 

 

 

 

 

Научно исследовательская работа по теме:

 

«Золотое сечение – красота и гармония в математических расчетах.»

 

 

Автор: Макоева Жанна ученица  6 класса МКОУ

 СОШ  сп Хамидие

 

Руководитель: Гогунокова Мадинат Муаедовна, учитель  математики.

 

 

 

                                                    

 

 

 

 

 

Содержание работы:

 

Введение  _______________________________________________3

·        цель работы, основные задачи  _______________________ 3

·        актуальность темы ___________________________________3

·        обзор литературы __________________________________  4 

Теоретические сведения по теме исследования  ____________   5

·        история возникновения «тайны золотой пропорции» ____ 5

·        числовое значение золотой пропорции _________________5

·        построение золотого сечения _________________________6

·        золотой прямоугольник  _____________________________6

·        числа Фибоначчи    __________________________________

·        использование золотого сечения в строительстве, искусстве_7

·        золотое сечение в природе __________________________7

Исследование___________________________________________7

·        выбор фоторамки ___________________________________7

·        выбор дерева с самыми красивыми листьями  __________8

·        строение кленового листа ____________________________9

·        эксперимент «Узел»_________________________________10

·        Золотое сечение в растениях__________________________12

·        Золотое сечение в пропорциях человеческого тела_______13

Заключение  ____________________________________________15

Список использованных ресурсов__________________________16

 

 

 

 

ВВЕДЕНИЕ

«Геометрия владеет двумя сокровищами-

теоремой Пифагора и золотым сечением,

и если первое из них можно сравнивать с

мерой золота, то второе – с драгоценным

камнем…»

Иоганн Кеплер

Цель работы:     выявить,  что же такое золотое сечение, исследовать принцип “золотого сечения – красоты и гармонии” в окружающем мире.

Основные задачи:

Ø изучить красоту окружающих предметов с математической точки зрения,

Ø найти в математической литературе подтверждение гипотезы исследования,

Ø провести эксперименты по поиску идеальных пропорций в красивых предметах

       Этапы выполнения исследовательской работы:                            

 1.     Подбор и изучение, необходимой для исследования литературы.                    2.         Сбор и систематизация материала.                                                                            3.         Экспериментальная проверка фактов, подтверждающих гипотезу проекта.

           4.      Оформление результатов  исследовательской деятельности.

Актуальность темы

На уроках математики, я узнала о золотых пропорциях окружающего мира. Мне стало интересно:  - Откуда такая красота и гармония?

Где же прячутся – эти числа и математические закономерности во всём, что нас привлекает? А что же нас привлекает в жизни? Всё красивое и гармоничное! Но тогда, как же это связано между собой - красота, гармония и … математика?

Я обратилась к современному источнику информации – к Интернету. И обнаружила, что за высшее проявление совершенства целого и его частей в искусстве, науке, технике и природе «отвечает» принцип «золотого сечения».

Странная, загадочная, необъяснимая вещь: эта божественная пропорция мистическим образом сопутствует всему живому. Вы непременно увидите эту пропорцию и в изгибах морских раковин, и в форме цветов, и в облике жуков, и в красивом человеческом теле. Все живое и все красивое — все подчиняется божественному закону, имя которому — «золотое сечение».

Так что же такое «золотое сечение»?..

Что это за идеальное, божественное сочетание?

Может быть, это закон красоты?

Или все-таки он — мистическая тайна?

Научный феномен или этический принцип?

Ответ неизвестен до сих пор. Точнее — нет, известен.

«Золотое сечение» — это и то, и другое, и третье. Только не по отдельности, а одновременно... И в этом его подлинная загадка, его великая тайна.

Я захотела узнать о тайнах “золотого сечения”. Результатом моей деятельности и явилась данная исследовательская работа.

Гипотеза: За красоту и гармонию в природе «отвечает» математика. То есть особые числовые закономерности существуют во всем, что нас окружает.

Обзор литературы по теме исследования:

  Из книги Н.А. Васютинского  я узнала, что в основе гармонии природы и произведений искусства лежит золотая пропорция.  Васютинский Н.А. очень просто  и интересно рассказывает о сути этого замечательного соотношения, истории его открытия и исследований. Здесь описано проявление закономерностей золотой пропорции в архитектуре, музыке, поэзии, а также в химии, биологии, ботанике, геологии, астрономии, технике.

Интересную информацию о золотом сечении, золотых прямоугольниках, треугольниках и пентаграмме содержит  учебник «Наглядная геометрия»  для 5 -6  классов, авторами которого являются Шарыгин Н.Ф., Ерганжиева Л.Н. Очень понравилась мне статья «Золотое сечение» в журнале «Квант».  Автор статьи Бендукидзе А.Д. пишет не только об истории открытия золотого сечения, но и о связи этой пропорции с числами Фибоначчи.

   Много интересных сведений о золотом сечении я нашла на сайтах сети Интернет.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

История возникновения «тайны золотой пропорции»

С давних пор человек стремится окружать себя красивыми вещами.

На определенном этапе своего развития человек начал задаваться вопросом: почему тот или иной предмет является красивым и что является основой прекрасного? Ещё у древних греков родилось представление о том, что основой прекрасного является гармония.

О золотом сечении знали еще в древнем Египте и Вавилоне, в Индии и Китае. Великий Пифагор создал тайную школу, где изучалась мистическая суть «золотого сечения». Евклид применил его, создавая свою геометрию, а Фидий — свои бессмертные скульптуры. Платон рассказывал, что Вселенная устроена согласно «золотому сечению». А Аристотель нашел соответствие «золотого сечения» этическому закону. Высшую гармонию «золотого сечения» будут проповедовать Леонардо да Винчи и Микеланджело, ведь красота и «золотое сечение» — это одно и то же. А христианские мистики будут рисовать на стенах своих монастырей пентаграммы «золотого сечения», спасаясь от Дьявола. При этом ученые — от Пачоли до Эйнштейна — будут искать, но так и не найдут его точного значения.

Красота скульптуры, красота храма, красота картины, симфонии, поэмы... Что между ними общего? Разве можно сравнивать красоту храма с красотой ноктюрна? Оказывается можно, если будут найдены единые критерии прекрасного, если будут открыты общие формулы красоты, объединяющие понятие прекрасного самых различных объектов - от цветка ромашки до красоты человеческого тела...". И эта формула – формула золотого сечения – некий универсальный информационный код красоты, соединяющий разные искусства и разные века в интуитивном постижении прекрасного.

Эта формула отвечает такому делению целого на две части, при котором отношение большей части к меньшей равно отношению целого к большей части. Эту пропорцию называли по-разному - "золотой", "божественной", "золотым сечением", "золотым числом". Она оказалась близкой к 1,6.

 Понятие «Золотого сечения»

Золотое сечение – это деление отрезка, при котором длина всего отрезка так относится к длине его большей части, как длина большей части к меньшей.

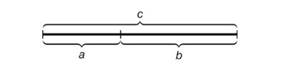с:в=в:а

Отношение обозначают буквой j;

j= 1,618 = 8/5

Золотое сечение математики часто называли божественной пропорцией

   Скульпторы, архитекторы, художники использовали и используют золотое сечение в своих произведениях.

   К примеру, в храме Парфенон в Афинах отношение высоты здания к его длине равно j.

Есть  предположение, что Пифагор понятие золотого сечения позаимствовал у египтян и вавилонян. И, действительно пропорции пирамиды Хеопса, барельефы предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношением золотого сечения при их создании.

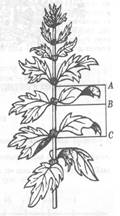Рассматривая расположение листьев на стебле растений можно заметить, что между каждыми двумя парами листьев (А и С) третья расположена в месте золотого сечения (В).

Очень совершенна форма стрекозы, которая создана по законам золотой пропорции: отношение длин хвоста и корпуса равно отношению общей длины к длине хвоста

Холст, на котором написана «Тайная вечеря» Сальвадора Дали, имеет форму золотого прямоугольника, стороны которого находятся в золотом отношении.

Задача 1. Пусть дан отрезок длиной 10 см и разделить его приблизительно в золотом отношении.

(6,2 см и 3,8 см) одна часть отрезка больше другой в 1,6 раза.

Части “золотого сечения” составляют приблизительно 62% и 38% всего отрезка.

В эпоху Возрождения “золотое сечение» было очень популярным среди художников, скульпторов, архитекторов. Так, выбирая размеры картины, художники старались, чтобы отношение ее сторон равнялось Ф. Такой прямоугольник стали называть “золотым”.

Задача 2.

Построим золотой прямоугольник.

Начертим квадрат и разделим его на два равных прямоугольника.

В одном из прямоугольников проведем диагональ АВ.

Циркулем проведем окружность радиуса АВ с центром в точке А.

Продолжим основание квадрата до пересечения с дугой в точке Р и проведем под прямым углом вторую сторону искомого прямоугольника.

Измерьте линейкой длины сторон построенного прямоугольника MNKP и вычислите отношения большей стороны к меньшей. (Отношение сторон должно быть примерно равно 1,6).

Числа Фибоначчи - удивительных числа, которые были открыты итальянским математиком средневековья Леонардо Пизанским, более известным под именем Фибоначчи (род. ок. 1170 - умер после 1228), итальянский математик. Путешествуя по Востоку, познакомился с достижениями арабской математики. После его открытия числа эти так и стали называться именем известного математика. Удивительная суть последовательности чисел Фибоначчи состоит в том, что каждое число в этой последовательности получается из суммы двух предыдущих чисел.

Числа, образующие последовательность 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, ... называются "числами Фибоначчи", а сама последовательность - последовательностью Фибоначчи. В числах Фибоначчи существует одна очень интересная особенность. При делении любого числа из последовательности на число, стоящее перед ним в ряду, результатом всегда будет величина, колеблющаяся около иррационального значения 1.... и через раз то превосходящая, то не достигающая его.

Более того, после 13-ого числа в последовательности этот результат деления становится постоянным до бесконечности ряда… Именно это постоянное число деления в средние века было названо Божественной пропорцией, а ныне в наши дни именуется как золотое сечение, золотое сpеднее или золотая пропорция.

В математике это число обозначается гpеческой буквой фи (Ф)

Итак, Золотая пропорция = 1 : 1,618

 Исследования.

Мне захотелось проверить, что «Золотая пропорция» действительно является универсальным информационным кодом. И я провела следующие эксперименты:

1.     Выбор фоторамки

Цель исследования: выявить, действительно ли форма золотого прямоугольника создает впечатление красоты и гармонии

Оборудование: лист ватмана с рисунками фоторамок различных размеров.

Вопрос: какая фоторамка лучше подходит для предложенной фотографии?

В опросе участвовало 30 человек: учащиеся 5 - 6 классов МКОУ СОШ сп Хамидие.

Результаты опроса

№	Размеры рамки, мм	Отношение ширины к длине	Количество голосов, отданных за рамку
1	120×200	0,6	23
2	100×200	0,5	3
3	135×190	0,71	2
4	90×150	0,6	1
5	120×150	0,8	1

 

Основная часть опрашиваемых выбрали фоторамки,  в которых отношение ширины к длине приблизительно равно числу φ=0,6.

Вывод:

Большинство участников исследования выбрало рамки, имеющие форму золотого прямоугольника,  значит,  соотношение сторон золотого прямоугольника действительно создаёт впечатление красоты и гармонии.

2. Выбор дерева с самыми красивыми листьями

Цель исследования: выяснить, листья какого дерева считаются самыми красивыми

Оборудование: гербарий с листьями различных деревьев

Вопрос: листья, какого дерева вы считаете самыми красивыми?

В опросе приняло  участие  30  человек.

Результаты опроса

№	Дерево	Количество голосов, отданных за листья данного дерева
1	Клен	24
2	Береза	2
3	Тополь	2
4	Осина	1
5	Дуб	1
6	Липа	0

 

80% опрашиваемых считают самыми красивыми листья клена, 6% опрашиваемых выбрали листья березы и тополя; 3% - листья дуба и осины.

Вывод:  самые красивые  листья у клена.

  3. Строение кленового листа

Цель исследования: выяснить, почему лист клена считается самым красивым.

Оборудование: лист клена, сканер, принтер, бумага, чертежные инструменты

Ход исследования:

1. Сбор листьев клена

2. Сканирование и печать изображения листьев клена

3. Выполнение измерений

С

4. Поиск соотношений

D

F

Е

В

А

    

При проведении исследования использовались 5  кленовых листьев, и в строении каждого из них были обнаружены пропорции золотого сечения.

Вывод:

 В строении кленового листа присутствуют пропорции золотого сечения и симметрия, поэтому лист клена создает впечатление красоты и гармонии.

4. Эксперимент «Узел»

Цель: исследовать форму узла

Оборудование: полоска бумаги постоянной ширины, чертежные инструменты, мужской галстук.

Ход эксперимента:

Бумажную ленту постоянной ширины завяжем простым узлом и расправим так, чтобы узел был плоским. Получается узел, имеющий форму пятиугольника. Измерения сторон и углов  пятиугольника доказывают, что ABCDE  - правильный пятиугольник.

 

С

          -                      

Отношение стороны правильного пятиугольника к диагонали равно числу.

У Пифагора и его учеников пентаграмма была священным символом телесно-духовной гармонии и на этом основании стала знаком здоровья.

Вывод:  узел имеет форму правильного пятиугольника, т.е. пентаграммы. Пентаграмма – это геометрический символ гармонии, здоровья и мистических сил.

Может быть, поэтому мужчины выбрали себе в качестве украшения галстук, ведь узел галстука имеет форму пентаграммы.

 

“Золотое сечение” в растениях.

Рассматривая расположение листьев на общем стебле растений: фикус,  золотой ус, традесканция и алоэ, я выяснила, что между каждыми двумя из листьев третий расположен в определенном месте.

  

Фикус

Для начала я измерила высоту фикуса - 40 см и расстояние между листами. 

Расстояние между листьями	В см	Вычисления отношения
от 1 до 2	15,9	(15,9+9,8):15,9=1,62
от 2 до 3	9,8	15,9: 9,8=1,62
от 3 до 4	6,1	(6,1+3,8)=9,9 9,9:6,1=1,62
от 4 до 5	3,8	6,1: 3,8=1,60
от 5 до 6	2,4	2,4+1,5=3,9 3,9:2,4=1,63
от 6 до 7	1,5	2,4:1,5=1,6

На основе данных была сделана диаграмма, в которой показаны изменения расстояния между листьями по мере его роста.

Заметила, что отношение   примерно равно числу φ ≈ 1,6.

Вывод:

В моих исследованиях,  я подтвердила, что окружающие нас предметы содержат золотую пропорцию, характеризующую соразмерность и гармоничность их строения.

Фикус содержат искомые «золотые пропорции».

Золотое сечение, действительно, универсальный закон живых систем.

Золотое сечение заложено в пропорциях человеческого тела.

Итак, золотое сечение является математическими символами идеального соотношения формы и роста. В древности считалось, что если человек имеет золотое сечение, то он великий человек

Среди своих знакомых и друзей я провела исследование: измерил их рост, расстояние до талии. Мне стало интересно, обладает ли кто-нибудь из нас «золотым сечением», то есть «божественной пропорцией». Ниже в таблице приведены данные измерений и вычислен коэффициент пропорциональности. Наиболее приближенные данные получились у Александра (0,62 / 0, 61).

 

 

 

	Рост, см	Расстояние от талии до макушки, см	Расстояние до талии, см	j  (0,618)
Я	152	60	92	0,6 / 0,65
Мама	166	68	98	0,59 / 0,69
Папа	179	73	106	0,59 / 0,68
Сеня	123	51	72	0,58 / 0,7
Юра	169	67	102	0,6 / 0,65
Виталя	137	49	88	0,64 / 0,56
Александр	167	63	104	0,62 / 0, 61
Сергей	150	55	95	0,63 / 0,58
Юля	164	59	105	0,64 / 0,56
Алена	160	60	100	0,62 / 0,6

 

	Расстояние от талии до макушки, см	Расстояние от талии до головы, см	Расстояние от головы до макушки, см	j  (0,618)
Я	60	39	21	0,53 / 0,65
Мама	68	48	20	0,42 / 0,7
Папа	73	53	20	0,38 / 0,72
Сеня	51	33	18	0,54 / 0,64
Юра	67	47	20	0,42 / 0,7
Виталя	49	27	22	0,81 / 0,55
Александр	63	43	20	0,46 / 0, 68
Сергей	55	37	18	0,49 / 0,67
Юля	59	38	21	0,55 / 0,64
Алена	60	42	18	0,43 / 0,7

 

Вывод:

 

Творения человека тоже подчиняются удивительному закону золотого сечения. Всё красивое и гармоничное, что сумеет сделать человек, содержит в себе золотые пропорции.

Я убедился, что все-таки существует связь между математикой и литературой, между математикой и архитектурой, между математикой и живописью. И это не случайно, ведь каждому искусству присуще стремление к стройности, соразмерности, гармонии. Природа совершенна, и у нее есть свои законы, выраженные с помощью математики и проявляющиеся в различных видах искусства.

Меня поразил тот факт, что даже планеты солнечной системы обращаются вокруг солнца по орбитам с «золотым сечением», а Земля имеет самую совершенную орбиту из всех планет. Это доказали математики!

Также я увидела строгую математику в расположении листьев фикуса, золотого уса. Узнала, что и человек в соотношении отдельных частей тела и расстояний между ними, подчиняется законам "золотого сечения". И даже в его генетическом коде заложены закономерности золотой симметрии.

Эти свойства не выдуманы людьми. Они отражают свойства самой природы. А один из важных инструментов для познания тайн природы – это математика. Явления всей вселенной подчинены определенным числовым соотношениям. Число-это закон и связь мира, сила, царящая над богами и смертными. Все упорядочивается в соответствии с числами.

ЗАКЛЮЧЕНИЕ

Красота спасет мир.

Ф.Достоевский

Наблюдая за окружающей природой и создавая произведения искусства, люди искали закономерности, которые позволяли бы определить прекрасное, т.е. пытались вывести формулу красоты. Ряд формул красоты  известен. Это правильные геометрические формы: квадрат, круг, равносторонний треугольник. В ходе выполнения исследовательской работы я выяснила, что действительно существует «формула красоты», которая не является выдумкой человека. Скорее всего, это закон природы. В наибольшей степени определение «формула красоты» подходит к понятию «золотая пропорция» -золотое сечение. Эта пропорция обладает наиболее отчетливыми признаками  гармоничности прекрасного. Золотая пропорция не только является господствующей во многих произведениях искусства, она определяет закономерности развития многих организмов, её присутствие отмечают почвоведы, химики, биологи, геологи, математики, астрономы.

Золотое сечение являлось критерием гармонии и красоты ещё во времена Пифагора и является настоящей  формулой красоты в настоящее время.  Понять это мне помогла математика. Математика является  не только стройной системой законов, теорем, задач, но и уникальным средством познания красоты. Аристотель говорил: «В наслаждении красотою есть элемент наслаждения мышлением».Золотое сечение, золотой прямоугольник и золотая спираль являются математическими символами идеального соотношения формы и роста. Великий немецкий поэт Гете считал их математическим символом жизни и духовного развития. Остается открытым вопрос: почему природа предпочла золотую пропорцию всем остальным пропорциям? Золотая пропорция делит целое на неравные части, почему же она более привлекательна, чем симметричные пропорции? Очевидно, золотая пропорция обладает каким-то особым свойством, в ней скрыта загадка природы, которую ещё предстоит открыть. Золотая пропорция – понятие математическое и её изучение – задача науки. Но она же является критерием красоты и гармонии, а это уже категории искусства. Поэтому я закончу свою исследовательскую работу стихами. «Чему бы жизнь нас ни учила,

Но сердце верит в чудеса.

Есть нескудеющая сила,

Есть и нетленная краса»

Ф. Тютчев

 

Список использованных ресурсов

1. Бендукидзе А.Д. Золотое сечение – М.: ж. «Квант», 1973, №8

2. Васютинский Н.А. Золотая пропорция. – М.: Мол. гвардия, 1990

3. Золотое сечение. Страницы Википедии. http://ru.wikipedia.org/wiki/%C7%EE%EB%EE%F2%EE%E5_%F1%E5%F7%E5%ED%E8%E5

4.  Лаврус В.  «Золотое сечение»  http://n-t.ru/tp/iz/zs.htm

5. Математика и законы красоты http://mathkrasota.ucoz.ru/index/0-11

6. Музей гармонии и золотого сечения  http://www.goldenmuseum.com/

7.  Шарыгин Н.Ф., Ерганжиева Л.Н. Нагляднаягеометрия 5- 6 кл. Учебник для общеобразоват. учрежд. – М.: Мнемозина, 2009

 

 

 

 

 

 

 

 

 

 

 

Сканированные изображения листьев для проведения исследований

         

 

 

     

 

Приложение 2

Иллюстрации к разделу «Золотое сечение в строительстве, искусстве»

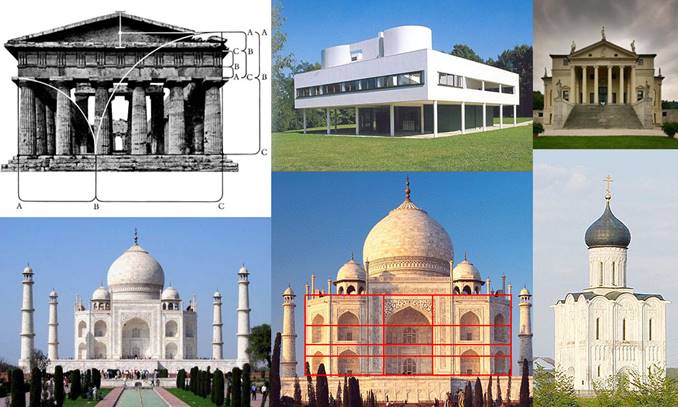
http://kak.ru/vimg/article/9ae90016b6aaaf590cf8fc77b5ae938b.gif

 

http://nordisk.pp.ru/jj/0883855348.01.LZZZZZZZ.jpg

 

Приложение 3

Иллюстрации к разделу «Золотое сечение в природе»

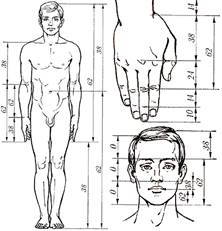 http://www.gamedev.ru/files/images/zolotoe-sechenie.jpg

 http://kak.ru/vimg/article/0c2ba9949857c6b2a56fe71f971401cd.gif

 http://kak.ru/vimg/article/3a755b3d88bbefbbfadf906deda9d30d.gif

Золотое сечение в квантовом мире http://www.redicecreations.com/ul_img/9388goldenratio.jpg

 

Скачано с www.znanio.ru