
Публикация является частью публикации:
Софизмы в математике
Секция: Математические науки.
Автор: Шеметова Анастасия, Глазунова Екатерина, 8 класс МБОУ «СОШ №18».
Научный руководитель: Лукьянова Ольга Георгиевна, учитель математики МБОУ «СОШ №18».
Г. Миасс
Челябинская область
Оглавление
Введение
I. Софизм и история его возникновения
1.1. Софизм и софистика
1.2. Экскурс в историю
II. Математические софизмы и их классификация
2.1. Софизмы и типичные ошибки в них
2.2. Математические софизмы
2.3. Разбор математических софизмов
2.4. Логические софизмы
2.5. Источники софизмов
III. «Софизмы из наших школьных тетрадей»
Заключение
Список литературы
Приложение 1.
Приложение 2. Арифметические софизмы
Приложение 3. Алгебраические софизмы
Приложение 4. Геометрические софизмы
В математических вопросах нельзя пренебрегать даже самыми мелкими ошибками.
И. Ньютон
У ученых есть такое свойство - поставят в тупик все человечество, а потом целое поколение или даже несколько поколений с трудом из него выбираются, проявляя чудеса изобретательности и изворотливости. И одним из средств не только учёных, но и любознательных остроумных людей, любящих ставить окружающих в тупик, является «софизм». Нас заинтересовал факт глубокой древности зарождения софизмов и популярности их у ученых.
Актуальность: Наверное, каждый человек хоть раз в жизни слышал фразу: «Дважды два равно пяти» или «Два равно трем». Что они обозначают? Кто их выдумал? Имеют ли они какое-нибудь логическое объяснение или же это лишь вымысел? Чтобы ответить на эти и подобные им вопросы, мы в своей работе рассматриваем математические софизмы. Математический софизм – удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки. Поэтому нам представляется актуальным изучение ошибок в софизмах, потому что их понимание ведёт к пониманию математике в целом, помогает развивать логику и навыки правильного мышления. Если нашел ошибку в софизме, значит, ты ее осознал, а осознание ошибки предупреждает от ее повторения в дальнейших математических рассуждениях.
Цель: изучение типичных ошибок, которые возникают у учащихся в процессе изучения математики, их причин и способов предупреждения на примере математических софизмов.
Задачи:
1. изучить понятие софизма и историю его возникновения;
2. рассмотреть виды софизмов и дать классификацию их ошибок;
3. составить сборник разбора задач на софизмы по различным разделам математики для 6 - 9 классов.
Гипотеза исследования: если в процессе обучения математике целенаправленно и систематически организовывать работу учащихся над типичными ошибками, на примере софизмов, то это будет способствовать повышению качества математической подготовки учащихся.
1.1. Софизм и софистика
Софизм в переводе с греческого означает дословно: уловка, выдумка или мастерство. Этим термином называют утверждение, являющееся ложным, но не лишенным элемента логики, за счет чего при поверхностном взгляде на него кажется верным. Софизмы основаны на сознательном и преднамеренном обмане, нарушении логики.
Софизм - преднамеренная ошибка, совершаемая с целью запутать противника и выдать ложное суждение за истинное.
Софистика – направление философии, которое возникло в V - IV вв. до н.э. в Греции и стало очень популярным в Афинах.
1.2. Экскурс в историю
Во второй половине V века до н.э. в Греции появились софисты. Софистами называли группу древнегреческих философов достигших большого искусства в логике. Они появились во время становления демократии в Афинах и на подвластных Афинам территориях. Софисты - это мудрецы, но мудрецы особого рода. Этих мудрецов истина не интересовала. Они были, как правило, платными «учителями мудрости». Их нанимали политики для того, чтобы организовать свою предвыборную компанию, в частности, переспорить оппонентов на собрании, а также для того, чтобы выиграть судебное дело. В Греции софистами называли и простых ораторов - философов-учителей, задачей которых было научить своих учеников «мыслить, говорить и делать». Одним из представителей софистов был философ Протагор, который говорил: «Я обучаю людей риторике, а это и есть гражданское искусство» (приложение 1, рис. 1).
Чтобы выйти победителем в словесном поединке, софисты часто пользовались тем, что противник недостаточно глубоко знает предмет, о котором идет речь, недостаточно внимателен и наблюдателен, и поэтому не в состоянии отличить ложь от истины. В результате словесного поединка противник должен был согласиться с доводами софиста и признать себя побежденным, хотя истина, казалось, была на его стороне. Софизмы существуют и обсуждаются более двух тысячелетий, причем острота их обсуждения не снижается с годами. Если софизмы — всего лишь хитрости и словесные уловки, выведенные на чистую воду еще Аристотелем, то долгая их история и устойчивый интерес к ним непонятны. Однако софизмы существовали задолго до философов-софистов, а наиболее известные и интересные были сформулированы позднее в сложившихся под влиянием Сократа философских школах.(Приложение 1,рис.2)
Термин «софизм» впервые ввел Аристотель (приложение 1, рис.3), охарактеризовавший софистику как мнимую, а не действительную мудрость. К софизмам им были отнесены и «апории Зенона» (внешне парадоксальные рассуждения на тему о движении и множестве), направленные против движения и множественности вещей, и рассуждения собственно софистов, и все те софизмы, которые открывались в других философских школах. Это говорит о том, что софизмы не были изобретением одних софистов, а являлись скорее чем-то обычным для многих школ античной философии. Аристотель называл софизмом «мнимые доказательства», в которых обоснованность заключения кажущаяся и обязана чисто субъективному впечатлению, вызванному недостаточностью логического анализа. Убедительность на первый взгляд многих софизмов, их «логичность» обычно связана с хорошо замаскированной ошибкой, с использованием, например, «неразрешённых» или даже «запрещённых» правил или действий.
Современный софизм, основной задачей которого является манипуляция общественным сознанием, существует в многочисленных формах. Современные софисты, прежде всего, - специалисты по пиару. Работа, которых заключается в навязывании обществу тех или иных политических деятелей.
В обычном и распространенном понимании софизм - это умышленный обман, основанный на нарушении правил. Но обман тонкий и завуалированный. Цель софизма – выдать ложь за истину.
В нашей работе мы рассматриваем математические софизмы.
2.1. Софизмы и типичные ошибки в них
Математический софизм - удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки.
История математики полна неожиданных и интересных софизмов, разрешение которых порой служило толчком к новым открытиям. Математические софизмы приучают внимательно и настороженно продвигаться вперед, тщательно следить за точностью формулировок, правильностью записи чертежей, за законностью математических операций. Поиск и нахождение ошибок в софизме способствует пониманию математики в целом и развивает логическое мышление.
К типичным ошибкам в софизмах относятся:
· запрещенные действия;
· пренебрежение условиями теорем, формул и правил;
· ошибочный чертеж;
· опора на ошибочные умозаключения.
Нередко, ошибки, допущенные в софизме, настолько умело скрыты, что даже опытный математик не сразу их выявит. Именно в этом и проявляется связь математики и философии в софизмах.
2.2. Математические софизмы
Математические софизмы делятся на:
1. Арифметические софизмы - это числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда.
Пример: « Дважды два - пять!».
Возьмем в качестве исходного соотношения следующее очевидное равенство: 4:4= 5:5. После вынесения за скобки общего множителя из каждой части равенства будем иметь: 4∙(1:1)=5∙(1:1) или (2∙2)(1:1)=5(1:1) Наконец, зная, что 1:1=1, из соотношения 4(1:1)=5(1:1) устанавливаем: 4=5, 2∙2=5.
Ошибка.
Распределительный закон умножения применяется только для сложения и вычитания: ав + ас = а(в + с).
2. Алгебраические софизмы - намеренно скрытые ошибки в уравнениях и числовых выражениях.
Алгебра — один из больших разделов математики, принадлежащий наряду с арифметикой и геометрией к числу старейших ветвей этой науки. Задачи, а также методы алгебры отличаются от других отраслей математики.
Приёмы эти заключаются обычно в составлении и решении уравнений.
Пример: «Любое отрицательное число больше положительного, имеющего то же абсолютное значение».
Этот софизм основан на очевидной истине: «Если в равенстве числитель левой дроби больше знаменателя в n раз, то и в правой части равенства соотношение внутри дроби будет таким же».
Напишем следующие равенства:
![]() и
и ![]() ; т.е.
; т.е. ![]() .
.
Другими словами, если в левой части равенства + a > - a, то и в правой части равенства должно соблюдаться то же соотношение.
Т.е. – a > + a.
Ошибка.
Чтобы получить из равенства +a > -a равенство –a>+a, нужно первое равенство умножить на -1, но при это нужно сменить знак неравенства (–a<+a).
3.Геометрические софизмы – это умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость, абсурд или противоречивое утверждение, связанное с геометрическими фигурами и действиями над ними.
Пример: «Из точки на прямую можно опустить два перпендикуляра.»
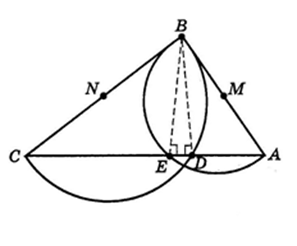
Рассмотрим треугольник АВС.
Разделим стороны АВ и ВС пополам точками M и N. На этих сторонах, как на диаметрах, опишем окружности с центрами в точках M и N. Окружности пересекут сторону АС в точках D и E.
Углы AEB и BDC опираются на диаметры АВ и ВС соответственно, значит они прямые.
Следовательно, отрезки BD и BE, исходящие из точки В, будут перпендикулярны, стороне АС, следовательно, из точки В можно опустить два перпендикуляра на сторону АС.
Ошибка.
Действительно, опустив из B перпендикуляр на AC , получим два прямоугольных треугольника, гипотенузами которых будут стороны BC и AB, и если вокруг этих треугольников описать окружности, их гипотенузы будут диаметрами. Неправильный чертеж. Известно, что окружности, построенные на двух сторонах треугольника как на диаметрах, пересекаются в одной точке, лежащей на третьей стороне.
2.3. Разбор математических софизмов
В математических софизмов выделяются 6 основных ошибок:
1. Деление на 0.
Софизм №1 «Пять равно шести».
Возьмем тождество 35+10-45=42+12-54.
В каждой части вынесем за скобки общий множитель:
5(7+2-9)=6(7+2-9).
Теперь, получим, что 5=6.
Ошибка.
При делении верного равенства 5(7+2-9)=6(7+2-9) на число 7+2-9, равное 0. Этого нельзя делать. Любое равенство можно делить только на число, отличное от 0.
Софизм №2 «Уравнение x-a=0 не имеет корней».
Дано уравнение x –a = 0. Разделив обе части этого уравнения на x-a, получим, что 1 = 0. Поскольку это равенство неверное, то это означает, что исходное уравнение не имеет корней.
Ошибка.
Поскольку x = a – корень уравнения, то, разделив на выражение x-a обе его части, мы потеряли этот корень и поэтому получили неверное равенство 1=0.(x-a=0 -на ноль делить нельзя).
2. Неправильные выводы из равенства дробей;
Софизм №3 «Отклонение от алгоритма может привести к приобретению посторонних корней данного уравнения».

3. Неправильное извлечение квадратного корня из квадрата выражения.
Софизм №4 ![]() =
= ![]() =
= 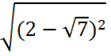 =2-
=2-![]()
Ошибка.
При
вычислении квадратного корня 2-![]() < 0
< 0
![]() =
= ![]() =
= 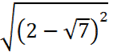 =ç2-
=ç2-![]() ç=
ç= ![]() - 2
- 2
4. Нарушения правил действия с величинами.
Софизм №5 «Один метр не равен ста сантиметрам».
Известно, что любые два равенства можно перемножить почленно, не нарушая при этом равенства, т. е. если а = b и c = d, то ac = bd. Применим это положение к двум очевидным равенствам: 1 метр = 100сантиметрам и 10 метров = 1000 сантиметрам. Перемножая эти равенства почленно, получим 10 метров = 100000 сантиметров и, разделив последнее равенство на 10, получим, что 1 метр = 10000 сантиметров .
Ошибка.
Она состоит в нарушении правила действий с именованными величинами: все действия, совершаемые над величинами, необходимо совершать также и над их размерностями.
«Один рубль не равен ста копейкам».
Возьмем верное равенство: 2р. = 200к. и возведем его по частям в квадрат. Мы получим: 4 р. = 40 000 к.
Ошибка.
Здесь надо вспомнить, что возведение в квадрат денег не имеет смысла. В квадрат возводятся числа, а не величины.
5. Проведение преобразований над математическими объектами, не имеющими смысла.
Софизм №6 «Два неодинаковых натуральных числа равны между собой».
Решим систему двух уравнений:
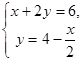 .
.
Сделаем это подстановкой у из 2-го уравнения в 1-е, получаем х+8-х=6, откуда 8=6.
Ошибка
Уравнение (2)
можно записать как х+2у=8, так, что исходная система запишется в виде: ![]() .
.
В этой системе уравнений коэффициенты при переменных одинаковы, а правые части не равны между собой, из этого следует, что система несовместна, т.е. не имеет ни одного решения.
Графически это
означает, что прямые у=3-![]() и у=4-
и у=4-![]() параллельны и не совпадают. Перед
тем, как решать систему линейных уравнений, полезно проанализировать, имеет ли
система единственное решение, бесконечно много решений или не имеет решений
вообще.
параллельны и не совпадают. Перед
тем, как решать систему линейных уравнений, полезно проанализировать, имеет ли
система единственное решение, бесконечно много решений или не имеет решений
вообще.
6. Неравносильный переход от одного неравенства к другому.
Софизм №7 «Если А больше В, то А всегда больше, чем 2В».
Возьмем два произвольных положительных числа А и В, такие, что А>В. Умножив это неравенство на В, получим новое неравенство АВ>В*В, а отняв от обеих его частей А*А, получим неравенство АВ-А*А>В*В-А*А, которое равносильно следующему: А(В-А)>(В+А)(В-А). (1)
После деления обеих частей неравенства (1) на В-А получим, что А>В+А (2), А прибавив к этому неравенству почленно исходное неравенство А>В, имеем 2А>2В+А, откуда А>2В. Итак, если А>В, то А>2В. Это означает, к примеру, что из неравенства 6>5 следует, что 6>10.
Ошибка.
Здесь совершен неравносильный переход от неравенства (1) к неравенству (2). Действительно, согласно условию А > В, поэтому В – А < 0.Это означает, что обе части неравенства (1) делятся на отрицательное число. Но согласно правилу преобразования неравенств при делении или умножении неравенства на одно и то же отрицательное число знак неравенства необходимо изменить на противоположный. С учетом сказанного из неравенства (1) вместо неравенства (2) получим неравенство А<В+А, прибавив к которому почленно исходное неравенство В<А, получим просто исходное неравенство А+В<В+2А.
7. Выводы и вычисления по неверно построенным чертежам;
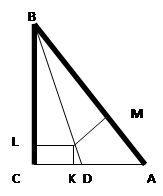 Софизм
№8 ∟С=90, ВД - биссектриса угла СВА, СК=КА, ОК перпендикулярна СА, О -
точка пересечения прямых ОК и ВД, ОМ перпендикулярна АВ, ОL перпендикулярна ВС.
Софизм
№8 ∟С=90, ВД - биссектриса угла СВА, СК=КА, ОК перпендикулярна СА, О -
точка пересечения прямых ОК и ВД, ОМ перпендикулярна АВ, ОL перпендикулярна ВС.
∟С=90, ВД - биссектриса ∟ СВА, СК=КА, ОК ^ СА, О - точка пересечения прямых ОК и ВД, ОМ ^ АВ, ОL ^ ВС.
Имеем: D LВО=D МВО, ВL = ВМ, ОМ = ОL = СК = КА,
D КОА=D ОМА (ОA- общая сторона, КА = ОМ, ∟ ОКА и
∟ ОМА - прямые), ∟ ОАК = ∟ МОА, ОК = МА = СL, ВА = ВМ + МА, ВС = ВL + LС, но ВМ = ВL, МА = СL, и потому ВА = ВС
Ошибка.
 |
Рассуждения о том, что катет равен гипотенузе, опирались на ошибочный чертеж. Точка пересечения прямой, определяемой биссектрисой ВD и серединного перпендикуляра к катету АС, находится вне треугольника АВС.
2.4. Логические софизмы
Один из видов математических софизмов является логический софизм.
Пример № 1: «Полупустое или полуполное».
Полупустое есть то же, что и полуполное. Если равны половины, значит, равны и целые. Следовательно, пустое есть то же, что и полное
Ошибка.
Полупустое не является половиной чего либо пустого, а является чем либо наполовину наполненным.
Пример №2: «Когда же учиться?»
1. По ночам занятий нет, половина суток свободна.
Остаётся: 365-182=183 дня. 2.
2. В школе ученики занимаются половину дня, значит, вторая половина (или четвёртая часть суток) может быть свободна. Остаётся:183-183:4=137 дней. 3. В году 52 воскресенья. Из них на каникулы приходится 15 дней, таким образом, выходных в учебном году52-15=37 дней.
Итого остаётся 137-37=100 дней.
4. Есть ещё каникулы: осенние (5 дней), зимние (10 дней), весенние (7 дней), летние (78 дней). Всего 5+10+7+78=100 дней.
5. Итак, школьники заняты в году 100-100=0 дней. Когда же учиться?!
2.5. Источники софизмов
Источниками софизмов может выступать терминология, которая используется во время спора. Многие слова имеют несколько смыслов (доктор может быть врачом или же научным сотрудником, имеющим ученую степень), за счет чего и происходит нарушение логики. Софизмы в математике, например, основаны на изменении чисел путем перемножения их и последующего сравнения исходных и полученных данных. Неправильное ударение тоже может быть оружием софиста, ведь множество слов при изменении ударения меняют и смысл. Построение фразы иногда очень запутанно, как, например, «два умножить на два плюс пять». В данном случае непонятно имеется ли в виду сумма двойки и пятерки, умноженная на два, или же сумма произведения двоек и пятерки.
Разбор и решение любого рода математических задач, а в особенности нестандартных, помогает развивать смекалку и логику. Математические софизмы относятся именно к таким задачам.
III. «Софизмы из наших школьных тетрадей»
Цель практической работы: проанализировать наши тетради для контрольных работ по математике, выявить софизмы и найти ошибки, заключенные в них.
Известная истина гласит «Умные люди учатся на чужих ошибках». В математике приходится учиться, в основном, на собственных ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь необходимая и полезная. Нужно лишь правильно относиться к ошибке, правильно ее использовать.
Обидно получать плохие оценки из-за ошибок «на ровном месте». Глупые ошибки – проблема многих учеников: случайная потеря знака, скобки, необоснованное изменение чисел, пропуски переменных и всевозможные ляпы. Сами ученики не могут объяснить, чем вызваны эти ошибки.
С помощью задач, содержащих противоречие в условии, можно предупредить ошибки учащихся, связанные с работой над математическими объектами, которые не существуют при заданных условиях. Если учащиеся решают задачу, работая с несуществующими объектами, то происходит выход за границы применяемости теоремы, свойства и т.д. Эти ошибки возникают по той причине, что большинство учебных задач содержит информацию непротиворечивую и приводящую к единственному решению.
|
Софизм |
Ошибка |
|
№1 |
Неправильный порядок действий:
|
|
№2
|
Нарушение правил приведения дробей к общему знаменателю:
|
|
|
|
|
№4
ОДЗ: все числа, кроме 2.
Умножим обе части уравнение на x-2 2 Разложили на множители квадратный трёхчлен 2 = (x - 2) (2x + 1) (x - 2) (2x + 1) = x2 (x - 2) Разделим обе части уравнения на х - 2,получим 2x + 1 = x2 X2 -2x -1 =0 Д=4+4=8 X1= X2=1- Корни удовлетворяют ОДЗ. Ответ:
1- |
Ошибка: при делении уравнения (x-2)(2x+1)=x2 (x-2) , на x-2произошла потеря корня Верное решение: x2 (x-2) – (x-2) (2x+1)=0 (x-2) (x2-2x-1)=0 х - 2=0 или x2 - 2x - 1=0 x = 2 или x1=1 + Уравнение имеет три корня: 2; 1 +
Но 2 - не удовлетворяет ОДЗ. Ответ:
1 +
|
|
№5
|
Верное
решение:
Ошибка:
Правило: при умножении степеней с одинаковым основанием, показатели складываются, а основание остаётся прежним.
|
|
№6 Периметр треугольника равен 6, его стороны относятся как 1:2:3. Чему равна его средняя по величине сторона. |
Задача провоцирует учащихся на то, чтобы дать ответ 2. При этом не выполняется неравенство треугольника. |
|
|
Известные элементы (радиус окружности и угол, образуемый радиусом ОА с основанием АВ вписанного равнобедренного треугольника), заданные в условии этой задачи, определяют две сложные фигуры: а) окружность центра О радиуса 8 см и вписанный в эту окружность остроугольный равнобедренный треугольник АВС; б) та же окружность и вписанный в нее тупоугольный равнобедренный треугольник АВС1.
|
Заключение
Исторические сведения о софистике и софистах помогли нам разобраться, откуда же все-таки началась история софизмов. Вначале мы думали, что софизмы бывают исключительно математические. Причем в виде конкретных задач, но, начав исследование в этой области, мы поняли, что софистика - это целая наука, а именно математические софизмы - это лишь часть большого течения.
Разбор софизмов развивает логическое мышление, помогает сознательному усвоению изучаемого материала, воспитывая вдумчивость, наблюдательность, критическое отношение к тому, что изучается. Кроме того, разбор софизмов увлекателен. Мы с большим интересом воспринимали софизмы, чем труднее софизм, тем большее удовлетворение доставляет его разбор. Порой сам попадаешься на уловки софиста.
Гипотеза, которую мы ставили в начале работы «Если в процессе обучения математике целенаправленно и систематически организовывать работу учащихся над типичными ошибками, на примере софизмов, то это будет способствовать повышению качества математической подготовки учащихся», подтвердилась.
Благодаря знанию софизмов можно научиться искать ошибки в рассуждениях других, научится грамотно строить свои рассуждения и логические объяснения. Когда ребенок раз притронется к горячему предмету, то впоследствии он постарается этого не делать. Он будет много осторожнее. Так, изучающий математику, впоследствии проявит больше осторожности, чтобы не повторить осознанную ошибку. Значит, математические софизмы заставляют внимательно и настороженно продвигаться вперед, тщательно следить за точностью формулировок, правильностью записей и чертежей, за допустимостью обобщений, за законностью выполняемых операций. Все это нужно и полезно. Только очень сухого человека не может увлечь интересный софизм. Как приятно бывает обнаружить ошибку в математическом софизме и тем как бы восстановить истину в ее правах. Математические софизмы показали нам, как важно строго соблюдать правила и формулировки теорем при логических умозаключениях.
Нам было очень интересно работать над данной темой. Мы создали сборник «Софизмы из наших школьных тетрадей».
Задания, предложенные нами в работе, можно использовать как на уроках алгебры и геометрии, так и на внеклассных мероприятиях.
Список литературы
1. «Софисты» под редакцией Б.С. Чернышева
2. «Софизмы. Алгебра. Геометрия. Тригонометрия» под редакцией Т.Н. Михеевой
3. http://gamzatovasm.ru/node/88 - Алгебраические софизмы
4. http://reshit.ru/sofizm - Геометрические софизмы
5. http://sophisms.ucoz.ru/index/arifmeticheskie_sofizmy/0-6 - Арифметические софизмы
6. http://referatwork.ru/category/logika/view/131832_sofizmy - Логические софизмы
7. https://ru.wikipedia.org/wiki/Апории_Зенона - Апории Зенона
Приложения
 Рис. 1 Протагор
Рис. 1 Протагор
 Рис.
2 Сократ
Рис.
2 Сократ
 Рис. 3 Аристотель
Рис. 3 Аристотель
1. Верно ли равенство 7 = 8?
35 + 14 – 49 = 40 + 16 - 56
7(5 + 2 - 7)=8(5 + 2 - 7)
Следовательно, 7 = 8
Ошибка.
Обе части равенства разделили на (5 + 2 - 7), но нарушено правило, что на "0" делить нельзя (5 + 2 – 7 = 0)
2.
Некто утверждал, что 45-45=45. Рассуждал он так: «Записываем вычитаемое в виде суммы последовательных натуральных чисел от 1 до 9, а уменьшаемое в виде суммы тех же чисел, но взятых в обратном порядке (от 1 до 9):
9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9
8 + 6 + 4 + 1 + 9 + 7 + 5 + 3 + 2
Будем последовательно вычитать числа второй строки из чисел первой. Например, так как 9 из 1 вычесть нельзя, то занимаем единицу из двух, имеем 11-9=2 и т. д. Теперь нетрудно установить,
8 + 6 + 4 + 1 + 9 + 7 + 5 + 3 + 2 = 45.
Итак, 45 – 45 = 45.
Ошибка состоит в том, что занимаемую единицу возводили в ранг десятка.
3.Меньшее число больше, чем большее».
Очевидно,что7 > 5 и что – 8 = - 8
Тогда:7 – 8 > 5 - 8 или – 1 > - 3
Это не противоречит основному понятию об отрицательных величина, на основании которого мы считаем меньшей ту отрицательную величину, численное значение которой больше, и наоборот.
Умножим обе части последнего неравенства на (- 4).
Получим (-1)*(-4)>(-3)*(-4) или 4 > 12
Ошибка.
При умножении неравенства на отрицательное число, знак неравенства изменяется на противоположный.
1.«Отрицательное число больше положительного».
Возьмем два положительных
числа а и с. Сравним два отношения: ![]() и
и ![]()
Они равны, так как каждое из них равно –(а/с). Можно составить
пропорцию: ![]()
Но если в пропорции предыдущий член первого отношения больше последующего, то предыдущий член второго отношения также больше своего последующего. В нашем случае а > - с, следовательно, должно быть –а > с, т.е. отрицательное число больше положительного.
Ошибка.
Данное свойство пропорции может оказаться неверным, если некоторые члены пропорции отрицательны.
2. « Если одно число больше другого, то эти числа равны»
Возьмем два произвольных числа т и п, такие, что m > n , и другие три произвольных числа а, b и с, сумма которых равна d, т.е. а + b + c = d. Умножив обе части этого равенства на n, а затем на m, получим:
ma + mb + mc = md, na + nb + nc = nd.
Сложив почленно равенства:
ma + mb + mc = md и nd = na + nb + nc
получим: ma + mb + mc + nd = na + nc + nb + md.
Перенося здесь nd вправо, а md влево, имеем
ma + mb + mc – md = na + nb + nc - nd.
Вынося слева число m, а справа число n за скобки, придем к соотношению m (a + b + c - d) = n (a + b + c - d).
Разделив обе части последнего равенства на
(a + b + c - d), находим, что m = n.
Ошибка.
a + b + c – d =0, на ноль делить нельзя.
4. «Любое число равно нулю»
Возьмем произвольное положительное число а и рассмотрим сумму х бесконечного числа слагаемых, равных а: х = а + а + а + а +… Очевидно, что мы можем представить эту сумму как х = а + (а + а + а +….) в которой сумма, стоящая в скобках, также равна х как сумма бесконечного числа слагаемых, равных а. Так что можем записать, что х = а + х, откуда заключаем, что а=0.
Ошибка допущена в равенстве (1) , в котором бесконечная сумма чисел а обозначена конечным числом х.
4.
Решим систему двух уравнений:
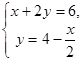
Сделаем это подстановкой у из 2го уравнения в 1, получаем х + 8 - х = 6, откуда
8 = 6
Ошибка.
Уравнение (2) можно записать как х + 2у = 8,
так что исходная система запишется в виде: ![]()
В этой системе уравнений коэффициенты при переменных одинаковы, а правые части не равны между собой, из этого следует, что система несовместна, т.е. не имеет ни одного решения.
Графически это
означает, что прямые у=3 - ![]() и у = 4
-
и у = 4
-![]() параллельны и не совпадают. Перед
тем, как решать систему линейных уравнений, полезно проанализировать, имеет ли
система единственное решение, бесконечно много решений или не имеет решений
вообще.
параллельны и не совпадают. Перед
тем, как решать систему линейных уравнений, полезно проанализировать, имеет ли
система единственное решение, бесконечно много решений или не имеет решений
вообще.
5. «Если “a” больше “b”, то “a” всегда больше, чем “2b”»
Возьмем два произвольных положительных числа a и b, такие, что a > b. Умножив это неравенство на b, получим новое неравенство:
ab > bb, а отняв от обеих его частей a·a, получим неравенство:
ab-aa > bb - aa, которое равносильно следующему: a(b-a) > (b+a)(b-a).(1)
После деления обеих частей неравенства (1) на b-a получим, что a > b+a (2),
Прибавив к этому неравенству почленно исходное неравенство a> b, имеем
2a > 2b + a, откуда a > 2b.
Итак, если a > b, то a > 2b.
Ошибка совершена при переходе от равенства (1) к (2).
Т.к. a > b, то b - a<0, следовательно, при делении неравенства (1) на b – a, мы должны поменять знак неравенства на противоположный.
6.«Единица равна двум»
Простым вычитанием легко убедиться в справедливости равенства
1 - 3 = 4-6.
Добавив к обеим частям этого равенства число 9/4, получим новое равенство
1 - 3 + 9/4 = 4 - 6 + 9/4,
в котором, как нетрудно заметить, правая и
левая части представляют собой полные квадраты, т. е. (1 - 3/2)![]() =(2 - 3/2)
=(2 - 3/2)
Извлекая из правой и левой частей предыдущего равенства квадратный корень, получаем равенство: 1 - 3/2 =2 - 3/2
откуда следует, что 1=2.
Ошибка.
По определению ![]() представляет собой некоторое
неотрицательное число, которое, будучи возведено в квадрат, даст х. Ясно, что
этому определению удовлетворяют два числа, а именно х и -х. Итак, если число х
неотрицательно (х ≥ 0), то
представляет собой некоторое
неотрицательное число, которое, будучи возведено в квадрат, даст х. Ясно, что
этому определению удовлетворяют два числа, а именно х и -х. Итак, если число х
неотрицательно (х ≥ 0), то![]() = х; если же число х отрицательно (х<0), то есть число –х положительно, то
= х; если же число х отрицательно (х<0), то есть число –х положительно, то ![]() = - x. Отсюда заключаем, что
= - x. Отсюда заключаем, что ![]() (свойство
арифметического квадратного корня), что не учитывается в содержании этих
софизмов и приводит к ложным выводам.
(свойство
арифметического квадратного корня), что не учитывается в содержании этих
софизмов и приводит к ложным выводам.
7. «Всякое число равно своей половине.»
Запишем очевидное для любого числа a тождество a2- a2= a2- a2,где а - любое число.
Вынесем a в левой части за скобку, а правую часть разложим на множители по формуле разности квадратов, получим
a(a – a) = (a + a)(a - a).
Разделив обе части на a - a, получим a = a + a, или a=2a.
Разделим на 2 и получим а = а/2
Ошибка.
Мы делим обе части на ноль, а деление на ноль запрещено
1. ![]() , а длина всякой окружности равна ее
диаметру.
, а длина всякой окружности равна ее
диаметру.
Построим
на отрезке МN как на диаметре окружность. Радиус окружности обозначим через ![]() . Тогда длина окружности будет
равна:
. Тогда длина окружности будет
равна: ![]()
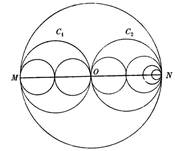
Поделим
MO и NO пополам точками ![]() и
и![]() и построим новые окружности с центрами в
этих точках радиусами
и построим новые окружности с центрами в
этих точках радиусами ![]() .
.
Найдем
длины новых окружностей: ![]()
Сумма
их длин будет равна ![]()
т.е. равна длине большой окружности C.
Таким же образом будем строить окружности и далее и находить сумму их длин.
Так,
сумма длин окружностей ![]() и
и ![]() . и будет равна
. и будет равна![]()
Продолжая
деление далее, мы будем делить диаметр NM на все меньшие части, а радиусы новых
окружностей будут равны ![]() и т.д. При этом сумма длин всех этих
окружностей всегда будет равна
и т.д. При этом сумма длин всех этих
окружностей всегда будет равна ![]() .
.
Так
как число делений большого диаметра будет бесконечно большим, окружности станут
настолько малыми, что сольются с диаметром, и сумма их длин в пределе будет
равна длине диаметра, так что она будет равна![]() .
.
С
другой стороны, сумма длин этих окружностей постоянна и равна ![]() , следовательно,
, следовательно,![]()
Из
этого равенства получаем ![]() или, деля на
или, деля на ![]() :
:![]()
Ошибка: Так как сумма
длин бесконечно малых окружностей постоянна, то она и в пределе равна ![]() . Пусть
. Пусть ![]() — длина малой
окружности
— длина малой
окружности![]() ,
— ее радиус. Как бы такая окружности ни была мала, всегда имеем
,
— ее радиус. Как бы такая окружности ни была мала, всегда имеем ![]() или
или
![]()
Отсюда
видим, что эта бесконечно-малая окружность никогда не будет равна своему
диаметру ,![]() что следовало бы из результата софизма.
что следовало бы из результата софизма.
2.« Отрезки параллельных прямых, заключенные между сторонами угла, равны»
Рассмотрим произвольный угол с вершиной в точке Е и пересечем их стороны двумя параллельными прямыми, отрезки которых АВ и CD заключены между сторонами этого угла.
Как известно параллельные прямые отсекают от сторон угла пропорциональные отрезки, следовательно, АЕ : CE = BE : DE,
Откуда АЕ·DE = BE·CE
Умножив обе части последнего равенства на отличную от нуля разность (АВ –CD), запишем
AE·DE·AB - AE·DE·CD = AE·DE·CD - BE·CE·CD,
или
AB(AE·DE - BE·CE) = CD(AE·DE - BE·CE)
Разделив обе части последнего равенства на (AE·DE - BE·CE), получим равенство АВ=CD.
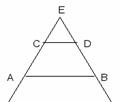
Ошибка.
AE·DE - BE·CE=0
3.Все треугольники равнобедренные.
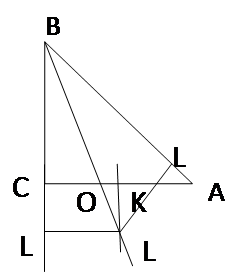
Рассмотрим произвольный ∆АВС (рис.2).
Проведем в нем биссектрису угла B и серединный перпендикуляр к стороне АС. Точку их пересечения обозначим через О.
Из точки O опустим перпендикуляр OD на сторону АВ и перпендикуляр ОЕ на сторону ВС. Очевидно, что ОА = ОС и OD = ОЕ. Но тогда ∆AOD = ∆СОЕ по катету и гипотенузе. Поэтому ∟DAO = ∟ЕСО. В то же время ∟ОАС = ∟ОСА, так как ∆АОС -равнобедренный.
Получаем: ∟ВАС = ∟DAO + ∟ОАС = ∟ЕСО + ∟ОСА = ∟ВСА
Итак, угол ВАС равен углу ВСА, поэтому ∆АВС - равнобедренный: АВ=ВС.
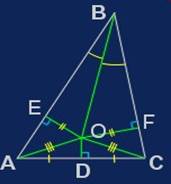
Ошибка. При построения чертежа. Серединный перпендикуляр к стороне и биссектриса противоположного ей угла для не равнобедренного треугольника, пересекаются вне этого треугольника.
Приложение 4.
Логические софизмы.
1. Лекарство, принимаемое больным, есть добро. Чем больше делать добра, тем лучше. Значит, лекарств нужно принимать как можно больше".

2. Одна песчинка не есть куча песка. Если n песчинок не есть куча песка, то и n+1 песчинка – тоже не куча. Следовательно, никакое число песчинок не образует кучу песка. К этому парадоксу можно сделать следующий комментарий: метод полной математической индукции нельзя применять, как показывает парадокс, к объёмно неопределённым понятиям, каковым является понятие «куча песка».

3. Что появилось раньше: яйцо или курица. Для того чтобы появилось яйцо, должна существовать курица, но ведь курица может вылупиться только из яйца, а значит, первичным является именно оно.

4.«Может ли всемогущий маг создать камень, который не сможет поднять?»
Если не может – значит, он не всемогущий. Если может – значит, всё равно не всемогущий, т.к. он не может поднять это камень.

6.В мире нет ни одного человека, говорящего на моем языке; или короче: ни одного человека, говорящего; или еще короче: ни одного человека.

Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.