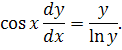Некоторые аспекты психолого-педагогического сопровождения проектно-исследовательской деятельности учащихся в учебно-воспитательном процессе.

Некоторые аспекты психолого-педагогического сопровождения проектно-исследовательской деятельности учащихся в учебно-воспитательном процессе.

 

        Современное общество предъявляет новые требования к образованию в плане формирования личности, готовой к решению поставленных перед ней проблем с по­зиции личностно-творческой сопричастности. Это обусловлено объективными факторами. Че­ловечество сегодня претерпевает ряд глубинных трансформаций, меняющих облик цивилизации в це­лом, и только яркие творческие личности могут найти выход из экономических, политических и социальных проблем сегодняшнего дня; личности с развитым твор­ческим мышлением, способные к поиску новых пу­тей в обществе. Исходя из этого, существует запрос на личность, способную уходить своей дея­тельностью от стереотипов, умеющую адаптировать­ся в изменяющихся условиях. По мнению психологов, современные подростки отличаются повышенной интеллектуальной активностью, которая стимулируется не только естественной возрастной любознательностью, но и желанием развить когнитивные стратегии, демонстрировать окружающим свои способности, получить высокую оценку с их стороны. Подростки могут формулировать гипотезы, рассуждать пред­положительно, исследовать и сравнивать между собой различ­ные альтернативы при решении одних и тех же задач. Сфера познавательных, в том числе учебных, интересов подростков выходит за пределы школы и приобретает форму познаватель­ной самодеятельности — стремления к поиску и приобретению знаний, к формированию полезных умений и навыков, к дальнейшему развитию когнитивных стратегий. Стремление к самообразованию — характерная особенность и подростково­го, и раннего юношеского возраста способствует. Согласно теории Пиаже, признаком когнитивных изменений у подростка является формирование у него абстрактного мышления. Абстрактное мышление требует способности формулировать, проверять и оценивать гипотезы. Оно предполагает манипулирование не только известными элементами, которые можно проверить, но и вещами, противоречащими фактам. У подростков также возрастает способность планировать и предвидеть. Поэтому в условиях обновляющейся школы требуются такие методы обучения, которые фор­мировали бы активную, инициативную позицию учащихся в учении; развивали бы общеучебные умения и навыки: исследовательские, рефлексив­ные, самооценочные; формировали бы творчес­кое мышления учащихся и на этой основе приоритетно направлены на формирование и разви­тие творческой личности. Ведущее место среди таких методов принадлежит учебному проекту и исследовательской деятельности.

        Исследовательская деятельность является интегративным дидактическим средством формирования творческого мышления, которое позволяет укреп­лять способности нестандартно мыслить, выра­батывать и развивать рефлексивные, исследова­тельские, презентационно - творческие умения, связанные с открытием субъективно нового знания, с реше­нием задач, с творческим преобразованием дей­ствительности; деятельность, направленная на создание новых идей, отвечающих конкретной цели, созданию проекта, проведению исследования. Учебный проект и исследовательская деятельность предполагают: наличие проблемы, требующей интегрированных знаний и исследовательского поиска ее решения; практическую, теоретическую, познавательную значимость предполагаемых результатов; самостоятельную деятельность ученика; структурирование содержательной части проекта (исследования) с указанием поэтапных результатов; использование исследовательских методов, определение проблемы, вытекающих из нее задач исследования, выдвижения гипотезы их решения. Обсуждение методов исследования, оформление конечных результатов. Анализ полученных данных, подведение итогов, корректировка, выводы. Использование метода проекта и исследовательской деятельности предусматривает хорошо продуманное, обоснованное сочетание методов, форм и средств обучения. Использование проектной технологии в работе требует от учителя серьезной подготовительной работы. В методической литературе выделяют следующие этапы работы.

Содержание работы на этапе	Деятельность учащихся	Деятельность учителя
Подготовительный этап
а) выбор темы и целей	Обсуждают тему с учителем и	Знакомит с сутью проектной
проекта, исследования (через проблемную	получают при необходимости	технологии и мотивирует учащихся.
ситуацию, беседу,	дополнительную	Помогает в постановке целей
анкетирование и т.д.)	информацию, устанавливают
б) определение количества	цели
участников проекта(исследования), состава
группы
Планирование работы
а) определение источников	Вырабатывают план	Предлагает идеи, высказывает
информации	действий. Формулируют	предположения, определяет сроки
б) планирование способов	задачи.	работы (поэтапно)
сбора и анализа информации
в) планирование итогового
продукта (формы
представления результата)
Продукт:
- отчет (устный, письменный,
устный с демонстрацией
материалов)
- издание сборника, фильма,
макета - организация
конференций и т.д.
г) установление процедур и
критериев оценки процесса
работы, результатов
д) распределение
обязанностей среди членов
команды
Исследовательская деятельность
Сбор информации, решение	Проводят исследования,	Наблюдает, советует, косвенно
промежуточных задач.	решая промежуточные задачи	руководит деятельностью,
Основные формы работы:		организует и координирует в случае
интервью, опросы,		необходимости отдельные этапы
наблюдения, изучение		проекта, исследования.
литературных источников,
исторического материала,
и т.д.. Организация
экскурсий, экспериментов,
экспедиций и т.д.
Результаты или выводы
Анализ информации. Формулировка выводов. Оформление результата.	Анализируют информацию. Оформляют результаты.	Наблюдает, советует.
Предоставление готового продукта
Представление разнообразных форм результата работы.	Отчитываются, отстаивают свою точку зрения, делают окончательные выводы.	Слушает. задает вопросы в роли рядового участника.
Оценка процесса и результатов работы
	Участвуют в оценке путем коллективного обсуждения и самооценок.	Оценивает усилия учащихся, креативность мышления, качество использования источников, потенциал продолжения работы по выбранному направлению, качество отчета

 

План работы:

I. Теоретические аспекты методов решения дифференциальных уравнений,         изучаемых в школьном курсе.

1.1  Анализ учебника «Алгебра и начала анализа» автор А. Н. Колмогоров:

Уравнения показательного роста.

Уравнения гармонических колебаний.

1.2  Решение заданий № 568 – 573 из учебника «Алгебра и начала анализа» автор А. Н. Колмогоров.

II.    Обыкновенные дифференциальные уравнения Л.С. Понтрягина.

2.1  Вклад Л.С.Понтрягина в методы решения дифференциальных уравнений.

2.2  Уравнения показательного роста в книге Л.С.Понтрягина.

2.3  Уравнения гармонических колебаний в книге Л.С.Понтрягина.

2.4  Уравнения в полных дифференциалах.

2.5  Дифференциальное уравнение с разделяющимися переменными.

2.6  Решение заданий № 568-573 из учебника  «Алгебра и начала анализа» автор А. Н. Колмогоров методами Л.С. Понтрягина.

III.Практикум  для изучения методов решения дифференциальных уравнений, основанных на выводах Понтрягина.

3.1  Уравнения с разделяющимися переменными.

3.2  Уравнения в полных дифференциалах.

IV.   Выводы

V.           Список используемой литературы.

 

 ВВЕДЕНИЕ

 Мой интерес к участию во II городских физико-математических чтениях, посвященных 100-летию со дня рождения великого ученого Льва Понтрягина, вызван проведенной большой исследовательской работой по теме: « Уравнения показательного роста и гармонических колебаний».

 Изучив тему «Понятие о дифференциальных уравнениях» по учебнику «Алгебра и начала анализа» автор А. Н. Колмогоров, я обнаружила задания, которые автор предлагает решить с помощью нахождения производной. Это № 568 -573. Данные задания заставили меня задуматься над вопросом: «Можно ли решить указанные примеры, не прибегая к последовательному нахождению производной?».

Сложившаяся противоречивая ситуация с одной стороны в задачнике школьного учебника «Алгебра и начала анализа» автор А. Н. Колмогоров присутствуют упражнения на нахождение решения дифференциальных уравнений, а с другой стороны в учебнике не изложены методы решения дифференциальных уравнений, что создает большие трудности и заставляет искать пути решения данного противоречия.

 Цель исследования: выявление и исследование методов решения дифференциальных уравнений, позволяющих решать все упражнения по теме дифференциальные уравнения, предложенные в задачнике.

Объект исследования: методы решения дифференциальных уравнений: уравнений показательного роста и гармонических колебаний.

Предмет исследования: обыкновенные дифференциальные уравнения Л.С.Понтрягина.              

В качестве гипотезы было выдвинуто предположение, что использование знаний о методах решения дифференциальных уравнений, использование теории решения обыкновенных дифференциальных уравнений Понтрягина, позволяет решить упражнения, находящиеся в задачнике.

 

Для проверки гипотезы были поставлены следующие задачи:

1.      Провести теоретический анализ школьного учебника «Алгебра и начала анализа» автор А. Н. Колмогоров по теме: «Понятие о дифференциальных уравнениях: уравнения показательного роста и уравнения гармонических колебаний».

2.      Изучить работу Понтрягина «Обыкновенные дифференциальные уравнения» и решить задания № 568 -573 из школьного учебника «Алгебра и начала анализа» автор А. Н. Колмогоров методами, рассмотренными Л.С.Понтрягиным.

3.      Разработать практикум для изучения методов решения  дифференциальных уравнений, основанных на изученном материале и теории Понтрягина.

Были выделены следующие этапы исследовательской работы:

 

№ п/п	Этап исследования	Содержание деятельности	Срок исполнения
1	Проектировочный	Сбор и изучение исходной информации, необходимый для выполнения исследования	Сентябрь
2	Диагностический	Выявление методов решения дифференциальных уравнений (анализ учебника)	Октябрь
3	Практический	Изучение методов решения дифференциальных уравнений и теории обыкновенных дифференциальных уравнений Понтрягина	Ноябрь-декабрь
4	Контрольно-диагностический	Решение задач из школьного учебника изученными методами	Январь
5	Обобщающий	Создание практикума	Февраль

 

Актуальность данной работы состоит в рассмотрении, изучении и практическом применении методов решения дифференциальных уравнений: уравнений показательного роста и гармонических колебаний, основанных на выводах теории Понтрягина об обыкновенных дифференциальных уравнениях, позволяющих решить все задания из школьного учебника по теме «Понятие о дифференциальных уравнениях».  

      Поставив цель и определив задачи, необходимо отобрать способы и методы проведения дальнейшего исследования.   Знаменитый французский философ Рене Декарт по этому поводу заметил: «...Уж лучше совсем не помышлять об открытии каких бы то ни было истин, чем делать это без вся­кого метода, ибо совершенно несомненно то, что подобные бес­порядочные занятия и темные мудрствования помрачают естес­твенный свет и ослепляют ум»¹.

 ¹ Цит. по С. 90. Латыпов Н. Минута на размышление: Основы интеллекту­ального тренинга. - СПб.: Питер, 2005. - 336 с.

      От  выбора метода зависит все исследование, начиная с его организации и включая получение определенного результата. В данном случае уместно привести слова академика Ивана Пет­ровича Павлова: «Метод — самая первая и основная вещь. От ме­тода, от способа действия зависит вся серьезность исследования. Все дело в хорошем методе»². Не во всех исследовательских работах, представленных на конкурс, были выделены методы исследования, возможно данный этап работы вызывает затруднение, поэтому приведу краткую характеристику основных методов иссле­дования, встречающуюся в психолого-педагогической литературе³:

       Наблюдение-метод познания, состоящий в преднамеренном, целенаправ­ленном восприятии реальных объектов.

      Виды наблюдения: структурированное наблюдение — это наблюдение, осущест­вляемое по плану; неструктурированное наблюдение — это наблюдение, при котором определен только объект наблюдения;  полевое наблюдение — это наблюдение в естественной об­становке;  лабораторное наблюдение — это наблюдение, при ко­тором объект находится в искусственно созданных условиях;  непосредственное наблюдение — это наблюдение, в процессе которого объект прямо воздействует на органы чувств наблю­дателя; опосредованное наблюдение — это наблюдение, в ко­тором воздействие объекта на органы чувств наблюдателя опо­средовано прибором. Наблюдение осуществляют в соответствии со следующим ал­горитмом:

1.      Определение цели наблюдения.2. Выбор объекта наблюдения.3. Выбор способов достижения цели наблюдения 4. Выбор способа регистрации полученной информации.5. Обработка и интерпретация полученной информации.

      Эксперимент-метод познания, предполагающий целенаправленное изме­нение объекта для получения знаний, которые невозможно выявить в результате наблюдения.

Структура программы эксперимента

1. Актуальность исследования. 2. Проблема исследования.3. Объект и предмет исследования.4. Гипотеза исследования.5. Цель и задачи исследования.6. Этапы экспериментальной работы, ожидаемые результаты по каждому этапу в форме документов, основные методы иссле­дования.7. Научная новизна исследования.

1. Актуальность исследования. Актуальность исследования — это обоснование необходимости решения той или иной пробле­мы. Актуальность исследований характеризуется степенью рас­хождения между спросом на научные идеи, технологии, мето­дические рекомендации и предложениями, которые может дать наука и практика в настоящее время.

 ²  Павлов И.П. Лекции по физиологии. 1912-1913 гг. - М.: Изд-во АМН СССР, 1949.-С. 16.

      ³ Татьянченко Д.В., Воровщиков С.Г. Культура познания — познание культу-

ры. - Челябинск: Брегет, 1998. — 193 с.

 

 

2. Проблема исследования. В основе проблемы исследования лежит противоречие, которое необходимо разрешить в ходе эксперимента и которое обосновывалось при определении ак­туальности исследования.

3. Объект и предмет исследования. Объект исследования — это область изучения; предмет — это аспект изучения объекта.

4. Гипотеза исследования. Гипотеза исследования — это науч­но обоснованное предположение о разрешении проблемы.

5. Цели и задачи исследования. Цель исследования — это пред­полагаемая деятельность, промежуточные и конечные резуль­таты проверки гипотезы. Задачи - конкретизация цели иссле­дования, ее декомпозиция (расчленение).

6. Этапы экспериментальной работы, ожидаемые результаты по каждому этапу в форме документов, основные методы исследо­вания.

7. Научная новизна исследования. Новизна отражает обще­ственно значимые новые знания, факты, данные, полученные в результате исследования. Критерий новизны отражает содер­жательную сторону результата. В зависимости от результата на первый план может быть выдвинута теоретическая новизна (концепция, принцип и т.д.), практическая (правило, реко­мендация, методика, требование, средство и т.д.) или оба вида одновременно.

         Моделиро­вание: Модели — это материальные и мысленно представленные объ­екты, которые в процессе изучения замещают объект-ориги­нал, сохраняя некоторые важные для определенного исследо­вания свойства. Виды моделирования: 1. Материальное (предметное) моделирование:  физическое моделирование — это моделирование, при ко­тором реальный объект замещается на его увеличенную или уменьшенную копию, позволяющую проводить изуче­ние свойств объекта; аналоговое моделирование — это моделирование на анало­гии процессов и явлений, которые имеют различную фи­зическую природу, но одинаково описываемые формально (одними и теми же математическими уравнениями, логи­ческими схемами и т.п.). 2. Мысленное (идеальное) моделирование: интуитивное моделирование — это моделирование, основан­ное на интуитивном представлении об объекте исследова­ния, не поддающимся или не требующим формализации; знаковое моделирование — это моделирование, использу­ющее в качестве моделей знаковые преобразования како­го-либо вида: схемы, графики, чертежи, формулы, набор символов и т.д.

         Анкетирова­ние - метод опроса посредством самостоятельного заполнения опросного листа (т.е. анкеты) респондентом (т. е. опрашивае­мым) по указанным в нем правилам. В анкете могут использоваться следующие виды вопросов: Закрытый вопрос — это вопрос, на который в анкете приводит­ся полный набор вариантов ответов. Закрытые вопросы быва­ют альтернативные (т.е. предполагающие выбор только одного ответа) и неальтернативные (т. е. предполагающие выбор более одного ответа). Открытый вопрос — это вопрос, который не содержит подсказ­ки и не навязывает респонденту варианты ответов.

          Интервьюи­рование-метод опроса, осуществляемый в форме целенаправленной беседы по заранее подготовленному плану с каким-либо ли­цом или группой лиц, ответы которых на поставленные перед ними вопросы служат исходным источником информации. Различают два основных вида интервью: Формализованное интервью предполагает, что общение ин­тервьюера и респондента строго регламентировано детально разработанными вопросником и инструкцией. Свободное интервью (беседа) проводится без заранее под­готовленного опросника, определяется только тема беседы. Беседа применяется на стадии подготовки массовых анкетных опросов для определения области исследования, пополнения и уточнения данных массовой статистики и как самостоятель­ный метод сбора информации.

          Анализ и синтез. Анализ — это способ познания объекта посредством изучения его частей и свойств. Синтез — это способ познания объекта посредством объединения в целое частей и свойств, выделен­ных в результате анализа. Анализ и синтез не изолированы друг от друга, а сосуществуют, друг друга дополняя. Говоря об анализе и синтезе, нельзя думать, что в начале идет чистый анализ, а затем начинается чистый синтез. Уже в нача­ле анализа исследователь имеет какую-то общую идею об изу­чаемом объекте, так что анализ начинается в сочетании с син­тезом. Затем, изучив несколько частей целого, исследователь уже начинает делать первые обобщения, приступая к синтезу первых данных анализа. И таких ступеней может быть не­сколько, перед тем как будут изучены все части целого.

          Сравнение- это способ познания посредством установле­ния сходства и/или различия объектов. Сходство — это то, что у сравниваемых объектов совпадает, а различие — это то, чем один сравниваемый объект отличается от другого. Общий алгоритм сравнения: 1. Определение объектов сравнения. 2. Определение аспекта сравнения объектов. 3. Анализ и синтез объектов в соответствии с аспектом сравне­ния. Если существенные признаки сравниваемых объектов известны, то их выбирают в соответствии с аспектом срав­нения. 4. Сопоставление существенных признаков сравниваемых объ­ектов, т. е. определение общих и/или отличительных сущест­венных признаков сравниваемых объектов. 5. Определение различия у общих признаков. 6. Вывод. Необходимо представить общие и/или отличитель­ные существенные признаки сравниваемых объектов и ука­зать степень различия общих признаков. В некоторых слу­чаях необходимо привести причины сходства и различия сравниваемых объектов.

         Обобщение — это способ познания посредством определения общих существенных признаков объектов. Из данного опре­деления следует, что обобщение базируется на анализе и син­тезе, направленных на установление существенных признаков объектов, а также на сравнении, которое позволяет определить общие существенные признаки. Определяют два основных обобщения: индуктивное и дедук­тивное: Индуктивное обобщение (от единичного достоверного к об­щему вероятностному) предполагает определение общих су­щественных признаков двух и более объектов и фиксировании их в форме понятия или суждения. Понятие — это мысль, отражающая общие существенные при­знаки объектов. Суждение — это мысль, в которой что-либо утверждается или отрицается о признаках объектов. Индуктивное обобщение осуществляется по следующему ал­горитму:

 1. Актуализируйте существенные признаки объектов обобще­ния.

2.  Определите общие существенные признаки объектов.

3.  Зафиксируйте общность объектов в форме понятия или суж­дения.

        Обобщение — это не только определение сходных признаков объектов; оно предполагает рассмотрение объектов, как части чего-то общего, части какого-то рода, вида, семейства, клас­са, отряда. Без обобщения не может быть познания вообще, ибо познание всегда выходит за рамки отдельного, индивиду­ального. Только на основе обобщения возможно образование общих понятий, суждений, умозаключений, построение тео­рий и т.д. Индуктивному обобщению всегда предшествует анализ, синтез и сравнение. Анализ и синтез направлены на установление су­щественных признаков объектов. Сравнение позволяет выявить отличительные и общие существенные признаки объектов. Сле­дует отметить, что определение общих существенных признаков уже является началом обобщения. Однако обобщение предпо­лагает не только установление общих существенных признаков, но и определение их «ближайшего общего», выяснения их при­надлежности к конкретному роду. Род — это совокупность объ­ектов, в состав которой входят другие объекты, являющиеся ви­дом этого рода. Дедуктивное обобщение (подведение единичного достоверно­го под общее достоверное) предполагает актуализацию поня­тия или суждения и отождествления с ним соответствующих существенных признаков одного и более объектов. Дедуктивное обобщение осуществляется по следующему ал­горитму:

1. Актуализируйте существенные признаки объектов, зафик­сированные в понятии или суждении.

2.  Актуализируйте существенные признаки заданного объекта или объектов.

3. Сопоставьте существенные признаки и определите при­надлежность объекта или объектов к данному понятию или суждению.

           Определение понятий - способ познания посредством раскрытия содержания понятий. Понятие — это мысль, отражающая общие существенные при­знаки объектов. Всякое понятие имеет содержание и объем.  Содержанием понятия называют существенные признаки объекта или объектов, отраженных в понятии. Объемом понятия называют объект или объекты, сущест­венные признаки которых зафиксированы в понятии. Понятие — это слово или словосочетание, обозначающее отдельный объект или совокупность объектов и их существенные свойства. Родовидовое определение понятий предполагает нахождение ближайшего рода объектов определяемого понятия и их отли­чительных существенных признаков.

К математическим методам относятся статистические мето­ды, методы моделирования, методы программирования и др.

            Исходя из выше сказанного, можно сделать вывод о многообразии методов исследования. Приведу пример использования некоторых из них  в нашей работе. Одним из применяемых нами методов стал метод анализа и синтеза. С помощью анализа учебника был изучен объект исследования - это методы решения дифференциальных уравнений,  посредством этого выделены методы решения уравнений показательного роста и гармонических колебаний.

          Анализ учебника «Алгебра и начала анализа», автора А. Н. Колмогорова, по теме «Понятие о дифференциальных уравнениях» показал, что используя рассмотренные автором примеры можно составить алгоритм решения уравнений показательного роста и гармонических колебаний. Таким образом, на основе проведенного анализа и синтеза мы сделали обобщение в виде выделенного нами  алгоритма решения дифференциальных уравнений. С помощью этого алгоритма были решены задания из школьного учебника по теме «Понятие о дифференциальных уравнениях». Приведу пример, как эта часть отражена в исследовательской работе.

 

1.1 Анализ учебника «Алгебра и начала анализа» автор А. Н. Колмогорова

           Я провела анализ учебника «Алгебра и начала анализа», автора А. Н. Колмогорова, по теме «Понятие о дифференциальных уравнениях» и выяснила, что решение дифференциального уравнения

                                          

можно рассматривать как первообразную  для функции , где  - данная функция, - решение этого уравнения.

     В учебнике дан ряд примеров, рассмотрев которые можно выделить алгоритм решения дифференциальных уравнений с помощью последовательного нахождения производной.

 

Пример   Согласно второму закону Ньютона при движении по прямой материальной точки постоянной массы m справедлива формула, где– сила, вызывающая движение,  – ускорение точки. Пусть сила зависит только от времени t, т. е.. Вспоминая, что ускорение есть вторая производная координаты по времени , получаем дифференциальное уравнение относительно функции:

),  т. е. ,

Для решения которого сначала находим как первообразную для решения функции  , а затем и x(t) как первообразную функции .

Общее решение зависит от двух произвольных постоянных. Для того чтобы их найти, обычно задают координату и скорость в какой-либо момент времени

Выделяем алгоритм решения

1.      Найти как первообразную для решения функции

2.      Найти   x(t) как первообразную функции .

3.      Записать ответ.

       Решение многих задач физики, техники, биологии и социальных наук сводится к задаче нахождения функций, удовлетворяющих дифференциальному уравнению

,

где  – некоторая константа.

       Зная формулу производной показательной функции, легко догадаться, что решением уравнения является любая функция вида

,

где  - постоянная. Так как  произвольно, у дифференциального уравнения бесконечно много решений. В работе дается ряд примеров уравнений показательного роста  и гармонический колебаний, решаемых с помощью выделенного алгоритма.

         Рассмотренные примеры позволяют понять, насколько мощным аппаратом исследования являются дифференциальные уравнения. Очень часто элементарные законы, управляющие каким-либо процессом, записываются в виде дифференциальных уравнений. Для того чтобы выяснить как процесс развертывается во времени, приходится решать эти дифференциальные уравнения.

       Практическое применение выделенного алгоритма и алгоритма, обратного данному, т.е. с помощью последовательного нахождения производной, нашло своё отражение в исследовательской работе, где представлено решение многих примеров из школьного учебника, здесь я предлагаю несколько из них.

Решение заданий из учебника «Алгебра и начала анализа» автор А. Н. Колмогоров с помощью выделенного нами алгоритма.

 

568.  Проверьте, что функция  является решением данного дифференциального уравнения:

568.(а)      

 Решение:

Найдем производную функции:

,

Найдем вторую производную функции:

,

  - верно;

 

                  569.    Докажите, что функция  удовлетворяет уравнению .

                  Решение:

,

.

 

572.    Найдите какое-нибудь отличное от нуля решение дифференциального уравнения:

572.(б)    ;

Решение:

,

,

, где , например, .

                  573. Напишите дифференциальное уравнение гармонического колебания:

573.(б)  ;

Решение:

,

        Дальнейшее исследование было направлено на поиск методов решения дифференциальных уравнений без последовательного нахождения производной и первообразной. На этом этапе мы обратились к работам Л.С.Понтрягина. Выяснили, какой вклад внёс Л.С. Понтрягин в методы решения дифференциальных уравнений, в том числе уравнений гармонического колебания и показательного роста. Далее мы в своей работе использовали один из рассмотренных выше методов исследования - это сравнение. Для проведения сравнения использовали общий алгоритм сравнения:

1. Определили объект сравнения – решение дифференциальных уравнений.
2. Определили аспект сравнения объектов - методы решения дифференциальных уравнений.
3. Провели анализ решения дифференциальных уравнений в соответствии с методами, изложенными в школьном учебнике и представленными в работе Л.С.Понтрягина «Обыкновенные дифференциальные уравнения».
4. Определили общие подходы к решению дифференциальных уравнений, уравнений показательного роста и гармонических колебаний.
5. Выявили некоторые различия в методах решения данных уравнений, в том числе установили, что в школьном учебнике не изложен метод решения дифференциальных уравнений с разделяющимися переменными, с помощью которого можно решить все дифференциальные уравнения, предложенные в учебнике «Алгебра и начала анализа», автора А. Н. Колмогорова, по теме «Понятие о дифференциальных уравнениях».  

      Далее мы сделали вывод о том, что нам необходимо изучить метод решения дифференциальных уравнений с разделяющимися переменными, описанный  Л.С.Понтрягиным, чтобы доказать выдвинутое нами в качестве гипотезы  предположение, что использование знаний о методах решения дифференциальных уравнений, использование теории решения обыкновенных дифференциальных уравнений Понтрягина, позволяет решить упражнения, находящиеся в задачнике.

  Практическое применение изученных методов решения дифференциальных уравнений, уравнений гармонического колебания и показательного роста методами Л.С.Понтрягина нашло своё отражение в исследовательской работе, где представлено решение многих примеров из школьного учебника, здесь я предлагаю несколько из них.

2.4               Решение заданий № 568-573 из учебника «Алгебра и начала анализа»   автор А. Н. Колмогоров методами Л.С. Понтрягина.

 

№ 568. Проверьте, что функция  является решением данного дифференциального уравнения:

568.(а)      

 

Решение:

,

,

,

,

,

,

 - верно.

 

569.    Докажите, что функция  удовлетворяет уравнению .

 

Решение:

,

,

,

 

,

.

 

570.   Докажите, что функция  удовлетворяет уравнению

.

Решение:

,

 

,

,

,

.

 

571.   Докажите, что функция   удовлетворяет уравнению

.

 

Решение:

,

  ,

,

,

.  

 

572.    Найдите какое-нибудь отличное от нуля решение дифференциального уравнения:

572.(а)    

 

Решение:

,

,

,

,

,

.

      После изучения методов решения дифференциальных уравнений, уравнений гармонического колебания и показательного роста методами Л.С.Понтрягина и решения примеров из школьного учебника мы смогли решать более сложные дифференциальные уравнения, выходящие за рамки школьной программы. Мы разработали практикум для изучения методов решения дифференциальных уравнений, основанный на изученном материале и теории Л.Л.Понтрягина. Привожу фрагмент данного практикума и выводы, представленные в работе.

 

 

 

 

Практикум для изучения методов решения дифференциальных         уравнений, основанных на выводах Понтрягина.

 

Теория	Образцы	Задания
Решением дифференциального уравнения называется такая дифференцируемая функция, которая при подстановке в уравнение вместо неизвестной функция обращает его в тождество. Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения. Дифференциальное уравнение вида  относится к типу уравнений с разделяющимися переменными. Если ни одна из функций , , , не равна тождественна нулю, то в результате деления исходного уравнения на   оно приводится к виду , Которое и определяет решение исходного уравнения	1.Найти частный интеграл уравнения у'cosx=y/lny, удовлетворяющий начальному условию y(0)I. Полагая  y' перепишем данное уравнение в виде Разделяем переменные: . Проинтегрируем обе части уравнения:  или Используя начальное условие    y = I при , находим С=0. Окончательно получаем 2. Найти  частное  решение дифференциального  уравнения (1+ при начальном условии Преобразуем данное уравнение  к виду  Интегрируя, получим Это и есть общий интеграл данного уравнения. Теперь, используя начальное условие, найдём производную постоянную С; имеем  откуда получаем искомое частное решение . 3.Найти общий интеграл уравнения  Полагая  и разделяя переменные, приходим к уравнению . Интегрирую, имеем , или . Отсюда находим , или  (общий интеграл).	1. 2.  y 3.  +2y’ 4.  y’-2xy 5.  ( 6.  -1) 7.  2

Выводы

1.    Проведенный теоретический анализ школьного учебника «Алгебра и начала анализа»  автор  А.  Н.  Колмогоров  по  теме:  «Понятие  о дифференциальных уравнениях» выявил некоторые теоретические аспекты методов решения дифференциальных уравнений, изучаемых в школьном курсе.

2.    Изученная работа Л.С.Понтрягина «Обыкновенные дифференциальные уравнения»,     расширяет     представления     о     методах     решения дифференциальных   уравнений,   уравнений   показательного   роста   и гармонических колебаний.

3.   Рассмотренные в работе методы решения дифференциальных уравнений позволяют подтвердить выдвинутую гипотезу.

4.  Разработанный     практикум     для     изучения     методов     решения дифференциальных уравнений, основанных на выводах Л.С.Понтрягина, позволяет выработать навык решения дифференциальных уравнений, уравнений показательного роста и гармонических колебаний.

5.   Данная    работа    способствовала    развитию    у    меня    умению исследовательской деятельности, активно включила в процесс познания, творческой    реализации    и    создала    условия    для    личностного самоопределения.

      Хочется также отметить, что при  использовании методов исследования, для  решения поставленных задач,  необходимо помнить об эффективных приемах творческой деятельности, применяемых  в психолого-педагогической практике. Знакомство с данными приемами поможет учащимся учиться приобретать знания самостоятельно и использовать их для решения новых познавательных и практических задач; приобретать коммуникативные навыки и умения; овладевать  практическими умениями исследовательской работы: собирать необходимую информацию, учиться анализировать факты, делать выводы и заключения.

 

 

Приемы творческой и исследовательской деятельности по О.Б.Епишевой

Метод многомерных матриц

1. Уточнить, если нужно, формулировку проблемы.

2. Выделить все возможные параметры объекта исследования, изобре­тения (признаки, процессы, идеи, методы и приемы и т. д.).

3. Систематизировать и по возможности классифицировать выделен­ные параметры.

4. Построить возможные комбинации выделенных параметров (внача­ле двумерную, затем многомерную матрицу).

5. Проанализировать и критически оценить все построенные комбина­ции с точки зрения оптимальности и реальности их практического примене­ния для достижения поставленной цели.

6. Отобрать из возможных комбинаций наиболее приемлемую и рацио­нальную.

Метод инверсии

1. Начинать решать задачу, проблему с ее переформулировки; посмотреть, нель­зя ли сформулировать задачу, обратную данной.

2. Искать идею решения в направлениях, противоположных традици­онным.

3. Для всякой идеи искать контридею.

4. Стремиться использовать в процессе решения творческих задач про­тивоположные средства и приемы.

Метод синектики (объединения разнородных элементов)

1. Максимально использовать свой личный опыт, если есть — специ­альные знания и умения.

2. Многократно переформулировать проблему.

3. В процессе выдвижения идей использовать различные виды анало­гий, инверсии.

4. Анализировать объект исследования с самых неожиданных точек зрения — научных и житейских, внешних и внутренних.

5. Рассуждать вслух.

Стратегия поиска идеи, противоположной общепринятой или наибо­лее очевидной предполагает, что если в процессе решения все стремились расширить поле поиска, то возможно целесообразнее его сузить; все анали­зировали прошлое, а возможно лучше осмыслить будущее и т. п.

Стратегия принятия решений:

1) мысленно проиграть, представить на­иболее оригинальное решение задачи в его окончательном варианте;

2) отменить решение, обосновать почему;                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                    

3) принять оригинальное, но временное решение;

4) проанализировать все возможные решения, продиктованные здра­вым смыслом, и выбрать из них наиболее эффективные;

5) проанализировать все возможные решения, которые выдвигаются вопреки здравому смыслу, оценить их эффективность;

6) искать серию поэтапных решений;

7)  принять окончательное решение.

       В заключении хочется обратить внимание ещё на одну трудность, с которой сталкиваются учащиеся на заключительном этапе – это устное выступление. Существуют правила устного выступления, которые можно рекомендовать учащимся.

Правила устного выступления

1. Излагать выступление по плану, выделяя его смысловые части.

2. Соблюдать грамматические правила, шире использовать свой сло­варный запас (полезно почаще пользоваться толковым словарем).

3. Стараться усилить эмоциональность выступления и говорить выра­зительно (с правильной интонацией).

4. Следить за своей дикцией, совершенствовать ее.

5. Следить за тем, как вас слушают и воспринимают, устанавливать контакт со слушателями и обратную связь.