Обобщающий урок в 10 классе по теме «Основные свойства функций»

Обобщающий урок в 10 классе по теме «Основные свойства функций»

Цели урока:

1) Образовательные – обеспечить повторение, обобщение и систематизацию материала темы. Создать условия контроля усвоения знаний и умений.

2) Развивающие – способствовать развитию мышления и речи, внимания, формированию умений переноса знаний в новую ситуацию.

3) Воспитательные – содействовать воспитанию интереса к математике, активности, мобильности, умения общаться, общей культуры.

Тип урока: урок обобщения и систематизации знаний.

Формы организации урока: индивидуальная, групповая.

Оборудование: доска, мел, указка, интерактивная доска, проектор, компьютер, карточки с заданиями, фломастеры, альбомные листы с системой координат (на рабочем столе компьютера «Презентация» и система координат)

Организационный момент

Функция – это одно из основных математических и общенаучных понятий, выражающее зависимость между переменными величинами. Каждая область знаний : физика, химия, биология и т.д. – имеет свои объекты изучения, устанавливает свойства, и что особенно важно, взаимосвязи между этими объектами

Сегодня у нас заключительный урок по теме «Основные свойства функций». На уроке повторяем основные свойства функций, строим графики функций различными способами, исследуем функции, находим им применение в окружающей нас жизни.

Класс разбит на группы. Каждый из вас участвует как в личном зачёте, так и в зачёте вашей группы. Каждое правильно выполненное задание оценивается в баллах и набрав определённое количество баллов вы  получаете оценку.

Работаем по плану:  (презентация)

1) Проверка теоретических знаний а) кроссворд (5 баллов)

                                      б) определение свойств функций (по 2 баллу)

                                      в) графическое проявление свойств (по 2 баллу)

                                      г) «Чтение» графика (5 баллов)

2) Построение графиков:     а) основных функций (5 баллов)

                            б) по свойствам (5 баллов)

                            в) на основании чётности и периодичности (5 баллов)

                            г) преобразование графиков функций  (5 баллов)

3) Исследование функций:  а) нули функции (5 балла)

                            б) чётность (5 балла)

                             в) монотонность (5 балла)

                            г) область определения (5 балла)

4) Прояви смекалку: пословицы в графиках, графики в физике (5 баллов)

5) Домашнее задание         6) Итог урока

1) Проверка теоретических знаний.

-Каждая группа выбирает карточку с заданием, на обдумывание 5 минут, подумайте, кто будет отвечать, кроссворд заполняете на доске, формулировку определений даёте у доски.

1 карточка:  Кроссворд «Математические термины»

1 Абсциссы точек пересечения графика функции с осью Ох

2 Значения функции в точках, в которых возрастание сменяется убыванием или наоборот

3 Функция, описывающая повторяющийся процесс

4 Для этой функции справедливо равенство f(-x) = f(x)

5 Для этой функции большему значению аргумента соответствует большее значение

   функции

6 Промежутки, на которых функция только возрастает или только убывает

7 Для этой функции большему значению аргумента соответствует меньшее значение

   функции

8 Промежутки, на которых функция принимает только положительные значения или

  только отрицательные.

2 карточка  Формулировка определений

Дайте определение каждому свойству, названному в кроссворде: чётная, нечётная, возрастающая, убывающая, экстремумы, знакопостоянство, нули,  периодическая, монотонность.

3 карточка  Графическое проявление свойств

Объясните, как проявляется каждое свойство функции, названное в кроссворде: чётная, нечётная, возрастающая, убывающая, экстремумы, знакопостоянство, нули, периодическая, монотонность. Приведите примеры.

4 карточка  «Чтение» графиков

              «Прочитайте» график                       

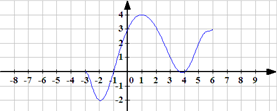
Проверка (Презентация)

1) Кроссворд заполнить на интерактивной доске

2) Дать определение и графическое проявление свойств с примером

3) Чтение графика 

Итог: В ходе устной работы мы повторили основные свойства функций, а сейчас эти знания будем применять при построении графиков функций и исследовании функций.      

2) Построение графиков.

(На каждом столе альбомный лист с изображением координатной плоскости, фломастер)

- Какие способы построения графиков функций вам известны? (по точкам,   по свойствам, путём преобразования графиков)

- Каждый стол получает карточку с заданием «Построить график функции», построение выполняете на альбомном листе фломастером, затем обосновываете правильность его выполнения и соответствие с условием задания.

1 карточка   Постройте график функции  

2 карточка Постройте график функции по свойствам

3 карточка Постройте эскиз графика функции на основании чётности и периодичности.

Функция у = f (x)  определена на всей числовой прямой и является чётной периодической функцией с периодом, равным 6. На отрезке [0; 3]  функция задана равенством  f (x) = -х² + 4х – 1.

4 карточка Постройте график функции путём преобразования.

В одной системе координат постройте графики функций                                                          у = cosx,   y = cos2x,   y = 2cos2x  

y = 2cos2x + 2

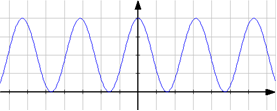
Итог: Мы повторили построение графиков функций разными способами. Сделайте вывод (Все графики функций можно построить любым способом, но одни удобнее и быстрее по точкам, другие – используя свойства функций)

3) Исследование функций

- Переходим к исследованию функций. Решение каких задач предусматривает исследование функций?   (Область определения, область значений, чётность, периодичность, точки пересечения с осями координат, промежутки знакопостоянства, промежутки монотонности, экстремумы) 

- Каждый стол получает карточку с одной из перечисленных задач, решает и оформляет их на доске.

1 карточка Найдите нули функции:   

 а) у = 1 – х⁴        б) у = х + 2|x + 3|            в) у =             г) у = 3х³ + 5х² + 5х + 3

х₁ = -1; х₂ = 1     х+2х+6=0  х-2х-6=0        х = -1                     (х+1)(3х²+2х+3)=0

                            х₁ = 2;        х₂ = -6                                            х = -1

2 карточка    Определите чётность функции

а) f(x) = х²cosx        б) f(x) =                  в) f(x)=                  г) f(x) = sinx+ctgx-x

1)D(f) = R              1)D(f)=(-∞;0)и(0;∞)      1)D(f)=(-∞;1)и(1;∞)    1)кроме ч вида πn

2) f(-x)=f(x) чёт    2) f(-x)=-f(x) нечёт       2) ни – ни                      2) f(-x)=-f(x) нечётн 

- Закончите предложение:1)произведение двух чётных функций является..(пример)

                                           2)сумма нечётных функций является…(пример)

3 карточка     Найдите область определения функции

а) у =                   в) у =            г) у =

                                                                                                 х-1-2=0     -х+1-2=0

(-∞;-2]и[1;3)и(3;∞)           [ - 2,5; 3 ]                               (-∞; -1) и (-1; 3) и (3; ∞ 

4 карточка Найдите промежутки возрастания и убывания функции

                а) у = 2х² + 4x                               б) у = 1 + 1,5cosx

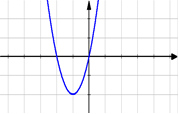
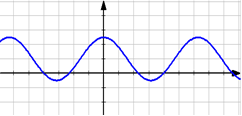
Убывает на (-∞; -1]                                 Убывает на [0+2πn;  π + 2πn] nЄZ

Возрастает на [-1; +∞)                         Возрастает на [-π + 2πn;  0 + 2πn] nЄZ

Итог:  Можем ли мы полностью исследовать любую функцию, не обращаясь         к графику функции? (нет)  К этой теме мы вернёмся в конце 10 класса после изучения темы «производная».

4) Прояви смекалку 

1) Чтобы проиллюстрировать характерные свойства функций, обратимся к пословицам, ведь пословицы – это отражение устойчивых закономерностей, выверенных многовековым опытом. Изобразите пословицу в виде графика – как вы его понимаете, а затем обоснуйте своё решение.

а) Чем дальше в лес, тем больше дров.    

б) Выше меры конь не скачет                   

в) Тише едешь, дальше будешь                

г) Семь раз отмерь – один раз отрежь.    

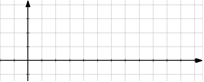
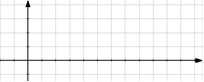
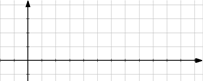
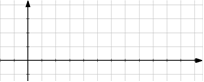
2) Графики в физике. Определите вид графика. Какой из данных графиков является…

- графиком движения тела брошенного горизонтально

- графиком движения тела брошенного под углом к горизонту

- графиком скорости при равноускоренном движении

- графиком скорости при равнозамедленном движении